To have an optimal design of an energy system, a hybrid power system is designed in MATLAB SIMULINK with the principle as shown in
Figure 3. The design simply works on the principle that in order to propel the ship at a certain advance speed, it has to overcome all the resistance that it would encounter which includes hull, waves, and air resistances. If the power supplied overcomes these resistances, the ship will start moving at the desired speed.
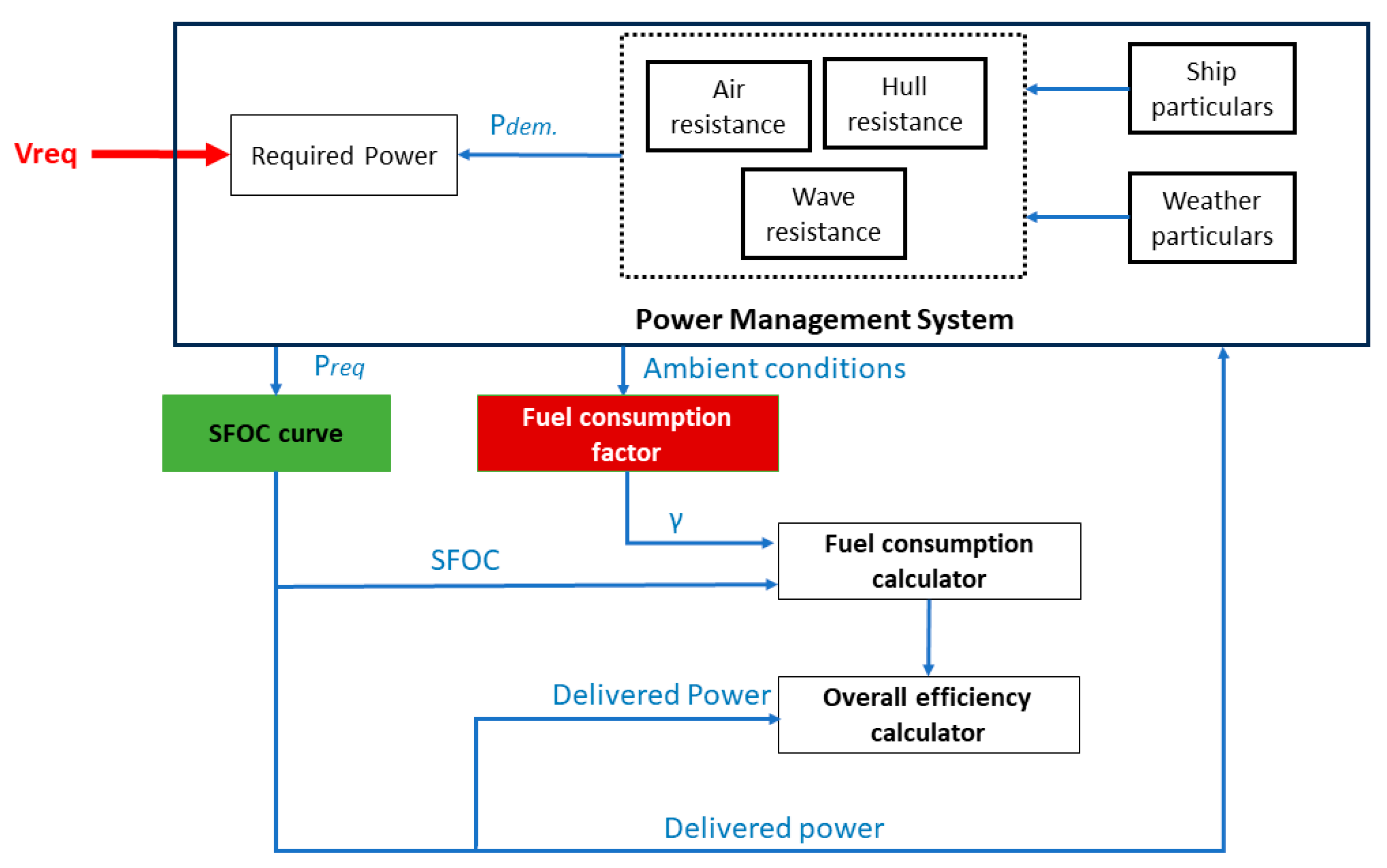
The power needed by the ship is influenced by various external forces as previously mentioned. An outlined representation of the power required is depicted in
Figure 5, incorporating factors such as the instantaneous wave height (ξ
wave), water-specific weight (σ
wave), wind speed (v
air), actual wind direction (θ
air), air pressure (P
air), air density (ρ
air), resulting ship speed (v
ship), and direction (θ
ship). To provide this power demand, a modular FC with a unit capacity of 200 kW inspired by Ballard’s FcWave module [
23] is used in this study. The characteristic and efficiency curves of this FC are assumed as shown in
Figure 6 and
Figure 7, respectively.
The FC module generates varying voltage and current outputs, necessitating the use of a DC–DC boost converter to maintain a constant voltage for the propulsion motor. Multiple simulations were conducted, altering the number of FC modules to determine the optimal module numbers. A crucial determining factor is the annual hydrogen consumption, directly influencing the operating expense (OPEX). To calculate the hydrogen used, the hydrogen mass flow is required, which is calculated during the simulation for every simulation step using Equation (2):
where
is the power delivered by the FC,
is the FC efficiency for the corresponding load, and
is the lower heating value of hydrogen. The DC–DC boost converter stabilizes the voltage output to 815 V corresponding to the voltage requirements of the DC propulsion motor (because of high torque). The motor used here is an ABB DC motor with Cat. No. 3BSM003050-XVJ with a power rating of 1355 kW at 970 rpm.
Apart from the power requirement of the propulsion, the power system in this study is also designed to supply energy to the ship’s auxiliary demands. The auxiliary system includes all the necessary equipment like communication, navigation, fire management systems, etc., along with all the devices required for comfortable movements of crew and passengers like air conditioning system, lighting, power ramps, etc. This study assumes that this power is fixed at a constant value of 50 kW. The power supplied while in port is sourced from a battery power pack. In the designed hybrid power system, if the number of FC modules is less (while using a simulation to track different module numbers) but there is a higher power demand exceeding FC capacity, the battery pack supplements the FC system for propulsion. This leads to an increase in the battery size to accommodate the combined power needs. Apart from this, the battery also provides interim power until the FC catches up. Equation (3) represents the total power available in the bus bar where
and
are currently drawn from the battery and the fuel cell modules, respectively, and
is the bus bar voltage:
3.1.1. Power Management System (PMS)
The PMS evaluates real-time conditions acting on the vessel, and their effects are compared with required power, i.e., the desired speed. After evaluation, as a result, its output is the net required power for the ferry to continue to propel at the set speed, which instructs the energy producers either to increase or decrease the power. This is accomplished in simultaneous stages by performing simultaneous calculations. The PMS calculates the difference between the delivered power and the power opposing the propulsion ship due to environmental forces (namely, wave and wind forces and air resistance).
The PMS senses the difference in power and guides the energy providers either to increase or decrease power delivery. These decisions are defined as per Equations (4)–(7):
where
is the generated difference,
is the total power opposing the propulsion,
is the power delivered by the propulsion motor,
is the power requirement except for auxiliary power, and
are the controller constants which are obtained after repeated trials of many combinations. Lastly,
are the external environment forces. The total forces are calculated in SIMULINK as shown in
Figure 8;
is the total required power estimated by the PMS and
is the ship’s surge velocity. The power is limited by maximum motor power (
). Here,
is estimated by using a PID controller. This controller varies the amount of hydrogen and oxygen (or battery power in the case of battery operation) using the standard PID Equation (5). Auxiliary power demand is added to this, making the total demand power
, whereas the opposing forces demands
. Fundamentally, this
has to be satisfied. After all the system losses,
is the power that has been delivered by the propeller which has to satisfy
need. If there is a mismatch,
appears, resulting in an increase or decrease in
. This process of repetitive iterations will continue until
reaches zero (or to a minimum error limit).
The wave resistance is calculated via Equation (8) [
24]. The wave height (
ξ(
t)) in this equation is dynamic and is different for every month.
Here,
σ is the specific weight of water,
L is the length of the ship, and
B corresponds to the breadth of the ship. For the simulation performed in this study, the average of each month is used for every second of the ship’s operational day. Similarly, the air resistance is governed via Equation (9) where the density of air varies each month of the year. This density depends on ambient temperature and pressure conditions:
where
is the drag coefficient of the ship that depends on the angle of attack of the incoming wind;
is the density of air;
is the projected sectional area of the ship for incoming wind that depends on the angle of the incoming wind. Lastly,
is the resultant velocity of incoming wind. This velocity is relative to the actual wind speed and direction in addition to the ship’s speed and direction. This resultant wind velocity and direction is calculated as a vector product of both the velocities as represented in
Figure 9.
Lastly, the hull force (the force exerted by water) is calculated in the simulation. This force depends on the draft of the ship as the higher the draft, the higher the hull force. Therefore, this force is simulated by varying the draft using a randomizer block of the SIMULINK library depicting change in the ship’s draft (passenger + cars). This randomizer block generates a random signal for each voyage that changes the number of passengers and vehicles transported. The number of passengers and vehicles changes the displacement of the ship and hence affects the draft according to Equations (10) and (11). A CFD analysis of the designed model satisfying the physical parameters was conducted using the CFD simulation ANSYS Fluent software [
25] to calculate the force exerted by moving water at various drafts. The results are input into the SIMULINK model as a 2D lookup table (see
Figure 10). During the simulations, this 2D lookup table provides the force corresponding to the calculated draft.
Here, T is the calculated draft, is the light weight draft of the ship, is the draft added due to the added weight in meters, is the added draft in centimeters, is the total weight added, and is the parameter of the ship that represents the weight needed to change the draft by 1 cm. The study involves the meticulous consideration of monthly data, wherein environmental parameters were meticulously recorded every second throughout the ship’s operational duration. The process involved calculating the average environmental parameters for each specific time instance (e.g., 6:31 a.m.) across the entire month. This method was consistently applied across various months within the year, enabling the representation of average environmental parameters for each month.
The sum of all these forces results in the total force, and consequently the product of this total force and the actual velocity of the ship provides the opposing power .