1. Introduction
Floating offshore wind turbines (FOWTs) has been emerging in both research and development for the last several decades. This is because unlike fixed-foundation wind turbines, FOWTs can be placed far offshore, which provides advantages such as stronger and steadier wind, limited or no noise and visual pollution to human beings, and increased space availability. FOWTs are considered a key piece of technology to achieve future clean energy targets around the world.
Despite these positive aspects of FOWTs, the current high offshore energy cost is impeding the uptake of FOWTs. Forming a wind farm by installing multiple turbines close to each other will help reduce the wind energy cost due to scale and cost distribution per turbine. However, wind farms are subject to a phenomenon known as the “wake effect”, which reduces the efficiency of the wind farm [
1]. This is caused by the upwind turbines extracting energy from the wind, which causes downwind turbines to operate less efficiently. This reduction in efficiency ultimately increases the cost of electricity, which makes wind turbines less attractive as a means to generate electricity. Therefore, effort should be made to reduce the impacts of the wake effect.
There have been many ways proposed to reduce the wake interactions between wind turbines. One general method is to reduce the overlap of the wind turbine rotors when looking at the turbines in the downwind direction. Several methods have been proposed to achieve this reduction in overlap. The wake overlap reduction method, which is unique to turbines with floating platforms, is to dynamically reposition the FOWTs within the wind farm, either with actuators to generate the force to move the platform such as winches [
2] and thrusters [
3,
4], or with utilization of aerodynamic force [
5]. Given a turbine with a sufficient movable range and knowledge of the mean wind direction, turbines can be relocated relative to one another to reduce the wake overlap between upwind and downwind turbines.
So far, numerous investigations have been performed related to analyzing the fatigue loading on FOWTs. The work in Ref. [
6] analyzed fatigue on a FOWT at various locations using a wide range of environmental conditions. Their results provided recommendations for how to select environmental conditions and necessary simulation length (recommended 1-h), as well as fatigue results specific to the FOWT in question. Work studying nacelle yaw offset for fixed-base onshore wind turbines was conducted in Ref. [
7], which provided an assessment of the factors which may drive the fatigue loading in these circumstances. Various aspects of the effects of modeling choices were studied in Ref. [
8]; of note, the authors claim it is possible to decouple wind and wave loading to find the fatigue damage based on stress superposition, thus decreasing simulation requirements. To corroborate this, it was found in Ref. [
9] that direct addition of tower-base fatigue damage from decoupled simulations did not accurately predict the fatigue loading. From the same work, it was also found that 1-h simulations should be used. In contrast, a suggestion was made in Ref. [
10] that simulations need not be longer than 10 min, but care must be taken during the cycle counting portion of the fatigue analysis. The effects of the wind and wave loading were studied by Ref. [
11] who found that wave loading dominated tower-base fatigue while wind loading dominated mooring line fatigue. Finally, the work performed in Ref. [
12] showed the increase in fatigue damage when operating a wind turbine with a fixed base versus a floating base.
A variety of controllers have also been designed for wind turbines in order to reduce the fatigue loading on the various structural elements. In Ref. [
13], a controller was designed that varies the generator speed set-point in an effort to reduce fore-aft oscillations. The addition of multiple, decoupled control loops was studied in Ref. [
14] with the aim to use both platform pitch and tower-top velocity as feedback signals in separate control loops to minimize fatigue at the tower base. Model Predictive Control (MPC) was implemented in Refs. [
15,
16,
17], which reduced fatigue loads on the FOWT and floating offshore wind farm, respectively, by online minimization of the MPC cost function. The performance of a standard FOWT controller and an optimal controller (LQR) were compared in Ref. [
18] showing that LQR provides improved performance, but struggles to reduce the impacts of wave loading. Through a number of different works, Namik and Stol [
19,
20,
21] designed a number of different controllers for a variety of FOWT platform types. Their results showed the effectiveness of more advanced controllers and the various challenges that different platform types posed to the control design problem. Finally, a method of tuning individual blade pitch controllers using a Bayesian optimization process was proposed in Ref. [
22]. A different approach to fatigue reduction using machine learning control was presented in Ref. [
23]. Recently, a FOWT control strategy combining a resonant controller and an individual blade pitch controller was developed to alleviate the blade root flapping moment [
24]. It should be noted that none of these controllers are applied to position controlled FOWTs, which are the major focus of the work presented in this paper.
Finally, beyond fatigue control, a number of position controllers have been proposed. A linear quadratic integrator was presented, which used pitch-to-stall blade pitching to control the
x-
y position of a FOWT [
25]. This was then further refined in Ref. [
26] using a more advanced control with an aim to regulate position and reduce platform motions. Pitch-to-feather blade pitching was then investigated in Refs. [
27,
28] as a method to use more standard wind turbine operation to achieve position control. These works implemented more simple proportional-integral [
27] and proportional-derivative [
28] control while using elongated mooring lines to improve the movable range of the FOWT. The concept of increased mooring line length was proposed in Ref. [
5]. This study found the necessary movable range, as well as optimization techniques to choose FOWT positions.
Despite a number of studies on fatigue load controller design for floating offshore wind turbines mentioned above, one of the outstanding questions that has not been addressed in current literature is whether fatigue reducing controllers can still be effectively applied to a position controlled FOWT. The main objective of this paper is to demonstrate that the turbine repositioning can be achieved while allowing for the inclusion of a fatigue reducing controller. For the demonstration, the LQR-based individual blade pitch controller is optimized over various environmental conditions while the position controller regulates the turbine location. The LQR tuning parameters (i.e., weighting matrices Q and R) are optimized through wind turbine dynamic simulations, fatigue calculations, and surrogate optimization. The simulation study using a baseline 5 MW semisubmersible turbine shows that the fatigue damage at the tower base is maintained at the same level as that without repositioning, over different operating conditions such as average wind speeds and nacelle yaw angles. To the best of the authors’ knowledge, this is the first paper that analyzes the fatigue load in turbine repositioning wind farm control strategy.
The paper is organized as follows. In
Section 2, the fatigue reduction problem with FOWT repositioning is stated for a baseline semisubmersible FOWT.
Section 3 presents the fatigue reduction controller design procedure. Finally, in
Section 4, simulations results are shown for a chosen FOWT and fatigue location.
For the readability, we collect all notations used in this paper in
Table 1.
2. Fatigue Reduction Problem in FOWT Repositioning
In this section, we will formulate the fatigue reduction problem of a floating offshore wind turbine (FOWT) with the repositioning capability. To this end, we will first briefly review the baseline FOWT (
Section 2.1) and its general control objectives (
Section 2.2). To achieve these objectives, we will introduce a control system structure with several feedback loops (
Section 2.3). Finally, we will state the fatigue reduction controller design problem (
Section 2.4).
Throughout the paper, we assume that the platform position is controlled only in the sway direction. This assumption is due to the assumption that multiple wind turbines in a wind farm are aligned in the surge direction with the wind blowing in the surge direction, and wake overlap reduction can be achieved mainly by the sway direction repositioning.
2.1. NREL 5 MW Baseline FOWT
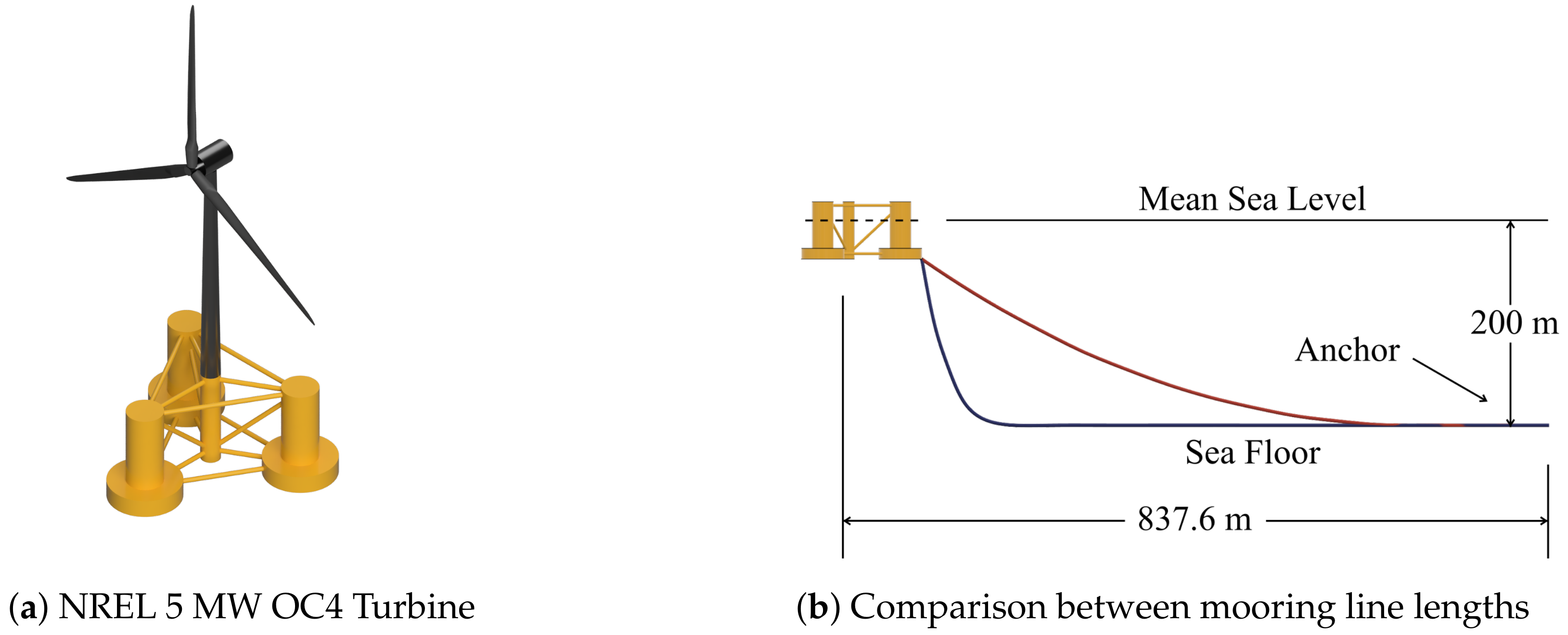
The baseline FOWT to be considered in this paper is illustrated in
Figure 1. It is referred to as NREL 5 MW OC4 wind turbine (WT) [
29,
30]; it was developed by National Renewable Energy Laboratory (NREL) in the US, its rated power is 5 MW, its rated wind speed is 11.4 [m/s] but it can operate between 3 and 25 [m/s], and its platform is a semisubmersible one, as shown in
Figure 1a. NREL 5 MW OC4 WT has the manipulable variables for control purpose, namely, nacelle yaw angle
[rad], three blade pitch angles
where
[rad],
, is the angle for
i-th blade, and generator torque
[Nm].
This baseline turbine has been widely used for research and development [
8,
12,
31], and a computational tool, called OpenFAST [
32], is available for simulating dynamic behaviors of this turbine. For the present work, all the mechanical and electrical properties of the NREL 5 MW OC4 WT are unmodified, except the mooring line length. The length has been extended from 835 [m] (red curve in
Figure 1b) to 925 [m] (blue curve in
Figure 1b) to enable the large range of platform motion.
2.2. Control Objectives for NREL 5 MW OC4 WT
For the NREL 5 MW OC4 WT, we would like to accomplish the following control objectives simultaneously.
- (O1)
Power maximization for below rated wind speed and power regulation for above rated wind speed;
- (O2)
Fatigue load minimization;
- (O3)
Platform repositioning.
Here, the objectives (O1) and (O2) are standard in all wind turbine control. In fact, there have been many works which develop controllers to attain (O1) and (O2) simultaneously. The objective (O3) is added here to mitigate the wake effect and to optimize the efficiency of a wind farm by dynamically modifying the farm layout.
The floating platform with long mooring lines gives an opportunity to utilize the lateral motion of the platform for wake mitigation within a wind farm. However, by adding the objective (O3), it is not clear that fatigue levels achieved by the controllers without repositioning objective can be maintained at various platform locations. Although there have been some work on position control of FOWTs [
2,
25,
26], so far, no work has considered the addition of fatigue control to a position controlled FOWT.
2.3. Control System Structure
To achieve the control objectives (O1)–(O3), the control system structure depicted in
Figure 2 is proposed in this paper.
As shown in the figure, the NREL 5 MW OC4 WT is connected to three sub-controllers, that is, NREL baseline controller for (O1), position controller for (O3), and then fatigue controller for (O2). Next, each controller block will be explained in order. Note that our contribution in this paper is the fatigue controller block, and the other two blocks will be presented below for review purposes only.
2.3.1. NREL Baseline Controller Block
For the control objective (O1), we adopt the baseline controller developed by NREL. This controller uses the generator speed
[rad/s] to command the generator torque
and the collective blade pitch angle
[rad], in order to maximize the power for low wind speed cases and to regulate the power for high wind speed cases. the NREL baseline controller assumes that the nacelle yaw angle
is set to face directly into the wind. As such, there is no yaw controller implemented. See Ref. [
29] for the details of the baseline controller.
2.3.2. Position Controller Block
The position control block in
Figure 2 determines the nacelle yaw angle
based on the platform position
y [m], to reposition the floating platform in the sway direction by manipulating the direction of the aerodynamic thrust force applied on the rotor plane. The controller is fully described in Ref. [
28]. It is a proportional-derivative controller whose primary goal is station-keeping of the wind turbine at a desired location, rather than trajectory-tracking from one position to another.
Figure 3 shows a top-down view of the FOWT in the
x-
y plane. For offshore structures, the
x and
y directions are often referred to as the surge and sway directions, respectively. The figure shows that the FOWT moved some arbitrary distance from its neutral position
. Specific to this work, we show the position error signal
which is the difference between the reference sway position
and the current sway position
y. Finally, the wind is shown as blowing in the positive surge direction, and this is assumed to be the only wind direction in this paper.
In order to avoid unduly increasing the fatigue load while station-keeping at repositioned locations, we limit the operating range of the nacelle yaw angle to the range of .
2.4. Fatigue Reduction Controller Design Problem
Now, we consider NREL 5 MW OC4 WT combined with NREL baseline controller and position controller, i.e., the dashed-rectangle part in
Figure 2, as an augmented system to be controlled. This augmented system has the input vector
, which consists of the three blade pitch angle deviations from the NREL baseline command
. As the sensor outputs of the augmented system, we assume the signals
are measurable, where
y [m] denotes the platform sway position relative to the platform location when there is no wind (see the
-location in
Figure 3),
[rad/s] is the generator speed, and
[rad] is the azimuth angle of a specific blade (say the first blade
). In addition, we assume the following variables to be available for fatigue feedback control:
Here,
[rad] and
[rad] are respectively platform pitch and roll angles,
and
are the tower-top fore-aft and side-to-side displacements, respectively. See the variables in the simulation tool OpenFAST corresponding to these sensor outputs in
Table 1.
For the augmented system, the problem considered in this paper is to design a controller (Fatigue Control block in
Figure 2) such that the fatigue loads are reduced at the tower base of the turbine, over operating (i.e., between cut-in and cut-out) wind speeds and at platform positions which correspond to the nacelle yaw angles within
.
Remark 1. In this paper, we focus on fatigue loads only at the tower base, for simplicity of discussions. However, we can deal with fatigue loads at other FOWT components analogously, as well as simultaneously with a multi-objective cost function having weighting factors.
3. Fatigue Reduction Controller Design
In this section, we will propose the controller structure for fatigue reduction (
Section 3.2) and explain the design of the LQR controller embedded in the controller structure (
Section 3.1.3), to solve the design problem in
Section 2.4.
Our proposed controller, to be embedded into ‘Fatigue Control’ block in
Figure 2, is depicted in the block diagram in
Figure 4. Signals and blocks in the block diagram will be explained below. The controller design procedure consists of the following steps.
Selection of an operating point;
Linearization around the selected operating point;
LQR design based on the linearized model.
3.1. Design Steps
3.1.1. Selection of An Operating Point
In this paper, we select three operating points, each of which represents an operating point for below-rated wind speed region (Region 2), transition wind speed region (Region 2.5), and above-rated wind speed region (Region 3). These three points, denoted by
,
, and
, are determined by specifying the wind speed and then obtaining the linear model states
in (
1).
The software OpenFAST, v2.6.0 which was the latest version when the work in this paper was conducted, developed at the National Renewable Energy laboratory at Golden, CO, US, has the capability of finding the operating point when the operating wind speed is specified. We denote the state corresponding to the wind speeds , and as , and , respectively.
Remark 2. For the linearization, we fixed the wind turbine at the neutral position with zero nacelle yaw. This is because of the limitation of the linearization using the mooring line model called MAP++ in OpenFAST v2.6.0, which was the most recent version available when this analysis was performed.
3.1.2. Linearization Around the Operating Point
The linearization module in OpenFAST is used to find the linearized model of the WT at each of the three operating points according to wind speed. The linearization module allows for the control variable (generator torque, blade pitch, or nacelle yaw) to be trimmed. In this case, the linearization is performed with a constant rotor speed. Therefore, the trim solution is used only to help the simulation forces converge (i.e., trimming the blade pitch does not change the rotor speed but does change the rotor thrust). The trim solution uses either generator torque or blade pitch depending on which region the model represents. The linearization is performed at many different rotor azimuth positions, which gives the periodic state-space model
We then use MBC3 [
33] to convert to a steady-state state-space model by averaging and converting rotating states to non-rotating. In this case, only the B-matrix has rotating states. The final result of the MBC3 process is a constant coefficient model of the form
3.1.3. LQR Design
For providing the blade pitch command
in (
2), the linear quadratic regulator (LQR) is employed. This is because LQR is suitable to solve the multi-objective (in the sense of minimizing eight states and three inputs) control problem for the multivariable system under consideration.
The LQR controller in the form of
is designed using the operating point and steady-state model presented above, and it is tuned by fixing the
R-matrix and adjusting only the
Q-matrix. The
Q-matrix is tuned using an optimization method from Matlab (surrogateopt) that repeatedly adjusts the
Q-matrix and tests the controller using turbulent OpenFAST simulations with all states enabled. The optimization searches for a solution which minimizes the fatigue for the given OpenFAST simulations. It searches for a solution using a surrogate model of the actual process. It globally optimizes within user-specified boundaries and is able to handle computationally expensive objective functions and discontinuities.
Due to the nonlinearity of the WT system with respect to the wind speed, we will generate three controllers, namely, a controller for low (below-rated) wind speed
, a controller for high (above-rated) wind speed
, and a controller for middle (around-rated) wind speed
. The three controllers are then combined as a gain-scheduling controller and validated in
Section 4.
3.2. Fatigue Reduction Controller Structure
The proposed structure of the fatigue reducing controller is shown in
Figure 4. The controller is a periodic gain-scheduled controller that is periodic with respect to the rotor azimuth angle
and has the generator torque
as a gain-scheduling parameter. The matrix
is the multi-blade coordinate (MBC) transformation matrix [
33] given by
The MBC transformation matrix is useful for reducing the periodically time-varying control problem into a time-invariant one.
The input to the controller is the plant state vector
. Using the operating point
, the state deviation vector is defined as
3.3. Design Process Overview
Since the controller design procedure is the same for
,
, and
, our explanation will be for a general wind speed region, and the controller to be designed is denoted by
K. The design is conducted by solving a short-term fatigue minimization problem:
where the cost function is given by
Here, is short-term fatigue calculated for i-th environmental profile , and denotes the index set for environmental profiles corresponding to the design environmental conditions . Each is based on the calculated LQR gain matrix for that simulation. Therefore, the cost function represents a simple minimization problem where, for a fixed set of simulations, the optimization will search for an LQR gain matrix that results in a minimum fatigue.
The flowchart for the design of
K is displayed in
Figure 5. The optimization variables are the positive semi-definite matrix
and the positive definite matrix
for the quadratic cost function
First, we give the initial optimization variables, denoted by
. This, in combination with the linearized model in
Section 3.1.2, will lead to the initial linear quadratic regulator gain
. This controller gain is used for simulations with various wind and wave profiles
in the medium-fidelity wind turbine simulator OpenFAST [
32]. The simulation results are input to the fatigue load calculation software MLife [
34], and the objective function in (
7) is evaluated. Based on the evaluated objective function, the surrogate optimization algorithm, implemented by the Matlab command surrogateopt.m, will update the weighting matrices
. The rationale for adopting the surrogate optimization is that it can deal with the optimization of computationally expensive objective functions. The objective function being evaluated here requires running multiple simulations per optimization iteration, leading to long evaluation times. The algorithm will be terminated when either the fatigue is not reduced compared to that in the previous iteration, or the pre-specified maximum number of iterations is reached.
For the optimized controller, denoted by , the controller analysis is conducted. This analysis step is necessary because the design uses only a small subset of the environmental conditions due to the computational expense to run simulations. In the controller analysis, the fatigue loads are calculated for a comprehensive set of environmental conditions , where denotes the index set for environmental profiles for the controller analysis.