UAV Relay Energy Consumption Minimization in an MEC-Assisted Marine Data Collection System
Abstract
:1. Introduction
1.1. Related Literature
1.2. Motivations and Contributions
- To prolong the lifetime of a marine data collection system, we constructed a two-hops relay network, where one aerial relay node collaborates with several MEC-enabled USVs to efficiently perform data collection tasks. Considering the restricted communication and energy resources in marine wireless communication scenarios, a partial computing offloading scheme was applied in the proposed network. Accordingly, an aerial node energy minimization problem was formulated, constrained by limited communication and computing resources as well as system latency requirements.
- We developed an energy optimal parallel partial computing and relay strategy to solve the nonconvex energy minimization problem based on a parallel computing and transmit scheme, and we obtained the optimal partial offloading factor vector in closed form. We acquired the optimal USV transmission power and optimal UAV relay transmission power using a two-step iterative optimizing method.
- The numerical results verified the effectiveness of our proposed strategy, which offers a feasible solution to prolong the lifetime of aerial-assisted marine data collection systems. Our strategy outperforms the benchmark methods in terms of aerial relay energy savings.
2. System Model
2.1. System Architecture Design
2.2. Partial Computational Offloading Model
2.3. Data Relaying Model
3. Problem Formulation
4. Energy Optimal Parallel Data Computation and Relaying Strategy
4.1. Partial Computation Ratio Vector Optimization
- In Case 1, all received data are processed in the nth USV. Simultaneously, and are satisfied. Thus, the computing time of the nth USV is . There are no remaining data to be transmitted to the nth USV, i.e., and . Therefore, no data transmission energy is consumed by the UAV from the nth USV.
- In Case 2, the computational capability of the nth USV is constrained by transmission latency T. Thus, the computing time of the nth USV is , and is the already-processed data volume. The remaining to-be-transmitted data volume in the nth USV is .
- In Case 3, the computational capability of the nth USV is constrained by the maximum computing energy budget , and is the already-processed data volume. The computing time of the nth USV is . The remaining to-be-transmitted data volume in the nth USV is .
4.2. Transmission Latency Optimization
4.2.1. Partial Computing-Dominated Latency
- Step 1. Given a value of , C8 can be transformed asWe setThe optimal power allocation parameter can be iteratively derived through (27).
- Step 2: After acquiring the optimal , the optimal can be obtained by using the bisection search method in its feasible region.
4.2.2. Data Transmission-Dominated Latency
| Algorithm 1: The Energy Optimal Parallel Partial Computing and Relay Strategy. |
|
5. Simulation Results
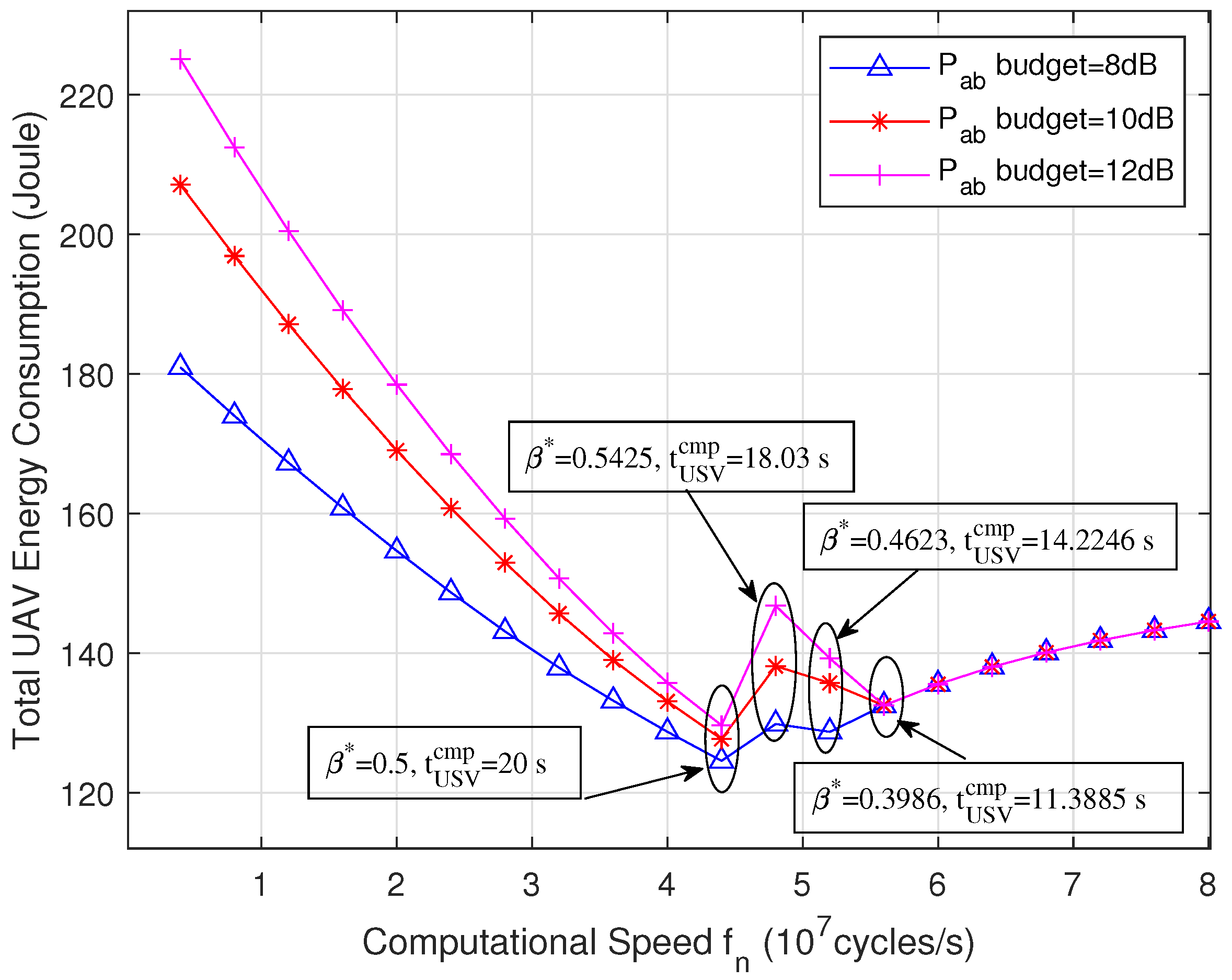
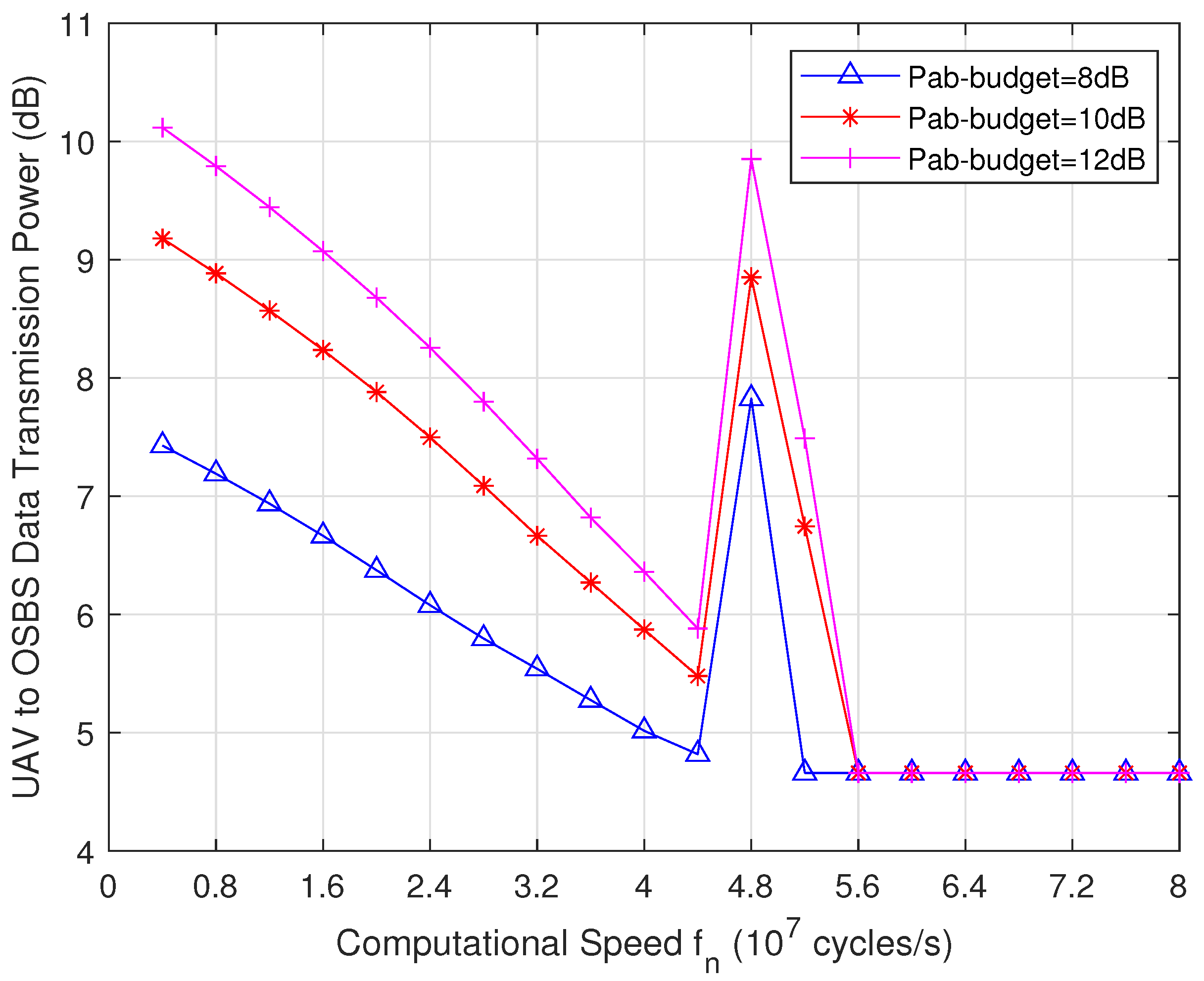
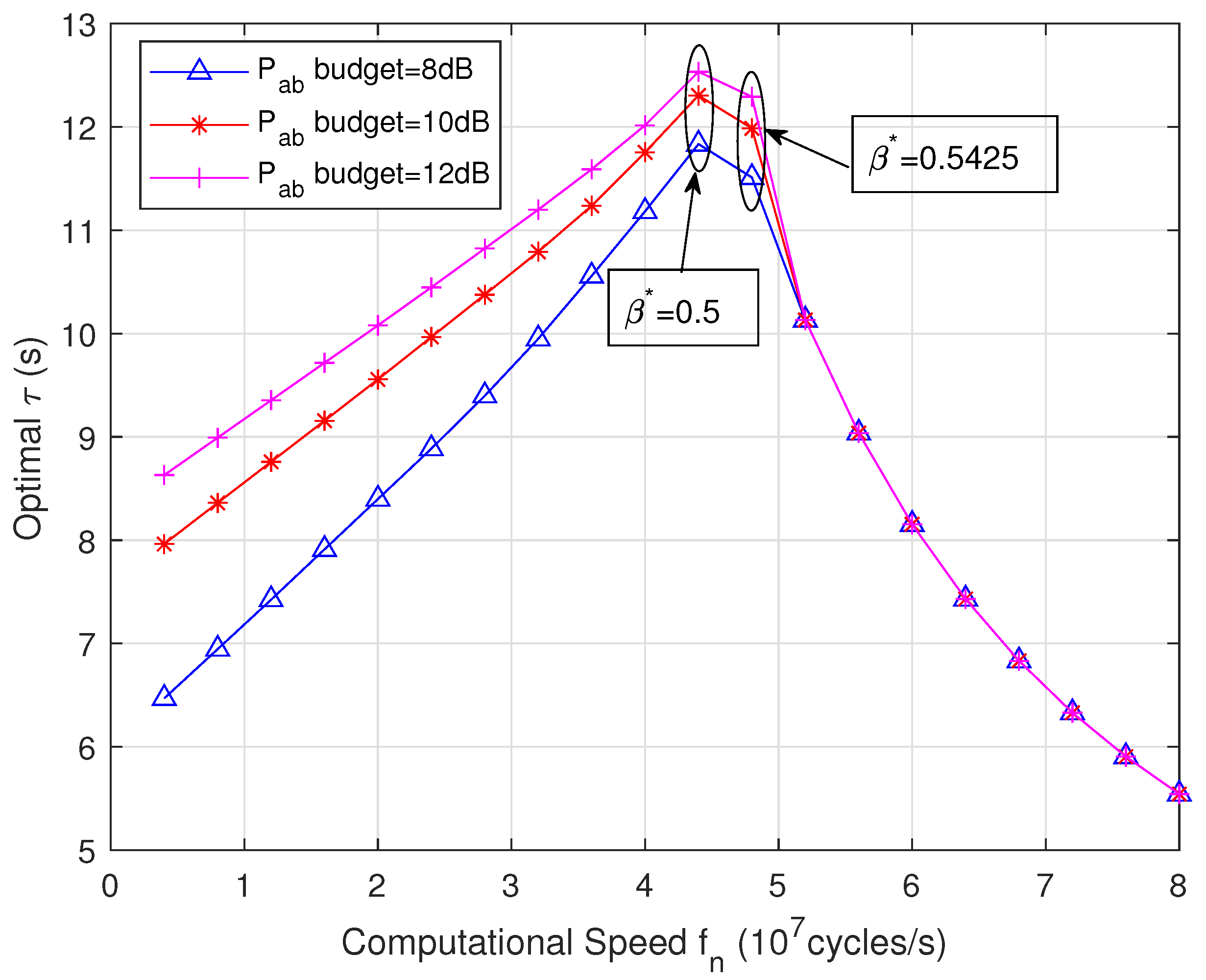
5.1. Proposed Strategy Performance for Different Values
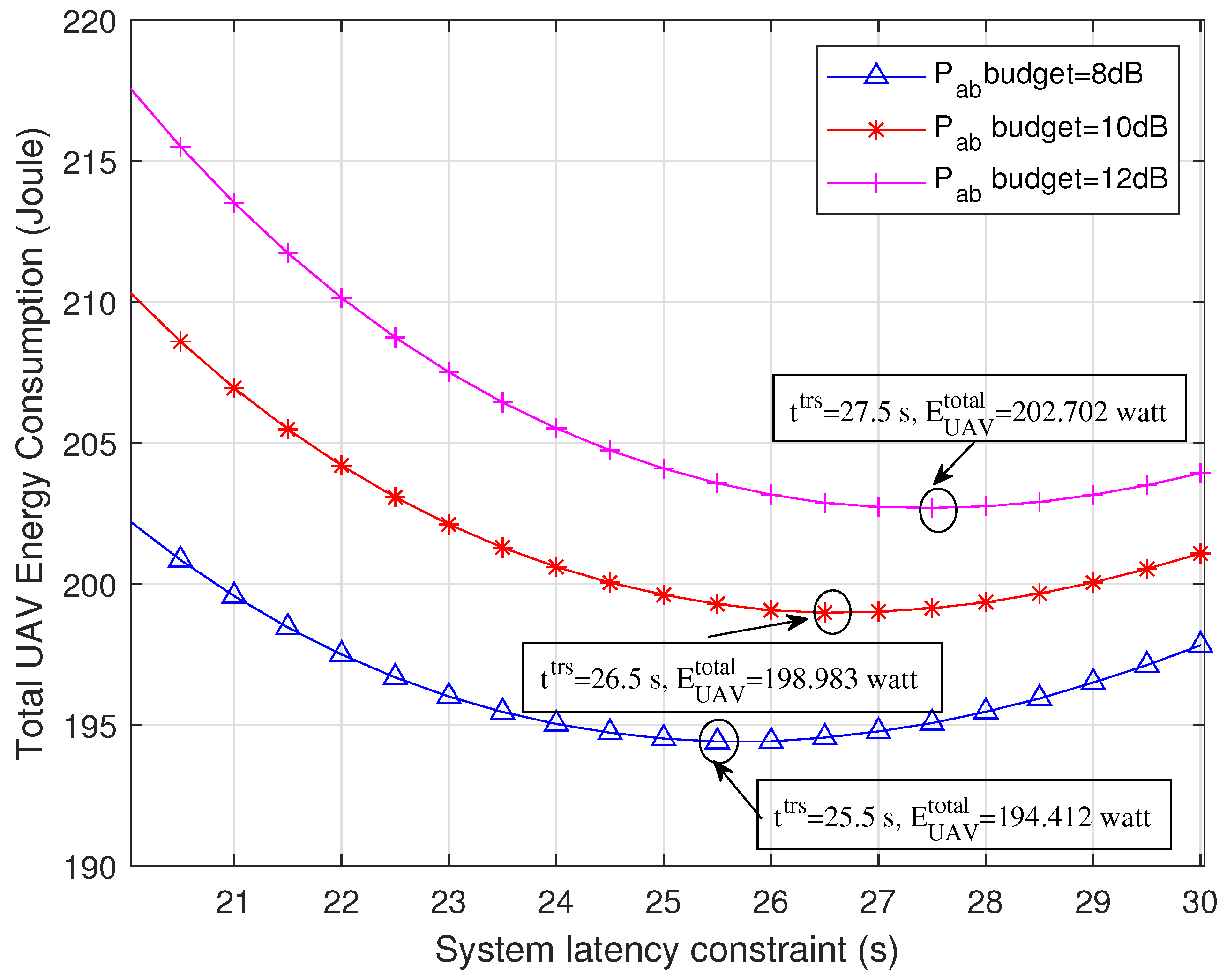
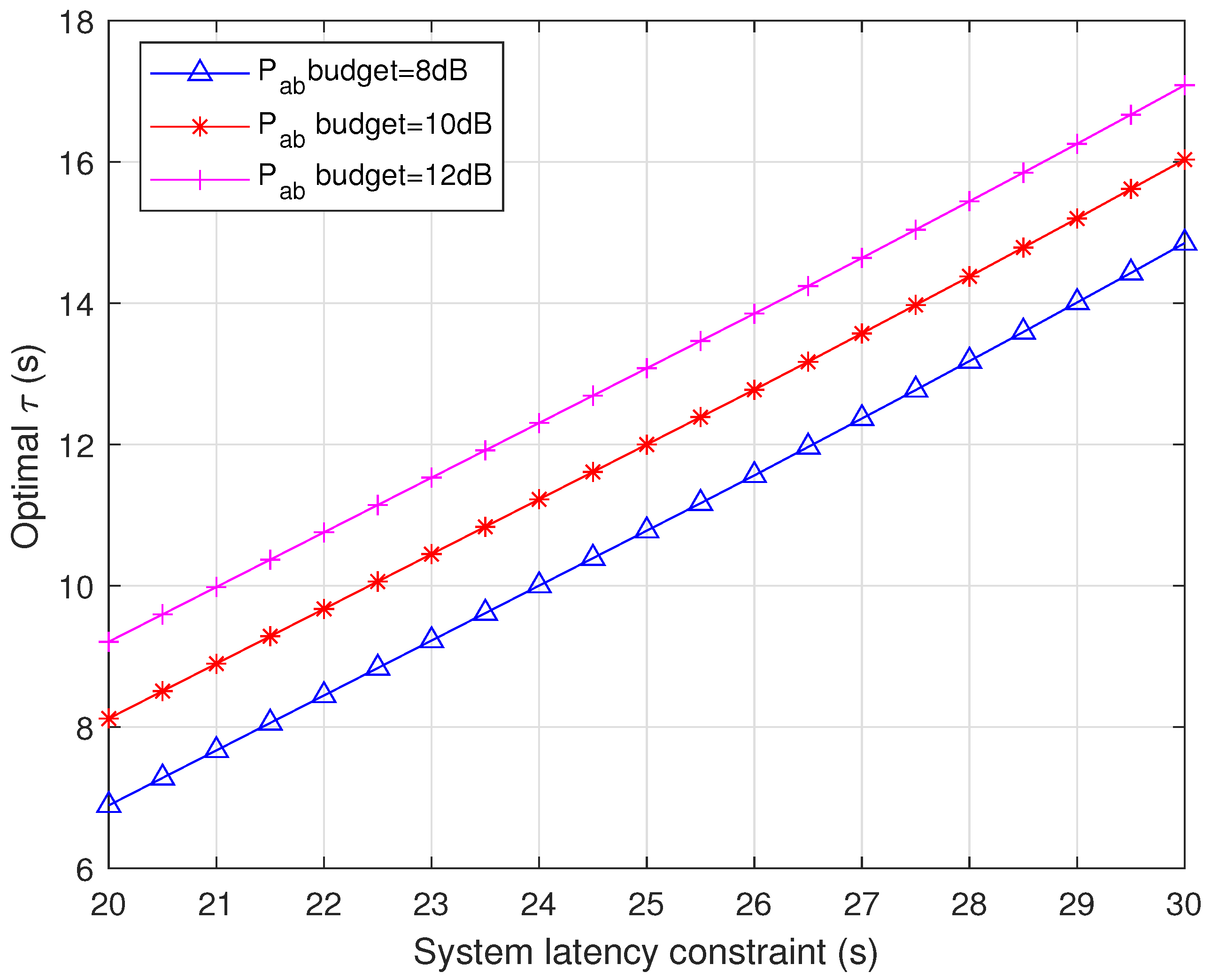
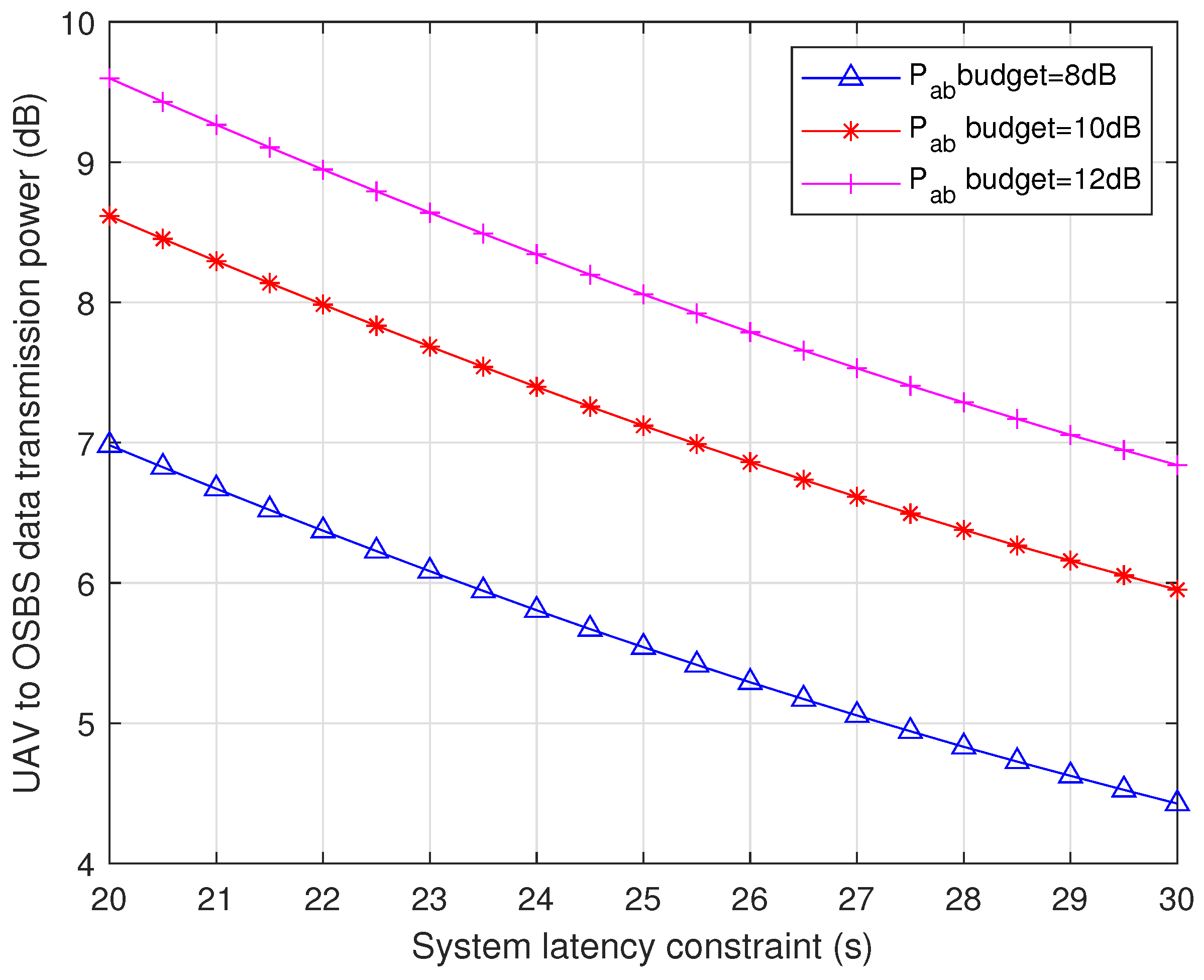
5.2. Proposed Strategy Performance for Different T Values
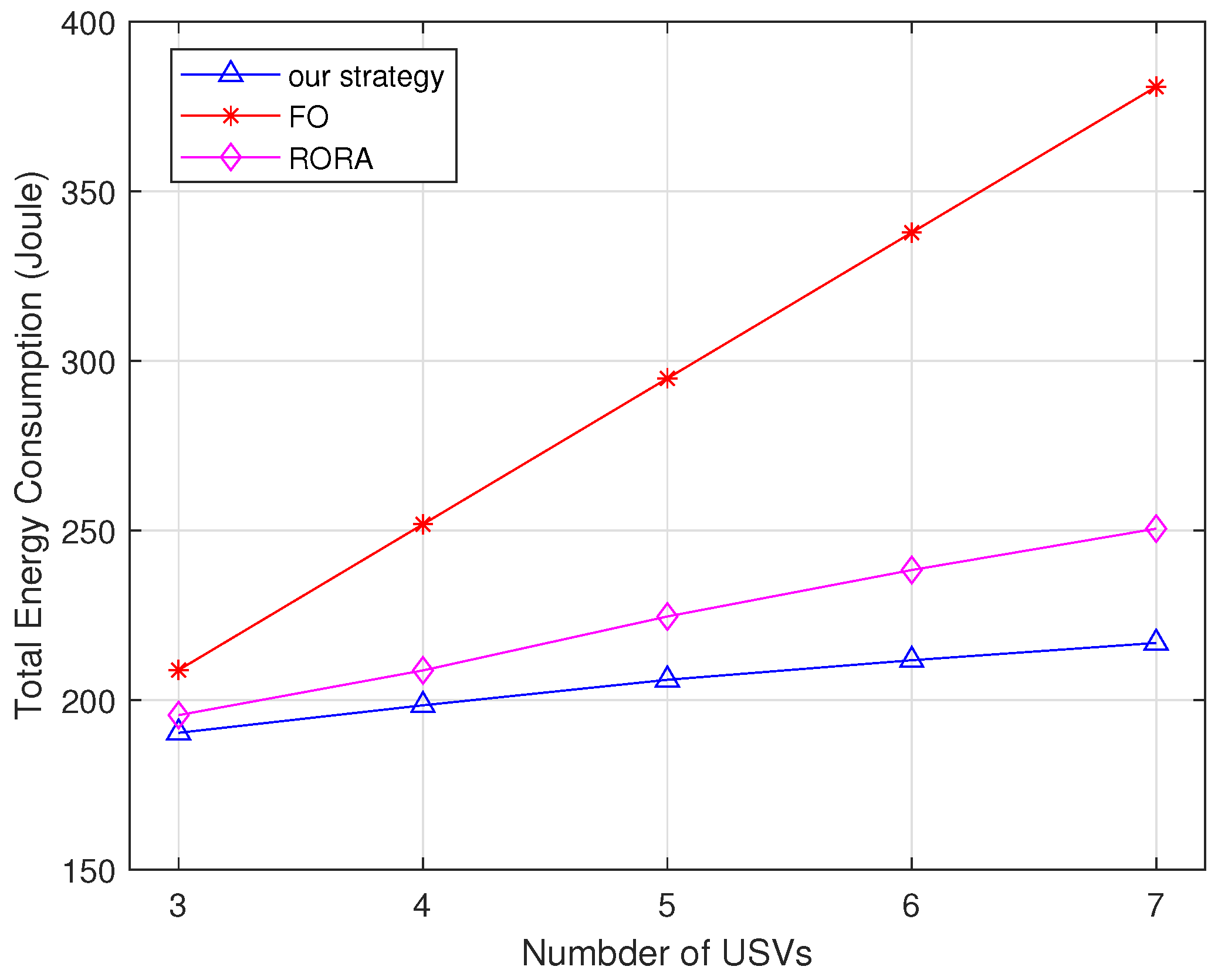
5.3. Performance Comparison
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, M.M.; Zhang, J.; You, X. Machine-type communication for maritime Internet of Things: A design. IEEE Commun. Surv. Tutor. 2020, 22, 2550–2585. [Google Scholar] [CrossRef]
- Jiang, S.M. Networking in oceans: A Survey. ACM Comput. Surv. 2020, 54, 33. [Google Scholar] [CrossRef]
- Kim, M.; Lee, S.; Park, C.; Lee, J.; Saad, W. Ensuring data freshness for blockchain-enabled monitoring networks. IEEE Internet Things J. 2022, 9, 9775–9788. [Google Scholar] [CrossRef]
- Abedin, S.F.; Munir, M.S.; Tran, N.H.; Han, Z.; Hong, C.S. Data freshness and energy-efffcient UAV navigation optimization: A deep reinforcement learning approach. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5994–6006. [Google Scholar] [CrossRef]
- Wang, D.; Wu, M.; Wei, Z.; Yu, K.; Min, L.; Mumtaz, S. Uplink secrecy performance of RIS-based RF/FSO three-dimension heterogeneous networks. IEEE Trans. Wirel. Commun. 2023, 99, 1. [Google Scholar] [CrossRef]
- Wang, D.; He, T.; Zhou, F.; Cheng, J.; Zhang, R.; Wu, Q. Outage-driven link selection for secure buffer-aided networks. Sci. China Inf. Sci. 2022, 65, 182303. [Google Scholar] [CrossRef]
- Seid, A.M.; Boateng, G.O.; Anokye, S.; Kwantwi, T.; Sun, G.; Liu, G. Collaborative computation offloading and resource allocation in multi-UAV-assisted IoT networks: A deep reinforcement learning approach. IEEE Internet Things J. 2021, 8, 12203–12218. [Google Scholar] [CrossRef]
- Guo, H.; Liu, J. UAV-enhanced intelligent offloading for internet of things at the edge. IEEE Trans. Ind. Inf. 2020, 16, 2737–2746. [Google Scholar] [CrossRef]
- Yang, T.; Feng, H.; Gao, S.; Jiang, Z.; Qui, M.; Cheng, N. Two-Stage offfoading optimization for energy–latency tradeoff with mobile edge computing in maritime internet of things. IEEE Internet Things J. 2020, 7, 5954–5963. [Google Scholar] [CrossRef]
- Dai, Y.; Lin, B.; Che, Y.; Lyu, L. UAV-assisted data offloading for smart container in offshore maritime communications. China Commun. 2022, 19, 153–165. [Google Scholar] [CrossRef]
- Qian, L.P.; Zhang, H.; Wang, Q.; Wu, Y.; Lin, B. Joint multi-domain resource allocation and trajectory optimization in UAV-assisted maritime IoT networks. IEEE Internet Things J. 2023, 10, 539–552. [Google Scholar] [CrossRef]
- Xu, W.; Tian, J.; Gu, L.; Tao, S. Joint placement and power optimization of UAV-relay in NOMA enabled maritime IoT system. Drones 2022, 6, 304. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, F.; Lin, W.; Ding, Z.; Al-Dhahir, N. Cooperative Hybrid Nonorthogonal Multiple Access-Based Mobile-Edge Computing in Cognitive Radio Networks. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 1104–1117. [Google Scholar] [CrossRef]
- Liu, B.; Liu, C.; Peng, M. Resource allocation for energy-efficient MEC in NOMA-enabled aassive IoT networks. IEEE J. Sel. Areas Commun. 2021, 39, 1015–1027. [Google Scholar] [CrossRef]
- Ding, Z.; Xu, J.; Dobre, O.A.; Poor, H.V. Joint power and time allocation for NOMA–MEC offloading. IEEE Trans. Veh. Technol. 2019, 68, 6207–6211. [Google Scholar] [CrossRef]
- Tripathi, S.; Pandey, O.J.; Cenkeramaddi, L.R.; Hegde, R.M. A socially-aware radio map framework for improving QoS of UAV-assisted MEC networks. IEEE Trans. Netw. Serv. Manag. 2023, 20, 342–356. [Google Scholar] [CrossRef]
- Park, Y.M.; Hassan, S.S.; Tun, Y.K.; Han, Z.; Hong, C.S. Joint trajectory and resource optimization of MEC-assisted UAVs in Sub-THz networks: A resources-based multi-agent proximal policy optimization DRL with attention mechanism. arXiv 2023, arXiv:2209.07228. [Google Scholar] [CrossRef]
- Nguyen, L.X.; Tun, Y.K.; Dang, Y.M.; Park, Z.H.; Hong, C.S. Dependency Tasks Offloading and Communication Resource Allocation in Collaborative UAV Networks: A Metaheuristic Approach. IEEE Internet Things J. 2023, 10, 9062–9076. [Google Scholar] [CrossRef]
- Lakew, D.S.; Tran, A.-T.; Dao, N.-N.; Cho, S. Intelligent offloading and resource allocation in heterogeneous aerial access IoT networks. IEEE Internet Things J. 2023, 10, 5704–5718. [Google Scholar] [CrossRef]
- Tri-Hai, N.; Laihyuk, P. HAP-assisted RSMA-enabled vehicular edge computing: A DRL-based optimization Framework. Mathematics 2023, 11, 2376. [Google Scholar]
- Truong, T.P.; Dao, N.-N.; Cho, S. HAMEC-RSMA: Enhanced aAerial computing systems with rate splitting multiple access. IEEE Access 2022, 10, 52398–52409. [Google Scholar] [CrossRef]
- Nasir, A.A.; Tuan, H.D.; Duong, T.Q.; Poor, H.V. UAV-enabled communication using NOMA. IEEE Trans. Commun. 2019, 67, 5126–5138. [Google Scholar] [CrossRef]
- Matolak, D.W.; Sun, R. Air-ground channel characterization for unmanned aircraft systems—Part I: Methods, measurements, and models for over-water settingse. IEEE Trans. Veh. Technol. 2017, 66, 26–44. [Google Scholar] [CrossRef]
- Sardellitti, S.; Scutari, G.; Barbarossa, S. Joint optimization of radio and computational resources for multicell mobile-edge computing. IEEE Trans. Signal Inf. Process. Over Netw. 2015, 1, 89–103. [Google Scholar] [CrossRef]
- Munoz, O.; Pascual-Iserte, A.; Vidal, J. Optimization of radio and computational resources for energy efficiency in latency-constrained application offloading. IEEE Trans. Veh. Technol. 2015, 64, 4738–4755. [Google Scholar] [CrossRef]
- Zhang, W.; Wen, Y.; Guan, K.; Kilper, D.; Luo, H.; Wu, D.O. Energy-optimal mobile cloud computing under stochastic wireless channel. IEEE Trans. Commun. 2013, 12, 4569–4581. [Google Scholar] [CrossRef]
- Wang, Y.; Sheng, M.; Wang, X.; Wang, L.; Li, J. Mobile-edge computing: Partial computation offloading using dynamic voltage scaling. IEEE Trans. Commun. 2016, 64, 4268–4282. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Truong, T.P.; Tuong, V.D.; Dao, N.-N.; Cho, S. FlyReflect: Joint Flying IRS Trajectory and Phase Shift Design Using Deep Reinforcement Learning. IEEE Internet Things J. 2023, 10, 4605–4620. [Google Scholar] [CrossRef]
- Hua, D.-T.; Do, Q.T.; Dao, N.-N.; Nguyen, T.-V.; Shumeye Lakew, D.; Cho, S. Learning-Based Reconfigurable-Intelligent-Surface-Aided Rate-Splitting Multiple Access Networks. IEEE Internet Things J. 2023, 10, 17603–17619. [Google Scholar] [CrossRef]
- Nguyen, T.-H.; Nguyen, L.V.; Dang, L.M.; Hoang, V.T.; Park, L. TD3-Based Optimization Framework for RSMA-Enhanced UAV-Aided Downlink Communications in Remote Areas. Remote Sens. 2023, 15, 5284. [Google Scholar] [CrossRef]



| Refs. | Scenarios | UAV Functions | Techniques | Metrics |
|---|---|---|---|---|
| [7] | Terrestrial | BS and computing | Full offloading | Task executive delay |
| [8] | Terrestrial | Relay and computing | Full offloading | Energy efficiency |
| [9,10] | Marine | Relay and computing | Partial offloading | System latency |
| [12] | Marine | Relay | no MEC | Energy efficiency |
| [16,17,18,19,20] | Terrestrial | Relay and computing | Full offloading | Rate and latency |
| [21] | Terrestrial | BS & computing | Partial offloading | Rate and task success rate |
| Ours | Marine | Relay | Partial offloading | UAV life time |
| Notation | Description |
|---|---|
| Index, the number, and the set of USVs | |
| Coordinates of the nth USV | |
| Coordinates of the UAV | |
| Coordinates of the OSBS | |
| Distance between the nth USV and the UAV | |
| Distance between the UAV and the OSBS | |
| Channel gain from the nth USV to the UAV | |
| Rician fading component of | |
| Large-scale fading coefficient of | |
| Parameters of | |
| Channel gain from the UAV to the OSBS | |
| Rician fading component of | |
| Parameters of ’s large-scale fading coefficient | |
| Reference distance | |
| Computing speed and a coefficient at the nth USV | |
| , | Data volume received at the nth USV and its computing cycles |
| Computational multiplied factor | |
| Partial computational offloading ratio of the nth USV | |
| Computing latency at the nth USV | |
| Overall computing latency of USVs | |
| , | Transmission latency from USVs-to-UAV and UAV-to-OSBS |
| Transmit power of the nth USV and the UAV | |
| Hovering power value of the UAV | |
| Computing energy consumed at the nth USV and its budget | |
| Transmit energy consumed at the nth USV and the UAV | |
| Transmit power budgets of the nth USV and the UAV | |
| T | System latency requirement |
| Bandwidth and background noise of NOMA links | |
| Bandwidth and background noise of UAV-to-OSBS |
| Parameter | Description | Value |
|---|---|---|
| Coordination of onshore BS | m | |
| Coordination of UAV hovering position | m | |
| Reference distance | 1 m | |
| Carrier frequency from USVs to UAV | 50 MHz | |
| Carrier frequency from UAV to OSBS | 100 MHz | |
| Background noise | dBm | |
| A2S link path loss at | 116.7 | |
| A2S link path loss exponent | 20 | |
| Standard deviation of | 0.1 | |
| A2S link Rician factor | 40 | |
| A2A link path loss at | 46.4 | |
| A2A link path loss exponent | 15 | |
| standard deviation of | 0.1 | |
| A2A link Rician factor | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Gu, L. UAV Relay Energy Consumption Minimization in an MEC-Assisted Marine Data Collection System. J. Mar. Sci. Eng. 2023, 11, 2333. https://doi.org/10.3390/jmse11122333
Xu W, Gu L. UAV Relay Energy Consumption Minimization in an MEC-Assisted Marine Data Collection System. Journal of Marine Science and Engineering. 2023; 11(12):2333. https://doi.org/10.3390/jmse11122333
Chicago/Turabian StyleXu, Woping, and Li Gu. 2023. "UAV Relay Energy Consumption Minimization in an MEC-Assisted Marine Data Collection System" Journal of Marine Science and Engineering 11, no. 12: 2333. https://doi.org/10.3390/jmse11122333
APA StyleXu, W., & Gu, L. (2023). UAV Relay Energy Consumption Minimization in an MEC-Assisted Marine Data Collection System. Journal of Marine Science and Engineering, 11(12), 2333. https://doi.org/10.3390/jmse11122333






