A Study on the Vibration Analysis of Thick-Walled, Fluid-Conveying Pipelines with Internal Hydrostatic Pressure
Abstract
:1. Introduction
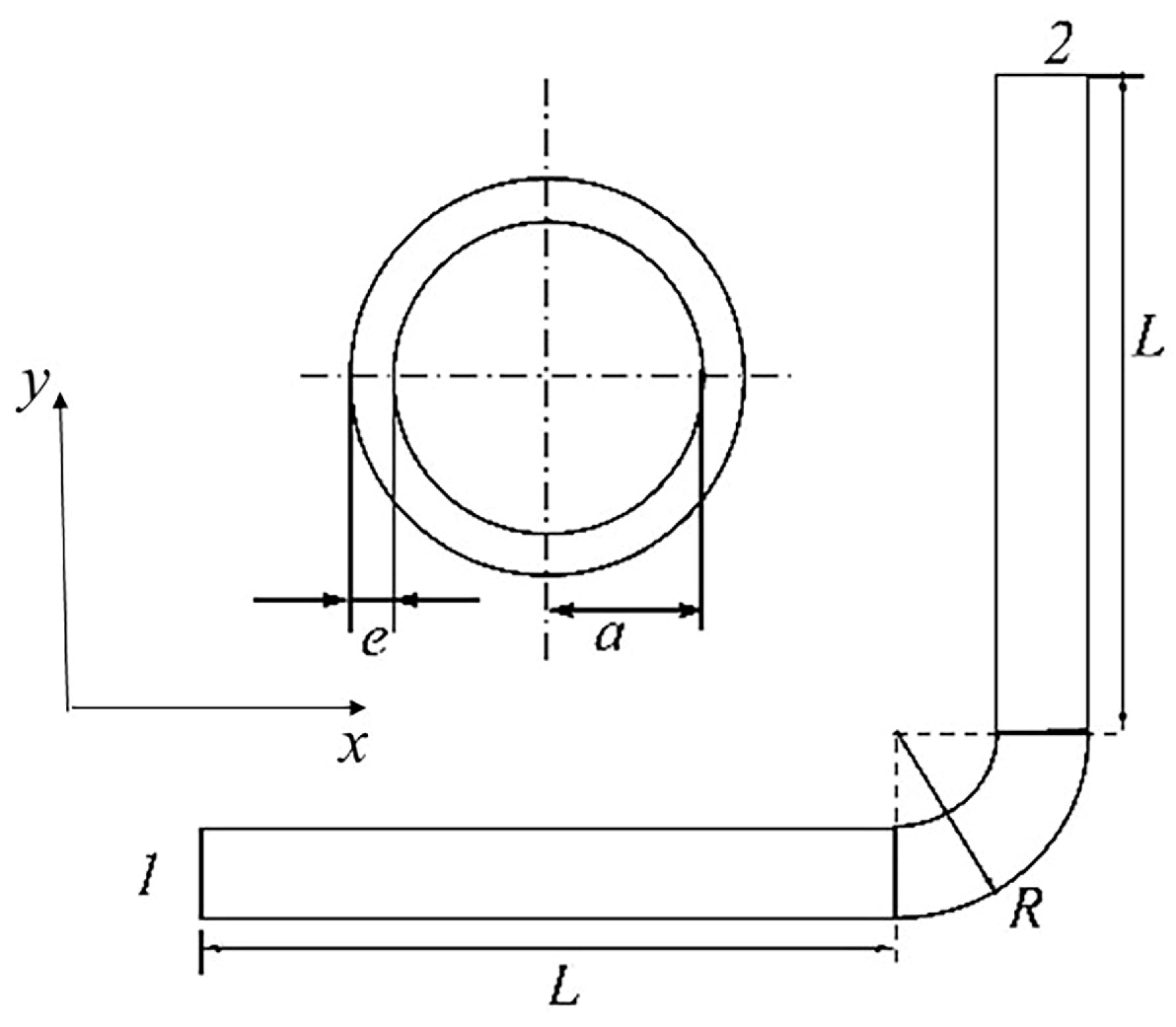
2. The Fluid–Structure Coupled Equation of Thick-Walled Pressurized Pipe in Plane
2.1. Vibration Equation of Pipe
2.2. Fluid Equations
2.3. The Governing FSI Equations for Pressurized Thick-Walled Pipeline
2.4. Pseudo-Excitation Method for Pipes Subjected to Random Loads
3. Results and Discussion
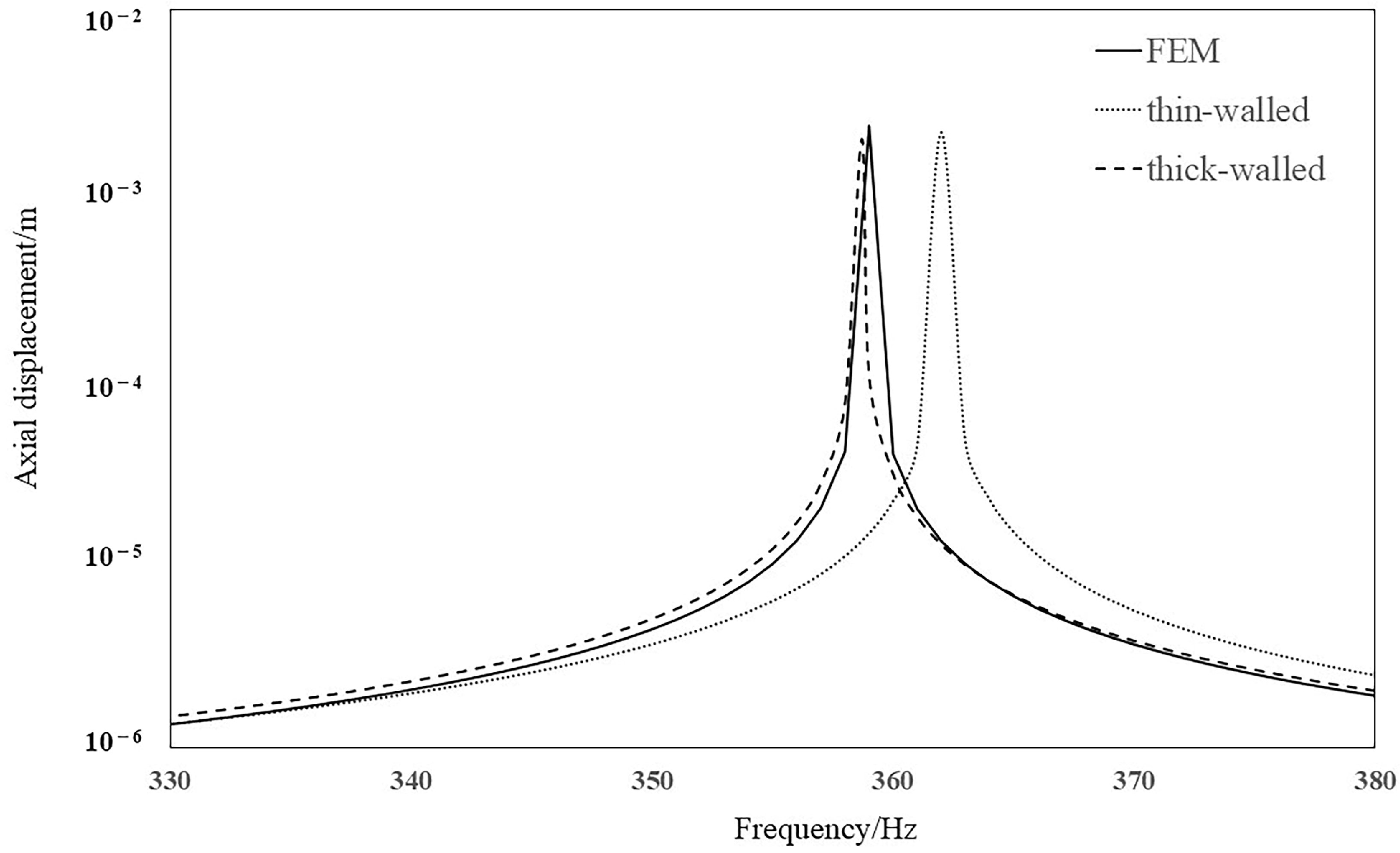
3.1. Validation of the Current Calculation Method
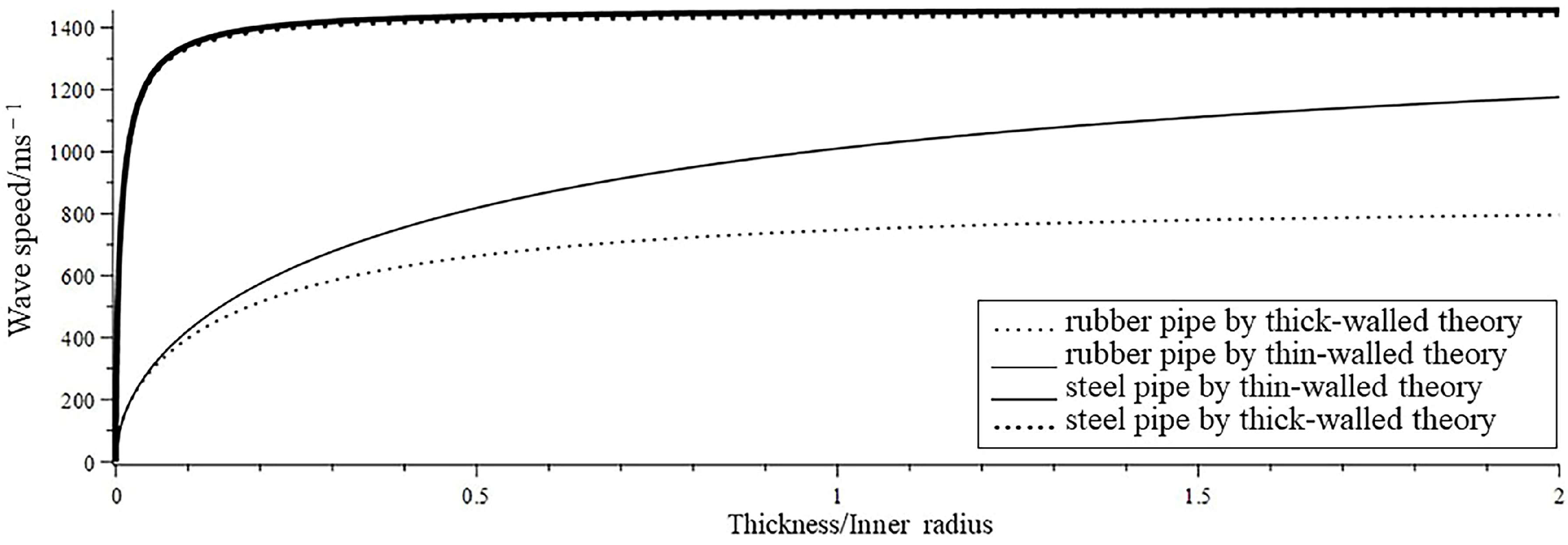
3.2. The Applicability Analysis of the Thick-Walled Theory and the Thin-Walled Theory
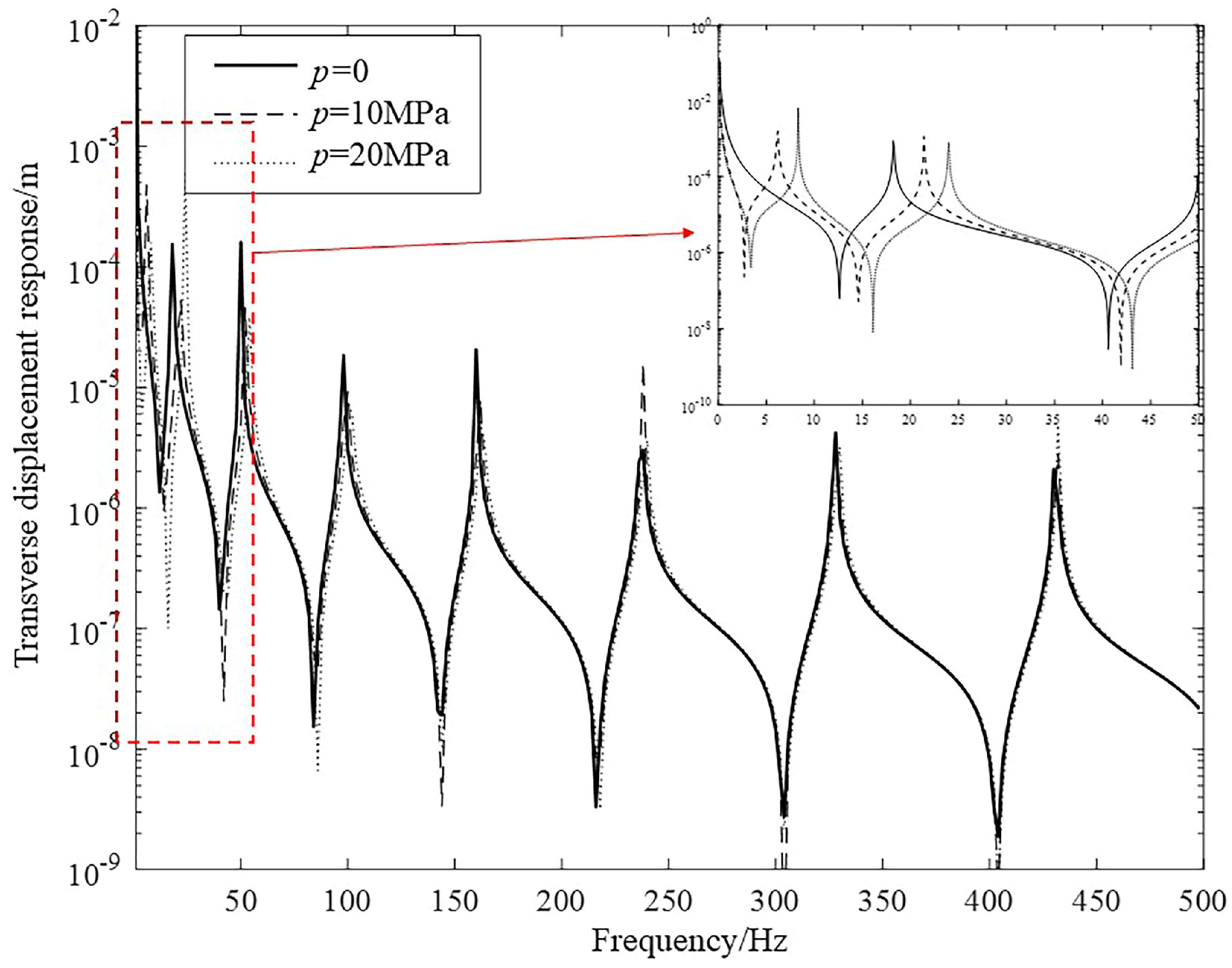
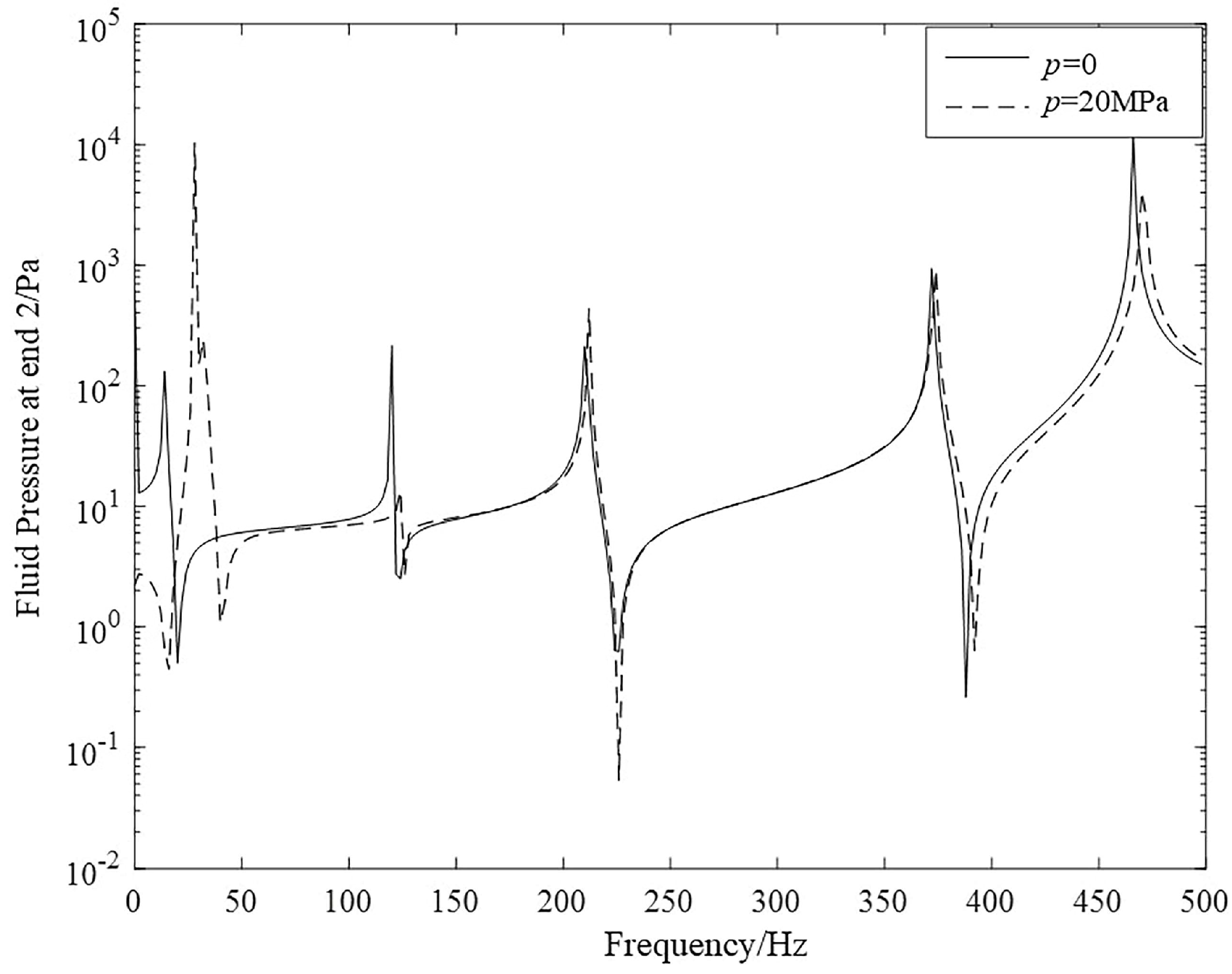
3.3. The Influences of Internal Hydrostatic Pressure under Harmonic Excitation
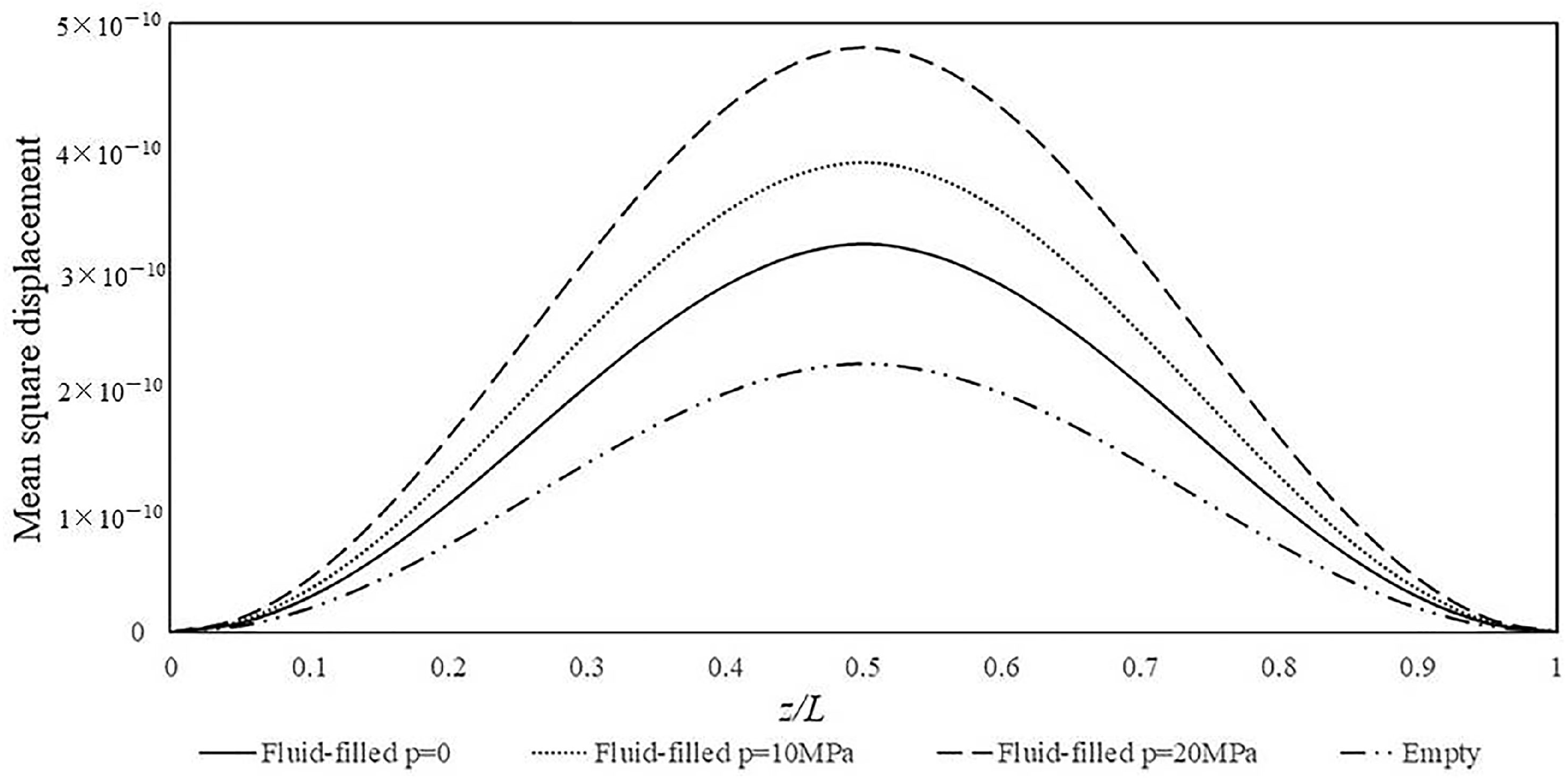
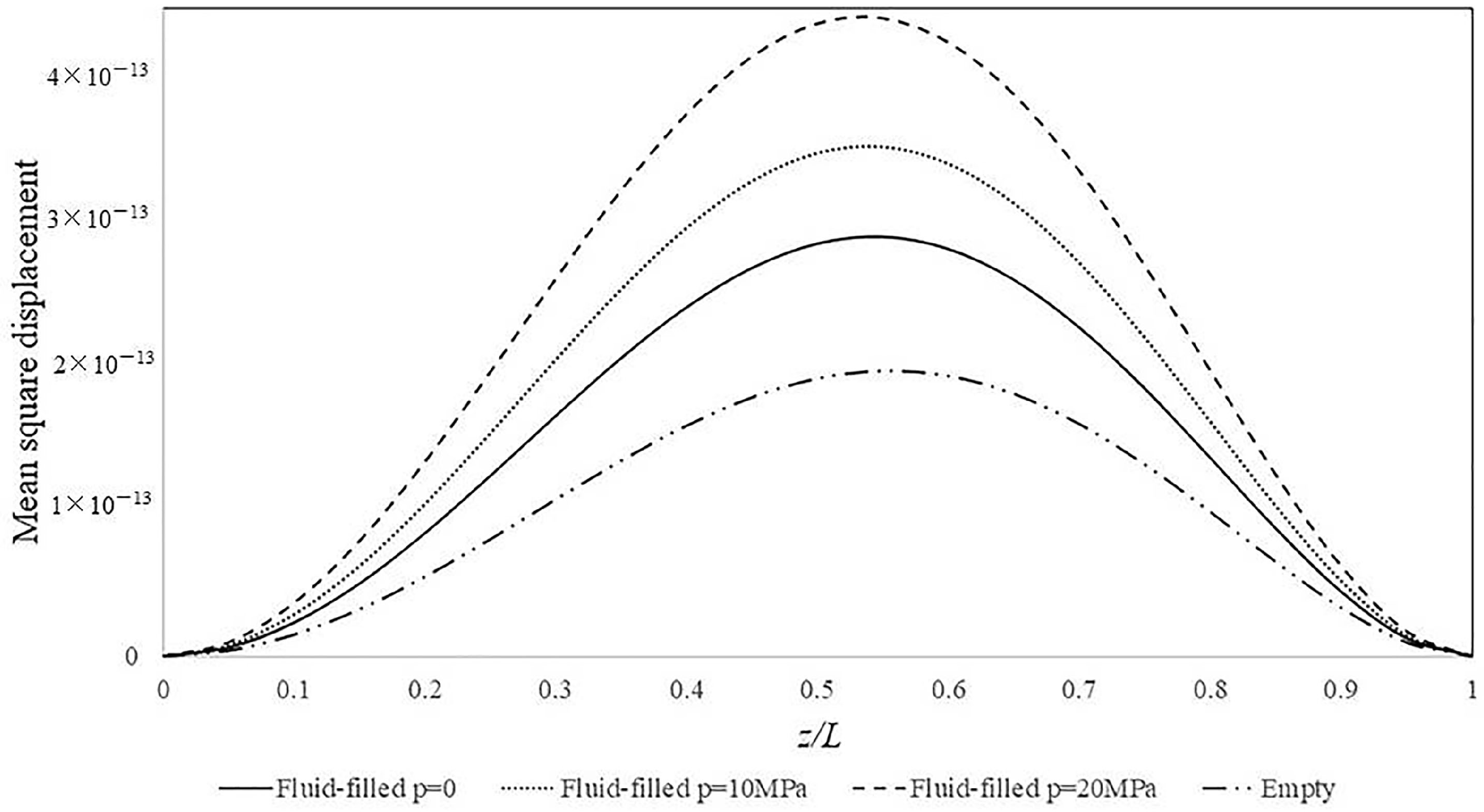
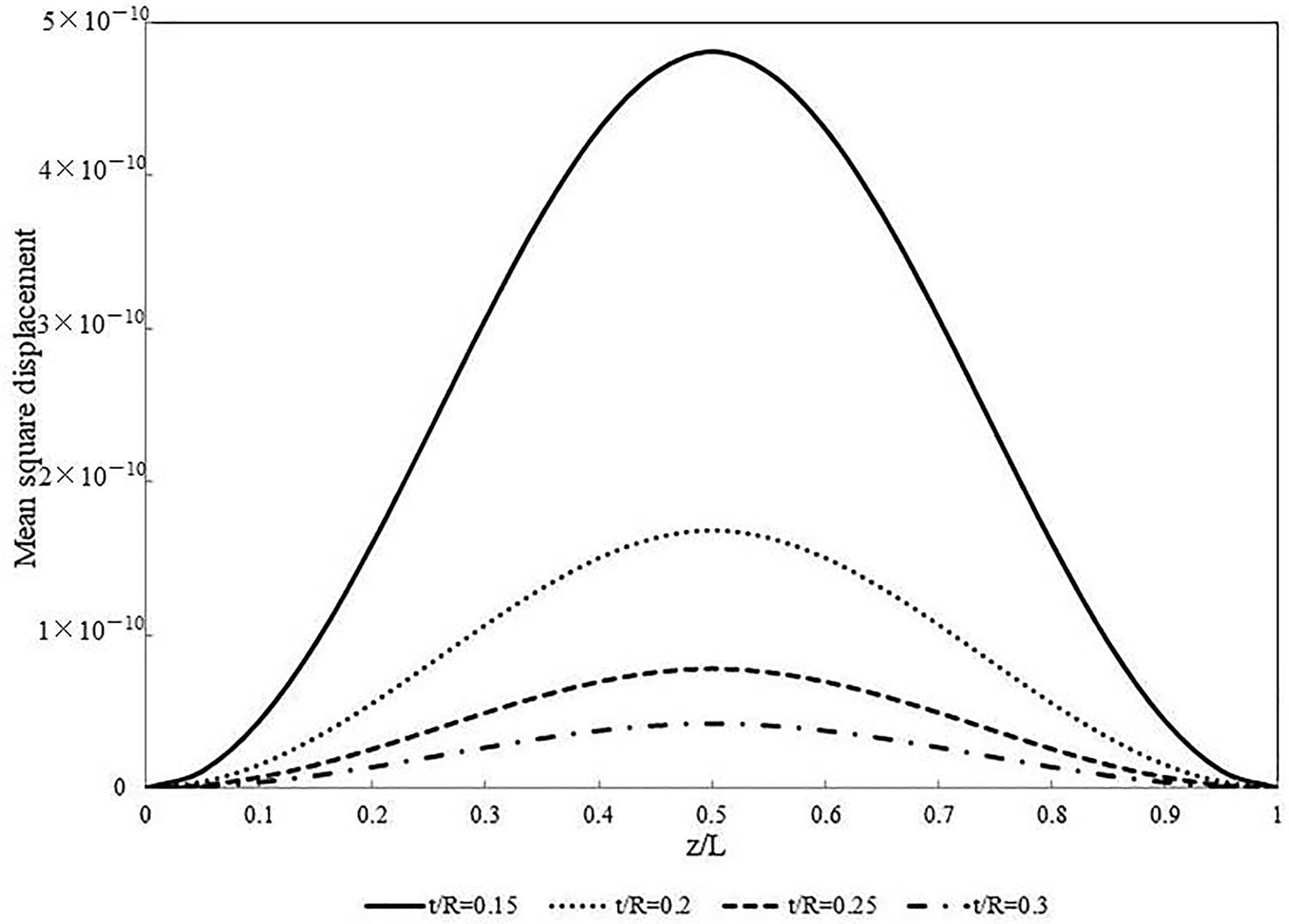
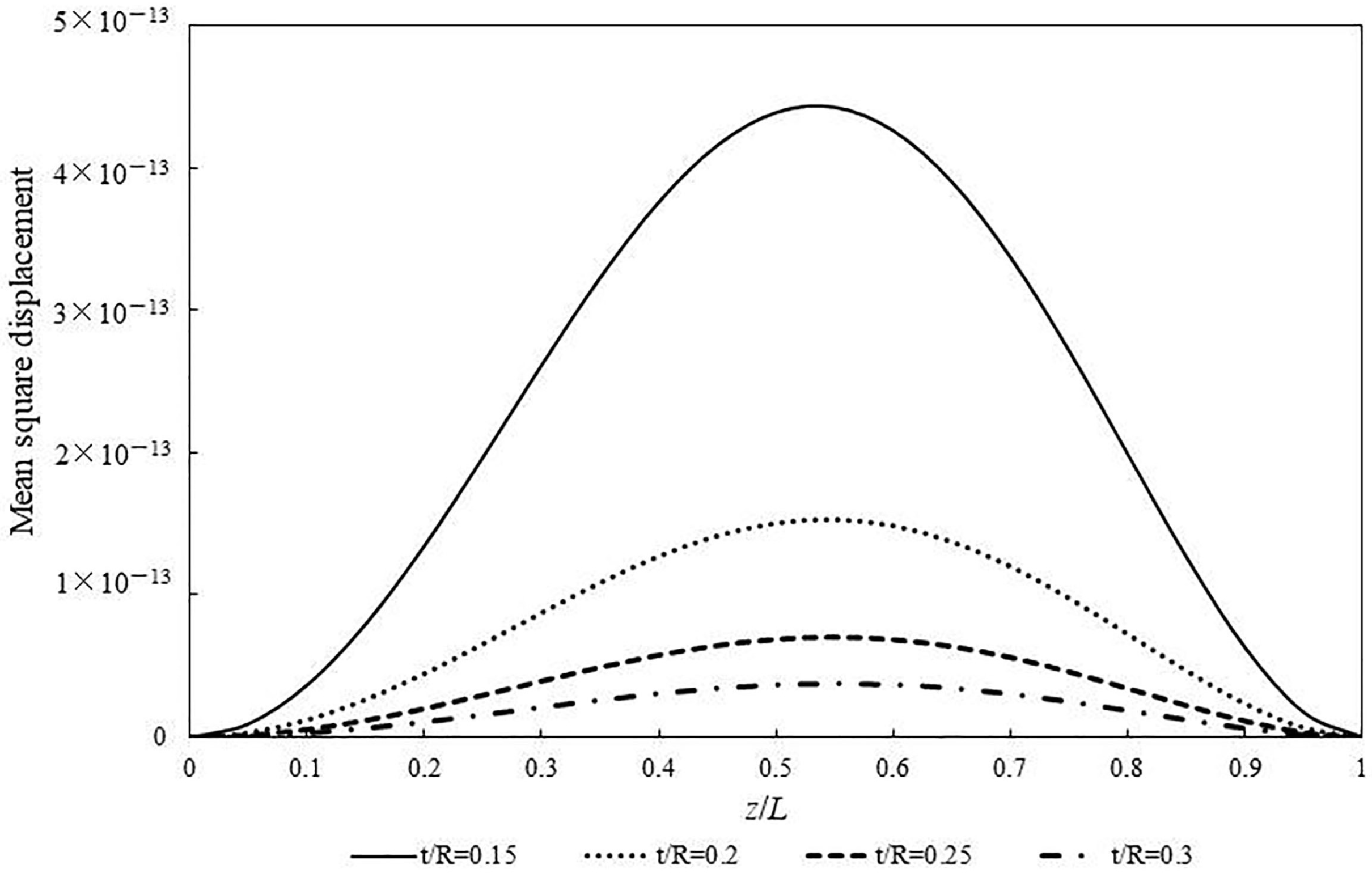
3.4. The Influences of Internal Hydrostatic Pressure under Random Loads
4. Conclusions
- (1)
- The axial wave speeds are different in the thick-walled theory and thin-walled theory. With an increase in the ratio of the thickness and radius, the differences also increase, especially for flexible pipes.
- (2)
- The internal hydrostatic pressure mainly affects the transverse vibration but has little effect on axial vibration transmissions.
- (3)
- The transverse natural frequencies become larger with increasing internal pressure. Such influences are especially significant in the lower frequency domain.
- (4)
- The downstream overall vibration velocity level increases due to the existence of internal pressure, which indicates that the hydrostatic pressure would increase the vibration transmission. Introducing flexible pipes may improve this condition.
- (5)
- The internal pressure also increases the mean square displacement along the pipeline when subjected to random loads. Relatively smaller displacements are presented by relatively thick-walled pipelines or under distributed random loads, as expected.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, X.L. On the ship pipeline system. Sci. Technol. Vision 2012, 25, 211–301. [Google Scholar]
- Wei, Z.D.; Li, B.R.; Du, J.M. Theoretical and experimental investigation of flexural vibration transfer properties of high-pressure periodic pipe. Chin. Phys. Lett. 2016, 33, 141. [Google Scholar] [CrossRef]
- Huang, P. Study on Hydroelastic Instability and Random Response Analysis of Tube Arrays. Ph.D. Thesis, Tsinghua University, Beijing, China, 2006. [Google Scholar]
- Fung, Y.C.; Kaplan, A.; Sechler, E.E. On the vibration of thin cylindrical shells under internal pressure. J. Aeronaut. Sci. 1957, 24, 650–660. [Google Scholar] [CrossRef]
- Miserentino, R.; Vosteen, L.F. Vibration Tests of Pressurized Thin-Walled Cylindrical Shells; TND-3066; National Aeronautics and Space Administration: Washington, DC, USA, 1965. [Google Scholar]
- Keltie, R.F. The effect of hydrostatic pressure fields on the structural and acoustic response of cylindrical shells. J. Acoust. Soc. Am. 1986, 79, 595–603. [Google Scholar] [CrossRef]
- Xie, G. Influence of hydrostatic pressure on sound radiation of cylindrical shell with ring ribs. J. Wuhan Univ. Technol. 1995, 1, 77–79. [Google Scholar]
- Zhang, Y.L.; Gorman, D.G.; Reese, J.M. Vibration of prestressed thin cylindrical shells conveying fluid. Thin-Walled Struct. 2003, 41, 1103–1127. [Google Scholar] [CrossRef]
- Liu, Z.; Li, T.; Liu, J. Analysis of dispersion characteristics of liquid-filled cylindrical shells considering hydrostatic pressure. Ship Mech. 2009, 13, 635–640. [Google Scholar]
- Iakovlev, S.; Dooley, G.; Williston, K.; Gaudet, J. Evolution of the reflection and focusing patterns and stress states in two-fluid cylindrical shell systems subjected to an external shock wave. J. Sound Vib. 2011, 330, 6254–6276. [Google Scholar] [CrossRef]
- Chen, L.; Li, L.; Zhang, Y. Analysis of acoustic radiation characteristics of cylindrical shell structures with local prestress. J. Shanghai Jiaotong Univ. 2014, 48, 1084–1089. [Google Scholar]
- Gao, H.; Shuai, C.; Ma, J.; Xu, G. Free Vibration of Rubber Matrix Cord-Reinforced Combined Shells of Revolution Under Hydrostatic Pressure. J. Vib. Acoust. Trans. ASME 2022, 144, 011002. [Google Scholar] [CrossRef]
- Hua, G.; Sang, C.; Ma, J.; Cheng, Y. Vibro-acoustic characteristics of rubber matrix cord-reinforced combined shells of revolution under hydrostatic pressure. Appl. Acoust. 2022, 190, 108642. [Google Scholar] [CrossRef]
- Neto, H.R.; Cavalini, J.A.; Vedovoto, J.M.; Neto, A.S.; Rade, D.A. Influence of seabed proximity on the vibration responses of a pipeline accounting for fluid-structure interaction. Mech. Syst. Signal Pr. 2019, 114, 224–238. [Google Scholar] [CrossRef]
- Kiryukhin, A.V.; Mil’man, O.O.; Ptakhin, A.V.; Serezhkin, L.N.; Isaev, S.A. Investigation of Pressure Pulsations and Power Loads in the Compensator with the Aim of Reducing Vibration Transfer in a Pipeline with a Liquid. J. Eng. Phys. Thermophys. 2019, 92, 1517–1523. [Google Scholar] [CrossRef]
- Yamilev, M.Z.; Masagutov, A.M.; Nikolaev, A.K.; Pshenin, V.V.; Zaripova, N.A.; Plotnikova, K.I. Modified equations for hydraulic calculation of thermally insulated oil pipelines for the case of a power-law fluid. Nauka Tehnol. Trubopr. 2021, 11, 388–395. [Google Scholar]
- Korshak, A.A.; Pshenin, V.V. Modeling of water slug removal from oil pipelines by methods of computational fluid dynamics. Neft. Khozyaystvo-Oil Ind. 2023, 10, 117–122. [Google Scholar] [CrossRef]
- Cao, Y.; Ma, H.; Guo, X.; Ge, H.; Li, H.; Lin, J. Experimental Study on Pressure Pulsation and Acceleration Response of Fluid Conveying Pipeline Under Multi-Excitation. ASME J. Press. Vessel Technol. 2023, 145, 051401. [Google Scholar] [CrossRef]
- Wiggert, D.C.; Hatfield, F.J.; Stuckenbruck, S. Analysis of Liquid and Structural Transients in Piping by the Method of Characteristics. ASME J. Fluids Eng. 1987, 109, 161–165. [Google Scholar] [CrossRef]
- Zhang, L.; Tijsseling, A.S.; Vardy, A.E. FSI analysis of liquid-filled pipes. J. Sound Vib. 1999, 224, 69–99. [Google Scholar] [CrossRef]
- Lesmez, M.W. Modal Analysis of Vibrations in Liquid-Filled Piping Systems. Ph.D. Thesis, Michigan State University, East Lancing, MI, USA, 1989. [Google Scholar]
- Tentarelli, S.C. Propagation of Noise and Vibration in Complex Hydraulic Tubing Systems. Ph.D. Thesis, Lehigh University, Bethlehem, PA, USA, 1990. [Google Scholar]
- Caf, J.D. Analysis of Pulsations and Vibrations in Fluid-Filled Pipe Systems. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 1994. [Google Scholar]
- Zhang, Z.Y. Study on Vibration Characteristics and Energy Flow in Fluid-Filled Pipe Systems Considering Fluid-Structure Interaction. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2000. [Google Scholar]
- Li, Y.H. Study on Vibration, Noise, and Characteristics of Fluid-Structure Coupled Pipe Systems. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2011. [Google Scholar]
- Everstine, G.C. Dynamic analysis of fluid-filled piping systems using finite element techniques. J. Press. Vessel.-Technol. ASME 1986, 108, 57–61. [Google Scholar] [CrossRef]
- Hansson, P.A.; Sandberg, G. Dynamic finite element analysis of fluid-filled pipes. Comput. Methods Appl. Mech. Eng. 2001, 190, 3111–3120. [Google Scholar] [CrossRef]
- Lee, U.; Kim, J. Dynamics of branched pipeline systems conveying internal unsteady flow. Trans. ASME 1999, 121, 114–122. [Google Scholar] [CrossRef]
- Sandvik, A.; Østby, E.; Thaulow, C. A probabilistic fracture mechanics model including 3D ductile tearing of bi-axially loaded pipes with surface cracks. Eng. Fract. Mech. 2008, 75, 76–96. [Google Scholar] [CrossRef]
- Kainat, M.; Lin, M.; Roger Cheng, J.J.; Martens, M.; Adeeb, S. Effects of the initial geometric imperfections on the buckling behavior of high-strength uoe manufactured steel pipes. J. Press. Vessel. Technol. 2016, 138, 051206. [Google Scholar] [CrossRef]
- Franci, A. Lagrangian finite element method with nodal integration for fluid–solid interaction. Comput. Part Mech. 2020, 8, 389–405. [Google Scholar] [CrossRef]
- Shahzamanian, M.M.; Lin, M.; Kainat, M.; Yoosef-Ghodsi, N.; Adeeb, S. Systematic literature review of the application of extended finite element method in failure prediction of pipelines. J. Pipeline Sci. Eng. 2021, 1, 241–251. [Google Scholar] [CrossRef]
- Hicham, F.; Abdelhamid, H.; Nabil Mohammed, O. Fluid-structure interactions of internal pressure pipeline using the hierarchical finite element method. Adv. Mech. Eng. 2021, 13, 16878140211041262. [Google Scholar] [CrossRef]
- Wu, G.X.; Zhao, X.L.; Shi, D.D.; Wu, X. Analysis of Fluid-Structure Coupling Vibration Mechanism for Subsea Tree Pipeline Combined with Fluent and Ansys Workbench. Water 2021, 13, 955. [Google Scholar] [CrossRef]
- Yu, T.; Zhang, Z.; Zhang, D.; Juan, M.; Jin, J. Vibration Analysis of Multi-Branch Hydraulic Pipeline System Considering Fluid—Structure Interaction. Appl. Sci. 2022, 12, 12902. [Google Scholar] [CrossRef]
- Zhu, H.Z.; Wang, W.B.; Yin, X.W.; Gao, C.F. Spectral element method for vibration analysis of three-dimensional pipes conveying fluid. Int. J. Mech. Mater. Des. 2019, 15, 345–360. [Google Scholar] [CrossRef]
- Wu, J.H.; Tijsseling, A.S.; Sun, Y.D. Vibration analysis by impedance synthesis method of three-dimensional piping connected to a large circular cylindrical shell. Mech. Syst. Signal Process. 2023, 188, 110063. [Google Scholar] [CrossRef]
- Wu, J.H.; Sun, Y.D. An exact solution for vibration analysis of pipe coupled with conical-ring stiffened cylindrical shells with arbitrary boundary condition. Ocean Eng. 2022, 266, 112861. [Google Scholar] [CrossRef]
- Lin, J.H.; Zhang, Y.H. The pseudo-excitation method and its industrial applications in China and abroad. Appl. Math. Mech. 2017, 38, 1–31. [Google Scholar]
- Lin, J.H.; Zhang, W.S.; Williams, F.W. Pseudo-excitation algorithm for non-stationary random seismic responses. Eng. Struct. 1992, 44, 683–687. [Google Scholar]
- Tijsseling, A.S. Water hammer with fluid-structure interaction in thick-walled pipes. Comput. Struct. 2007, 85, 844–851. [Google Scholar] [CrossRef]
- Xu, Z.L. Elasticity, 5th ed.; Higher Education Press: Beijing, China, 2016. [Google Scholar]
- Liang, Z.; Zhang, J.; Zhang, H. Submarine Pipeline Mechanics; Science Press: Beijing, China, 2018; pp. 38–40. [Google Scholar]





| Axial (Hz) [20] | 173 | 289 | 459 | 485 | 636 | 750 | 918 | 968 |
|---|---|---|---|---|---|---|---|---|
| Axial (present) (Hz) | 169 | 282 | 451 | 470 | 621 | 734 | 898 | 941 |
| Error (%) | −2.31% | −2.42% | −1.74% | −3.09% | −2.36% | −2.13% | −2.18% | −2.79% |
| Transverse (Hz) [20] | 13 | 36 | 70 | 116 | 173 | 241 | 320 | 411 |
| Transverse (present) (Hz) | 13 | 37 | 73 | 121 | 179 | 247 | 327 | 417 |
| Error (%) | 0% | 2.8% | 4.3% | 4.3% | 3.5% | 2.5% | 2.1% | 1.5% |
| R (mm) | t (mm) | t/R | Pressure | Natural Frequencies (Hz) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 40 | 5 | 0.125 | p = 20 MPa | 8 | 24 | 54 | 101 | 153 | 165 |
| p = 10 MPa | 6 | 21 | 52 | 99 | 154 | 162 | |||
| p = 0 | - | - | 50 | 98 | 155 | 160 | |||
| 40 | 8 | 0.2 | p = 20 MPa | 7 | 24 | 59 | 111 | 166 | 180 |
| p = 10 MPa | 5 | 23 | 57 | 110 | 166 | 179 | |||
| p = 0 | - | 21 | 56 | 109 | 166 | 178 | |||
| 40 | 10 | 0.25 | p = 20 MPa | 7 | 25 | 61 | 116 | 163 | 188 |
| p = 10 MPa | 5 | 23 | 60 | 115 | 163 | 187 | |||
| p = 0 | - | 22 | 59 | 114 | 163 | 187 | |||
| 40 | 12 | 0.3 | p = 20 MPa | 6 | 25 | 63 | 120 | 160 | 196 |
| p = 10 MPa | - | 24 | 62 | 120 | 160 | 195 | |||
| p = 0 | - | 23 | 61 | 119 | 160 | 194 | |||
| 40 | 15 | 0.375 | p = 20 MPa | 6 | 26 | 66 | 126 | 157 | 206 |
| p = 10 MPa | 4 | 25 | 65 | 126 | 157 | 205 | |||
| p = 0 | - | 24 | 65 | 125 | 157 | 205 | |||
| 40 | 20 | 0.5 | p = 20 MPa | 5 | 27 | 71 | 136 | 154 | 221 |
| p = 10 MPa | - | 26 | 70 | 135 | 154 | 221 | |||
| p = 0 | - | 26 | 70 | 135 | 154 | 221 | |||
| R (mm) | t (mm) | t/R | Steel–Rubber–Steel (dB) | Steel (dB) |
|---|---|---|---|---|
| 40 | 5 | 0.125 | 213.14 | 216.60 |
| 40 | 8 | 0.2 | 211.97 | 214.00 |
| 40 | 10 | 0.25 | 210.82 | 212.40 |
| 40 | 12 | 0.3 | 209.75 | 215.16 |
| 40 | 15 | 0.375 | 211.09 | 209.27 |
| 40 | 20 | 0.5 | 206.24 | 208.78 |
| Pipe Type | Inner Pressure | Overall Vibration Velocity Level (dB) | Overall Sound Pressure Level (dB) |
|---|---|---|---|
| Including rubber pipe | p = 0 | 152.6 | 175.7 |
| p = 20 MPa | 160.3 | 175.4 | |
| Pure metal pipe | p = 0 | 155.4 | 176.4 |
| p = 20 MPa | 171.6 | 174.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Wu, J. A Study on the Vibration Analysis of Thick-Walled, Fluid-Conveying Pipelines with Internal Hydrostatic Pressure. J. Mar. Sci. Eng. 2023, 11, 2338. https://doi.org/10.3390/jmse11122338
Zhu H, Wu J. A Study on the Vibration Analysis of Thick-Walled, Fluid-Conveying Pipelines with Internal Hydrostatic Pressure. Journal of Marine Science and Engineering. 2023; 11(12):2338. https://doi.org/10.3390/jmse11122338
Chicago/Turabian StyleZhu, Hongzhen, and Jianghai Wu. 2023. "A Study on the Vibration Analysis of Thick-Walled, Fluid-Conveying Pipelines with Internal Hydrostatic Pressure" Journal of Marine Science and Engineering 11, no. 12: 2338. https://doi.org/10.3390/jmse11122338




