Dynamic Analysis of Active Heave Compensation System for Marine Winch under the Impact of Irregular Waves
Abstract
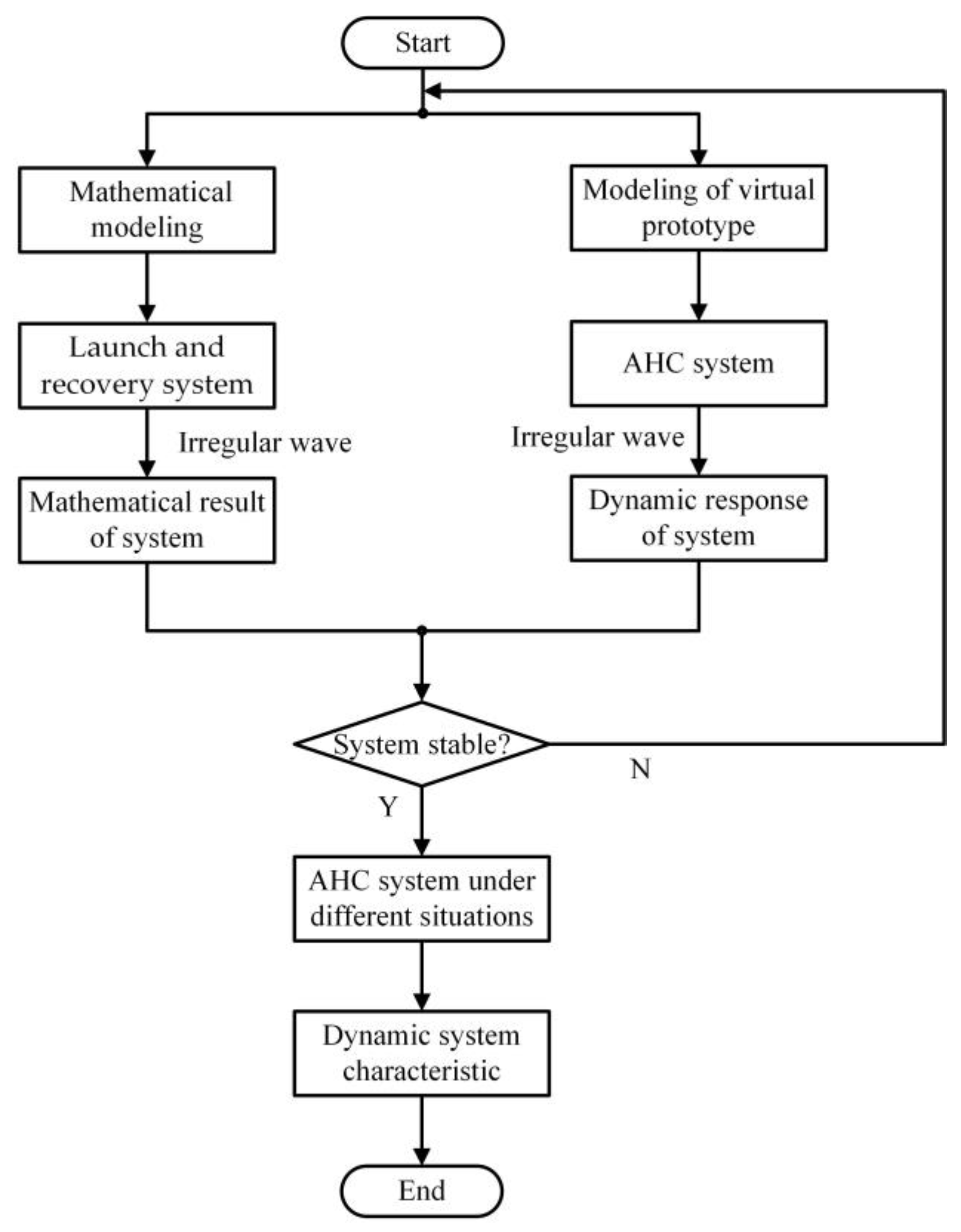
:1. Introduction
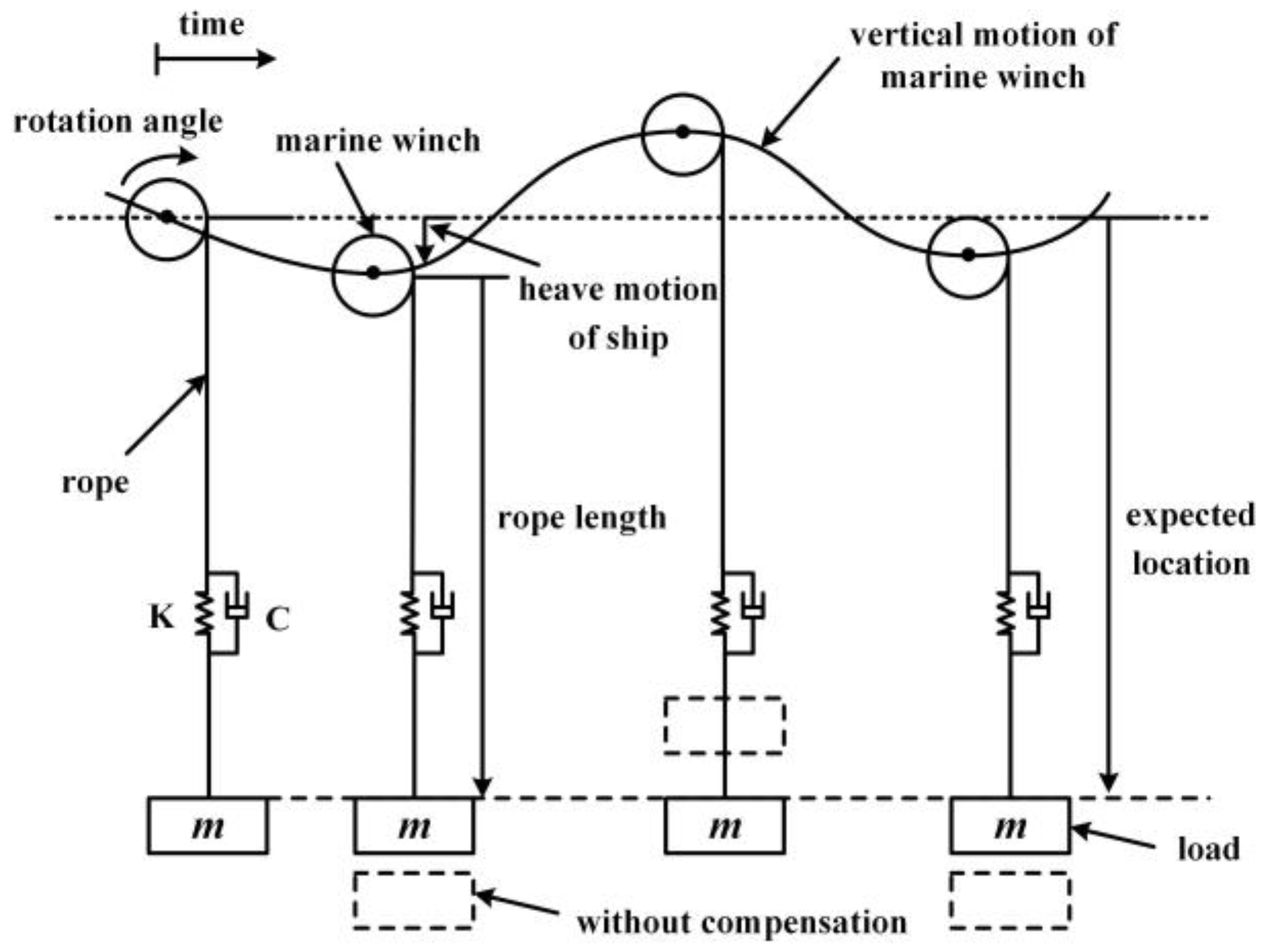
2. System Mathematical Model and Simulation without AHC Function
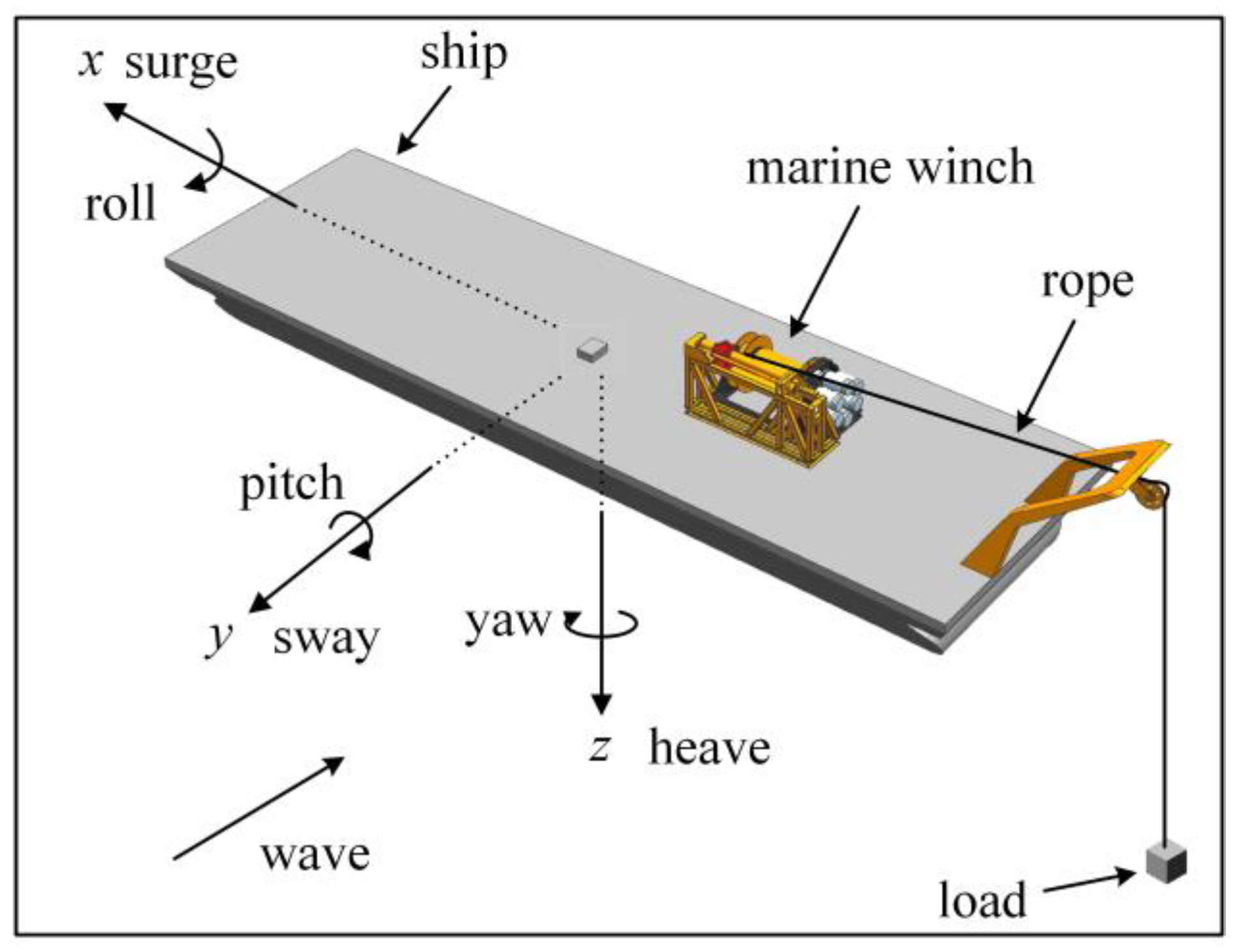
2.1. Model Assumptions
- (1)
- The work mainly studies the pitch and heave motions in 6-DOF motion.
- (2)
- The model assumes that the rope is a light rod without mass. Furthermore, the elasticity of the rope and retractable frame is ignored, which means both of them are regarded as rigid bodies.
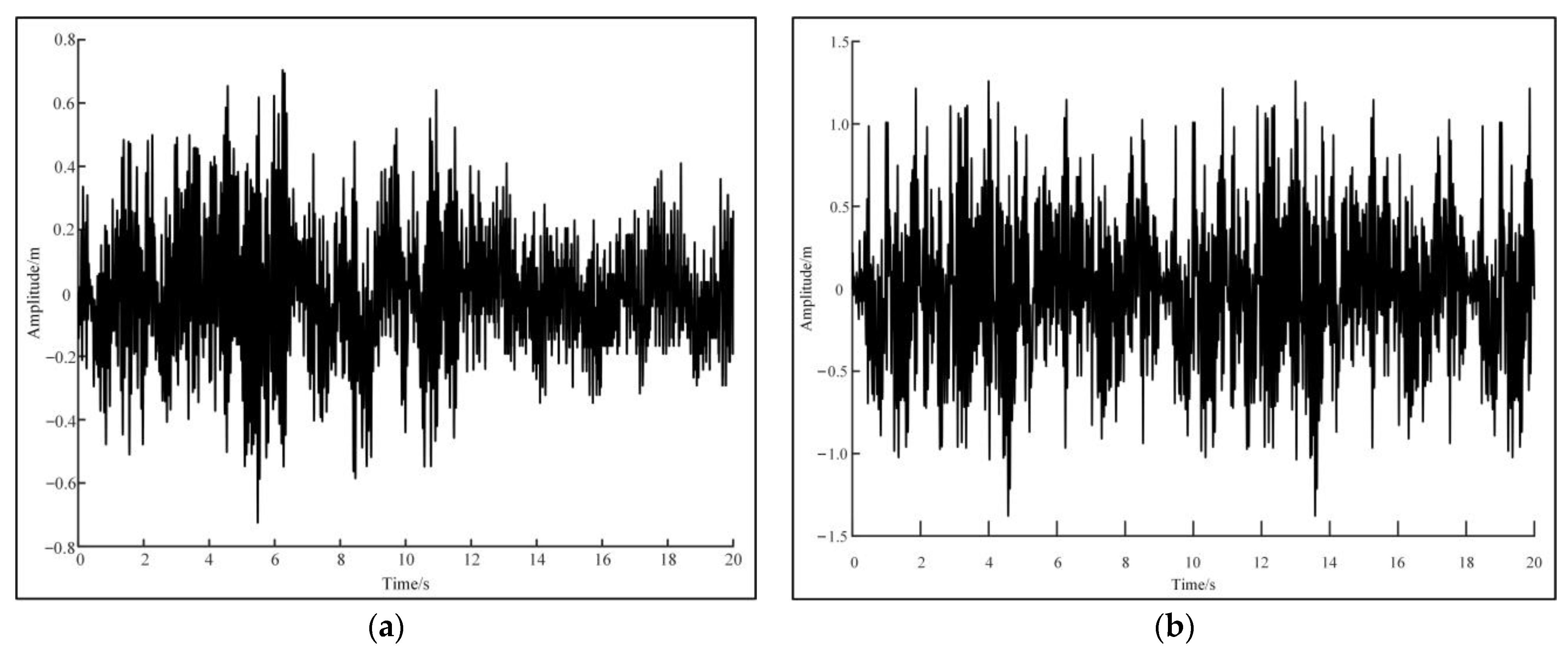
2.2. Model of Wave Motion
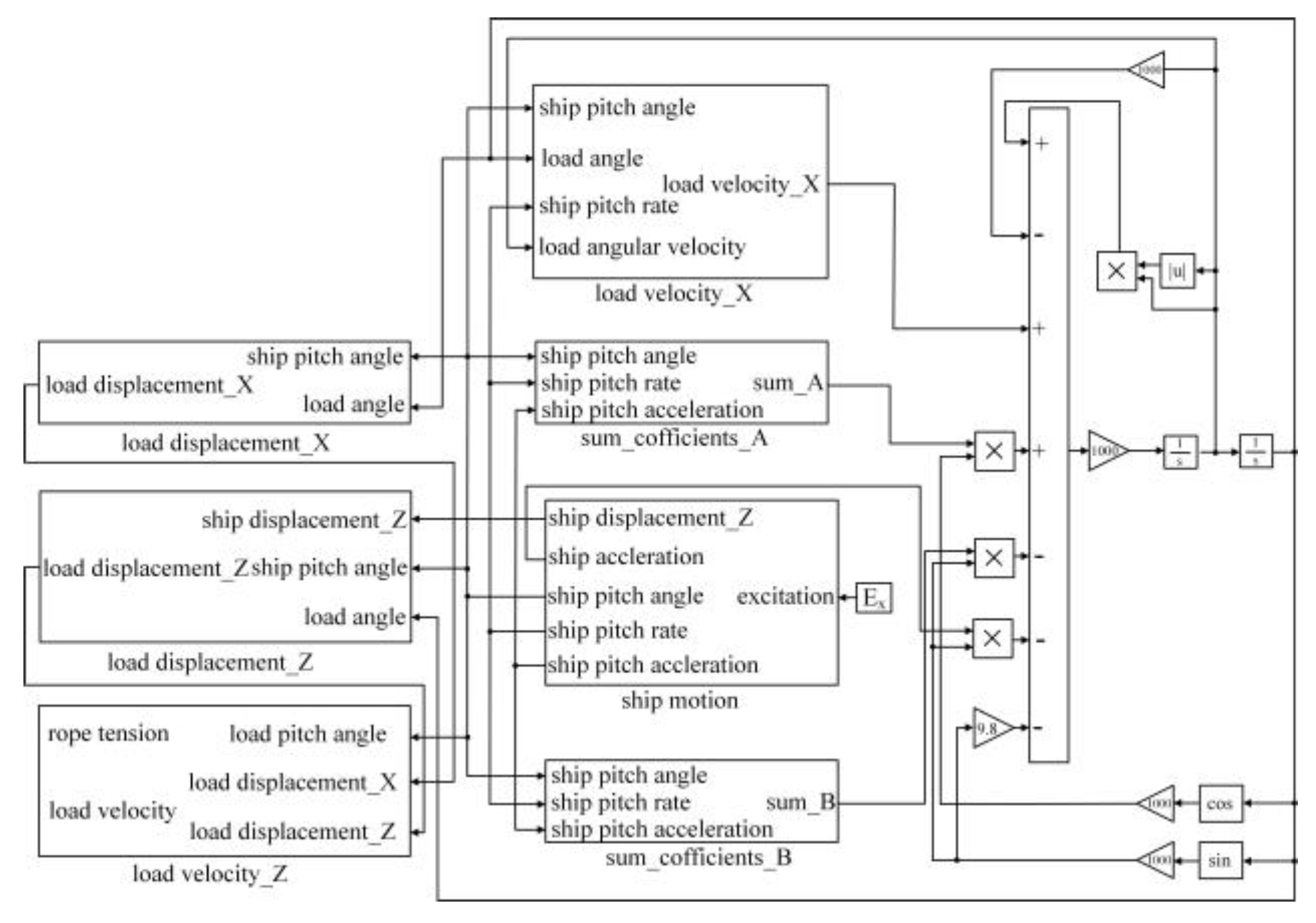
2.3. Model of Launch and Recovery System
2.4. Simulation of Launch and Recovery System
3. Modeling and Simulation of AHC System
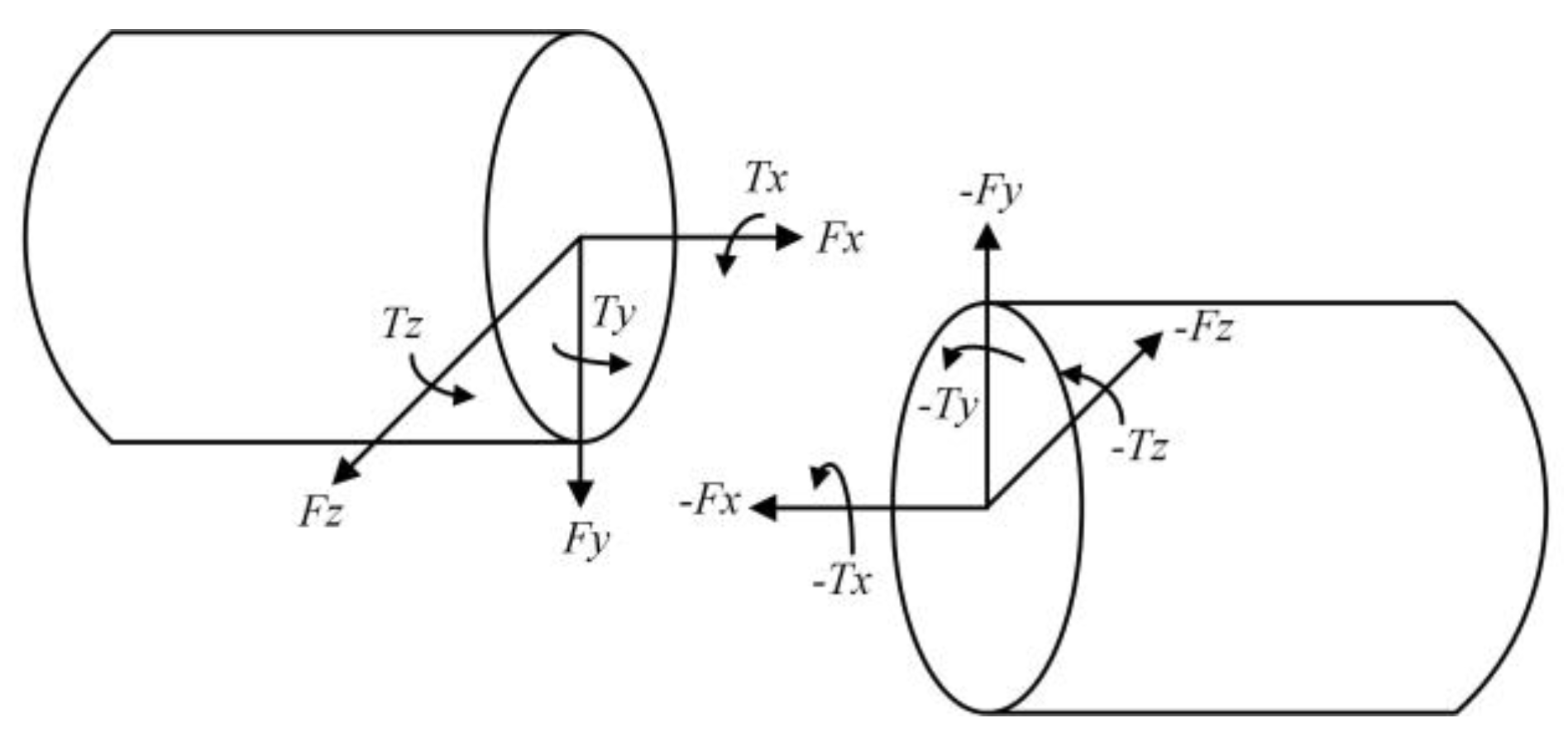
3.1. Model of Flexible Rope
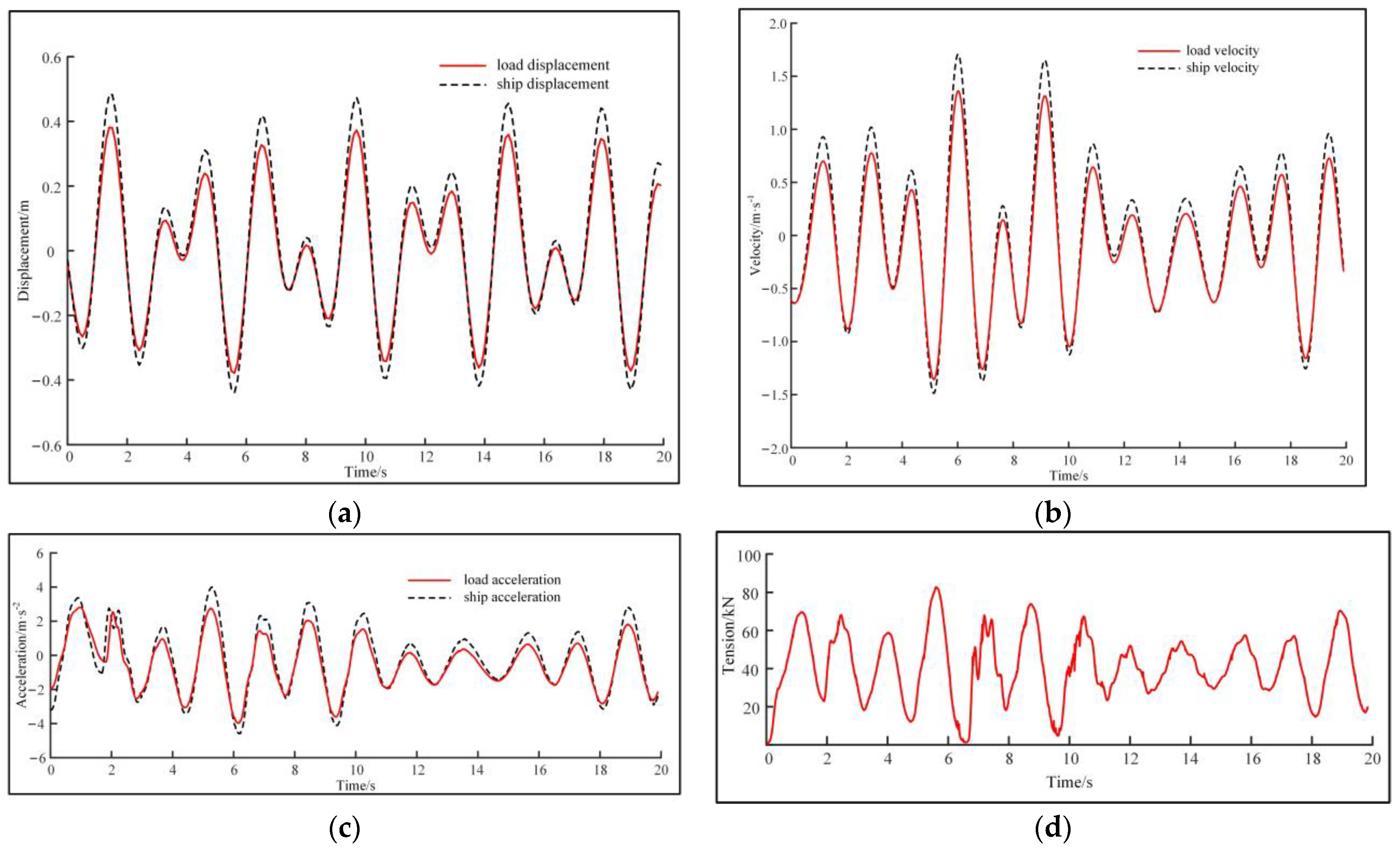
3.2. Simulation and Analysis of AHC System under Level 3 Sea Condition
3.3. Simulation and Analysis of AHC System under Level 4 Sea Condition
4. Conclusions
- (1)
- There are some differences between the results of simulation without AHC and those with AHC function, while this work still has a reliable reference for its ideal effect of AHC function. During the process of modeling and simulation, the launch and recovery system lacking AHC function is easily affected by harsh sea conditions, and the rope is easy to break away from the hoisting sheave. However, the rope runs normally under the effect of the AHC function.
- (2)
- On the whole, the increase of the load and underwater penetration will lead to the increase of the dynamic response of the system. Through the simulation results, it is strongly recommended to choose a light load and short rope in actual maritime operations.
- (3)
- A harsh sea condition will cause an increase of load displacement, load velocity, and load acceleration, as well as rope tension, and brings difficulty to the AHC system. Especially, the results of this work also demonstrate the importance of the AHC function in maritime operations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Woodacre, J.K.; Bauer, R.J.; Irani, R.A. A review of vertical motion heave compensation systems. Ocean Eng. 2015, 104, 140–154. [Google Scholar] [CrossRef]
- Woodacre, J.K.; Bauer, R.J.; Irani, R.A. Hydraulic valve-based active-heave compensation using a model-predictive controller with non-linear valve compensations. Ocean Eng. 2018, 152, 47–56. [Google Scholar] [CrossRef]
- Yu, L.; Wang, S.; Ma, N. Study on wave-induced motions of a turning ship in regular and long-crest irregular waves. Ocean Eng. 2021, 225, 108807. [Google Scholar] [CrossRef]
- Wan, B.; Zhang, G.; Huang, X. Research and development of seafloor shallow-hole multi-coring drill. In Proceedings of the Twentieth International Offshore and Polar Engineering Conference, Beijing, China, 20–25 June 2010; pp. 588–591. [Google Scholar]
- Sorensen, A.J. Structural issues in the design and operation of marine control systems. Annu. Rev. Control 2005, 29, 125–149. [Google Scholar] [CrossRef]
- Nishi, Y. Static analysis of axially moving cables applied for mining nodules on the deep sea floor. Appl. Ocean Res. 2012, 34, 45–51. [Google Scholar] [CrossRef]
- Posiadala, B. Influence of crane support system on motion of the lifted load. Mech. Mach. Theory 1997, 32, 9–20. [Google Scholar] [CrossRef]
- Schellin, T.E.; Jiang, T.; Sharma, S.D. Crane Ship Response to Wave Groups. J. Offshore Mech. Arct. Eng. 1991, 113, 211–218. [Google Scholar] [CrossRef]
- Gu, P.; Walid, A.A.; Iskandarani, Y.; Karimi, H.R. Modeling, simulation and design optimization of a hoisting rig active heave compensation system. Int. J. Mach. Learn. Cybern. 2013, 4, 85–98. [Google Scholar] [CrossRef] [Green Version]
- Masoud, Z.N.; Nayfeh, A.H.; Mook, D.T. Cargo pendulation reduction of ship-mounted cranes. Nonlinear Dyn. 2004, 35, 299–311. [Google Scholar] [CrossRef]
- Ellermann, K. Dynamics of a moored barge under periodic and randomly disturbed excitation. Ocean Eng. 2005, 32, 1420–1430. [Google Scholar] [CrossRef]
- Do, K.D.; Pan, J. Nonlinear control of an active heave compensation system. Ocean Eng. 2008, 35, 558–571. [Google Scholar] [CrossRef] [Green Version]
- Richter, M.; Schaut, S.; Walser, D.; Sawodny, O. Experimental validation of an active heave compensation system: Estimation, prediction and control. Control Eng. Pract. 2017, 66, 1–12. [Google Scholar] [CrossRef]
- Liu, T.; Iturrino, G.; Goldberg, D.; Meissner, E.; Swain, K.; Furman, C.; Fitzgerald, P.; Frisbee, N.; Chlimoun, J.; Van Hyfte, J.; et al. Performance evaluation of active wireline heave compensation systems in marine well logging environments. Geo-Mar. Lett. 2013, 33, 83–93. [Google Scholar] [CrossRef] [Green Version]
- Küchler, S.; Mahl, T.; Neupert, J.; Schneider, K.; Sawodny, O. Active Control for an Offshore Crane Using Prediction of the Vessel’s Motion. IEEE/ASME Trans. Mechatron. 2011, 16, 297–309. [Google Scholar] [CrossRef]
- Cuellar, W.H.; Fortaleza, E. Compact Hydropneumatic Heave Compensator. IFAC Pap. 2015, 48, 189–193. [Google Scholar] [CrossRef]
- Inman, D.J.; Singh, R.G. Engineering Vibration. In Prentice Hall Englewood Cliffs; Prentice-Hall: Englewood Cliffs, NJ, USA, 1994. [Google Scholar]
- Rao, S.S. Mechanical Vibrations; Addison-Wesley Longman Incorporated: Boston, MA, USA, 1986. [Google Scholar]
- Jeans, T.L.; Fagley, C.; Siegel, S.G.; Seidel, J. Irregular deep ocean wave energy attenuation using a cycloidal wave energy converter. Int. J. Mar. Energy 2013, 1, 16–32. [Google Scholar] [CrossRef]
- Pierson, W.J., Jr.; Moskowitz, L. A proposed spectral form for fully developed wind seas based on the similarity theory of SA Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Wang, X.; Liu, B.; Mei, X.; Wang, W.; Duan, W.; Wang, X. An adaptive laser focus auto-positioning method for non-datum complex components based on 3D vision. Opt. Lasers Eng. 2022, 149, 106834. [Google Scholar] [CrossRef]
- Lanni, C.; Ceccarelli, M.; Figliolini, G. An algebraic formulation and experimental analysis of two circular-arc cams. Trans. Can. Soc. Mech. Eng. 2001, 25, 29–49. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, D.; Kai, C.; Feng, C.; De, S. Longitudinal dynamic characteristics of steel wire rope in a friction hoisting system and its coupling effect with friction transmission. Tribol. Int. 2018, 119, 731–743. [Google Scholar] [CrossRef]
- Huang, Q.; Li, Z.; Xue, H. Multi-body dynamics co-simulation of hoisting wire rope. J. Strain Anal. Eng. Des. 2018, 53, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Ma, C.; Yao, J.; Xiao, X.; Di, X.; Jiang, Y. Vibration Analysis of Winding Hoisting System based on ADAMS/Cable. J. Phys. Conf. Ser. 2021, 1750, 012033. [Google Scholar] [CrossRef]
- Imanishi, E.; Nanjo, T.; Kobayashi, T. Dynamic Simulation of Wire Rope with Contact. J. Mech. Sci. Technol. 2009, 23, 1083–1088. [Google Scholar] [CrossRef]
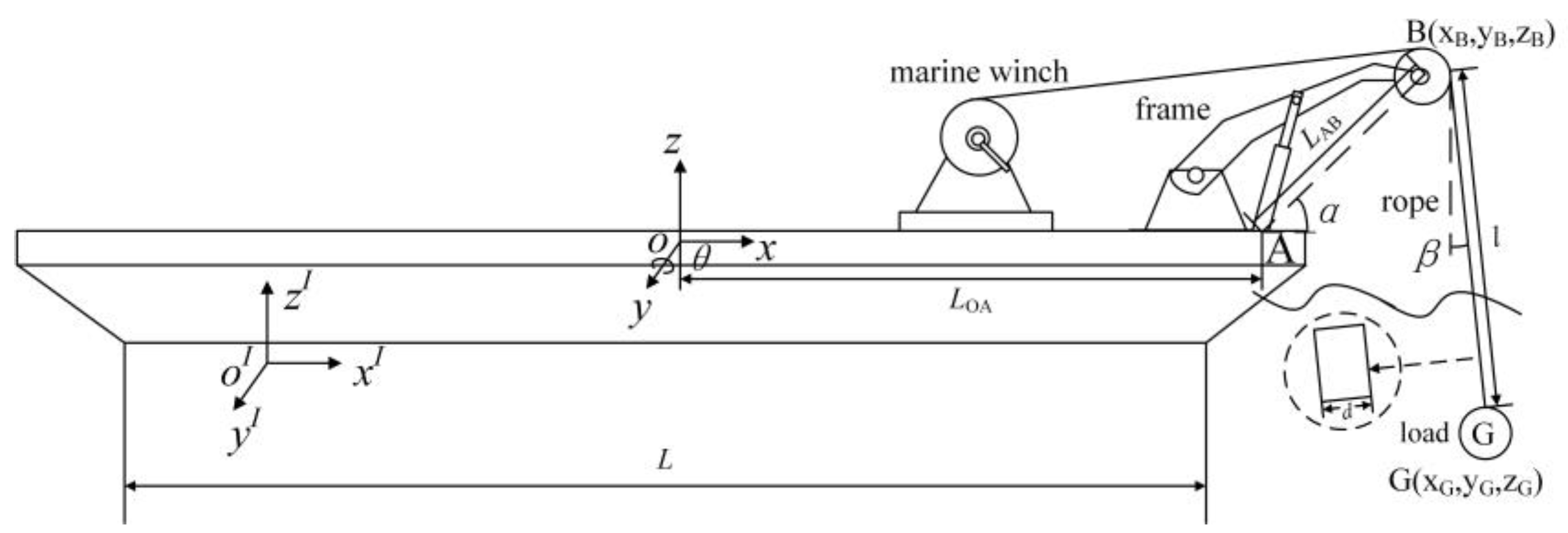



| Parameter | Description | Value | Parameter | Description | Value |
|---|---|---|---|---|---|
| L(m) | Length of ship | 73.3 | Cz | Resistance coefficient along X direction | 0.02 |
| B(m) | Width of ship | 10.2 | LOA(m) | Distance between O and A | 35 |
| d(mm) | Diameter of the rope | 32 | LAB(m) | Distance between A and B | 6 |
| mG(kg) | Quality of the load | 55,000 | V(m3) | Volume of the load | 3.375 |
| l(m) | Length of the rope | 1000 | Sx | Resistance area along X direction | 7.07 |
| Cx | Resistance coefficient along X direction | 1.53 | Sz | Resistance area along Z direction | 7.07 |
| (g/cm3) | Density of seawater | 1.025 | α(°) | Angle between frame and horizon | 45 |
| Cn | Damping coefficient of rope | 0.4 | g(m/s2) | Acceleration of gravity | 9.8 |
| Sea Condition | Object | Displacement (m) | Velocity (m·s−1) | Acceleration (m·s−2) | Tension (kN) |
|---|---|---|---|---|---|
| Level 3 | Ship | −0.48 to +0.50 | −1.50 to +1.70 | −5.0 to +3.9 | / |
| Load | −0.39 to +0.39 | −1.38 to +1.35 | −4.2 to + 2.9 | / | |
| Rope | / | / | / | 0 to +82.0 |
| Parameter | Description | Value | Parameter | Description | Value |
|---|---|---|---|---|---|
| E(N/mm2) | Elastic modulus of the rope | 140,000 | C11(N·s/mm) | Stiffness coefficient of the segments | 1 |
| Gr(GPa) | Shear modulus of the rope | 80 | C22(N·s/mm) | Stiffness coefficient of the segments | 1 |
| A(mm2) | Cross-sectional area of the segments | 804.25 | C33(N·s/mm) | Stiffness coefficient of the segments | 1 |
| R(mm) | Radius of the segments | 16 | C44(N·s/mm) | Stiffness coefficient of the segments | 10 |
| Lr(mm) | Length of the segments | 100 | C55(N·s/mm) | Stiffness coefficient of the segments | 10 |
| / | / | / | C66(N·s/mm) | Stiffness coefficient of the segments | 10 |
| Parameters | Descriptions | Values |
|---|---|---|
| Kc(N/m) | Stiffness coefficient of contact | 15,000 |
| xc(mm) | Penetration depth of objects | 0.1 |
| e | Nonlinear collision index | 1.5 |
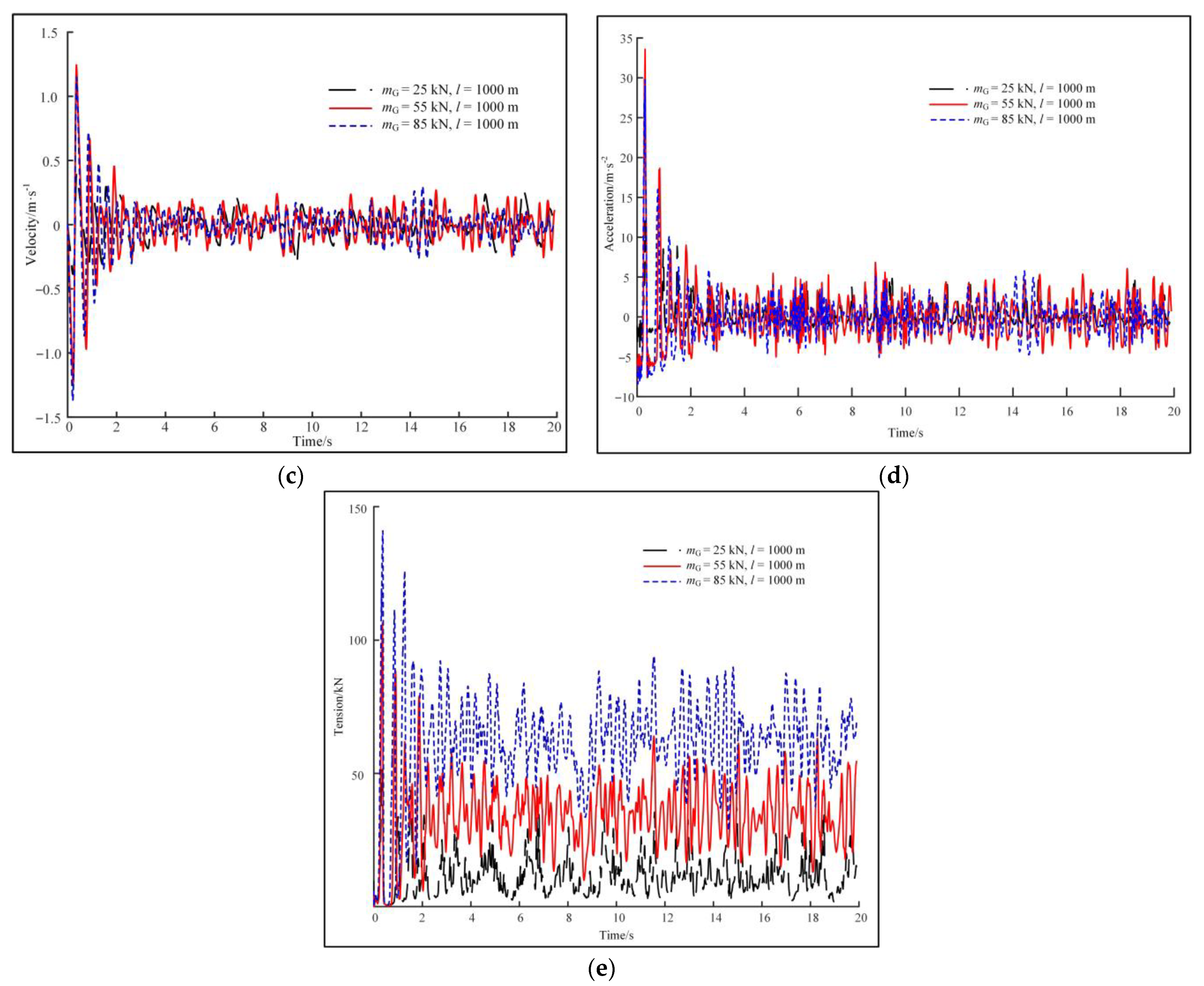
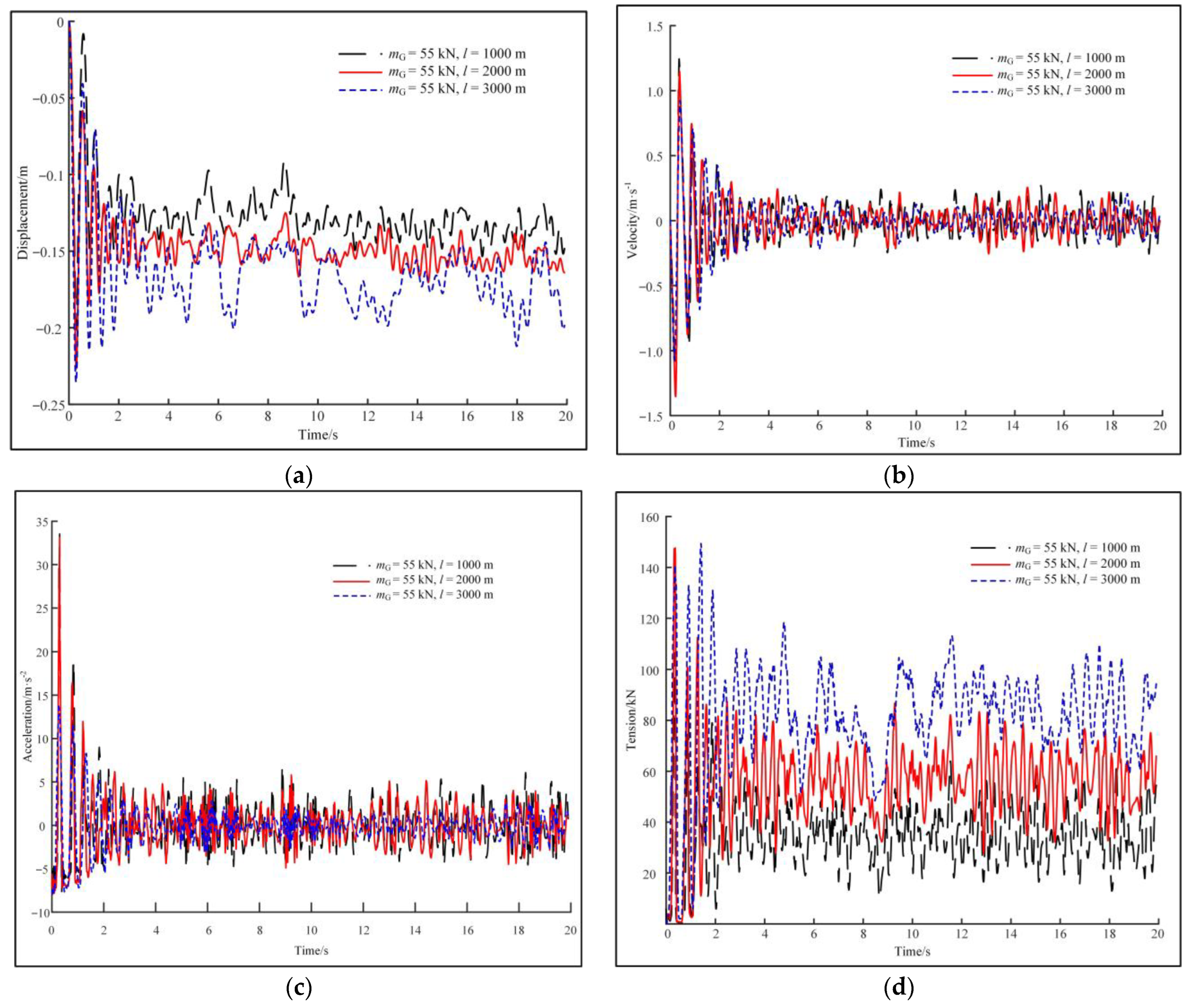
| Sea Condition | Subcondition | Load Displacement (m) | Load Velocity (m·s−1) | Load Acceleration (m·s−2) | Rope Tension (kN) |
|---|---|---|---|---|---|
| Level 3 | mG = 25 kN, l = 1000 m | −0.10 to 0 | −0.50 to +0.50 | −3.50 to +10.90 | 0 to +30 |
| mG = 55 kN, l = 1000 m | −0.20 to 0 | −1.20 to +1.25 | −7.50 to +33.70 | 0 to +105 | |
| mG = 85 kN, l = 1000 m | −0.25 to 0 | −1.40 to +1.20 | −8.50 to +29.3 | 0 to +140 | |
| mG = 55 kN, l = 2000 m | −0.225 to 0 | −1.45 to +1.10 | −7.80 to +34.0 | 0 to +146 | |
| mG = 55 kN, l = 3000 m | −0.235 to 0 | −1.10 to +0.95 | −8.00 to +14.8 | 0 to +148 | |
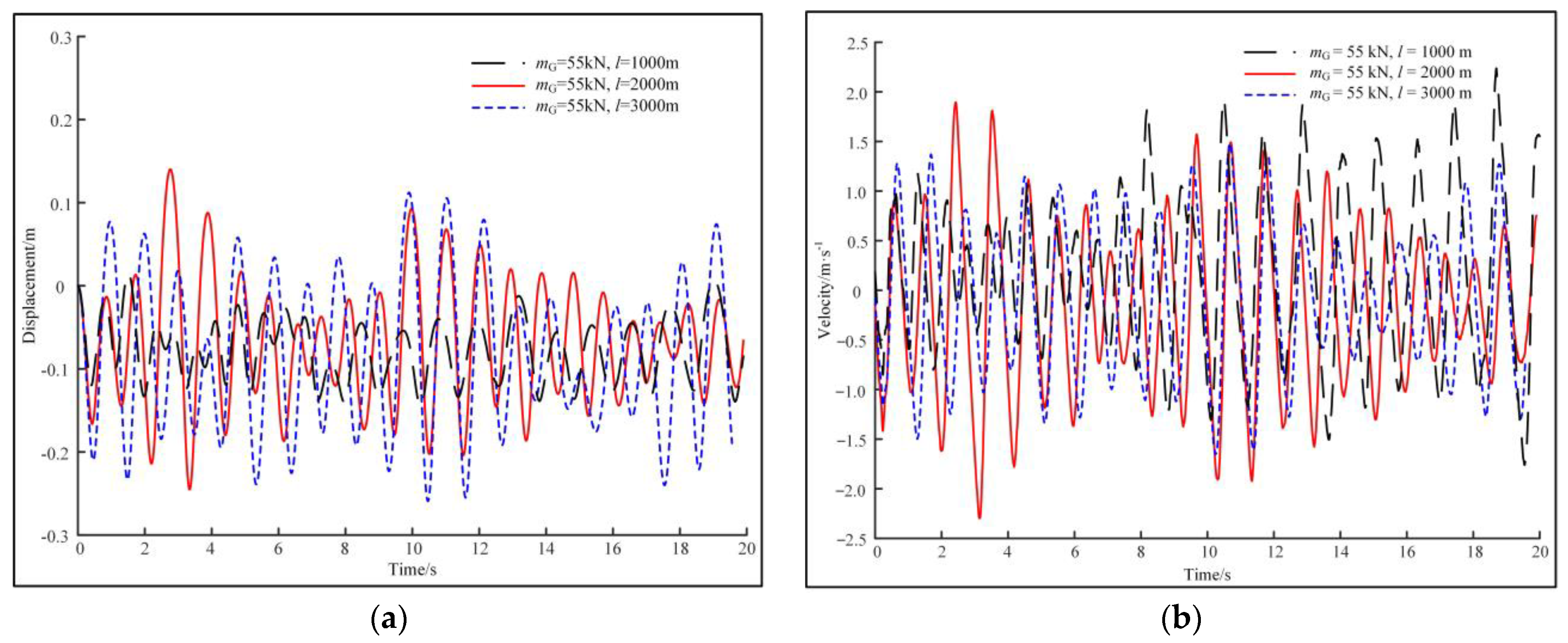
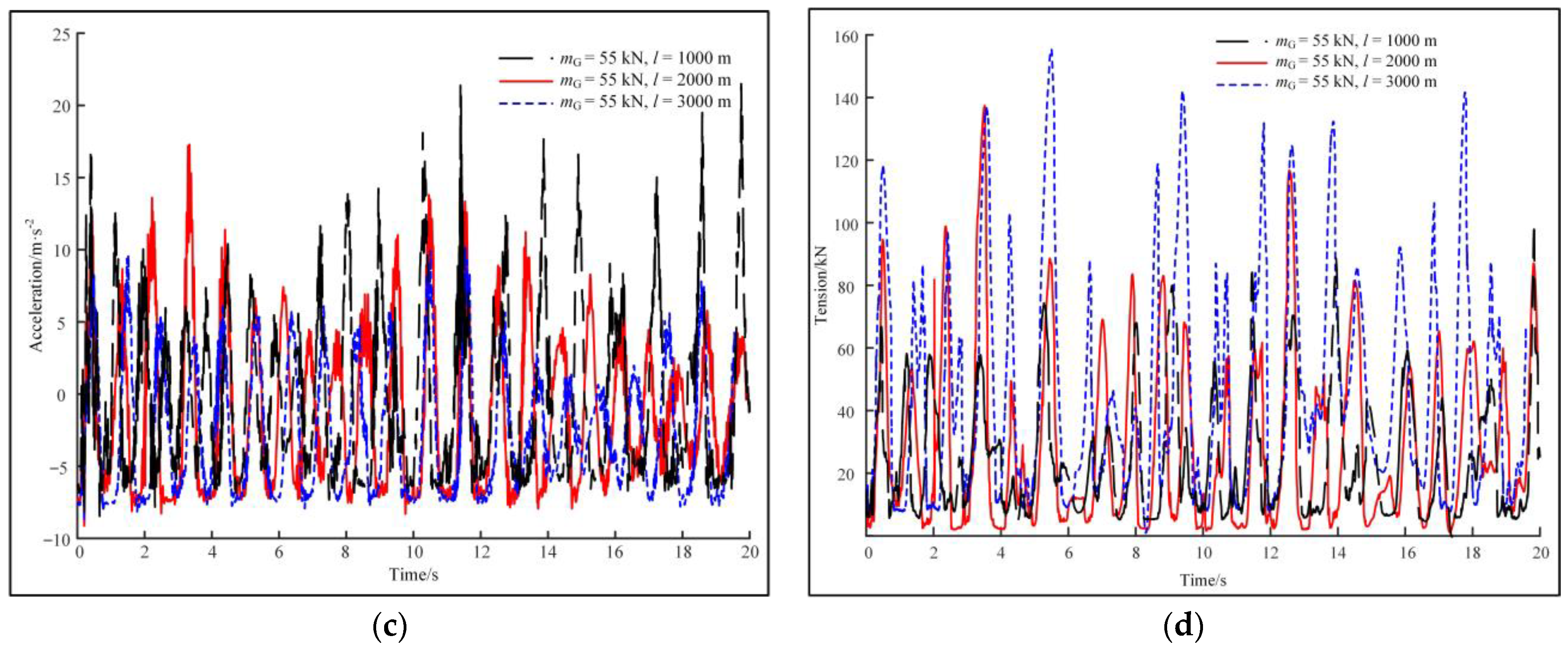
| Level 4 | mG = 25 kN, l = 1000 m | 0 to +0.13 | −0.36 to +0.37 | −9.60 to +4.90 | 0 to +31 |
| mG = 55 kN, l = 1000 m | −0.13 to +0.02 | −1.98 to +2.05 | −9.80 to +22.3 | 0 to +92 | |
| mG = 85 kN, l = 1000 m | −0.32 to +0.11 | −1.99 to +2.10 | −9.20 to +21.5 | 0 to +119 | |
| mG = 55 kN, l = 2000 m | −0.24 to +0.04 | −1.87 to +1.88 | −9.50 to +17.5 | 0 to +138 | |
| mG = 55 kN, l = 3000 m | −0.26 to +0.11 | −1.31 to +1.50 | −7.40 to +10.3 | 0 to +155 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, T.; Huang, L.; Xu, J.; Guo, Y.; Ou, Y. Dynamic Analysis of Active Heave Compensation System for Marine Winch under the Impact of Irregular Waves. J. Mar. Sci. Eng. 2023, 11, 240. https://doi.org/10.3390/jmse11020240
Xie T, Huang L, Xu J, Guo Y, Ou Y. Dynamic Analysis of Active Heave Compensation System for Marine Winch under the Impact of Irregular Waves. Journal of Marine Science and Engineering. 2023; 11(2):240. https://doi.org/10.3390/jmse11020240
Chicago/Turabian StyleXie, Tiancai, Liangpei Huang, Jingwei Xu, Yong Guo, and Yun Ou. 2023. "Dynamic Analysis of Active Heave Compensation System for Marine Winch under the Impact of Irregular Waves" Journal of Marine Science and Engineering 11, no. 2: 240. https://doi.org/10.3390/jmse11020240
APA StyleXie, T., Huang, L., Xu, J., Guo, Y., & Ou, Y. (2023). Dynamic Analysis of Active Heave Compensation System for Marine Winch under the Impact of Irregular Waves. Journal of Marine Science and Engineering, 11(2), 240. https://doi.org/10.3390/jmse11020240






