Comparative Study on Numerical Simulation of Wave-Current Nonlinear Interaction Based on Improved Mass Source Function
Abstract
:1. Introduction
2. Numerical Models
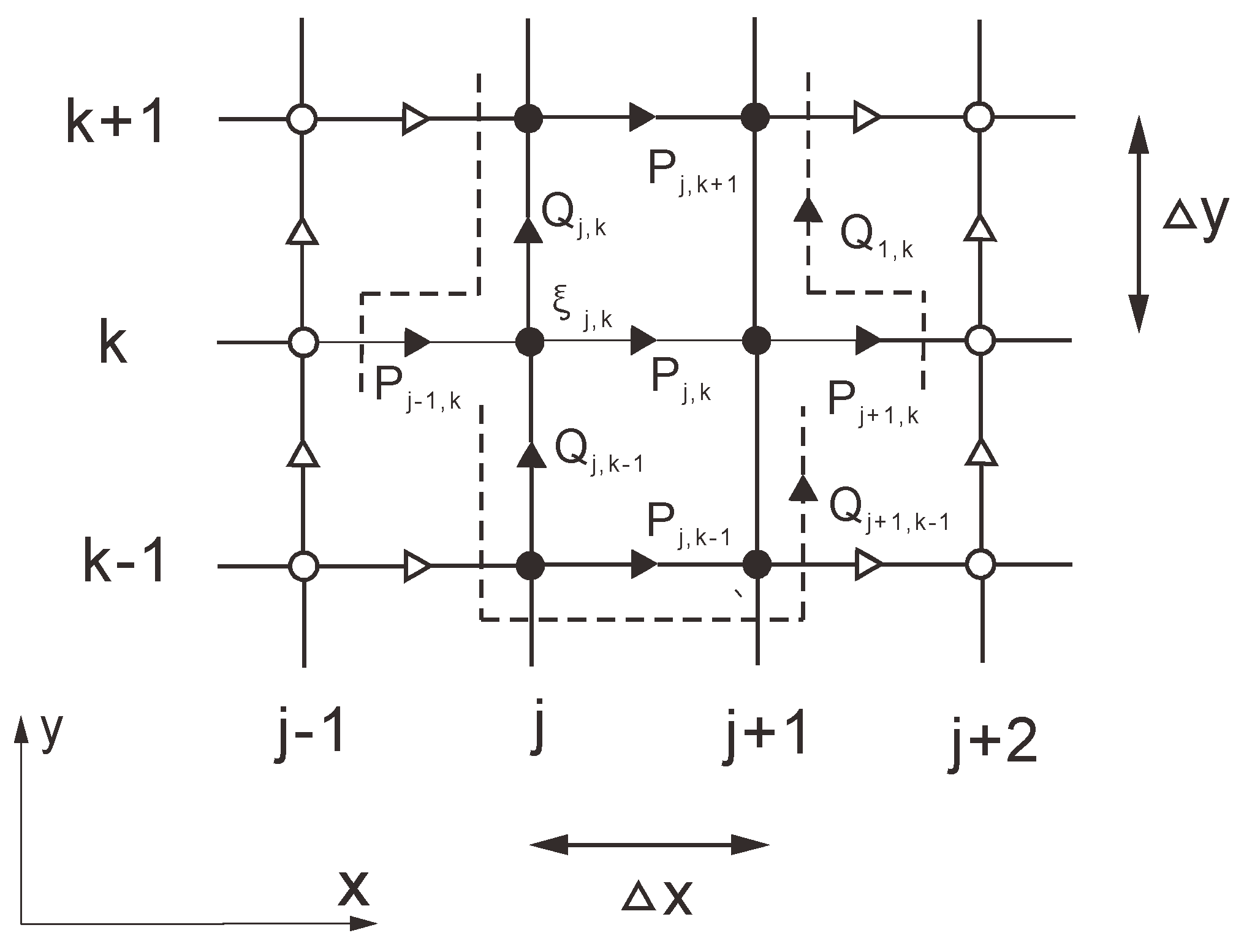
2.1. Control Equations and Solution Methods for the MIKE 21 BW Two-Dimensional Model
2.2. Numerical Model and Solution of the Navier–Stokes Equation
- has the following three values:
- : No phase fluid in the unit.
- : The unit is filled with phase fluid.
- : This unit is the intersection of phase liquid and other liquids.
3. Research Methods
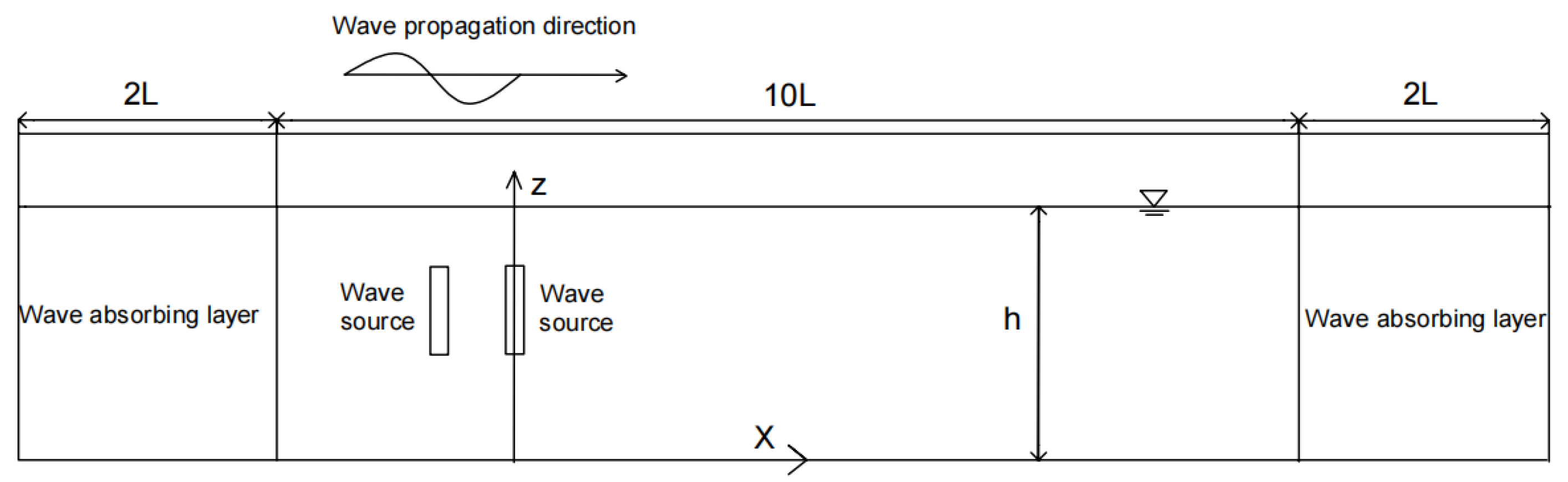
3.1. Mass Source Wave-Generation Method
3.2. Single-Frequency Waveform Generation
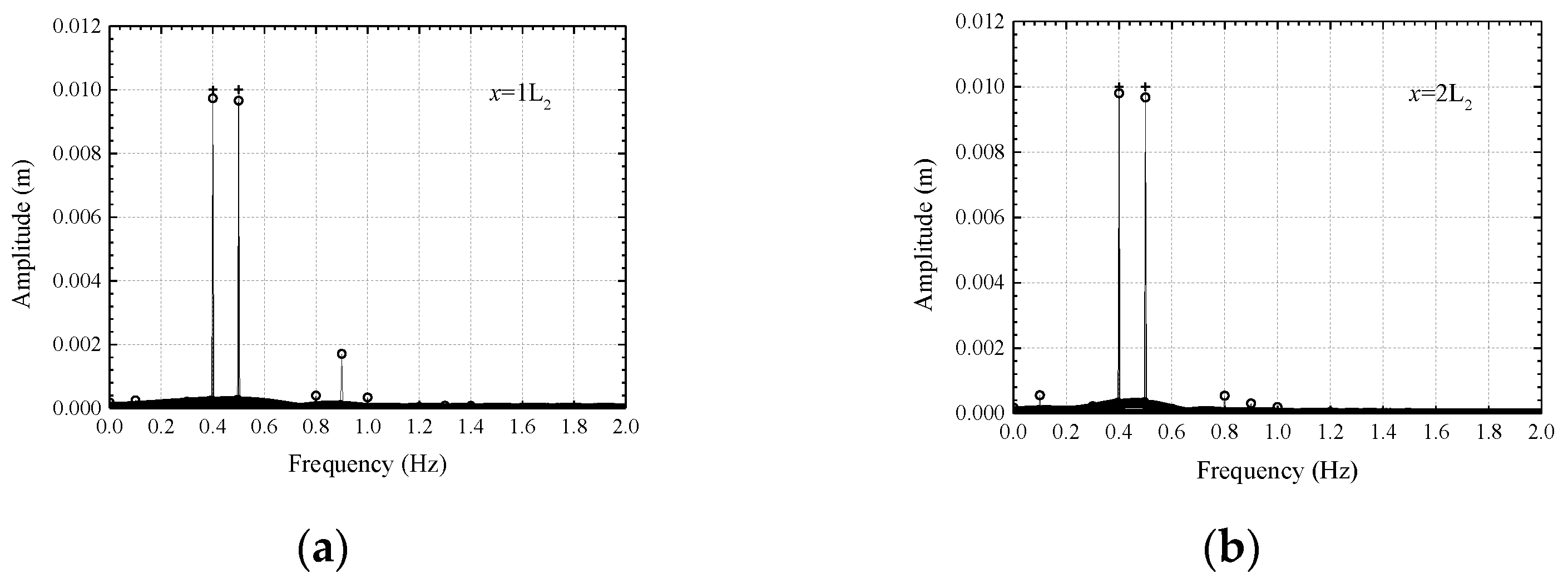
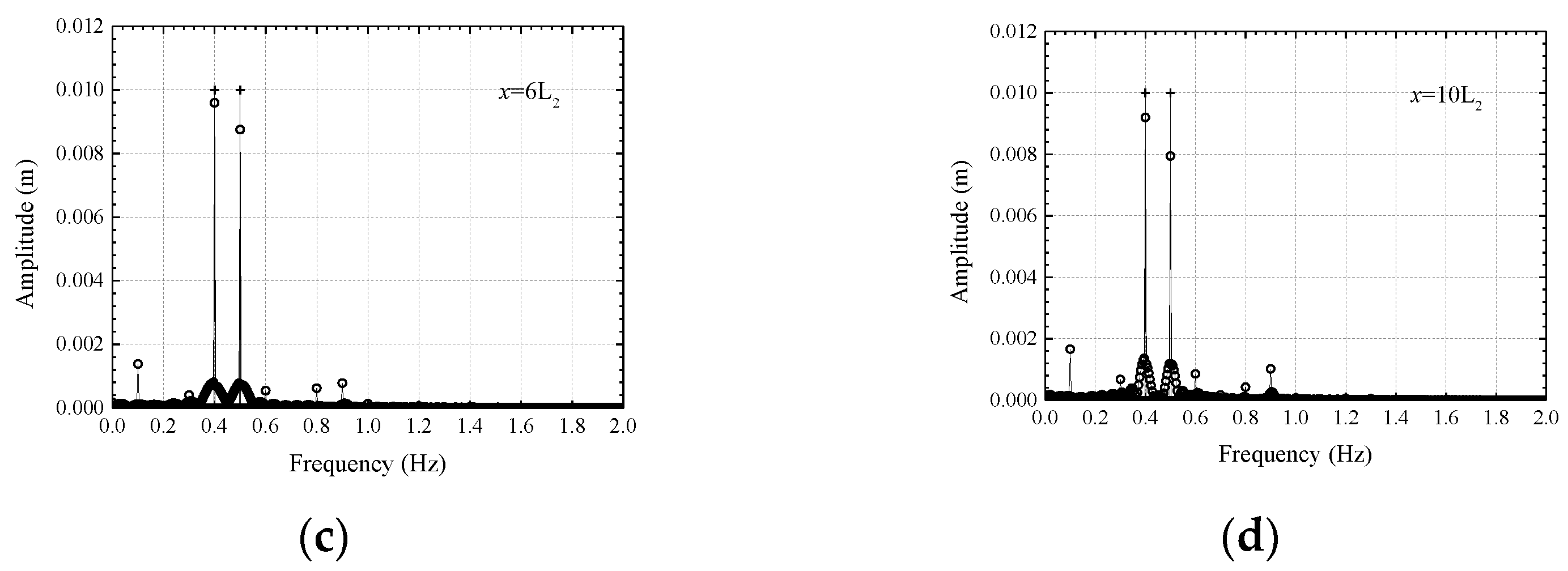
3.3. Interaction between Dual-Frequency Wave Generation and Wave-Current
3.4. Numerical Wave Elimination Methods
3.4.1. Numerical Extinction of the MIKE 21 BW Model
3.4.2. Numerical Wave Dissipation for the Navier–Stokes Equation Wave Model
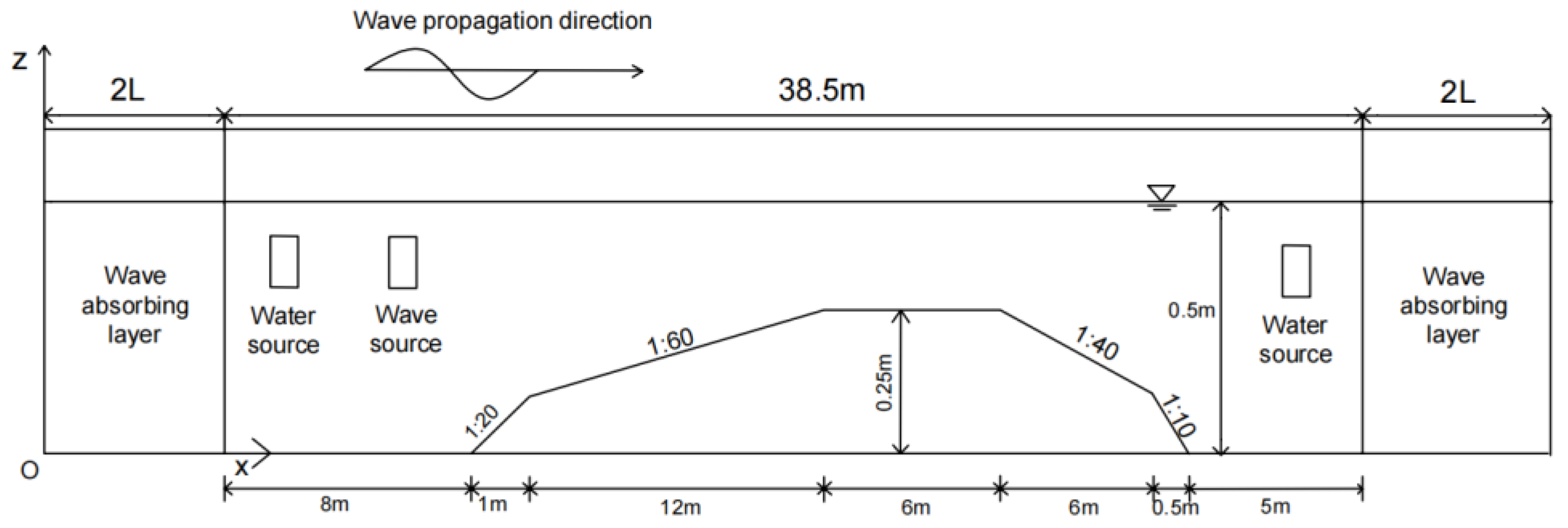
4. Numerical Simulation and Comparative Verification
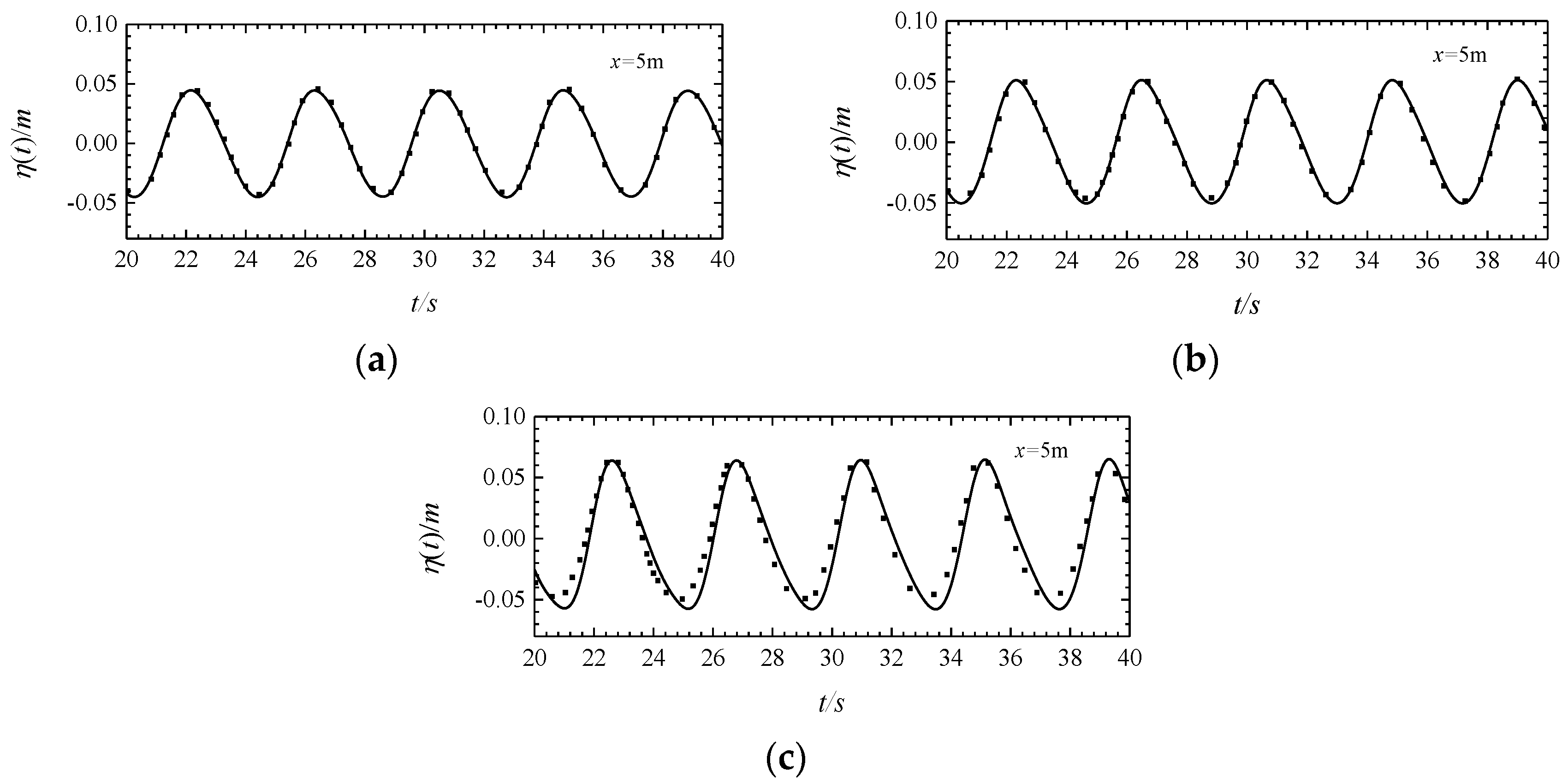
4.1. Wave-Wave Interactions
4.1.1. Numerical Extinction of the MIKE 21 BW Model
4.1.2. Comparison of the MIKE21 BW and Navier–Stokes Models
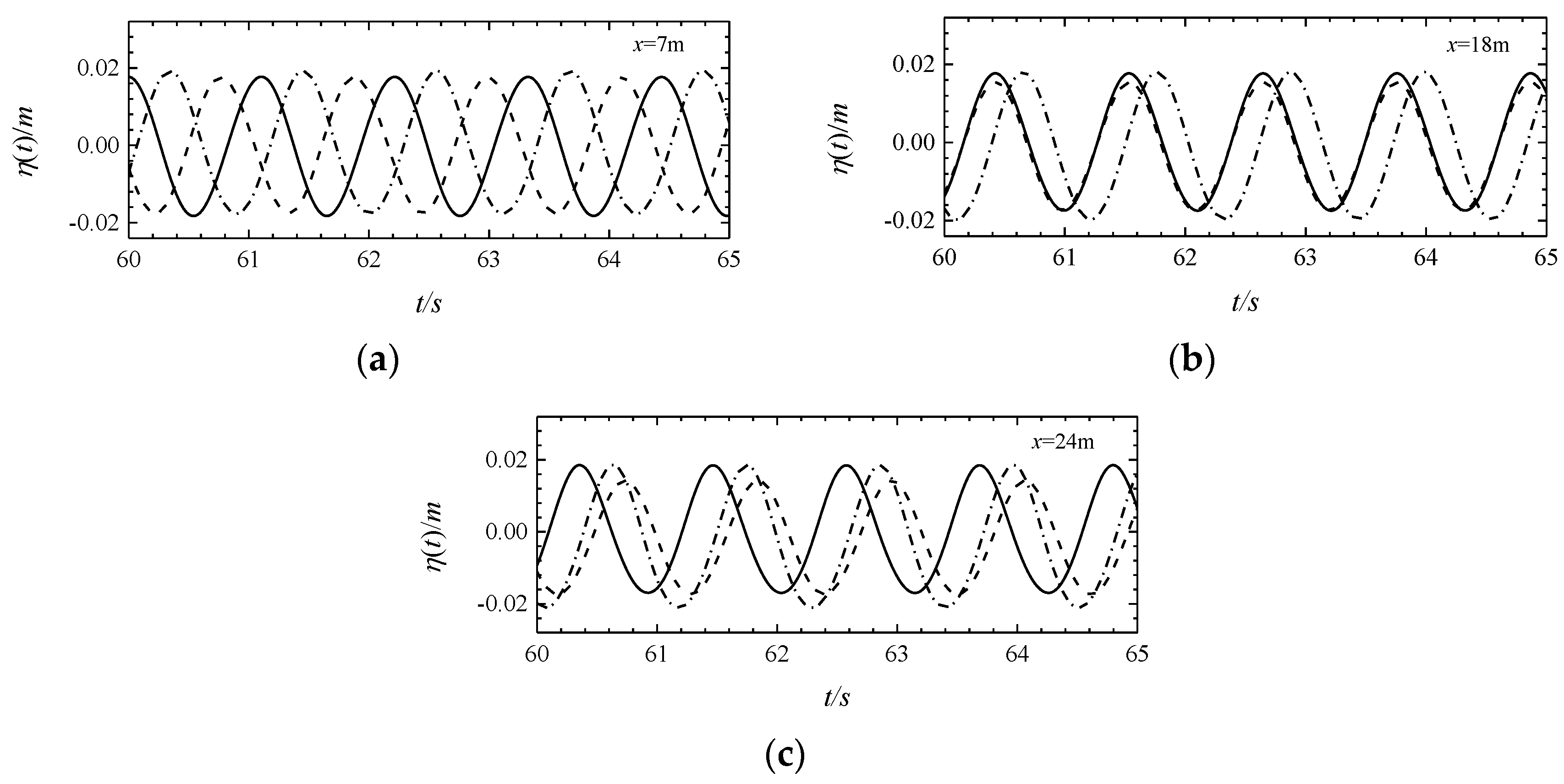
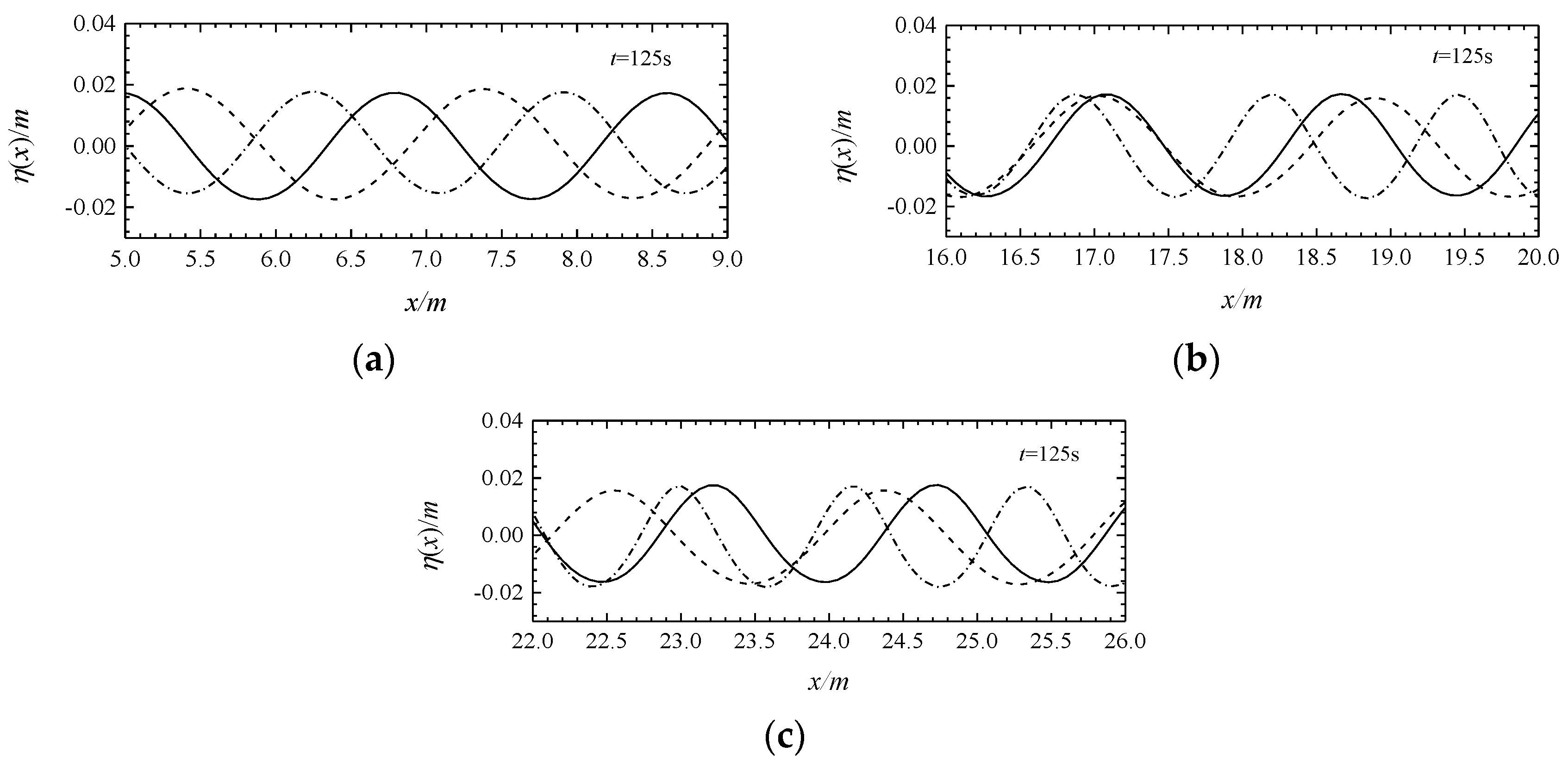
4.2. Wave-Current Interactions
4.2.1. Numerical Simulation of Wave-Current Interactions at a Uniform Water Depth
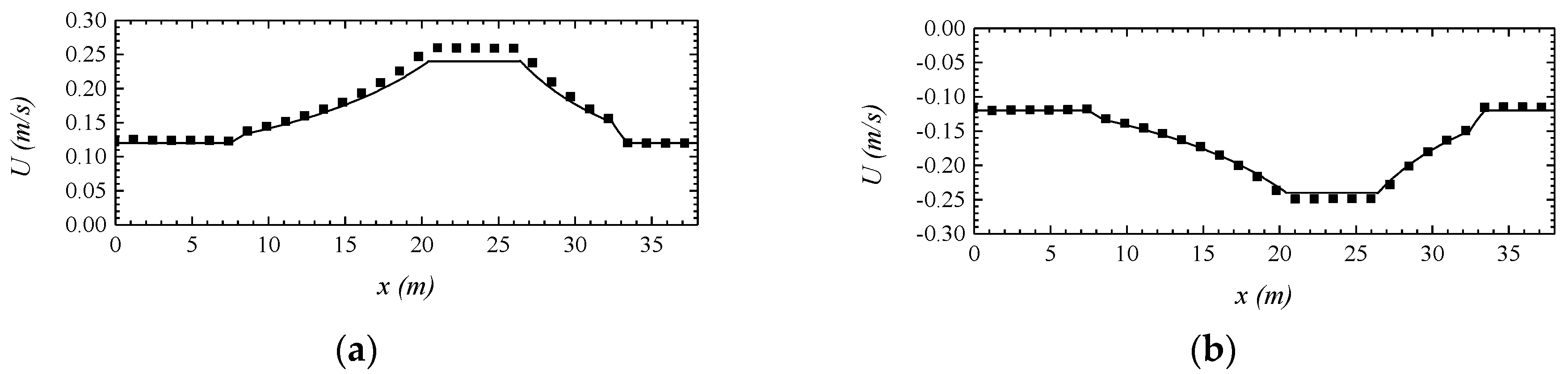
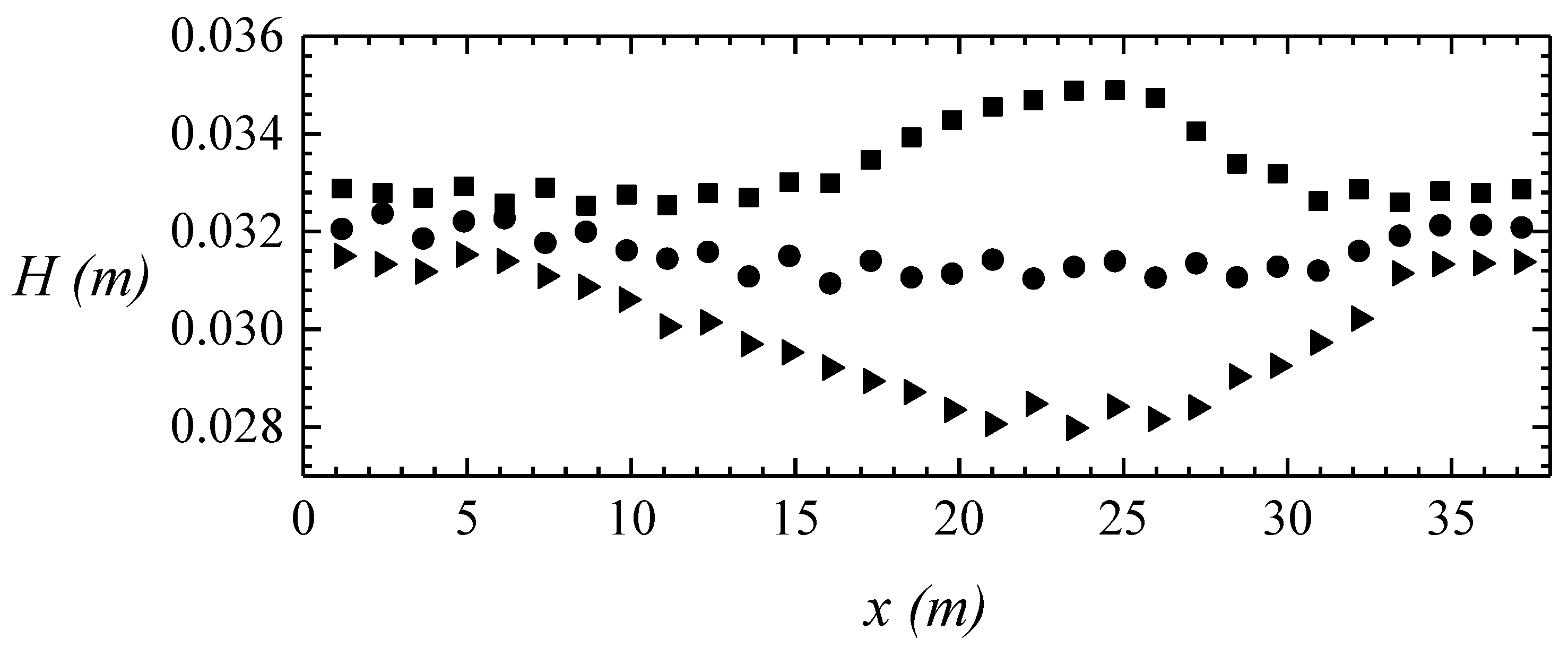
4.2.2. Numerical Simulation of Wave-Flow Interactions in Submerged Dike Topography
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Longuet-Higgins, M.S.; Stewart, R.W. Changes in the form of short gravity waves on long waves and tidal currents. J. Fluid Mech. 1960, 8, 565–583. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation stresses in water wave; a physical discussion with application. Deep Sea Res. 1964, 4, 529–562. [Google Scholar] [CrossRef]
- Hughes, B.A.; Stewart, R.W. Interaction between gravity waves and a shear flow. J. Fluid Mech. 1961, 10, 385–400. [Google Scholar] [CrossRef]
- Tao, W.; Jiachun, L. Research progress of wave current interaction. Adv. Mech. 1999, 3, 331–343. [Google Scholar]
- Jonsson, I.G. 3.2-Combinations of Waves and Currents. Dev. Geotech. Eng. 1978, 23, 162–203. [Google Scholar] [CrossRef]
- Jonsson, I.G. Wave action flux: A physical interpretation. J. Fluid Mech. 1998, 368, 155–164. [Google Scholar] [CrossRef]
- Brevik, I.; Bjørn, A. Flume experiment on waves and currents. I. Rippled bed. Coast. Eng. 1979, 3, 149–177. [Google Scholar] [CrossRef]
- Brevik, I. Flume experiment on waves and currents II. Smooth bed. Coast. Eng. 1980, 4, 89–110. [Google Scholar] [CrossRef]
- Li, Y.; Herbich, J.B. Effect of wave-current interaction on the wave parameter. In Proceedings of the 18th Conference on Coastal Engineering, Cape Town, South Africa, 14–19 November 1982. [Google Scholar] [CrossRef]
- Swan, C.; Cummins, I.P.; James, R.L. An experimental study of two-dimensional surface water waves propagating on depth-varying currents. Part 1. Regular waves. J. Fluid Mech. 2001, 428, 273–304. [Google Scholar] [CrossRef]
- Lian, J.J.; Zhao, Z.D. Velocity distribution of full depth water flow in wave current coexistence field. Mar. Bull. 1994, 3, 1–10. [Google Scholar]
- Alfonsi, G.; Lauria, A.; Primavera, L. The field of flow structures generated by a wave of viscous fluid around vertical circular Cylinder Piercing the Free Surface. Process. Eng. 2015, 116, 103–110. [Google Scholar] [CrossRef] [Green Version]
- Dong, G.; Fu, R.; Ma, Y.; Fang, K. Simulation of unidirectional propagating wave trains in deep water using a fully non-hydrostatic model. Ocean Eng. 2019, 180, 254–266. [Google Scholar] [CrossRef]
- Ai, C.F.; Ma, Y.X.; Yuan, C.F.; Dong, G.H. Development and assessment of semi-implicit nonhydrostatic models for surface water waves. Ocean Modell. 2019, 144, 101489. [Google Scholar] [CrossRef]
- Ruffini, G.; Briganti, R.; Alsina, J.M.; Brocchini, M.; Dodd, N.; McCall, R. Numerical modelling of flow and bed evolution of bichromatic wave groups on an intermediate beach using nonhydrostatic xbeach. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 04019034. [Google Scholar] [CrossRef]
- Thomas, G.P. Wave-current interactions: An experimental and numerical study. Part 1. Linear waves. J. Fluid Mech. 1981, 110, 457–474. [Google Scholar] [CrossRef]
- Thomas, G.P. Wave-current interactions: An experimental and numerical study. Part 2. Nonlinear waves. J. Fluid Mech. 1990, 216, 505–536. [Google Scholar] [CrossRef]
- Wolf, J.; Prandle, D. Some observations of wave–current interaction. Coast. Eng. 1999, 37, 471–485. [Google Scholar] [CrossRef]
- Sørensen, O.R.; Kofoed-Hansen, H.; Jones, O.P. Numerical modeling of wave-current interaction in tidal areas using an unstructured finite volume technique. Coastal Eng. 2007, 1, 653. [Google Scholar] [CrossRef]
- Baschek, B. Wave-current interaction in tidal fronts. In 14th ‘Aha Huliko’a Winter Workshop 2005: Rogue Waves; Muller, P., Garrett, C., Eds.; Honolulu, HI, USA, 2005; pp. 131–138. Available online: http://www.soest.hawaii.edu/PubServices/2005pdfs/Baschek.pdf (accessed on 22 November 2022).
- Yan, Y.X. Mathematical model of wave current interaction in tidal estuary area. Ocean. Eng. 1989, 3, 47–56. [Google Scholar]
- Li, Y.C.; Zhang, Y.G. Theoretical study of nonlinear wave current interaction using Boussinesq equation. Res. Dev. Hydrodyn. Part A 1996, 2, 205–211. [Google Scholar]
- Chen, Q.; Madsen, P.A.; Schäffer, H.A.; Basco, D.R. Wave-current interaction based on an enhanced Boussinesq approach. Coast. Eng. 1998, 33, 11–39. [Google Scholar] [CrossRef]
- Zou, Z.L.; Hu, P.C.; Fang, K.Z.; Liu, Z.B. Boussinesq-type equations for wave–current interaction. Wave Motion 2013, 50, 655–675. [Google Scholar] [CrossRef]
- Wang, Y.L.; Zhang, H.S. Numerical simulation of nonlinear wave propagation in non-uniform flow. J. Mech. 2007, 6, 732–740. [Google Scholar]
- Zhang, H.S.; Zhao, H.J.; Ding, P.X.; Miao, G.P. Wave propagation deformation in non-uniform flow waters. J. Mech. 2007, 3, 325–332. [Google Scholar]
- Hong, G.W.; Feng, W.B.; Zhang, H.S. Numerical simulation of wave propagation in coastal and estuarine waters. J. Hohai Univ. Nat. Sci. Ed. 1999, 2, 4–12. [Google Scholar]
- Wu, Y.S.; Lian, J.J.; Wang, Z.Y.; Zhang, Q.H. Wave current interaction model. Water Resour. 2002, 04, 13–17. [Google Scholar]
- Liu, Y.Z.; Shi, Z. Mathematical model of wave current interaction in estuaries. Mar. Sci. 2001, 05, 42–46. [Google Scholar]
- Teles, M.J.; Pires-Silva, A.A.; Benoit, M. Numerical modelling of wave current interactions at a local scale. Ocean Modell. 2013, 68, 72–87. [Google Scholar] [CrossRef]
- Li, H.T.; Zhou, E.X.; Gou, J.F.; Ha, J.Q.; Liu, Y.F.; Wang, G.; Qin, L.R.; Li, H.H. Research on wave making method for numerical simulation of bichromatic wave. Water Conserv. Hydropower Technol. 2019, 50, 155–166. [Google Scholar]
- Brorsen, M.; Larsen, J. Source generation of nonlinear gravity waves with the boundary integral equation method. Coast. Eng. 1987, 11, 93–113. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P.L.-F. Internal wave-maker for Navier–Stokes equations models. J. Waterw. Port Coastal Ocean Eng. 1999, 125, 207–215. [Google Scholar] [CrossRef]
- Wei, G.; Kirby, J.T.; Sinha, A. Generation of waves in Boussinesq models using a source function method. Coast. Eng. 1999, 36, 271–299. [Google Scholar] [CrossRef]
- Chen, M.Y.; Zhang, H.S.; Zhou, E.X.; Xu, D. Numerical bichromatic wave generation using designed mass source function. J. Math. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Ha, T.; Lin, P.; Cho, Y. Generation of 3D regular and irregular waves using Navier–Stokes equations model with an internal wave maker. Coast. Eng. 2013, 76, 55–67. [Google Scholar] [CrossRef]
- Li, B.X.; Yu, L.X.; Zhang, N.C. Establishment and application of a numerical two-dimensional random wave flume. Mar. Bull. 2004, 5, 1–9. [Google Scholar]
- Gao, X.P.; Zeng, G.D.; Zhang, Y. Wave creation and damped wave dissipation in irregular wave value flumes. J. Oceanogr. 2002, 2, 127–132. (In Chinese) [Google Scholar]
- Wang, X.; Lin, Z.Y.; You, Y.X. Numerical wave generation methods for internally isolated wave mass sources in two-layer fluids. J. Shanghai Jiaotong Univ. 2014, 6, 850–855. [Google Scholar]
- Ning, D.Z.; Teng, B.; Zhou, B.Z.; Liu, Z. Application of the source wave creation method to a three-dimensional fully non-linear numerical wave flume. J. Dalian Marit. Univ. 2008, 2, 1–5. [Google Scholar]
- Gobbi, M.F.; Kirby, J.T. Wave evolution over submerged sills: Tests of a high-order Boussinesq model. Coast. Eng. 1999, 37, 57–96. [Google Scholar] [CrossRef]
- Andrzej, M. Energy conserving numerical solutions of simplified turbulence equations. Math. Tech. Report. 1990, 1175–1180. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Fonseca, R.B.; Guedes Soares, C. Comparison of analytical and numerical simulations of long no linear internal solitary waves in shallow water. J. Coastal. Res. 2018, 34, 928–938. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Gadelho, J.F.M.; Guedes Soares, C. Effect of interfacial tension on internal waves based on Bousinesq equations in two-layer fluids. J. Coastal. Res. 2019, 35, 445–462. [Google Scholar] [CrossRef]
- Dinvay, E. Well-posedness for a Whitham–Boussinesq system with surface tension. Math. Phys. Anal. Geom. 2020, 23, 1–27. [Google Scholar] [CrossRef]
- Karaagac, B.; Ucar, Y.; Esen, A. Dynamics of modified improved Boussinesq equation via Galerkin finite element method. Math. Meth. Appl. Sci. 2020, 43, 1–17. [Google Scholar] [CrossRef]
- Yao, S.W.; Islam, M.E.; Akbar, M.A.; Inc, M.; Adel, M.; Osman, M.S. Analysis of parametric effects in the wave profile of the variant Boussinesq equation through two analytical approaches. Open Phys. 2022, 20, 778–794. [Google Scholar] [CrossRef]
- Fang, K.Z.; Liu, Z.B.; Wang, P.; Wu, H.; Sun, J.W.; Yin, J. Modeling solitary wave propagation and transformation over complex bathymetries using a two-layer Boussinesq model. Ocean. Eng. 2022, 265, 112549. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Part 2. A slowly-varying bathymetry. Coast. Eng. 1992, 18, 183–204. [Google Scholar] [CrossRef]
- Madsen, P.A.; Murray, R.; Sørensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Coast. Eng. 1991, 15, 371–388. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.R.; Schäffer, H.A. Surf zone dynamics simulated by a Boussinesq type model. Part I: Model description and cross-shore motion of regular waves. Coast. Eng. 1997, 32, 255–288. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.R.; Schäffer, H.A. Surf zone dynamics simulated by a Boussinesq type model. Part II: Surf beat and swash zone oscillations for wave groups and irregular waves. Coast. Eng. 1997, 32, 289–320. [Google Scholar] [CrossRef]
- Sørensen, O.R.; Schäffer, H.A.; Madsen, P.A. Surf zone dynamics simulated by a Boussinesq type model. Part III: Wave-induced horizontal nearshore circulations. Coast. Eng. 1998, 33, 155–176. [Google Scholar] [CrossRef]
- Sørensen, O.R.; Schäffer, H.A.; Sørensen, L.S. Boussinesq-type modelling using an unstructured finite element technique. Coast. Eng. 2004, 50, 181–198. [Google Scholar] [CrossRef]
- Ning, D.Z.; Chen, L.F.; Tian, H.G. Fully non-linear numerical flume model for wave-flow mixing action. J. Harbin Eng. Univ. 2010, 11, 1450–1455. [Google Scholar]

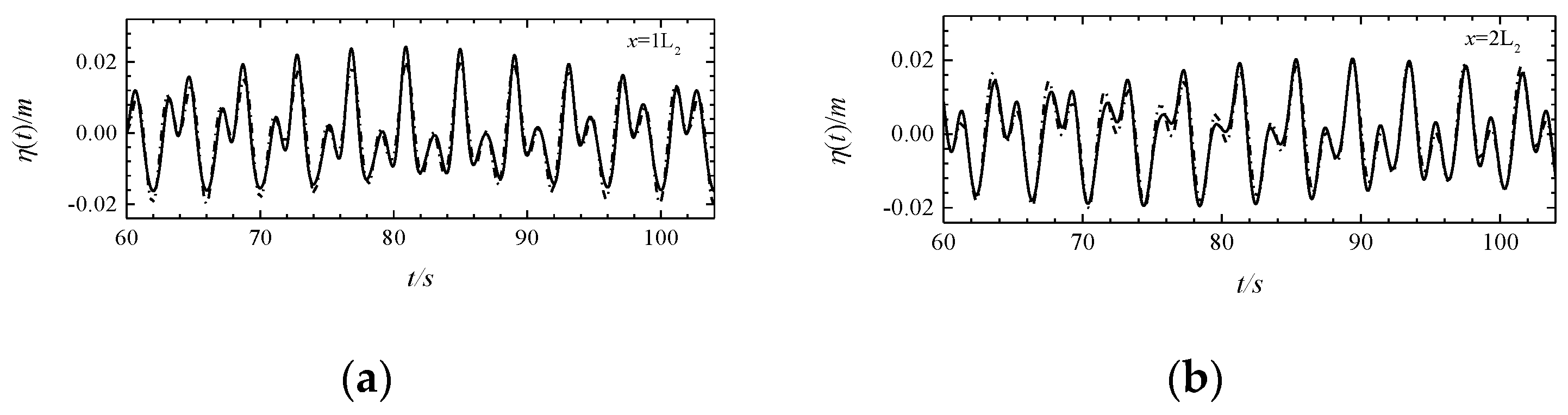
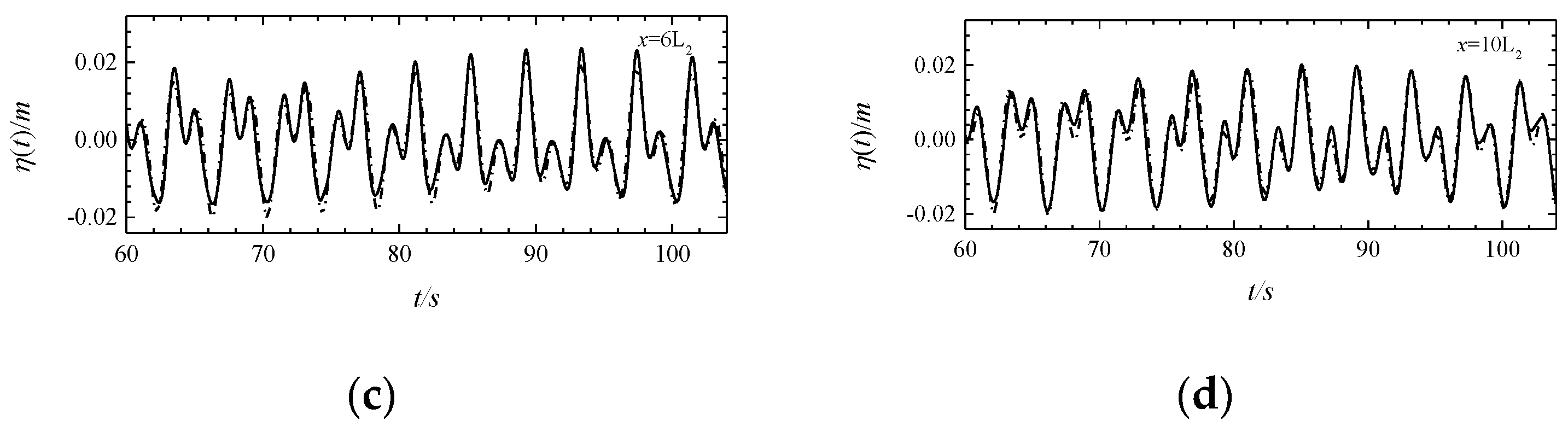
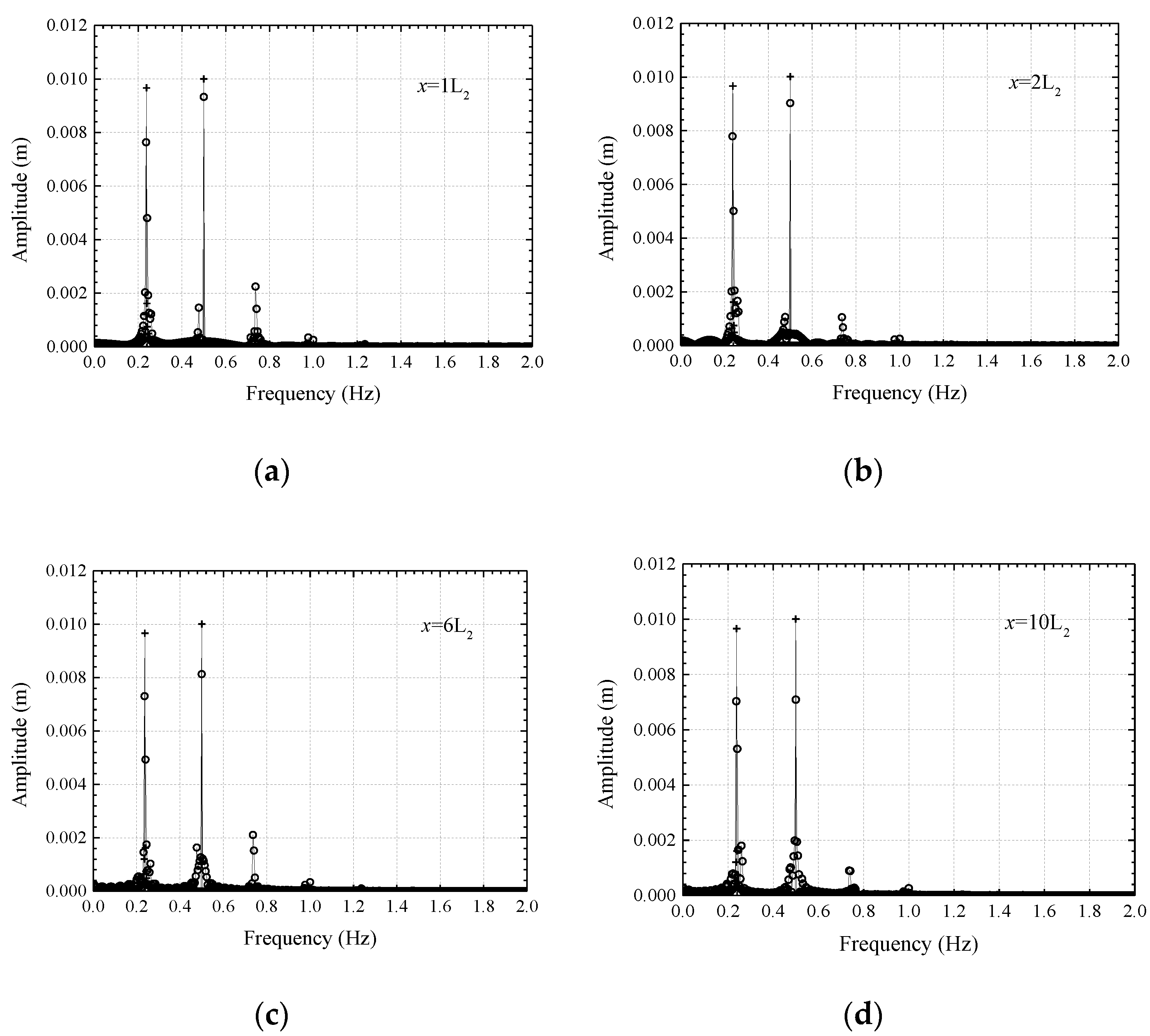
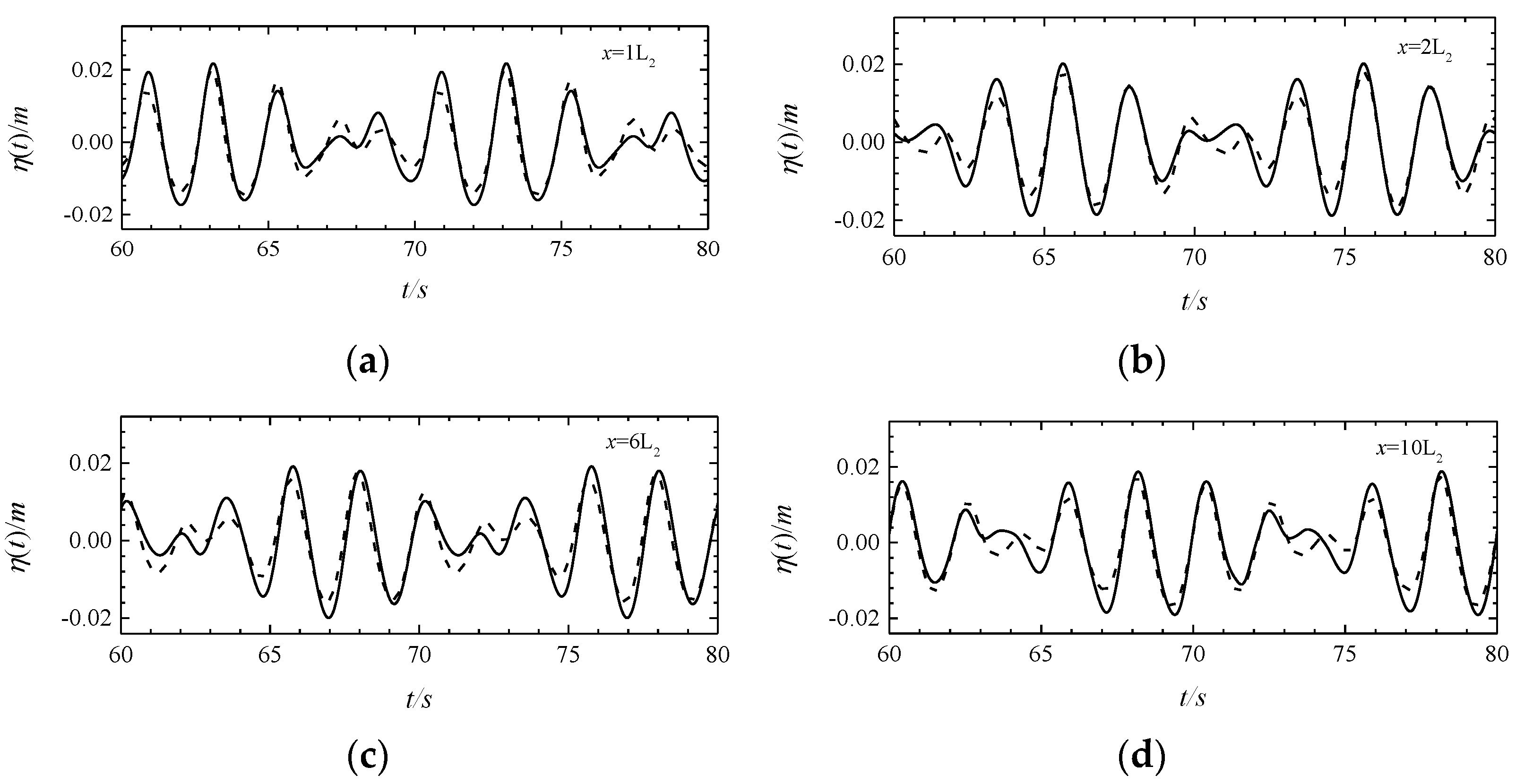






| Wave 1 | Wave 2 | |||||
|---|---|---|---|---|---|---|
| T1/s | L1/m | μ1 | T2/s | L2/m | μ2 | |
| C1 | 2 | 3.88 | 0.12 | 2.5 | 5.00 | 0.090 |
| C2 | 2 | 3.88 | 0.12 | 4.2 | 8.67 | 0.052 |
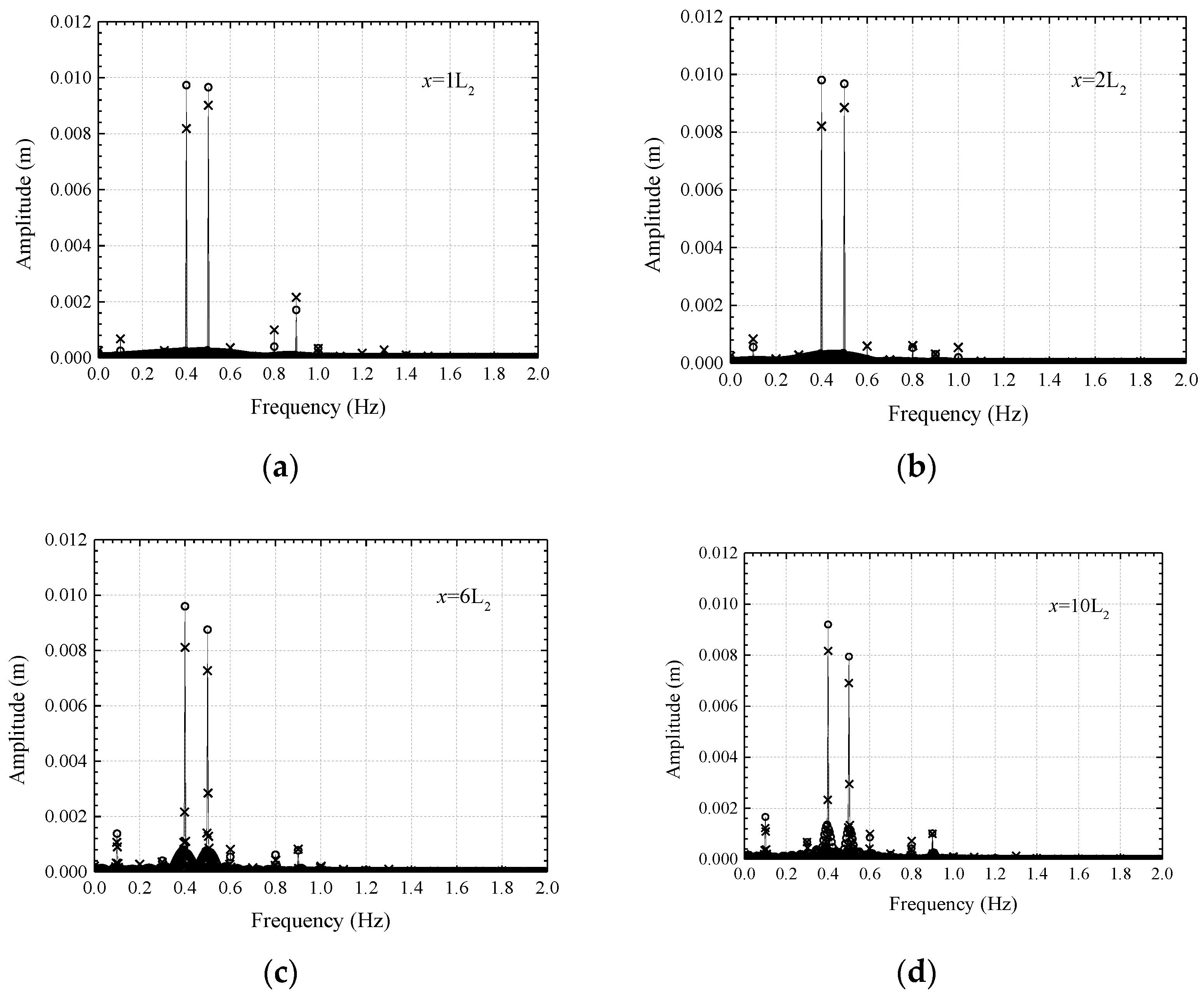
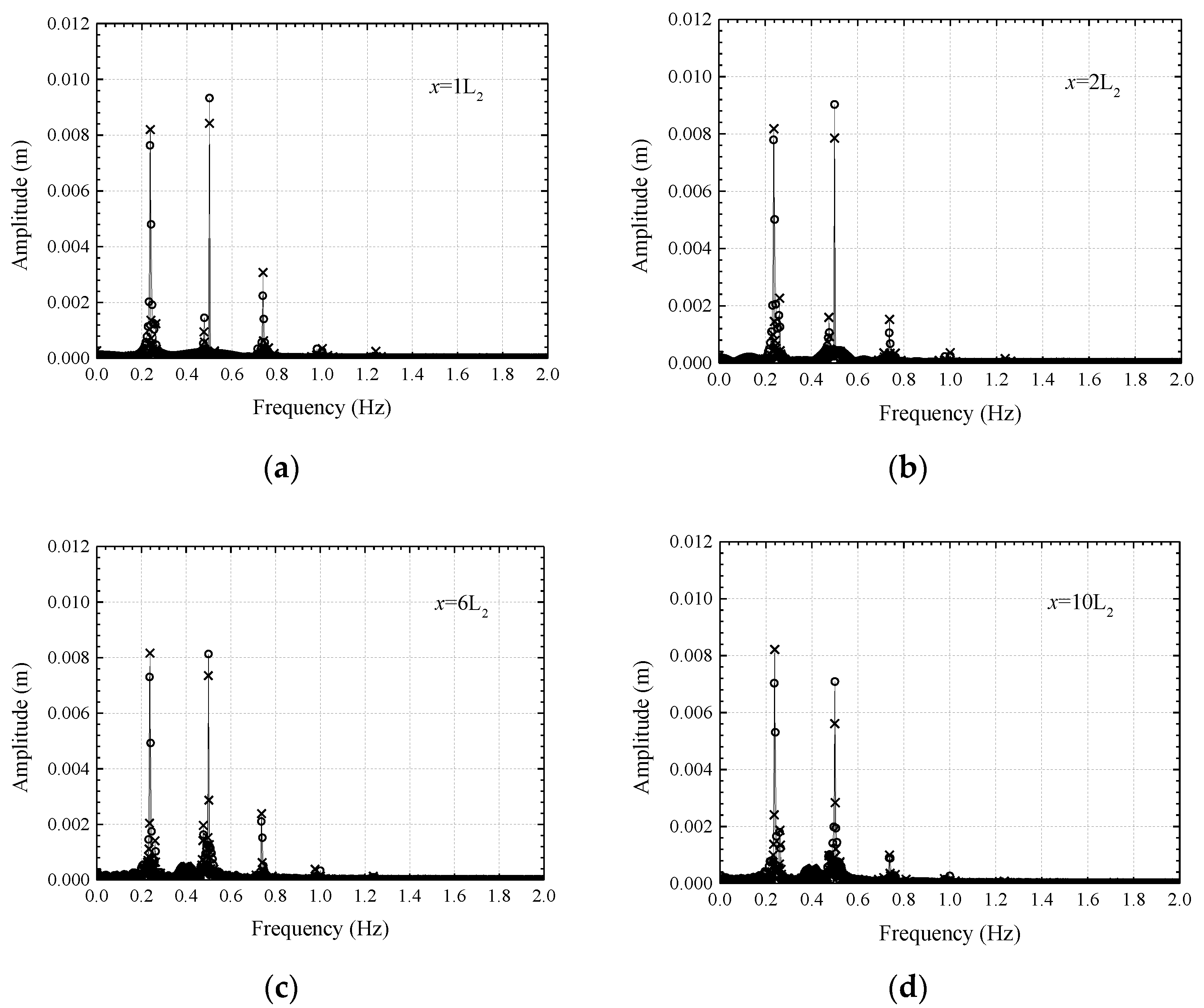
| f1 | f2 | 2f1 | 2f2 | f1 + f2 | f1 + 2f2 | 2f1 + f2 | 2f1 + 2f2 | f1 − f2 | 2f2 − f1 | 2f1 − f2 | 2f1 − 2f2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequency (Hz) | 0.50 | 0.40 | 1.00 | 0.80 | 0.90 | 1.30 | 1.40 | 1.80 | 0.10 | 0.30 | 0.60 | 0.20 |
| f1 | f2 | 2f1 | 2f2 | f1 + f2 | f1 + 2f2 | 2f1 + f2 | 2f1 + 2f2 | f1 − f2 | f1 − 2f2 | 2f1 − f2 | 2f1 − 2f2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequency (Hz) | 0.50 | 0.24 | 1.00 | 0.48 | 0.74 | 0.98 | 1.24 | 1.48 | 0.26 | 0.02 | 0.76 | 0.52 |
| x/m | Downstream | No-Current | Counter-Current |
|---|---|---|---|
| 7 | 2.01 | 1.78 | 1.69 |
| 18 | 1.85 | 1.62 | 1.31 |
| 24 | 1.85 | 1.51 | 1.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Lian, J.; Zhou, E.; Wang, G. Comparative Study on Numerical Simulation of Wave-Current Nonlinear Interaction Based on Improved Mass Source Function. J. Mar. Sci. Eng. 2023, 11, 299. https://doi.org/10.3390/jmse11020299
Li H, Lian J, Zhou E, Wang G. Comparative Study on Numerical Simulation of Wave-Current Nonlinear Interaction Based on Improved Mass Source Function. Journal of Marine Science and Engineering. 2023; 11(2):299. https://doi.org/10.3390/jmse11020299
Chicago/Turabian StyleLi, Haitao, Jijian Lian, Enxian Zhou, and Gang Wang. 2023. "Comparative Study on Numerical Simulation of Wave-Current Nonlinear Interaction Based on Improved Mass Source Function" Journal of Marine Science and Engineering 11, no. 2: 299. https://doi.org/10.3390/jmse11020299




