Fatigue Strength of AH36 Thermal Cut Steel Edges at Sub-Zero Temperatures
Abstract
:1. Introduction
2. Materials and Methods
3. Results
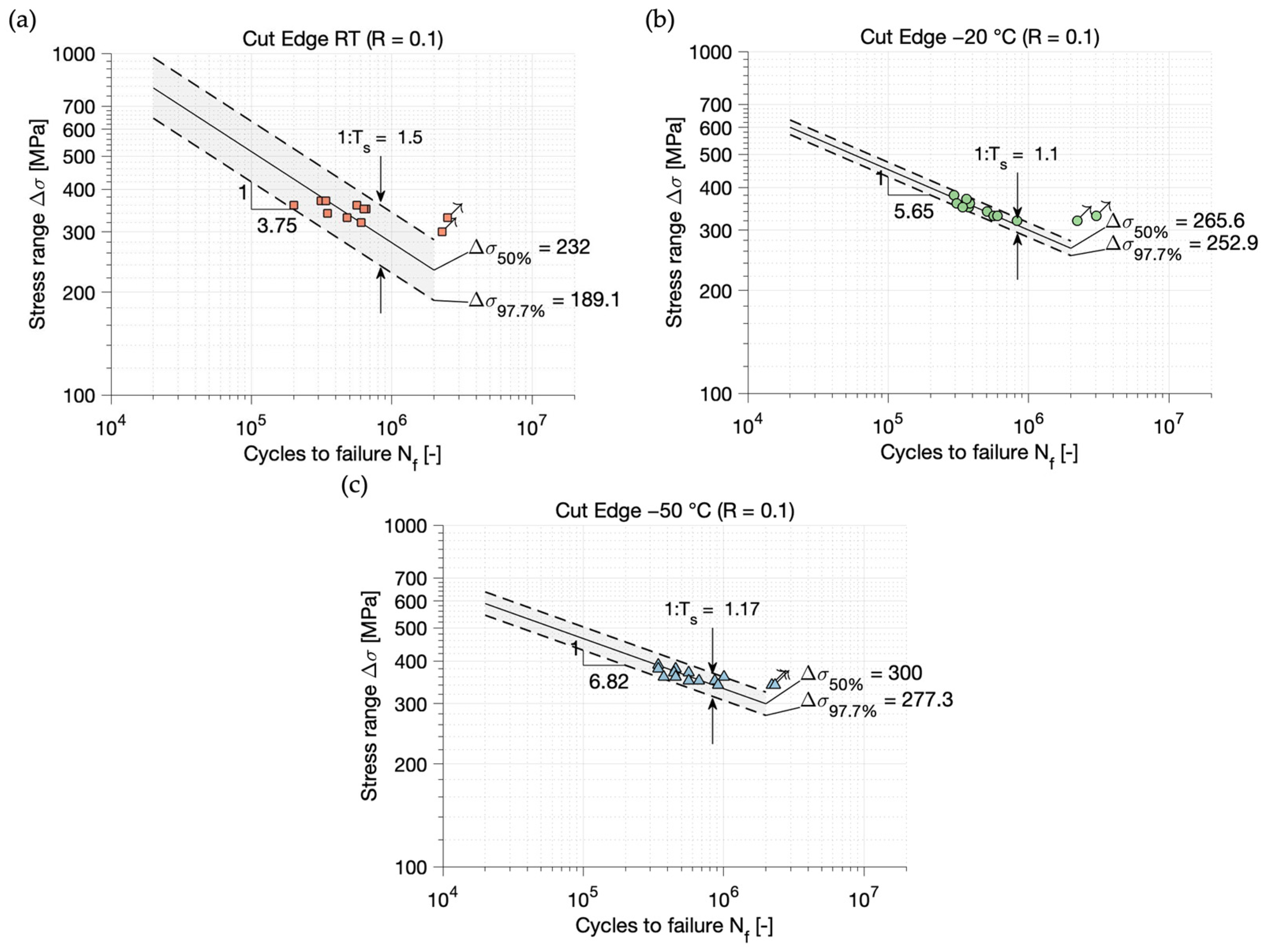
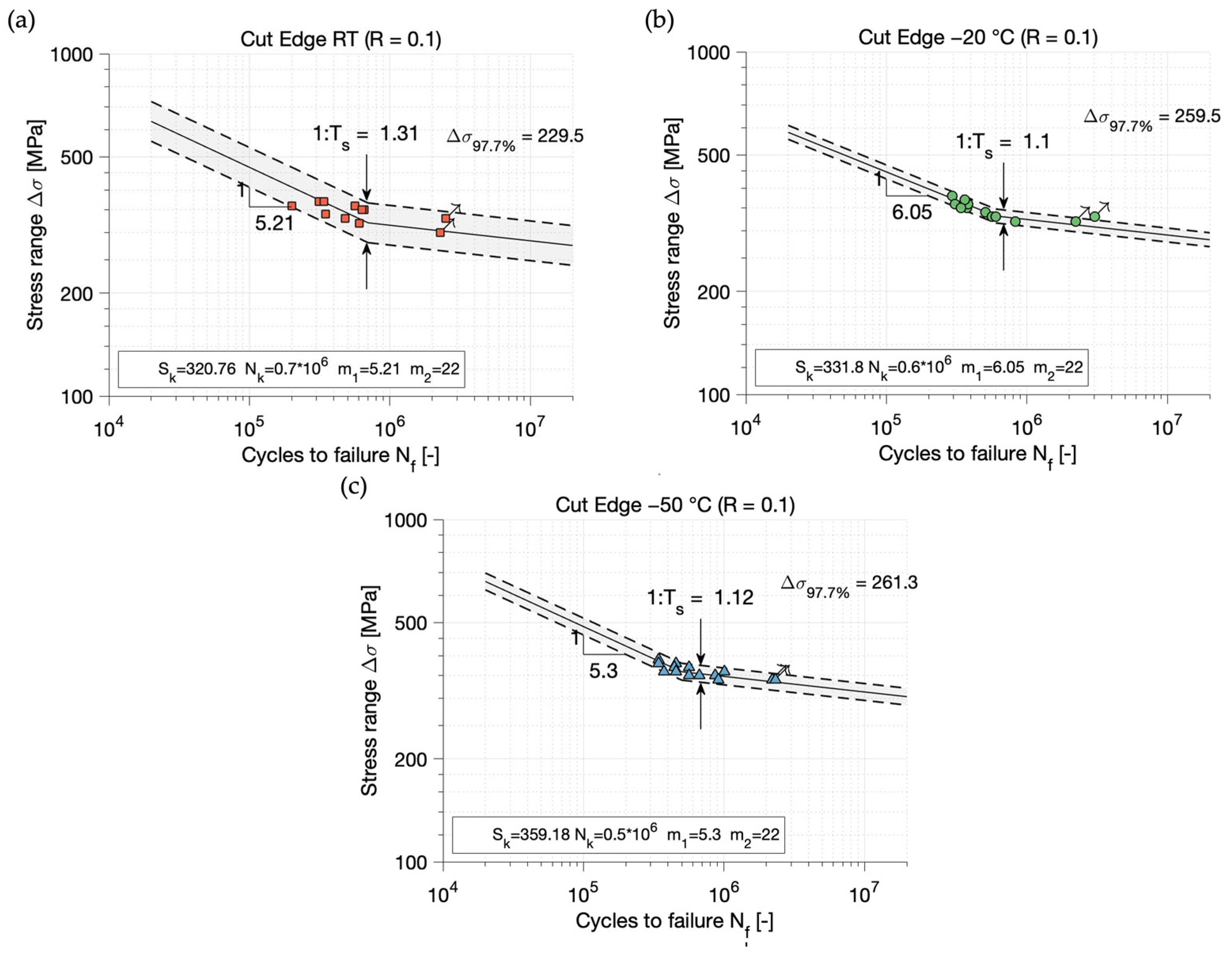
3.1. Statistical Evaluation of Test Results
- Slope in the high cycle fatigue regime ;
- Stress range at the knee point ;
- Standard deviation stdv, as a measure of the scatter in the direction of the stress range;
- Cycles to failure at the knee point ;
- Slope in the long-life fatigue regime .
- Specimens that failed before the knee point ();
- Specimens that failed behind the knee point ();
- Specimens that have not failed (runouts).
3.2. Fracture Surface
3.3. Influence of the Crack Position.
3.4. Linear Regression with Constant Slope
4. Discussion
5. Conclusions
- After analyzing the statistically evaluated best-fit S-N curves, it is clear that the fatigue strength of thermal cut steel edges of AH36 increase at sub-zero temperatures in comparison to room temperature. This is independent of the statistical method and corresponds to the experience gained with welds at sub-zero temperature [9,10].
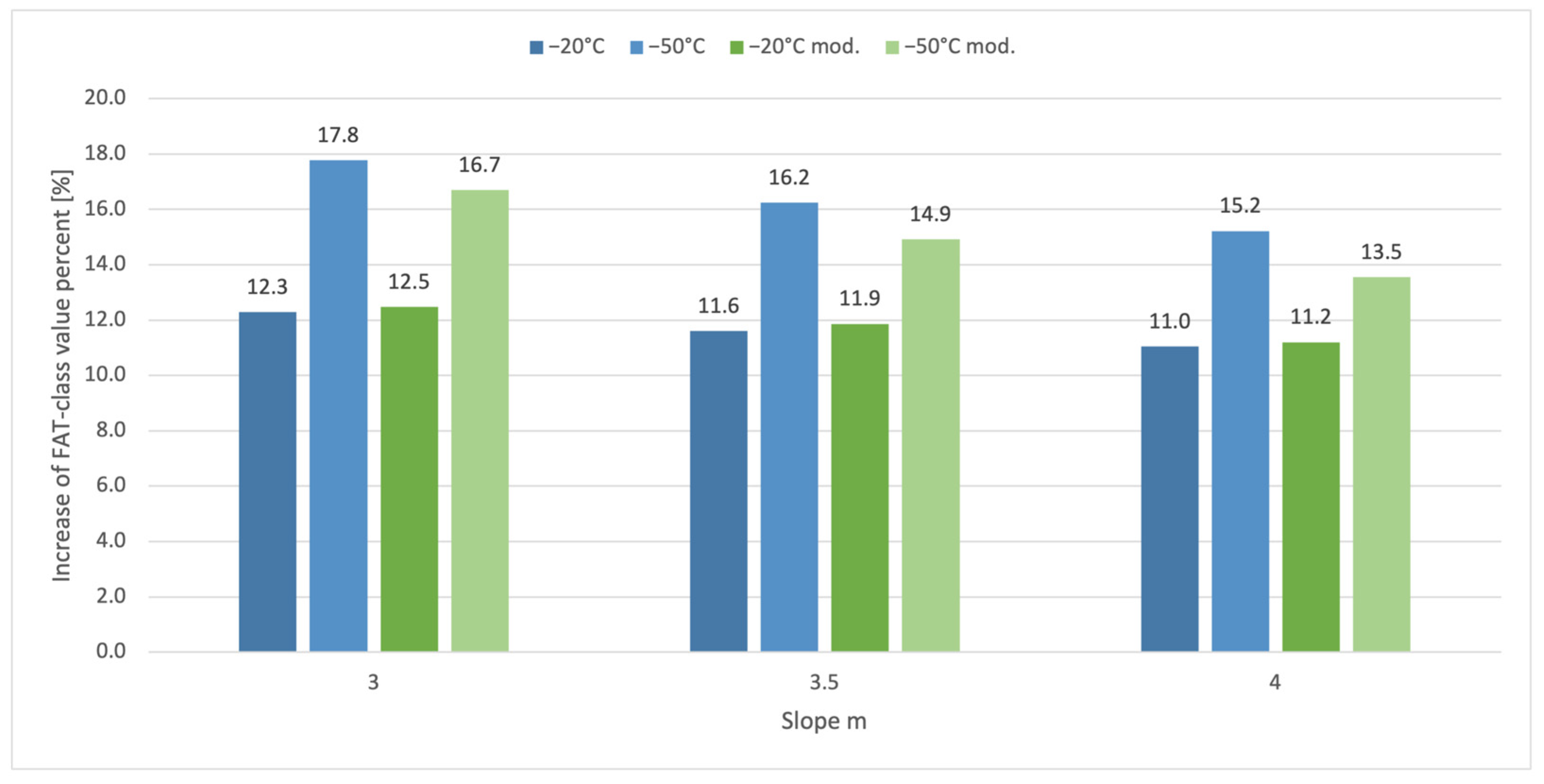
- A fixed slope of m = 4 seems applicable for the evaluation with fixed slopes as the slopes that are found in the evaluation of the best fit S-N curves are close to that or greater. The modification of the stress range leads to steeper S-N curves, which are even closer to a slope of m = 4.
- Using fixed slopes shows the increase in fatigue strength in an even clearer manner. The highest increase in fatigue strength evaluated with a fixed slope of m = 4 is about 15.2% at a test temperature of −50 °C and in the case of the modified data, the increase is still about 13.5%.
- The comparison with the FAT-class values of the design curves of the common guidelines has shown that all test series surpass the FAT-class recommendations. This shows that the design curves are very conservative for thermal cut edges, especially at sub-zero temperatures.
- A difference in the crack location is not found. All cracks occur in the corner of the cut edges, independent to the test temperature.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | Unit | Description |
| - | Scatter ratio in strength | |
| - | Slope of S-N curve in linear regression | |
| - | Slope before the knee point in maximum likelihood method | |
| - | Slope behind the knee point in maximum likelihood method | |
| Cycles | Cycles to failure | |
| Cycles | Number of cycles at knee point | |
| MPa | Stress range | |
| MPa | Stress range at the knee point | |
| - | Stress ratio | |
| MPa | Stress range at knee point | |
| - | Highest probability of occurrence | |
| - | Probability of occurrence for one test point | |
| - | Probability of occurrence for a failure | |
| - | Probability of occurrence for a runout | |
| - | Standard deviation in the direction of the stress range |
Abbreviations
| FDBT | Fatigue ductile–brittle transition |
| FTT | Fatigue transition temperature |
| RT | Room temperature |
References
- von Bock und Polach, F.; Kahl, A.; Braun, M.; von Selle, H.; Ehlers, S. Analysis of governing parameters on the fatigue life of thermal cut edges. In Proceedings of the International Conference on Ships and Offshore Structures ICSOS, Orlando, FL, USA, 4–8 November 2019. [Google Scholar]
- Lipiäinen, K.; Ahola, A.; Skriko, T.; Björk, T. Fatigue strength characterization of high and ultra-high-strength steel cut edges. Eng. Struct. 2021, 228, 111544. [Google Scholar] [CrossRef]
- Diekhoff, P.; Hensel, J.; Nitschke-Pagel, T.; Dilger, K. Fatigue Stregth of Thermal Cut Edges-Influence of ISO 9013 Quality Groups; XIII-2687-17; International Institute of Welding: Liguria, Italy, 2017. [Google Scholar] [CrossRef]
- Hobbacher, A.F. Recommendations for Fatigue Design of Welded Joints and Component, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Walters, C.; Alvaro, A.; Johan, M. The effect of low temperatures on the fatigue crack growth of S460 structural steel. Int. J. Fatigue 2016, 82, 110–118. [Google Scholar] [CrossRef]
- Von Bock und Polach, F.; Klein, M.; Kubiczek, J.; Kellner, L.; Braun, M.; Herrnring, H. State of the art and knowledge gaps on modelling structures in cold regions. In Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering, Glasgow, UK, 9–14 June 2019. [Google Scholar] [CrossRef]
- Wallin, K. A Simple Theoretical Charpy-V–KIc correlation for irradiation embrittlement. ASME-PVP 1989, 170, 93–100. [Google Scholar]
- Dzioba, I.; Lipiec, S. Fracture Mechanism of S355 Steel–Experimental Research, FEM Simulation and SEM Observation. Materials 2019, 12, 3959. [Google Scholar] [CrossRef] [PubMed]
- Braun, M.; Scheffer, R.; Fricke, W.; Ehlers, S. Fatigue strength of fillet-welded joints at subzero temperatures. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 403–416. [Google Scholar] [CrossRef]
- Braun, M.; Milaković, A.; Ehlers, S.; Kahl, A.; Willems, T.; Seidel, M.; Fischer, C. Sub-zero temperatures fatigue strength of Butt-welded normal and high-strength steel joints for ships and offshore structures in arctic regions. In Proceedings of the ASME 2020 39th International Conference on Ocean, Offshore and Arctic Engeneering, Virtual, 3–7 August 2020. [Google Scholar] [CrossRef]
- Sperle, J.-O. Influence of Parent Metal Strength on the Fatigue Strength of Parent Material with Machined and Thermally Cut Edges; IIW Document XIII-2174-07; International Institute of Welding: Paris, France, 2007. [Google Scholar]
- Grimm, J.-H.; Castro, J.; von Selle, H.; Braun, M.; von Bock und Polach, F.; Ehlers, S.; Hensel, J.; Hesse, A.-C.; Dilger, K. The influence of edge treatment on fatigue behavior of thermal cut edges. In Proceedings of the ASME 2022 41st International Conference on Ocean, Offshore and Arctic Engineering, Hamburg, Germany, 5–11 June 2022. [Google Scholar]
- Deutsche Fassung EN ISO 9013:2017; Thermisches Schneiden–Einteilung Thermischer Schnitte–Geometrische Produktspezifikation und Qualität (ISO 9013:2017). Deutsches Institut für Normung: Berlin, Germany, 2017.
- Merkblatt DVS 2403. Empfehlung für die Durchführung, Auswertung und Dokumentation von Schwingfestigkeitsversuchen an Schweißverbindungen Metallischer Werkstoffe; Deutscher Verband für Schweißen und verwandte Verfahren: Düsseldorf, Germany, 2019.
- Störzel, K.; Baumgartner, J. Statistical Evaluation of Fatigue Tests Using Maximum Likelihood; Walter de Gruyter GmbH: Berlin, Germany; Boston, MA, USA, 2021. [Google Scholar] [CrossRef]
- von Bock und Polach, F.; Kahl, A.; Braun, M.; Sperle, J.-O.; von Selle, H.; Ehlers, S. Analysis of the scatter in fatigue life testing of thick thermal cut plate edges. Ships Offshore Struct. 2023, 18, 217–230. [Google Scholar] [CrossRef]
- Diekhoff, P.; Hensel, J.; Nitschke-Pagel, T.; Dilger, K. Investigation on Fatigue Strength of Cut Edges of High Strength Steels (S355M, S690Q); IIW Annual Assembly, Document XIII—2732-18; University of Braunschweig: Braunschweig, Germany, 2018. [Google Scholar]
- Haibach, E. Betriebsfestigkeit, Verfahren und Daten zur Bauteilberechnung; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- DNVGL. Fatigue Assessment of Ship Structures; DNVGL-CG-0129; Class Guideline, Edition October 2015; DNV GL AS: Oslo, Norway, 2015. [Google Scholar]

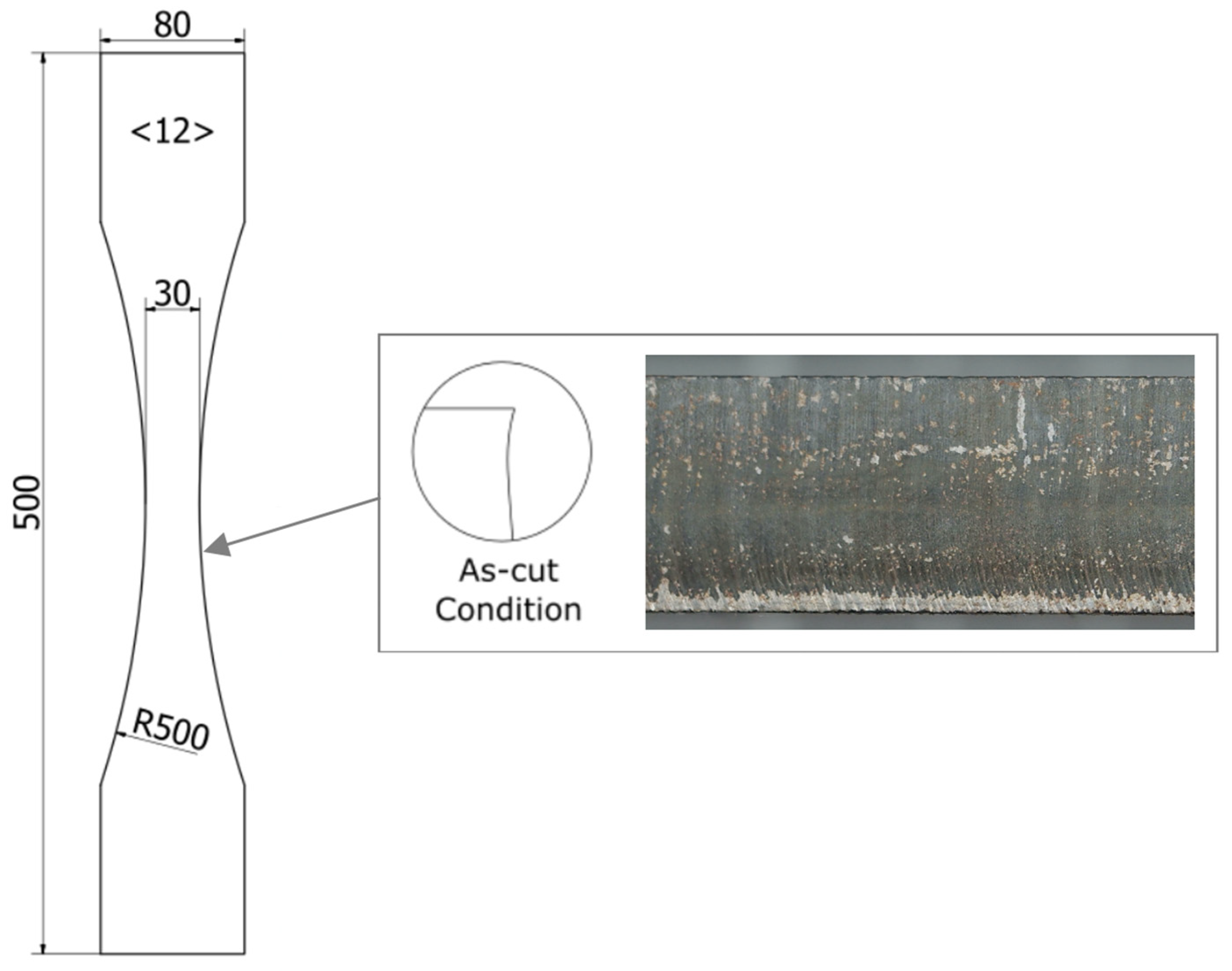
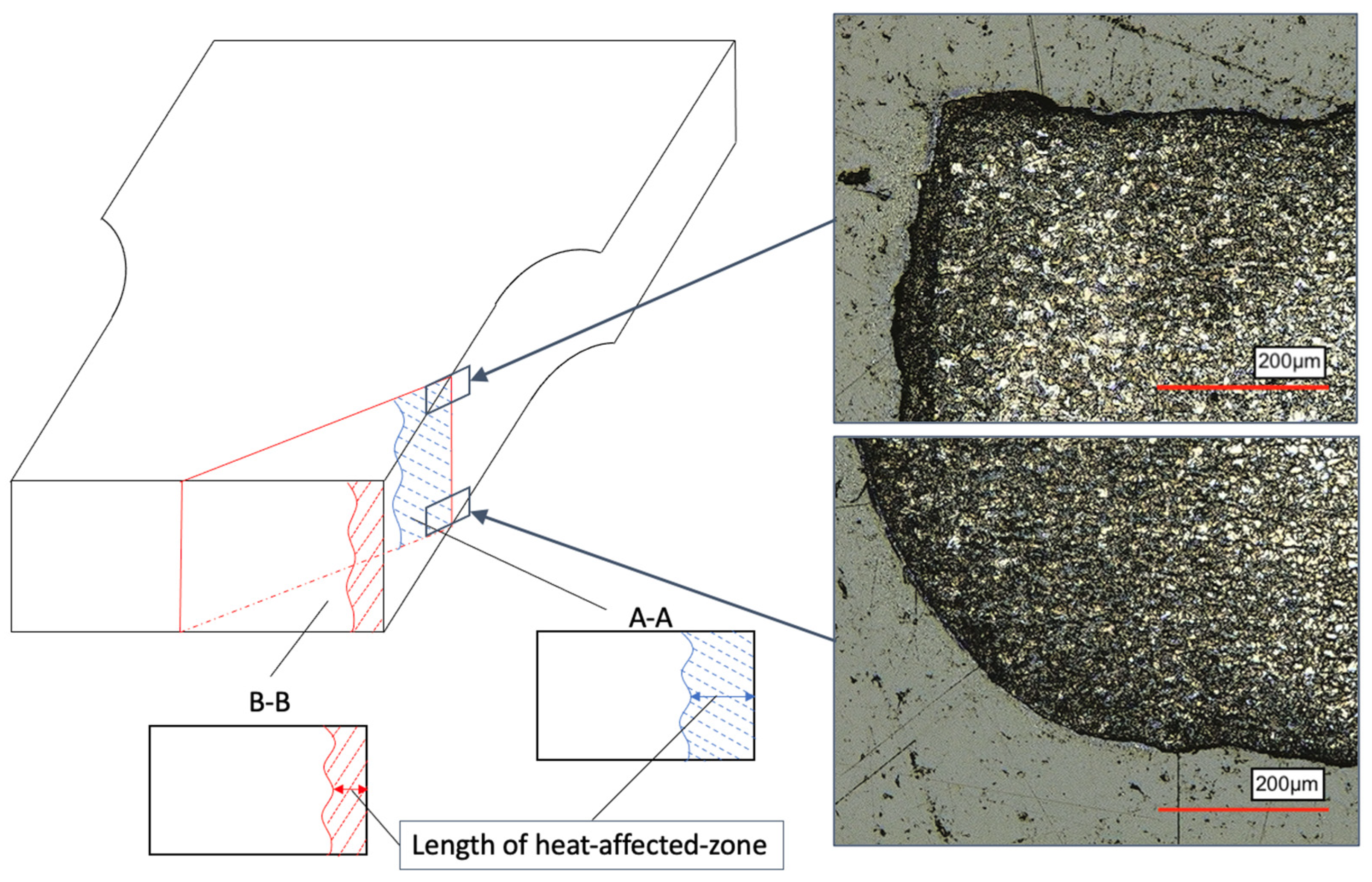
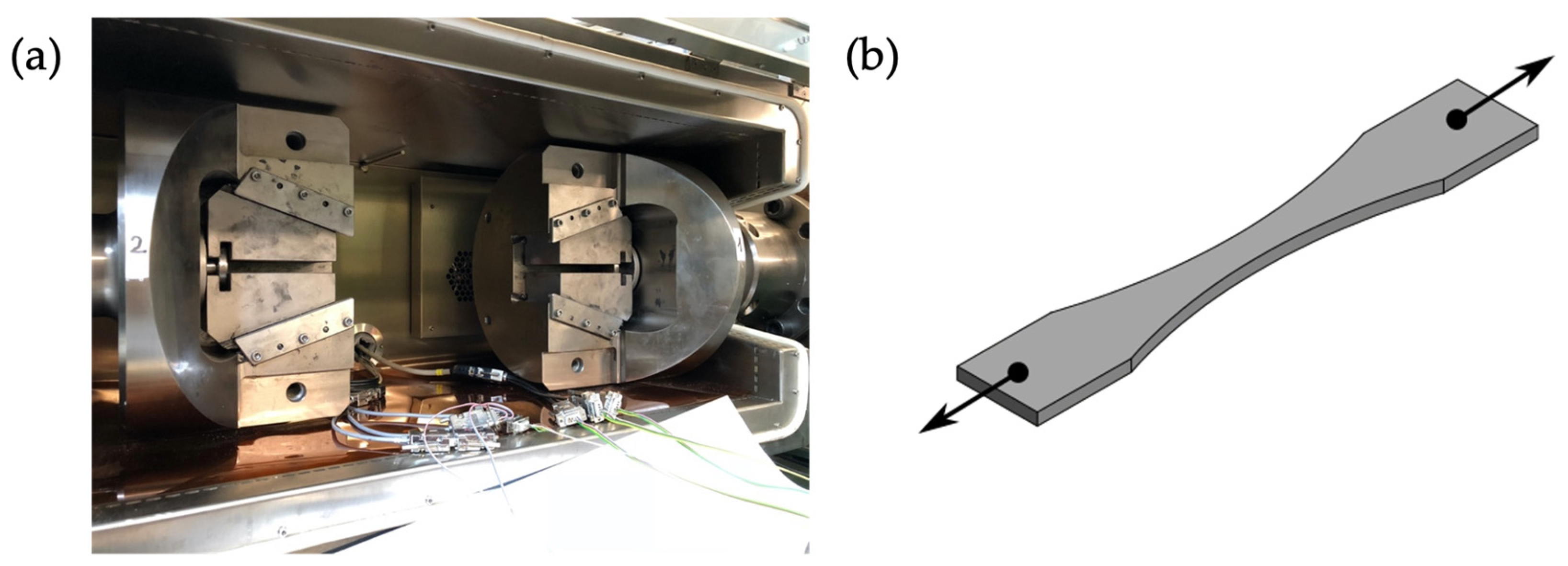



| C | Si | Mn | P | S | Al | N |
| 0.09 | 0.25 | 1.16 | 0.017 | 0.006 | 0.028 | 0.007 |
| Cr | Cu | Ni | Ti | V | Nb | Mo |
| 0.09 | 0.22 | 0.12 | 0.001 | 0.001 | 0.024 | 0.001 |
| CEV | Tensile Strength(MPa) | Yield Strength(MPa) | Failure Strain (%) | |||
| 0.32 | 538 | 423 | 29.2 |
| Statistical Method | Linear Regression | Maximum Likelihood Method | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | FAT (MPa) | (MPa) | FAT (MPa) | ||||||
| RT | 3.75 | 1.5 | 189.1 | 5.21 | 22 | 1.31 | 320.76 | 229.5 | |
| −20 °C | 5.65 | 1.1 | 252.9 | 6.05 | 22 | 1.1 | 331.8 | 259.5 | |
| −50 °C | 6.82 | 1.17 | 277.3 | 5.3 | 22 | 1.12 | 359.18 | 261.3 | |
| RT mod. | 3.57 | 1.51 | 179.3 | 4.8 | 22 | 1.33 | 310.11 | 216.5 | |
| −20 °C mod. | 5.12 | 1.12 | 237.9 | 5.26 | 22 | 1.13 | 323.92 | 242.2 | |
| Test Series | RT (MPa) | −20 °C (MPa) | −50 °C (MPa) | RT Mod. (MPa) | −20 °C Mod. (MPa) | −50 °C Mod. (MPa) | Guideline (IIW Case No. 122, DNV Case B2 and C) |
|---|---|---|---|---|---|---|---|
| m = 3 | 162 | 181.9 | 190.8 | 158.7 | 178.5 | 185.2 | 125 (IIW) |
| m = 3.5 | 181 | 202.0 | 210.4 | 177.0 | 198.0 | 203.4 | 125 (DNV) |
| m = 4 | 196.5 | 218.2 | 226.4 | 191.9 | 213.4 | 217.9 | 140 (DNV) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beiler, M.; Grimm, J.-H.; Bui, T.-N.; von Bock und Polach, F.; Braun, M. Fatigue Strength of AH36 Thermal Cut Steel Edges at Sub-Zero Temperatures. J. Mar. Sci. Eng. 2023, 11, 346. https://doi.org/10.3390/jmse11020346
Beiler M, Grimm J-H, Bui T-N, von Bock und Polach F, Braun M. Fatigue Strength of AH36 Thermal Cut Steel Edges at Sub-Zero Temperatures. Journal of Marine Science and Engineering. 2023; 11(2):346. https://doi.org/10.3390/jmse11020346
Chicago/Turabian StyleBeiler, Marten, Jan-Hendrik Grimm, Trong-Nghia Bui, Franz von Bock und Polach, and Moritz Braun. 2023. "Fatigue Strength of AH36 Thermal Cut Steel Edges at Sub-Zero Temperatures" Journal of Marine Science and Engineering 11, no. 2: 346. https://doi.org/10.3390/jmse11020346
APA StyleBeiler, M., Grimm, J.-H., Bui, T.-N., von Bock und Polach, F., & Braun, M. (2023). Fatigue Strength of AH36 Thermal Cut Steel Edges at Sub-Zero Temperatures. Journal of Marine Science and Engineering, 11(2), 346. https://doi.org/10.3390/jmse11020346








