Assessment of Hydrodynamic Loads on an Offshore Monopile Structure Considering Hydroelasticity Effects

Abstract

Regular and irregular waves were numerically generated in a wave canal to investigate hydrodynamic loads acting on a wind turbine monopile and to predict its structural response. The monopile was implemented in the canal and modeled as a flexible structure, with the turbine blades and rotors considered as a point mass situated at the top of the monopile. Fluid–structure interaction (FSI) simulations were performed by coupling a structure solver based on a finite element method (FEM) with an unsteady Reynolds-averaged Navier–Stokes (URANS) equations solver of the finite volume method (FVM). The FSI simulations considered the two-way interaction between the deformable structure and the fluid flow. The URANS equations solver was coupled with the volume of fluid (VoF) method to account for the two-phase flow. In regular waves, numerically predicted total load coefficients occurring at the monopile’s first eigenfrequency compared favorably to experimental measurements. A deviation between calculations and measurements was observed for the total loads in irregular waves. This deviation occurred due to the smaller wave energy density of the numerically predicted irregular wave. Hydroelasticity effects increased wave-induced forces by about 6% and wave induced bending moments by about 16% in regular waves. A relatively strong whipping event was observed, which characterized the hydroelasticity response bending moment of the monopile in irregular long-crested waves. This whipping event also had a significant influence on the loads on the monopile. These investigations demonstrated the favorable use of FSI simulations to predict hydroelasticity effects on a monopile.

1. Introduction

The demand for offshore wind turbines has increased in recent decades and will continue to increase as many countries intend to reduce greenhouse gas emissions [1]. Offshore wind turbines (OWTs) are expected to generate more than 70 GW of electricity in the period from 2021 to 2025 [2]. These wind turbines are subject to wave-induced loads, which need to be investigated as these loads significantly influence the ultimate strength and the fatigue life of OWTs.

Many authors have performed numerical and experimental investigations to address impact loads. The spatial detection of a slamming event, the identification of the relevant parameters for the slamming, and the selection of a reliable mathematical model to evaluate slamming effects are necessary to properly assess the structural integrity of OWTs [3]. Computational fluid dynamics (CFD) has been used to investigate the influence and the characteristics of breaking waves on OWTs installed on a slope [4], the impact on the foundation due to spilling and plunging breaking waves [5], the breaking wave forces and maximum impact pressures on the cylindrical structure [6], and the physical processes prevailing during breaking wave impacts [7]. The intensity of the impact of a plunging breaking wave on a cylindrical structure depends on the wave’s shape immediately before impact. Maximum impact occurs just before the wave tongue is below the wave crest; minimum impact occurs when the wave breaks behind the cylindrical structure [8]. The distance between the location of a breaking wave and the cylindrical structure is important to predict the extreme loads [9].

Experimental investigations were performed to determine the hydroelasticity response of cylindrical structures subject to breaking waves [10,11,12]. Different intensities of breaking waves from plunging to spilling were considered to measure pressures and accelerations. Maximum accelerations were obtained for moderately plunging waves and maximum pressures for severe plunging waves [10]. A wind turbine undergoes its largest response in steep breaking waves, and this response may be a combination of slamming-induced and a first-order ringing responses [11]. To predict bending moments at the seabed of an OWT under ultimate limit sea state conditions, it is necessary to accurately determine at least the first and second eigenmodes for the wind turbine [12].

To numerically explore hydroelasticity effects, simulations of Fluid–structure interaction (FSI) were performed to account for the associated structural response [13]. The authors used a method based on solving the Reynolds-averaged Navier–Stokes (RANS) equations, two-way coupled with a three-dimensional structure solver based on the finite element method (FEM). The first and second bending modes and the nodal deformations in areas of highest displacement per bending mode were considered. In regular waves, the first bending mode was predominantly excited, whereas the second bending mode was of minor relevance. In a focused wave, however, the overturning moment of the second bending mode turned out to be 40% of the overturning moment of the first bending mode. Furthermore, the dynamic effects of hydrodynamic loads acting on the structure were significant in focused waves and less significant in regular waves [13]. The bending moment of a monopile was investigated at the mud line for different wave periods and wave steepness in regular waves [14]. The authors developed a new tool for FSI simulations, which couples a nonlinear potential flow solver with an FEM tool using a Euler-Bernoulli beam model. The accuracy of this simulation tool decreased with increasing wave steepness. Results compared favorably only to the first two load harmonics; the agreement with higher load harmonics was poor [14]. Numerical FSI simulations were performed to investigate the contribution of hydroelasticity effects on fatigue loads [15]. As expected, fatigue damage increased in sea states that generated a ringing response. The influence of a damped and a lightly damped structure on fatigue damage was also investigated. The fatigue damage increased considerably in sea states with a significant wave height greater than one-half of the monopile’s diameter [15]. Bending moments at the mud line were experimentally measured and numerically calculated for a monopile in long-crested irregular waves [16]. The 90th percentile of the bending moments was then compared over a 30 min time period in irregular waves. Band pass filtering of the bending moment in the vicinity of the first and the second eigenfrequencies, as well as the remaining eigenfrequencies, obtained the total unfiltered bending moment of the structure. The bending moment of the second eigenfrequency did not agree with the experimental data. No significant structural response resulted for the second eigenfrequency [16].

The focus of this paper was to investigate hydroelasticity effects on the loads acting on a monopile in regular and irregular waves using an unsteady Reynolds-averaged Navier–Stokes (URANS) equations solver coupled in an implicit way (two-way-coupling) with a 3D FEM solver for structural dynamics [17]. We validated our numerical model against experiments [18]. Moreover, we performed a systematic spatial and temporal discretization study. We did not consider vortex-induced vibration.

We generated regular and irregular waves to examine not only the total response loads, but also the low-pass and high-pass filtered response loads at a cutoff frequency of about 90% of the monopile’s first eigenfrequency. This allowed us to investigate the response loads in greater detail and to extract the whipping event that characterized the hydroelasticity response loads of the monopile in long-crested irregular waves, which was not observed by the previous investigations cited above. We validated our numerical FV structure model and the associated free surface elevation in the fluid domain surrounding the monopile against experiments [18]. A spatial and temporal study was performed for the fluid domain without implementing the monopile to obtain a suitable mesh and time step for generating regular and irregular waves. The computed free surface elevations were used and validated against the measured free surface elevations for the regular waves. Further on, the energy density spectrum of the measured seaways was used to validate the numerical method in irregular waves. Finally, we compared experimentally measured total force and bending moment coefficients with computed total force and bending moment coefficients, and these coefficients compared favorably to measurements. All simulations were performed with the numerical tool STAR-CCM+ [17].

The progress in this paper, compared to the current state of the art, consisted in the quantification of hydroelasticity effects of hydrodynamic loads acting on a monopile in irregular seas. The nonlinear hydrodynamic effects (breaking waves, slamming) were taken into account by the URANS solver.

2. Test Case Description

The simulations were performed and described for the model scale. The fluid domain had a width of 0.818 m and a length of 30 m, representing the wave canal. The monopile was situated on the centerline of the fluid domain at a longitudinal distance of x = 13.5 m. As in reality, the bottom of the fluid domain was considered to be the mud line. To permit structural deformations at the mud line, the monopile was fixed below the bottom of the fluid domain.

Table 1. Main dimensions of the monopile.

Parameter	Value
Height (m)	4.1700
Diameter at 0.1% of height (m)	0.2300
Diameter at 0.5% of height (m)	0.1800
Diameter at 0.9% of height (m)	0.1600
Wetted surface area $A_{yz}$ (m2)	0.2026
Wetted length (m)	0.8842

lists the main dimensions of the monopile.

Our study comprised four scenarios. The first scenario identified the (dry) eigenfrequencies and the eigenmodes of the monopile for comparison with experimental measurements. The second scenario was configured to evaluate the influence of the hydrodynamic added mass on the structure’s first two eigenfrequencies. The water level was set at a relative height of 22.44% of the height of the monopile. Figure 1 depicts the numerical wave canal with the implemented monopile. This figure also presents the boundary conditions for the third and fourth scenario. Numerical hammering tests were performed for the first two scenarios under dry and wet conditions. The structure was exposed to one triangular impulsive force in the longitudinal direction of the canal. The triangular impulsive force was applied for a simulation time of 0.1 s at the relative height of about 95% of the monopile’s height.

Table 2. Test matrix of parameters for hammering tests in the first and second scenario.

Scenario	Canal Condition	Relative Water Level (%)	Relative Height of Applied Triangular Force (%)	Duration and Amplitude of Triangular Force	Number of Investigated
					Eigen- Frequencies	Eigenmodes
1	Dry	0	95	0.1 s; 200 N	2	2
2	Wet	22.44	95	0.1 s; 200 N	2	2

presents the test matrix of the parameters for the hammering tests. The accelerations were calculated in the time domain at five different heights of the monopile structure and converted, via the fast Fourier transform (FFT), to the frequency domain for a simulation time of 29 s. This process yielded the structure’s first two eigenfrequencies and eigenmodes.

In the third scenario, regular waves were generated with a wave height of H = 0.3272 m and a wave period of T = 1.809 s. The waves advanced in the longitudinal direction of the fluid domain. The fourth scenario dealt with hydroelasticity effects on loads acting on the monopile in irregular waves. Ocean wave spectra from the Joint North Sea Wave Observation Project (JONSWAP) were used to generate the irregular waves of significant wave height H_s = 0.2238 m, peak wave period T_P = 2.344 s, and peak shape enhancement factor $\gamma$ = 3.3. The third and fourth scenarios compared the computed total forces and total bending moments with experimental measurements for a water level at a relative height of 20.48% of the height of the monopile.

Table 3. Wave parameters and relative water level relative to the monopile’s height for the third and fourth scenario.

Scenario	Relative Water Level (%)	$\mathit{H}$ (m)	Hs (m)	T (s)	${\mathit{T}}_{\mathit{P}}$ (s)	$\mathit{\gamma }$
3	20.48	0.32720	-	1.8089	-	-
4	20.48	-	0.22382	-	2.3444	3.3

lists the associated wave parameters for the regular and irregular waves specified in the third and fourth scenarios.

3. Numerical Method

3.1. Fluid Domain

To solve the URANS equations, the fluid domain was assumed to consist of a liquid water phase and a gaseous air phase. The free surface is computed using the VOF method [17,19]. Appropriate exchange terms for mass and momentum account for the interaction between the two phases [20]. The high-resolution interface capturing (HRIC) scheme [21] discretizes the transport equation for the volume fraction of the phases. The shear stress transport (SST) k–ω model of Menter [22] approximates turbulence in the URANS solver. A segregated flow solver resolves the conservation equation of mass and momentum consecutively, using the semi-implicit method for pressure linked equations (SIMPLE) algorithm. This SIMPLE algorithm couples the velocity and pressure fields via the predictor-corrector approach. For more details, see our previous paper [23] and the user manual of STAR-CCM+ [17].

A fifth-order Stokes wave theory modeled the regular waves [24]. However, as this wave theory is only valid for Ursell numbers $U_R$ below a value of 30, its applicability had to be verified [25]. The Ursell number is expressed as follows:

$$U_R=\frac{H{\lambda }^2}{h^3},$$

(1)

where $\lambda$ is wavelength, h is water depth, and H is wave height. As this value turned out to be about 10.1, it was appropriate to implement this wave theory.

The JONSWAP wave spectrum $S_J\left(\omega \right)$ [25] is used to generate the irregular waves:

$$S_J\left(\omega \right)=A_{\gamma }{S}_{PM}(\omega ){\gamma }^{\exp \left(-0.5{\left(\frac{\omega -{\omega }_P}{\sigma {\omega }_P}\right)}^2\right)},$$

(2)

where $\omega$ is the wave angular frequency, $A_{\gamma }$ is a normalizing factor, $S_{PM}\left(\omega \right)$ is the Pierson–Moskowitz spectral density, ${\omega }_P$ is the angular spectral peak frequency, and $\sigma$ is the spectral band width parameter.

The normal and tangential velocity vector components were defined as 0 for the boundary conditions at the tank walls with the no-slip wall condition:

$$\mathit{v}·\mathit{n}=0,$$

(3)

$$\mathit{v}-(\mathit{v}·\mathit{n})·\mathit{n}=\mathbf{0},$$

(4)

where $\mathit{v}$ is the velocity vector and $\mathit{n}$ is the unit normal to the boundary.

3.2. Solid Domain

A three-dimensional solid stress FEM idealized the structure of the monopile. Regarding the conservation of mass and momentum, the fundamentals of the governing equations for a solid model are the same as those for a fluid model. We used a Lagrangian approach instead of a Eulerian approach for the solid model. The mass m is conserved at any time, so that the deformed volume of the structure had the same mass as the undeformed volume. This mass is written as follows:

$$\mathrm{m}={\int }_V^{}\rho \left(t\right)dV={\int }_{V_0}^{}{\rho }_{0}dV=const,$$

(5)

where V is the deformed volume of the structure, $\rho \left(t\right)$ is the density of the deformed material, and $V_0$ and ${\rho }_0$ are the volume and density of the undeformed structure, respectively. The deformation of the volume slightly changes the density $\rho \left(V\right)$ of the material as mass remains constant. This density is expressed as follows:

$$\rho \left(V\right)=\frac{m_0}{V}=\frac{{\int }_{V_0}^{}{\rho }_{0}dV}{{\int }_V^{}dV},$$

(6)

where $m_0$ is the mass of the undeformed structure.

The material properties were assumed as isotropic linearly elastic. Therefore, the volume change is defined as follows:

$$\frac{V-V_0}{V}=\frac{{\sigma }_m}{K}=\mathsf{\epsilon },$$

(7)

where ${\sigma }_m$ is the mean stress, $K$ is the bulk modulus, and $\mathsf{\epsilon }$ is the infinitesimal strain.

The variation of the density is derived from the mean stress for the isotropic linear elastic model:

$$\rho ({\sigma }_m)={\rho }_0\left(1-\frac{{\sigma }_m}{K}\right).$$

(8)

The convective term in the momentum equation is omitted due to the Lagrangian approach for the solid structure, and the Cauchy equilibrium is implemented into the momentum equation:

$$\rho \ddot{\mathit{u}}-\nabla \mathbf{\sigma }-\mathbf{b}=0,$$

(9)

where $\ddot{\mathit{u}}$ is the acceleration derived from the displacement of the solid structure, $\mathbf{\sigma }$ is the Cauchy stress tensor, and $\mathbf{b}$ is the body force per unit volume. Boundary conditions defined as constraints and loads follow the Neumann and the Dirichlet conditions:

$$\mathbf{u}=\stackrel{-}{\mathit{u}},$$

(10)

$$\mathit{\sigma }=\frac{\stackrel{-}{\mathit{\tau }}}{\mathit{n}},$$

(11)

where Equation (14) describes the Dirichlet boundary condition for a constrained motion, Equation (15) expresses the Neumann boundary condition for a defined load, $\stackrel{-}{\mathit{u}}$ is a specified displacement of a surface, $\stackrel{-}{\mathit{\tau }}$ is a specified traction vector on a surface, and $\mathit{n}$ is the surface normal.

The fluid forces deform the solid structure. The resulting deformation of the mesh of the solid and in the fluid domains has to be considered in the momentum equation of the solid domain and in the mass and momentum equations of the fluid domain. More details may be found in [17].

4. Numerical Setup

For the first two scenarios, the monopile was placed in the center of the domain and its bottom at z = −0.3345 m below the canal’s bottom. The first scenario considered the canal to be empty; the second scenario considered the canal to be filled with water. The water was assumed to be calm in the second scenario and only slightly moving on account of the deformations of the monopile structure during the numerical hammering tests.

A numerical hammering test was performed by applying, at the top of the monopile, a triangularly varying impulsive force described as follows:

$$F_x(\mathrm{t})=200\mathrm{N}\ast \left(1-\frac{t}{0.1}\right)\hspace{0.17em}for\hspace{0.17em}t\le 0.1,$$

(12)

where $F_x$ is the force in the x-direction, and t is the simulated time. As the monopile was symmetrical, it was sufficient to apply this triangular impulsive force only in the x-direction. The monopile’s top was excited until the simulated time of 0.1 s, see Equation (12). The accelerations of the monopile’s structure were monitored with probe points installed at five different height positions over a simulation time of 29 s. The eigenfrequencies and eigenmodes were obtained by transforming the accelerations of the monopile at these five probe points from the time domain into the frequency domain.

The surface of the monopile and all walls, except the top and the side walls in the fluid domain, were defined as walls with the no-slip condition. The side walls were defined as walls with the slip condition, and the top wall was defined as a pressure outlet. A floating condition was specified for the top wall and the contact area between the fluid domain and the solid domain to account for the interaction between both domains and thus to allow these surfaces to deform. All the other boundaries were specified as fixed because they did not deform. A constraint motion condition was specified for the bottom surface of the monopole. Velocities and pressures were defined as zero for the initial conditions in the first scenario. The hydrostatic pressure of the water level and the velocity of zero were defined as initial conditions in the second scenario.

For the third and the fourth scenarios, the domain length was extended to 30 m to facilitate generating regular and irregular waves. The wave heights and velocities needed space and time to develop before hitting the structure. The water level was about 20.48% of the monopile’s height. The side walls in these scenarios were specified as walls with the slip condition. Velocities were specified at the inlet wall, i.e., at x = 0 m. Regular and irregular waves were generated at this boundary. The top wall and the end wall (at x = 30 m) represented pressure outlets. The bottom was specified as a wall with the no-slip condition. Boundary conditions regarding the FSI simulations were the same as those for the first and the second scenarios. The pressure of the fifth-order Stokes wave and zero velocity were defined as initial conditions for the third scenario, and the pressure of the irregular wave and zero velocity were defined as initial conditions for the fourth scenario.

A second-order scheme discretized space. Time was discretized implicitly to the second order. The ambient air was assumed to be compressible and the water to be incompressible. The HRIC scheme was employed for the multi-phase VoF model. The Courant–Friedrichs–Lewy (CFL) number was on average lower than 0.2. Accurate results were obtained in previous investigations using a sharpening factor of 0.1 for the HRIC scheme [26]. The thickness of the first prism layer was small enough to retain an averaged wall y+ value of less than 1.0 at the monopile’s surface in the FSI simulations. The turbulent kinetic energy k was set to 0.001 J/kg; the specific dissipation rate, $\omega$, to 1.0 × 10⁻⁴ 1/s [23]. Rayleigh damping was used. To model the structure of the monopile as accurately as possible, we used an isotropic linear elasticity model for the monopile structure with the corresponding material properties.

A total of about 20,000 hexahedral control volumes (CVs) modeled the structure of the monopile. The FEM was made up of 10 cylindrical segments. A mapped contact interface connected these cylinders with each other, and they were meshed individually. This ensured that we established a high-quality mesh for the entire monopile structure. As shown in Figure 2, the diameter of the monopile was subdivided into 56 elements; its thickness, into 3 elements.

To investigate hydroelasticity effects of the monopile in regular and irregular waves, two separate validation studies were performed. One study compared computed and measured time histories of free surface elevation of regular waves; the other study compared computed and measured time histories of the free surface elevation and the energy density spectrum of irregular waves. The discretization studies were performed without the monopile.

Each discretization study was performed on three successively finer grids refined by the factor $\sqrt{2}$. The same CFL number was obtained for each grid. The number of cells in the width of the tank was reduced to two cells. From [13,27,28], we extracted the recommended number of CVs per wave height and the associated time steps. For each grid,

Table 4. Number of CVs, time step size, number of time steps per wave period, and number of CVs per wave height for hydroelastic computations on the coarse, medium, and fine grids.

	Regular Wave				Irregular Wave
Grid	Control Volumes	Time Step (s)	$\frac{\mathit{T}}{\mathit{T}\mathit{i}\mathit{m}\mathit{e} \mathit{s}\mathit{t}\mathit{e}\mathit{p}}$	Cells per Wave Height	Control Volumes	Time Step (s)	$\frac{{\mathit{T}}_{\mathit{P}}}{\mathit{T}\mathit{i}\mathit{m}\mathit{e} \mathit{s}\mathit{t}\mathit{e}\mathit{p}}$	Cells per Wave Height
Coarse	35,972	5.17 × 10−3	350	11.3	49,120	5.86 × 10−3	400	9
Medium	69,936	3.65 × 10−3	495	16	93,204	4.14 × 10−3	566	12.7
Fine	136,240	2.58 × 10−3	700	22.6	184,984	2.93 × 10−3	800	18

lists the number of CVs, the time step, the number of time steps per wave period, T, and the number of CVs per wave height.

Hexahedral cells were used to generate the mesh in the fluid domain, which are widely employed in various hydrodynamic modeling [29,30]. A mesh alignment location was defined at the intersection between the liquid and gaseous phases. The CVs in the vicinity of the free surface had a height equal to one-half of a CV’s length. The specified free surface mesh ranged from z = −0.25 m below the free surface to z = 0.28 m above the free surface.

For the validation study in regular waves, the CVs’ height and length in the region of the free surface were, respectively, $∆z$ = 0.02892 m and $∆x$ = 0.05784 m for the coarse grid, $∆z$ = 0.02045 m and $∆x$ = 0.0409 m for the medium grid, and $∆z$ = 0.01446 m and $∆x$ = 0.02892 m for the fine grid. For the validation study of irregular waves, the CVs’ height and length in the region of the free surface were, respectively, $∆z$ = 0.02487 m and $∆x$ = 0.04974 m for the coarse grid, $∆z$ = 0.01759 m and $∆x$ = 0.03517 m for the medium grid, and $∆z$ = 0.012435 m and $∆x$ = 0.02487 m for the fine grid.

An additional volume meshing was performed with a hyperbolic tangent extrusion type mesh. At the end wall of the numerical domain, ranging from x = 30 m to x = 60 m, the existing mesh was extended by ten layers to generate the additional volume. A stretching factor of 1.4 was used for these ten layers. This extruder meshing model increased the length of the CV and, therefore, increased the iteration errors and the numerical discretization. However, it dampened the waves and prevented their reflection [31]. Figure 2 presents the side view of the fine mesh used for the irregular wave simulations in the vicinity of x = 30 m, where the extruded mesh began. The area of the free surface was additionally locally refined.

A first prism layer thickness of 8.0 × 10⁻⁵ m was defined for the monopile structure in the fluid domain. The total thickness of the prism layer was limited to 0.00405 m for the FSI simulations with the regular wave train and to 0.00348 m for the FSI simulations with the irregular wave train. We used a total of seven prism layers. Figure 2 shows a side view of the monopile structure situated in the canal and the associated mesh of the solid and fluid domains. As vortex-induced vibrations were not considered, the loads were induced by the waves.

5. Validation

We started by validating the dry and wet eigenfrequencies of the monopile structure. Then we compared the structure’s first two computed eigenmodes with experimental measurements. The accelerations from the associated hammering tests were obtained at five selected probe points located at different heights along the monopile. These accelerations were recorded in the time domain and transformed into the frequency domain via an FFT. This procedure yielded the eigenfrequencies of the structure. At the first eigenfrequency, the first eigenmode was derived from the maximum amplitude of the accelerations of the respective probe points; at the second eigenfrequency, the second eigenmode was in this way derived. The displacements of the recorded probe points of the first two eigenmodes were estimated using the following equation:

$$u_{x_{ij}}=\frac{{\ddot{u}}_{x_{ij}}}{{\left(2\pi f_i\right)}^2},$$

(13)

where $u_x$ is the displacement in the x-direction, ${\ddot{u}}_x$ is the acceleration in the x-direction, and $f$ is the eigenfrequency. Index $i$ refers to the first and second eigenfrequencies; index j, to the probe points.

Figure 3a plots the spectrum of axial accelerations ${\ddot{u}}_x$ at the five positions (probe points 1 to 5). The x-shaped markings in Figure 3b depicted the percentage deviation from the highest displacements ${u_{xmax}}_i$ of the corresponding eigenmode and the percentage deviation from the maximum height $z_{max}$ of the monopile for the respective probe point. The graphs in Figure 3b were extrapolated from the x-shaped markings. Probes 1, 2, 3, 4 and 5 are located at the heights of 0.19%, 0.30%, 0.47%, 0.71%, and 0.96% of the monopile’s height. Figure 3b depicts the computed and measured displacements of the first and the second eigenmodes, showing a favorable agreement for the first eigenmode between the physical and the numerical model. Although the second eigenmode was not captured as favorably as the first eigenmode, it was within an acceptable range. The higher eigenmodes and eigenfrequencies were considered to be of minor importance. The computed first two (dry) eigenfrequencies of 1.632 Hz and 7.479 Hz compared favorably to the corresponding measured eigenfrequencies of 1.634 Hz and 7.458 Hz.

To investigate the effect of the hydrodynamic added mass on the first two eigenfrequencies, hammering tests were performed. The computed eigenfrequencies of the wetted monopile were 1.629 Hz and 7.192 Hz; the corresponding measured eigenfrequencies, 1.633 Hz and 6.594 Hz.

Figure 4 presents the experimental and numerical results of the decay test for the monopile in water. The computed and measured displacements of the center of the monopile were low-pass and band-pass filtered. The displacements were normalized against the maximum displacement of the corresponding mode. The computed and measured damping ratios (Rayleigh) were 0.0128 and 0.0134 for the first mode and 0.0186 and 0.0160 for the second mode, respectively. The computed damping ratios of the first and second modes deviated by about 4.5% and 16.3%, respectively, from the measured damping ratios.

The added mass hardly affected the first eigenfrequency, but it did noticeably influence the second eigenfrequency. The computed and measured deviations between the wet and dry second frequencies were 3.56% and 11.58%, respectively. The deviation between the computed and the measured second wet frequencies was 9.07%. Similar deviations were observed in [13]. This deviation may have been due to the difference in stiffness [16]. The first eigenfrequency was influenced by the mass distribution at the top and the second eigenfrequency by the mass distribution at the center of the monopile. This latter mass distribution was closer to the area surrounded by water. Therefore, there was a noticeable influence of hydrodynamic added mass on the second eigenfrequency.

Table 5. First and second computed eigenfrequencies and their deviation from experimentally measured eigenfrequencies for the monopole situated in an empty (dry) and in a filled (wet) canal computed damping ratios for the first two modes and their deviation from experimentally measured eigenfrequencies in the wet condition.

	Dry		Wet
	1st	2nd	1st	Damping Ratio	2nd	Damping Ratio
Exp. (Hz)	1.634	7.458	1.633	0.0134	6.594	0.0160
Num. (Hz)	1.632	7.479	1.629	0.0128	7.192	0.0186
Devi. (%)	0.12	0.28	0.24	4.48	9.07	16.25

lists the measured and computed first and second eigenfrequencies and the associated damping ratios.

To estimate discretization errors, we first performed simulations on three successively finer spatial and temporal grids for the regular and the irregular waves without the monopile.

Figure 5a plots the normalized free surface elevation, i.e., the free surface elevation divided by the maximum measured wave height at the position of the monopile versus the normalized time, i.e., the time divided by the wave period. A dashed blue line identifies computed free surface elevations obtained on the coarse grid consisting of 35,972 control volumes (CVs) with a corresponding time step of 5.17 × 10⁻³ s; a dashed red line, computed free surface elevations obtained on the medium grid consisting of 69,936 CVs with a corresponding time step of 3.65 × 10⁻³ s; a dashed yellow line, computed free surface elevations obtained on the fine grid consisting of 136,240 CVs with a corresponding time step of 2.58 × 10⁻³ s. A solid black line identifies the free surface elevations obtained from experimental measurements [18]. Figure 5b depicts box plots [32] of free surface elevations peaks obtained over about 50 wave periods. The median peak value of the normalized free surface elevation from numerical simulations was 0.565 for the coarse grid, 0.576 for the medium grid, and 0.581 for the fine grid. The median peak of the normalized free surface elevation from the experiments was 0.585. Note that the computed free surface elevation obtained on the finest grid agreed closest to the measured free surface elevation. The computed normalized median peak of the free surface elevation deviated by 0.68% from the experimentally measured normalized median peak.

To quantify the discretization errors, we applied the procedure by Oberhagemann [33]. Figure 6a plots the refinement ratio of the time step versus the refinement ratio of the grid spacing. The refinement ratio of the time step $t_k$ is defined as follows:

$$t_k=\frac{t_{{grid}_k}}{t_{{grid}_1}},$$

(14)

where k = 1, 2, and 3 are the indices for the coarse, medium, and fine grids, respectively. The refinement ratio of the grid spacing $x_k$ is defined as follows:

$$x_k=\frac{{Grid\_spacing}_{{grid}_k}}{{Grid\_spacing}_{{grid}_1}},$$

(15)

where $Grid\_spacing$ is the length of the control volume in the x-direction. The refinement factor of the grid spacing and the time step was $\sqrt{2}$.

Figure 6b plots the discretization-independent normalized free surface elevation of the median of the peak values versus the refinement ratio. The value of the green line at the refinement ratio of 0.0 yielded a discretization independent normalized wave elevation of 0.598, which was a deviation of 2.39% from the experimental median value.

Figure 7a plots the normalized free surface elevation, i.e., the free surface elevation divided by the significant wave height (H_s = 0.22382 m) versus the normalized simulation time, i.e., the time divided by the seaway’s peak period (T_p = 2.3444 s). A blue line identifies computed free surface elevations obtained on the coarse grid consisting of 49,120 CVs; a red line, computed free surface elevations obtained on the medium grid consisting of 93,204 CVs; a yellow line, computed free surface elevations obtained on the fine grid consisting of 184,984 CVs. A solid black line identifies the experimental data. Figure 7b depicts the energy density spectra. The calculated and measured normalized free surface elevations obtained over 9.8 min (model scale) were used to calculate the wave energy density spectra [34]. The area below the energy density spectra based on simulations and experiments was calculated and compared. The area from numerical simulations on the coarse grid was 0.000523 ${\mathrm{m}}^2$; the area from numerical simulations on the medium grid, 0.000548 ${\mathrm{m}}^2$; and the area from numerical simulations on the fine grid, 0.000551 ${\mathrm{m}}^2$. The area from the experiments was 0.000590 ${\mathrm{m}}^2$. The area obtained on the fine grid deviated by a mere 6.6% from the area obtained from experiments.

Figure 8a plots the numerically simulated refinement ratio of the time step versus the refinement ratio of the grid spacing for the irregular wave cases. Figure 8b plots the area of the discretization-independent energy density of the associated grids and their time steps for the irregular waves, which turned out to be about 0.000583 ${\mathrm{m}}^2$. This discretization-independent value would have been obtained with an infinitesimally small grid spacing and time step. The deviation of the discretization independent value from the experimental value was about 1.2%.

Table 6. Median values of normalized free surface elevations obtained on the coarse, the medium, and the fine grid areas below the energy density spectra, and discretization independent normalized free surface elevations, discretization independent area of the energy density spectra, and their deviation from experimental measurements (in brackets) for the regular and irregular wave cases.

	Regular Waves		Irregular Waves
Grid	Norm. Free Surface Elevation (-) and Deviation from Experiments (%)	Discretization Independent Norm. Free Surface Elevation (-) and Deviation from Experiments (%)	Energy Density $\left(\frac{{\mathbf{m}}^2}{\mathbf{H}\mathbf{z}}\right)$ and Deviation from Experiments (%)	Discretization Independent Norm. Energy Density $\left(\frac{{\mathbf{m}}^2}{\mathbf{H}\mathbf{z}}\right)$ and Deviation from Experiments (%)
Coarse	0.565 (3.42)	0.598 (2.22)	0.523 × 10−3 (11.37)	0.583 × 10−3 (1.20)
Medium	0.576 (1.54)		0.548 × 10−3 (7.13)
Fine	0.581 (0.68)		0.551 × 10−3 (6.63)

lists median values of normalized free surface elevations for different grid sizes and their time steps, the area below the energy density spectra, the discretization independent normalized free surface elevation, and the discretization independent area of the energy density spectra for the numerically simulated regular and irregular wave cases. Values in brackets identify the deviation from the experimentally measured values.

Figure 9 plots the exceedance probability of computed and measured normalized free surface elevations (scaled by Hs = 0.22382 m) for the irregular wave case. As expected, the finer the discretization, the closer was the agreement with experiments. Simulated free-surface elevations performed on the coarsest grid deviated most from measurements because the relatively rougher discretization was unable to adequately resolve the high waves. Consequently, all subsequent computations were performed on the finest grid.

Table 7. Control volumes and time steps for the FSI simulations in regular and irregular waves.

	Regular Waves		Irregular Waves
Grid	Control Volumes	Time Step (s)	Control Volumes	Time Step (s)
Fine	1,763,733	2.58 × 10−3	2,759,498	2.93 × 10−3

lists associated number of control volumes and time step sizes.

6. The Monopile’s Response Loads

The normalized force coefficient c_x [26] expressed the monopile’s total longitudinal force in the (longitudinal) x-direction as follows:

$$c_x=\frac{F_x}{\rho ·\left(2{\pi }^2·\frac{1}{{T_P}^2}·{H_s}^2\right)·A_{yz}},$$

(16)

where $T_P$ and $H_s$ are, respectively, period and wave height for the regular wave case and peak period and significant wave height for the irregular wave cases, and $A_{yz}=0.2026 {\mathrm{m}}^2$ is the projected wetted surface area of the monopile. The bending moment coefficient cm_y expressed the monopile’s normalized bending moment about the y-axis as follows:

$${cm}_y=\frac{M_y}{\rho ·\left(2{\pi }^2·\frac{1}{{T_P}^2}·{H_s}^2\right)·A_{yz}·l},$$

(17)

where $M_y$ is the bending moment about the y-axis, and $l=0.8842 \mathrm{m}$ is the monopile’s wetted length.

Figure 10a–d presents calculated and measured longitudinal force and bending moment coefficients in regular waves. Figure 10a plots computed (blue line) and measured (black line) amplitude spectra of longitudinal force coefficients. As seen, our numerical simulations captured the measured response loads favorably. Note that the first peak of force coefficients in the spectrum occurred at a frequency of 0.557 Hz, which corresponded to the wave frequency. The second peak of the force coefficients corresponds at a frequency of 1.107 Hz to the second-order force. The peaks at frequencies of 1.629 Hz and 7.192 Hz represented the first and second eigenfrequencies of the monopile. Figure 10b plots the amplitude spectrum of the bending moment coefficient. In contrast to the force coefficient, a higher third peak occurred at 1.629 Hz.

Figure 10c presents time histories of calculated and measured longitudinal force coefficients for twelve wave periods. Generally, our numerical simulations favorably captured the force response of the monopile although maxima and minima of the force coefficient peaks were slightly underestimated. Figure 10d plots the corresponding time histories of computed and measured bending moment coefficients. Here, too, our numerical simulations slightly underestimated the maxima and minima of the bending moment coefficient peaks; however, the agreement with measurements was fair.

Figure 11a–d depicts the filtered calculated and measured force and bending moment coefficients in regular waves for the simulations that were presented in Figure 10a–d. To demonstrate the hydroelasticity effects on total load response, these values were low-pass and high-pass filtered about the first eigenfrequency of the monopile. A red line identifies coefficients that were low-pass filtered at the cutoff frequency of about 90% of the first eigenfrequency of the monopile; a cyan line, coefficients that were high-pass filtered at the same cutoff frequency. Figure 11a plots the amplitude spectrum of force coefficients. The first amplitude peak (red curve) at 0.557 Hz corresponded to the first order force; the second amplitude peak, to the second-order force. The amplitude peak (cyan curve) at 1.629 Hz corresponded to the first order vibration mode. The remaining peaks corresponded to higher order vibration modes. The response of the bending moment coefficient was similar (see Figure 11b). Figure 11c presents time histories of the lower frequency (red curve, wave load on rigid body) and the higher frequency (cyan curve, hydroelasticity-induced load) force coefficients. As seen, wave-induced forces were dominant. The amplitudes of wave-induced force coefficients considering hydroelasticity (see Figure 10c blue line) were about 5.9% higher than the amplitudes of wave-induced force coefficients without considering hydroelasticity (see Figure 11c red line). Figure 11d presents time histories of the associated filtered response bending moment coefficients. The amplitudes of wave-induced bending moment coefficients considering hydroelasticity (see Figure 10d blue line) were now about 16.14% higher than the amplitude of the bending moment coefficient that did not consider hydroelasticity (see Figure 11d red line). These plots demonstrated the significant influence of hydroelasticity effects on total loads acting on the monopile. The first and second-order wave loads, without accounting for hydroelasticity, were lower than the loads that did consider hydroelasticity effects and, as expected, these hydroelasticity effects were stronger for bending moments than for forces.

Figure 12a–d depicts the calculated and measured response force and bending moment coefficients in irregular waves. Figure 12a represents the FFT of the calculated and measured force coefficients. Blue lines identify numerically calculated values; black lines, experimental measurements. As expected, the first computed and measured amplitude peaks occurred at the peak frequency of the seaway $\left(\frac{1}{T_P}=0.427 \mathrm{H}\mathrm{z}\right)$. The second calculated and measured amplitude peaks occurred at about 1.633 Hz, which corresponded to the first eigenfrequency of the monopile. The bending moment response was similar (see Figure 12b). As with regular waves, hydroelasticity effects on the bending moment were more pronounced than on the force. Figure 12c,d presents time histories of force and bending moment coefficients for a representative time interval.

To quantitatively compare the computed and measured loads in irregular seas, we determined short-term statistics. Figure 13 and Figure 14 show a comparison of computed and measured exceedance probabilities of the force and moment coefficients, respectively. Generally, the simulations agreed favorably with measurements. Higher deviations occurred in the vicinity of rarely occurring events. This applied in particular to the bending moment.

Overall, the agreement between calculations and measurements was satisfactory, particularly for the bending moment.

Figure 15a–d presents the low-pass and high-pass filtered force and bending moment coefficients at the cutoff frequency of 90% of the monopile’s first eigenfrequency for simulations in irregular waves. Figure 15a,b plots the amplitude spectra of the filtered force and bending moment coefficients, respectively, versus frequency. Red lines identify low-pass filtered load response coefficients; cyan lines, high-pass filtered load response coefficients. The time histories plotted in Figure 15c,d shows that wave-induced force and moment coefficients (low-pass filtered) were significantly higher than the hydroelasticity-induced force and moment coefficients (high-pass filtered). Hydroelasticity-induced force coefficients were hardly affected. The influence of hydroelasticity on the bending moment was more pronounced. This demonstrated that vibratory stresses characterizing the hydroelasticity-induced bending moment response may significantly influence fatigue loads. 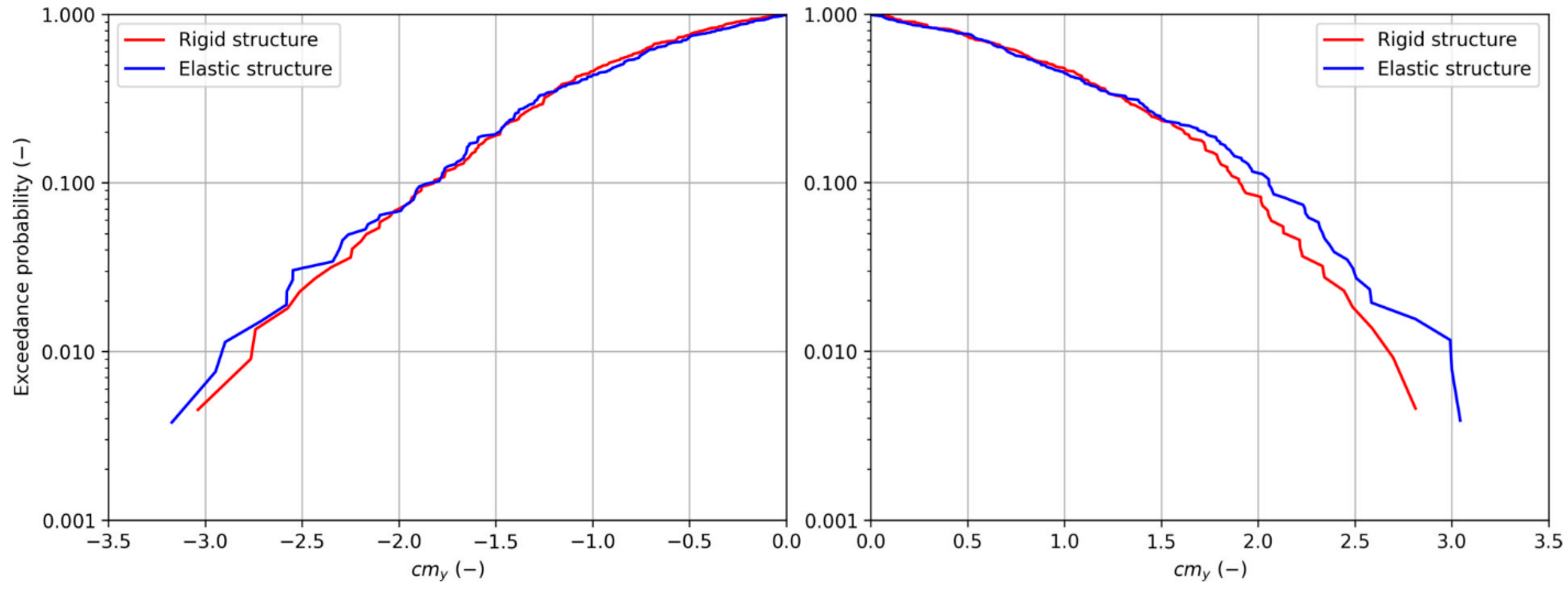Figure 16 and Figure 17 depict, respectively, the exceedance probabilities of wave-induced force and bending moment coefficients obtained without accounting for hydroelasticity (rigid structure) and wave-induced force and bending moment coefficients that did consider hydroelasticity (elastic structure). Figure 16 and Figure 17 demonstrate the influence of hydroelasticity on total loads acting on the monopile. The wave-induced loads that considered hydroelasticity were higher than the wave-induced loads without considering hydroelasticity. The bending moment coefficients, in particular, were notably higher when considering hydroelasticity. Figure 18 depicts velocities of the flow around the monopile in a horizontal plane closely below the free surface and the associated pressure distribution acting on the monopile right before the first wave impact. This figure shows the deformation of the monopile which was captured with the FSI simulations.

7. Conclusions and Outlook

Hydrodynamic loads caused by regular and irregular waves acting on a flexible monopile were numerically predicted using a URANS equations solver implemented with a VoF method to account for the two-phase flow. The URANS solver is coupled with a FEM of the structure. First, we performed validation studies of the monopile’s FEM to estimate dry eigenfrequencies and eigenmodes. Then, we calculated eigenfrequencies, eigenmodes, and damping of the monopile in water. Our numerically predicted first and second eigenfrequencies, as well as damping, compared favorably to experimental measurements. Our predicted second eigenfrequencies deviated only by 9.07%, which was likely caused by the deviation in the stiffness.

We first performed validation studies for the free surface elevation of regular and irregular waves generated without the presence of the monopile. We obtained predictions on three successively refined grids and time steps and validated our numerical results against experimental measurements. We then used the finest grid and its associated time step to carry out the FSI simulations, now with the monopile.

We computed longitudinal forces and bending moment coefficients. These load coefficients were low-pass and high-pass filtered at the monopile’s first eigenfrequency to assess the effects of hydroelasticity on load responses.

In regular waves, our numerically predicted total force and bending moment coefficients compared favorably to experimental measurements. Overall, hydroelasticity effects on bending moments were significantly greater than on forces. Wave-induced forces considering hydroelasticity were about 5.9% higher and wave induced bending moments considering hydroelasticity were about 16.14% higher than their respective wave-induced values in regular waves that did not consider hydroelasticity. The same trend was observed also in irregular waves.

Our investigations demonstrated the favorable use of FSI simulations to predict hydroelasticity effects on a monopile subject to wave-induced loads.