Optimization of Waypoints on the Great Circle Route Based on Genetic Algorithm and Fuzzy Logic

Abstract

Determining the appropriate number and position of waypoints on a great circle route (GCR) helps to shorten the sailing distance, reduce the number of course changes, and well-approximate the GCR through a small number of rhumb line (RL) legs. In this study, a genetic algorithm-based method (i.e., the GA method) is proposed to optimize the positions of waypoints on the GCR when the number of waypoints is given. Furthermore, a fuzzy logic-based evaluation method for the number of waypoints (i.e., the FL method) is proposed to judge whether to add a new waypoint or stop the process by using the non-fixed values while considering both the number of waypoints and the remaining benefit of the GCR. According to the example demonstration results, the two methods proposed in this study can well-determine the number and position of waypoints and provide effective support for ocean route planning.

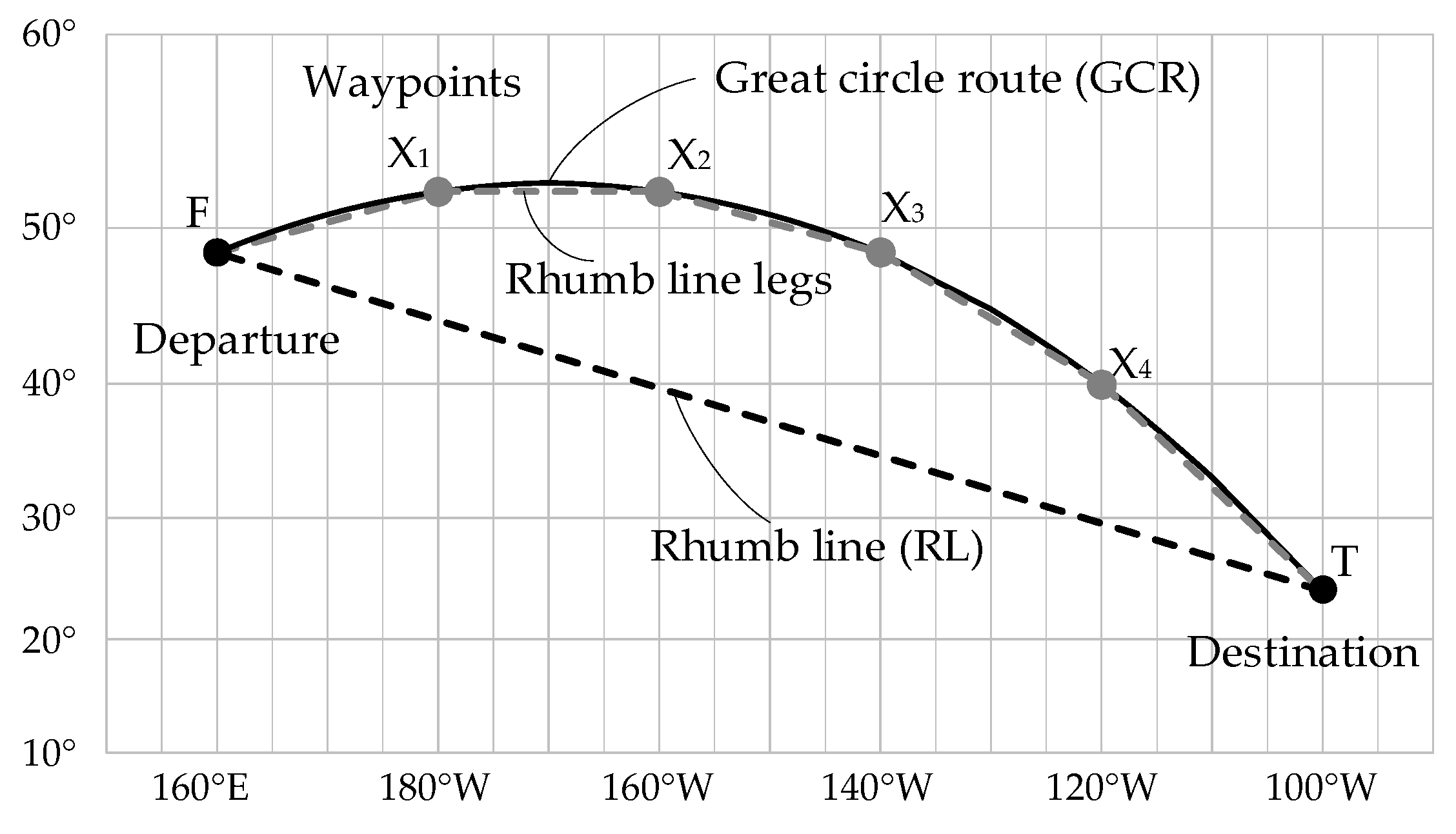
1. Introduction

In recent years, with the continuous development of the global economy, maritime transportation has increased its dominance as the principal mode of transportation in international trade. For ships sailing in the ocean, the quality of route planning directly affects the economy and safety of navigation. There are two kinds of important basic routes for ocean navigation, namely the great circle route (GCR) and the rhumb line (RL). When the GCR meets safety conditions, choosing the GCR has the advantage of shortening the voyage; however, since the intersection angles of the great circle arc and all the meridians are not equal, the course must be constantly changed when sailing strictly along the GCR. Although it is more convenient to choose the RL because the fixed course allows simpler operation, the sailing distance is longer. On the Mercator map, the GCR is depicted as an arc concave to the equator, and the RL is depicted as a straight line, as shown in Figure 1. In practice, when the ship adopts the GCR, it does not sail strictly along the great circle arc; instead, it will determine several waypoints (such as $X_1$, $X_2$, …, $X_4$) on the GCR, and sail along the RL legs (such as $\overline{\mathrm{F}{X}_1}$, $\overline{X_1{X}_2}$, …, $\overline{X_4\mathrm{T}}$) between each waypoint. Therefore, the key issue of great circle navigation is how to determine the number and position of waypoints on the GCR. Too many waypoints will increase the number of course changes and the complexity of ship maneuvering; on the contrary, too few waypoints will lead to a poor total distance benefit of the RL legs that approximate the GCR. How to balance the number of waypoints and distance benefit is an important issue that should be considered in the design of the GCR.

Before computers were popular, in order to reduce calculation variables, textbooks [1,2,3] and studies [4,5] often applied the formulae of the right spherical triangle in Napier’s rules and the vertex to solve the positions of waypoints. Baric et al. solved the great circle initial course angle through the vertex [6], and Chen et al. applied the formulae of the quadrantal spherical triangle in Napier’s rules and the equator crossing point to solve the positions of waypoints [7]. Subsequently, studies of the GCR focused on formula derivation and geometric analysis from different aspects, including a linear equation method [8], linear combination methods [9,10,11,12], vector algebra methods [5,7,13,14], a rotation transformation method [15], a graphic method [16], etc. The above studies all used fixed intervals to determine the waypoints, such as: fixed longitude intervals (generally use 5° or 10° longitude intervals), fixed distance intervals (generally use one-day sailing distance), and fixed latitude intervals (since one latitude may correspond to two longitudes, it is rarely used and requires an additional pre-judgment step). In addition, Levin and Murray conducted some studies on the direction-facing of Muslims, discussing how mosques were built precisely according to the initial compass direction of the GCR [17,18]. Although these studies have made great contributions to the understanding of the GCR, they did not pay particular attention to the number and position of waypoints.

Different from traditional methods of solving waypoints at fixed intervals, Hsu and Hsieh proposed the longitude bisection method (LBM) using non-fixed intervals to add new waypoints, stopping the process when the remaining benefit of distance becomes less than an hour of sailing time [19]. While the research considered the number of waypoints, there are still two problems: (1) the positions of waypoints obtained by the LBM are not optimal, and (2) the condition for stopping the process is a fixed value. Therefore, in the era of computer popularization, to improve the above problems, this study proposes the idea of using intelligent algorithms to directly find the optimal position of waypoints and flexibly increase the number of waypoints to fill the research gap.

In recent years, intelligent algorithms have been widely used to solve route planning problems. For example, Tsou et al. applied the genetic algorithm to plan a ship collision avoidance route [20]. Tsou and Hsueh used fuzzy logic to construct ship safety domain rules, and applied the ant colony algorithm to design a ship collision avoidance route [21]. Mao et al. used three different statistical models (i.e., auto-regression, least square estimates, maximum likelihood method) to predict sailing speed [22]. Vettor and Guedes Soares used the genetic algorithm to find the Pareto frontier while optimizing the path and speed [23]. Wang et al. used the artificial neural network and developed a real-time energy efficiency optimization model to determine the optimal engine speed [24]. Lee et al. applied the Non-dominated Sorting Genetic Algorithm (NSGA)-II algorithm to solve the ship routing optimization problem [25]. Wang et al. proposed a quadratic optimization genetic algorithm combining with the ship motion characteristics to complete automatic route planning [26]. Zhao et al. proposed a hybrid multi-criteria ship route planning method based on an improved particle swarm optimization-genetic algorithm [27]. Zhang et al. clustered the automatic identification system (AIS) data based on fuzzy adaptive density-based spatial clustering of applications with noise (FA-DBSCAN) technology to design the automatic ship route for coastal seas [28]. These studies have made great contributions to the solution of route planning, especially in confirming that the genetic algorithm and fuzzy logic can obtain better optimization results and perform more flexible decision-making. However, they also did not pay special attention to the number and position of waypoints. Therefore, this study proposes an optimization method for the waypoints on the GCR based on a genetic algorithm (i.e., the GA method) and an evaluation method for the number of waypoints based on fuzzy logic (i.e., the FL method) to optimize the position and number of waypoints.

In brief, this study presents two methods for determining the number and position of waypoints on the GCR to optimize the sailing distance and change course. Section 2 lists related formulae of the GCR for the use in subsequent sections. Section 3 proposes the GA method, and Section 4 proposes the FL method. Then, several examples are demonstrated for verification in Section 5. Finally, the research work is concluded in Section 6.

2. Great Circle Route-Related Formulae

Both a sphere and a spheroid can be used as a model of the earth. In Earle’s research, it was found that the difference between the great circle distance on the sphere and the spheroid is within 0.5%, and the sphere model is considered sufficient to meet the needs of teaching and practice [29]. In order to simplify the calculation, this study regards the earth as a sphere, and under the condition that the positions of departure (F) and destination (T) are known, the related formulae required to design the waypoints on the GCR are summarized below.

2.1. Great Circle Distance and Initial Course Angle

The great circle distance ($D$) and the great circle initial course angle ($C$) can be obtained by the following formulae:

$$\cos D=\sin {\phi }_{\mathrm{F}}\sin {\phi }_{\mathrm{T}}+\cos {\phi }_{\mathrm{F}}\cos {\phi }_{\mathrm{T}}\cos \Delta \lambda$$

(1)

$$\tan C=\frac{\cos {\phi }_{\mathrm{T}}\sin \mathsf{\Delta }\lambda }{\cos {\phi }_{\mathrm{F}}\sin {\phi }_{\mathrm{T}}-\sin {\phi }_{\mathrm{F}}\cos {\phi }_{\mathrm{T}}\cos \mathsf{\Delta }\lambda }$$

(2)

where $D$ represents the great circle distance from F to T, expressed in degrees, which should be converted into nautical miles (nm), $1°={60}^{\prime }$, 1′$\cong 1 \mathrm{nm}$, ${\phi }_{\mathrm{F}}$ represents the latitude of F, ${\phi }_{\mathrm{T}}$ represents the latitude of T, $\mathsf{\Delta }\lambda$ represents the difference of longitude between F and T, expressed in degrees, and $C$ represents the great circle initial course angle.

2.2. Rhumb Line Course and Distance

The rhumb line course ($c$) and the rhumb line distance ($d$) can be yielded by the following formulae:

$$M_{\mathrm{F}}=\frac{10800}{\pi }\left[\ln \tan \left(45°+\frac{{\phi }_{\mathrm{F}}}{2}\right)\right]$$

(3)

$$\tan c=\frac{60^{\prime }\mathsf{\Delta }\lambda }{M_{\mathrm{T}}-M_{\mathrm{F}}}$$

(4)

$$d=\{\begin{array}{l}60^{\prime }\left({\phi }_{\mathrm{T}}-{\phi }_{\mathrm{F}}\right)\sec c ,c\ne 90°\\ 60^{\prime }\Delta \lambda \cos {\phi }_{\mathrm{F}} , c=90°\end{array}$$

(5)

where $M_{\mathrm{F}}$ represents the meridional parts of F, namely, the arc length of a meridian from the equator to a given latitude parallel circle, expressed in units of 1 min of longitude at the equator, $c$ represents the rhumb line course, $M_{\mathrm{T}}$ represents the meridional parts of T, and $d$ represents the rhumb line distance from F to T, expressed in nm.

2.3. Waypoint at a Given Longitude

When the longitude of the waypoint is known, the latitude of the waypoint (${\phi }_X$) can be obtained by the following formula:

$$\tan {\phi }_X=\frac{\cos C\sin \mathsf{\Delta }{\lambda }_{\mathrm{F}X}+\sin {\phi }_{\mathrm{F}}\sin C\cos \mathsf{\Delta }{\lambda }_{\mathrm{F}X}}{\cos {\phi }_{\mathrm{F}}\sin C}$$

(6)

where ${\phi }_X$ represents the latitude of the waypoint, and $\mathsf{\Delta }{\lambda }_{\mathrm{F}X}$ represents the difference of longitude between F and the waypoint.

2.4. Remaining Benefit of the GCR

The remaining benefit ($RB$) of the GCR can be obtained by the following formula:

$$RB=\left|D-\left(d_{\mathrm{F}{X}_1}+d_{X_1{X}_2}+\cdots +d_{X_n\mathrm{T}}\right)\right|$$

(7)

where $RB$ represents how much the sum of each RL leg distance compares to the GCR, and $d_{\mathrm{F}{X}_1}$ represents the RL leg distance from F to the first waypoint, which can be calculated through Equations (3)–(5).

The $RB$ is a key index for judging the benefit of the GCR. As shown in Figure 2, its meaning is the distance difference between the GCR and the approximate route (namely, the sum of each RL leg distance), that is, the degree to which the total RL legs approximate the GCR. According to the suggestion of the Royal Navy, it is worthwhile to use the GCR when it can save more than an hour of sailing time [3]. Assuming that the average speed of the ship is 15 knots, there is no need to add a new waypoint for approximation when the $RB$ of the distance becomes less than 15 nm.

In fact, the idea in this study can also be applied to the spheroid model. When the accuracy is high, the spheroid equation can be used instead of the sphere equation. For example, the large-ellipse distance formula can be obtained by direct solutions [30,31,32], replacing Equation (1). Equations (3)–(5) can be replaced by the formulae of course and distance of the ellipsoidal rhumb line proposed by Bennett [33], and the latitude formula of the waypoint at a given longitude is obtained by inverse solutions [31,34], replacing Equation (6).

3. Optimization Method for the Waypoints on the GCR based on the Genetic Algorithm

To optimize the positions of the waypoints on the GCR, this study applied the genetic algorithm [35,36] to propose a genetic algorithm-based optimization method for the waypoints on the GCR (i.e., the GA method). As shown in Figure 3, the method mainly includes three parts:

Part 1: Calculate the basic properties’ information of the GCR. When the longitude and latitude of the departure (F) and destination (T) are known, the basic information, such as great circle distance ($D$) and great circle initial course angle ($C$), can be calculated through Equations (1) and (2).

Part 2: After initializing the number of waypoints ($n=1$), enter the genetic algorithm calculation process. The problem of waypoints on the GCR is encoded in chromosome form, and the positions of waypoints are optimized through the steps of population initialization, fitness evaluation, survivor selection, operator reproduction, population update, and termination.

Part 3: Add a new waypoint or stop the process. If the $RB$ of the optimal individual is greater than or equal to 15 nm, a new waypoint ($n=n+1$) will be added, and the genetic algorithm calculation process will be re-entered to find the optimal position of the $n$ waypoints. If the $RB$ becomes less than 15 nm, the process will be stopped, and the chromosome of the optimal individual will be decoded to obtain the optimal position distribution of $n$ waypoints on the GCR.

Among them, the steps of the genetic algorithm calculation process in Part 2 are explained below.

3.1. Population Initialization

Genes are the basic units located on chromosomes, chromosomes can be used to express the characteristics of individuals, and several individuals can constitute a population. This study encoded the problem of waypoints on the GCR. A gene represents the difference of longitude between a waypoint and F. The value range of any waypoint should be between F and T and should be randomly and uniformly distributed in the whole solution space. A chromosome composed of $n$ genes represents a feasible solution of the position distribution of $n$ waypoints, as shown in Equation (8). The $m$ individuals represent $m$ feasible solution options with the same number of waypoints and different position distributions, and the set of these options constitutes the population, as shown in Equation (9).

$$R_j=\left[\mathsf{\Delta }{\lambda }_{\mathrm{F}X1},\cdots ,\mathsf{\Delta }{\lambda }_{\mathrm{F}Xi},\cdots ,\mathsf{\Delta }{\lambda }_{\mathrm{F}Xn}\right]$$

(8)

$$pop=\left[R_1,\cdots ,R_j,\cdots ,R_m\right]$$

(9)

where $R_j$ represents the $j$-th feasible solution, $\mathsf{\Delta }{\lambda }_{\mathrm{F}Xi}$ represents the difference of longitude between F and the $i$-th waypoint, $0<\mathsf{\Delta }{\lambda }_{\mathrm{F}Xi}<\mathsf{\Delta }\lambda$, and $pop$ represents a population containing $m$ individuals, and the number of individuals was set to 50 in this study.

3.2. Fitness Evaluation

To find the feasible solution options of the optimal position distribution of waypoints, the fitness function was used to evaluate the fitness of each individual in the population. In this study, $RB$ was used to evaluate each feasible solution, as shown in Equation (10).

$$fit=\left[R{B}_1,\cdots ,R{B}_j,\cdots ,R{B}_M\right]$$

(10)

where $R_j$ represents a vector of $M$ fitness values, and $R{B}_j$ represents the $RB$ of the $j$-th individual, which can be obtained through Equation (7).

3.3. Survivor Selection

The individual structures with high fitness were copied from the current population to the next-generation population. This study adopted the technique of stochastic universal sampling (SUS) [37] to select survivors.

3.4. Operator Reproduction

To maintain the diversity of the population and avoid the algorithm falling into a local optimal solution, this study adopted the method of random crossover and mutation for gene recombination, setting the crossover probability to 0.8 and the mutation probability to 0.01.

3.5. Population Update and Termination

After the population was updated, the process will be repeated until the given termination condition was reached. In this study, the algorithm was terminated when the average change in the fitness value became less than ${10}^{-6}$.

4. Evaluation Method for the Number of Waypoints Based on Fuzzy Logic

To optimize the number of waypoints on the GCR in a non-fixed way and avoid the phenomenon of adding a new waypoint when the $RB$ was only slightly greater than 15 nm, this paper applied fuzzy logic [38,39] and the Mamdani fuzzy system [40] to propose a fuzzy logic-based evaluation method for the number of waypoints (i.e., the FL method). As shown in Figure 4, while considering both the $RB$ and the number of waypoints ($n$), the method used fuzzification, fuzzy logic operators, and defuzzification processes to judge whether to continue the iteration; that is, to add a new waypoint or stop the process. This can replace Part 3 of the GA method in Section 3 to more flexibly and reasonably determine $n$.

4.1. Fuzzification

This paper used a triangular membership function for fuzzy variables. As shown in Figure 5a,b, the $RB$ was divided into three levels of uncertainty: low, medium, and high, and its degree of membership can be calculated through Equations (11)–(13). $n$ was divided into three levels of uncertainty: lower, medium, and higher, and its degree of membership can be calculated through Equations (14)–(16).

$$f\left(R{B}_L\right)=\{\begin{array}{c}1, 0<10\\ \frac{17-RB}{7}, 10\le RB<17\\ 0, RB\le 17\end{array}$$

(11)

$$f\left(R{B}_M\right)=\{\begin{array}{c}0, RB<13\\ \frac{RB-13}{7}, 13\le RB<20\\ \frac{27-RB}{7}, 20\le RB<27\\ 0, RB\ge 27\end{array}$$

(12)

$$f\left(R{B}_H\right)=\{\begin{array}{c}0,RB<23\\ \frac{RB-23}{7},23\le RB<30\\ 1,RB\ge 30\end{array}$$

(13)

$$f\left(n_L\right)=\{\begin{array}{c}\frac{5-n}{4},1\le n<5\\ 0,n\ge 5\end{array}$$

(14)

$$f\left(n_M\right)=\{\begin{array}{c}0,n<2\\ \frac{n-2}{6},2\le n<8\\ \frac{14-n}{6},8\le n<14\\ 0,n\ge 14\end{array}$$

(15)

$$f\left(n_H\right)=\{\begin{array}{c}0,n<11\\ \frac{n-11}{4},11\le n<15\\ 1, n\ge 15\end{array}$$

(16)

According to the suggestion of the Royal Navy [3], this study assumed that when $RB\ge 30$, it means that the $RB$ was still obvious. According to the results of the example demonstration by Hsu and Hsieh [15], this study assumed that when $n\ge 15$, it means that too many waypoints have been used. Users can adjust the range of semantic levels of variables according to their preferences.

4.2. Fuzzy Logic Operators and Defuzzification

This paper established a fuzzy rule base for measuring $RB$ and $n$, as shown in

Table 1. Fuzzy rule base.

	n	Low	Medium	High
RB
Lower		stop	continue	continue
Medium		stop	stop	continue
Higher		stop	stop	continue

, and adopted the max–min composition method for fuzzy reasoning. Firstly, we compared the membership degree of $RB$ and $n$, and used the minimum value to determine the weight of a single rule; then, we compared the weights among multiple rules, and used the rule with maximum weight to determine whether to add a new waypoint or stop the process by referring to Table 1.

5. Example Demonstration

5.1. Example Demonstration for the GA Method

To demonstrate the GA method proposed in this study, the example of the GCR from San Francisco (34°00.0′ N, 120°40.0′ W) to Luzon Strait (20°10.0′ N, 122°00.0′ E) was selected to optimize the waypoints. First, when the longitude and latitude of F and T were known, the basic information of the GCR was calculated: the great circle distance ($D$) was 5968.25 nm, and the great circle initial course angle ($C$) was N57.7°W. Next, the genetic algorithm was used to optimize the positions of waypoints, as shown in

Table 2. Using the GA method to optimize the waypoints.

Number of Waypoints	Number of Iterations	$\Delta \mathit{\lambda }F{\mathit{X}}_{\mathit{i}}(°)$	$\mathbf{Waypoint} \left({\mathit{X}}_{\mathit{i}}\right)$	RB (nm)
$n=1$	55	57.39	X1 (45°09.6′ N, 178°03.6′ W)	98.39
$n=2$	197	38.42	X1 (45°03.6′ N, 159°05.4′ W)	44.32
		76.46	X2 (41°57.0′ N, 162°52.8′ E)
$n=3$	248	28.91	X1 (43°48.0′ N, 149°34.8′ W)	25.01
		57.42	X2 (45°09.0′ N, 178°04.8′ W)
		86.02	X3 (38°54.6′ N, 153°18.6′ E)
$n=4$	305	23.20	X1 (42°37.2′ N, 143°52.2′ W)	16.02
		46.01	X2 (45°28.8′ N, 166°40.2′ W)
		68.81	X3 (43°39.6′ N, 170°31.8′ E)
		91.82	X4 (36°30.6′ N, 147°31.2′ E)
$n=5$	330	19.39	X1 (41°38.4′ N, 140°03.0′ W)	11.13
		38.41	X2 (45°03.6′ N, 159°04.2′ W)
		57.40	X3 (45°09.0′ N, 178°04.2′ W)
		76.41	X4 (41°57.6′ N, 162°55.2′ E)
		95.74	X5 (34°38.4′ N, 143°36.0′ E)

. The process is as follows:

When the number of waypoints $n=1$, the termination condition is reached after 55 iterations, and the optimal solution is $\mathsf{\Delta }{\lambda }_{\mathrm{F}X1}=57.39°$, as shown in Figure 6a. The $RB$ value of 98.39 nm is still greater than 15 nm, and a new waypoint should be added. When the $n=2$, the termination condition is reached after 197 iterations, and the optimal solution is $\mathsf{\Delta }{\lambda }_{\mathrm{F}X1}=38.42°$ and $\mathsf{\Delta }{\lambda }_{\mathrm{F}X2}=76.46°$, as shown in Figure 6b. The $RB$ value of 44.32 nm is still greater than 15 nm, and a new waypoint should be added. When the $n=3$, the termination condition is reached after 248 iterations, and the optimal solution is $\mathsf{\Delta }{\lambda }_{\mathrm{F}X1}=28.91°$, $\mathsf{\Delta }{\lambda }_{\mathrm{F}X2}=57.42°$, and $\mathsf{\Delta }{\lambda }_{\mathrm{F}X3}=86.02°$, as shown in Figure 6c. The $RB$ value of 25.01 nm is still greater than 15 nm, and a new waypoint should be added. When the $n=4$, the termination condition is reached after 305 iterations, and the optimal solution is $\mathsf{\Delta }{\lambda }_{\mathrm{F}X1}=23.20°$, $\mathsf{\Delta }{\lambda }_{\mathrm{F}X2}=46.01°$, $\mathsf{\Delta }{\lambda }_{\mathrm{F}X3}=68.81°$, and $\mathsf{\Delta }{\lambda }_{\mathrm{F}X4}=91.82°$, as shown in Figure 6d. The $RB$ value of 16.02 nm is still greater than 15 nm, and a new waypoint should be added. When the $n=5$, the termination condition is reached after 330 iterations, and the optimal solution is $\mathsf{\Delta }{\lambda }_{\mathrm{F}X1}=19.39°$, $\mathsf{\Delta }{\lambda }_{\mathrm{F}X2}=38.41°$, $\mathsf{\Delta }{\lambda }_{\mathrm{F}X3}=57.40°$, $\mathsf{\Delta }{\lambda }_{\mathrm{F}X4}=76.41°$, and $\mathsf{\Delta }{\lambda }_{\mathrm{F}X5}=95.74°$, as shown in Figure 6e. The $RB$ value of 11.13 nm becomes less than 15 nm, and the process is stopped. The optimal position distributions of five waypoints obtained by decoding were: $X_1$(41$°$38.4′ N, 140$°$03.0′ W), $X_2$(45$°$03.6′ N, 159$°$04.2′ W), $X_3$(45$°$09.0′ N, 178$°$04.2′ W), $X_4$(41$°$57.6′ N, 162$°$55.2′ E), and $X_5$(34$°$38.4′ N, 143$°$36.0′ E).

Comparing the GA method and the longitude bisection method (LBM) under the same example, the condition for both methods to stop the process was set such that they no longer added a new waypoint when the $RB$ became less than 15 nm. As shown in Figure 7, the GA method only needs 5 waypoints, while the LBM needs 6 waypoints; moreover, the $RB$ of each waypoint of the GA method became less than that of the LBM, which shows that the GA method has indeed optimized the position and number of waypoints through the optimization process. It is worth noting that when the number of waypoints was an even number, the difference of $RB$ between the GA method and LBM was more obvious.

In fact, the disadvantages of the LBM process were most obvious when the number of waypoints was even. As shown in Figure 8a, when the first waypoint ($X_1$) has been obtained, the LBM will select the part between $\mathrm{F}{X}_1$ and $X_1\mathrm{T}$ where the distance difference between the GC and RL leg is larger and will add the second waypoint ($X_2$) through longitude bisection, resulting in an uneven position distribution of waypoints. In contrast, as shown in Figure 8b, the optimal position distribution of waypoints yielded by the GA method was more uniform through global search optimization.

In order to make more comparisons, the other five routes were listed in

Table 3. Comparison of the GA method and LBM in the other five routes.

Route	Departure (F)	Destination (T)	Method	n	RB
1	Yokohama (35°27.0′ N, 139°38.0′ E)	San Francisco (34°00.0′ N, 120°40.0′ W)	GA LBM	4 4	10.84 13.83
2	Busan (35°07.0′ N, 129°02.0′ E)	Seattle (47°42.0′ N, 122°22.0′ W)	GA LBM	5 6	11.34 10.80
3	Shanghai (31°23.0′ N, 121°30.0′ E)	Vancouver (49°14.0′ N, 123°11.0′ W)	GA LBM	5 6	13.78 12.99
4	New York (40°43.0′ N, 74°00.0′ W)	London (51°30.0′ N, 0°05.0′ W)	GA LBM	2 3	13.67 7.69
5	Los Angeles (33°43.0′ N, 118°17.0′ W)	Shanghai (31°23.0′ N, 121°30.0′ E)	GA LBM	5 6	14.34 14.08

. It can be seen that under the same stopping process conditions, the $n$ used by the GA method was less; when the $n$ was the same, the $RB$ of the GA method was lower. These results confirm again that the optimal position distribution of waypoints on the GCR can be achieved through the optimization process of the GA method, which solves the problem that the position of waypoints obtained by LBM is not the optimal solution.

5.2. Example Demonstration for the FL Method

Using the same example in Section 5.1 to demonstrate how the FL method proposed in this study determines whether to add a new waypoint or stop the process in a non-fixed way, as shown in

Table 4. Membership degree calculation and rules’ judgment.

n	Lower	Medium	Higher	RB	Low	Medium	High	Rule (n/RB)	Result
1	1	0	0	98.39	0	0	1	Lower/High	Continue
2	0.75	0	0	44.32	0	0	1	Lower/High	Continue
3	0.50	0.17	0	25.01	0	0.28	0.29	Lower/High	Continue
4	0.25	0.33	0	16.02	0.14	0.43	0	Medium/Medium	Stop

, the process was as described below.

When the $n=1$ and $RB=98.39$, one rule is activated: $n$ is lower (the membership is 1) and $RB$ is high (the membership is 1), and the obtained weight is 1 (i.e., min (1, 1)). Refer to Table 1 to know that the iteration should continue, and a new waypoint should be added. When the $n=2$ and $RB=44.32$, one rule is activated: $n$ is lower (the membership is 0.75) and $RB$ is high (the membership is 1), and the obtained weight is 0.75 (i.e., min (0.75, 1)). Refer to Table 1 to know that the iteration should continue, and a new waypoint should be added. When the $n=3$ and $RB=25.01$, four rules are activated. Rule 1: $n$ is lower (the membership is 0.50) and $RB$ is medium (the membership is 0.28), and the obtained weight is 0.28 (i.e., min (0.50, 0.28)). Rule 2: $n$ is lower (the membership is 0.50) and $RB$ is high (the membership is 0.29), and the obtained weight is 0.29 (i.e., min (0.50, 0.29)). Rule 3: $n$ is medium (the membership is 0.17) and $RB$ is medium (the membership is 0.28), and the obtained weight is 0.17 (i.e., min (0.17, 0.28)). Rule 4: $n$ is medium (the membership is 0.17) and $RB$ is high (the membership is 0.29), and the obtained weight is 0.17 (i.e., min (0.17, 0.29)). Among them, the maximum weight is 0.29 of Rule 2 (i.e., max (0.28, 0.29, 0.17, 0.17)). Refer to Table 1 to know that the iteration should continue, and a new waypoint should be added. When the $n=4$ and $RB=16.02$, four rules are activated. Rule 1: $n$ is lower (the membership is 0.25) and $RB$ is low (the membership is 0.14), and the obtained weight is 0.14 (i.e., min (0.25, 0.14)). Rule 2: $n$ is lower (the membership is 0.25) and $RB$ is medium (the membership is 0.43), and the obtained weight is 0.25 (i.e., min (0.25, 0.43)). Rule 3: $n$ is medium (the membership is 0.33) and $RB$ is low (the membership is 0.14), and the obtained weight is 0.14 (i.e., min (0.33, 0.14)). Rule 4: $n$ is medium (the membership is 0.33) and $RB$ is medium (the membership is 0.43), and the obtained weight is 0.33 (i.e., min (0.33, 0.43)). Among them, the maximum weight is 0.33 of Rule 4 (i.e., max (0.14, 0.25, 0.14, 0.33)). Refer to Table 1 to know that the process should stop, and no new waypoint should be added. In this study, the fixed values of $n$ and $RB$ were converted into three levels, respectively, and the membership degrees of each level range from 0 to 1. The combined nine rules cover all possibilities. Therefore, the evaluation result can be obtained by referring to Table 1.

In fact, as shown in Table 2, when $n=4$, the $RB$ is 16.02 nm; when $n=5$, the $RB$ is 11.13 nm, and the benefit that can be saved by adding a new waypoint is no longer obvious. The results show that, compared with a fixed judgment constraint of 15 nm for the LBM or GA method, the FL method proposed in this study can reduce unnecessary waypoints and provide a more flexible decision process for stopping the calculation process. By means of non-fixed value judgment, the problem of adding one more waypoint when it was only slightly more than 15 nm was solved.

6. Conclusions

To better determine the positions of waypoints on the GCR, this study proposed the GA method, which is an optimization method for the waypoints on the GCR based on the genetic algorithm. When the number of waypoints was known, in addition to optimizing the position distribution of waypoints, this study also found that the longitude bisection method (LBM) has the disadvantage of uneven position distribution when the number of waypoints was even. To optimize the number of waypoints on the GCR in a smooth way, this study proposed the FL method, which is an evaluation method for the number of waypoints based on fuzzy logic. Compared with the traditional 15 nm threshold, it can more flexibly and reasonably determine the number of waypoints. This study mainly proposed ideas and methods for optimizing the number and position of waypoints on the GCR and provided theoretical support for the optimization and planning of ocean routes.

The advantage of this study is to optimize the position distribution of waypoints on the GCR with a reasonable number of waypoints. It allows the navigator to reduce unnecessary frequent course changes when sailing along the GCR, while maintaining the benefit of shortening the voyage. However, there are two limitations: (1) In order to simplify the problem, this study mainly considered the distance factor to evaluate the waypoint, without considering other factors such as weather and sea conditions. (2) Many parameters in the genetic algorithm and fuzzy logic used in this study were only set to reasonable values, and users can adjust the values according to their preferences.

On the basis of this paper, in the next stage of research work, we intend to consider the weather, fuel consumption, and ship maneuvering characteristics, with the goal of safety and energy saving, to further study the maneuverability of the GCR. In addition, the GCR is widely used in aviation, aerospace, and other fields, and it is expected to apply the research results of this paper to different professional fields in the future.