Stress–Strain Assessment of Honeycomb Sandwich Panel Subjected to Uniaxial Compressive Load
Abstract
:1. Introduction
2. Compressive Test of Honeycomb Sandwich Panel
2.1. Research Object
2.2. Research Methodology
2.2.1. Experimental Analysis
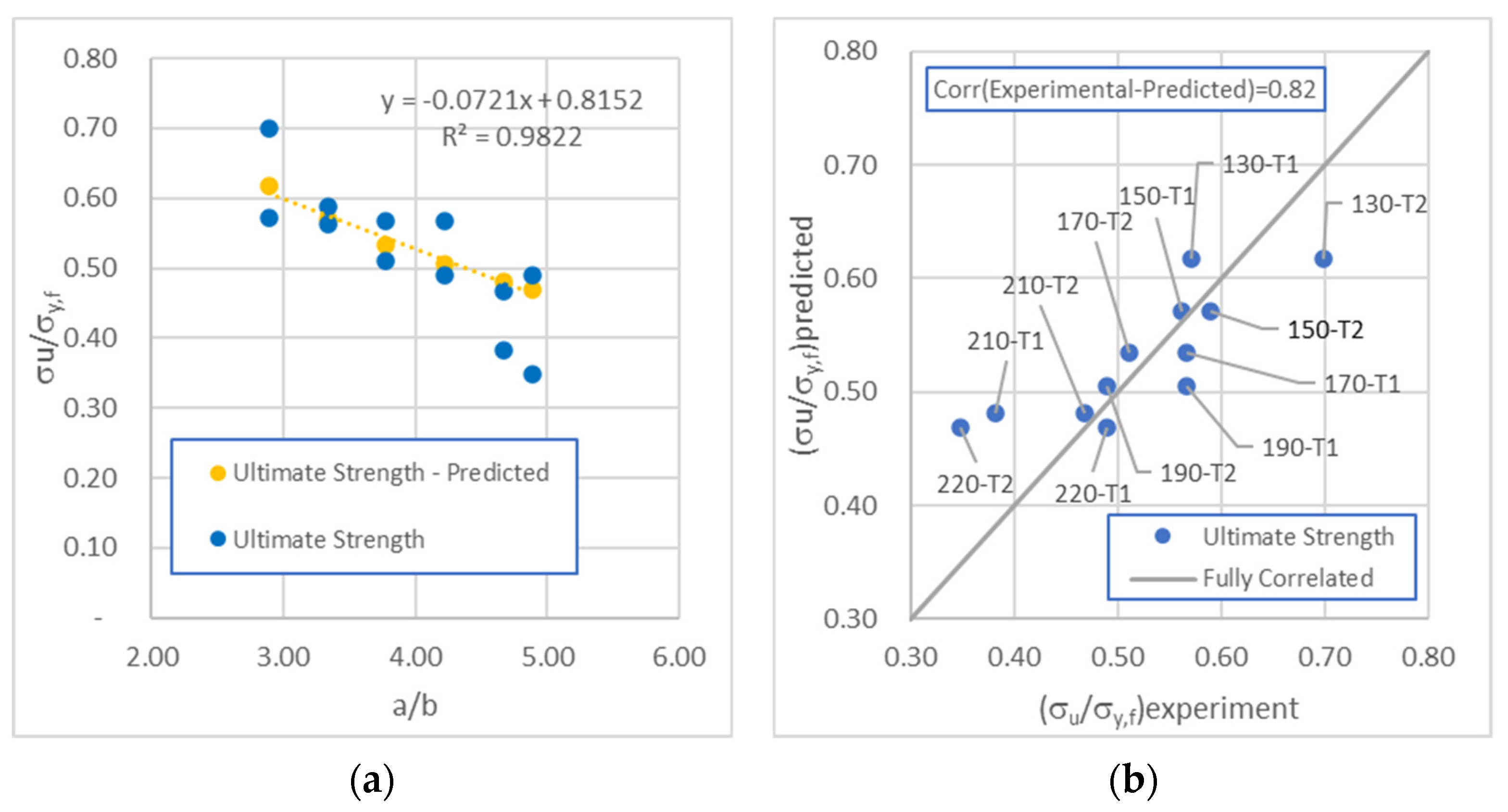
2.2.2. Prediction Model
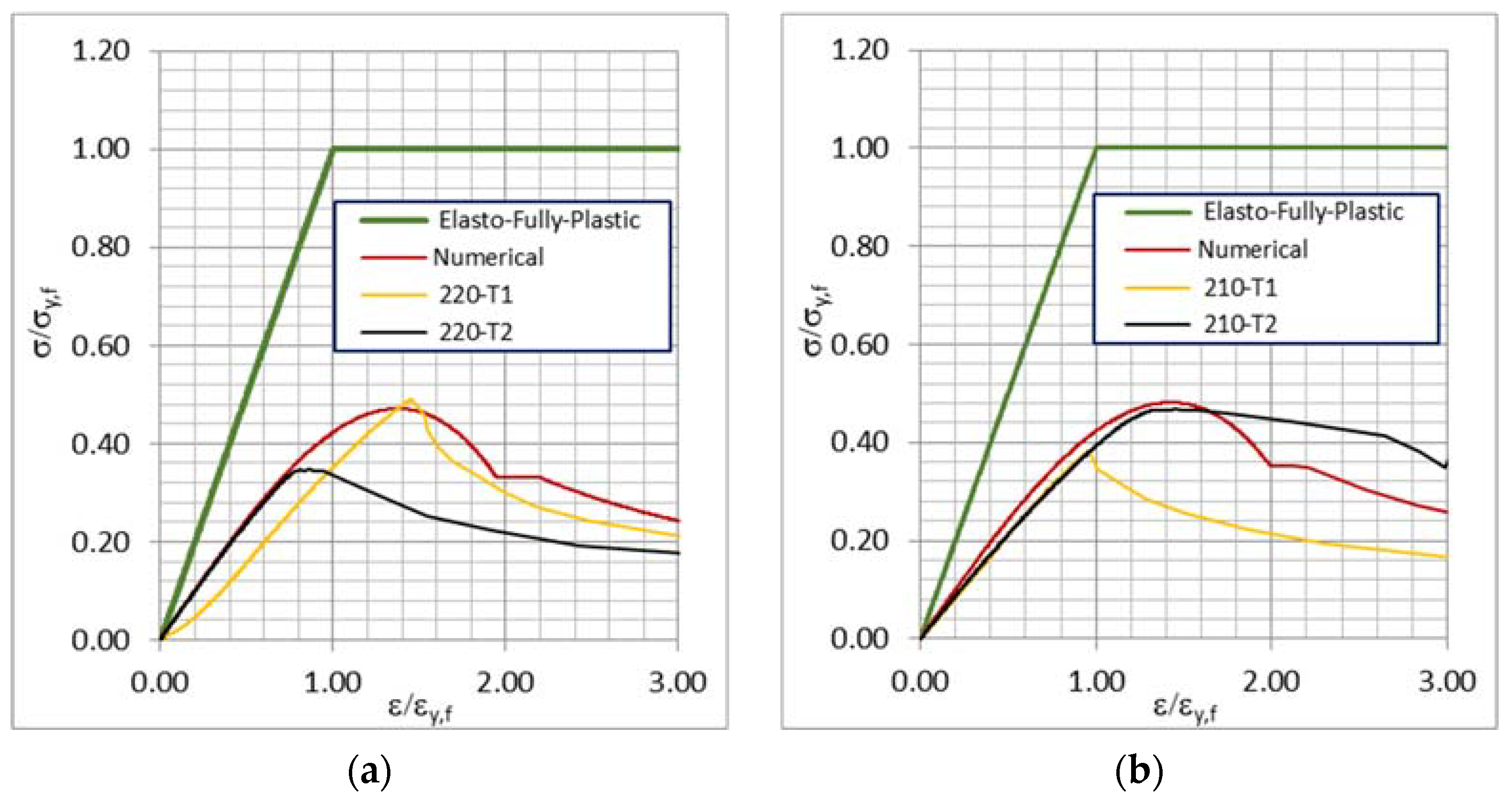
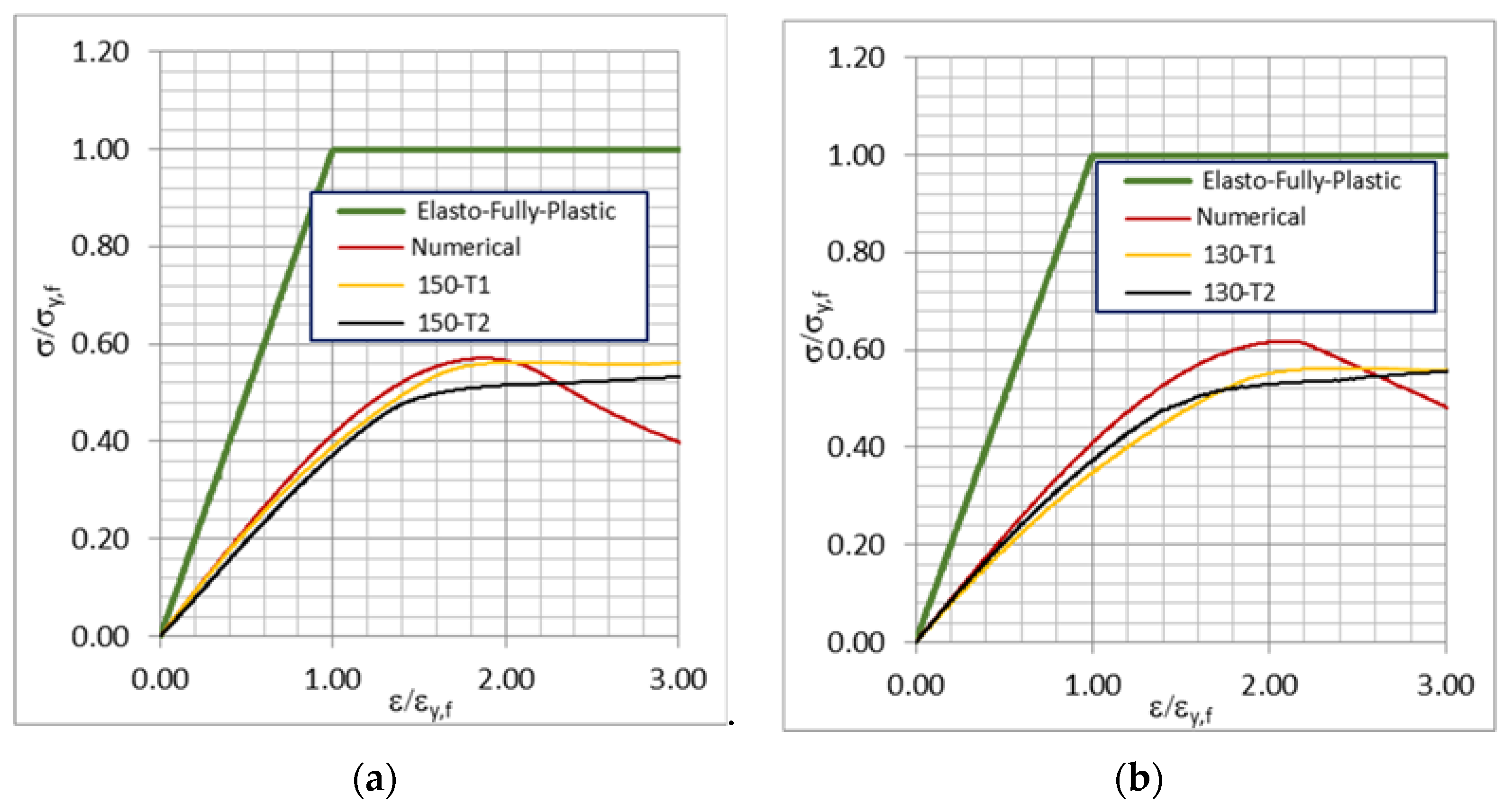
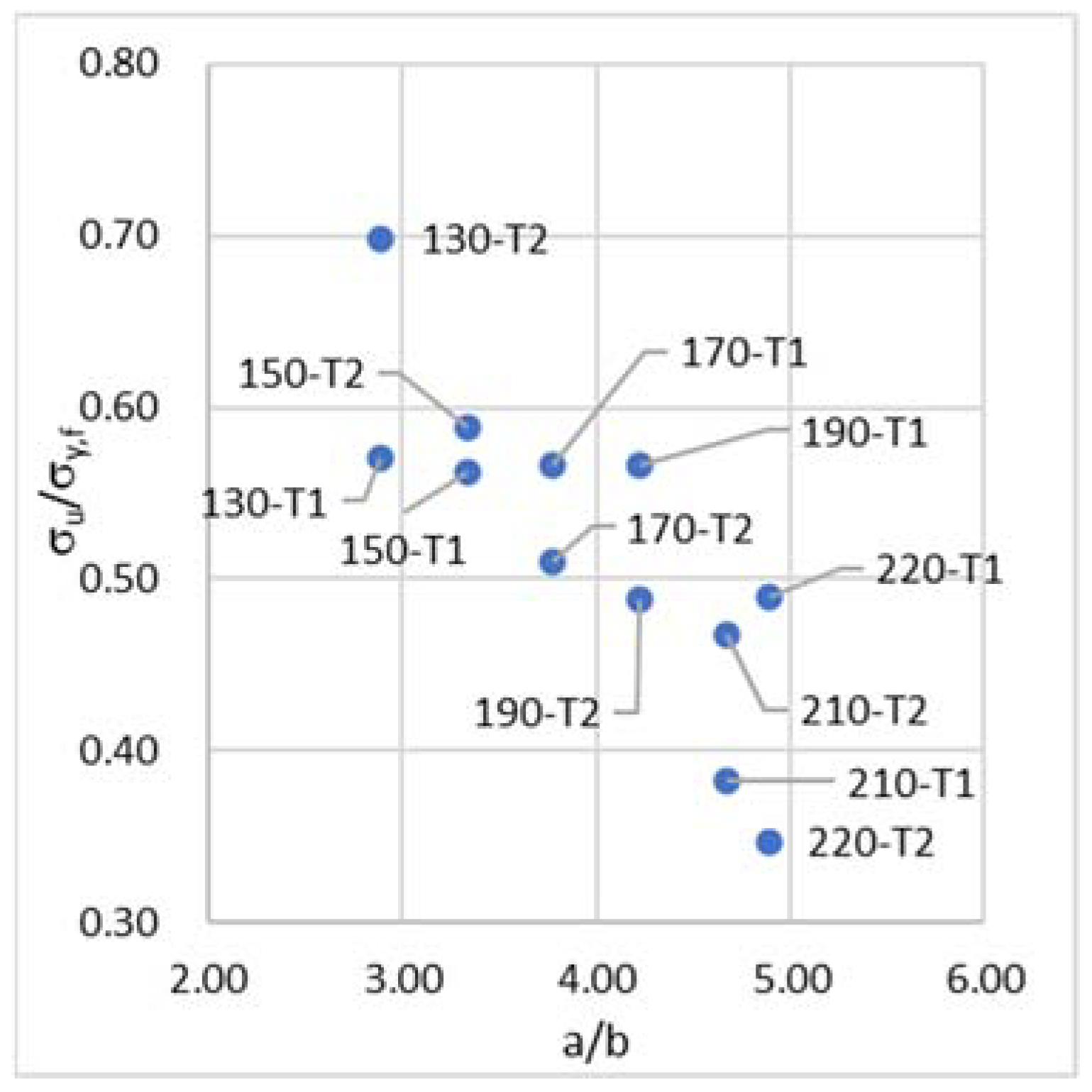
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Paik, J.K.; Lee, D.H.; Noh, S.H.; Park, D.K.; Ringsberg, J.W. Full-Scale Collapse Testing of a Steel Stiffened Plate Structure under Cyclic Axial-Compressive Loading. Structures 2020, 26, 996–1009. [Google Scholar] [CrossRef]
- Doukas, H.; Spiliotis, E.; Jafari, M.A.; Giarola, S.; Nikas, A. Low-Cost Emissions Cuts in Container Shipping: Thinking inside the Box. Transp. Res. Part D 2021, 94, 102815. [Google Scholar] [CrossRef]
- Palomba, G.; Marchese, S.S.; Crupi, V.; Garbatov, Y. Cost, Energy Efficiency and Carbon Footprint Analysis of Hybrid Light-weight Bulk Carrier. J. Mar. Sci. Eng. 2022, 10, 957. [Google Scholar] [CrossRef]
- Palomba, G.; Epasto, G.; Sutherland, L.; Crupi, V. Aluminium Honeycomb Sandwich as a Design Alternative for Light-weight Marine Structures. Ships Offshore Struct. 2021, 17, 2355–2366. [Google Scholar] [CrossRef]
- Kortenoeven, J.; Boon, B.; de Bruijn, A. Application of Sandwich Panels in Design and Building of Dredging Ships. J. Ship Prod. 2008, 3, 125–134. [Google Scholar] [CrossRef]
- Nguyen, T.T.T.; Le, T.A.; Tran, Q.H. Composite Sandwich Structures in the Marine Applications. In Sandwich Composites; CRC Press: Boca Raton, FL, USA, 2022; pp. 277–291. ISBN 9781003143031. [Google Scholar]
- Palomba, G.; Corigliano, P.; Crupi, V.; Epasto, G.; Guglielmino, E. Static and Fatigue Full-Scale Tests on a Lightweight Ship Balcony Overhang with Al/Fe Structural Transition Joints. J. Mar. Sci. Eng. 2022, 10, 1382. [Google Scholar] [CrossRef]
- Li, Y.; Wu, X.; Xiao, W.; Wang, S.; Zhu, L. Experimental Study on the Dynamic Behaviour of Aluminium Honeycomb Sandwich Panel Subjected to Ice Wedge Impact. Compos. Struct. 2022, 282, 115092. [Google Scholar] [CrossRef]
- Wu, X.; Li, Y.; Cai, W.; Guo, K.; Zhu, L. Dynamic Responses and Energy Absorption of Sandwich Panel with Aluminium Honeycomb Core under Ice Wedge Impact. Int. J. Impact Eng. 2022, 162, 104137. [Google Scholar] [CrossRef]
- IMO. Fourth IMO GHG Study 2020; IMO: Singapore, 2020. [Google Scholar]
- Grimes, S.; Donaldson, J.; Gomez, G.C. Report on the Environmental Benefits of Recycling; Bureau of International Recycling: Brussels, Belgium, 2008. [Google Scholar]
- Schlesinger, M.E. Aluminum Recycling, 2nd ed.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2014; ISBN 9781466570252. [Google Scholar]
- Garbatov, Y.; Saad-Eldeen, S.; Guedes Soares, C. Hull Girder Ultimate Strength Assessment Based on Experimental Results and the Dimensional Theory. Eng. Struct. 2015, 100, 742–750. [Google Scholar] [CrossRef]
- Woloszyk, K.; Garbatov, Y.; Kowalski, J.; Samson, L. Experimental and Numerical Investigations of Ultimate Strength of Imperfect Stiffened Plates of Different Slenderness. Pol. Marit. Res. 2020, 4, 120–129. [Google Scholar] [CrossRef]
- Corigliano, P. On the Compression Instability during Static and Low-Cycle Fatigue Loadings of AA 5083 Welded Joints: Full-Field and Numerical Analyses. J. Mar. Sci. Eng. 2022, 10, 212. [Google Scholar] [CrossRef]
- SANDCORe Co-Ordination Action. Best Practice Guide for Sandwich Structures in Marine Applications; NewRail, University of Newcastle: Newcastle upon Tyne, UK, 2013. [Google Scholar]
- Andric, J.; Prebeg, P.; Palaversa, M.; Zanic, V. Influence of Different Topological Variants on Optimized Structural Scantlings of Passenger Ship. Mar. Struct. 2021, 78, 102981. [Google Scholar] [CrossRef]
- Wang, Z.; Yuan, T.; Kong, X.; Wu, W. A Universal Similarity Method and Design Procedure for Buckling Assessment of Stiffened Plates under Compression Load on Real Ships. Thin-Walled Struct. 2022, 181, 110025. [Google Scholar] [CrossRef]
- IMO. RESOLUTION MSC.454(100)—Revised Guidelines for Verification of Conformity with Goal-Based Ship Construction Standards for Bulk Carriers and Oil Tankers; IMO: London, UK, 2018. [Google Scholar]
- Lloyd’s Register. Rules and Regulations for the Classification of Ships; Lloyd’s Register: London, UK, 2022. [Google Scholar]
- Liu, B.; Yao, X.; Lin, Y.; Wu, W.; Guedes Soares, C. Experimental and Numerical Analysis of Ultimate Compressive Strength of Long-Span Stiffened Panels. Ocean Eng. 2021, 237, 109633. [Google Scholar] [CrossRef]
- Liu, B.; Chen, C.; Garbatov, Y. Material Failure Criterion in the Finite Element Analysis of Aluminium Alloy Plates under Low-Velocity Impact. Ocean Eng. 2022, 266, 113260. [Google Scholar] [CrossRef]
- Liu, B.; Doan, V.T.; Garbatov, Y.; Wu, W.; Soares, C.G. Study on Ultimate Compressive Strength of Aluminium-Alloy Plates and Stiffened Panels. J. Mar. Sci. Appl. 2020, 19, 534–552. [Google Scholar] [CrossRef]
- Wysmulski, P. The Effect of Load Eccentricity on the Compressed CFRP Z-Shaped Columns in the Weak Post-Critical State. Compos. Struct. 2022, 301, 116184. [Google Scholar] [CrossRef]
- Kubiak, T.; Kolakowski, Z.; Swiniarski, J.; Urbaniak, M.; Gliszczynski, A. Local Buckling and Post-Buckling of Composite Channel-Section Beams—Numerical and Experimental Investigations. Compos. B Eng. 2016, 91, 176–188. [Google Scholar] [CrossRef]
- Wysmulski, P.; Teter, A.; Debski, H. Effect of Load Eccentricity on the Buckling of Thin-Walled Laminated C-Columns. In AIP Conference Proceedings; American Institute of Physics Inc.: Woodbury, Long Island, NY, USA, 5 January 2018; Volume 1922. [Google Scholar]
- Wang, J.; Yi, B.; Zhou, H. Framework of Computational Approach Based on Inherent Deformation for Welding Buckling Investigation during Fabrication of Light-weight Ship Panel. Ocean Eng. 2018, 157, 202–210. [Google Scholar] [CrossRef]
- Eyvazian, A.; Taghizadeh, S.A.; Hamouda, A.M.; Tarlochan, F.; Moeinifard, M.; Gobbi, M. Buckling and Crushing Behavior of Foam-Core Hybrid Composite Sandwich Columns under Quasi-Static Edgewise Compression. J. Sandw. Struct. Mater. 2021, 23, 2643–2670. [Google Scholar] [CrossRef]
- Wei, X.; Wu, Q.; Gao, Y.; Yang, Q.; Xiong, J. Composite Honeycomb Sandwich Columns under In-Plane Compression: Optimal Geometrical Design and Three-Dimensional Failure Mechanism Maps. Eur. J. Mech. A/Solids 2022, 91, 104415. [Google Scholar] [CrossRef]
- Kardomateas, G.A.; Simitses, G.J.; Shen, L.; Li, R. Buckling of Sandwich Wide Columns. Int. J. Non-Linear Mech. 2002, 37, 1239–1247. [Google Scholar] [CrossRef]
- Léotoing, L.; Drapier, S.; Vautrin, A. First Applications of a Novel Unified Model for Global and Local Buckling of Sandwich Columns. Eur. J. Mech. A/Solids 2002, 21, 683–701. [Google Scholar] [CrossRef]
- Salazar-Domínguez, C.M.; Hernández-Hernández, J.; Rosas-Huerta, E.D.; Iturbe-Rosas, G.E.; Herrera-May, A.L. Structural Analysis of a Barge Midship Section Considering the Still Water and Wave Load Effects. J. Mar. Sci. Eng. 2021, 9, 99. [Google Scholar] [CrossRef]
- HexCel HexWeb Honeycomb Sandwich Design Technology. HexWeb Honeycomb sandwich design technology 2000, 1–28.
- Smith, C.S. Influence of Local Compressive Failure on Ultimate Longitudinal Strength of a Ship’s Hull. In Proceedings of the International Symposium on Practical Design in Shipbuilding, Tokyo, Japan, 17–21 October 1977; pp. 73–79. [Google Scholar]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; McGraw-Hill: New York, NY, USA, 1985; ISBN 0-07-Y85821-7. [Google Scholar]
- Frankland, J.M. The Strength of Ship Plating under Edge Compression. US EMB Rep. 1940, 469, 13–14. [Google Scholar]
- Faulkner, D. A Review of Effective Plating for Use in the Analysis of Stiffened Plating in Bending and Compression. J. Ship Res. 1975, 19, 1–17. [Google Scholar] [CrossRef]

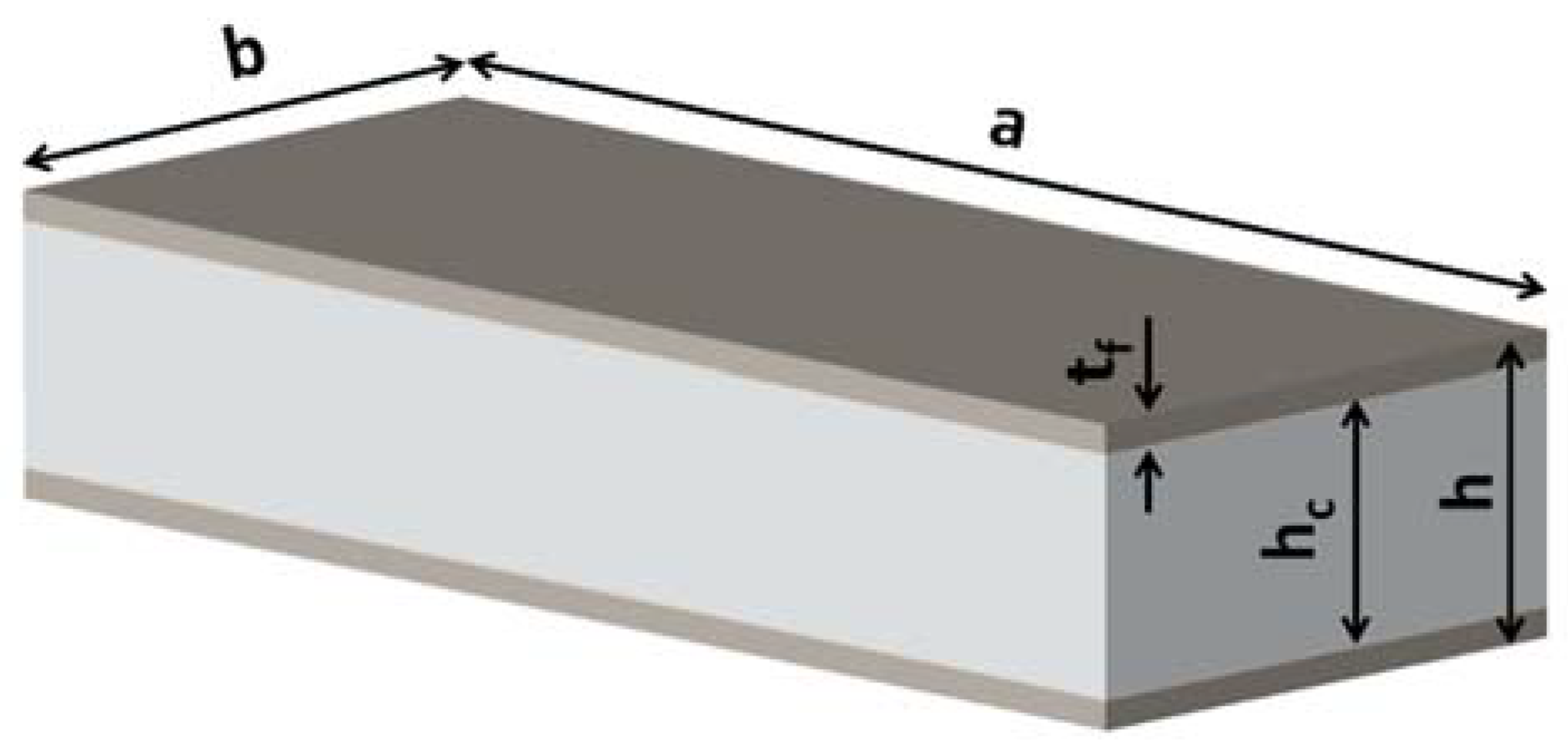




| Skin material | AA5754 |
| Core material | AA5052 |
| Skin Young’s modulus Ef [GPa] | 68 |
| Skin yield stress σy,f [MPa] | 155 |
| Core shear modulus Gw [MPa] 1 | 372 |
| Core density, ρ [kg/m3] 1 | 130 |
| Cell diameter [mm] | 3 |
| Cell wall thickness [μm] | 70 |
| Specimen width b [mm] | 45 |
| Skin thickness [mm] | 1 |
| Core thickness [mm] | 9 |
| Overall thickness [mm] | 11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corigliano, P.; Palomba, G.; Crupi, V.; Garbatov, Y. Stress–Strain Assessment of Honeycomb Sandwich Panel Subjected to Uniaxial Compressive Load. J. Mar. Sci. Eng. 2023, 11, 365. https://doi.org/10.3390/jmse11020365
Corigliano P, Palomba G, Crupi V, Garbatov Y. Stress–Strain Assessment of Honeycomb Sandwich Panel Subjected to Uniaxial Compressive Load. Journal of Marine Science and Engineering. 2023; 11(2):365. https://doi.org/10.3390/jmse11020365
Chicago/Turabian StyleCorigliano, Pasqualino, Giulia Palomba, Vincenzo Crupi, and Yordan Garbatov. 2023. "Stress–Strain Assessment of Honeycomb Sandwich Panel Subjected to Uniaxial Compressive Load" Journal of Marine Science and Engineering 11, no. 2: 365. https://doi.org/10.3390/jmse11020365
APA StyleCorigliano, P., Palomba, G., Crupi, V., & Garbatov, Y. (2023). Stress–Strain Assessment of Honeycomb Sandwich Panel Subjected to Uniaxial Compressive Load. Journal of Marine Science and Engineering, 11(2), 365. https://doi.org/10.3390/jmse11020365









