Effects of Internal Waves on Acoustic Temporal Coherence in the South China Sea
Abstract
:1. Introduction
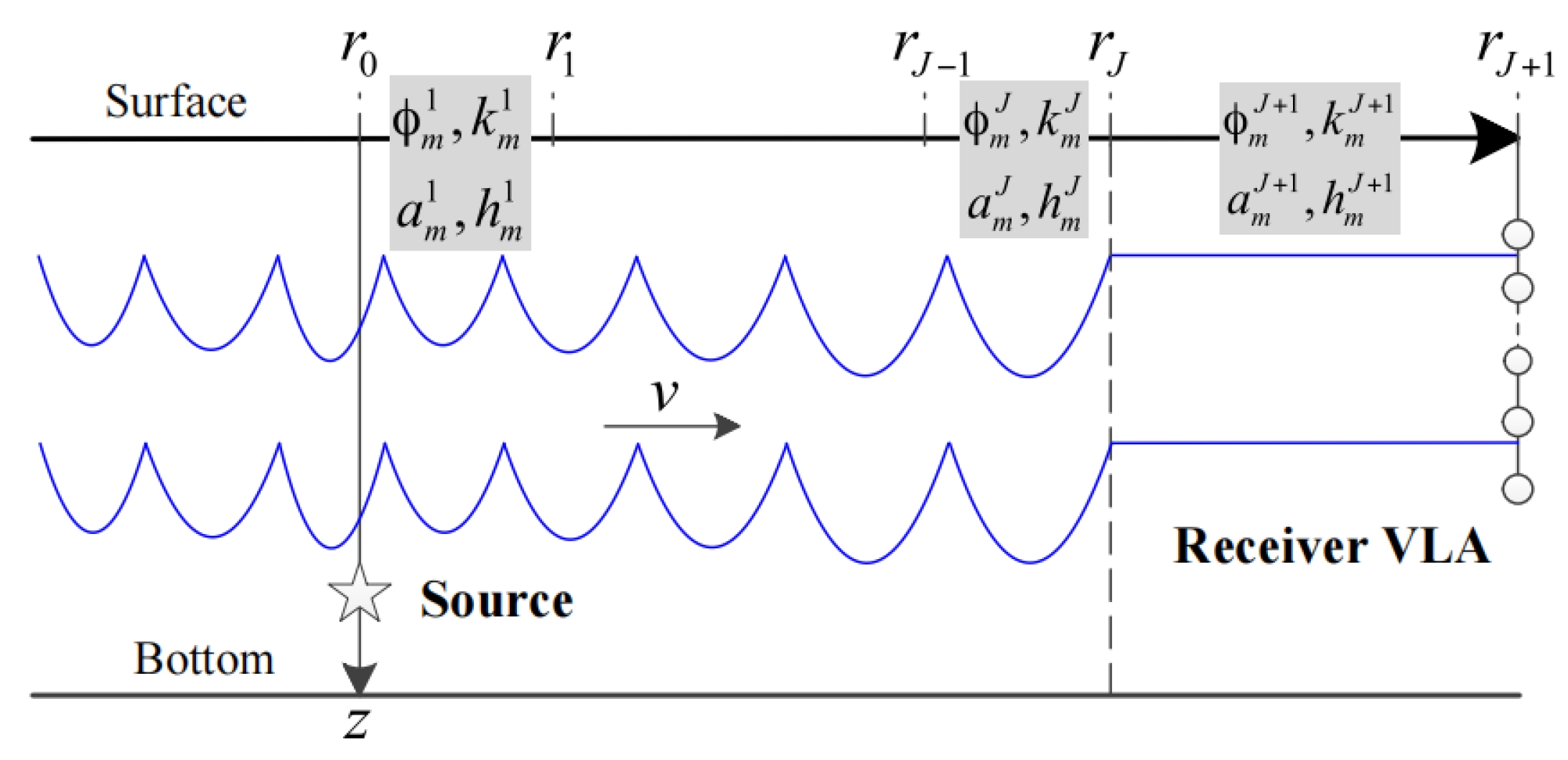
2. Method and Experiment
2.1. Temporal Coherence Function
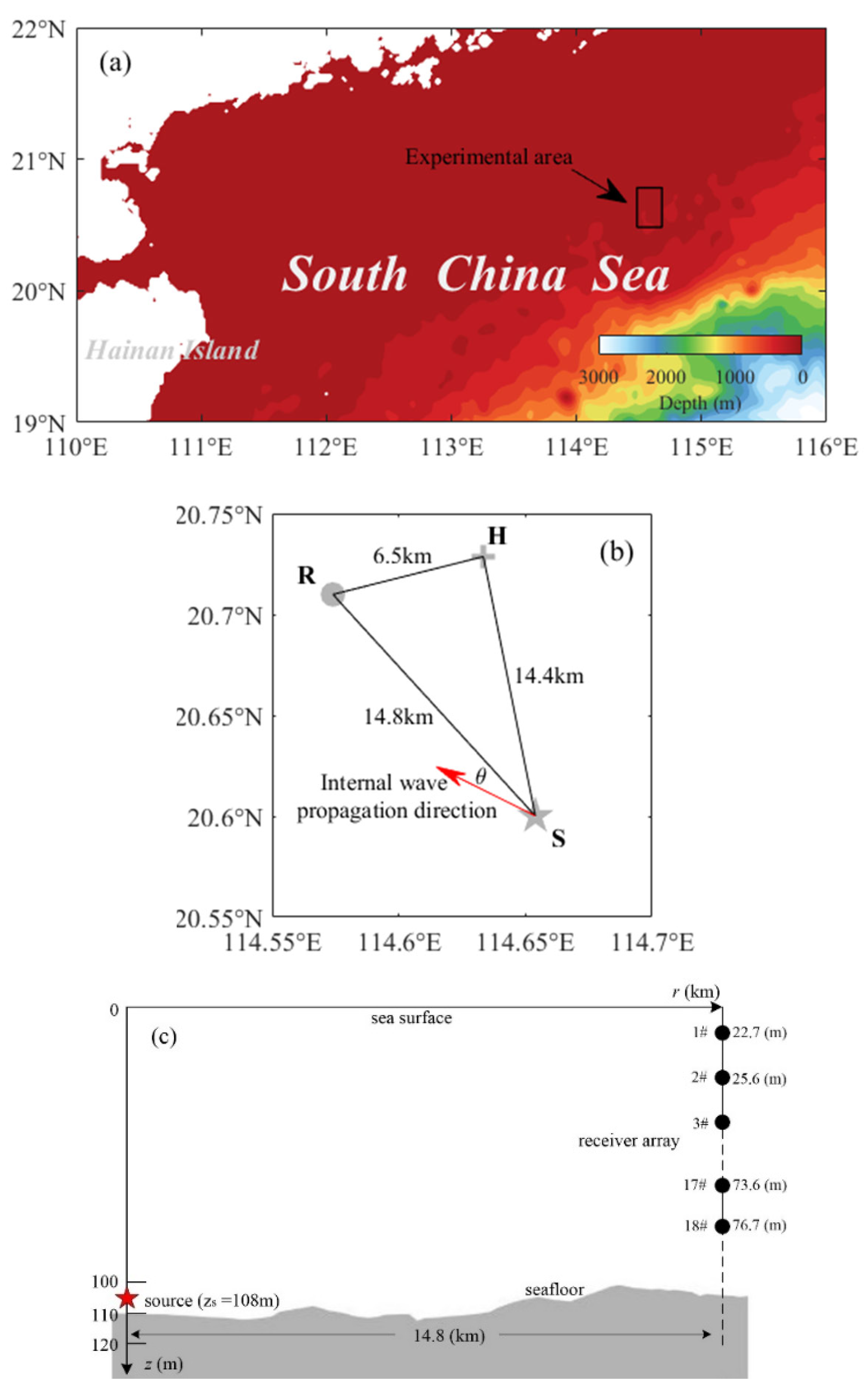
2.2. Acoustic Experiment Descriptions
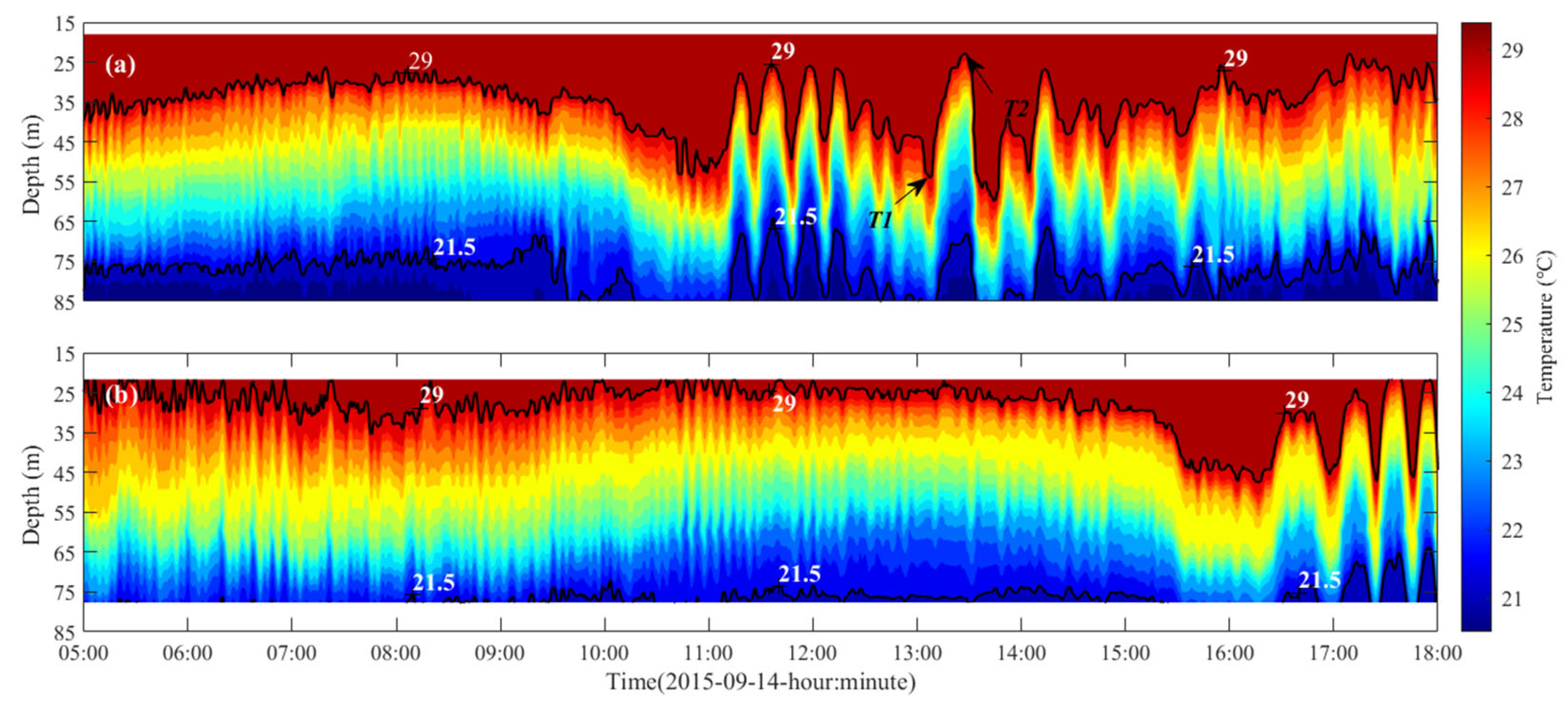
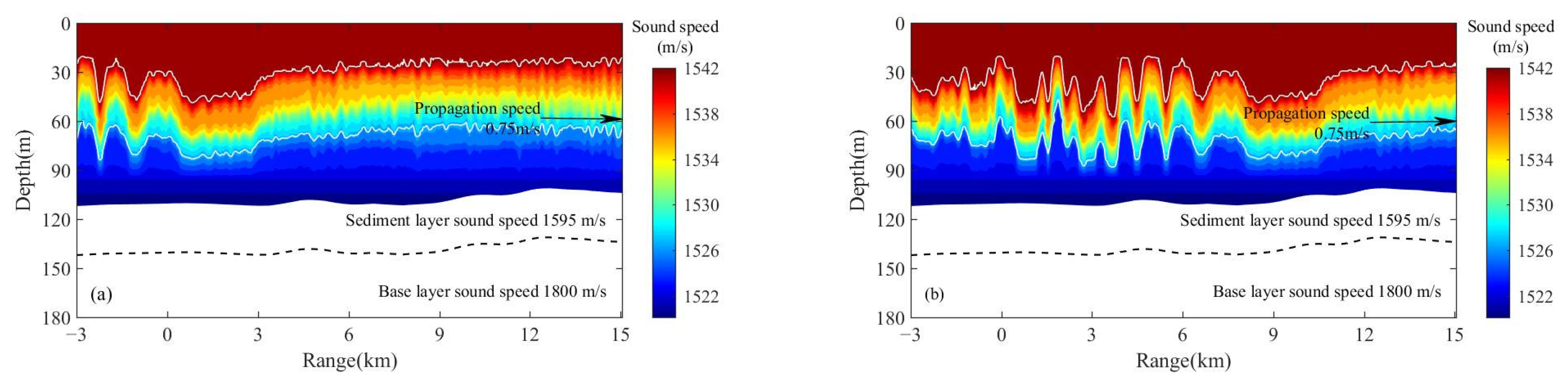
2.3. Internal Wave Analysis
3. Simulation and Experimental Data Analysis
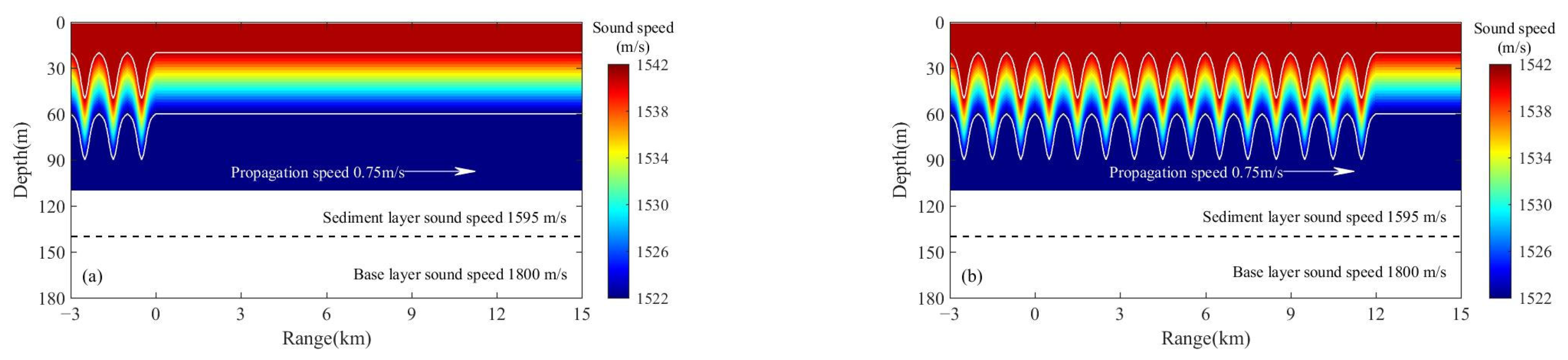
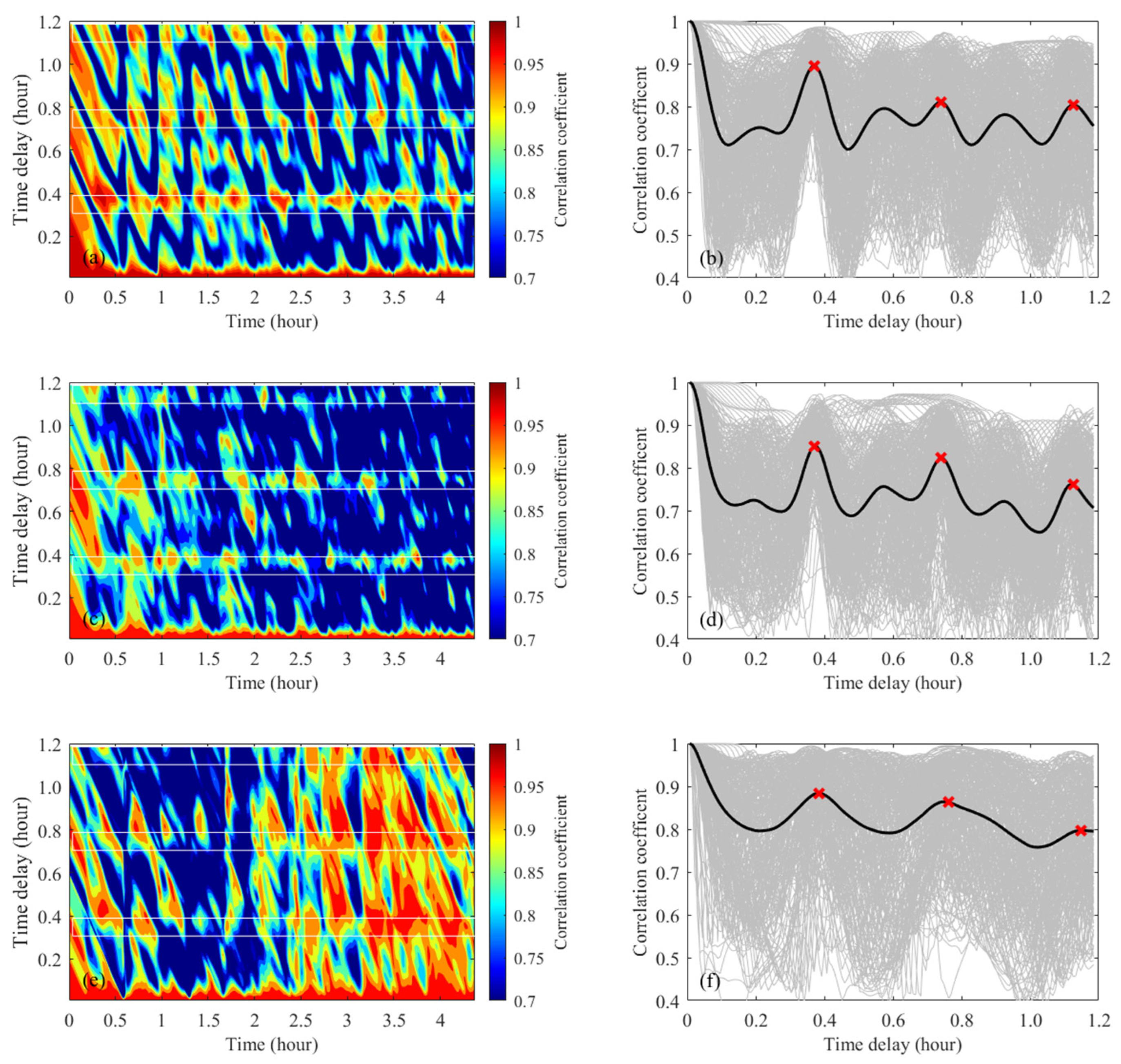
3.1. Simulations in an Ideal ISWs Environment
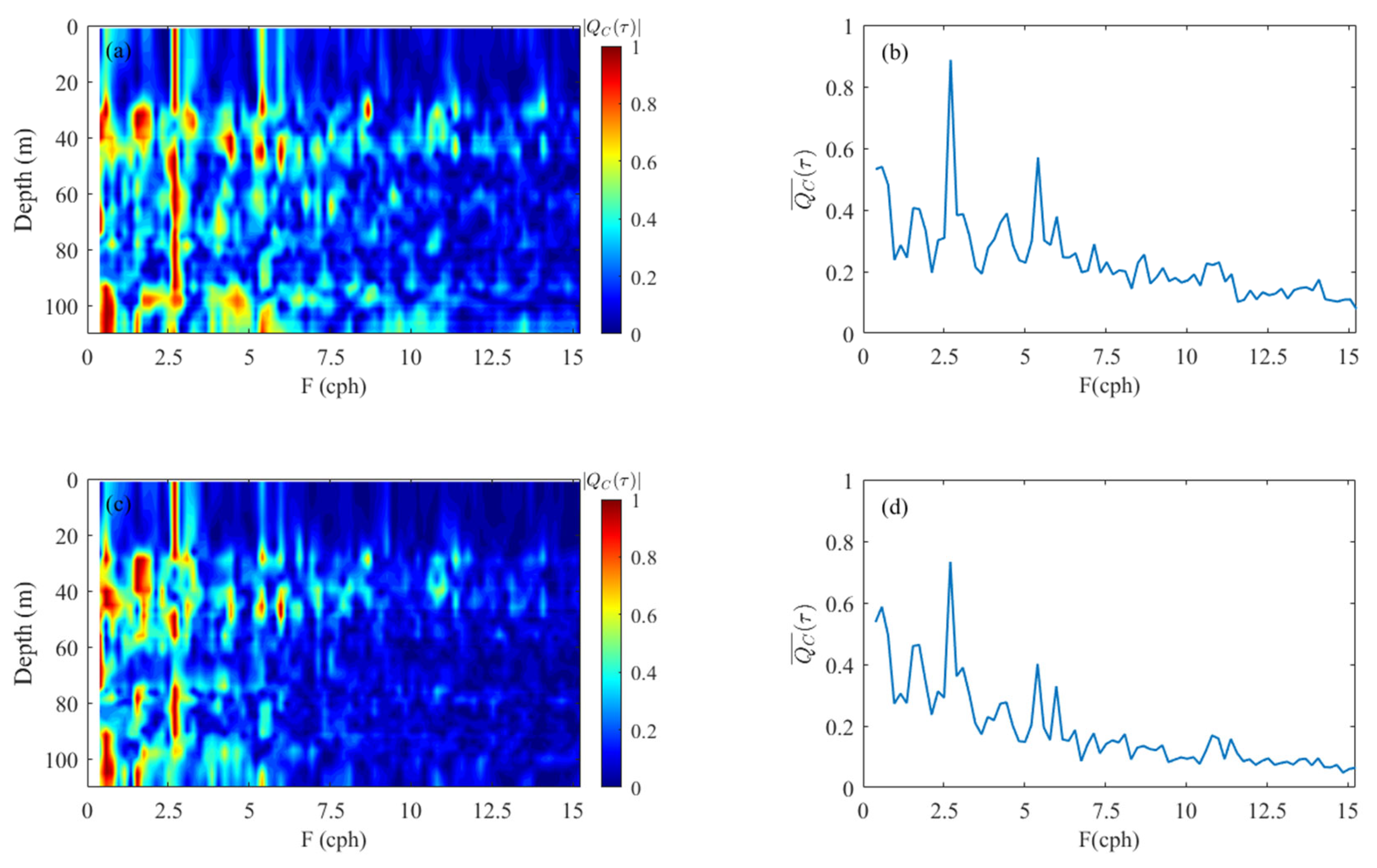
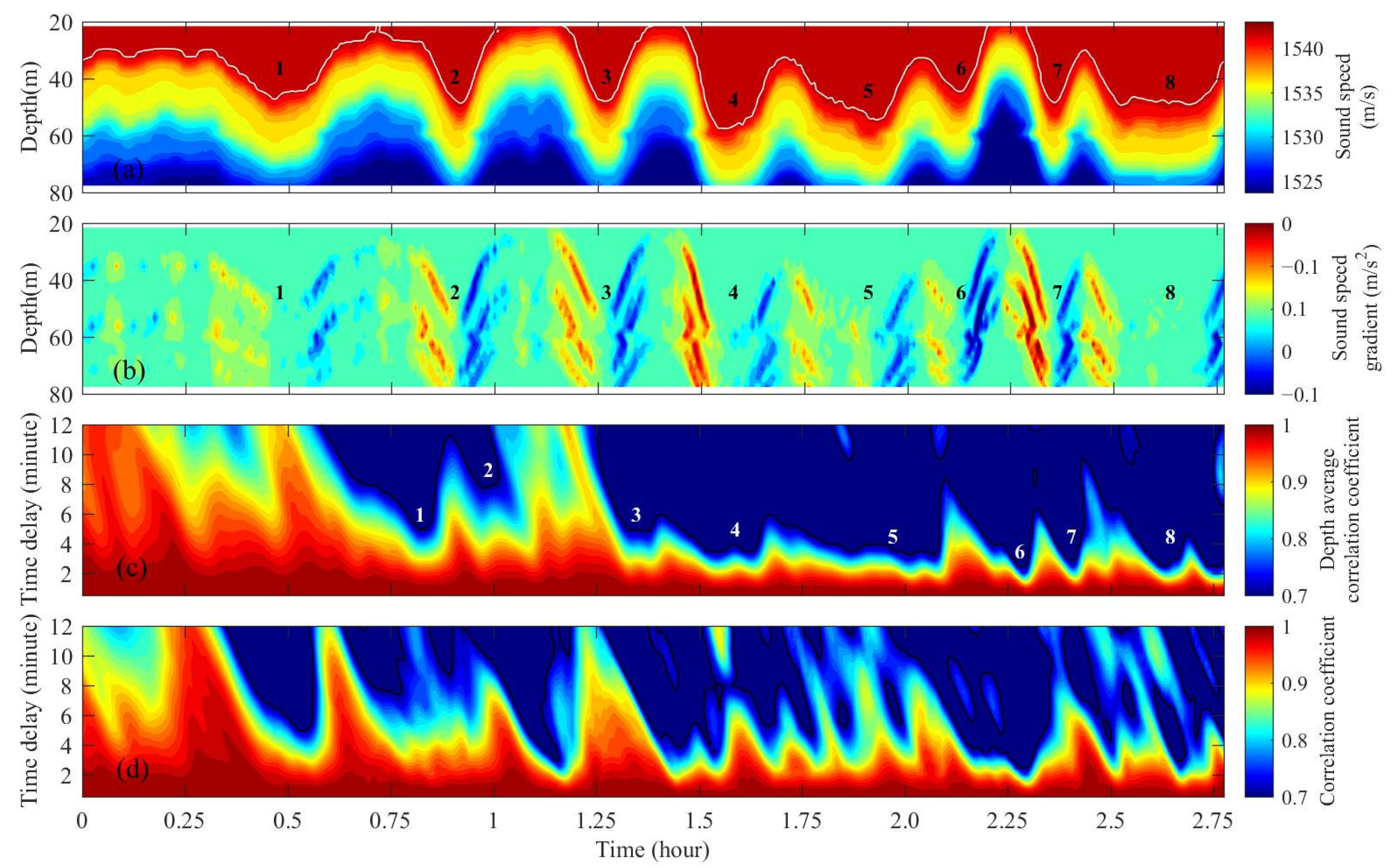
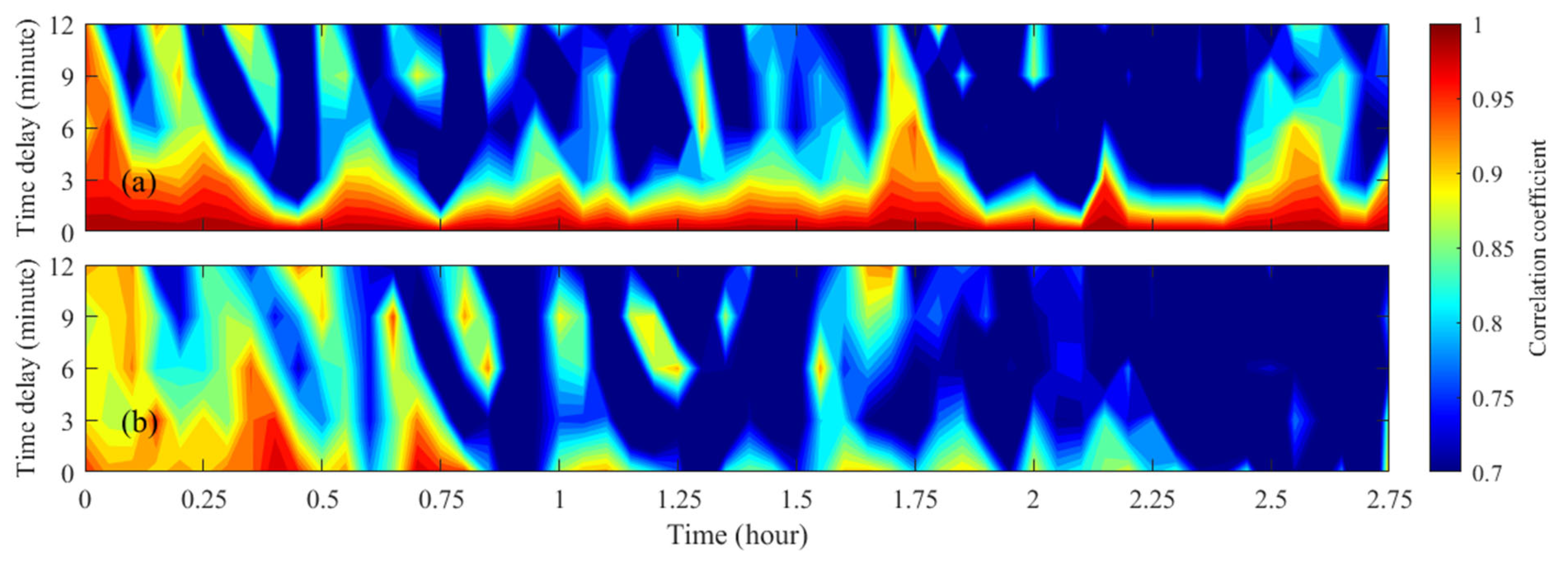
3.2. Simulations in the Experiment Environment and Verification with Experimental Data
4. Discussion
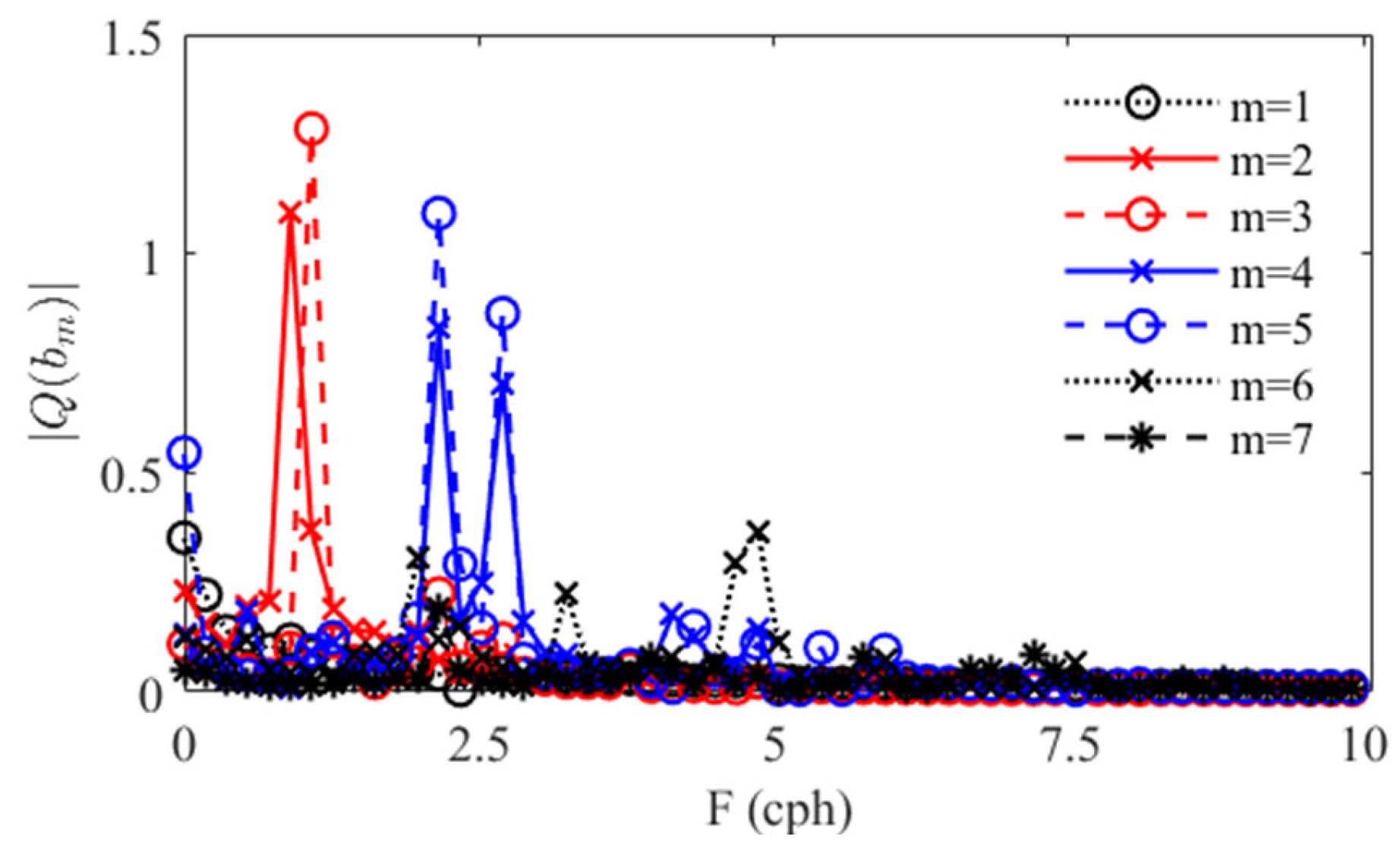
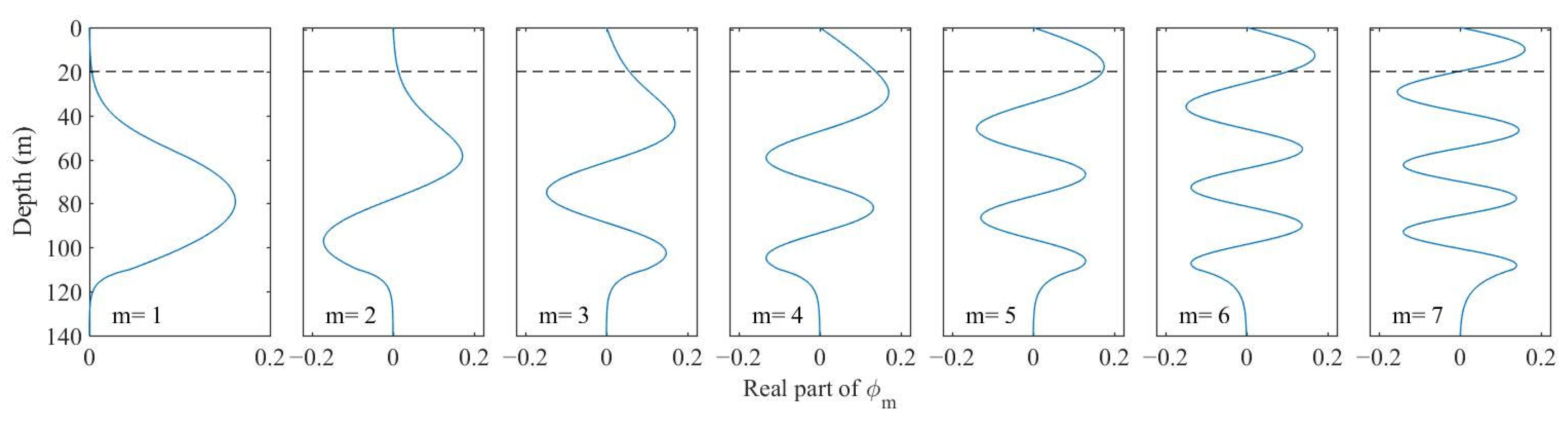
4.1. Quasi-Periodical Sound Field in the ISWs Environment
4.2. Mechanism Interpretation Using Coupled Normal Mode Theory
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, Q.A.; Xie, L.L.; Xiong, X.J.; Hu, X.M.; Chen, L. Progress in research of submesoscale processes in the South China sea. Acta Oceanol. Sin. 2020, 39, 1–13. [Google Scholar] [CrossRef]
- Wang, J.F.; Yu, F.; Nan, F.; Ren, Q.; Chen, Z.F.; Zheng, T.T. Observed three dimensional distributions of enhanced turbulence near the Luzon Strait. Sci. Rep. 2021, 11, 14835. [Google Scholar] [CrossRef] [PubMed]
- Whalen, C.B.; de Lavergne, C.D.; Garabato, A.C.N.; Klymak, J.M.; MacKinnon, J.A.; Sheen, K.L. Internal wave-driven mixing: Governing processes and consequences for climate. Nat. Rev. Earth Environ. 2020, 1, 606–621. [Google Scholar] [CrossRef]
- Apel, J.R.; Ostrovsky, L.A.; Stepanyants, Y.A.; Lynch, J.F. Internal solitons in the ocean and their effect on underwater sound. J. Acoust. Soc. Am. 2007, 121, 695–722. [Google Scholar] [CrossRef]
- Lynch, J.F.; Lin, Y.-T.; Duda, T.F.; Newhall, A.E. Acoustic ducting, reflection, refraction, and dispersion by curved nonlinear internal waves in shallow water. IEEE J. Ocean. Eng. 2010, 35, 12–27. [Google Scholar] [CrossRef]
- Dossot, G.A.; Smith, K.B.; Badiey, M.; Miller, J.H.; Potty, G.R. Underwater acoustic energy fluctuations during strong internal wave activity using a three-dimensional parabolic equation model. J. Acoust. Soc. Am. 2019, 146, 1875. [Google Scholar] [CrossRef]
- Zhou, J.X.; Zhang, X.Z.; Rogers, P.H. Resonant interaction of sound wave with internal solitons in the coastal zone. J. Acoust. Soc. Am. 1991, 90, 2042–2054. [Google Scholar] [CrossRef]
- Preisig, J.C.; Duda, T.F. Coupled acoustic mode propagation through continental-shelf internal solitary waves. IEEE J. Ocean. Eng. 1997, 22, 256–269. [Google Scholar] [CrossRef]
- Duda, T.F. Acoustic mode coupling by nonlinear internal wave packets in a shelfbreak front area. IEEE J. Ocean. Eng. 2004, 29, 118–125. [Google Scholar] [CrossRef]
- Gao, F.; Xu, F.H.; Li, Z.L.; Qin, J.X. Mode coupling and intensity fluctuation of sound propagation over continental slope in presence of internal waves. Acta Phys. Sin. 2022, 71, 204301–204314. (In Chinese) [Google Scholar] [CrossRef]
- Katsnel’son, B.G.; Pereselkov, S.A. Low-frequency horizontal acoustic refraction caused by internal wave solitons in a shallow sea. Acoust. Phys. 2000, 46, 684–691. [Google Scholar] [CrossRef]
- Badiey, M.; Katsnelson, B.G.; Lynch, J.F.; Pereselkov, S.; Siegmann, W.L. Measurement and modeling of three-dimensional sound intensity variations due to shallow-water internal waves. J. Acoust. Soc. Am. 2005, 117, 613–625. [Google Scholar] [CrossRef]
- Lin, Y.; Duda, T.F.; Lynch, J.F. Acoustic mode radiation from the termination of a truncated nonlinear internal gravity wave duct in a shallow ocean area. J. Acoust. Soc. Am. 2009, 126, 1752–1765. [Google Scholar] [CrossRef] [PubMed]
- Frank, S.D.; Badiey, M.; Lynch, J.F.; Siegmann, W.L. Experimental evidence of three-dimensional acoustic propagation caused by nonlinear internal waves. J. Acoust. Soc. Am. 2005, 118, 723–734. [Google Scholar] [CrossRef]
- Katsnelson, B.G.; Grigorev, V.; Badiey, M.; Lynch, J.F. Temporal sound field fluctuations in the presence of internal solitary waves in shallow water. J. Acoust. Soc. Am. 2009, 126, EL41–EL48. [Google Scholar] [CrossRef]
- Qin, J.X.; Katsnel’son, B.G.; Li, Z.L.; Zhang, R.H.; Luo, Y.W. Intensity fluctuations due to the motion of internal solitons in shallow water. Acta Acust. 2016, 41, 145–153. (In Chinese) [Google Scholar] [CrossRef]
- Rouseff, D.; Turgut, A.; Wolf, S.N.; Finette, S.; Orr, M.H.; Pasewark, B.H.; Apel, J.R.; Badiey, M.; Chiu, C.S.; Headrick, R.H.; et al. Coherence of acoustic modes propagating through shallow water internal waves. J. Acoust. Soc. Am. 2002, 111, 1655–1666. [Google Scholar] [CrossRef]
- Li, Q.R.; Sun, C.; Xie, L. Research on the modal intensity fluctuation during the dynamic propagation of internal solitary waves in the shallow water. Acta Phys. Sin. 2022, 71, 024302-1-13. (In Chinese) [Google Scholar] [CrossRef]
- Headrick, R.H.; Lynch, J.F.; Kemp, J.N.; Newhall, A.E.; von der Heydt, K.; Apel, J.; Badiey, M.; Chiu, C.; Finette, S.; Orr, M.; et al. Acoustic normal mode fluctuation statistics in the 1995 SWARM internal wave scattering experiment. J. Acoust. Soc. Am. 2000, 107, 201–220. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.C. Measurements of temporal coherence of sound transmissions through shallow water. J. Acoust. Soc. Am. 2006, 120, 2595–2614. [Google Scholar] [CrossRef]
- Ji, G.; Zhi, J.; Yong-Bo, S.; Wei, C.; Xian-Tai, W.; Gao-Peng, C.; Xin-Yu, L. A Physics-Based Charge-Control Model for InP DHBT Including Current-Blocking Effect. Chin. Phys. Lett. 2009, 26, 077302. [Google Scholar] [CrossRef]
- Duda, T.F. Temporal and cross-range coherence of sound traveling through shallow-water nonlinear internal wave packets. J. Acoust. Soc. Am. 2006, 119, 3717–3725. [Google Scholar] [CrossRef]
- Lunkov, A.A.; Petnikov, V.G. The coherence of low-frequency sound in shallow water in the presence of internal waves. Acoust. Phys. 2014, 60, 61–71. [Google Scholar] [CrossRef]
- Yoo, K.B.; Yang, T.C. Broadband source localization in shallow water in the presence of internal waves. J. Acoust. Soc. Am. 1999, 106, 3255–3269. [Google Scholar] [CrossRef]
- Yoo, K.B. Shallow water temporal coherence of broadband acoustic signals in the presence of internal waves. IEEE J. Ocean. Eng. 2005, 30, 391–405. [Google Scholar] [CrossRef]
- Collins, M.D. A split-step Padé solution for the parabolic equation method. J. Acoust. Soc. Am. 1993, 93, 1736–1742. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B.W. ETOPO1 1 arc-minute global relief model: Procedures, data sources and analysis. Psychologist 2009, 16, 20–25. [Google Scholar]
- Guo, C.C.; Chen, X.E. A review of internal solitary wave dynamics in the northern South China Sea. Prog. Oceanogr. 2014, 121, 7–23. [Google Scholar] [CrossRef]
- Wang, J.; Huang, W.G.; Yang, J.S.; Zhang, H.G.; Zheng, G. Study of the propagation direction of the internal waves in the South China sea using satellite imagines. Acta Oceanol. Sin. 2012, 32, 42–50. [Google Scholar] [CrossRef]
- Li, D.; Chen, X.; Liu, A. On the generation and evolution of internal solitary waves in the northwestern South China sea. Ocean Model. 2011, 40, 105–119. [Google Scholar] [CrossRef]
- Zheng, Q. Satellite SAR Detection of Sub-Mesoscale Ocean Dynamic Processes; World Scientific Publishing Co. Inc.: Singapore, 2017. [Google Scholar]
- Dozier, L.B.; Tappert, F.D. Statistics of normal mode amplitudes in a random ocean. I. Theory. J. Acoust. Soc. Am. 1978, 63, 353–365. [Google Scholar] [CrossRef]
- Liu, J.Q.; Piao, S.C.; Gong, L.J.; Zhang, M.H.; Guo, Y.C.; Zhang, S.Z. The effect of mesoscale eddy on the characteristic of sound propagation. J. Mar. Sci. Eng. 2021, 9, 787. [Google Scholar] [CrossRef]
- Jiang, Y.Y.; Grigorev, V.; Katsnelson, B. Sound field fluctuations in shallow water in the presence of moving nonlinear internal waves. J. Mar. Sci. Eng. 2022, 10, 119. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, F.; Hu, P.; Xu, F.; Li, Z.; Qin, J. Effects of Internal Waves on Acoustic Temporal Coherence in the South China Sea. J. Mar. Sci. Eng. 2023, 11, 374. https://doi.org/10.3390/jmse11020374
Gao F, Hu P, Xu F, Li Z, Qin J. Effects of Internal Waves on Acoustic Temporal Coherence in the South China Sea. Journal of Marine Science and Engineering. 2023; 11(2):374. https://doi.org/10.3390/jmse11020374
Chicago/Turabian StyleGao, Fei, Ping Hu, Fanghua Xu, Zhenglin Li, and Jixing Qin. 2023. "Effects of Internal Waves on Acoustic Temporal Coherence in the South China Sea" Journal of Marine Science and Engineering 11, no. 2: 374. https://doi.org/10.3390/jmse11020374
APA StyleGao, F., Hu, P., Xu, F., Li, Z., & Qin, J. (2023). Effects of Internal Waves on Acoustic Temporal Coherence in the South China Sea. Journal of Marine Science and Engineering, 11(2), 374. https://doi.org/10.3390/jmse11020374







