Modelling Manoeuvrability in the Context of Ship Collision Analysis Using Non-Linear FEM
Abstract
1. Introduction
1.1. General Overview
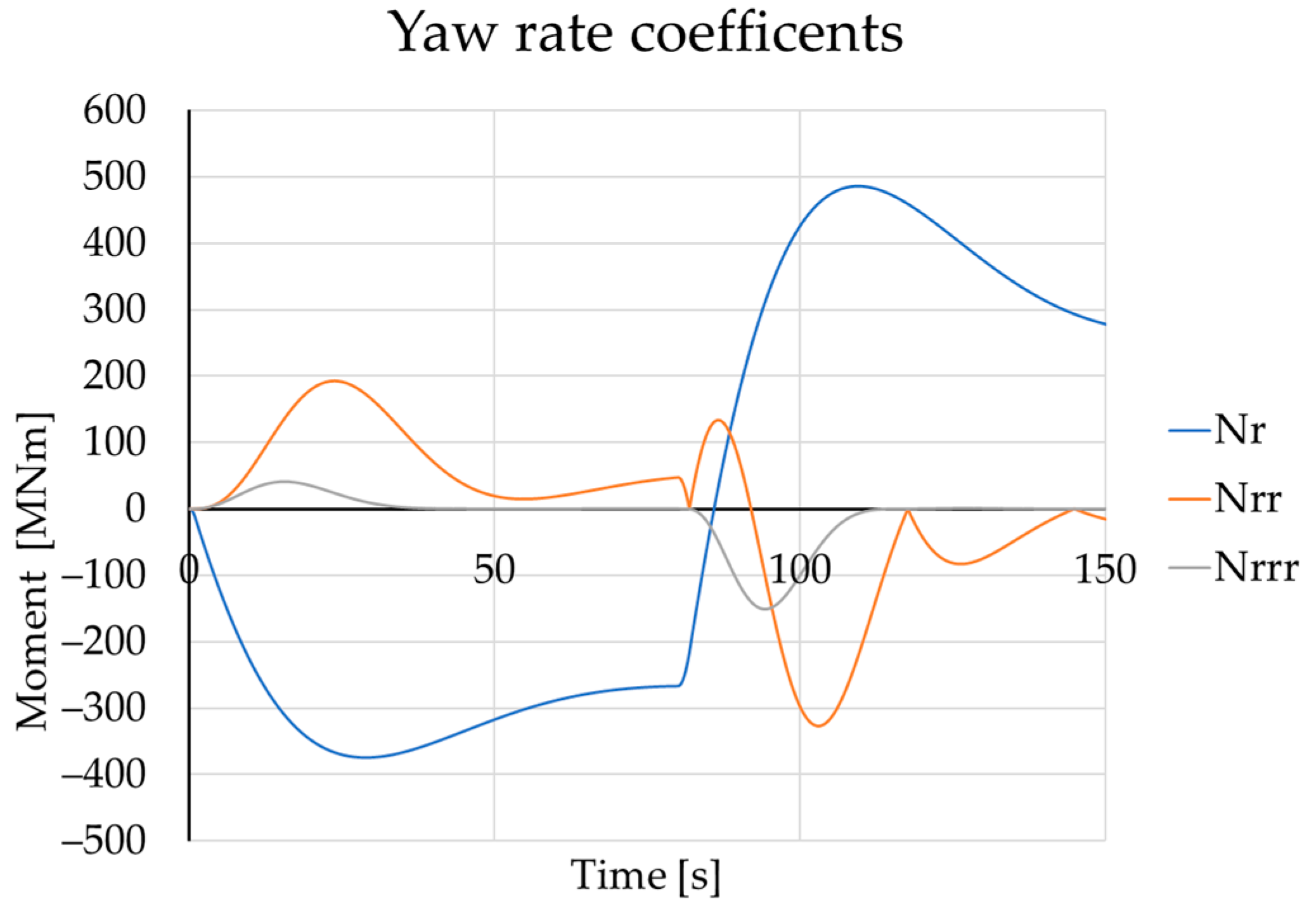
1.2. Hydrodynamic Derivatives
1.2.1. Hydrodynamic Set 1
1.2.2. Hydrodynamic Set 2
1.2.3. Hydrodynamic Set 3
1.3. Non-Dimensional to Dimensional Form of Hydrodynamic Coefficients
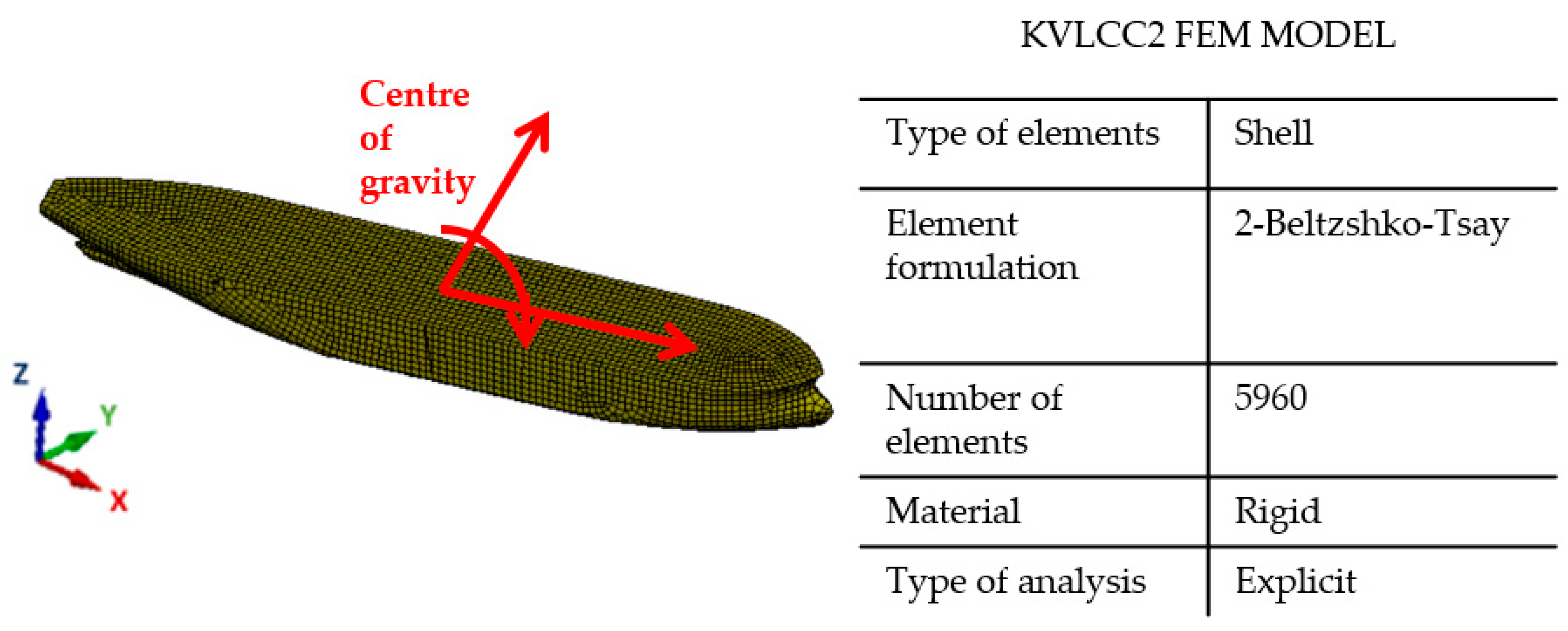
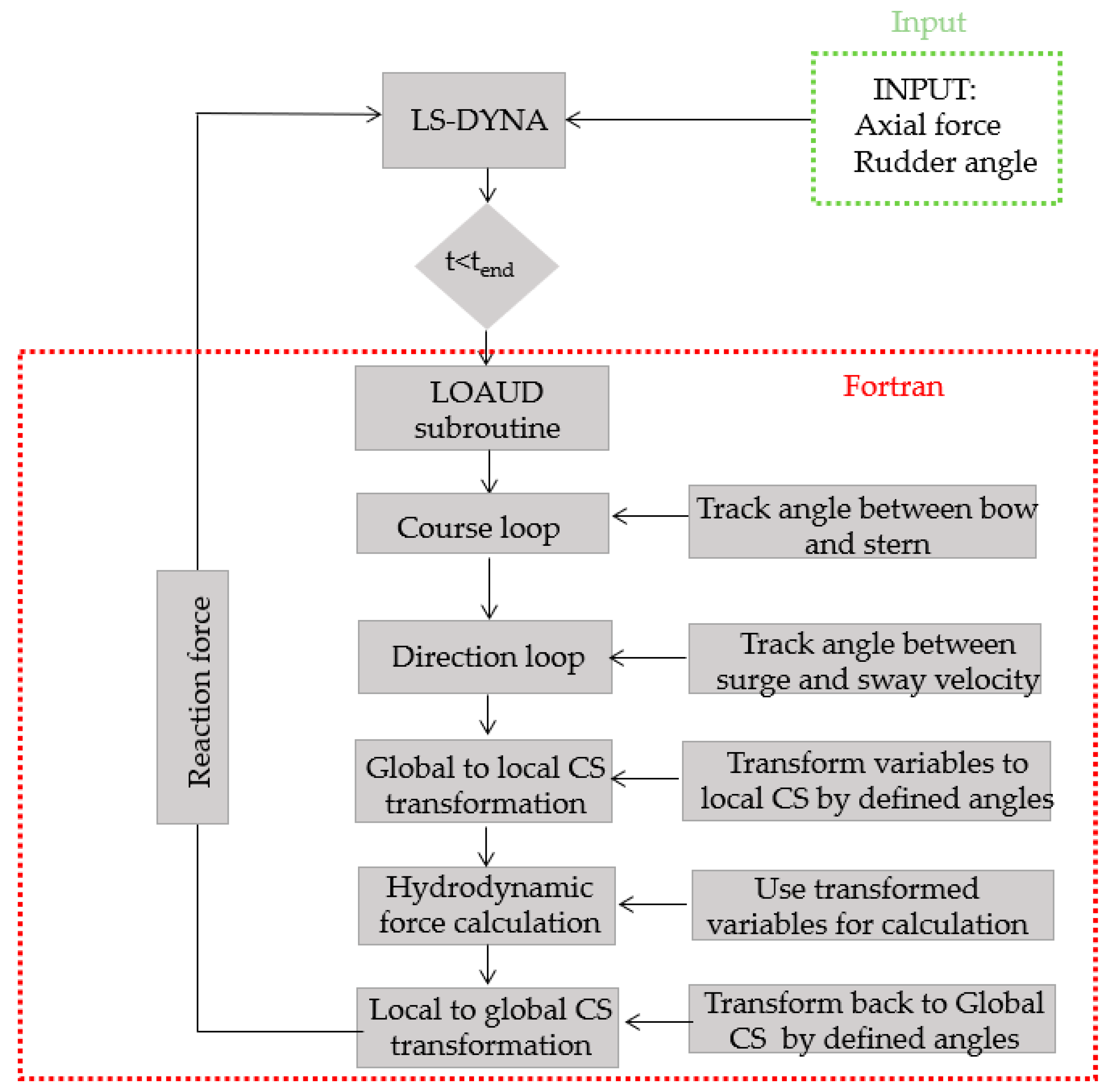
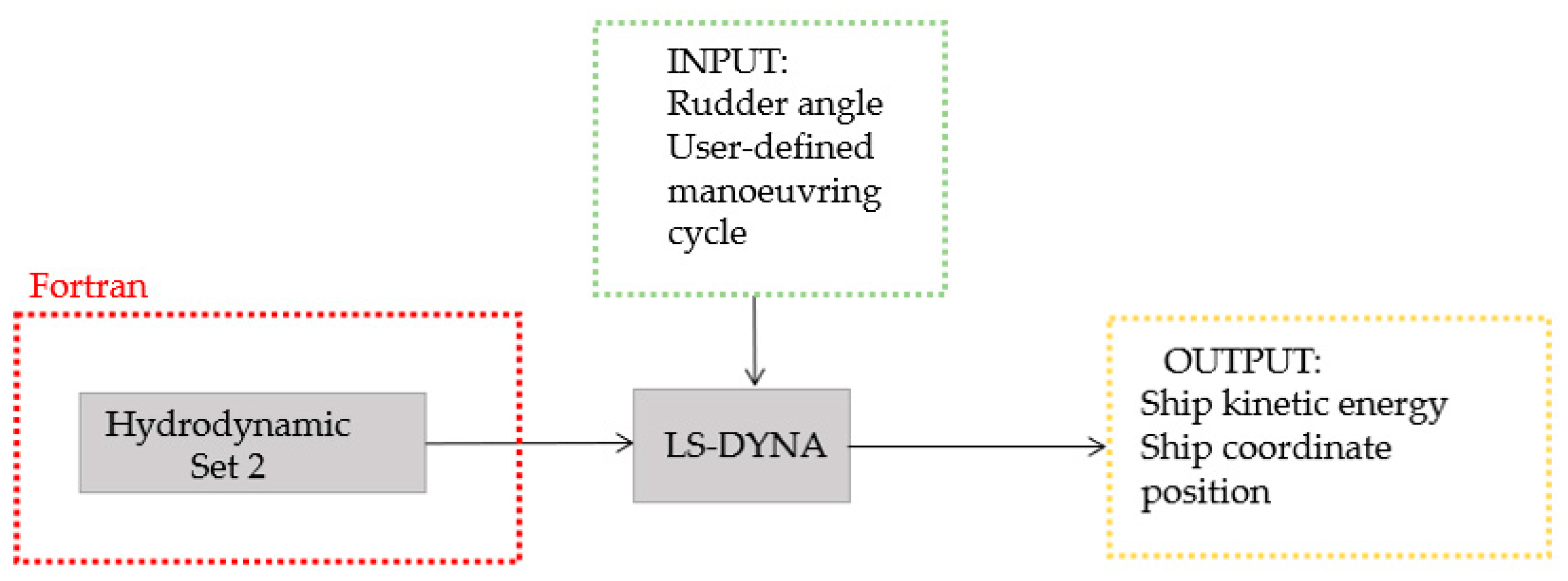
2. LOADUD Subroutine Implementation
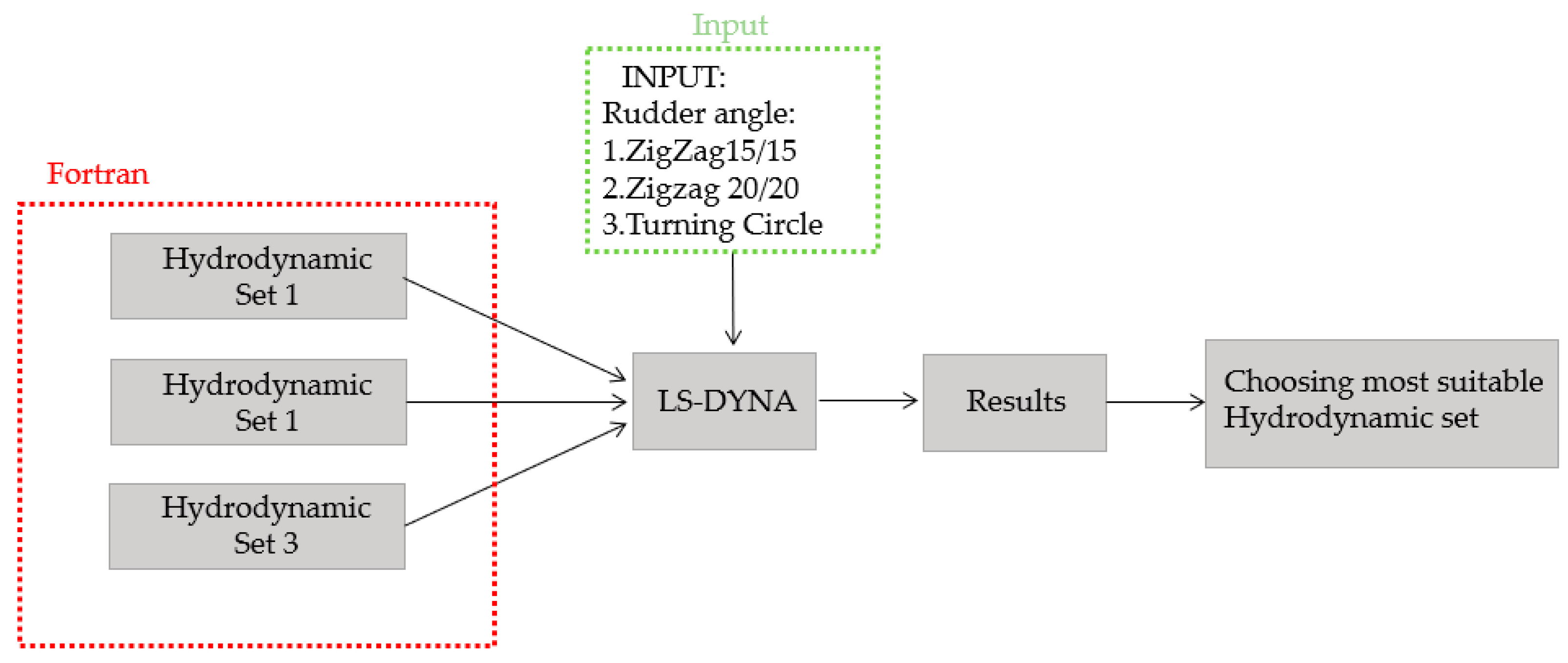
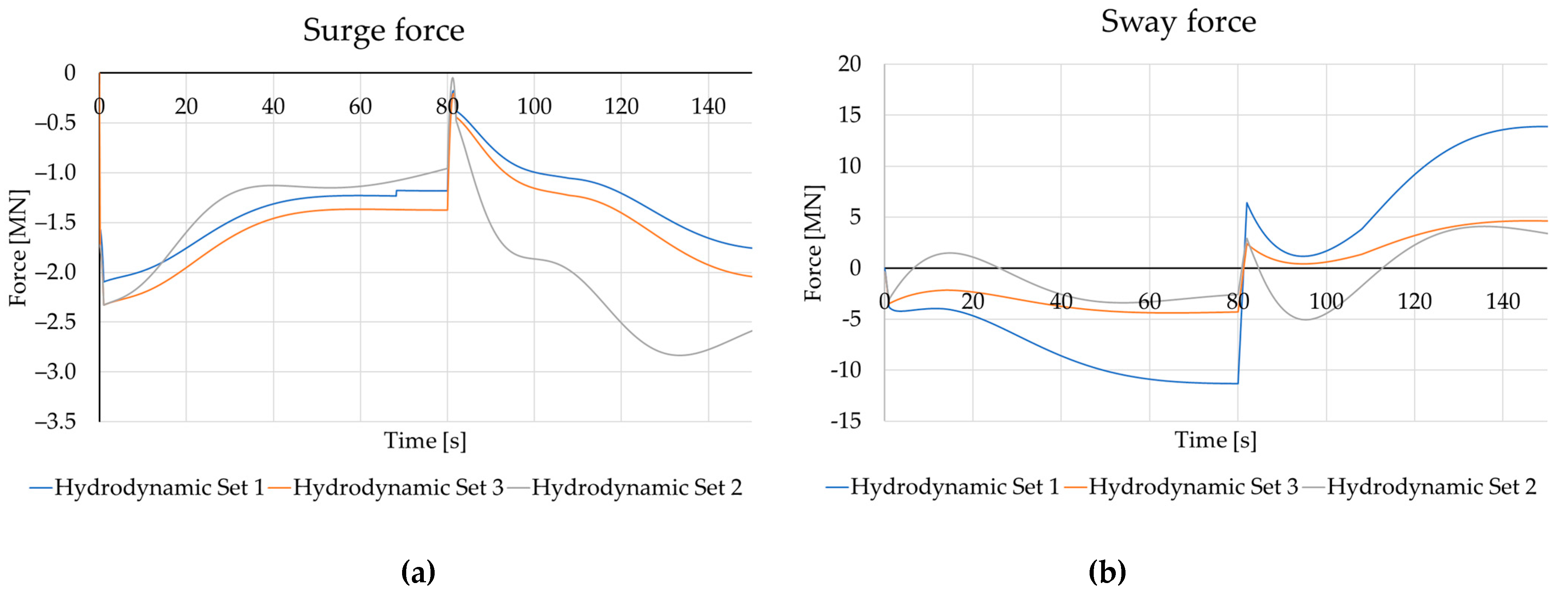
3. Validation of the Results
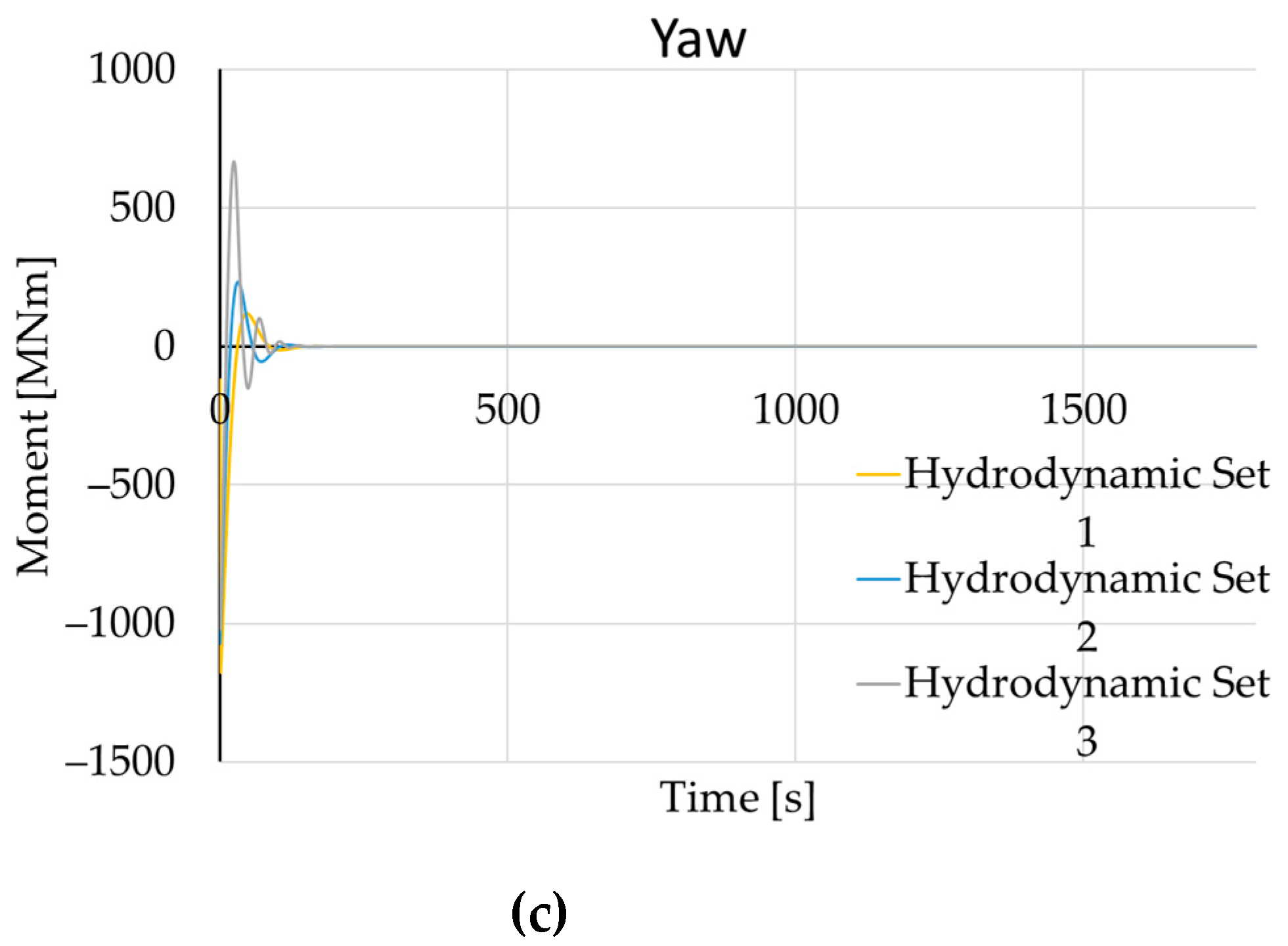
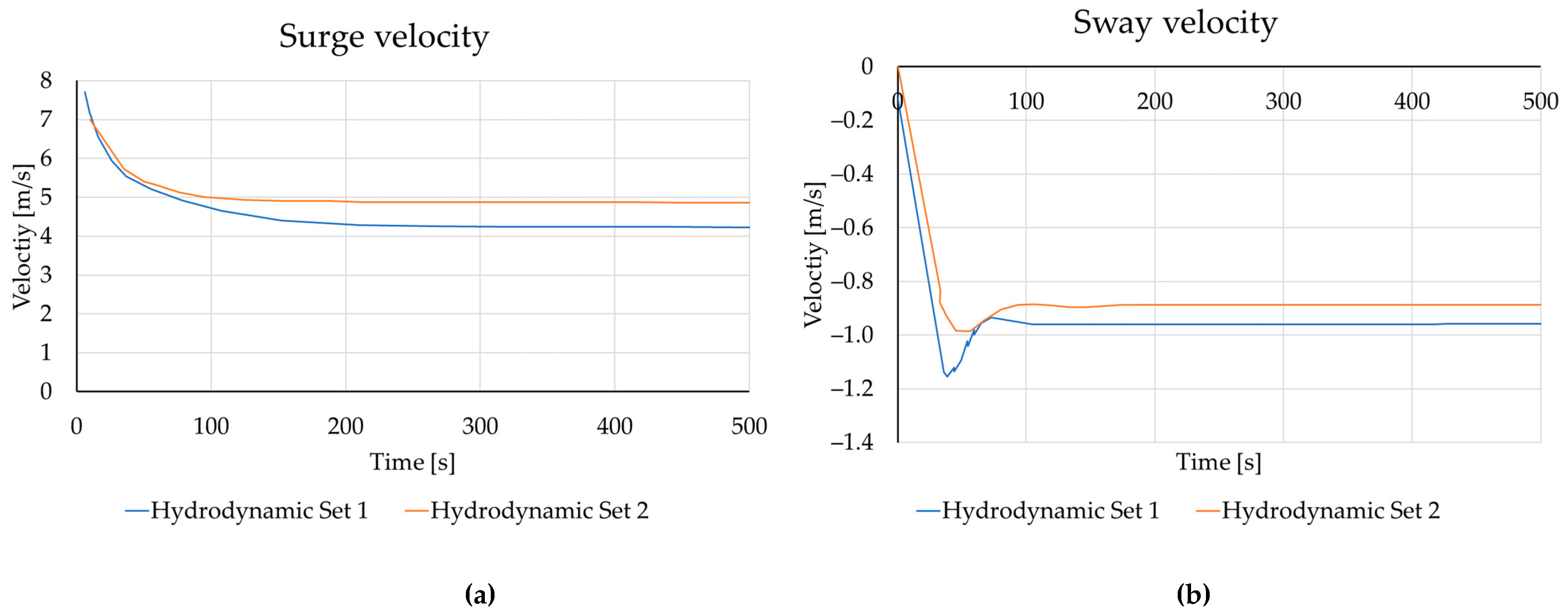
3.1. Half-Turn Comparison
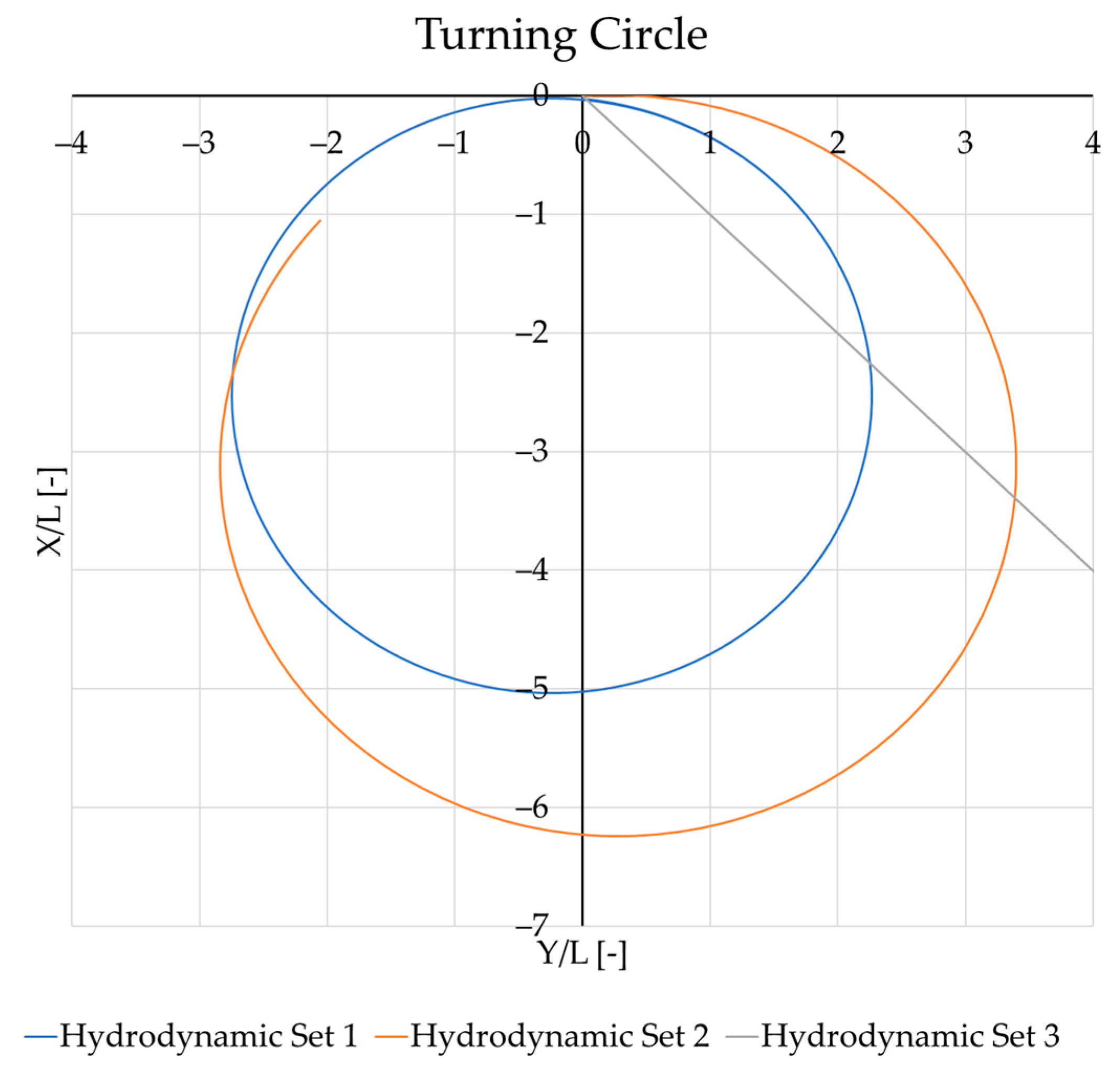
3.2. Turning Circle 35°
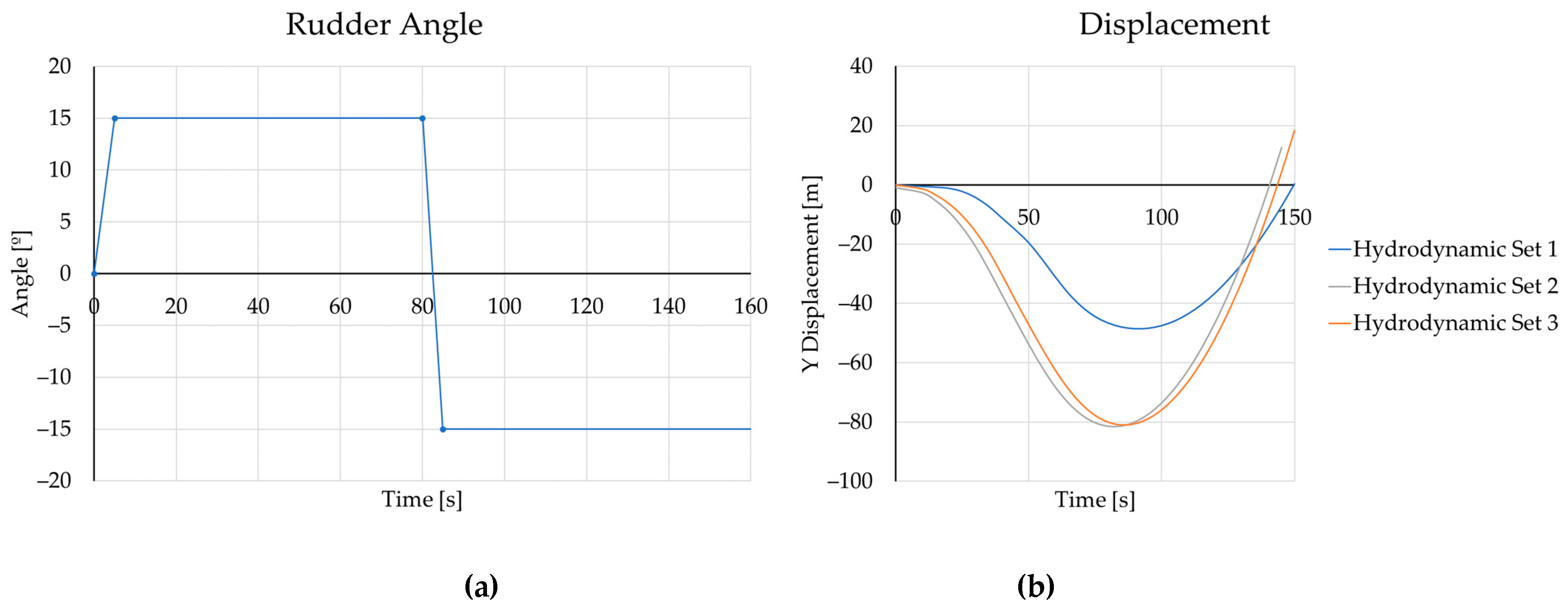
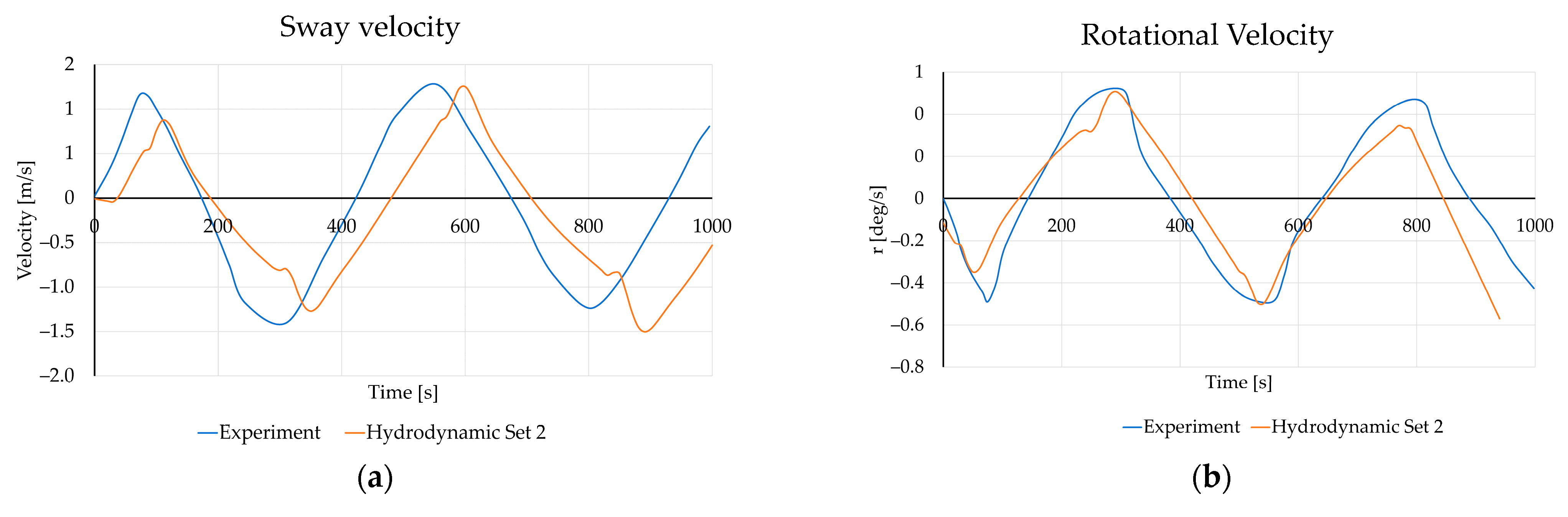
3.3. Validation on Zigzag 20/20 Test
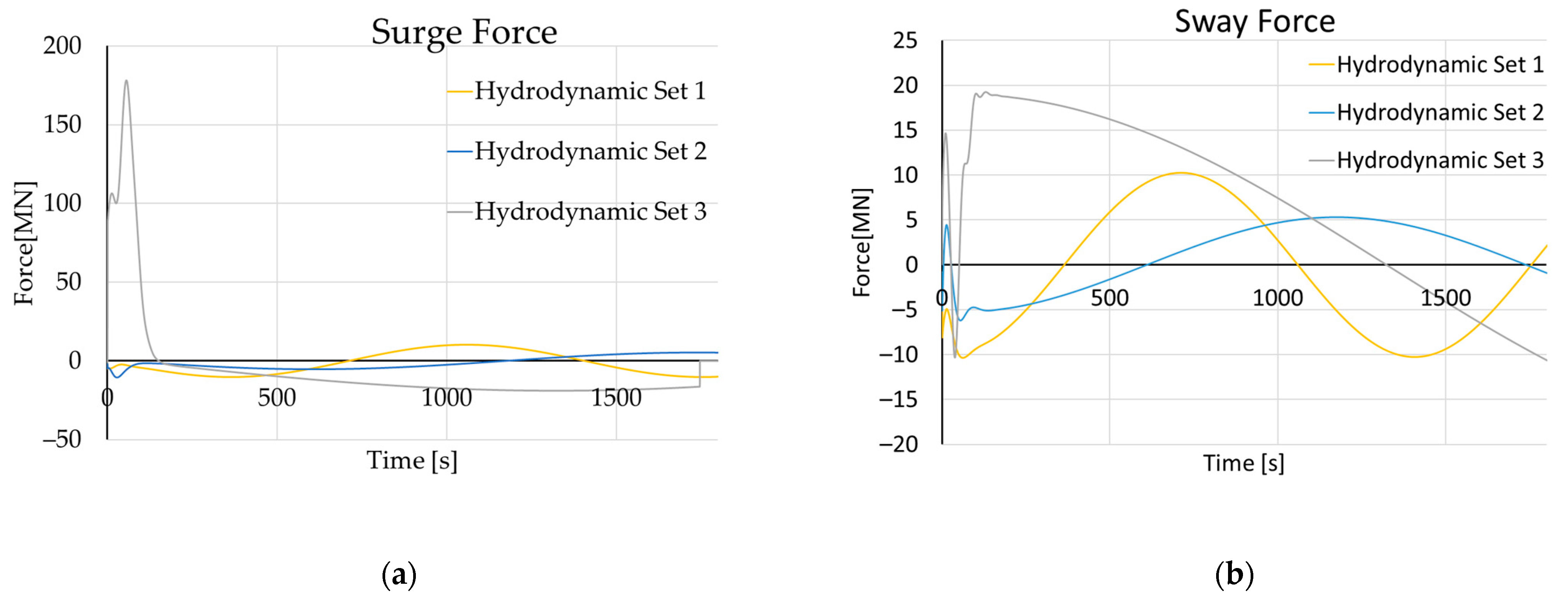
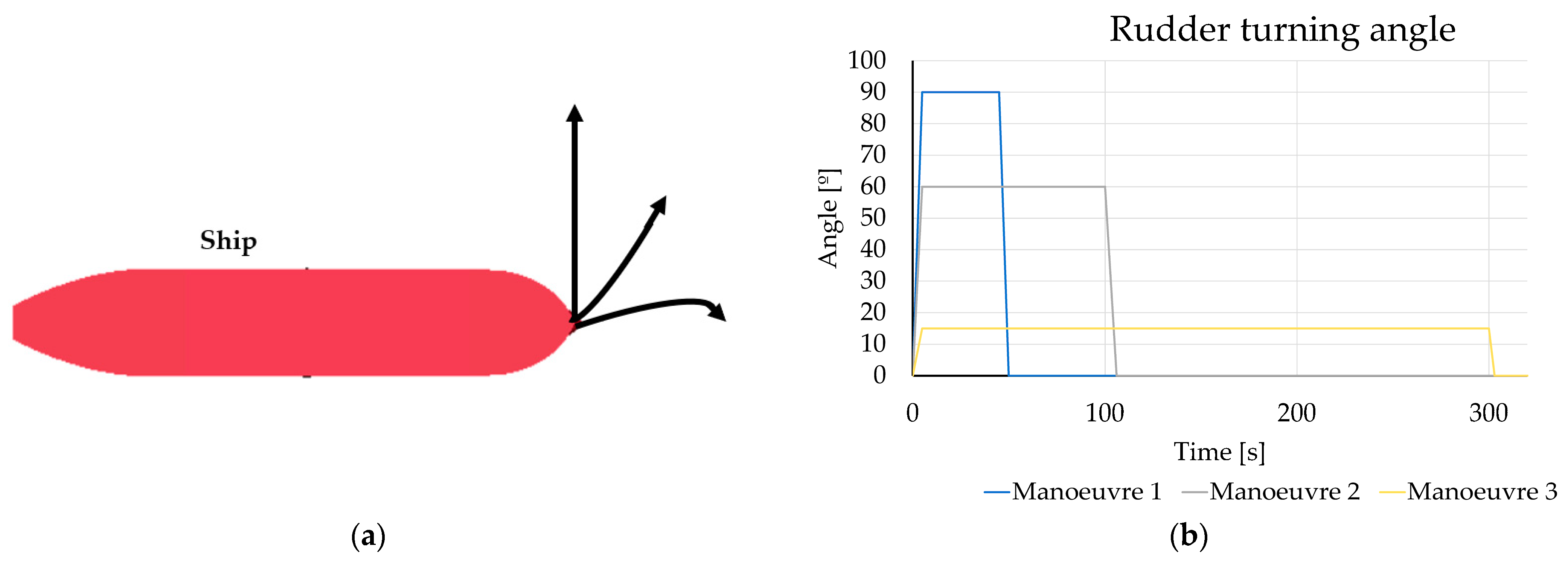
4. Prediction of Ship Collision Consequences
4.1. Kinetic Energy as a Function of Ship Manoeuvring
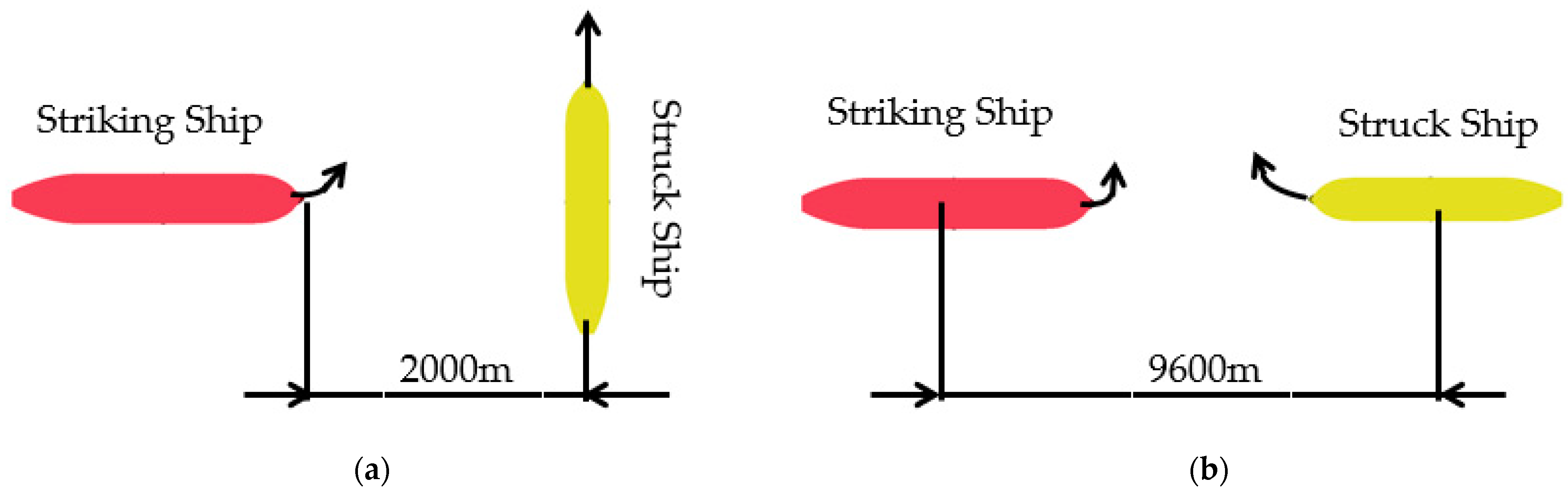
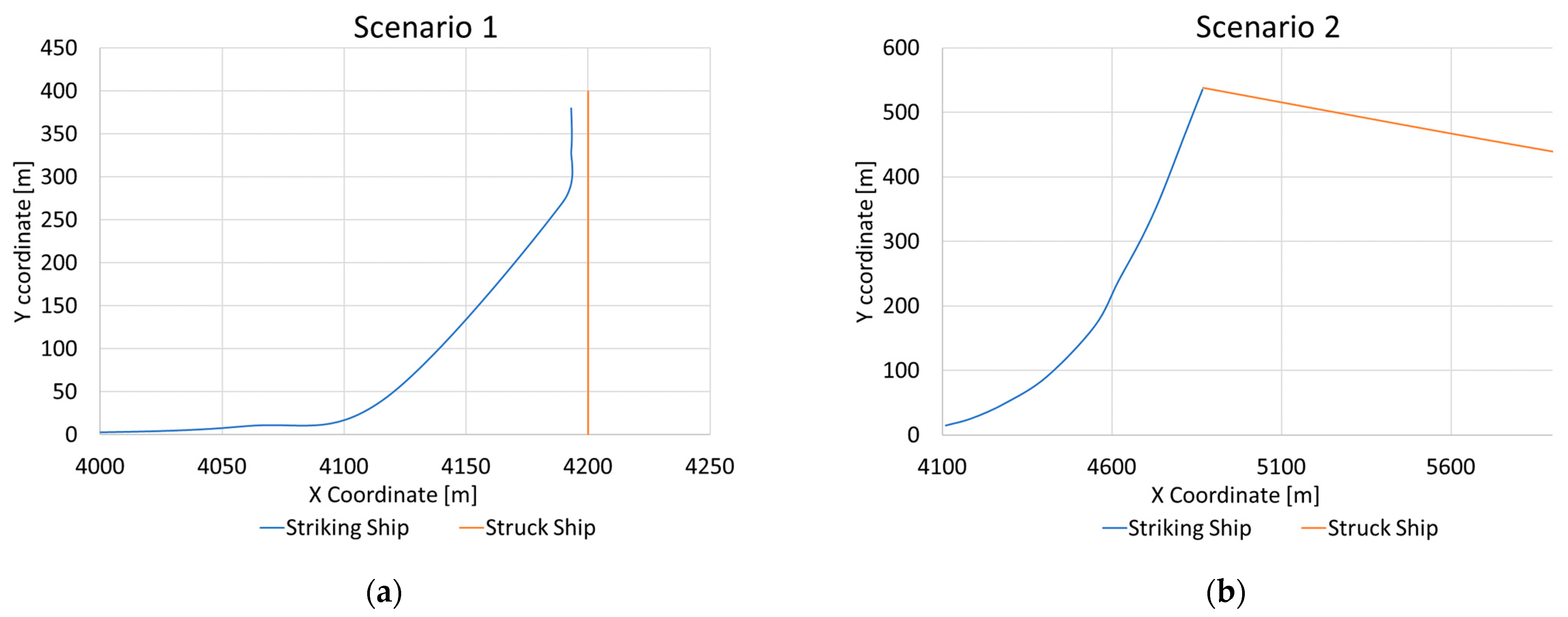
4.2. Multiple Ship Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| ABS | American Bureau of Shipping |
| ALE | Arbitrary Lagrange-Euler |
| CFD | Computational Fluid Dynamics |
| FEM | Finite Element Method |
| KVLCC2 | KRISO Very Large Cruder Carrier 2 |
| LOAUD | Load User-defined |
| MMG | Manoeuvring Modelling Group |
References
- Kuznecovs, A.; Ringsberg, J.W.; Ullal, A.M.; Bangera, P.J.; Johnson, E. Consequence analyses of collision-damaged ships—Damage stability, structural adequacy and oil spills. Ships Offshore Struct. 2022, 1–15. [Google Scholar] [CrossRef]
- Liu, B.; Villavicencio, R.; Zhang, S.; Soares, C.G. Guedes Soares, Assessment of external dynamics and internal mechanics in ship collisions. Ocean Eng. 2017, 141, 326–336. [Google Scholar] [CrossRef]
- Gao, Z.; Yang, S.; Hu, Z. The Resistance of Ship Web Girders in Collision and Grounding. Math. Probl. Eng. 2014, 2014, 720542. [Google Scholar] [CrossRef]
- Tabri, K.; Varsta, P.; Matusiak, J. Numerical and experimental motion simulations of nonsymmetric ship collisions. J. Mar. Sci. Technol. 2010, 15, 87–101. [Google Scholar] [CrossRef]
- Ringsberg, J.W.; Amdahl, J.; Chen, B.Q.; Cho, S.-R.; Ehlers, S.; Hu, Z.; Kubiczek, J.M.; Kõrgesaar, M.; Liu, B.; Marinatos, J.N.; et al. MARSTRUCT benchmark study on nonlinear FE simulation of an experiment of an indenter impact with a ship side-shell structure. Mar. Struct. 2018, 59, 142–157. [Google Scholar] [CrossRef]
- Minorsky, V.U. An Analysis of Ship Collision to Protection of Nuclear Powered Plant. J. Ship Res. 1959, 3, 1–4. [Google Scholar]
- Zhang, S.; Pedersen, P.T.; Villavicencio, R. Internal mechanics of ship collision and grounding. Probab. Mech. Ship Collis. Grounding 2019, 2019, 147–270. [Google Scholar] [CrossRef]
- Liu, B.; Pedersen, P.T.; Zhu, L.; Zhang, S. Review of experiments and calculation procedures for ship collision and grounding damage. Mar. Struct. 2018, 59, 105–121. [Google Scholar] [CrossRef]
- Le Sourne, H. A ship collision analysis program based on the super-element method coupled with a large rotational ship movement analysis tool. In Proceedings of the International Conference on Collision and Grounding of Ships, Hamburg, Germany, 9–12 September 2007; pp. 131–138. [Google Scholar]
- Rudan, S.; Ćatipović, I.; Berg, R.; Völkner, S.; Prebeg, P. Numerical study on the consequences of different ship collision modelling techniques. Ships Offshore Struct. 2019, 14, 387–400. [Google Scholar] [CrossRef]
- Rudan, S.; Karačić, J.; Ćatipović, I. Non-linear response of a moored LNG ship subjected to regular waves. Ships Offshore Struct. 2021, 16, 44–57. [Google Scholar] [CrossRef]
- Yu, Z.; Amdahl, J.; Storheim, M. A new approach for coupling external dynamics and internal mechanics in ship collisions. Mar. Struct. 2016, 45, 110–132. [Google Scholar] [CrossRef]
- Sukas, O.F.; Kinaci, O.K.; Bal, S. Theoretical background and application of MANSIM for ship maneuvering simulations. Ocean Eng. 2019, 192, 106239. [Google Scholar] [CrossRef]
- Yasukawa, H.; Yoshimura, Y. Introduction of MMG standard method for ship maneuvering predictions. J. Mar. Sci. Technol. 2014, 20, 37–52. [Google Scholar] [CrossRef]
- Jian-Chuan, Y.; Zao-Jian, Z.; Feng, X. Parametric Identification of Abkowitz Model for Ship Maneuvering Motion by Using Partial Least Squares Regression. J. Offshore Mech. Arct. Eng. 2015, 137, 31301. [Google Scholar] [CrossRef]
- Du, P.; Ouahsine, A.; Toan, K.T.; Sergent, P. Simulation of ship maneuvering in a confined waterway using a nonlinear model based on optimization techniques. Ocean Eng. 2017, 142, 194–203. [Google Scholar] [CrossRef]
- ABS. Guide for Vessel Manouverabitiy; Updated 2017; American Bureu of Shipping: Houston, TX, USA, 2017. [Google Scholar]
- Hu, Y.; Yao, J.; Liu, Z.; Song, L. Identification of Ship Hydrodynamic Derivatives Based on LS-SVM with Wavelet Threshold Denoising. J. Mar. Sci. Eng. 2021, 9, 1356. [Google Scholar] [CrossRef]
- Mucha, P. On Simulation-Based Ship Maneuvering Prediction in Deep and Shallow Water. Doctoral Thesis, University of Duisburg-Essen, Duisburg, Germany, 2017. [Google Scholar]
- Sheeja, J.; Krishnankutty, P. Determination of Linear and Non-linear Hydrodynamic Derivatives of a Surface Ship in Manoeuvring Using CFD Method. In Advances in Visualization and Optimization Techniques for Multidisciplinary Research; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]



| Chapter | Description |
|---|---|
| 1. Introduction | The literature research is presented regarding manoeuvrability with an introduction of hydrodynamic forces described by derivatives. |
| 2. LOADUD subroutine implementation | The procedure for implementation of the hydrodynamic forces into the finite element software is described. |
| 3. Validation of the results | Coupled manoeuvrability-FEM analysis is performed. Results are validated for the cases of Zigzag 15/15 half-turn, Zigzag 20/10, and turning circle. |
| 4. Prediction of ship collision consequences | A new method of analysing ship events prior to the collision is researched. The assessment of kinetic energy and coordinate tracking is presented. |
| 5. Discussion and conclusions | The final chapter states conclusions from the presented research as well as a proposal for future work. |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Ship length | 320 m | Draft | 20.8 m |
| Breadth | 58 m | Inertia IZ | 2.00 × 1012 kg/m2 |
| X Centre of gravity | 11.136 m | Approach speed | 7.956 m/s |
| X Coefficient [-] | Y Coefficient [-] | N Coefficient [-] | |||
|---|---|---|---|---|---|
| −0.0022 | −0.01902 | −0.007886 | |||
| 0.0015 | 0.000639 | −0.000308 | |||
| 0.00159 | −0.1287 | 0.00175 | |||
| −0.001135 | −0.014508 | −0.000388 | |||
| 0.0003338 | 0.005719 | −0.003701 | |||
| 0.01391 | −0.000002 | −0.000002 | |||
| −0.00272 | −0.000048 | −0.000707 | |||
| 0.001609 | −0.02429 | 0.003726 | |||
| −0.001034 | 0.0211 | −0.019 | |||
| 0.000048 | 0.00408 | −0.001834 | |||
| 0.002008 | −0.000114 | −0.000056 | |||
| 0.0001658 | −0.002059 | 0.001426 | |||
| −0.004716 | −0.00456 | 0.00232 | |||
| −0.000364 | 0.00326 | −0.001504 | |||
| a2 | −0.000894 | 0.003018 | −0.001406 | ||
| b2 | −0.000649 | −0.002597 | 0.001191 | ||
| c2 | 0.001543 | 0.000895 | −0.000398 | ||
| Coef. [N] | Dimension. Factor | Coef. [N] | Dimension. Factor | Coef. [Nm] | Dimension. Factor |
|---|---|---|---|---|---|
| 0.5ρL3 | 0.5ρL3 | 0.5ρL4 | |||
| 0.5ρL2 | 0.5ρL2 | 0.5ρL4 | |||
| 0.5ρL2 | 0.5ρL2 | 0.5ρL4 | |||
| 0.5ρL3 | 0.5ρL3 | 0.5ρL4 | |||
| 0.5ρL4 | 0.5ρL4 | 0.5ρL5 | |||
| 0.5ρL3 | 0.5ρL3 | 0.5ρL4 | |||
| 0.5ρL2V2 | 0.5ρL2V2 | 0.5ρL2V2 | |||
| 0.5ρL3 | 0.5ρL3 | 0.5ρL3 | |||
| 0.5ρL3V | 0.5ρL3/V | 0.5ρL4/V | |||
| 0.5ρL4 | 0.5ρL2V2 | 0.5ρL3 V2 | |||
| 0.5ρL3 | 0.5ρL2V2 | 0.5ρL3 V2 | |||
| 0.5ρL2V2 | 0.5ρL2V2 | 0.5ρL3 V2 | |||
| 0.5ρL3 | 0.5ρL3 | 0.5ρL4 | |||
| 0.5ρL3V | 0.5ρL3 | 0.5ρL4 | |||
| a2 | 0.5ρL2V2 | 0.5ρL3 | 0.5ρL4 | ||
| b2 | 0.5ρL2V2 | 0.5ρL3V | 0.5ρL4V | ||
| c2 | 0.5ρL2V2 | 0.5ρL3V | 0.5ρL4V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sviličić, Š.; Rudan, S. Modelling Manoeuvrability in the Context of Ship Collision Analysis Using Non-Linear FEM. J. Mar. Sci. Eng. 2023, 11, 497. https://doi.org/10.3390/jmse11030497
Sviličić Š, Rudan S. Modelling Manoeuvrability in the Context of Ship Collision Analysis Using Non-Linear FEM. Journal of Marine Science and Engineering. 2023; 11(3):497. https://doi.org/10.3390/jmse11030497
Chicago/Turabian StyleSviličić, Šimun, and Smiljko Rudan. 2023. "Modelling Manoeuvrability in the Context of Ship Collision Analysis Using Non-Linear FEM" Journal of Marine Science and Engineering 11, no. 3: 497. https://doi.org/10.3390/jmse11030497
APA StyleSviličić, Š., & Rudan, S. (2023). Modelling Manoeuvrability in the Context of Ship Collision Analysis Using Non-Linear FEM. Journal of Marine Science and Engineering, 11(3), 497. https://doi.org/10.3390/jmse11030497






