Optimal Assimilation Number of Phytoplankton in the Siberian Seas: Spatiotemporal Variability, Environmental Control and Estimation Using a Region-Specific Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Sources and Sampling
2.2. The Field Data
2.3. Statistical Analysis
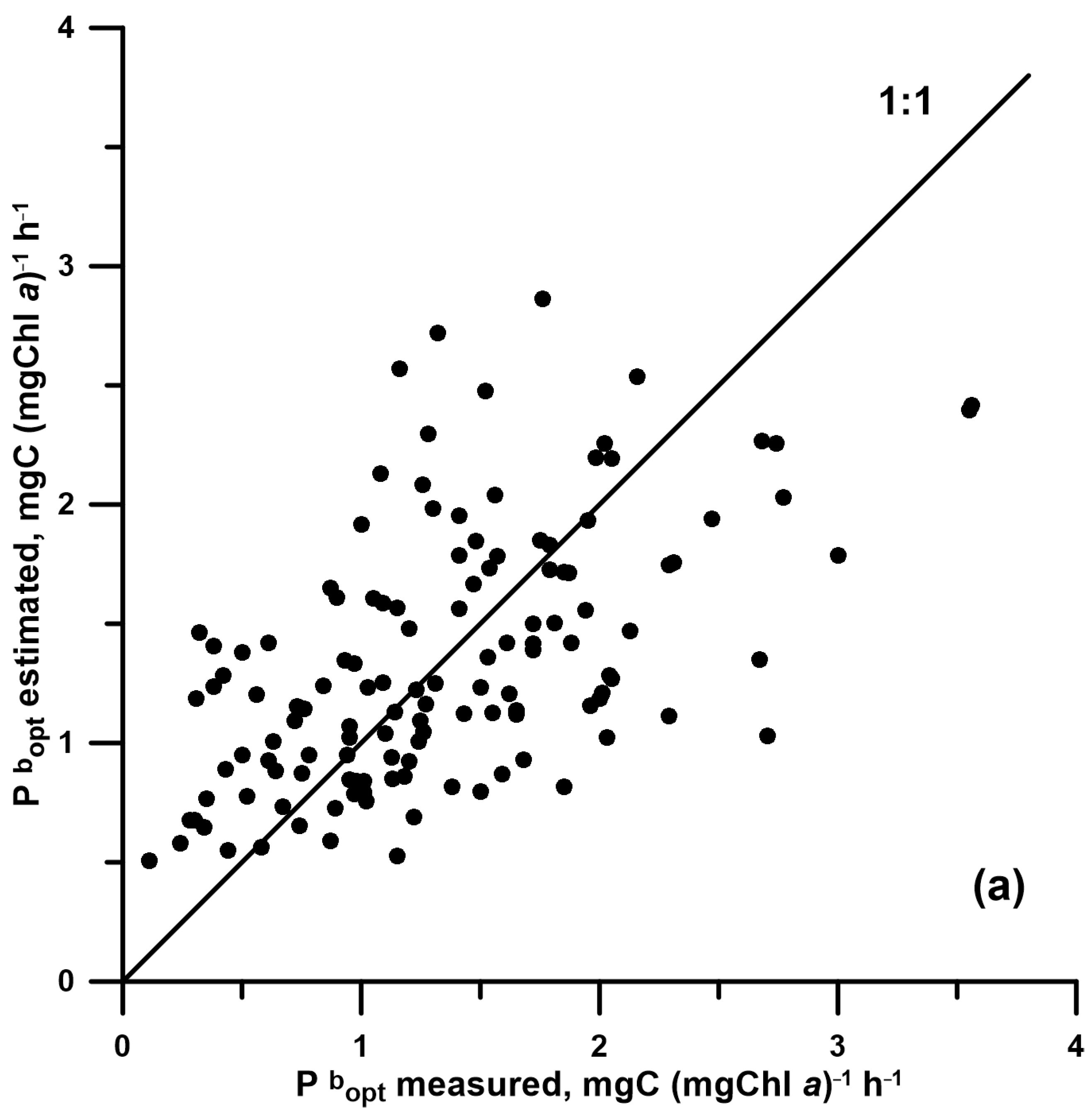
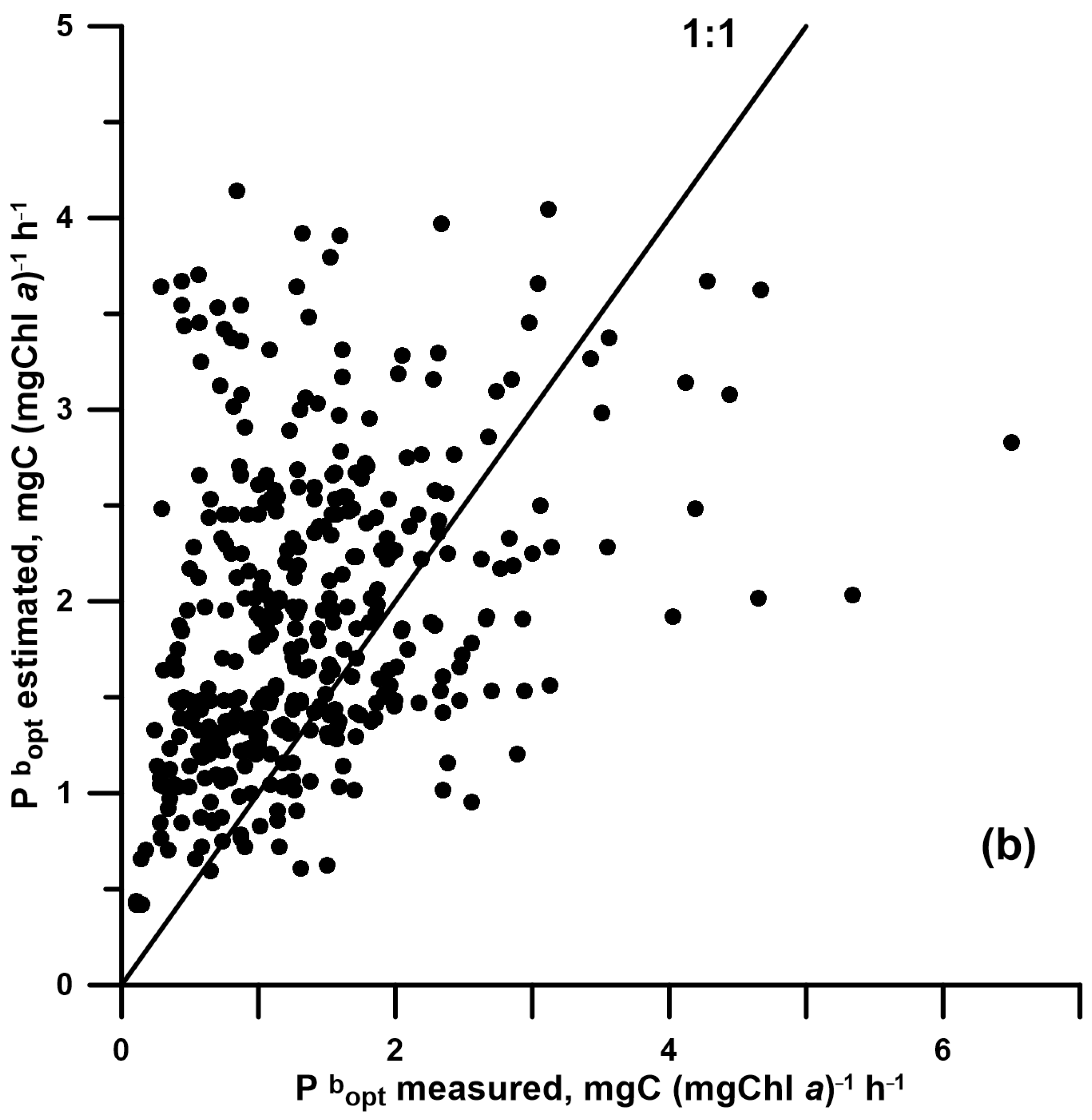
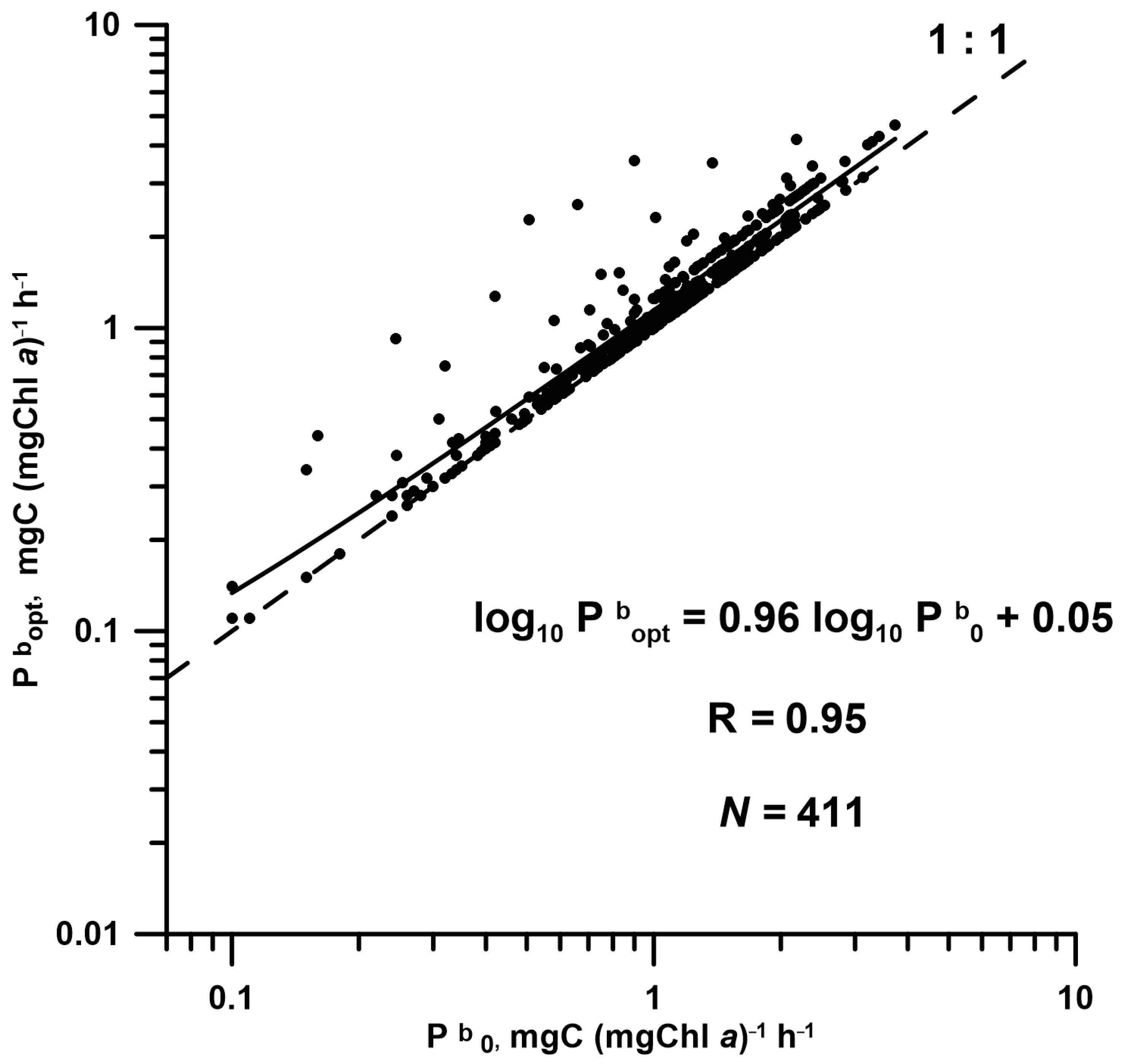
2.4. Development and Verification of Pbopt Models
2.5. Satellite-Derived Data of Photosynthetically Available Radiation (PAR)
3. Results
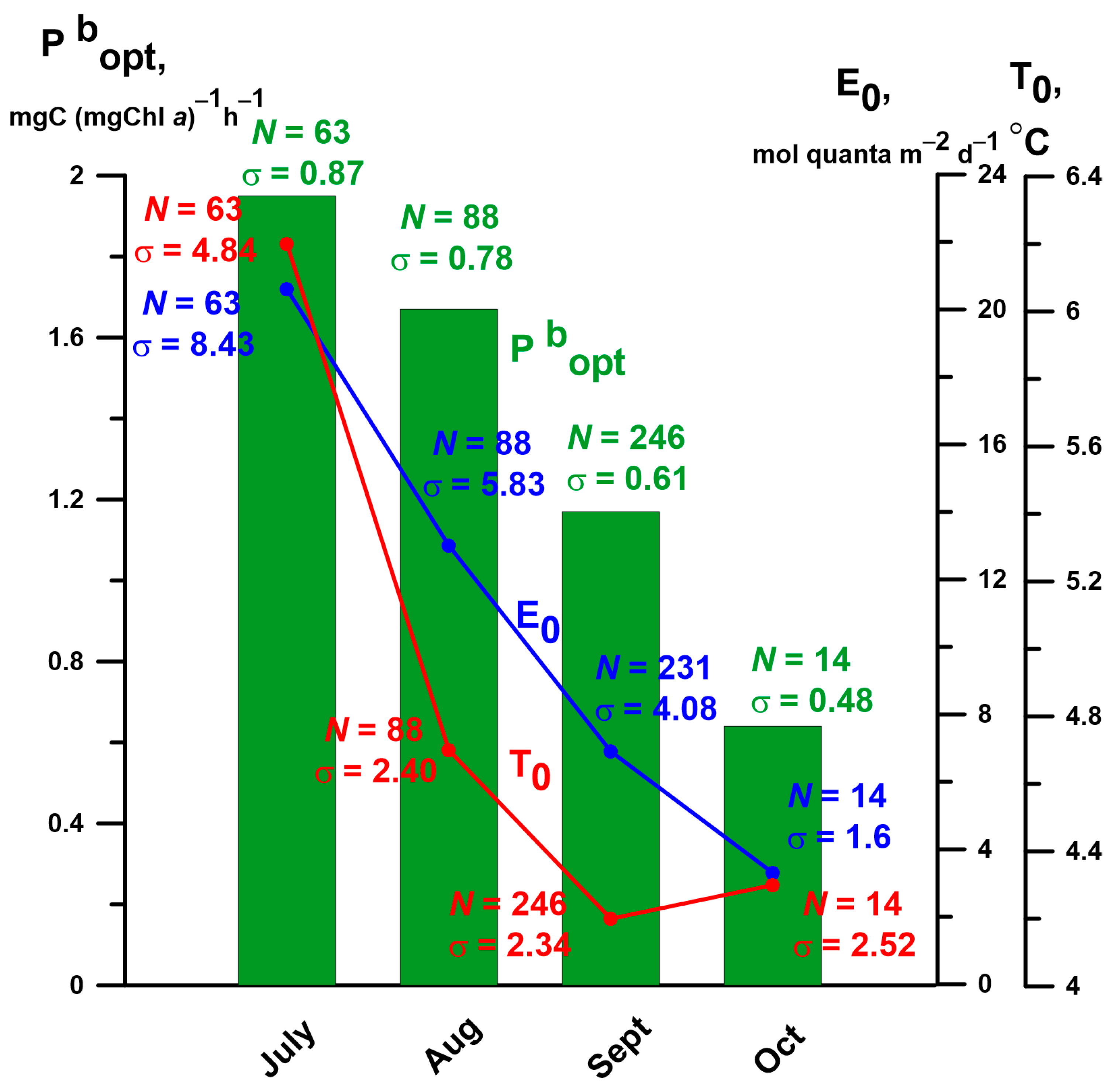
3.1. Values and Spatiotemporal Variability in Optimal Assimilation Number (Pbopt) in the Siberian Seas (SSs) Using Field Observations
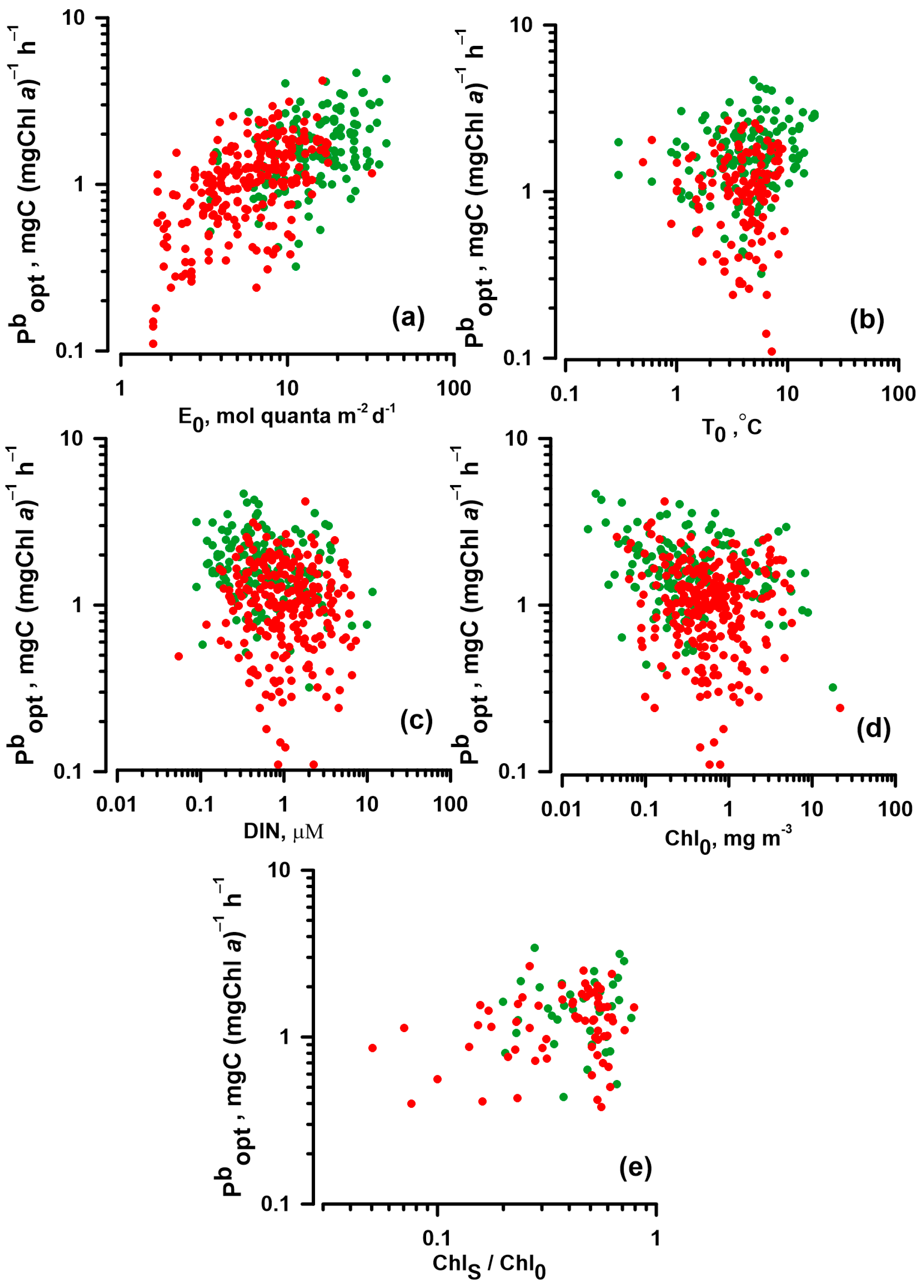
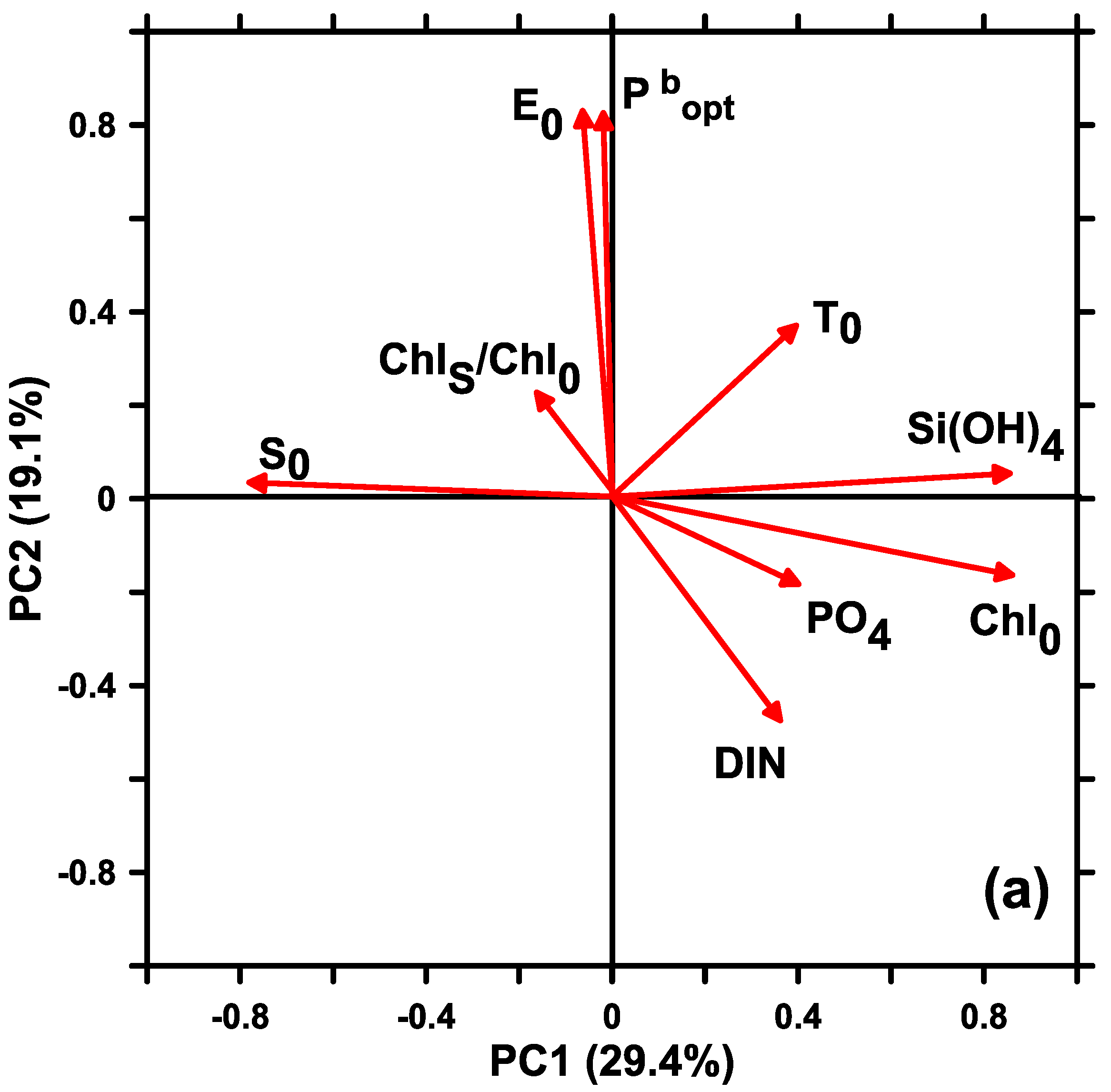
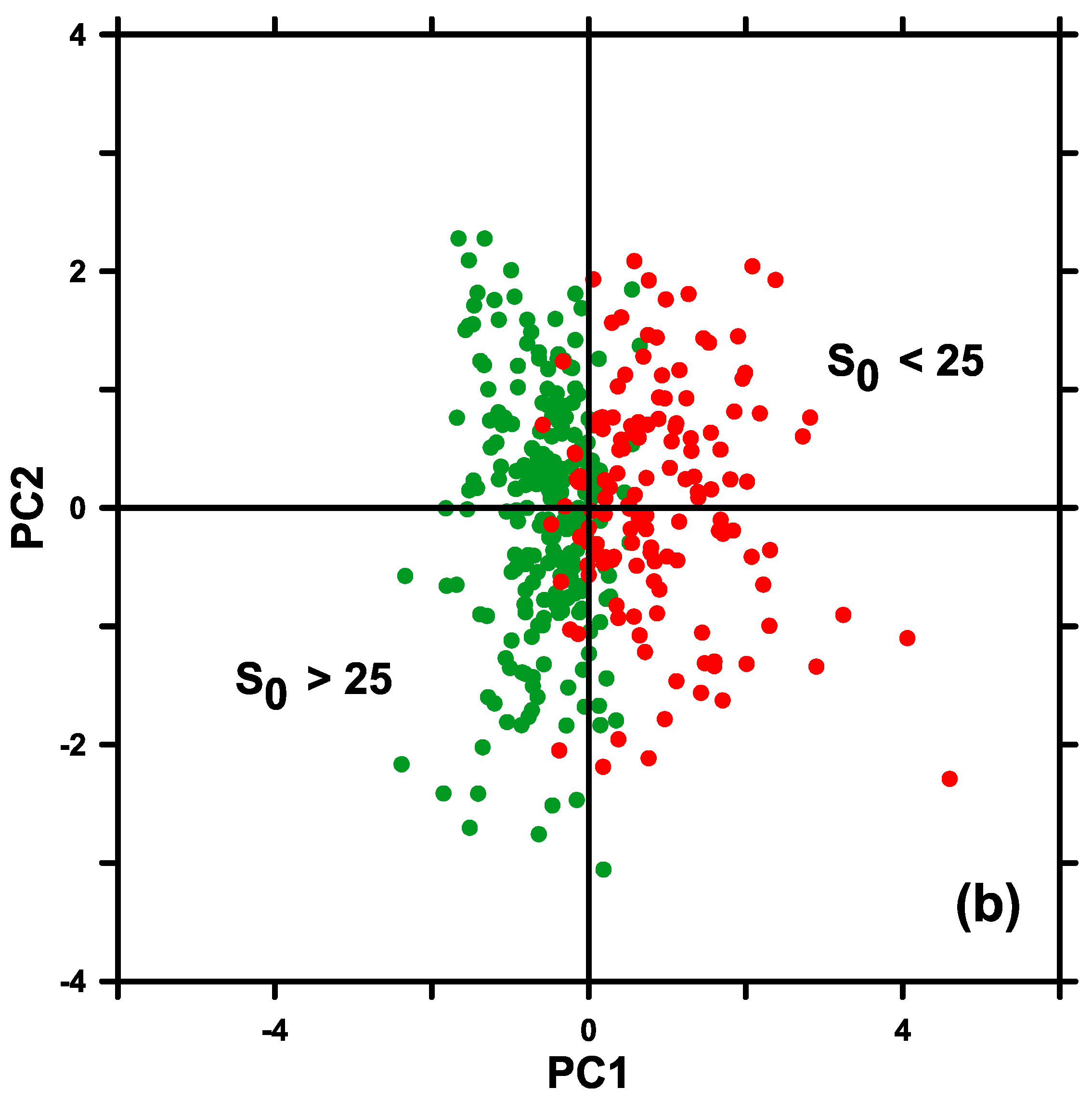
3.2. The Relationships between Pbopt and Environmental Factors
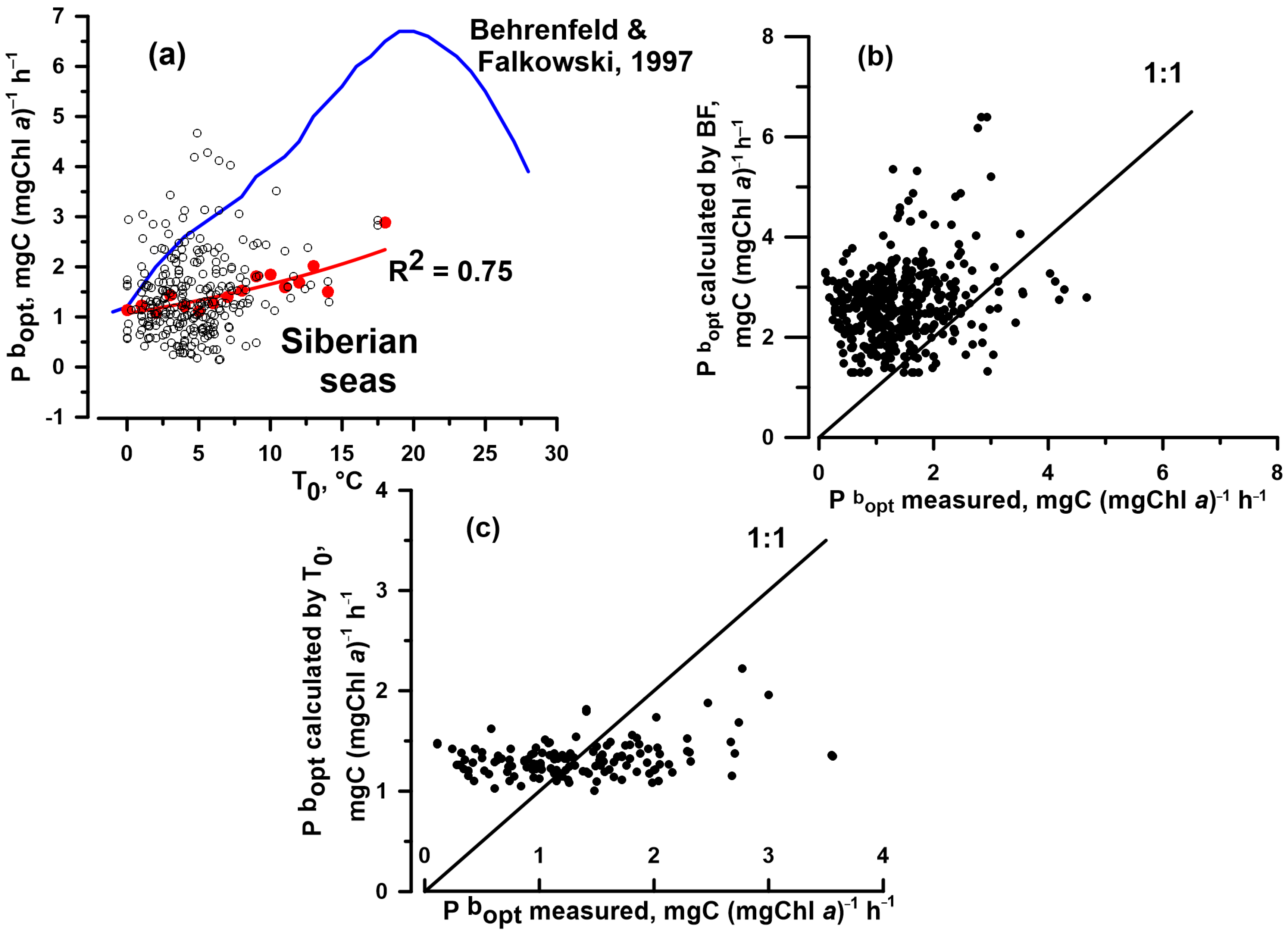
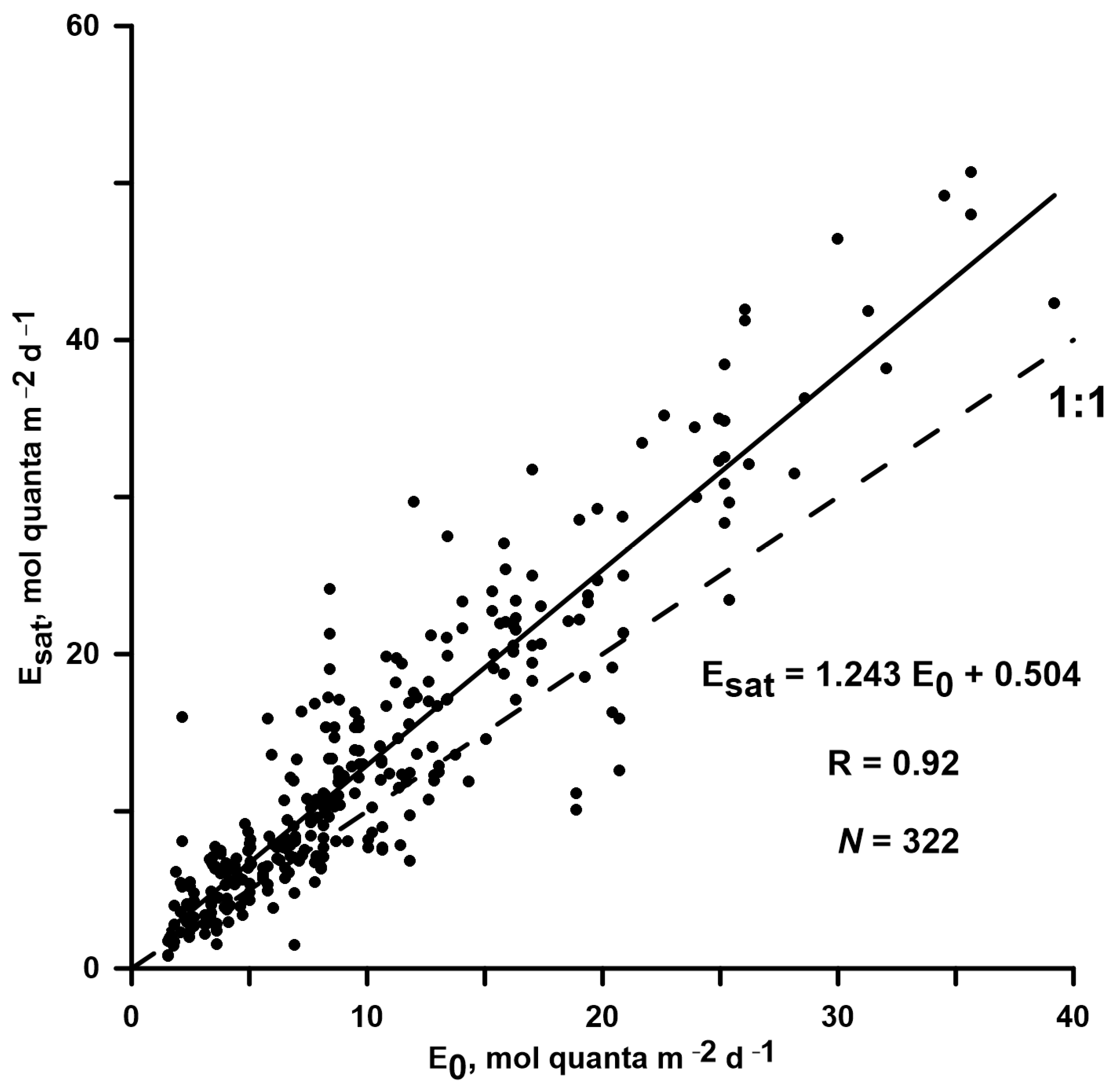
3.3. Pbopt Model Developed with E0, Its Efficiency, and a Comparison with T-Based Models
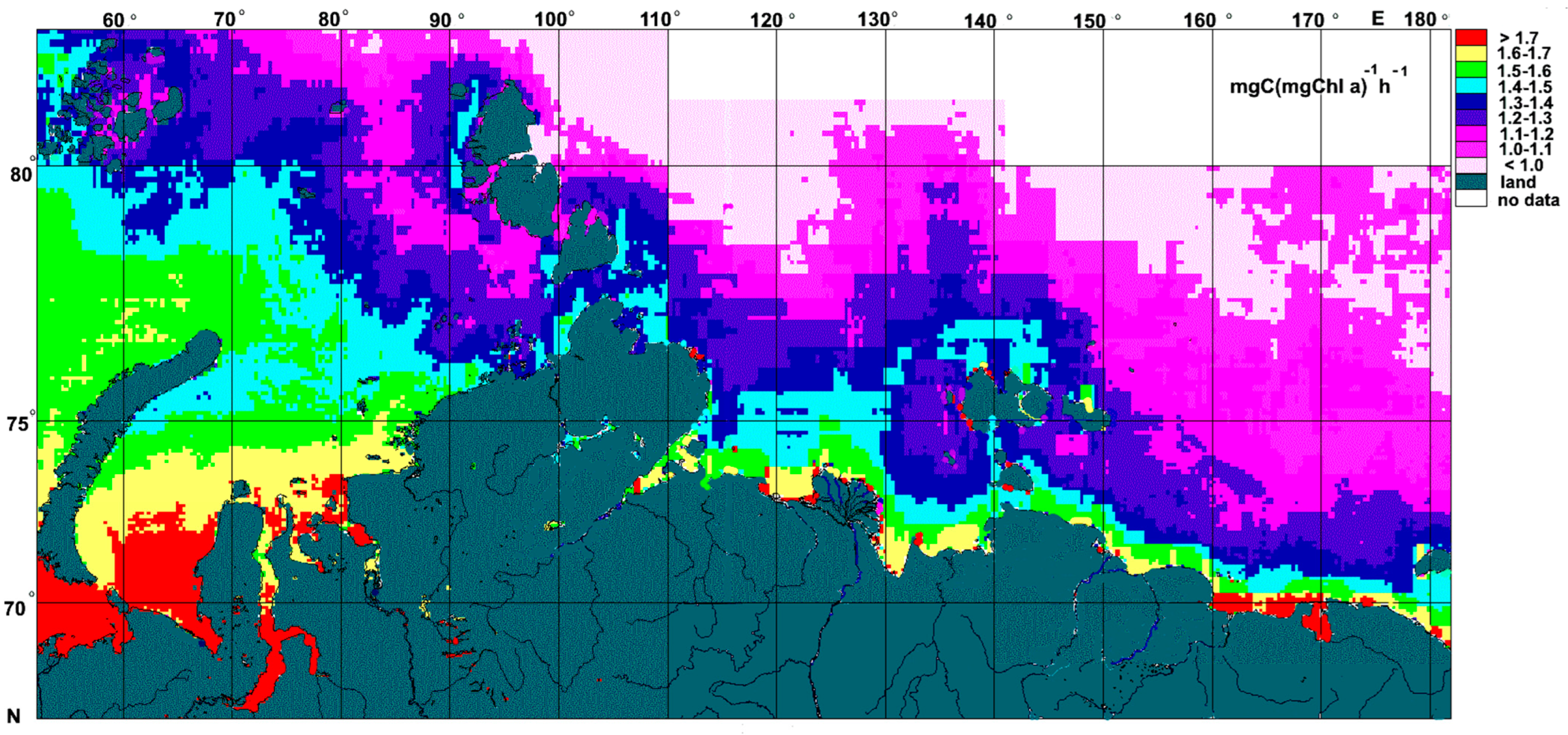
3.4. The Spatial Distribution in Pbopt Assessed Using Satellite-Derived Data
4. Discussion
4.1. The Average Values and Spatiotemporal Variations in the Optimal Assimilation Number (Pbopt) in the Siberian Seas (SSs)
4.2. Influence of Environmental Factors on Pbopt
4.2.1. Influence of PAR on Pbopt
4.2.2. Influence of Temperature and Nutrients on Pbopt
4.2.3. Modelling of Pbopt and Its Application for Remote Sensing
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Field, C.B.; Behrenfeld, M.J.; Randerson, J.T.; Falkowski, P. Primary production of the Biosphere: Integrating terrestrial and oceanic components. Science 1998, 281, 237–240. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; O’Malley, R.O.; Siegel, D.A.; McClain, C.R.; Sarmiento, J.L.; Feldman, G.C.; Milligan, A.J.; Falkowski, P.G.; Letelier, R.M.; Boss, E.S. Climate-driven trends in contemporary ocean productivity. Nature 2006, 444, 752–755. [Google Scholar] [CrossRef] [PubMed]
- Bopp, L.; Monfray, P.; Aumont, O.; Dufresne, J.-L.; Treut, H.L.; Madec, G.; Terray, L.; Orr, J.C. Potential impact of climate change on marine export primary production. Glob. Biogeochem. Cycles 2001, 15, 81–99. [Google Scholar] [CrossRef]
- Chavez, F.P.; Messié, M.; Pennington, J.T. Marine primary production in relation to climate variability and change. Annu. Rev. Mar. Sci. 2011, 3, 227–260. [Google Scholar] [CrossRef]
- Gregg, W.W.; Conkright, M.E.; Ginoux, P.; O’Reilly, J.E.; Casey, N.W. Ocean primary production and climate: Global decadal changes. Geophys. Res. Lett. 2003, 30, 1809. [Google Scholar] [CrossRef]
- Sarmiento, J.L.; Slater, R.; Barber, R.; Bopp, R.L.; Doney, S.C.; Hirst, A.C.; Kleypas, J.; Matear, R.; Mikolajewicz, U.; Monfray, P.; et al. Response of ocean ecosystems to climate warming. Glob. Biogeochem. Cycles 2004, 18, GB3003. [Google Scholar] [CrossRef]
- Taucher, J.; Oschlies, A. Can we predict the direction of marine primary production change under global warming? Geophys. Res. Lett. 2011, 38, L02603. [Google Scholar] [CrossRef]
- Kulk, G.; Platt, T.; Dingle, J.; Jackson, T.; Jönsson, B.F.; Bouman, H.A.; Babin, M.; Brewin, R.J.W.; Doblin, M.; Estrada, M.; et al. Primary production, an index of climate change in the ocean: Satellite-based estimates over two decades. Remote Sens. 2020, 12, 826. [Google Scholar] [CrossRef]
- Jassby, A.D.; Platt, T. Mathematical formulation of the relationship between photosynthesis and light for phytoplankton. Limnol. Oceanogr. 1976, 21, 540–547. [Google Scholar] [CrossRef]
- Platt, T.; Gallegos, C.L.; Harrison, W.G. Photoinhibition of photosynthesis in natural assemblages of marine phytoplankton. J. Mar. Res. 1980, 38, 103–111. [Google Scholar]
- Steemann Nielsen, E. Experimental methods for measuring organic production in the sea. Rapp. P.-v. Réun. Cons. Perm. Int. Explor. Mer. 1958, 144, 38–46. [Google Scholar]
- Lohrenz, S.E. Estimation of primary production by the simulated in situ method. ICES Mar. Sci. Symp. 1993, 197, 159–171. [Google Scholar]
- Behrenfeld, M.J.; Falkowski, P.G. Photosynthetic rates derived from satellite-based chlorophyll concentrations. Limnol. Oceanogr. 1997, 42, 1–20. [Google Scholar] [CrossRef]
- Banse, K.; Yong, M. Sources of variability in satellite-derived estimates of phytoplankton production in the eastern tropical Pacific. J. Geophys. Res. 1990, 95, 7201–7215. [Google Scholar] [CrossRef]
- Campbell, J.; Antoine, D.; Armstrong, R.; Arrigo, K.; Balch, W.; Barber, R.; Behrenfeld, M.; Bidigare, R.; Bishop, J.; Carr, M.-E.; et al. Comparison of algorithms for estimating ocean primary production from surface chlorophyll, temperature, and irradiance. Glob. Biogeochem. Cycles 2002, 16, 9-1–9-15. [Google Scholar] [CrossRef]
- Carr, M.-E.; Friedrichs, M.A.M.; Schmeltz, M.; Aita, M.N.; Antoine, D.; Arrigo, K.R.; Asanuma, I.; Aumont, O.; Barber, R.; Behrenfeld, M.; et al. A comparison of global estimates of marine primary production from ocean color. Deep-Sea Res. Part II 2006, 53, 741–770. [Google Scholar] [CrossRef]
- Friedrichs, M.A.M.; Carr, M.-E.; Barber, R.; Scardi, M.; Antoine, D.; Armstrong, R.; Asanuma, I.; Behrenfeld, M.; Buitenhuis, E.; Chai, F.; et al. Assessing the uncertainties of model estimates of primary productivity in the tropical Pacific Ocean. J. Mar. Syst. 2009, 76, 113–133. [Google Scholar] [CrossRef]
- Saba, V.; Marjorie, S.; Friedrichs, M.A.M.; Carr, M.-E.; Antoine, D.; Armstrong, R.A.; Asanuma, I.; Aumont, O.; Bates, N.R.; Behrenfeld, M.J.; et al. Challenges of modeling depth-integrated marine primary productivity over multiple decades: A case study at BATS and HOT. Glob. Biogeochem. Cycles 2010, 24, GB3020. [Google Scholar] [CrossRef]
- Saba, V.S.; Friedrichs, M.A.M.; Antoine, D.; Armstrong, R.A.; Asanuma, I.; Behrenfeld, M.J.; Ciotti, A.M.; Dowell, M.; Hoepffner, N.; Hyde, K.J.W.; et al. An evaluation of ocean color model estimates of marine primary productivity in coastal and pelagic regions across the globe. Biogeosciences. 2011, 8, 489–503. [Google Scholar] [CrossRef]
- Petrenko, D.; Pozdnyakov, D.; Johannessen, J.; Counillon, F.; Sychov, V. Satellite-derived multiyear trend in primary production in the Arctic Ocean. Int. J. Remote Sens. 2013, 34, 3903–3937. [Google Scholar] [CrossRef]
- Lee, Y.J.; Matrai, P.A.; Friedrichs, M.A.M.; Saba, V.S.; Antoine, D.; Ardyna, M.; Asanuma, I.; Babin, M.; Bélanger, S.; Benoît-Gagne, M.; et al. An assessment of phytoplankton primary productivity in the Arctic Ocean from satellite ocean color/in situ chlorophyll-a based models. J. Geophys. Res. 2015, 120. [Google Scholar] [CrossRef]
- Babin, M.; Bélanger, S.; Ellingsen, I.; Forest, A.; Le Fouest, V.; Lacour, T.; Ardyna, M.; Slagstad, D. Estimation of primary production in the Arctic Ocean using ocean colour remote sensing and coupled physical–biological models: Strengths, limitations and how they compare. Prog. Oceanogr. 2015, 139, 197–220. [Google Scholar] [CrossRef]
- Lobanova, P.; Tilstone, G.H.; Bashmachnikov, I.; Brotas, V. Accuracy Assessment of Primary Production Models with and without Photoinhibition Using Ocean-Colour Climate Change Initiative Data in the North East Atlantic Ocean. Remote Sens. 2018, 10, 1116. [Google Scholar] [CrossRef]
- Regaudie-de-Giouxa, A.; Huete-Ortega, M.; Sobrino, C.; López-Sandoval, D.C.; González, N.; Fernández-Carrera, A.; Vidal, M.; Marañón, E.; Cermeño, P.; Latasa, M.; et al. Multi-model remote sensing assessment of primary production in the subtropical gyres. J. Mar. Syst. 2019, 196, 97–106. [Google Scholar] [CrossRef]
- Ishizaka, J.; Siswanto, E.; Itoh, T.; Murakami, H.; Yamaguchi, Y.; Horimoto, N.; Ishimaru, T.; Hashimoto, S.; Saino, T. Verification of Vertically Generalized Production Model and estimation of primary production in Sagami Bay, Japan. J. Oceanogr. 2007, 63, 517–524. [Google Scholar] [CrossRef]
- Lee, Z.; Marra, J.; Perry, M.J.; Kahru, M. Estimating oceanic primary productivity from ocean color remote sensing: A strategic assessment. J. Mar. Syst. 2015, 149, 50–59. [Google Scholar] [CrossRef]
- Siegel, D.A.; Westberry, T.K.; O’Brien, M.C.; Nelson, N.B.; Michaels, A.F.; Morrison, J.R.; Scott, A.; Caporelli, E.A.; Sorensen, J.C.; Maritorena, S.; et al. Bio-optical modeling of primary production on regional scales: The Bermuda BioOptics project. Deep-Sea Res. Part II 2001, 48, 1865–1896. [Google Scholar] [CrossRef]
- Arrigo, K.R.; van Dijken, G.L. Secular trends in Arctic Ocean net primary production. J. Geophys. Res. 2011, 116, C09011. [Google Scholar] [CrossRef]
- Matrai, P.A.; Olson, E.; Suttles, S.; Hill, V.; Codispoti, L.A.; Light, B.; Steele, M. Synthesis of primary production in the Arctic Ocean: I. Surface waters, 1954–2007. Prog. Oceanogr. 2013, 110, 93–106. [Google Scholar] [CrossRef]
- Hill, V.J.; Matrai, P.A.; Olson, E.; Suttles, S.; Steele, M.; Codispoti, L.A.; Zimmerman, R.C. Synthesis of integrated primary production in the Arctic Ocean: II. In situ and remotely sensed estimates. Prog. Oceanogr. 2013, 110, 107–125. [Google Scholar] [CrossRef]
- Subba Rao, D.V.; Platt, T. Primary production of Arctic waters. Pol. Biol. 1984, 3, 191–201. [Google Scholar] [CrossRef]
- Harrison, W.G.; Cota, G.F. Primary production in polar waters: Relation to nutrient availability. Pol. Res. 1991, 10, 87–104. [Google Scholar] [CrossRef]
- Demidov, A.; Sukhanova, I.; Belevich, T.; Flint, M.; Gagarin, V.; Sergeeva, V.; Eremeeva, E.; Fedorov, A. Size-fractionated surface phytoplankton in the Kara and Laptev seas: Environmental control and spatial variability. Mar. Ecol. Prog. Ser. 2021, 664, 59–77. [Google Scholar] [CrossRef]
- Finkel, Z.V.; Beardall, J.; Flynn, K.J.; Quigg, A.; Rees, T.A.V.; Raven, J.A. Phytoplankton in a changing world: Cell size and elemental stoichiometry. J. Plankton Res. 2010, 32, 119–137. [Google Scholar] [CrossRef]
- Dittmar, T.; Kattner, G. The biogeochemistry of the river and shelf system of the Arctic Ocean: A review. Mar. Chem. 2003, 83, 103–120. [Google Scholar] [CrossRef]
- Hanzlick, D.; Aagaard, K. Freshwater and Atlantic water in the Kara Sea. J. Geophys. Res. 1980, 85, 4937–4942. [Google Scholar] [CrossRef]
- Holmes, R.M.; McClelland, J.W.; Peterson, B.J.; Tank, S.E.; Bulygina, E.; Eglinton, T.I.; Gordeev, V.V.; Gurtovaya, T.Y.; Raymond, P.A.; Repeta, D.J.; et al. Seasonal and annual fluxes of nutrients and organic matter from large rivers to the Arctic Ocean and surrounding seas. Estuaries Coasts. 2012, 35, 369–382. [Google Scholar] [CrossRef]
- Le Fouest, V.; Babin, M.; Ttemblay, J.-É. The fate of riverine nutrients on Arctic shelves. Biogeosciences 2013, 10, 3661–3677. [Google Scholar] [CrossRef]
- Stein, R. Circum Arctic river discharge and its geological record. Int. J Earth Sci. 2000, 89, 447–449. [Google Scholar] [CrossRef]
- Kubryakov, A.; Stanichny, S.; Zatsepin, A. River plume dynamics in the Kara Sea from altimetry-based lagrangian model, satellite salinity and chlorophyll data. Remote Sens. Environ. 2016, 176, 177–187. [Google Scholar] [CrossRef]
- Osadchiev, A.A.; Frey, D.I.; Shchuka, S.A.; Tilinina, N.D.; Morozov, E.G.; Zavialov, P.O. Structure of the freshened surface layer in the Kara Sea during ice-free periods. J. Geophys. Res. 2021, 126, e2020JC016486. [Google Scholar] [CrossRef]
- Zatsepin, A.G.; Zavialov, P.O.; Kremenetskiy, V.V.; Poyarkov, S.G.; Soloviev, D.M. The upper desalinated layer in the Kara Sea. Oceanology 2010, 50, 658–668. [Google Scholar] [CrossRef]
- Glukhovets, D.I.; Goldin, Y.A. Surface desalinated layer distribution in the Kara Sea determined by shipboard and satellite data. Oceanologia 2020, 62, 364–373. [Google Scholar] [CrossRef]
- Amon, R.M.W. The role of dissolved organic matter for the organic carbon cycle in the Arctic Ocean. In The Organic Carbon Cycle in the Arctic Ocean; Stein, R., Macdonald, R.W., Eds.; Springer: Berlin, Germany, 2004; pp. 83–100. [Google Scholar]
- Rachold, V.; Eicken, H.; Gordeev, V.V.; Grigoriev, M.N.; Hubberten, H.-W.; Lisitzin, A.P.; Shevchenko, V.P.; Schirrmeister, L. Modern terrigenous organic carbon input to the Arctic ocean. In The Organic Carbon Cycle in the Arctic Ocean; Stein, R., Macdonald, R.W., Eds.; Springer: Berlin, Germany, 2004; pp. 33–56. [Google Scholar]
- Vetrov, A.A.; Romankevich, E.A. Carbon Cycle in the Russian Arctic Seas; Springer: Berlin, Germany, 2004; p. 331. [Google Scholar]
- Demidov, A.B.; Mosharov, S.A.; Makkaveev, P.N. Patterns of the Kara Sea primary production in autumn: Biotic and abiotic forcing of subsurface layer. J. Mar. Syst. 2014, 132, 130–149. [Google Scholar] [CrossRef]
- Longhurst, A.R.; Sathyendranath, S.; Platt, T.; Caverhill, C. An estimate of global primary production in the ocean from satellite radiometer data. J. Plankton Res. 1995, 17, 1245–1271. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S. Spatial structure of pelagic ecosystem processes in the global ocean. Ecosystems 1999, 2, 384–394. [Google Scholar] [CrossRef]
- Saux Picart, S.; Sathyendranath, S.; Dowell, M.; Moore, T.; Platt, T. Remote sensing of assimilation number for marine phytoplankton. Rem. Sens. Environ. 2014, 146, 87–96. [Google Scholar] [CrossRef]
- Carmack, E.C.; Macdonald, R.W.; Jasper, S. Phytoplankton productivity on the Canadian Shelf of the Beaufort Sea. Mar. Ecol. Prog. Ser. 2004, 277, 37–50. [Google Scholar] [CrossRef]
- Tremblay, J.E.; Gagnon, J. The effect of irradiance and nutrient supply on the productivity of Arctic waters: A perspective on climate change. In Influence of Climate Change on the Changing Arctic and Sub-Arctic Condition; Nihpul, J.C.J., Kostianoy, A.G., Eds.; Springer: New York, NY, USA, 2009; pp. 73–94. [Google Scholar]
- Platt, T.; Harrison, W.G.; Horne, E.P.W.; Irwin, B. Carbon fixation and oxygen evolution by phytoplankton in the Canadian High Arctic. Pol. Biol. 1987, 8, 103–113. [Google Scholar] [CrossRef]
- Bélanger, S.; Babin, M.; Tremblay, J.E. Increasing cloudiness in the Arctic damps the increase in phytoplankton primary production due to sea ice receding. Biogeosciences Discussions. 2012, 9, 13987–14012. [Google Scholar] [CrossRef]
- Yun, M.S.; Chung, K.H.; Zimmerman, S.; Zhao, J.; Joo, H.M.; Lee, S.H. Phytoplankton productivity and its response to higher light levels in the Canada Basin. Pol. Biol. 2012, 35, 257–268. [Google Scholar] [CrossRef]
- Vedernikov, V.I.; Demidov, A.B.; Sud’bin, A.I. Primary production and chlorophyll in the Kara Sea in September 1993. Oceanology 1995, 34, 630–640. [Google Scholar]
- Mosharov, S.A. Distribution of the primary production and chlorophyll a in the Kara Sea in September of 2007. Oceanology 2010, 50, 885–893. [Google Scholar] [CrossRef]
- Mosharov, S.A.; Demidov, A.B.; Simakova, U.V. Peculiarities of the primary production process in the Kara Sea at the end of the vegetation season. Oceanology 2016, 56, 84–94. [Google Scholar] [CrossRef]
- Demidov, A.B.; Kopelevich, O.V.; Mosharov, S.A.; Sheberstov, S.V.; Vazyulya, S.V. Modelling Kara Sea phytoplankton primary production: Development and skill assessment of regional algorithms. J. Sea Res. 2017, 125, 1–17. [Google Scholar] [CrossRef]
- Demidov, A.B.; Gagarin, V.I.; Arashkevich, E.G.; Makkaveev, P.N.; Konyukhov, I.V.; Vorobieva, O.V.; Fedorov, A.V. Spatial Variability of Primary Production and Chlorophyll in the Laptev Sea in August–September. Oceanology 2019, 59, 678–691. [Google Scholar] [CrossRef]
- Demidov, A.B.; Gagarin, V.I.; Vorobieva, O.V.; Makkaveev, P.N.; Artemiev, V.A.; Khrapko, A.N.; Grigoriev, A.V.; Sheberstov, S.V. Spatial and vertical variability of primary production in the Kara Sea in July and August 2016: The influence of the river plume and subsurface chlorophyll maxima. Pol. Biol. 2018, 41, 563–578. [Google Scholar] [CrossRef]
- Demidov, A.B.; Gagarin, V.I. Primary Production and Associated Environmental Conditions in the East Siberian Sea in Autumn. Dokl. Earth Sci. 2019, 487, 1006–1011. [Google Scholar] [CrossRef]
- Fitzwater, S.E.; Knauer, G.A.; Martin, J.H. Metal contamination and its effect on primary production measurements. Limnol. Oceanogr. 1982, 27, 544–551. [Google Scholar] [CrossRef]
- Steemann Nielsen, E. The use of radioactive carbon (C14) for measuring organic production in the sea. J. Cons. Perm. Int. Pour Explor. Mer. 1952, 18, 117–140. [Google Scholar] [CrossRef]
- Jeffrey, S.W.; Humphrey, G.F. New spectrophotometric equations for determining chlorophylls a, b, c1 and c2 in higher plants, algae and natural phytoplankton. Biochem. Physiol. Pflanzen. 1975, 167, 191–194. [Google Scholar] [CrossRef]
- SCOR–UNESCO. Report of SCOR–UNESCO working group 17 on determination of photosynthetic pigments in Sea Water. In Monography of Oceanography Methodology; UNESCO: Paris, France, 1966; pp. 9–18. [Google Scholar]
- Holm-Hansen, O.; Lorenzen, C.J.; Holmes, R.W.; Strickland, J.D.H. Fluorometric determination of chlorophyll. J. Cons. Perm. Int. Explor. Mer. 1965, 30, 3–15. [Google Scholar] [CrossRef]
- Holm-Hansen, O.; Riemann, B. Chlorophyll a determination: Improvements in methodology. Oikos 1978, 30, 438–447. [Google Scholar] [CrossRef]
- Neveux, J.; Delmas, D.; Romano, J.; Algarra, P.; Ignatiades, L.; Herbland, A.; Morand, P.; Neori, A.; Bonin, D.; Barbe, J.; et al. Comparison of chlorophyll and phaeopigments determination by spectrophotometric, fluorometric, spectrofluorometric and HPLC methods. Mar. Microb. Food Webs. 1990, 4, 217–238. [Google Scholar]
- Mantoura, R.F.C.; Jeffrey, S.W.; Liewellyn, C.A.; Claustre, H.; Morales, C.E. Comparison between spectrophotometric, fluorometric and HPLC methods for chlorophyll analysis. In Phytoplankton Pigments in Oceanography: Guidelines to Modern Methods; Jeffrey, S.W., Mantoura, R.F.C., Wright, S.W., Eds.; UNESCO: Paris, France, 1997; pp. 361–380. [Google Scholar]
- Intergovernmental Oceanographic Commission. Chemical Methods for Use in Marine Environment Monitoring; UNESCO: Paris, France, 1983; p. 53. [Google Scholar]
- Grasshoff, K.; Kremling, K.; Ehrhardt, M. Methods of Seawater Analysis; Wiley: New York, NY, USA, 1999; p. 600. [Google Scholar]
- Millero, F.J. Thermodynamics of the carbon dioxide system in oceans. Geochim. Cosmochim. Acta 1995, 59, 661–677. [Google Scholar] [CrossRef]
- Pivovarov, S.; Schlitzer, R.; Novikhin, A. River run-off influence on the water mass formation in the Kara Sea. In Siberian River Run-off in the Kara Sea; Stein, R., Fahl, K., Fütterer, D.K., Galimov, E.M., Stepanets, O.V., Eds.; Elsevier: Amsterdam, The Netherlands, 2003; pp. 9–25. [Google Scholar]
- Doney, S.C.; Lima, I.; Moore, J.K.; Lindsay, K.; Behrenfeld, M.J.; Westberry, T.K.; Mahowald, N.; Glover, D.M.; Takahashi, T. Skill metrics for confronting global upper ocean ecosystem-biogeochemistry models against field and remote sensing data. J. Mar. Syst. 2009, 76, 95–112. [Google Scholar] [CrossRef]
- Stow, C.A.; Jolliff, J.; McGillicuddy, D.J.; Doney, C.S.; Allen, J.I.; Friedrichs, M.A.M.; Rose, K.A.; Wallhead, P. Skill assessment for coupled biological/physical models of marine systems. J. Mar. Syst. 2009, 76, 4–15. [Google Scholar] [CrossRef]
- Frouin, R.; McPherson, J.; Ueyoshi, K.; Franz, B.A. A time series of photosynthetically available radiation at the ocean surface from SeaWiFS and MODIS data. Proc. SPIE 2012, 12. [Google Scholar] [CrossRef]
- Siswanto, E.; Ishizaka, J.; Yokouchi, K. Optimal Primary Production Model and Parameterization in the Eastern East China Sea. J. Oceanogr. 2006, 62, 361–372. [Google Scholar] [CrossRef]
- Hill, V.J.; Zimmerman, R.C. Estimates of primary production by remote sensing in the Arctic Ocean: Assessment of accuracy with passive and active sensors. Deep Sea Res. Part I 2010, 57, 1243–1254. [Google Scholar] [CrossRef]
- Mei, Z.-P.; Legendre, L.; Gratton, Y.; Tremblay, J.-É.; LeBlanc, B.; Klein, B.; Gosselin, M. Phytoplankton production in the North Water Polynya: Size-fractions and carbon fluxes, April to July 1998. Mar. Ecol. Prog. Ser. 2003, 256, 13–27. [Google Scholar] [CrossRef]
- Hill, V.J.; Cota, G. Spatial patterns of primary production on the shelf, slope and basin of the Western Arctic in 2002. Deep-Sea Res. Part II 2005, 52, 3344–3354. [Google Scholar] [CrossRef]
- Apollonio, S.; Matrai, P. Marine primary production in the Canadian Arctic, 1956, 1961–1963. Polar Biol. 2011, 34, 767–774. [Google Scholar] [CrossRef]
- Bouman, H.; Platt, T.; Sathyendranath, S.; Stuart, V. Dependence of light-saturated photosynthesis on temperature and community structure. Deep-Sea Res. Part I 2005, 52, 1284–1299. [Google Scholar] [CrossRef]
- Kameda, T.; Ishizaka, J. Size-fractionated primary production estimated by a two-phytoplankton community model applicable to ocean color remote sensing. J. Oceanogr. 2005, 61, 663–672. [Google Scholar] [CrossRef]
- de Madariaga, I.; Joint, I. Photosynthesis and carbon metabolism by size-fractionated phytoplankton in the southern North Sea in early summer. Cont. Shelf Res. 1994, 14, 295–311. [Google Scholar] [CrossRef]
- Richardson, K.; Bendtsen, J.; Kragh, T.; Mousing, E.A. Constraining the distribution of photosynthetic parameters in the global ocean. Front. Mar. Sci. 2016, 3. [Google Scholar] [CrossRef]
- Robinson, A.; Bouman, H.A.; Tilstone, G.H.; Sathyendranath, S. Size class dependent relationships between temperature and phytoplankton photosynthesis-irradiance parameters in the Atlantic Ocean. Front. Mar. Sci. 2017, 4. [Google Scholar] [CrossRef]
- Raven, J.A. Small is beautiful: The picophytoplankton. Funct. Ecol. 1998, 12, 503–513. [Google Scholar] [CrossRef]
- Raven, J.A.; Finkel, Z.V.; Irwin, A.J. Picophytoplankton: Bottom-up and top-down controls on ecology and evolution. Vie et Milieu. 2005, 55, 209–215. [Google Scholar]
- Kremer, C.T.; Thomas, M.K.; Litchman, E. Temperature- and size-scaling of phytoplankton population growth rates: Reconciling the Eppley curve and the metabolic theory of ecology. Limnol. Oceanogr. 2017, 62, 1658–1670. [Google Scholar] [CrossRef]
- Harrison, W.G.; Irwin, B.; Platt, T. Primary production and nutrient assimilation by natural phytoplankton populations of the eastern Canadian Arctic. Can. J. Fish. Aquat. Sci. 1982, 39, 335–345. [Google Scholar] [CrossRef]
- Platt, T.; Harrison, W.G. Letter to the editor. Reconciliation of carbon and oxygen fluxes in the upper ocean. Deep-Sea Res. 1986, 33, 273–276. [Google Scholar] [CrossRef]
- Babin, M.; Arrigo, K.; Bélanger, S.; Forget, M.-H. Ocean Colour Remote Sensing in Polar Seas. IOCCG Rep. Series 2015, 16, 130. [Google Scholar]
- Lobbes, J.M.; Fitznar, H.P.; Kattner, G. Biogeochemical characteristics of dissolved and particulate organic matter in Russian rivers entering the Arctic Ocean. Geochem. Cosmochim. Acta 2000, 64, 2973–2983. [Google Scholar] [CrossRef]
- Bröder, L.; Tesi, T.; Salvadó, J.A.; Semiletov, I.P.; Dudarev, O.V.; Gustafsson, Ö. Fate of terrigenous organic matter across the Laptev Sea from the mouth of the Lena River to the deep sea of the Arctic interior. Biogeosciences 2016, 13, 5003–5019. [Google Scholar] [CrossRef]
- Ahn, S.H.; Kim, K.W.; Jo, N.; Kang, J.J.; Lee, J.H.; Whitledge, T.E.; Stockwell, D.A.; Lee, H.W.; Lee, S.H. Fluvial influence on the biochemical composition of particulate organic matter in the Laptev and Western East Siberian seas during 2015. Mar. Environ. Res. 2020, 155. [Google Scholar] [CrossRef]
- Harrison, W.G.; Platt, T. Photosynthesis-Irradiance Relationships in Polar and Temperate Phytoplankton Populations. Pol. Biol. 1986, 5, 153–164. [Google Scholar] [CrossRef]
- Li, W.K.W.; Smith, J.C.; Platt, T. Temperature response of photosynthetic capacity and carboxylase activity in Arctic marine phytoplankton. Mar. Ecol. Progr. Ser. 1984, 17, 237–243. [Google Scholar] [CrossRef]
- Rey, F. Photosynthesis-irradiance relationships in natural phytoplankton populations of the Barents Sea. Pol. Res. 1991, 10, 105–116. [Google Scholar] [CrossRef]
- Palmer, M.A.; van Dijken, G.L.; Mitchell, G.; Seegers, B.J.; Lowry, K.E.; Mills, M.M.; Arrigo, K.R. Light and nutrient control of photosynthesis in natural phytoplankton populations from the Chukchi and Beaufort seas, Arctic Ocean. Limnol. Oceanogr. 2013, 58, 2185–2205. [Google Scholar] [CrossRef]
- Huot, Y.; Babin, M.; Bruyant, F. Photosynthetic parameters in the Beaufort Sea in relation to the phytoplankton community structure. Biogeosciences 2013, 10, 3445–3454. [Google Scholar] [CrossRef]
- Coello-Camba, A.; Agustí, S.; Vaqué, D.; Holding, J.; Arrieta, J.M.; Wassmann, P.; Duarte, C.M. Experimental Assessment of Temperature Thresholds for Arctic Phytoplankton Communities. Estuaries Coasts 2014, 38, 873–885. [Google Scholar] [CrossRef]
- Demidov, A.B.; Sheberstov, S.V.; Gagarin, V.I.; Khlebopashev, P.V. Seasonal Variation of the Satellite-Derived Phytoplankton Primary Production in the Kara Sea. Oceanology 2017, 57, 91–104. [Google Scholar] [CrossRef]
- Demidov, A.B.; Sheberstov, S.V.; Gagarin, V.I. Seasonal Variability and Annual Primary Production of Phytoplankton in the Laptev Sea Assessed by MODIS-Aqua Data. Izv.-Atmos. Oceanic Phys. 2020, 56, 950–962. [Google Scholar] [CrossRef]
- Lee, S.H.; Whitledge, T.E. Primary and new production in the deep Canada Basin during summer 2002. Pol. Biol. 2005, 28, 190–197. [Google Scholar] [CrossRef]
- Goldman, J.C.; McCarthy, J.J.; Peavey, D.G. Growth rate influence on the chemical composition of phytoplankton in oceanic waters. Nature 1979, 279, 210–215. [Google Scholar] [CrossRef]
- Falkowski, P.G.; Stone, D.P. Nitrate Uptake in Marine Phytoplankton: Energy Sources and the Interaction with Carbon Fixation. Mar. Biol. 1975, 32, 77–84. [Google Scholar] [CrossRef]
- Estrada, M.; Bayer-Giraldi, M.; Felipe, J.; Marrasé, C.; Sala, M.M.; Vidal, M. Light and nutrient effects on microbial communities collected during spring and summer in the Beaufort Sea. Aquat. Microb. Ecol. 2009, 54, 217–231. [Google Scholar] [CrossRef]
- Moschonas, G.; Gowen, R.J.; Paterson, R.F.; Mitchell, E.; Stewart, B.M.; McNeill, S.; Glibert, P.M.; Davidson, K. Nitrogen dynamics and phytoplankton community structure: The role of organic nutrients. Biogeochemistry 2017, 134, 125–145. [Google Scholar] [CrossRef]
- Dogliotti, A.I.; Lutz, V.A.; Segura, V. Estimation of primary production in the southern Argentine continental shelf and shelf-break regions using field and remote sensing data. Rem. Sens. Environ. 2014, 140, 497–508. [Google Scholar] [CrossRef]

| Cruise | Months | Years | Location | Number of Stations | Publications |
|---|---|---|---|---|---|
| 49th Dmitry Mendeleev | August–September | 1993 | Kara Sea | 29 | [56] |
| 54th Akademik Mstislav Keldysh | September | 2007 | Kara Sea | 16 | [57] |
| 59th Akademik Mstislav Keldysh | September–October | 2011 | Kara Sea | 36 | [58] |
| 125th Professor Shtokman | September | 2013 | Kara Sea | 29 | [59] |
| 128th Professor Shtokman | August–September | 2014 | Kara Sea | 48 | Unpublished data |
| 63d Akademik Mstislav Keldysh | August–October | 2015 | Kara and Laptev Seas | 56 | [60] |
| 66th Akademik Mstislav Keldysh | July–August | 2016 | Kara Sea | 55 | [61] |
| 69th Akademik Mstislav Keldysh | August–September | 2017 | Kara, Laptev, and East Siberian Seas | 53 | [60,62] |
| 72nd Akademik Mstislav Keldysh | August–September | 2018 | Kara and Laptev Seas | 37 | [60] |
| 76th Akademik Mstislav Keldysh | July–August | 2019 | Kara Sea | 32 | Unpublished data |
| 81st Akademik Mstislav Keldysh | August–September | 2020 | Kara Sea | 28 | Unpublished data |
| Region | Statistics | >3 μm | <3 μm | Total |
|---|---|---|---|---|
| Kara Sea | M ± σ | 1.15 ± 0.59 | 1.78 ± 1.29 | 1.37 ± 0.79 |
| N | 60 | 59 | 333 | |
| Laptev Sea | M ± σ | 1.02 ± 0.55 | 1.30 ± 0.76 | 1.27 ± 0.58 |
| N | 33 | 33 | 59 | |
| East Siberian Sea | M ± σ | 1.21 ± 0.68 | 1.33 ± 0.97 | 1.77 ± 0.70 |
| N | 12 | 12 | 19 | |
| Siberian Seas | M ± σ | 1.05 ± 0.58 | 1.65 ± 1.24 | 1.38 ± 0.76 |
| N | 105 | 104 | 411 |
| Range of S0 | Season | Statistics | Phytoplankton Size Fractions | |||||
|---|---|---|---|---|---|---|---|---|
| >3 μm | <3 μm | Total | ||||||
| <25 | Summer (July, August) | M ± σ | 1.26 ± 0.43 | 1.10 ± 0.52 | 2.60 ± 1.96 | 1.73 ± 1.40 | 1.72 ± 0.48 | 1.35 ± 0.64 |
| N | 3 | 3 | 41 | |||||
| Autumn (September, October) | M ± σ | 1.07 ± 0.54 | 1.60 ± 1.32 | 1.22 ± 0.57 | ||||
| N | 21 | 21 | 117 | |||||
| >25 | Summer (July, August) | M ± σ | 1.13 ± 0.66 | 1.04 ± 0.60 | 1.99 ± 1.42 | 1.63 ± 1.19 | 1.81 ± 0.88 | 1.40 ± 0.84 |
| N | 35 | 35 | 110 | |||||
| Autumn (September, October) | M ± σ | 0.97 ± 0.54 | 1.35 ± 0.90 | 1.08 ± 0.64 | ||||
| N | 46 | 45 | 143 | |||||
| Parameter | Statistics | T0 | S0 | Chl0 | ChlS/Chl0 | E0 | PO4 | Si(OH)4 | DIN |
|---|---|---|---|---|---|---|---|---|---|
| Pbopt | R | 0.08 | 0.08 | −0.21 * | 0.23 * | 0.61 * | −0.02 | 0.10 | −0.20 * |
| N | 411 | 408 | 411 | 104 | 395 | 404 | 410 | 387 | |
| p | 0.109 | 0.092 | <10−3 | 0.020 | <10−2 | 0.723 | 0.12 | <10−3 | |
| Pbopt L | R | 0.20 * | 0.07 | 0.01 | 0.26* | 0.08 | 0.14 | 0.16 | 0.13 |
| N | 105 | 105 | 105 | 104 | 105 | 104 | 104 | 98 | |
| p | 0.04 | 0.468 | 0.947 | 0.008 | 0.394 | 0.154 | 0.106 | 0.201 | |
| Pbopt S | R | 0.07 | −0.04 | 0.12 | −0.09 | 0.24 * | −0.11 | −0.05 | −0.05 |
| N | 104 | 104 | 104 | 103 | 104 | 103 | 103 | 97 | |
| p | 0.457 | 0.652 | 0.208 | 0.379 | 0.014 | 0.291 | 0.594 | 0.596 |
| Parameter | Statistics | T0 | S0 | Chl0 | E0 | PO4 | Si(OH)4 | DIN |
|---|---|---|---|---|---|---|---|---|
| T | R | 1.00 | ||||||
| N | 411 | |||||||
| p | <10−3 | |||||||
| S0 | R | −0.22 * | 1.00 | |||||
| N | 408 | 408 | ||||||
| p | <10−3 | <10−3 | ||||||
| Chl0 | R | 0.30 * | −0.61 * | 1.00 | ||||
| N | 411 | 408 | 411 | |||||
| p | <10−3 | <10−2 | <10−3 | |||||
| E0 | R | 0.11 * | 0.07 | −0.20 * | 1.00 | |||
| N | 395 | 392 | 395 | 395 | ||||
| p | 0.036 | 0.163 | <10−3 | <10−3 | ||||
| PO4 | R | −0.14 * | −0.21 * | 0.19 * | −0.06 | 1.00 | ||
| N | 404 | 401 | 404 | 388 | 404 | |||
| p | 0.006 | <10−3 | <10−3 | 0.232 | <10−3 | |||
| Si(OH)4 | R | 0.21 * | −0.52 * | 0.67 * | −0.04 | 0.35 * | 1.00 | |
| N | 410 | 407 | 410 | 394 | 404 | 410 | ||
| p | <10−3 | <10−2 | <10−2 | 0.473 | <10−3 | <10−3 | ||
| DIN | R | −0.11 * | −0.20 * | 0.28 * | −0.23 * | 0.28 * | 0.25 * | 1.00 |
| N | 387 | 384 | 387 | 377 | 385 | 387 | 387 | |
| p | 0.027 | <10−3 | <10−3 | <10−3 | <10−3 | <10−3 | <10−3 |
| Model | Regression Statistics | Performance Indices | ||||||
|---|---|---|---|---|---|---|---|---|
| Slope | Intercept | R2 | N | p Value | B | σ | RMSD | |
| E0reg | 0.697 | 0.879 | 0.35 | 131 | <0.05 | 0.040 | 0.176 | 0.227 |
| BF-model | 0.060 | 0.405 | 0.02 | 410 | <0.05 | 0.343 | 0.409 | 0.444 |
| Treg | 0.036 | 0.115 | 0.03 | 137 | <0.05 | 0.066 | 0.055 | 0.279 |
| Esat | 0.289 | 0.226 | 0.19 | 373 | <0.05 | 0.183 | 0.190 | 0.321 |
| Parameter | Statistics | T0 | S0 | Chl0 | E0 | PO4 | Si(OH)4 | DIN |
|---|---|---|---|---|---|---|---|---|
| Pbopt S0 < 25 | R | 0.24 * | 0.21 * | −0.10 | 0.59 * | −0.09 | 0.19 * | −0.24 * |
| N | 159 | 156 | 159 | 150 | 154 | 158 | 147 | |
| p | 0.003 | 0.009 | 0.211 | <10−3 | 0.284 | 0.020 | 0.003 | |
| Pbopt S0 > 25 | R | 0.02 | −0.11 | −0.41 * | 0.63 * | 0.02 | 0.06 | −0.19 * |
| N | 245 | 254 | 254 | 247 | 252 | 254 | 242 | |
| p | 0.713 | 0.075 | <10−3 | <10−2 | 0.696 | 0.376 | 0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demidov, A.B.; Belevich, T.A.; Sheberstov, S.V. Optimal Assimilation Number of Phytoplankton in the Siberian Seas: Spatiotemporal Variability, Environmental Control and Estimation Using a Region-Specific Model. J. Mar. Sci. Eng. 2023, 11, 522. https://doi.org/10.3390/jmse11030522
Demidov AB, Belevich TA, Sheberstov SV. Optimal Assimilation Number of Phytoplankton in the Siberian Seas: Spatiotemporal Variability, Environmental Control and Estimation Using a Region-Specific Model. Journal of Marine Science and Engineering. 2023; 11(3):522. https://doi.org/10.3390/jmse11030522
Chicago/Turabian StyleDemidov, Andrey B., Tatiana A. Belevich, and Sergey V. Sheberstov. 2023. "Optimal Assimilation Number of Phytoplankton in the Siberian Seas: Spatiotemporal Variability, Environmental Control and Estimation Using a Region-Specific Model" Journal of Marine Science and Engineering 11, no. 3: 522. https://doi.org/10.3390/jmse11030522
APA StyleDemidov, A. B., Belevich, T. A., & Sheberstov, S. V. (2023). Optimal Assimilation Number of Phytoplankton in the Siberian Seas: Spatiotemporal Variability, Environmental Control and Estimation Using a Region-Specific Model. Journal of Marine Science and Engineering, 11(3), 522. https://doi.org/10.3390/jmse11030522







