Research on Multi-Fault Identification of Marine Vertical Centrifugal Pump Based on Multi-Domain Characteristic Parameters

Abstract

The marine vertical centrifugal pump is an important piece of auxiliary equipment for ships. Due to the complex operating conditions of marine equipment and the frequent swaying of the hull, typical pump failures such as rotor misalignment, rotor unbalance and mechanical loosening occur frequently, which seriously affect the service life of the marine vertical centrifugal pump. Based on multi-domain characteristic parameters, a fault identification method combining weighted kernel principal component analysis (WKPCA) and particle swarm optimization support vector machine (PSO-SVM) is proposed in this paper. It can effectively solve the problem of multi-fault classification of the centrifugal pump and provide reference for efficient maintenance of equipment. Firstly, a vertical centrifugal pump test bench is set up to simulate typical faults. The collected original fault data are denoised by Kalman filtering. Then, a multi-domain feature set composed of 20 feature parameters was constructed. However, due to high dimension, data redundancy and calculation time were increased. After dimensionality reduction, a fault feature set with 9 feature indexes was established by combining with the WKPCA method. Finally, the PSO-SVM model is used to realize multi-fault identification, and the recognition results of the traditional support vector machine and the genetic algorithm support vector machine (GA-SVM) are compared to verify the diagnosis results and classification performance of PSO-SVM. The results show that the accuracy of WKPCA and PSO-SVM fault recognition methods based on multi-domain characteristic parameters is 1, and it has good convergence.

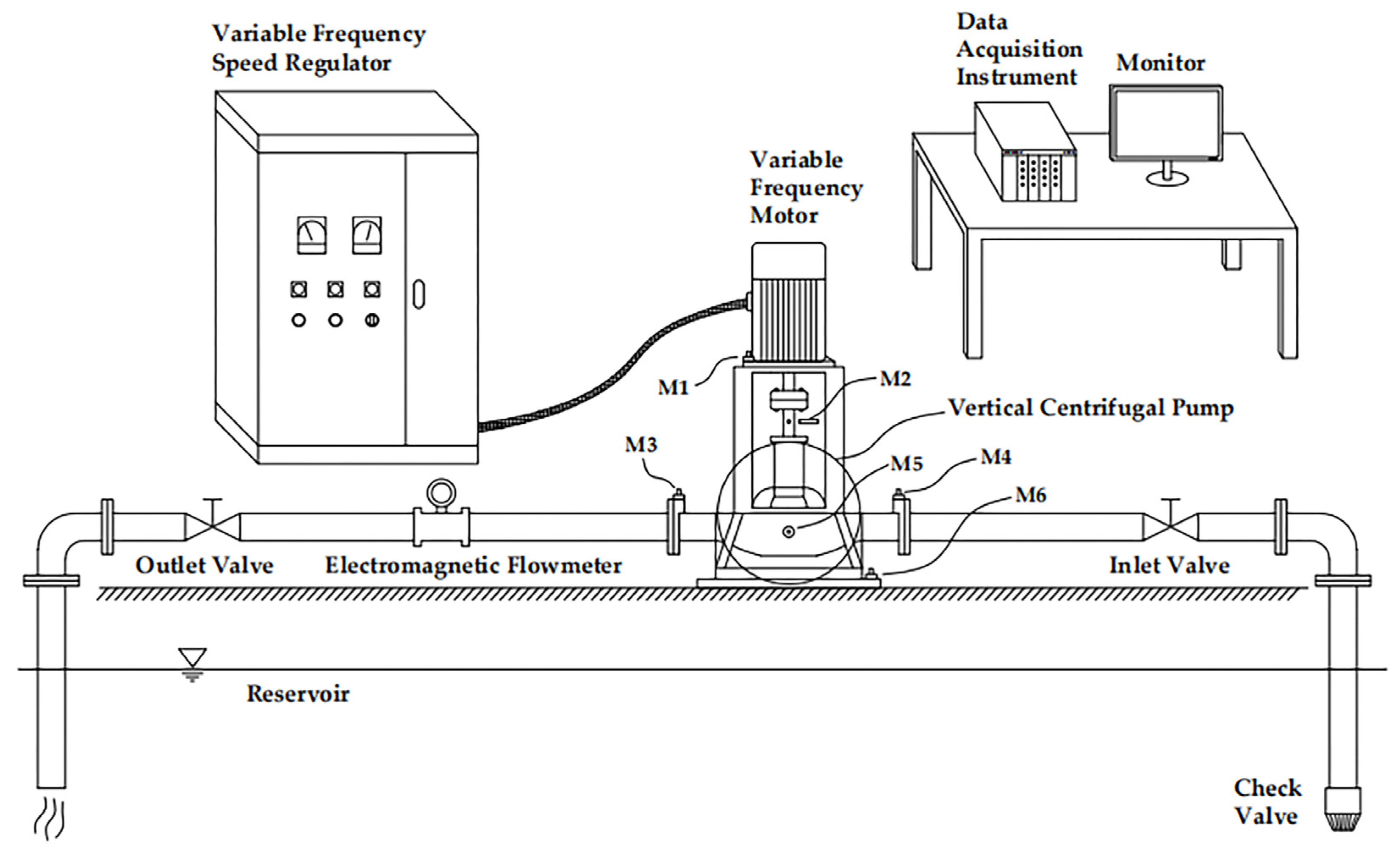
1. Introduction

The marine vertical centrifugal pump is a key component of a ship pipeline system, which is responsible for conveying a fluid working medium to maintain the normal operation of various parts of mechanical equipment. However, the ship’s swing, the vibration of the operating equipment and the long-term operation under a certain load easily cause the failure of the rotor components of the vertical centrifugal pump unit and reduce the service life of the equipment [1,2,3]. Therefore, the establishment of multi-fault classification and an identification method for the rotor fault and the mechanical loose fault of the marine vertical centrifugal pump has become a research hotspot. It is also a technical means to prevent the sudden failure of equipment and effectively improve the operating efficiency and service life of equipment.

In recent years, the fault diagnosis of rotating machinery has developed from traditionally relying on expert experience to the intelligent fault identification based on machine learning [4]. The fault diagnosis process of the rotating machinery system generally includes three key stages: (1) Obtaining the original signal of equipment fault information based on the field sensor. (2) Signal preprocessing and feature extraction are used to obtain fault signal features. (3) The trained diagnostic model is used to diagnose and identify the test samples [5]. In the industrial production scene, the data collected by the sensor usually have the characteristics of not obvious features and noise interference. Therefore, it is very important to mine signal characteristics and reduce noise in the rotating machinery fault diagnosis [6]. Zhang et al. proposed an image representation fault diagnosis method based on convolutional neural network (CNN) signal features, which overcomes the problem that information cannot fully reflect the fault mode, and has been verified in rotor tests [7]. Shao et al. proposed a multi-domain convolutional neural network method based on deep learning. Its features are composed of time domain and frequency domain characteristic parameters, and make full use of the characteristics of the two domains for fault diagnosis. The effectiveness of this method on the bearing data set is verified by a large number of experiments [8]. Pang et al. proposed a deep learning fault diagnosis method, which extracts features from time domain and frequency domain signals. Two sets of deep features in multiple domains are fused into intrinsic low-dimensional features. A lot of experiments on the gearbox, rotor and engine bearing show that the method has better diagnostic performance and stronger adaptability [9]. Sun et al. proposed a data-driven multi-wavelet denoising technique, which has been successfully applied in weak feature extraction of minor faults in bearing inner rings [10]. By product function selection and wavelet packet decomposition, Lee et al. effectively removed the high-frequency noise, effectively extracted the fault information hidden under the noise, and established a high-precision fault location feature set of bearing roller [11]. Therefore, signal noise reduction is essential for feature extraction of industrial production equipment fault signals, which is conducive to reflect the actual state of equipment earlier, more accurately and more truly.

William proposed a zero-crossing feature parameter extraction method for the early fault detection of rotating machinery [12]. In this method, zero-crossing characteristic parameters are extracted from time-domain signals by using continuous zero-crossing time intervals. When the data dimension is high, the direct use of machine learning for data classification will cause a long computing time, and the classification performance cannot be achieved. To solve these problems, kernel principal component analysis has advantages in dimensionality reduction. According to the eigenvalue of the kernel matrix, the kernel function weight is formed, and the data dimension is reduced by combining multiple kernel functions [13,14]. Du et al. proposed wavelet packet decomposition (WPD) and high-order cumulant to extract features from bearing failure vibration signals, and combined them with principal component analysis (PCA) to reduce the redundancy of feature data [15]. Shen et al. proposed a feature selection method based on the polling mode and the weighted kernel principal component analysis (WKPCA) method. Finally, this method can adaptively classify highly sensitive features with more fault information of rotating components, improving the separability of the fault sample subset [16]. In order to identify the fault state of centrifugal pump effectively, it is important to construct the feature space with the optimal dimension to improve the recognition ability.

Machine learning is an effective method of equipment fault diagnosis, and the accuracy of classification recognition can be used as a typical basis to judge the diagnosis model. Support vector machine (SVM) is a machine learning method widely studied by scholars. When combined with other intelligent algorithms, SVM can realize high-precision fault identification under limited fault samples [17]. Huang et al. proposed an SVM model based on the optimized genetic algorithm, which successfully identified the faults of the operating mechanism such as the loosening of the foundation screw and the failure of the buffer spring. Compared with traditional SVM, it has higher recognition accuracy [18]. The SVM classifier optimized by grid search technology can effectively identify the running state of centrifugal pumps [19]. Maamar uses wavelet packet transform for feature extraction at multiple decomposition levels, and studies two parent wavelets to verify the effectiveness of feature extraction. At the same time, a genetic algorithm was used to optimize the number of hidden layers and multilayer perceptual neurons, and the hybrid training method a combining genetic algorithm and a BP algorithm was applied to the fault classification of the centrifugal pump [20]. Rotating machinery fault diagnosis technology is usually proposed for a single fault. But compound failures of rotating machinery occur more frequently [21,22,23]. Liu proposed a hybrid intelligent model based on redundant second-generation wavelet packet transform, kernel principal component analysis and dual support vector machines to realize multi-fault detection of the rotating machinery. Experimental results have proved the effectiveness of this method [24]. Tang et al. proposed a particle swarm optimization support vector machine (PSO-SVM) multi-fault diagnosis method based on information fusion, and the accuracy distribution of this method for normal state, single fault mode and multi-fault mode can reach 98.3%, 97.6% and 94% [25]. Therefore, combining an intelligent algorithm to optimize the kernel function and penalty parameters in traditional SVM is an effective way to improve its fault recognition accuracy.

In the study of rotating machinery fault diagnosis, the above literature mainly considered the signal noise reduction ability of the diagnosis algorithm, the feature set screening of the optimal dimension and the fault recognition accuracy, but ignored the sensitivity of signals at different measuring points of the equipment to fault characteristics and the characterization ability of multi-domain signal features of a single measuring point. Due to the characteristics of marine vertical centrifugal pump, including complex structure, variable operating conditions, rotor dynamics and fluid dynamics and other factors, different measuring points have different sensitivity to fault characteristics. The limitation of single feature representation is an important factor affecting the diagnostic accuracy. This paper takes the marine vertical centrifugal pump as the research object to solve the problems of uncertainty of the fault signal, limitation of single feature representation and poor classification and identification effect of multiple faults. In this paper, the fault simulation test platform and data acquisition system of the Marine vertical centrifugal pump are built. The test point with the highest sensitivity to fault characteristics is selected from six typical test points of the Marine vertical centrifugal pump. Secondly, the multi-domain and multi-type feature parameter set is established, and the feature set dimension is reduced by the WKPCA method, which effectively solves the aliasing phenomenon of various fault features. Finally, the optimal parameters are selected based on the PSO algorithm to improve the performance of the support vector machine model in the classification and identification of multiple faults of Marine vertical centrifugal pumps.

2. Typical Fault Simulation Test System

2.1. Test Bench

In order to study the sensitivity of a typical fault signal of the vertical centrifugal pump and provide data support for fault signal feature extraction and an established diagnosis model, a vertical centrifugal pump fault simulation test-bed is built according to the requirement specified in GB/T 29531-2013 pump vibration measurement and evaluation methods, as shown in Figure 1.

The test model pump adopts a single-stage single-suction vertical centrifugal pump, and the main design parameters are: specific speed n_s is 67.09, rated flow Q_d is 100 m³/h, rated speed n is 2950 rpm. The test speed ratio n’/n is 0.8, that is, the impeller speed is 2360 rpm and the axial passing frequency (1f_APF) is 39.33 Hz. The arrangement of measuring points of the vertical centrifugal pump sensor is shown in Figure 2.

Table 1. Sensor measuring point number information table.

Number of Measuring Point	M1	M2	M3	M4	M5	M6
Location of measuring point	Motor bracket	Pump shaft surface	Pump outlet flange	Pump inlet flange	Pump body	Machine foot
Signal of measuring point	Vibration acceleration	Displacement in XY direction	Vibration acceleration	Vibration acceleration	Vibration acceleration	Vibration acceleration

shows the number information of sensor measuring points.

The data acquisition system of the test-bed adopts an INV3020 Series high-performance 24 bit sampling instrument, with sampling frequency of 25.6 kHz and sampling time of 30 s. The data acquisition and signal processing software is the supporting software DASP V10 engineering version of the system. The test sensor adopts INV9822 IEPE uniaxial acceleration sensor and LD980-Y integrated eddy current displacement sensor.

2.2. Fault Simulation Scheme

The typical fault of the vertical centrifugal pump is reproduced in the form of manual fault simulation. After one typical fault test is completed, the next typical fault simulation can be carried out after returning to the original state. The three typical fault simulation parameters are shown in

Table 2. Parameters of fault simulation.

Fault Type	Position	Fault Quantity
Rotor unbalance	Coupling at pump shaft end	The unbalance quantity is 15 g
Rotor misalignment	Motor shaft and pump shaft	Comprehensive misalignment
Mechanical looseness	Base machine foot	The number of loosened bolts is one

.

2.3. Signal Sensitivity Analysis

Vibration intensity is a comprehensive and effective characteristic quantity reflecting the vibration state of the centrifugal pump. It is widely used in the research of vibration monitoring and the condition evaluation of rotating machinery. The vibration intensity is the root mean square of the vibration speed of the centrifugal pump and reflects the total vibration energy of each harmonic energy [26]. The signal measured in the test is a discrete signal, and its expression is:

$$V_{ims}=\sqrt{\frac{1}{N}{\displaystyle \sum _{n=0}^{N-1}{v}^2\left(n\right)}}$$

(1)

where, N is the total number of discrete signals; $v\left(n\right)$ is the nth discrete speed signal. Using the discrete Fourier Transform Theory, the expression of the signal in the frequency domain $X\left(k\right)$ can be obtained:

$$X\left(k\right)={\displaystyle \sum _{n=0}^{N-1}x\left(n\right)}{e}^{-j2nk\pi /N},k=0,1,\cdot \cdot \cdot ,N$$

(2)

where, $x\left(n\right)$ is the measured N-point vibration signal. The single side amplitude spectrum $A_k$ and harmonic frequency of signal $f_k$ are obtained as follows:

$$A_k=\frac{2}{N}\left|X\left(k\right)\right|,k=0,1,\cdot \cdot \cdot ,\raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$$

(3)

$$f_k=\frac{k{f}_s}{N},k=0,1,\cdot \cdot \cdot ,\raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$$

(4)

If it is a vibration displacement signal, the unit is mm, then the vibration intensity within the frequency range $f_a\sim f_b$ is:

$$V_{mss}=\frac{2\sqrt{2}\pi f_s}{N^2}\sqrt{{{\displaystyle \sum _{k=k_a}^{k_b}\left(k\left|X\left(K\right)\right|\right)}}^2}$$

(5)

If it is a vibration acceleration signal, the unit is mm/s², then the vibration intensity within the frequency range $f_a\sim f_b$ is:

$$V_{msa}=\frac{1}{\sqrt{2}\pi f_s}\sqrt{{{\displaystyle \sum _{k=k_a}^{k_b}\left(\frac{\left|X\left(k\right)\right|}{k}\right)}}^2}$$

(6)

where, $f_s$ is the signal sampling frequency; $k_a$ is the smallest integer greater than $N{f}_a/f_s$; $k_b$ is the maximum integer greater than $N{f}_b/f_s$.

The average value of five groups of data is selected to calculate the vibration intensity of the signal at each measuring point under the four states of normal, rotor unbalance, rotor misalignment and mechanical looseness of the vertical centrifugal pump, as shown in Figure 3. It can be seen from the figure that the M2 signal at the measuring point is the most sensitive to the rotor unbalance and misalignment, and its vibration intensity is 53.9% and 65.3% higher than under normal conditions. The M6 signal of the measuring point is the highest sensitivity of the mechanical loosening state, and its vibration intensity is increased by 73.6%. Therefore, M2 and M6 measuring points can better reflect the typical fault characteristic information of the vertical centrifugal pump and will also be used as the measuring point signal source for algorithm verification.

3. Feature Extraction

3.1. Signal Preprocessing

The implementation process of Kalman Filter is to predict the current value by using the optimal result of the previous time, and modify the predicted current by using the measured value to finally obtain the optimal result. Its calculation formula is:

$${\widehat{x}}_t={\widehat{x}}_t^{-}+K_t(z_t-H{\widehat{x}}_t^{-})$$

(7)

$$K_t=P_t^{-}{H}^T{(H{P}_t^{-}{H}^T+R)}^{-1}$$

(8)

$$P_t^{-}=F{P}_{t-1}{F}^T+Q$$

(9)

where, ${\widehat{x}}_t$ is the optimal result; ${\widehat{x}}_t^{-}$ is the predicted current value; $z_t$ is the measured value; $K_t$ is Kalman gain; $P_t^{-}$ is the covariance of the predicted value [27,28].

3.2. Weighted Kernel Principal Component Analysis (WKPCA)

In order to realize the rapid screening of nonlinear characteristic parameters and eliminate the influence of irrelevant factors on pattern recognition, the Kernel Principal Component Analysis (KPCA) method is used to standardize and reduce the dimension of the characteristic matrix.

Standardize the original fault data with the number of characteristic parameters s and the number of samples k, and the calculation formula is as follows:

$$\stackrel{\ast }{x_{sk}}=\frac{x_{sk}-{\overline{x}}_k}{\sqrt{\mathrm{var}(x_k)}}(s=1,2,\cdot \cdot \cdot ,n;k=1,2,\cdot \cdot \cdot ,p)$$

(10)

where, ${\overline{x}}_k=\frac{1}{n}{\displaystyle \sum _1^n{x}_{sk}}$.

Select kernel function K to map matrix X to high-dimensional matrix C, and calculate the sample correlation coefficient matrix:

$$r_{sk}=\frac{1}{n-1}{\displaystyle \sum _{t=1}^n{x}_{ts}{x}_{tk}}(s,k=1,2,\cdot \cdot \cdot ,p)$$

(11)

The Jacobian method is used to solve the eigenvalues $({\lambda }_1,{\lambda }_2,\cdot \cdot \cdot ,{\lambda }_p)$ and corresponding eigenvectors $a_i=(a_{i1},a_{i2},\cdot \cdot \cdot ,a_{ip}),i=1,2,\cdot \cdot \cdot ,p$ of the correlation coefficient matrix R. The calculation formula of the characteristic contribution rate is as follows:

$$P_{\lambda }(i)=\frac{{\lambda }_i}{{\displaystyle \sum _{i=1}^p{\lambda }_i}}$$

(12)

According to the principle that the contribution rate of characteristic parameters is sorted from high to low and the index is greater than 0.85, the first m eigenvectors of the contribution rate are taken to form an eigenvalue matrix with s eigenvalues reduced into m principal elements [29].

3.3. Establishing Feature Set

The filtering noise reduction method eliminates and suppresses the influence of random noise components on signal feature extraction to a certain extent. The vibration signal of vertical centrifugal pump has nonlinear and unsteady characteristics. In order to improve the adaptability of multi-resolution analysis of vibration signal. The original signal is adaptively decomposed to obtain intrinsic mode functions (IMF) components at different characteristic time scales, so that the decomposed components have a single eigenfrequency, and the linearization and smoothing of the original signal are realized [30].

Taking the vibration displacement data of measuring point M2 in the rotor misalignment fault test as an example, the empirical mode decomposition (EMD) results are shown in Figure 4. It can be seen from the figure that the waveforms of the IMF4 and IMF5 are all approximate sinusoidal waves with period 2π, and according to the corresponding spectral diagram, obvious amplitude characteristics appear at 1f_APF and 2f_APF. The time-domain waveform data of IMF4 and IMF5 are extracted for signal reconstruction analysis, and the results are shown in Figure 5.

By observing the time-domain waveform of the reconstructed signal, it can be found that the time-domain waveform presents the characteristics of a sine wave, and there are depressions and double peaks at the peak. This is the main time-domain feature of the dual frequency rotation component in the corresponding frequency-domain diagram. By Fourier transform, it can be further found that the main frequency of the signal is 1f_APF, accompanied by a secondary frequency of 2f_APF, which accords with the spectrum characteristics of the rotor misalignment fault.

The vibration characteristics are different due to different faults. The number and order of the IMF component are also different. For example, the IMF5 component is selected to reconstruct the unbalanced rotor fault signal after decomposition. The time-domain signal of the IMF5 component presents a sinusoidal function with a period 2π. After mechanical loosening fault signal decomposition, IMF2, IMF5 and IMF6 components were selected for reconstruction. In order to cover different fault characteristic information, the first six IMF components after EMD decomposition are selected as the characteristic parameters in the time-frequency domain.

The characteristic energy is calculated as follows:

$$E_i={{\displaystyle {\int }_{-\infty }^{+\infty }\left|c_i(t)\right|}}^{2}dt$$

(13)

An eigenvector matrix is constructed by taking the energy characteristic of the first six IMF components decomposed as elements:

$$T=[E_1{E}_2{E}_3{E}_4{E}_5{E}_6]$$

(14)

Normalization:

$$E={\left({\displaystyle \sum _{i=1}^6{\left|E_i\right|}^2}\right)}^{\frac{1}{2}}$$

(15)

The normalized energy characteristic matrix is obtained:

$$T\prime =[E_1/E{E}_2/E\dots E_6/E]$$

(16)

The four operating states of normal, rotor unbalanced, rotor misalignment and mechanical looseness have different characteristics. In order to avoid the limitation of fault trend analysis caused by a single characteristic parameter or a single type characteristic parameter, a multi-domain and multi-class fault feature extraction method is used to form a fault feature set. The characteristic indexes include 10 time-domain indexes, 4 frequency-domain indexes and 6 time-frequency domain energy characteristic indexes, as shown in

Table 3. Signal characteristic index information table.

Name	Symbol	Formula	Name	Symbol	Formula
Mean	Pt1	$\frac{{\displaystyle \sum _{n=1}^{N}x(n)}}{N}$	Mean frequency	pf1	$\frac{{\displaystyle \sum _{i=1}^{m}U(i)}}{m}$
Kurtosis	Pt2	$\frac{{\displaystyle \sum _{n=1}^N{(x(n)-p_{t1})}^4}}{N{p}_{t5}{}^4}$	Center of gravity frequency	pf2	$\frac{{\displaystyle \sum _{i=1}^m{f}_i\times U(i)}}{{\displaystyle \sum _{i=1}^{m}U(i)}}$
Peak	Pt3	$\max (\left|x(n)\right|)$	Root mean square frequency	Pf3	$\sqrt{\frac{{\displaystyle \sum _{i=1}^m{(f_i)}^2\times U(i)}}{{\displaystyle \sum _{i=1}^{m}U(i)}}}$
Variance	Pt4	$\frac{{\displaystyle \sum _{n=1}^N{(x(n)-p_{t1})}^2}}{N}$	Frequency standard deviation	Pf4	$\sqrt{\frac{{\displaystyle \sum _{i=1}^m{(f_i-p_{f2})}^2\times U(i)}}{m}}$
Harmonic mean	Pt5	$\sqrt{\frac{1}{N}{{\displaystyle \sum _{n=1}^N(x(n))}}^2}$	IMF component 1	E1	${{\displaystyle {\int }_{-\infty }^{+\infty }\left|c_1(t)\right|}}^{2}dt$
Waveform index	Pt6	$\frac{p_{t5}}{p_t{}_1}$	IMF component 2	E2	${{\displaystyle {\int }_{-\infty }^{+\infty }\left|c_2(t)\right|}}^{2}dt$
Pulse index	Pt7	$\frac{p_{t3}}{\frac{1}{N}{\displaystyle \sum _{n=1}^N\left|x(n)\right|}}$	IMF component 3	E3	${{\displaystyle {\int }_{-\infty }^{+\infty }\left|c_3(t)\right|}}^{2}dt$
Peak index	Pt8	$\frac{p_{t3}}{p_{t5}}$	IMF component 4	E4	${{\displaystyle {\int }_{-\infty }^{+\infty }\left|c_4(t)\right|}}^{2}dt$
Margin index	Pt9	$\frac{p_{t3}}{{\left(\frac{1}{N}{\displaystyle \sum _{n=1}^N\sqrt{\left|x(n)\right|}}\right)}^2}$	IMF component 5	E5	${{\displaystyle {\int }_{-\infty }^{+\infty }\left|c_5(t)\right|}}^{2}dt$
Skewness index	Pt10	$\frac{p_{t3}}{\frac{1}{N}\sqrt{{\displaystyle \sum _{n=1}^N{\left|x(n)\right|}^2}}}$	IMF component 6	E6	${{\displaystyle {\int }_{-\infty }^{+\infty }\left|c_6(t)\right|}}^{2}dt$

.

According to the above table, a multi-domain and multi-type feature sample library is constructed for signals collected under four typical conditions of the marine vertical centrifugal pump, and a single fault sample contains 100 feature matrices. According to the needs of model training and verification, this paper divides the single fault sample library into training set and test set according to the ratio of 5:5. A total of 50 samples were selected to build a training set for training the diagnostic model, and 50 samples were selected to build a test set for verifying the fault classification and recognition effect of the diagnostic model. At the same time, labels are configured for four typical states of the Marine vertical centrifugal pump, which are used for training and verification of the diagnostic model.

Table 4. Fault sample database classification and label configuration.

Fault Category	Training Sample (PCS)	Test Sample (PCS)	Sample Label
Normal	50	50	1
Rotor unbalance	50	50	2
Rotor misalignment	50	50	3
Mechanical looseness	50	50	4
Total	200	200	-

describes the fault sample database classification and label configuration.

3.4. Data Dimensionality Reduction

Due to the rich variety of original signal feature parameters, the correlation between parameters results in information redundancy. In order to avoid aliasing between different faulty core principal components, the problem of information redundancy is reduced or eliminated. The original high-dimensional fault features are dimensionally reduced, and the weight index size of each feature parameter in the original fault feature set is calculated, as shown in Figure 6.

It can be seen from the graph analysis that the original 20 characteristic parameters are subjected to dimensionality reduction processing, and the 9 characteristic parameters that meet the conditions are Mean, Kurtosis, Peak, Harmonic Mean, Mean Frequency, E1, E2, E5, E6 respectively. The weight values are 0.21515, 0.2938, 0.317025, 0.35055, 0.109925, 0.319, 0.1441, 0.114, 0.1457. The feature matrix composed of 9 feature parameters is used as the target feature set for fault classification.

3.5. Feature Extraction Result

The distribution of the four operating state feature parameters kernel key element feature points obtained by the KPCA method is relatively concentrated. Among them, the core principal element feature points of mechanical loosening faults are relatively concentrated; that is, the intra-class spacing is small, and it is clearly distinguished from the principal element feature points in the normal state; that is, the inter-class spacing is obvious, and the distinguishing effect is good. However, the feature points of the two types of faults of rotor unbalance and rotor misalignment overlap with each other, and it is impossible to completely distinguish the core feature points of normal operating conditions and mechanical loose faults. The fault principal components extracted by the feature dimension reduction of KPCA have obvious aliasing, which cannot fully achieve the effect of classifying multiple faults of centrifugal pumps, as shown in Figure 7a. The WKPCA is an extension of the general KPCA method. Its basic idea is to strengthen the role of some fault features on fault classification by weighting each data feature in the data set. The two-dimensional distribution is shown in Figure 7b. The core principal element feature points of the four types of working conditions can be clearly distinguished, the distance between classes is obvious, and the discrimination degree of multiple fault categories is good.

It can be seen from the figure that compared with the feature parameter kernel pivot feature point extraction method of KPCA, the intra-class spacing of the kernel pivot feature points of the four operating states extracted by the WKPCA method is smaller. The inter-class spacing is larger. Accurate classification of kernel key element feature points in four operating states is achieved.

4. Diagnostic Algorithm

4.1. Support Vector Machines

Support vector machine based on statistical theory has obvious advantages in small sample, nonlinear and high-dimensional classification and recognition, and can achieve high fault classification performance. Its general form can be expressed as follows:

$$\left\{\begin{array}{l}\underset{w,b,\xi }{\min }\left(\frac{1}{2}{w}^{T}w+C{\displaystyle \sum _{i=1}^n{\xi }_i}\right)\\ y_i(w^T{x}_i+b)\ge 1-{\xi }_i\\ {\xi }_i\ge 0\\ i=1,\mathrm{\dots },n\end{array}\right.$$

(17)

where, C is the penalty factor of SVM; ${\xi }_i$ is the relaxation variable; $x_i$ is the fault characteristic sample; $y_i$ is the sample label. Radial basis function (RBF) is adopted as the kernel function, which can overcome the complexity of inner product operation in high-dimensional feature space. Its kernel function expression is:

$$K\left(x_i,x_j\right)=exp\left(-g{‖x_i-x_j‖}^2\right)$$

(18)

where, $x_i$ is the fault characteristic sample; $g$ is a kernel function.

The selection of RBF kernel parameter $g$ and SVM penalty parameter C ultimately affects the sample training and test results, which easily to causes the SVM classification results to fall into local optimization, affecting the accuracy of fault identification. Therefore, PSO is used to optimize the kernel parameter $g$ and penalty parameter C [31,32].

4.2. Particle Swarm Optimization

In a D-dimensional target search space, N Particles form a community, in which the i^th particle is represented as a D-dimensional vector:

$$X_i=\left(x_{i1},x_{i2},\mathrm{\dots }{,x}_{iD}\right),i=1,2,\mathrm{\dots },N$$

(19)

The optimization speed of the ith particle is also a D-dimensional vector, expressed as:

$$V_i=\left(v_{i1},v_{i2},\mathrm{\dots },v_{iD}\right),i=1,2,\mathrm{\dots },N$$

(20)

Particle velocity and position updates can be expressed as:

$$\left\{\begin{array}{l}{v}_{\mathrm{ij}}{}^{t+1}=\omega v_{ij}{}^t+c_1{r}_1{}^t\left(p_{ij}^t-x_{ij}^t\right)+c_2{r}_2{}^t\left(p_{gj}^t-x_{ij}^t\right)\\ x_{ij}^{t+1}=x_{ij}^t+v_{ij}^{t+1}\end{array}\right.$$

(21)

where, $v_{ij}^{t+1},x_{ij}^{t+1}$ are the velocity vector and position vector on the j dimension after the t + 1 iteration of the i^th particle, respectively; $\omega$ is the inertia weight that decreases linearly; $c_1,c_2$ are individual learning coefficient and global learning coefficient, respectively; $r_1,r_2$ are independent random numbers of [0,1]; $p_{ij}$ is the current optimal position of the i^th particle; $p_{gj}$ is the current optimal position of the whole group [33,34].

In summary, the steps of feature extraction and the multi-fault identification method of the marine vertical centrifugal pump based on WKPCA and PSO-SVM are as follows:

(1) Collect original data. A fault simulation test system is built, and the original data with high sensitivity are selected based on vibration intensity. The signal is denoised by Kalman filter.

(2) Extract signal features. Multi-domain and multi-type feature parameters are extracted, the feature matrix is normalized and dimensionality reduced, and the feature parameters are weighted based on the ReliefF algorithm. WKPCA is used to achieve accurate classification of the four fault states.

(3) Establish fault samples. 100 groups of samples are selected for each fault state, which are divided into 50 groups of training set and 50 groups of test set. Label different fault samples.

(4) Select kernel function. In order to select the appropriate kernel function, RBF kernel function with strong learning ability and generalization ability is selected as the mapping function of the model.

(5) Optimize parameters. For the selected mapping function, based on the existing fault feature set data samples, particle swarm optimization algorithm is selected to globally optimize the penalty factor C and kernel function g parameter values of SVM.

(6) Fault classification based on PSO-SVM recognition model. The obtained training set and test set are input into the recognition model respectively to analyze the effect of fault classification.

The flow of feature extraction and the fault classification model based on WKPCA and PSO-SVM algorithm is shown in Figure 8.

5. Results and Discussion

In order to further explore the contribution of multi-domain and multi-type characteristic parameters to the classification and recognition of multiple faults of the marine vertical centrifugal pump, the multi-domain and multi-type characteristic parameters established in Chapter 3 are divided into a single domain, two domains and three domains. A single domain is divided into three cases, including 4 features in the time domain (T), 1 feature in the frequency domain (F), and 4 features in the time-frequency domain (TF). The two domains are divided into three cases, including 5 features of the time domain and frequency domain (T + F), 8 features of the time domain and time frequency domain (T + TF), and 5 features of the frequency domain and time frequency domain (F + TF). The three domains contain 9 features of the time domain, frequency domain and time frequency domain (T + F + TF). The seven categories were used as input of the PSO-SVM model for multi-fault classification identification, and the results are shown in

Table 5. Influence of different characteristic parameters on classification of PSO-SVM model.

Characteristic Parameter	Single Domain			Two Domains			Three Domains
	T	F	TF	T + F	T + TF	F + TF	T + F + TF
Accuracy	0.85	0.69	0.87	0.89	0.95	0.92	1
F-1 score	0.91	0.73	0.93	0.94	0.97	0.96	1

.

As can be seen from Table 5, when a single domain is the input feature of the model, the average classification accuracy of the feature parameters of the three domains is 0.8. The average accuracy of classification in two domains is 0.92. The classification accuracy reaches 1 in three domains. At the same time, F-1 score is an indicator of the accuracy of the binary model. It can be regarded as a weighted average of model accuracy and recall rates. The average F-1 score of a single domain is 0.86; The average F-1 score of the two domains is 0.96; The F-1 score for all three domains is 1. When measured by classification accuracy and F-1 score, the classification performance of the PSO-SVM model is improved with the increase of the number of domains. It can be seen that the establishment of multi-domain and multi-type characteristic parameters has a positive contribution to the multi-fault classification of the marine vertical centrifugal pump.

The parameters of the SVM model are optimized based on the PSO optimization algorithm, and the diagnostic classification results are shown in Figure 9. It can be seen from the figure that the fitness value of the PSO algorithm reaches the maximum convergence accuracy of 98.8% in the 11th generation. It is obtained that the optimal solution of penalty parameter C is 56.22, and the optimal solution of kernel parameter g is 0.81. The accuracy of fault classification based on the PSO-SVM model has reached 1; that is, the four operating states have been accurately classified. Thus, it is verified that the proposed fault pattern recognition model has strong learning generalization ability.

In order to further verify the advantages of the proposed parameter optimization and pattern recognition algorithm in the multi-fault classification of the marine vertical centrifugal pump, 200 groups of test samples composed of four fault data sets are classified and compared with the traditional SVM model and GA-SVM model, respectively. The final classification performance is shown in Figure 10 and Figure 11, and the data comparison results are shown in

Table 6. Comparison of classification performance of three fault pattern recognition models.

Fault Type		Normal	Rotor Unbalance	Rotor Misalignment	Mechanical Looseness	Total
SVM	Exact quantity	40	38	37	50	165
	Accuracy	0.8	0.76	0.74	1	0.83
	F-1 score	0.89	0.86	0.85	1	0.9
GA-SVM	Exact quantity	44	48	50	50	192
	Accuracy	0.88	0.96	1	1	0.96
	F-1 score	0.94	0.98	1	1	0.98
PSO-SVM	Exact quantity	50	50	50	50	200
	Accuracy	1	1	1	1	1
	F-1 score	1	1	1	1	1

.

It can be found from Table 6 that the classification accuracy of test samples based on the traditional SVM model is only 0.83, and that the accuracy of those based on the GA-SVM model is 0.96. The classification accuracy of 200 groups of test samples based on the PSO-SVM recognition model is 1, the fitness is 98.8%, and the convergence speed is the fastest. The classification performance of the PSO-SVM model on test samples is significantly better than that of traditional SVM and GA-SVM models. The F-1 score based on the PSO-SVM model reached 1, which is higher than the both of the other models. The superiority of the proposed PSO-SVM algorithm in multi-fault classification of vertical centrifugal pumps is comprehensively verified.

6. Conclusions

Multi-fault identification of the Marine vertical centrifugal pump has been carried out by comprehensive testing and algorithm recognition research. The main contributions and future prospects of this work are summarized as follows:

(1)

The multi-fault simulation test system of the marine vertical centrifugal pump is established. The vibration data of 6 measuring points were obtained. Taking vibration intensity as the comprehensive evaluation index, the detection point with the highest sensitivity of fault characteristics is selected. It greatly simplifies the auxiliary parts of the cabin piping system and improves the reliability of the detection system.

(2)

A multi-domain and multi-category fault feature set with 20 feature indexes is established. Combined with the WKPCA method, the feature set was reduced in dimension, and 9 multi-domain and multi-class feature indexes were selected to realize feature extraction of four operating states of the Marine vertical centrifugal pump. It is proved that the multi-domain multi-class feature set is effective to improve the classification performance of the model.

(3)

The optimal penalty parameter C and kernel parameter g in the SVM model are obtained by using the PSO optimization algorithm, which successfully realizes the classification and recognition of multiple faults. At the same time, the traditional SVM model and GA-SVM model are compared to verify the advantages of the PSO-SVM model. The results show that this model has higher classification and recognition accuracy and faster convergence speed.

(4)

Based on the research in this paper, it is imperative to carry out health diagnostics for the marine auxiliary equipment in the future. The application includes data cleaning, transfer learning, digital-analog linkage and so on.