A Hybrid–Source Ranging Method in Shallow Water Using Modal Dispersion Based on Deep Learning
Abstract
:1. Introduction
2. The Modal-Dispersion and Modal-Based Source-Ranging Method
2.1. The Modal Dispersion
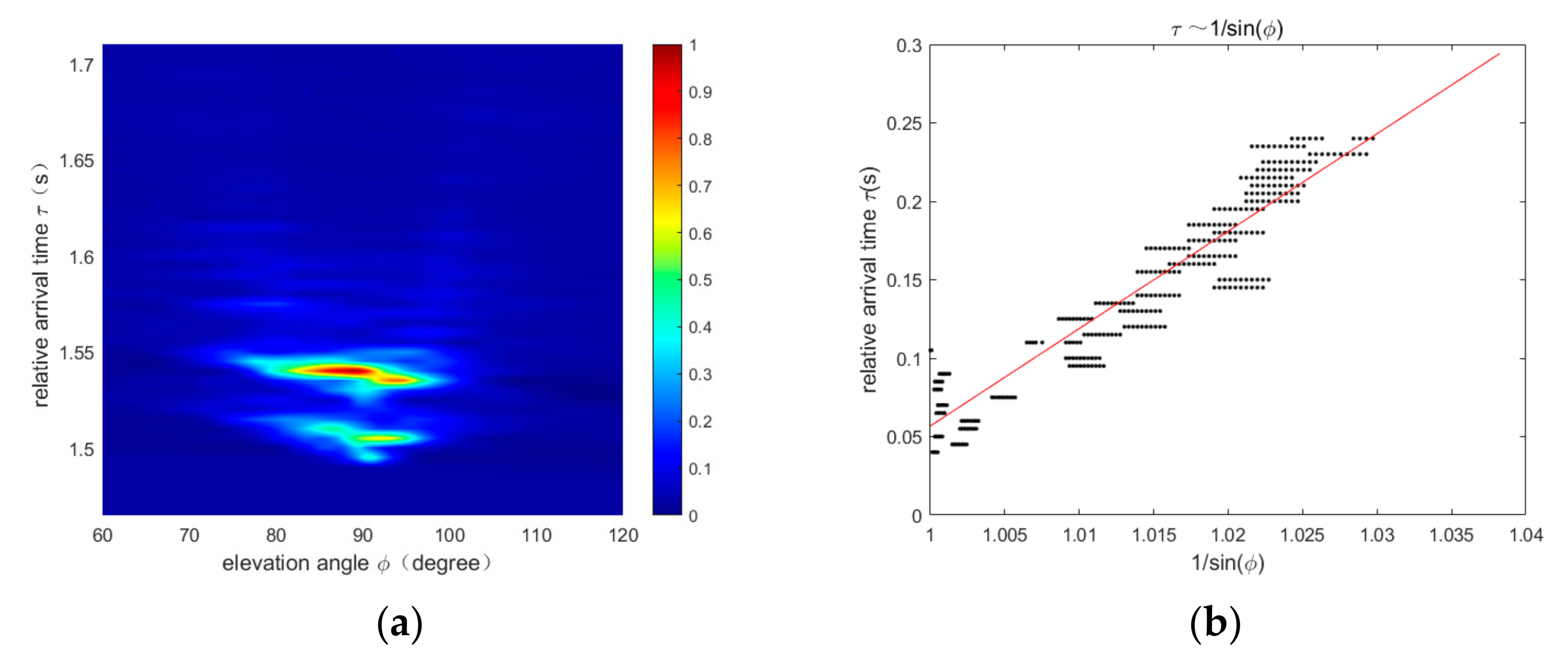
2.2. The Source-Ranging Method Based on Modal Dispersion
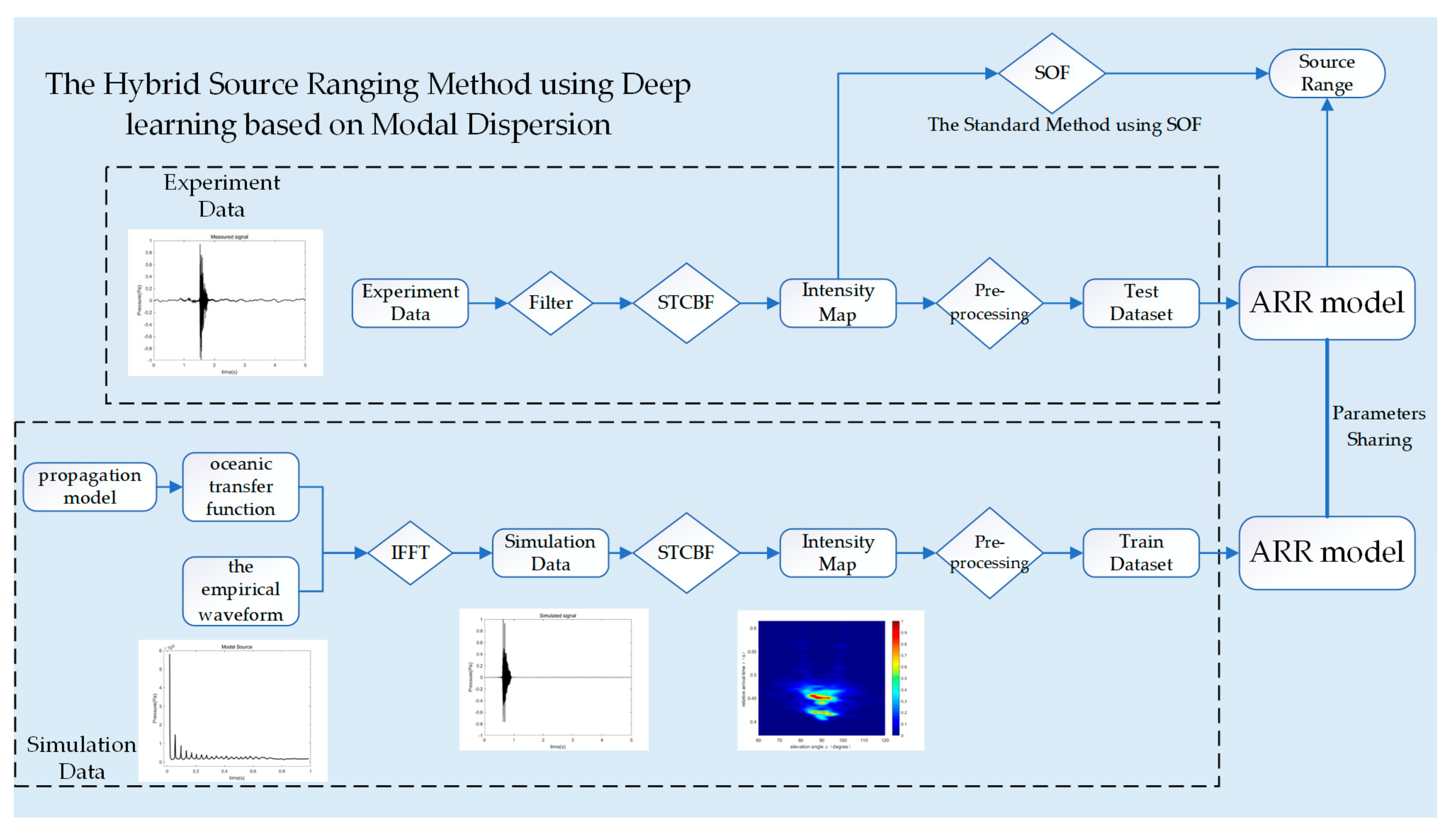
3. The Hybrid–Source Ranging Method
3.1. Input and Label
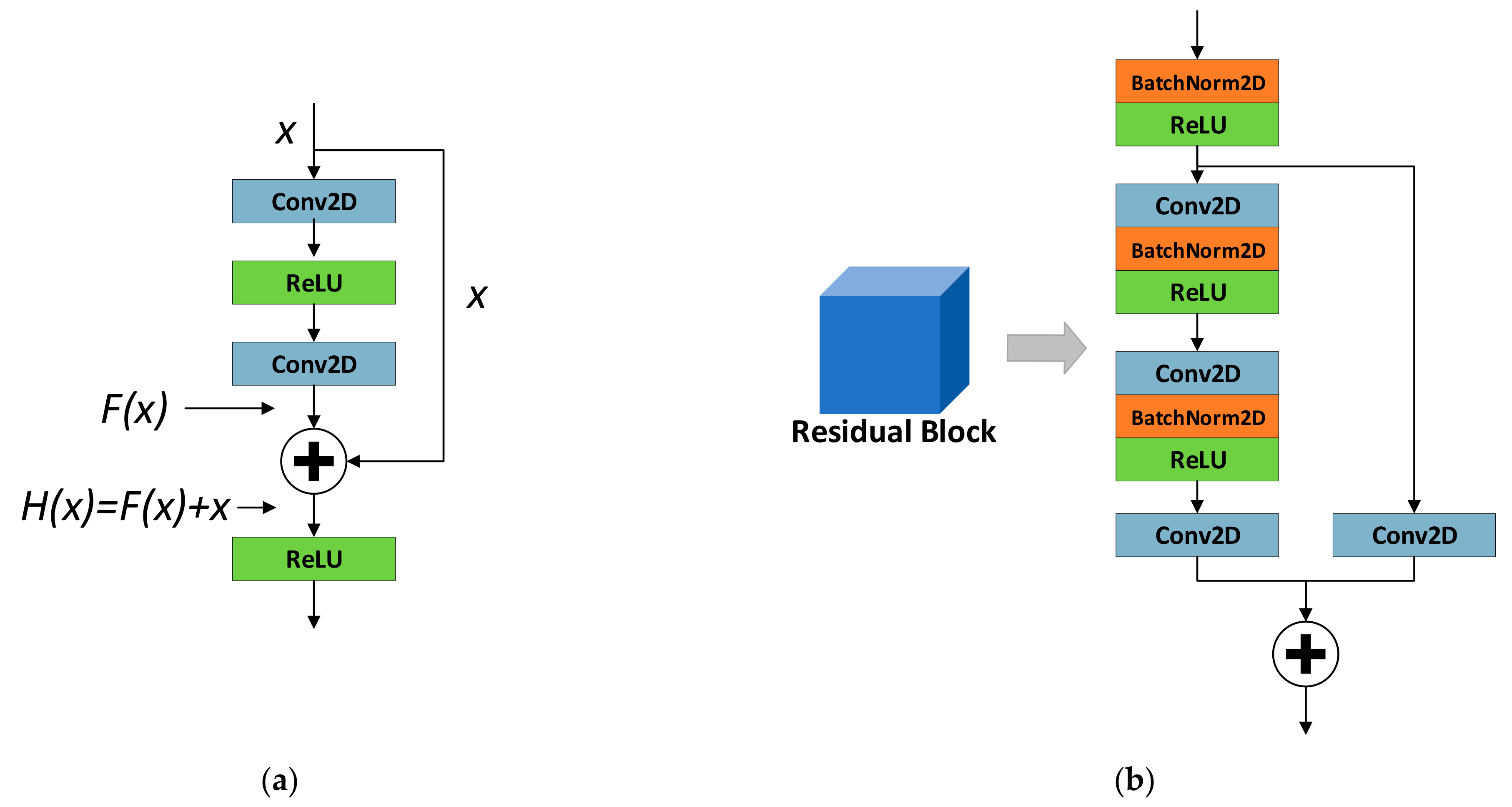
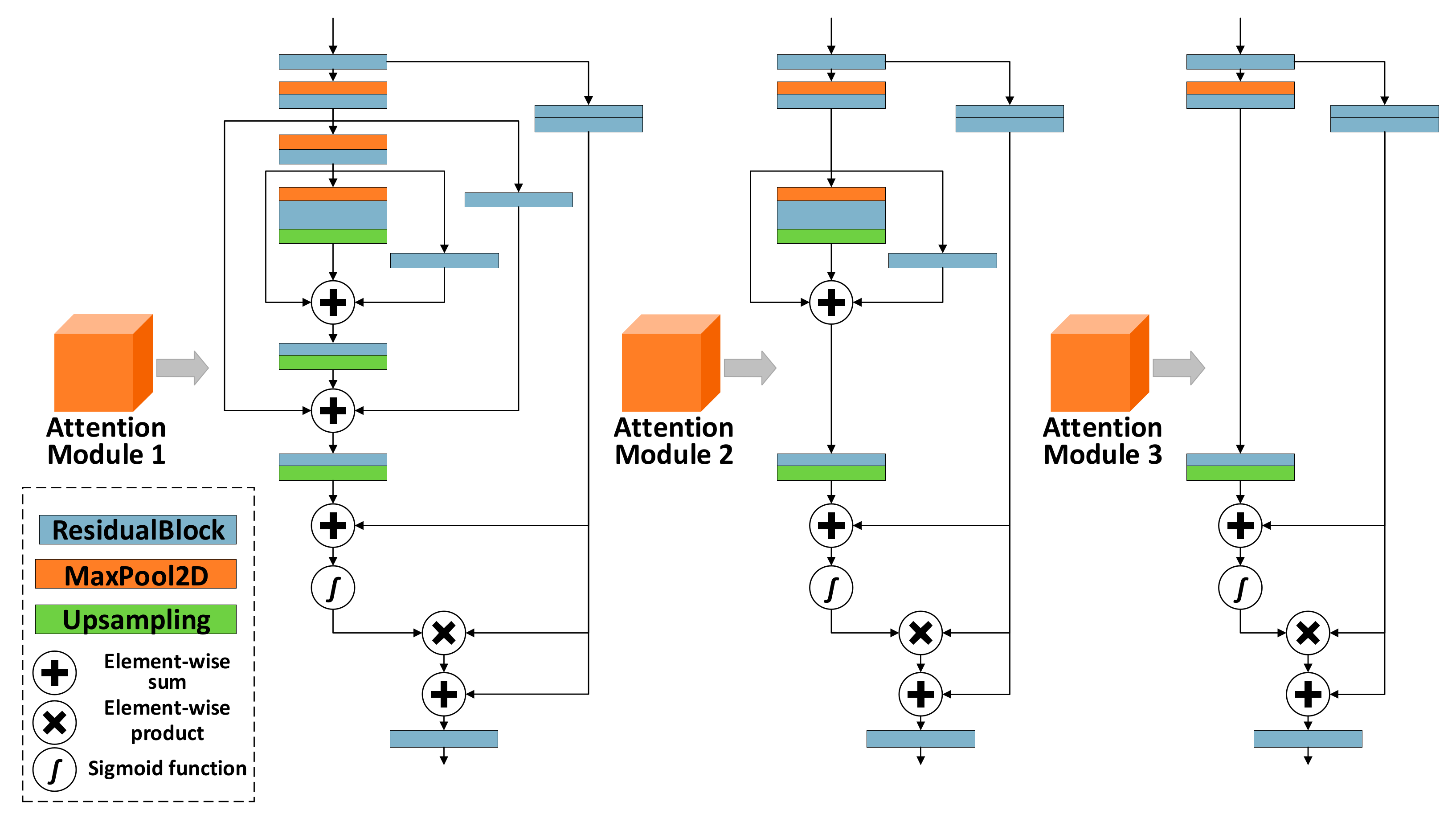
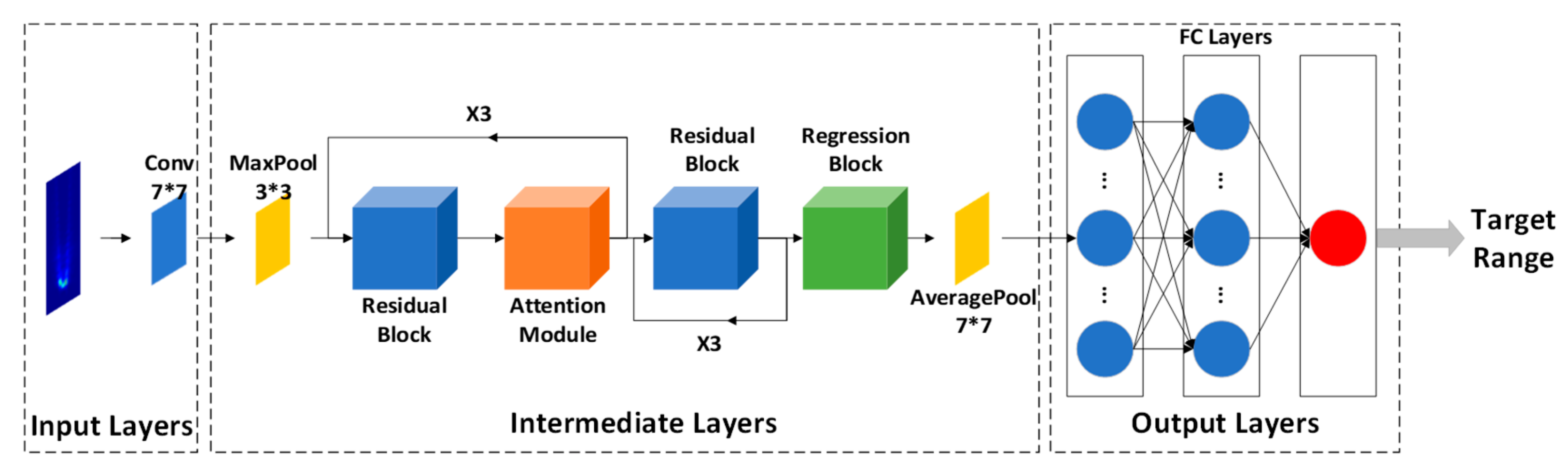
3.2. Attention-Based ResNet Regression Model(ARR)
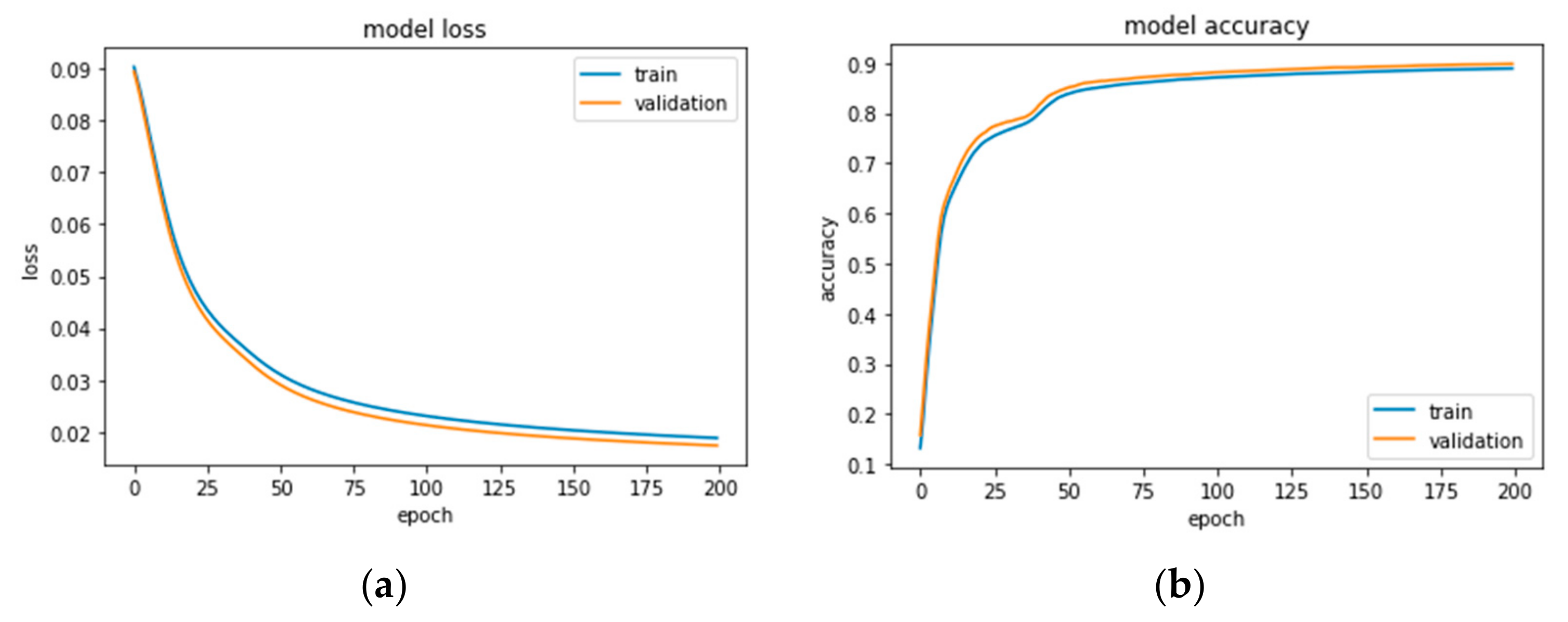
3.3. Model Training
4. Experimental Demonstration
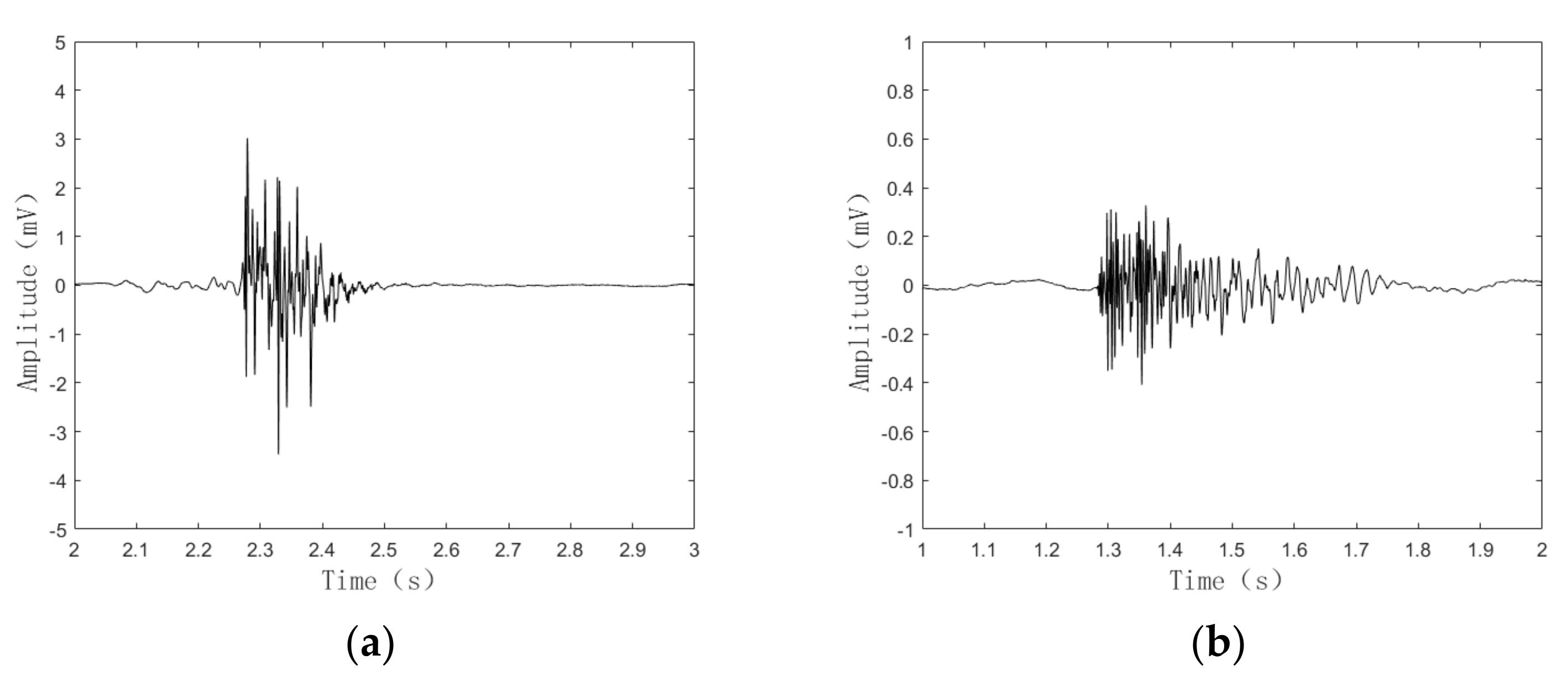
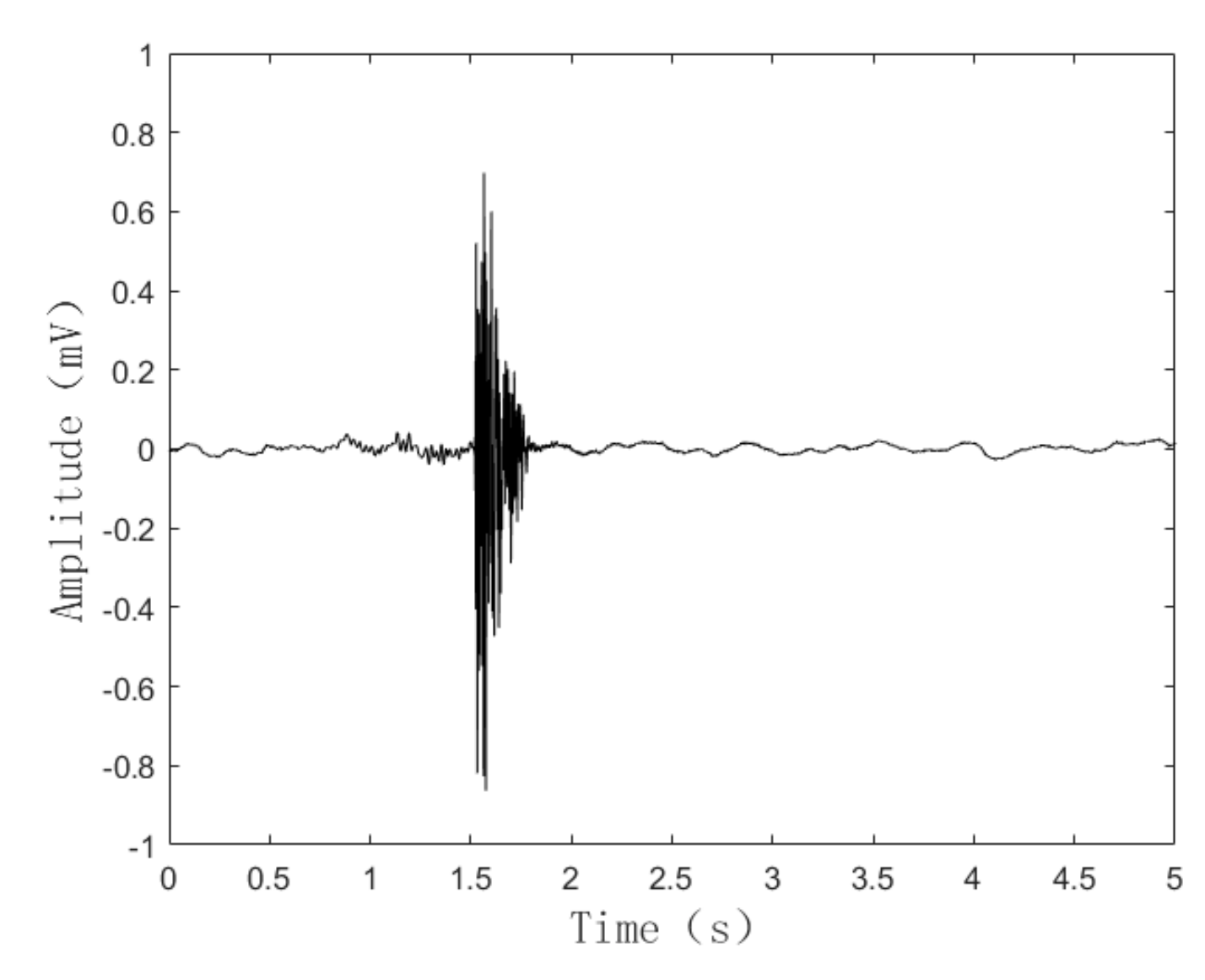
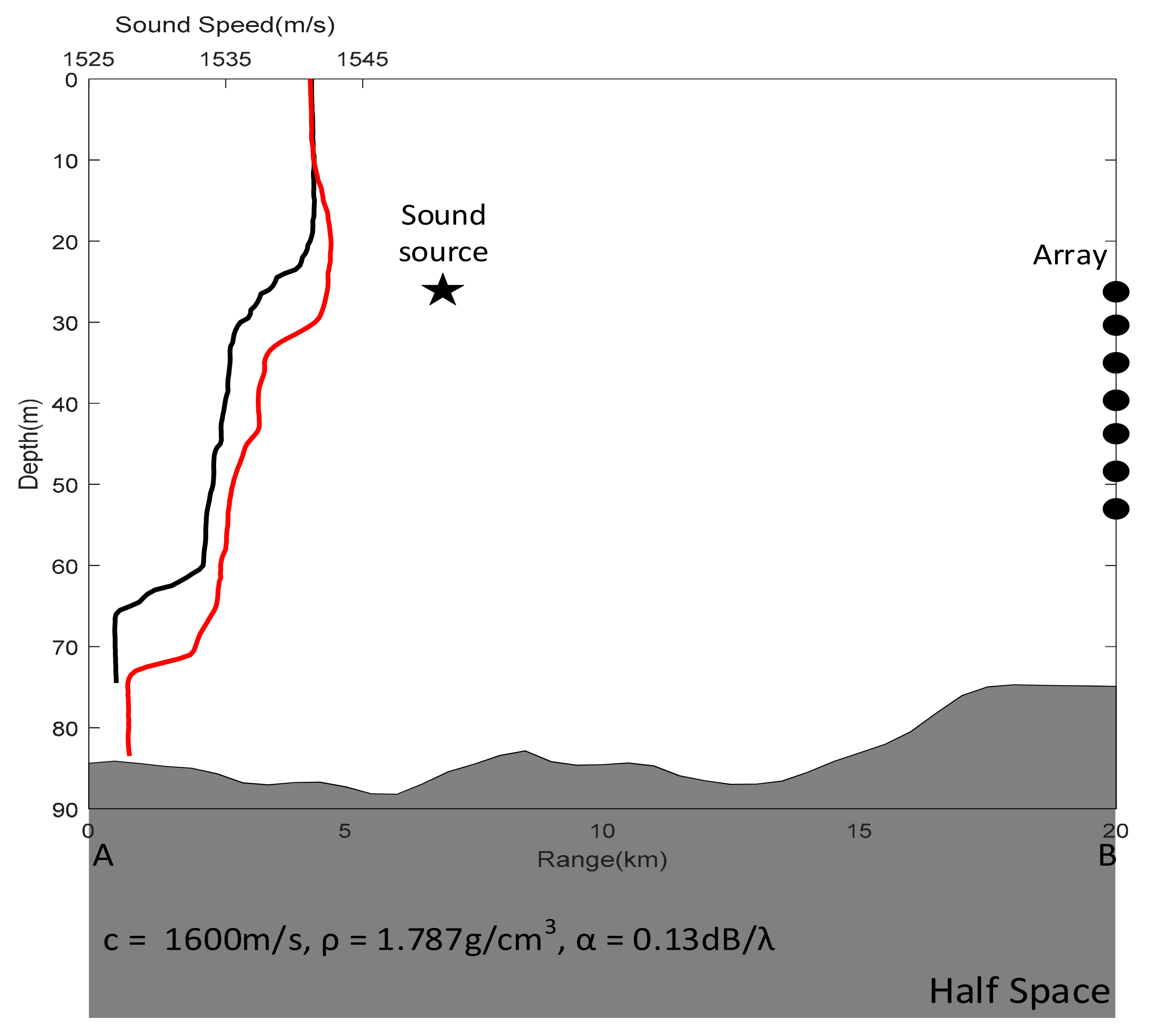
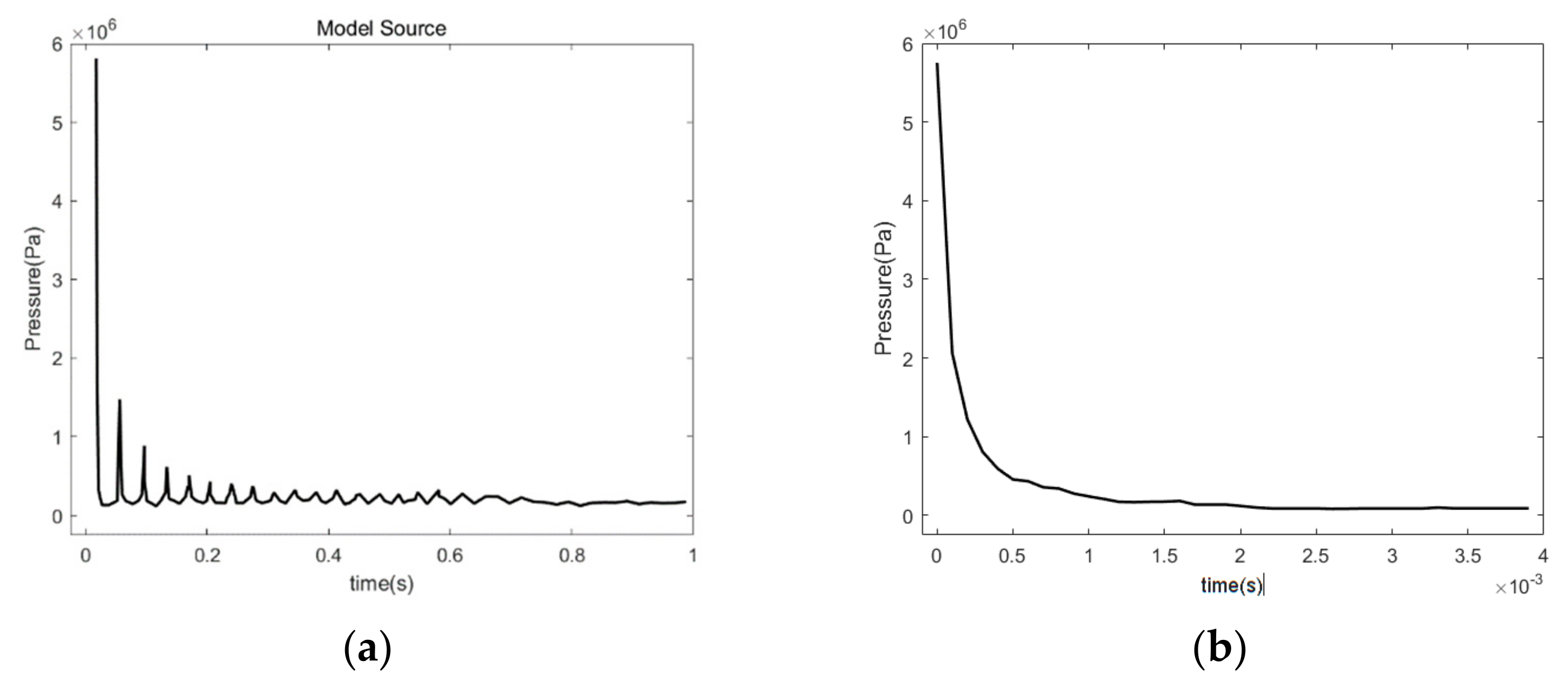
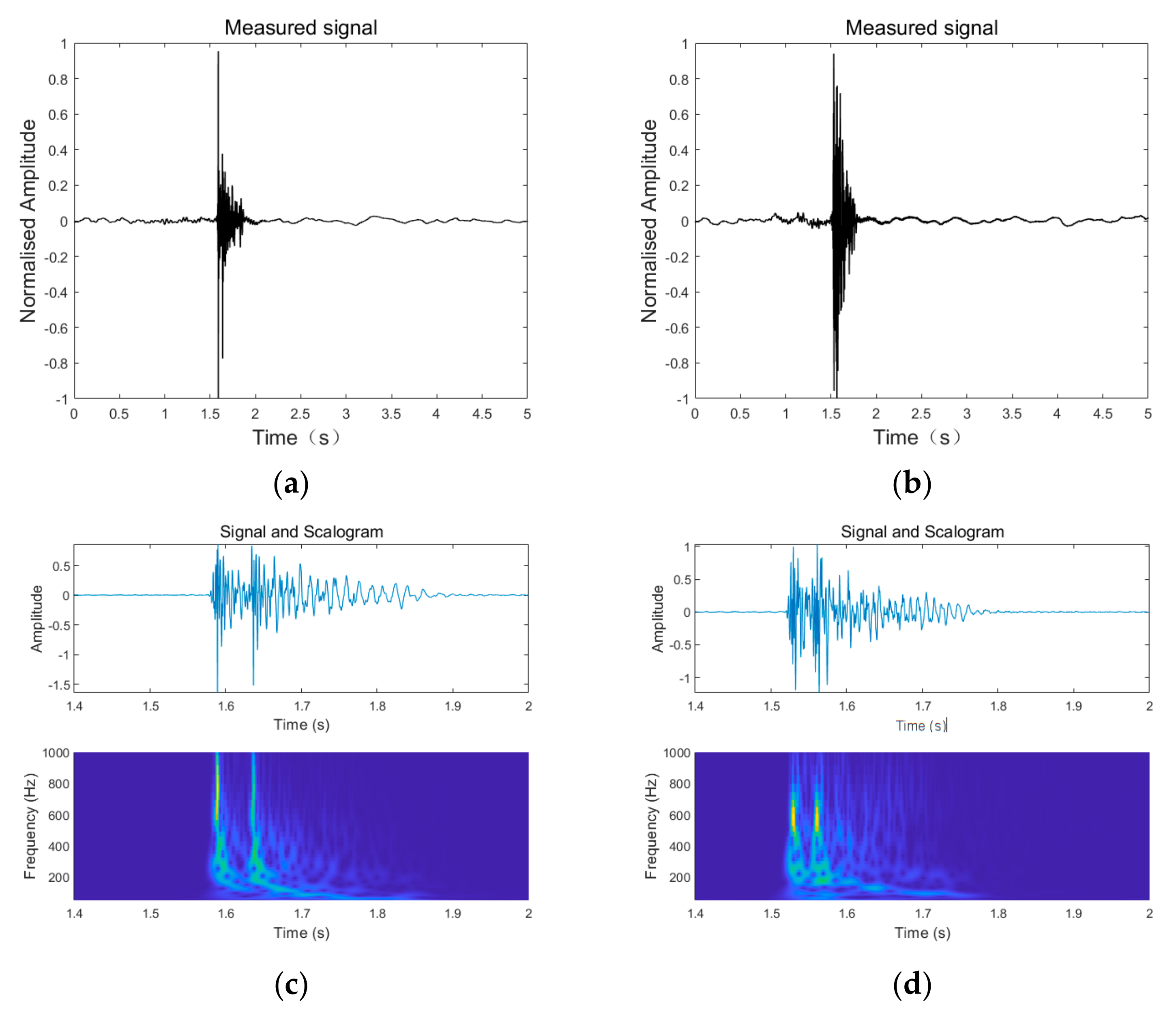
4.1. Experiment Introduction
4.2. Baseline Methods
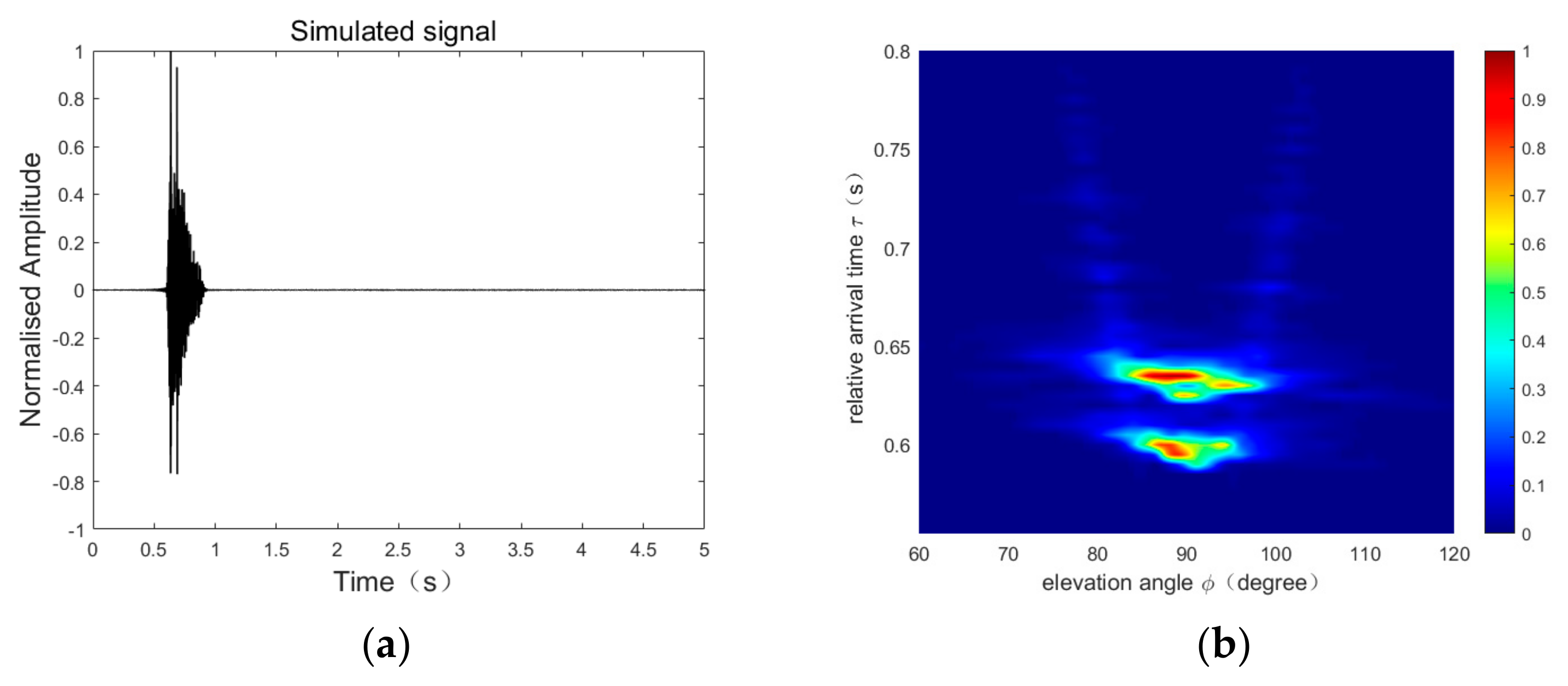
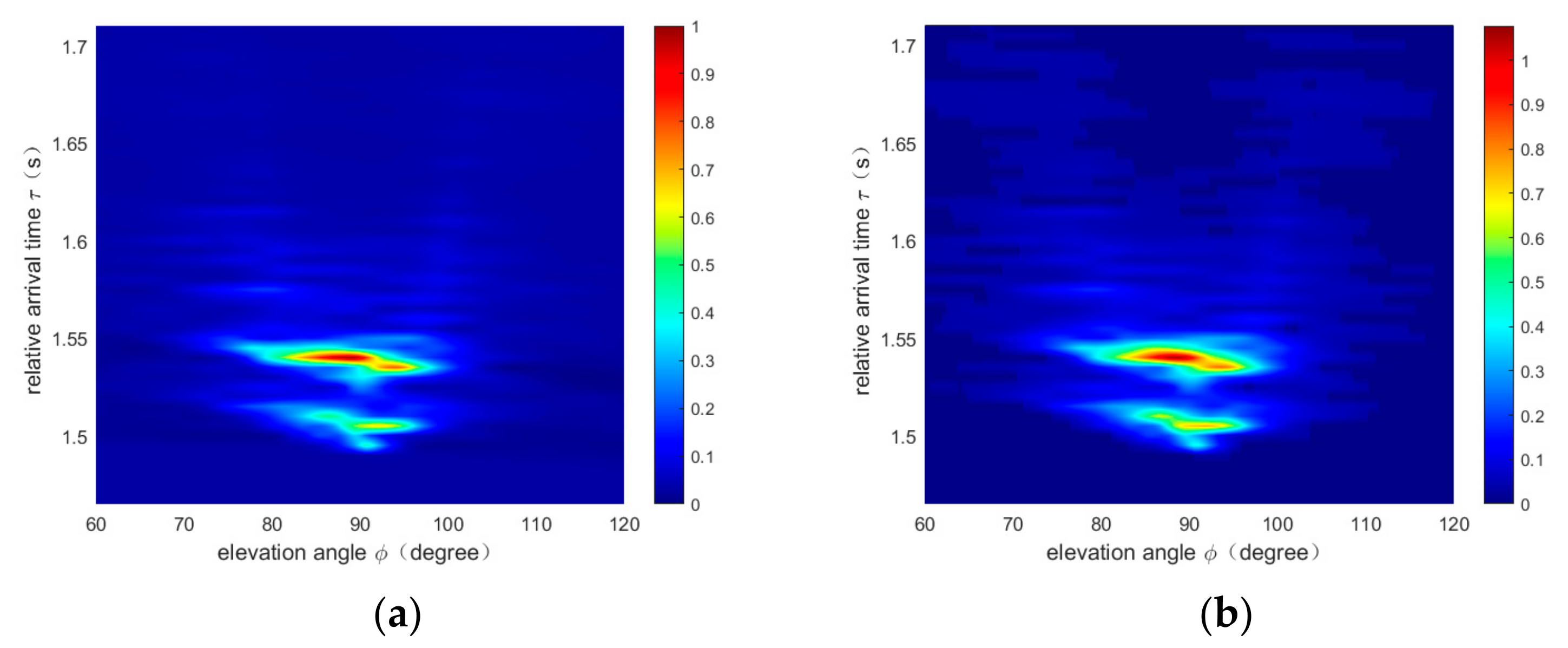
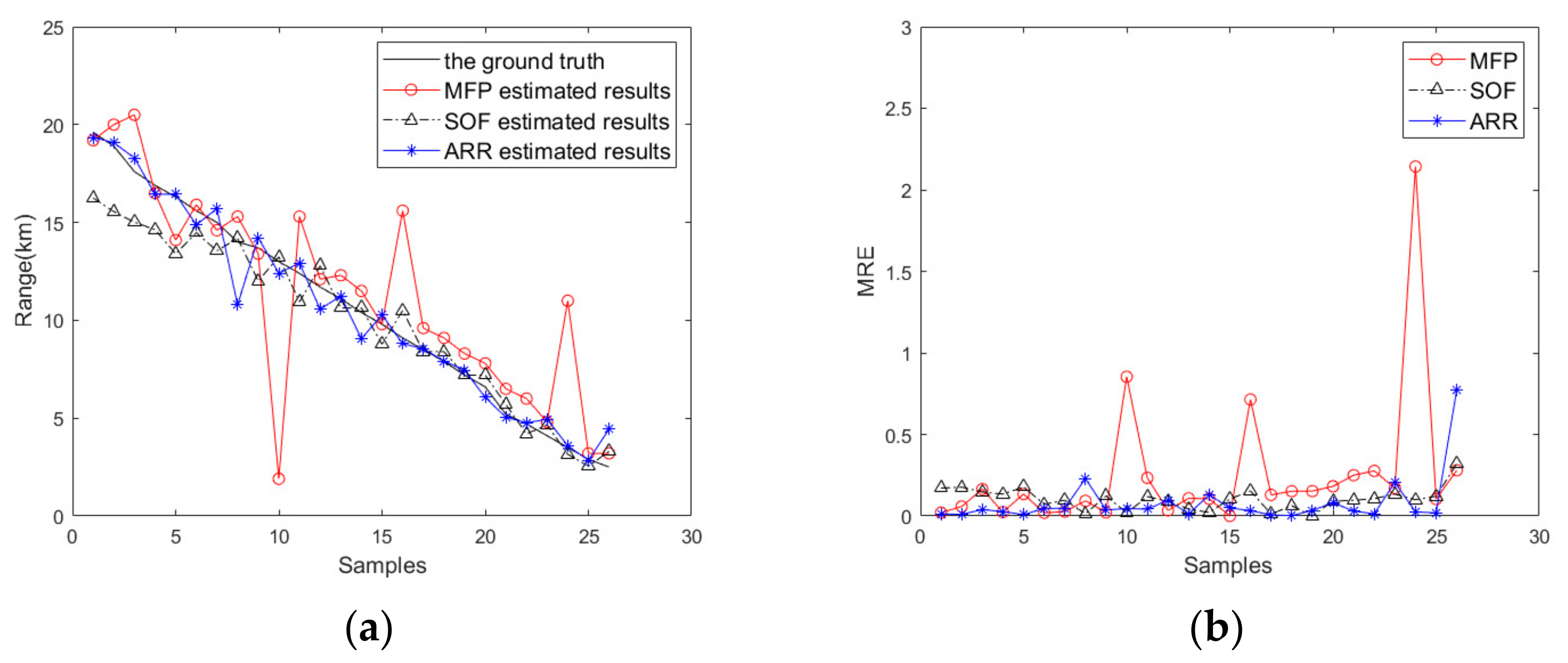
4.3. Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sazontov, A.G.; Malekhanov, A.I. Matched field signal processing in underwater sound channels (Review). Acoust. Phys. 2015, 61, 213–230. [Google Scholar] [CrossRef]
- Baggeroer, A.B.; Kuperman, W.A.; Schmidt, H. Matched field processing: Source localization in correlated noise as an optimum parameter estimation problem. J. Acoust. Soc. Am. 1998, 83, 571. [Google Scholar] [CrossRef]
- Jackson, D.R.; Ewart, T.E. The effect of internal waves on matched-field processing. J. Acoust. Soc. Am. 1994, 96, 2945–2955. [Google Scholar] [CrossRef]
- Dosso, S.E.; Nielsen, P.L.; Wilmut, M.J. Data Uncertainty Estimation in Matched-Field Geoacoustic Inversion. J. Acoust. Soc. Am. 2006, 119, 208–219. [Google Scholar] [CrossRef]
- Wilcox, P.D.; Lowe, M.; Cawley, P. A signal processing technique to remove the effect of dispersion from guided wave signals. Aip Conf. Proc. 2001, 557, 555–562. [Google Scholar]
- Chuprov, S.D. Interference structure of a sound field in a layered ocean. In Ocean Acoustics. Current State; Brekhovskikh, L.M., Andreevoi, I.B., Eds.; Nauka: Moscow, Russia, 1982; pp. 71–91. [Google Scholar]
- Turgut, A.; Orr, M.; Rouseff, D. Broadband source localization using horizontal-beam acoustic intensity striations. J. Acoust. Soc. Am. 2010, 127, 73. [Google Scholar] [CrossRef]
- Yun, Y.; Junying, H. Passive ranging based on acoustic field interference structure using double arrays(elements). Chin. J. Acoust. 2012, 31, 262–274. [Google Scholar] [CrossRef]
- Yang, T.C. Beam intensity striations and applications. J. Acoust. Soc. Am. 2003, 113, 1342–1352. [Google Scholar] [CrossRef]
- Wang, N. Dispersionless transform and potential application in ocean acoustics. In Proceedings of the 10th Western Pacific Acoustics Conference, Beijing, China, 21 September 2009. [Google Scholar]
- Gao, D.; Wang, N. Dispersionless transform and signal enhencement application. In Proceedings of the 2th International Conference on Shallow Water Acoustic, Shanghai, China, 13 April 2009. [Google Scholar]
- Gao, D.; Wang, N.; Wang, H. Artifical time reversal mirror by dedispersion transform in shallow water. In Proceedings of the 3th Oceanic Acoustics Conference, Beijing, China, 12 May 2012. [Google Scholar]
- Gao, D. Waveguide Invariant in Shallow Water: Theory and Application. Ph.D. Thesis, Ocean University of China, Qingdao, China, 2012. [Google Scholar]
- Xiao-Le, G.; Kun-De, Y.; Yuan-Liang, M.; Qiu-Long, Y. A source range and depth estimation method based on modal dedispersion transform. Acta Phys. Sin. 2016, 65, 214302. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Y.; Gao, S. Passive acoustic location with de-dispersive transform. In Proceedings of the 16th Western China Acoustics Conference, Leshan, Sichuan, China, 1 August 2016. [Google Scholar]
- Lee, S.; Makris, N.C. The array invariant. J. Acoust. Soc. Am. 2006, 119, 336–351. [Google Scholar] [CrossRef]
- Lee, S.; Makris, N.C. A new invariant method for instantaneous source range estimation in an ocean waveguide from passive beam-time intensity data. J. Acoust. Soc. Am. 2004, 116, 2646. [Google Scholar] [CrossRef]
- Lee, S. Efficient Localization in a Dispersive Waveguide: Applications in Terrestrial Continental Shelves and on Europa. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2006. [Google Scholar]
- Kong, Q.; Trugman, D.; Ross, Z.; Bianco, M.; Meade, B.; Gerstoft, P. Machine learning in seismology: Turning data into insights. Seismol. Res. Lett. 2018, 90, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Bergen, K.J.; Johnson, P.A.; de Hoop, M.V.; Beroza, G.C. Machine learning for data-driven discovery in solid earth geo-science. Science 2019, 363, eaau0323. [Google Scholar] [CrossRef]
- Zhenglin, L.I.; Haibin, W.A.N.G. Overview of Machine Learning Methods in Underwater Source Localization. J. Signal Process. 2019, 35, 1450–1459. [Google Scholar]
- Liang, X.; Yang, F. Underwater Acoustic Target Localization: A Review. IEEE J. Ocean. Eng. 2021, 46, 112–125. [Google Scholar] [CrossRef]
- Soylu, C.; Basyigit, B.; Tekin, A.C. Machine Learning Methods for Underwater Acoustic Localization: A Survey. IEEE Access 2020, 8, 130589–130611. [Google Scholar] [CrossRef]
- Li, L.; Chen, H. Underwater Acoustic Target Localization: A Review of Recent Progress and Challenges. Sensors 2020, 20, 6599. [Google Scholar] [CrossRef]
- Torres, D.; Casari, P.; Zuniga, M. A Review of Machine Learning Techniques for Acoustic Target Localization in Underwater Sensor Networks. Ad Hoc Netw. 2018, 73, 65–79. [Google Scholar] [CrossRef]
- Niu, H.; Ozanich, E.; Gerstoft, P. Ship localization in Santa Barbara Channel using machine learning classifiers. J. Acoust. Soc. Am. 2017, 142, EL455–EL460. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Wang, F.; Jiang, M.; Qian, C. Residual attention network for image classification. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21 July 2017; pp. 3156–3164. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:abs/1706.03762. [Google Scholar]
- Jensen, F. Computational Ocean Acoustics, 2nd ed.; Springer Science Business Media, LLC.: New York, NY, USA, 2011; pp. 611–617. [Google Scholar]
- Porter, M.B. “The KRAKEN Normal Mode Program”, SACLANT Undersea Research Centre Memorandum SM-245 and Naval Research Laboratory Memorandum Report No. 6920. 1991. Available online: http://oalib.hlsresearch.com/Modes/kraken.pdf (accessed on 1 March 2023).
- Chapman, N.R. Measurement of the waveform parameters of shallow explosive charges. J. Acoust. Soc. Am. 1985, 78, 672–681. [Google Scholar] [CrossRef]
- Gannon, L. Simulation of underwater explosions in close-proximity to a submerged cylinder and a free-surface or rigid boundary. J. Fluids Struct. 2019, 87, 189–205. [Google Scholar] [CrossRef]

| Parameters | Units | Lower Bound | Upper Bound | No. of Discrete Values |
|---|---|---|---|---|
| Source depth | m | 1 | 70 | 35 |
| Source range | km | 1 | 20 | 191 |
| SSP | m/s | 2 SSPs measured by CTD | 2 | |
| Water depth | m | 70 | 90 | 3 |
| Models | Simulation Dataset | Experimental Dataset | ||||
|---|---|---|---|---|---|---|
| MRE | RMSE | Accuracy | MRE | RMSE | Accuracy | |
| ARR Model | 0.01 | 0.18 | 93% | 0.07 | 0.90 | 85% |
| SOF | 0.14 | 1.90 | 61% | 0.18 | 2.54 | 54% |
| MFP | 0.01 | 0.10 | 99% | 0.25 | 3.15 | 35% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Su, L.; Ren, Q.; Li, H.; Jia, Y.; Ma, L. A Hybrid–Source Ranging Method in Shallow Water Using Modal Dispersion Based on Deep Learning. J. Mar. Sci. Eng. 2023, 11, 561. https://doi.org/10.3390/jmse11030561
Wang T, Su L, Ren Q, Li H, Jia Y, Ma L. A Hybrid–Source Ranging Method in Shallow Water Using Modal Dispersion Based on Deep Learning. Journal of Marine Science and Engineering. 2023; 11(3):561. https://doi.org/10.3390/jmse11030561
Chicago/Turabian StyleWang, Tong, Lin Su, Qunyan Ren, He Li, Yuqing Jia, and Li Ma. 2023. "A Hybrid–Source Ranging Method in Shallow Water Using Modal Dispersion Based on Deep Learning" Journal of Marine Science and Engineering 11, no. 3: 561. https://doi.org/10.3390/jmse11030561





