Wave Overtopping at Sea Dikes on Shallow Foreshores: A Review, an Evaluation, and Remaining Challenges
Abstract
:1. Introduction
2. Foreshore Classification
2.1. Based on Breaker Parameter
2.2. Wave Steepness
2.3. Based on Relative Water Depth (htoe/Hm0,o)
3. Existing Empirical Methods
3.1. Van Gent (1999)
3.2. Goda (2009)
3.3. Altomare et al. (2016) in EurOtop (2018)
3.4. Lashley et al. (2021)
4. Methods and Datasets
4.1. Physical Model Tests
4.2. CLASH Dataset
4.3. Performance Indicators
5. Results and Discussion
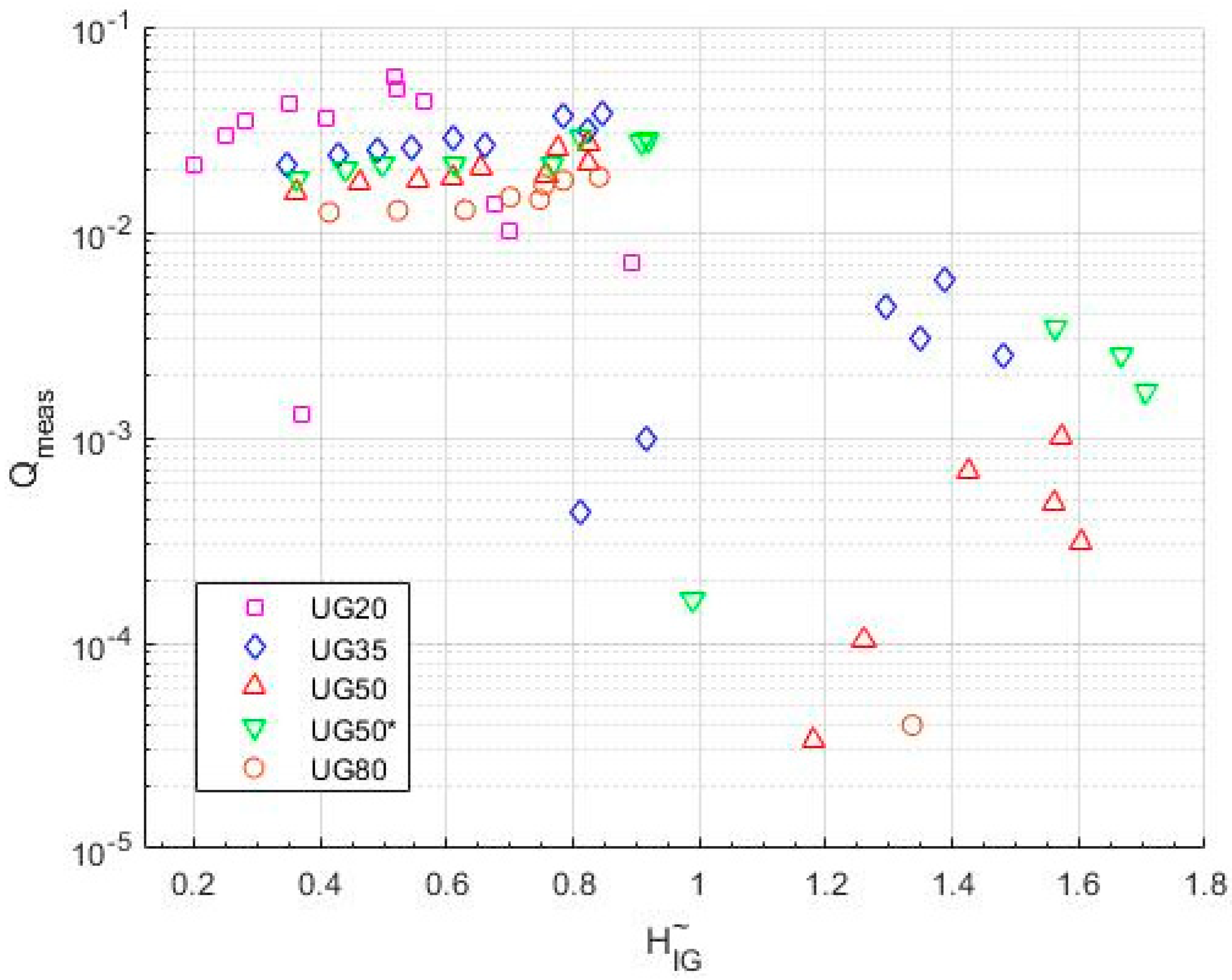
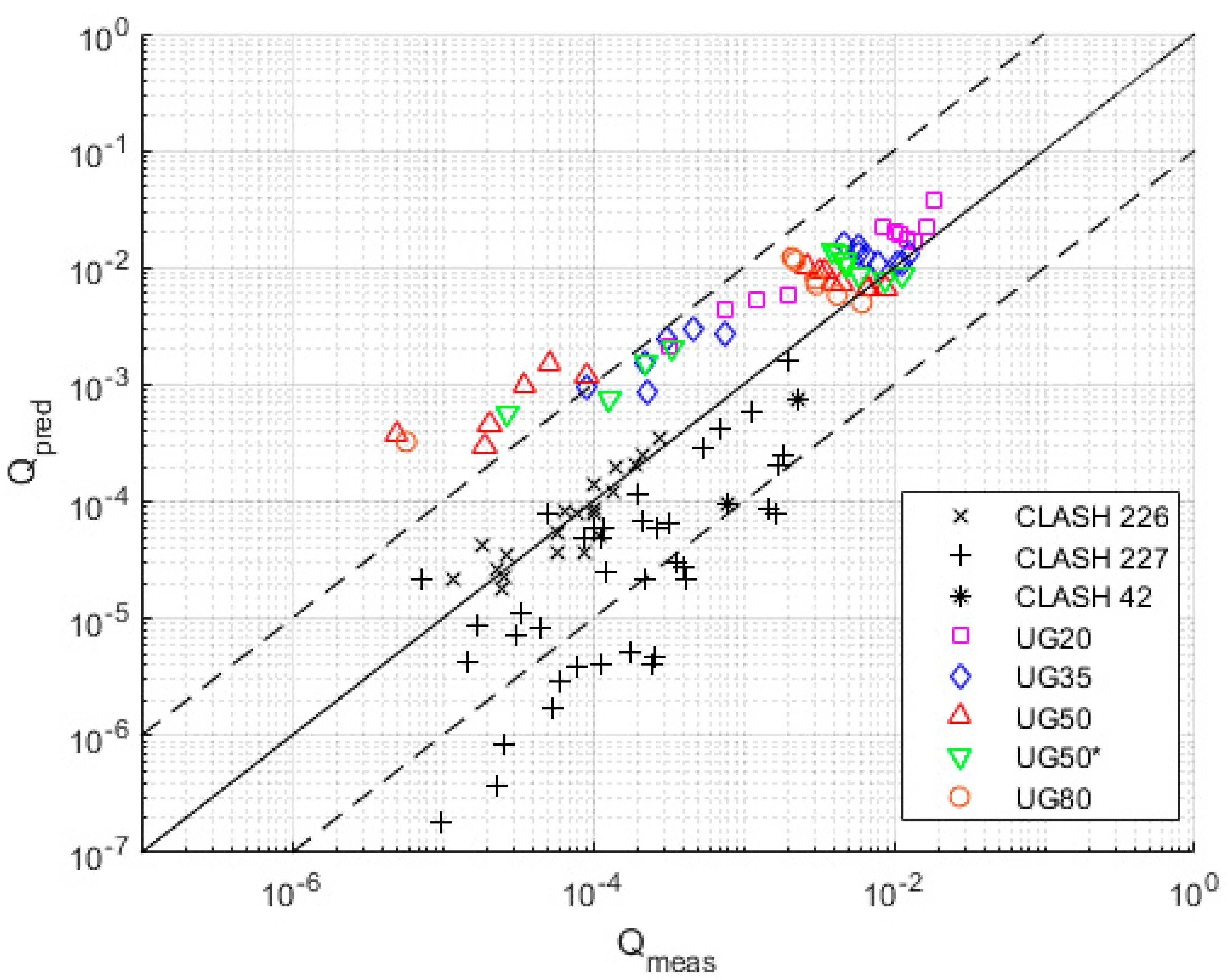
5.1. Analysis of Physical Model Tests
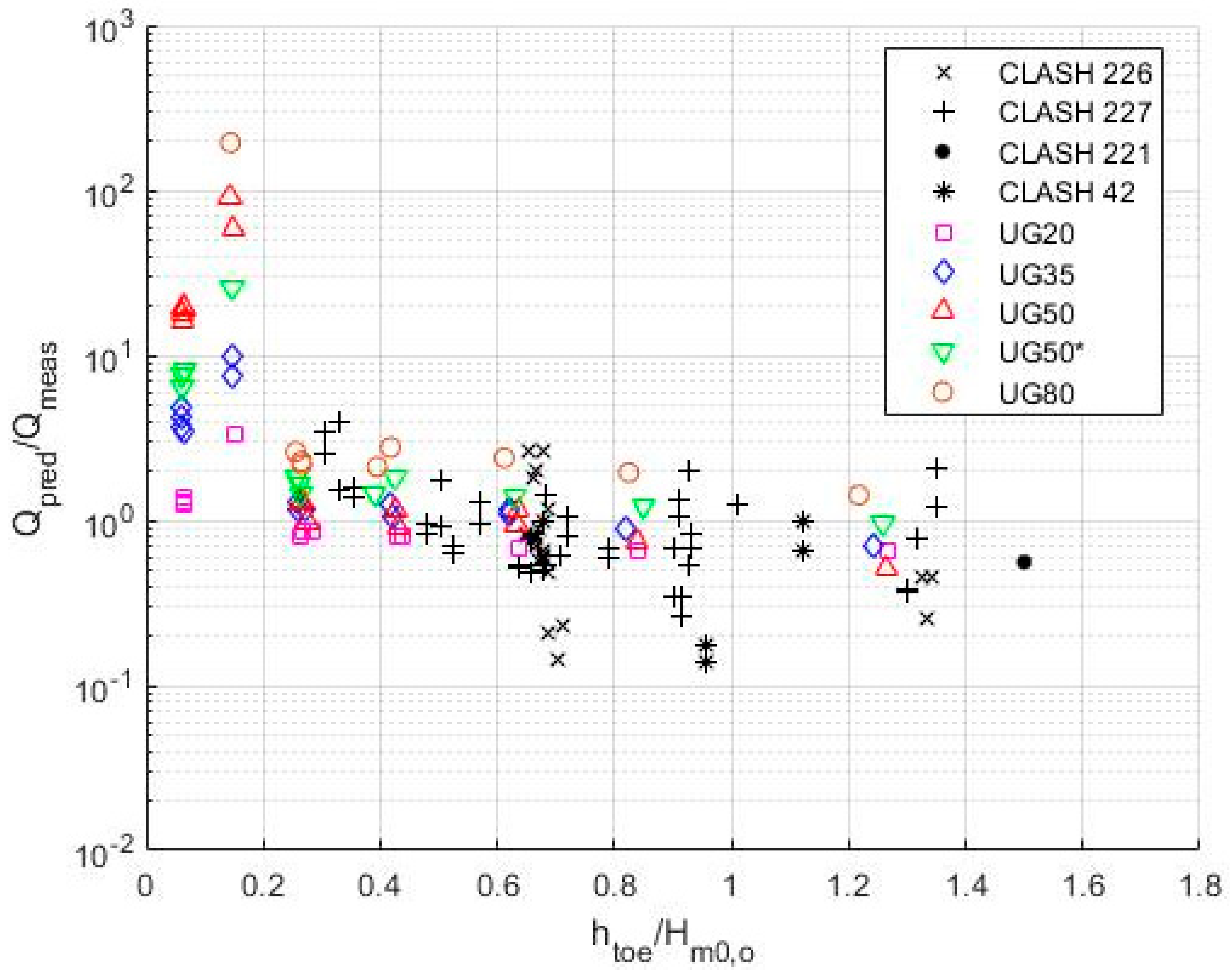
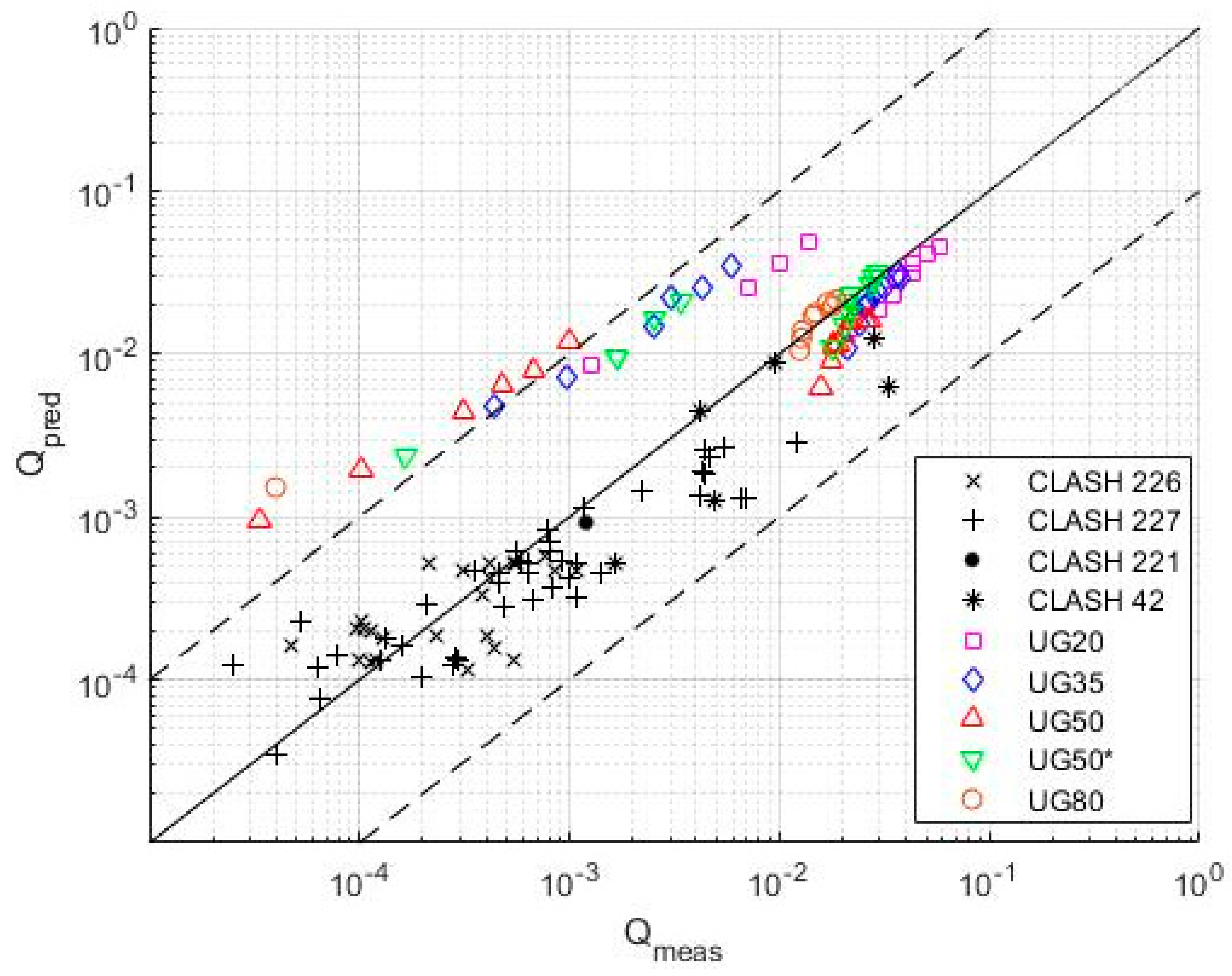
5.2. Performance of Existing Empirical Methods
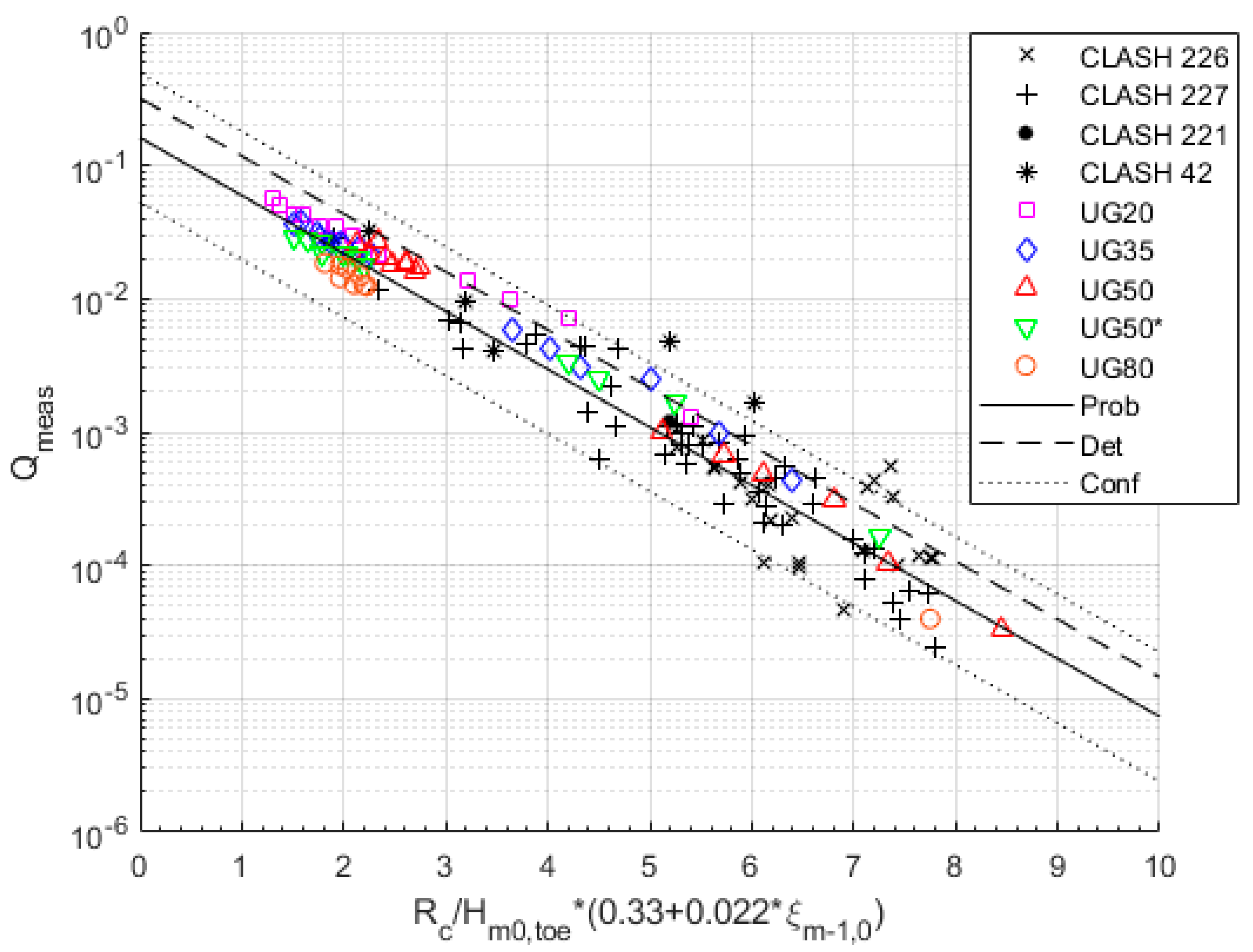
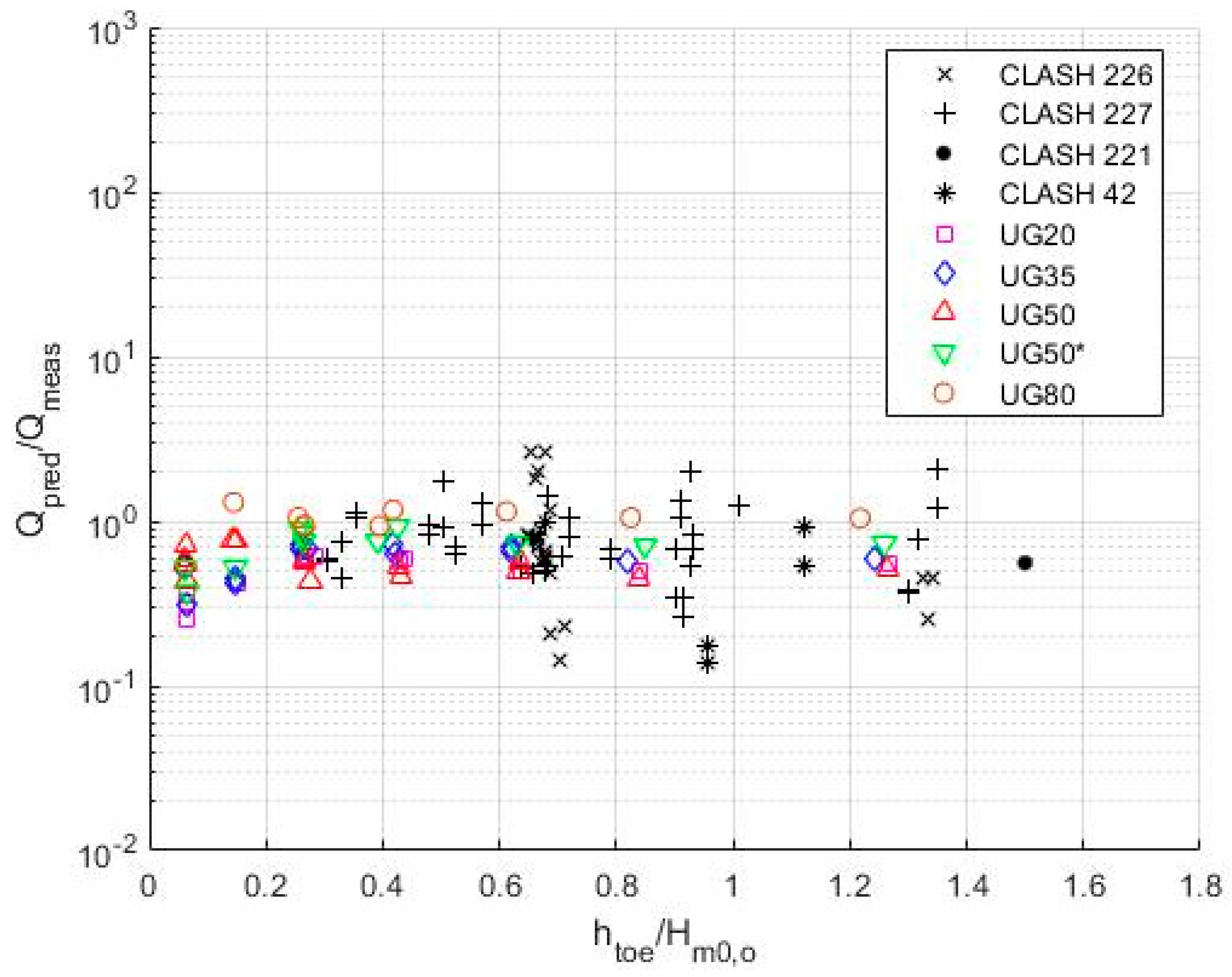
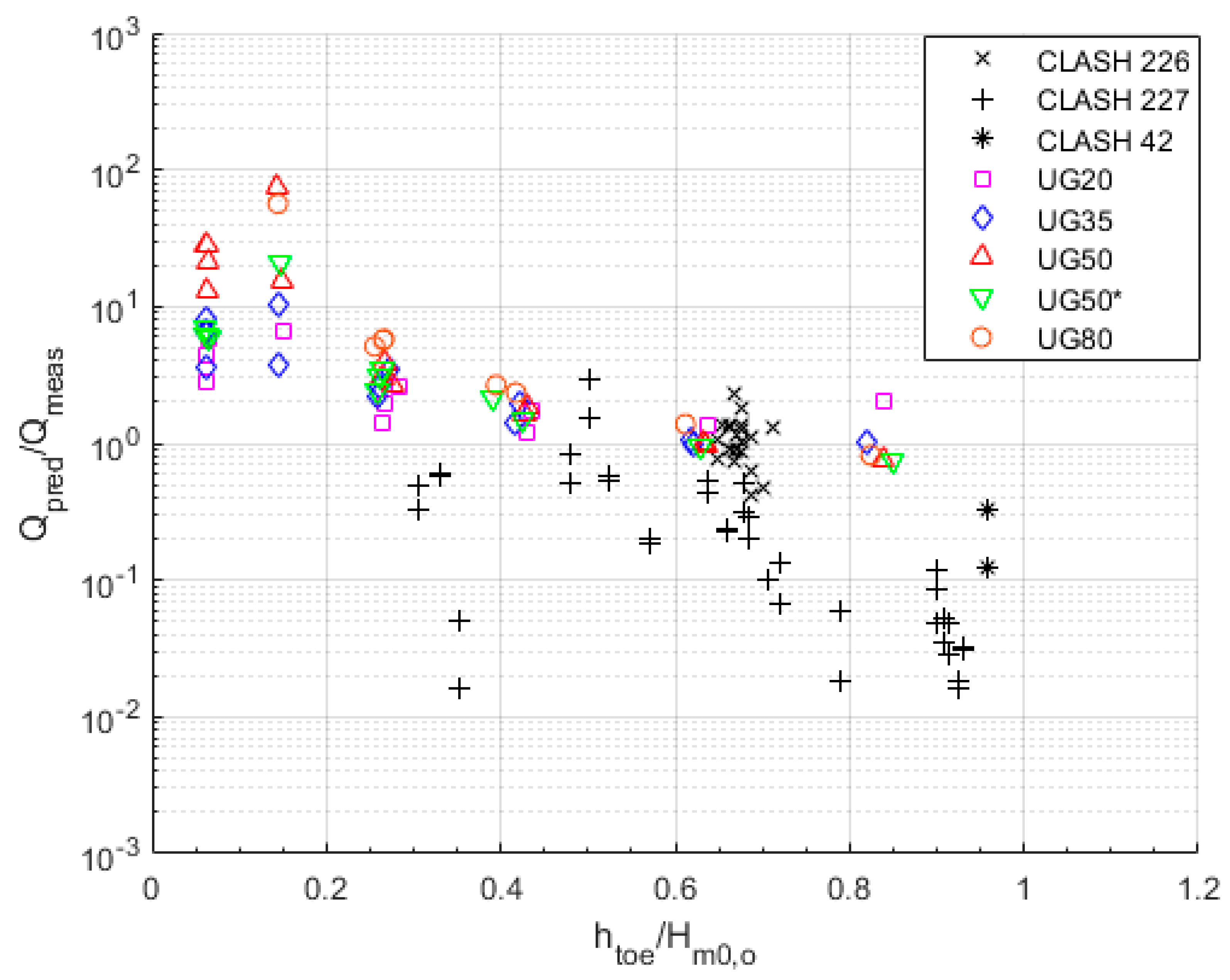
5.2.1. Van Gent (1999)
5.2.2. Goda (2009)
5.2.3. Altomare et al. (2016) in EurOtop (2018)
5.2.4. Lashley et al. (2021)
6. Conclusions and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hofland, B.; Chen, X.; Altomare, C.; Oosterlo, P. Prediction formula for the spectral wave period T m-1,0 on mildly sloping shallow foreshores. Coast. Eng. 2017, 123, 21–28. [Google Scholar] [CrossRef] [Green Version]
- Altomare, C.; Suzuki, T.; Chen, X.; Verwaest, T.; Kortenhaus, A. Wave overtopping of sea dikes with very shallow foreshores. Coast. Eng. 2016, 116, 236–257. [Google Scholar] [CrossRef]
- Van der Meer, J.W.; Allsop, N.W.H.; Bruce, T.; De Rouck, J.; Kortenhaus, A.; Pullen, T.; Schüttrumpf, H.; Troch, P.; Zanuttigh, B. (Eds.) EurOtop—Manual on Wave Overtopping of Sea Defences and Related Structures: An Overtopping Manual Largely Based on European Research, but for Worldwide Application; TU Delft: Delft, The Netherlands, 2018; Available online: www.overtopping-manual.com (accessed on 2 February 2022).
- Koosheh, A.; Etemad-Shahidi, A.; Cartwright, N.; Tomlinson, R.; van Gent, M.R.A. Distribution of individual wave overtopping volumes at rubble mound seawalls. Coast. Eng. 2022, 177, 104173. [Google Scholar] [CrossRef]
- Altomare, C.; Suzuki, T.; Verwaest, T.; Verwaest, T. Influence of directional spreading on wave overtopping of sea dikes with gentle and shallow foreshores. Coast. Eng. 2020, 157, 103654. [Google Scholar] [CrossRef] [Green Version]
- Gruwez, V.; Altomare, C.; Suzuki, T.; Streicher, M.; Cappietti, L.; Kortenhaus, A.; Troch, P. An inter-model comparison for wave interactions with sea dikes on shallow foreshores. J. Mar. Sci. Eng. 2020, 8, 985. [Google Scholar] [CrossRef]
- Lashley, C.H.; van der Meer, J.; Bricker, J.D.; Altomare, C.; Suzuki, T.; Hirayama, K. Formulating Wave Overtopping at Vertical and Sloping Structures with Shallow Foreshores Using Deep-Water Wave Characteristics. J. Waterw. Port Coast. Ocean Eng. 2021, 147, 04021036. [Google Scholar] [CrossRef]
- Nguyen, T.-H.; Hofland, B.; Chinh, V.D.; Stive, M.J.F. Wave Overtopping Discharge for Very Gently Sloping Foreshores. Water 2020, 12, 1695. [Google Scholar] [CrossRef]
- Goda, Y. Derivation of unified wave overtopping formulas for seawalls with smooth, impermeable surfaces based on selected CLASH datasets. Coast. Eng. 2009, 56, 385–399. [Google Scholar] [CrossRef]
- Mase, H.; Tamada, T.; Yasuda, T.; Hedges, T.S.; Reis, M.T. Wave runup and overtopping at seawalls built on land in very shallow water. J. Waterw. Port Coast. Ocean Eng. 2013, 139, 346–357. [Google Scholar] [CrossRef]
- Yuhi, M.; Mase, H.; Kim, S.; Umeda, S.; Altomare, C. Refinement of integrated formula of wave overtopping and runup modeling. Ocean Eng. 2020, 220, 108350. [Google Scholar] [CrossRef]
- Van Gent, M.R.A. Physical Model Investigations on Coastal Structures with Shallow Foreshores: 2D Model Tests with Single and Double-Peaked Wave Energy Spectra; H3608; TU Delft: Delft, The Netherlands, 1999; Available online: https://repository.tudelft.nl/islandora/object/uuid%3A1b4729de-2e86-4b8a-98d5-48d8e07d5902 (accessed on 2 February 2022).
- Goda, Y.; Kishara, Y.; Kamiyama, Y. Laboratory investigation on the overtopping rate of seawalls by irregular waves. Rep. Port Harb. Res. Inst. 1975, 14, 3–44. (In Japanese) [Google Scholar]
- Herbers, T.H.C.; Elgar, S.; Guza, R.T. Infragravity-Frequency (0.005–0.05 Hz) Motions on the Shelf. Part I: Forced Waves. J. Phys. Oceanogr. 1994, 24, 917–927. [Google Scholar] [CrossRef]
- Goda, Y. Random Seas and Design of Maritime Structures, 2nd ed.; Advanced Series on Ocean Engineering; World Scientific: Singapore, 2000; Volume 15. [Google Scholar]
- Lashley, C.H.; Zanuttigh, B.; Bricker, J.D.; van der Meer, J.; Altomare, C.; Suzuki, T.; Roeber, V.; Oosterlo, P. Benchmarking of numerical models for wave overtopping at dikes with shallow mildly sloping foreshores: Accuracy versus speed. Environ. Model. Softw. 2020, 130, 104740. [Google Scholar] [CrossRef]
- Okihiro, M.; Guza, R.T.; Seymour, R.J. Bound infragravity waves. J. Geophys. Res. 1992, 97, 11453–11469. [Google Scholar] [CrossRef] [Green Version]
- Verhaeghe, H.; van der Meer, J.W.; Steendam, G.J. Database on Wave Overtopping at Coastal Structures; CLASH Report Workpackage 2; Ghent University: Ghent, Belgium, 2004. [Google Scholar]
- TAW. Technical Report on Wave Run-Up and Wave Overtopping at Dikes; Technical Advisory Committee on Flood Defence: Delft, The Netherlands, 2002. [Google Scholar]
- Pullen, T.; Allsop, N.W.H.; Kortenhaus, A.; Schüttrumpf, H.; van der Meer, J.W. (Eds.) EurOtop—European Overtopping Manual for the Assessment of Wave Overtopping; TU Delft: Delft, The Netherlands, 2007. [Google Scholar]
- Tamada, T.; Inoue, M.; Tezuka, T. Experimental studies on diagrams for the estimation of wave overtopping rate on gentle slope-type seawalls and these reduction effects on wave overtopping. Proc. Coast. Eng. JSCE 2002, 49, 641–645. (In Japanese) [Google Scholar]
- Lashley, C.H.; Bricker, J.D.; van der Meer, J.; Van der Meer, J.W.; Altomare, C.; Suzuki, T. Relative magnitude of infragravity waves at coastal dikes with shallow foreshores: A prediction tool. J. Waterw. Port Coast. Ocean Eng.-Asce 2020, 146, 04020034. [Google Scholar] [CrossRef]
- Meinert, P.; Lykke Andersen, T.; Frigaard, P. AwaSys 7 User Manual; Aalborg University: Aalborg, Denmark, 2017. [Google Scholar]
- Kamphuis, J.W. Long waves in flume experiments. In Proceedings of the 26th Conference on Coastal Engineering, Copenhagen, Denmark, 22–26 June 1998. [Google Scholar]
- Ruessink, B.G.; Michallet, H.; Bonneton, P.; Mouaze, D.; Lara, J.; Silva, P.A.; Wellens, P. Globex: Wave dynamics on a gently sloping laboraty beach. In Proceedings of the Coastal Dynamics, Arcachon, France, 24–28 June 2013; pp. 1351–1362. Available online: http://dspace.library.uu.nl/handle/1874/310236 (accessed on 2 February 2022).
- Mansard, E.P.D.; Funke, E.R. The measurement of incident and reflected spectra using a least squares method. In Proceedings of the 17th Coastal Engineering Conference Proceedings, Sydney, Australia, 23–28 March 1980; pp. 154–172. [Google Scholar]
- Eldrup, M.R.; Lykke Andersen, T. Applicability of Nonlinear Wavemaker Theory. J. Mar. Sci. Eng. 2019, 7, 14. [Google Scholar] [CrossRef] [Green Version]
- Victor, L.; Troch, P. Development of a test set-up to measure large wave-by-wave overtopping masses. In Proceedings of the Third International Conference on the Application of Physical Modelling to Port and Coastal Protection, Barcelona, Spain, 28–30 September 2010. [Google Scholar]

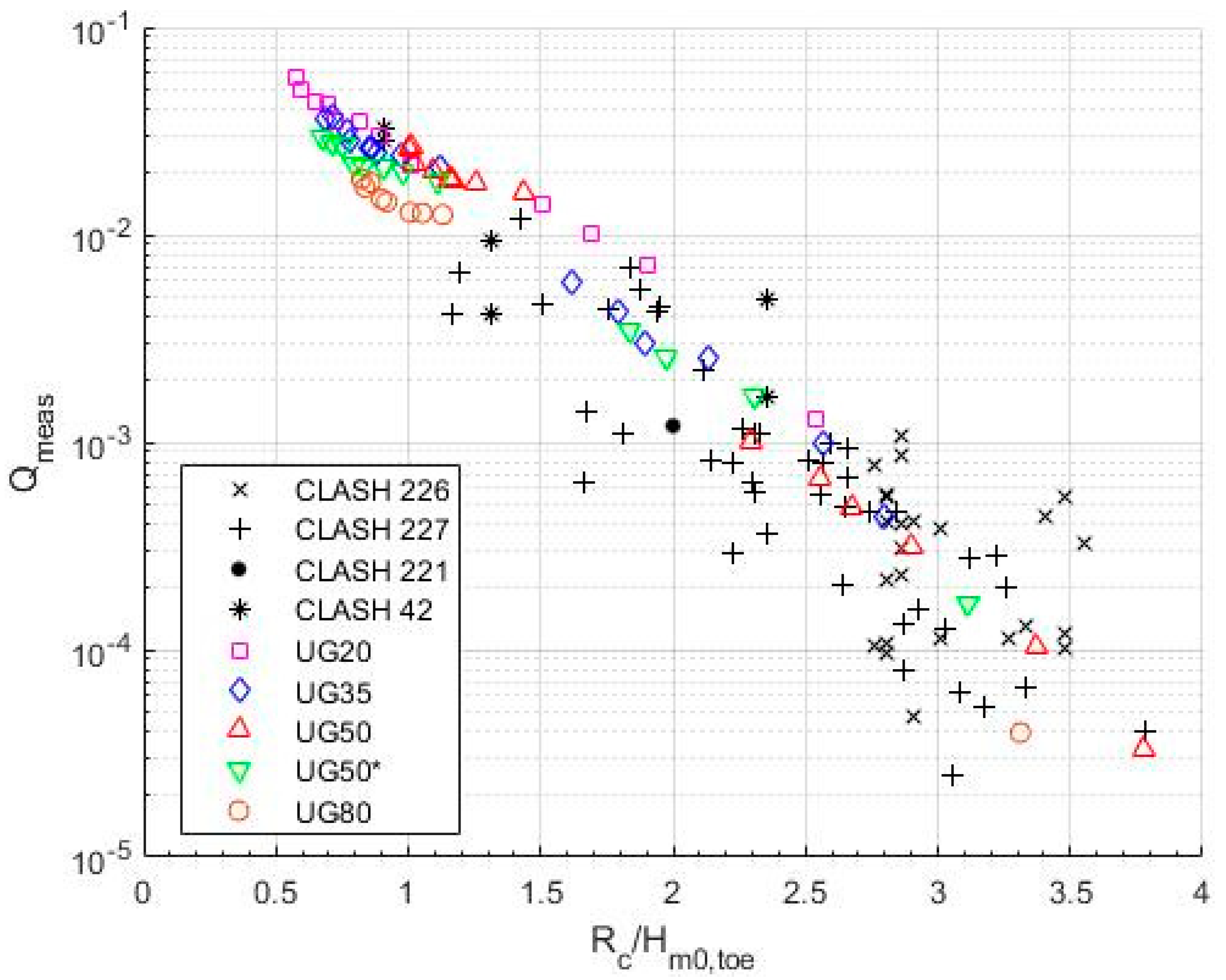
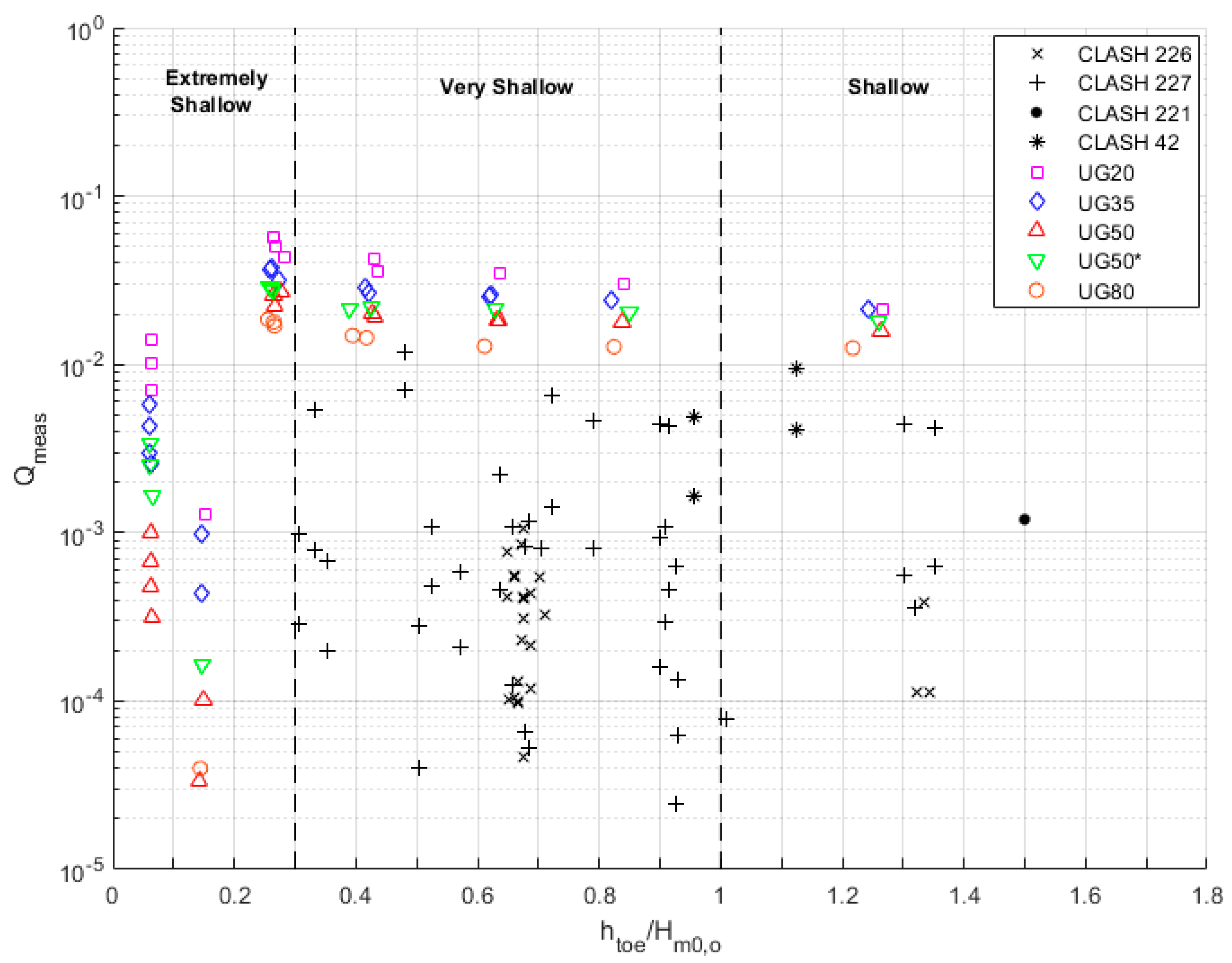
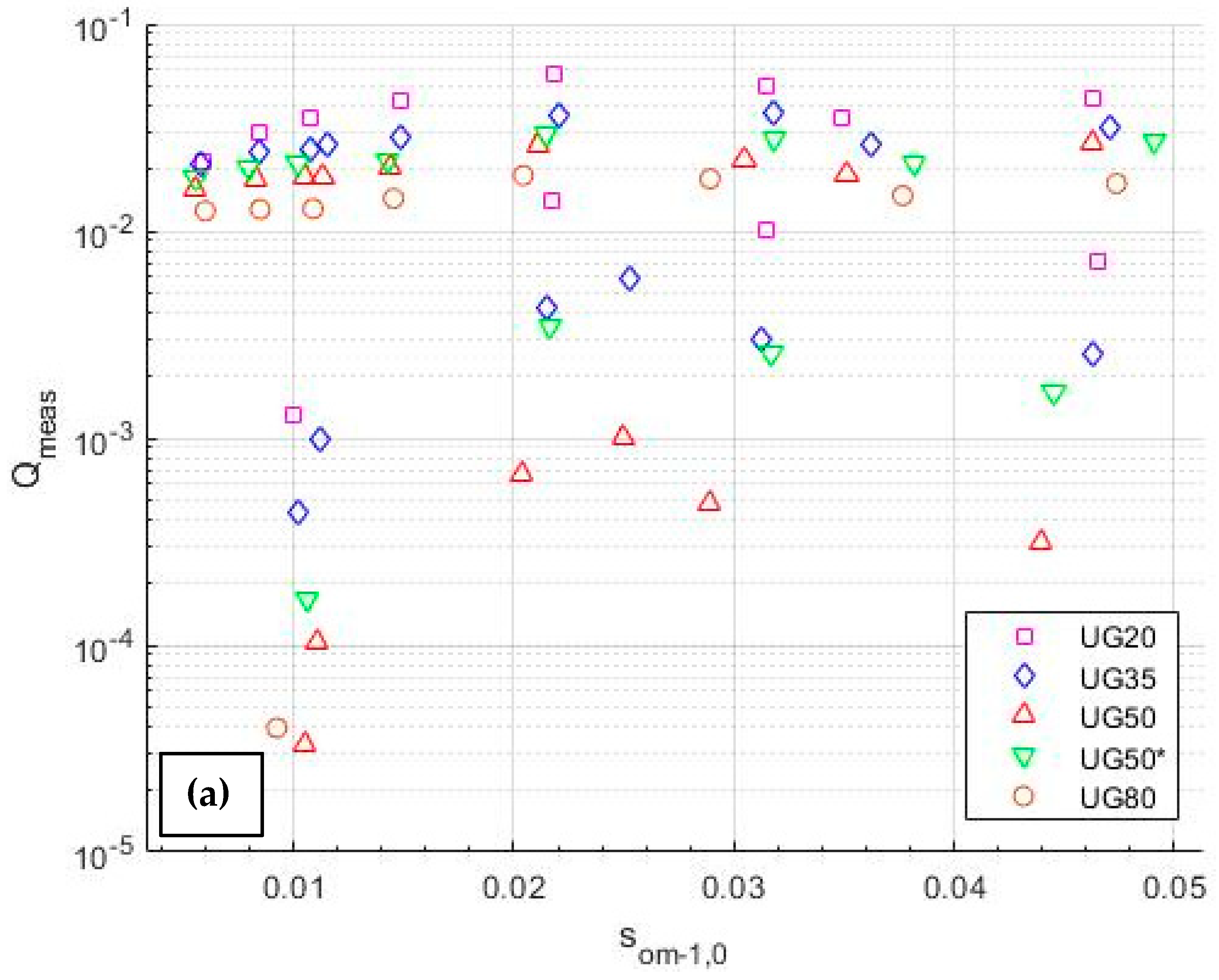
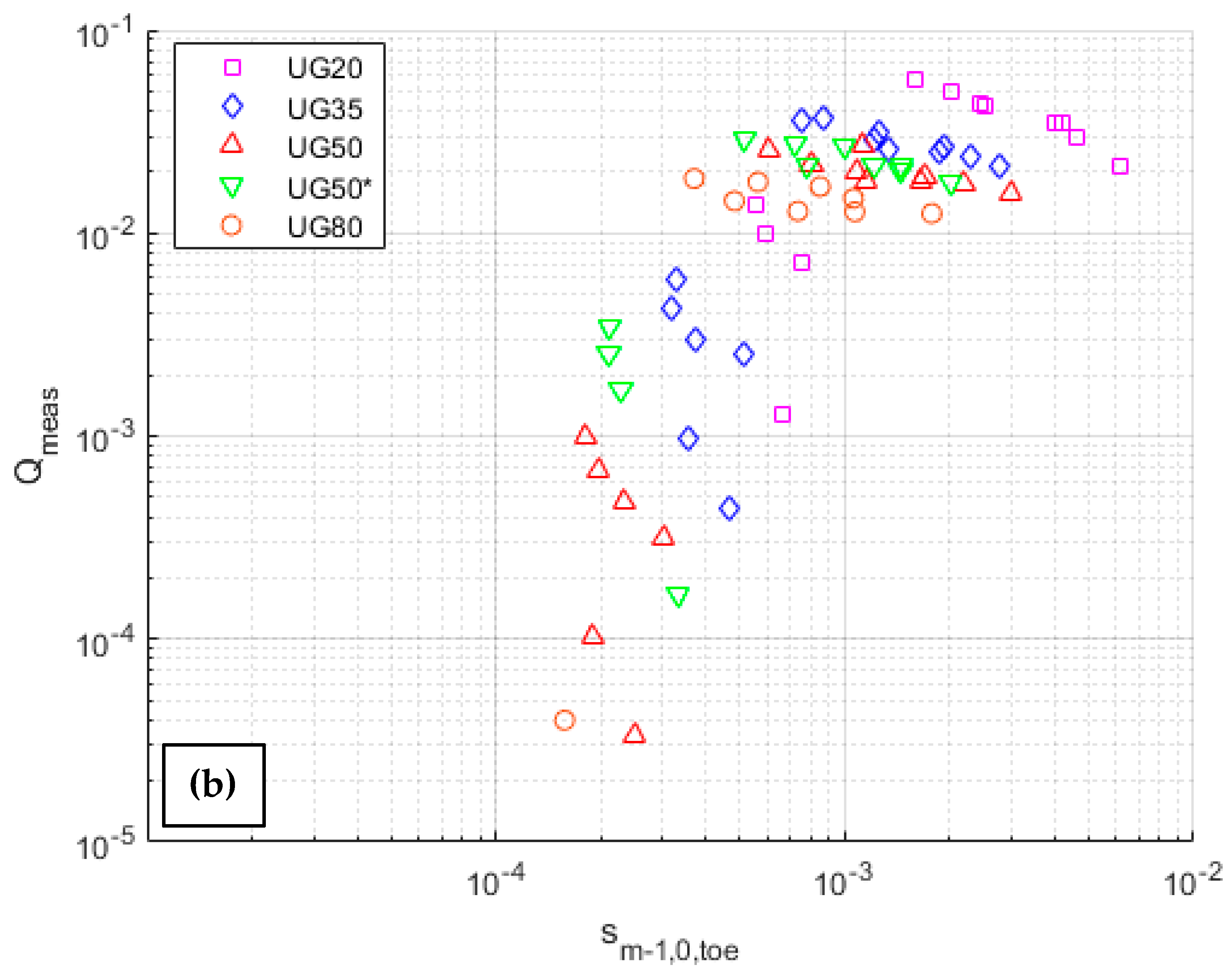



| Test ID | ho (m) | htoe (m) | Rc (m) | Hm0,o (m) | Top (s) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Scale | 1:25 | 1:35 | 1:25 | 1:35 | 1:25 | 1:35 | 1:25 | 1:35 | 1:25 | 1:35 |
| RS01 | 0.65 | 0.467 | 0.012 | 0.009 | 0.08 | 0.057 | 0.20 | 0.143 | 2.40 | 2.03 |
| RS02 | 0.65 | 0.467 | 0.012 | 0.009 | 0.08 | 0.057 | 0.20 | 0.143 | 2.00 | 1.69 |
| RS03 | 0.65 | 0.467 | 0.012 | 0.009 | 0.08 | 0.057 | 0.20 | 0.143 | 1.60 | 1.35 |
| RS05 | 0.65 | 0.467 | 0.012 | 0.009 | 0.08 | 0.057 | 0.08 | 0.057 | 2.40 | 2.03 |
| RS06 | 0.69 | 0.495 | 0.052 | 0.037 | 0.04 | 0.029 | 0.20 | 0.143 | 2.40 | 2.03 |
| RS07 | 0.69 | 0.495 | 0.052 | 0.037 | 0.04 | 0.029 | 0.20 | 0.143 | 2.00 | 1.69 |
| RS08 | 0.69 | 0.495 | 0.052 | 0.037 | 0.04 | 0.029 | 0.20 | 0.143 | 1.60 | 1.35 |
| RS09 | 0.69 | 0.495 | 0.052 | 0.037 | 0.04 | 0.029 | 0.12 | 0.086 | 1.60 | 1.35 |
| RS10 | 0.69 | 0.495 | 0.052 | 0.037 | 0.04 | 0.029 | 0.12 | 0.086 | 2.40 | 2.03 |
| RS11 | 0.69 | 0.495 | 0.052 | 0.037 | 0.04 | 0.029 | 0.08 | 0.057 | 2.40 | 2.03 |
| RS12 | 0.69 | 0.495 | 0.052 | 0.037 | 0.04 | 0.029 | 0.06 | 0.043 | 2.40 | 2.03 |
| RS13 | 0.69 | 0.495 | 0.052 | 0.037 | 0.04 | 0.029 | 0.04 | 0.029 | 2.40 | 2.03 |
| Dataset ID | cot m | cot α | Froude Scale | Hm0,toe (m) | Tm−1,0 (s) | Rc (m) | htoe/Hm0,o | No. of Tests |
|---|---|---|---|---|---|---|---|---|
| UG20 | 20 | 2 | 1:25 | 0.031–0.069 | 2.014–6.031 | 0.040, 0.080 | 0.062–1.318 | 12 |
| UG35 | 35 | 2 | 1:25 | 0.029–0.059 | 2.921–8.739 | 0.040, 0.080 | 0.060–1.285 | 15 |
| UG50 | 50 | 2 | 1:25 | 0.024–0.049 | 2.728–9.541 | 0.040, 0.080 | 0.061–1.305 | 15 |
| UG50* | 50 | 2 | 1:35 | 0.018–0.043 | 3.015–9.745 | 0.029, 0.057 | 0.073–1.356 | 12 |
| UG80 | 80 | 2 | 1:35 | 0.017–0.036 | 3.164–10.320 | 0.029, 0.057 | 0.058–1.263 | 12 |
| Dataset ID | cot m | cot α | Hm0,toe (m) | Tm−1,0 (s) | Rc (m) | htoe/Hm0,o | No. of Tests |
|---|---|---|---|---|---|---|---|
| CLASH 226 | 100, 250 | 2.5, 4 | 0.045–0.103 | 2.45–4.58 | 0.160–0.310 | 0.648–1.343 | 24 |
| CLASH 227 | 100 | 3, 4, 6 | 0.039–0.119 | 2.41–10.64 | 0.066–0.366 | 0.306–1.351 | 44 |
| CLASH 221 | 100 | 4 | 0.105 | 2.609 | 0.210 | 1.500 | 1 |
| CLASH 42 | 20, 50 | 2, 4 | 0.111–0.153 | 3.167–3.647 | 0.100–0.300 | 0.957–3.448 | 6 |
| Van Gent (1999) | Goda (2009) | Van Gent (1999) with Equivalent Slope | Altomare et al. (2016) in EurOtop (2018) | Lashley et al. (2021) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset ID | No. of Tests | Geo | GSD | Geo | GSD | Geo | GSD | Geo | GSD | Geo | GSD |
| CLASH 226 | 24 (21) | 0.684 | 2.081 | 0.997 | 1.952 | 0.684 | 2.081 | 0.921 | 2.081 | 1.014 | 1.488 |
| CLASH 227 | 44 (29) | 0.860 | 1.854 | 0.694 | 1.983 | 0.738 | 1.620 | 0.993 | 1.620 | 0.150 | 3.843 |
| CLASH 221 | 1 (0) | 0.559 | 1.000 | 0.770 | 1.000 | 0.559 | 1.000 | 0.752 | 1.000 | N/A | N/A |
| CLASH 42 | 6 (2) | 0.396 | 2.047 | 0.433 | 1.887 | 0.377 | 1.972 | 0.507 | 1.972 | 0.197 | 1.629 |
| UG20 | 12 (11) | 0.983 | 1.555 | 1.312 | 2.305 | 0.470 | 1.320 | 0.633 | 1.320 | 2.466 | 1.749 |
| UG35 | 15 (14) | 2.004 | 2.272 | 1.840 | 3.048 | 0.568 | 1.253 | 0.764 | 1.253 | 2.877 | 2.136 |
| UG50 | 15 (14) | 3.748 | 5.670 | 2.159 | 5.056 | 0.550 | 1.205 | 0.740 | 1.205 | 5.409 | 4.253 |
| UG50* | 12 (11) | 2.764 | 2.678 | 1.833 | 2.822 | 0.671 | 1.297 | 0.904 | 1.297 | 3.179 | 2.524 |
| UG80 | 12 (8) | 3.581 | 4.150 | 1.613 | 3.073 | 1.059 | 1.113 | 1.426 | 1.113 | 4.014 | 3.305 |
| TOTAL | 141 (119) | 1.259 | 3.166 | 1.108 | 2.885 | 0.649 | 1.663 | 0.873 | 1.663 | 0.976 | 5.850 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarakcioglu, G.O.; Kisacik, D.; Gruwez, V.; Troch, P. Wave Overtopping at Sea Dikes on Shallow Foreshores: A Review, an Evaluation, and Remaining Challenges. J. Mar. Sci. Eng. 2023, 11, 638. https://doi.org/10.3390/jmse11030638
Tarakcioglu GO, Kisacik D, Gruwez V, Troch P. Wave Overtopping at Sea Dikes on Shallow Foreshores: A Review, an Evaluation, and Remaining Challenges. Journal of Marine Science and Engineering. 2023; 11(3):638. https://doi.org/10.3390/jmse11030638
Chicago/Turabian StyleTarakcioglu, Gulizar Ozyurt, Dogan Kisacik, Vincent Gruwez, and Peter Troch. 2023. "Wave Overtopping at Sea Dikes on Shallow Foreshores: A Review, an Evaluation, and Remaining Challenges" Journal of Marine Science and Engineering 11, no. 3: 638. https://doi.org/10.3390/jmse11030638
APA StyleTarakcioglu, G. O., Kisacik, D., Gruwez, V., & Troch, P. (2023). Wave Overtopping at Sea Dikes on Shallow Foreshores: A Review, an Evaluation, and Remaining Challenges. Journal of Marine Science and Engineering, 11(3), 638. https://doi.org/10.3390/jmse11030638






