The Effect of the Fillets on Submarine Wake Field and Propeller Unsteady Bearing Force
Abstract
1. Introduction
2. Simulation Details
2.1. Governing Equations
2.2. Numerical Models
2.3. Test Case
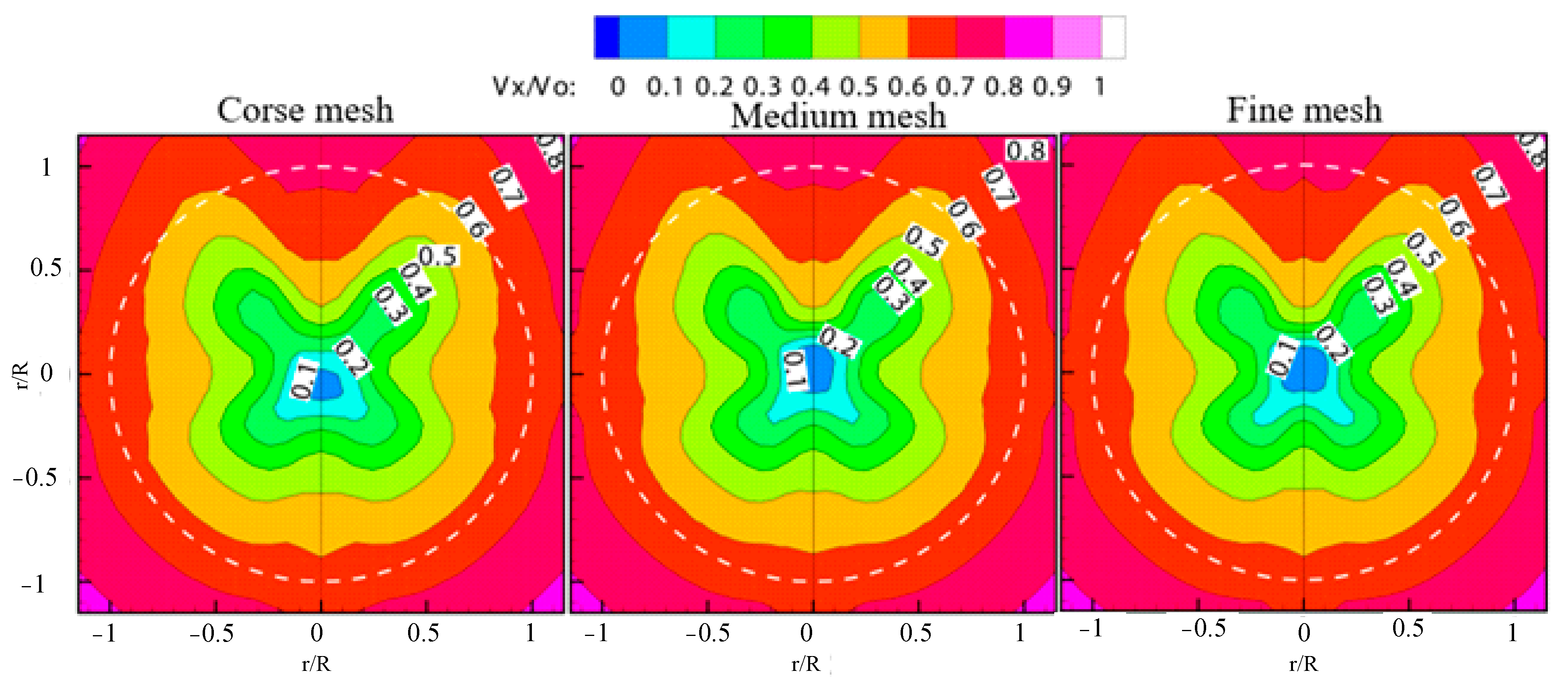
3. Mesh Verification
3.1. Meshing
3.2. Verification of Resistance
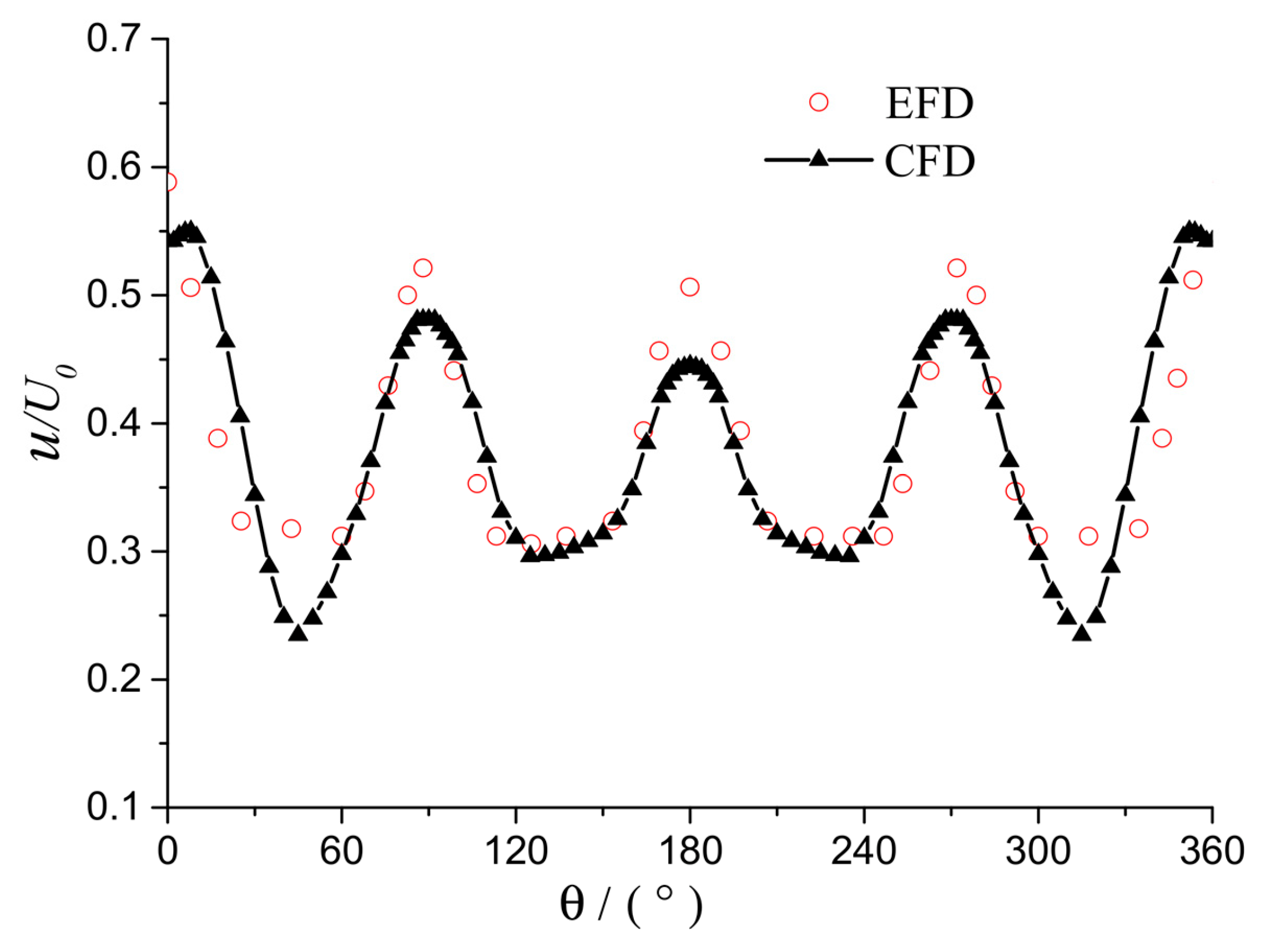
3.3. Verification of Wake Flow
4. Results Analysis and Discussion
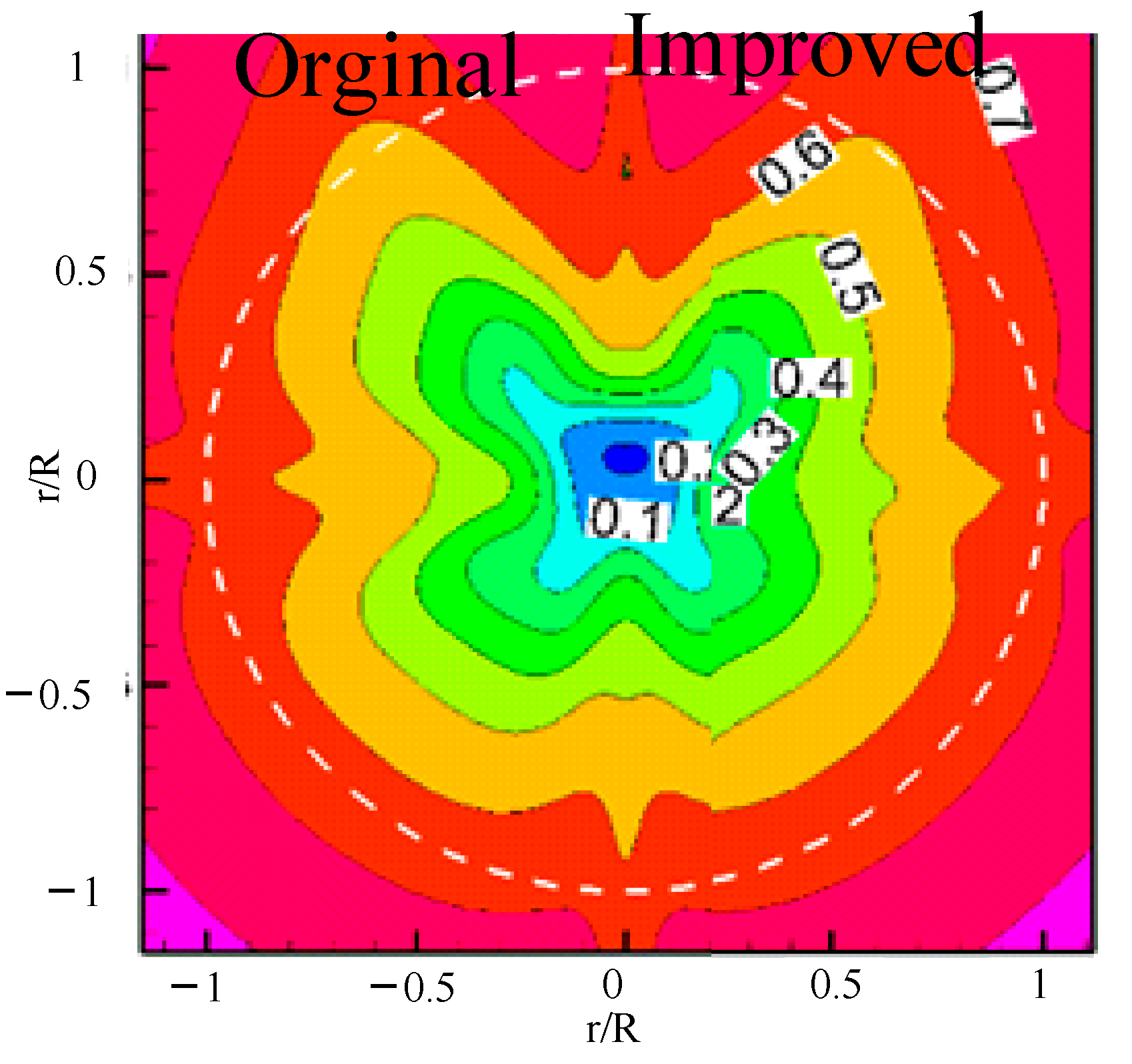
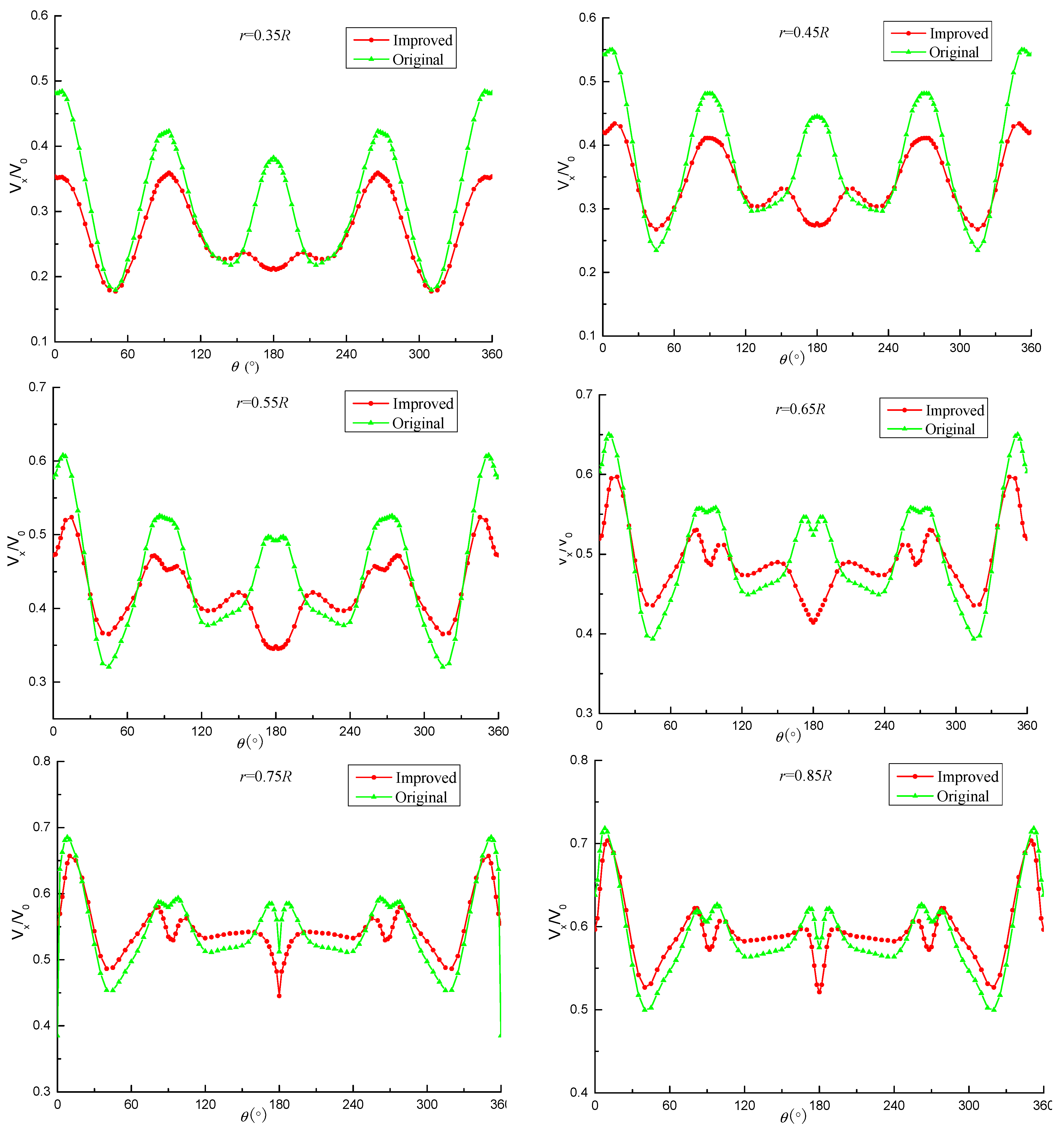
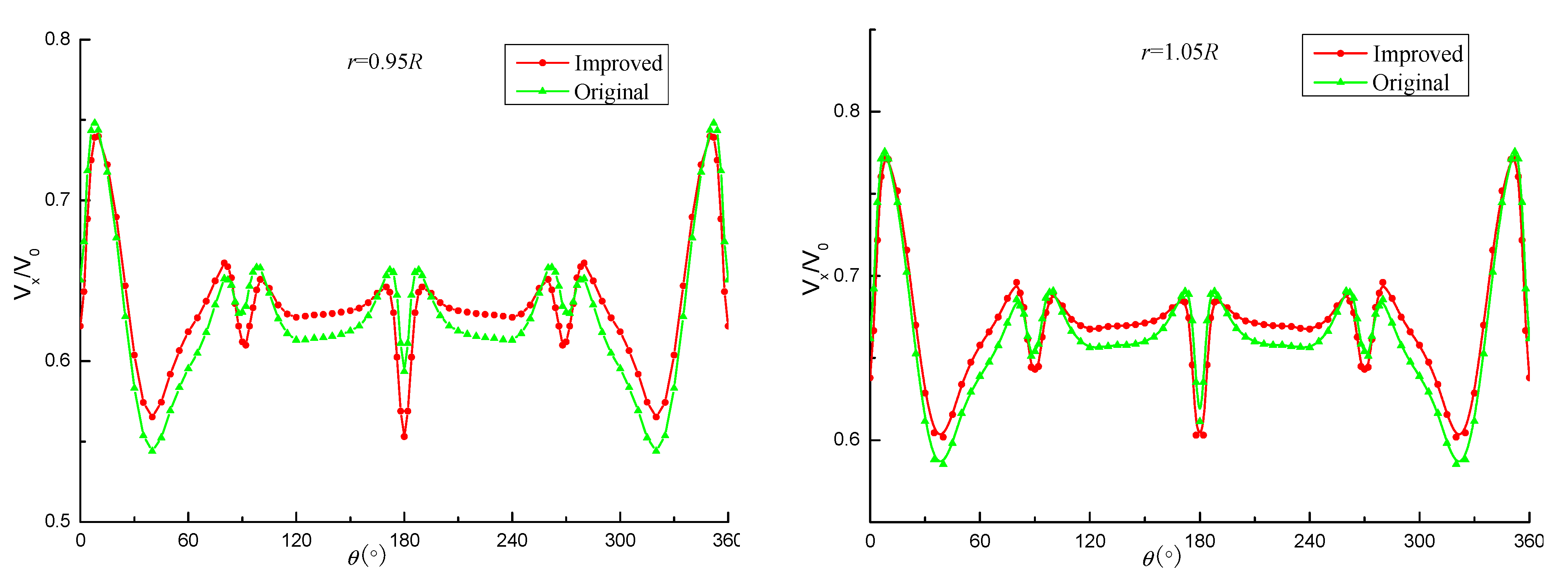
4.1. Distribution of Velocity
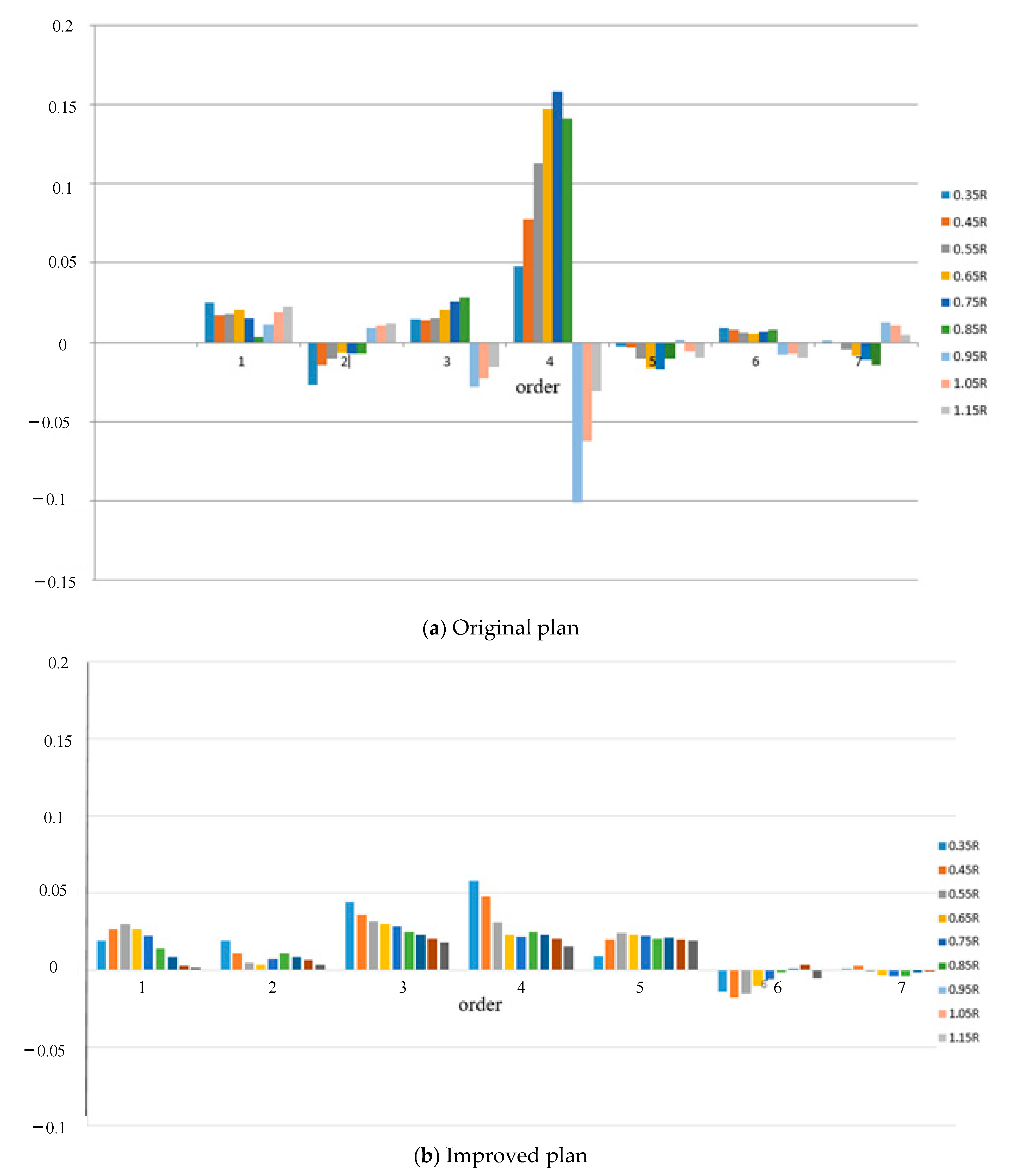
4.2. Uniformity of Wake Field
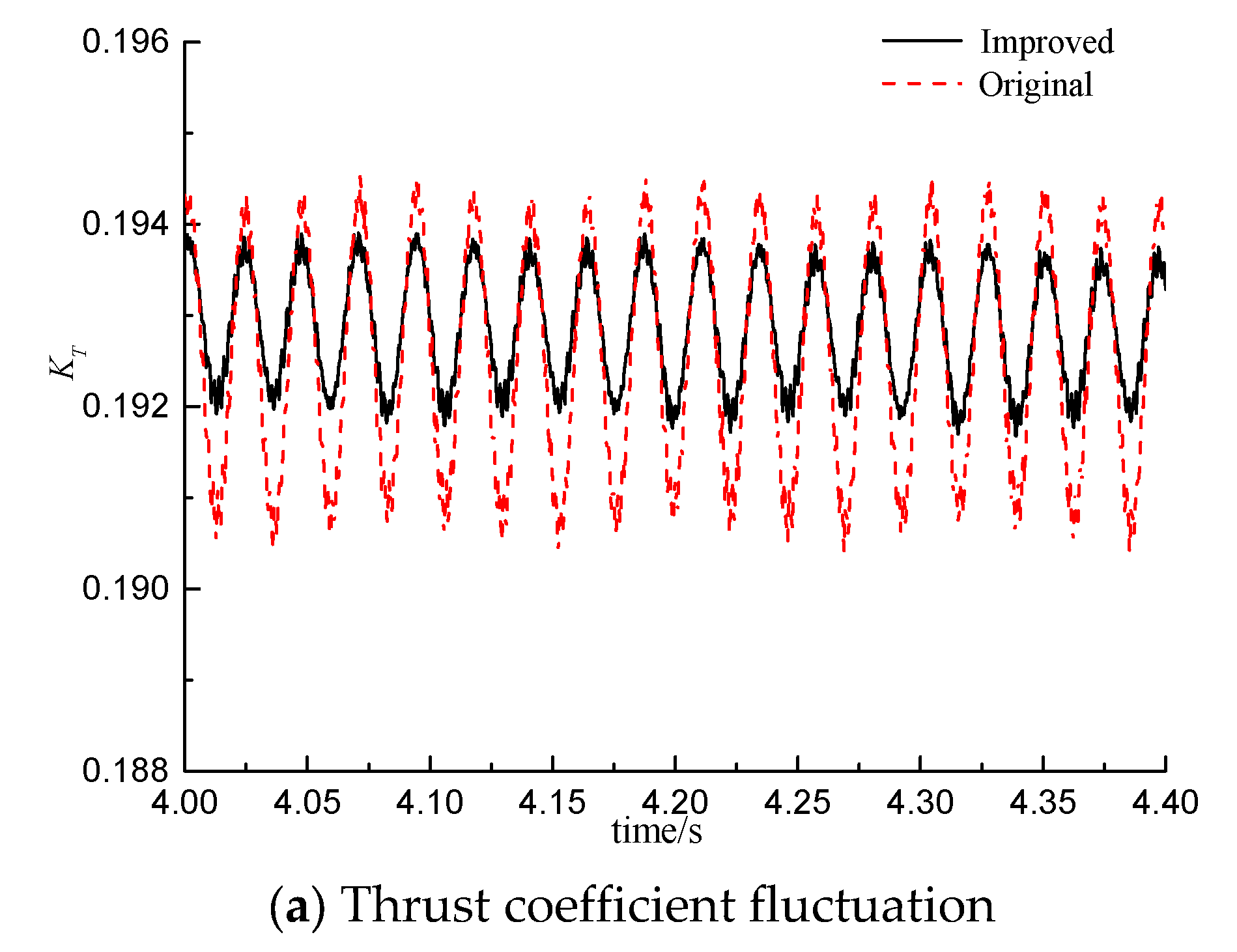
4.3. Analysis of Unsteady Bearing Force
5. Conclusions
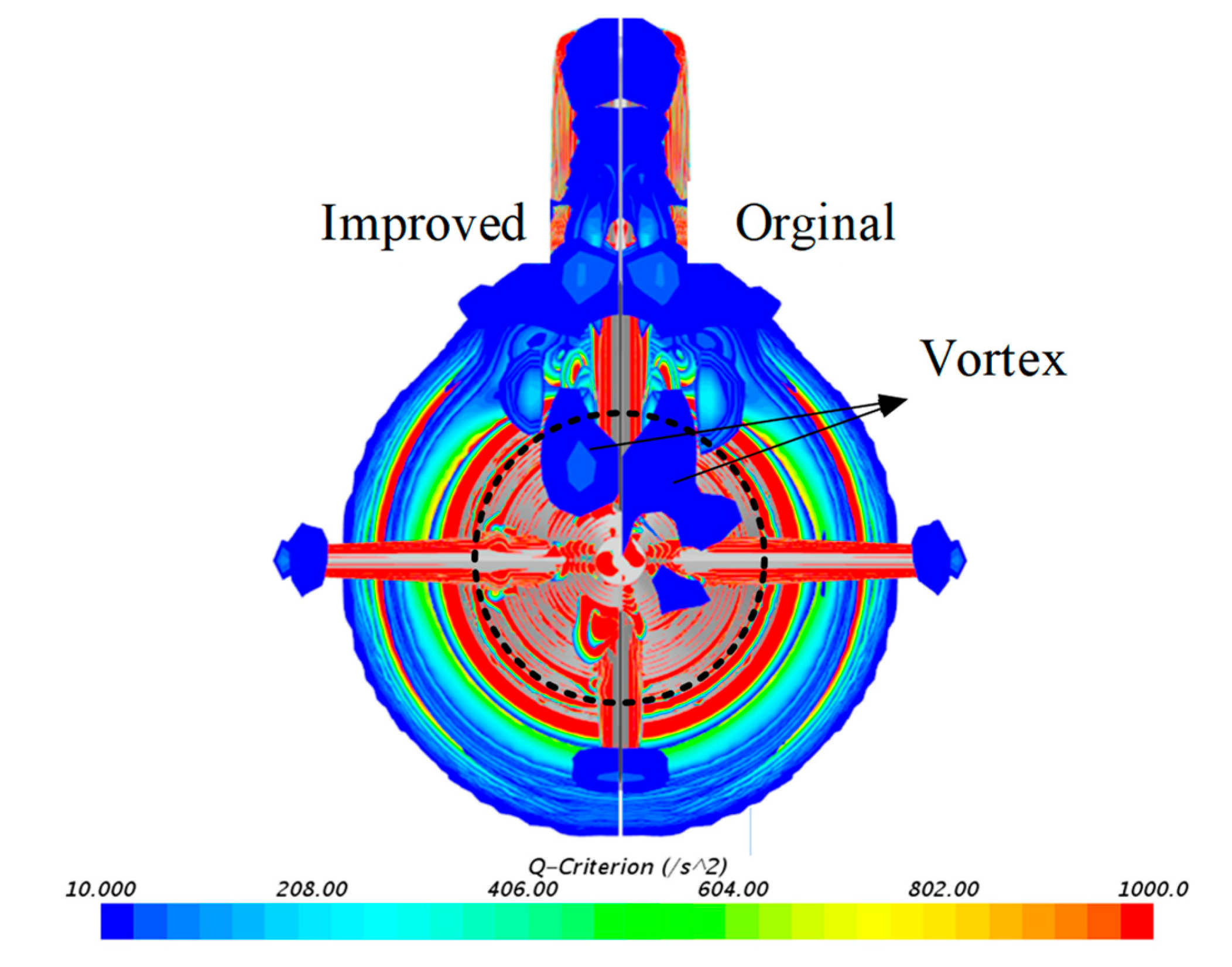
- The velocity distribution on the propeller disk shows that the fillets improve the wake field of the submarine by reducing the horseshoe vortex of the tail rudder, and they mainly affect the flow field characteristics in the inner radius area.
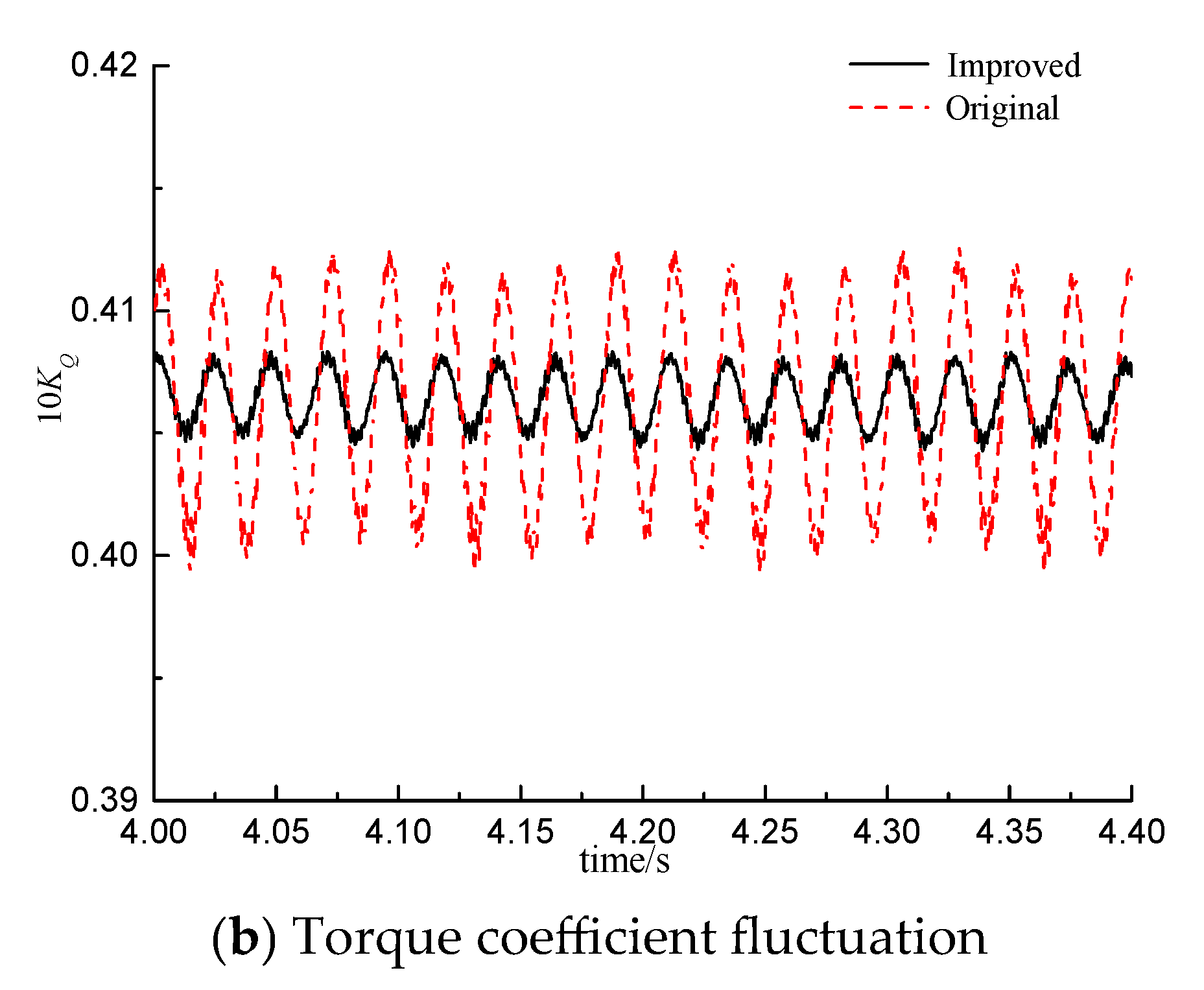
- The analysis of the harmonic components shows that the fillets can effectively reduce the axial velocity pulsation from 0.15 to 0.5, and the wake field of the improved model is more uniform.
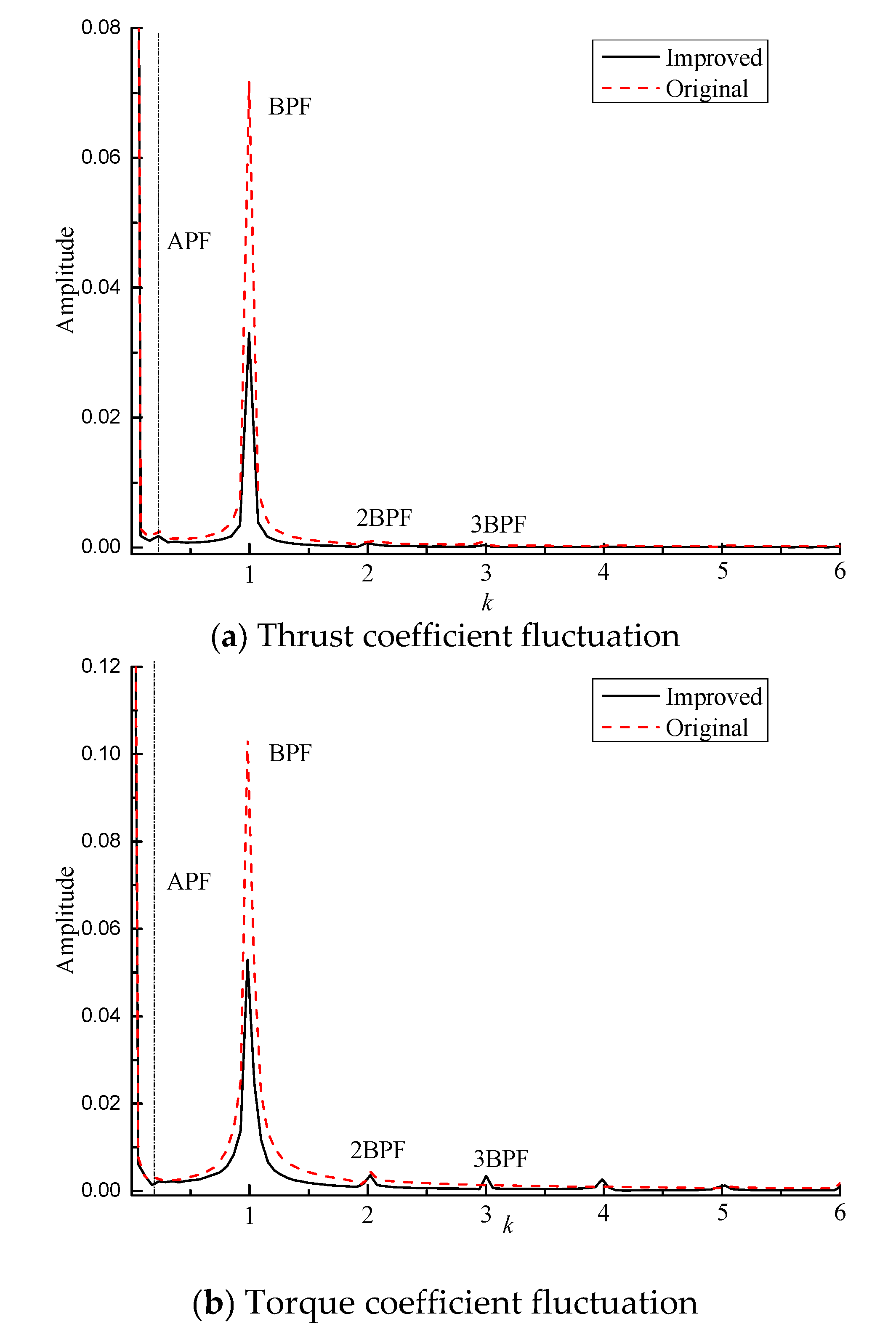
- The frequency–domain curve shows that the fillets can reduce the bearing force pulsation value from 0.07 to 0.03, indicating that the fillets are conducive to controlling the vibration and noise performance of the submarine propeller.
- The cavitation is not considered in this paper. In future research, the influence of the fillets on the unsteady excitation force of the submarine will be studied under the condition of considering cavitation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, L.; Zhu, H.C.; Qiu, X.J. Acoustic Theory and Engineering Application; Science Press: Beijing, China, 2006. [Google Scholar]
- Heng, L.; Wang, Z.Z.; Qi, W.J. Study on the influence of hull shape of submarine command platform on wake flow field. Ship Electron. Eng. 2016, 36, 151–156+187. [Google Scholar]
- Li, J.; Hou, L.; Huang, X.C. Experimental study on propeller vibration induced by spatial uneven flow field. China Ship Res. 2017, 12, 92–100. [Google Scholar]
- Zheng, X.L.; Wang, C.; Zhang, L.X.; Zhang, S. Prediction of propeller hydrodynamic and noise characteristics in non-uniform flow field. J. Wuhan Univ. Technol. 2014, 38, 122–125. [Google Scholar]
- Zhu, X.Q.; Li, Y.; Sun, H.X. Prediction of interaction noise between ship propeller blade and stern turbulent field. Acoust. Technol. 2006, 25, 361–364. [Google Scholar]
- Du, D.; Qian, Z.F.; Yang, D.; Chen, K.; Guo, F. Numerical simulation of complex flow field around Submarine Based on STAR CCM. In Proceedings of the Academic Conference Commemorating the 20th Anniversary of Ship Mechanics, Shanghai, China, 3 February 2017. [Google Scholar]
- Li, Y.; Fang, Z.Y.; Yao, Z.Q. Numerical simulation of submarine wake flow field with different stern wing types at corresponding positions. Shipbuild. Technol. 2007, 43, 19–22. [Google Scholar]
- Bai, T.C.; Lu, J.G. Effects of appendages on submarine drag and wake field. Ship Sci. Technol. 2013, 3, 51–55. [Google Scholar]
- Zhai, S.; Liu, Z.H. Numerical research on hydrodynamic performance and wake flow of conformal rudder. Shipbuild. China 2019, 60, 115–125. [Google Scholar]
- Zhai, S.; Liu, Z.H. Study on optimization effect of common airfoil rudder with local equal thickness on submarine wake flow field. Propuls. Technol. 2020, 41, 226–235. [Google Scholar]
- Lee, S.K.; Manovski, P.; Kumar, C. Wake of a cruciform appendage on a generic submarine at 10 yaw. J. Mar. Sci. Technol. 2020, 25, 787–799. [Google Scholar] [CrossRef]
- Zhang, N.; Lv, S.J.; Shen, H.C.; Xie, H. Numerical simulation on the effect of fairwater optimization to suppress the wall pressure fluctuations and flow induced noise. J. Ship Mech. 2014, 18, 448–458. [Google Scholar]
- Zhang, N.; Zhang, S.L.; Shen, H.C.; Xie, H. Large eddy simulation of vortical flow structure and wall pressure fluctuations around wing-plate junction. J. Ship Mech. 2013, 17, 729–740. [Google Scholar]
- Liu, Z.H.; Xiong, Y.; Wang, Z.Z.; Wang, S.; Tu, C.X. Design and Experimental Study on a New Wake Control Method of Submarine. Shipbuild. China 2010, 51, 47–55. [Google Scholar]
- Liu, Z.H.; Xiong, Y. Comparison on the submarine horseshoe vortex control effects by vortex control bafflers and fillets. J. Ship Mech. 2011, 15, 1102–1109. [Google Scholar]
- Liu, Z.H.; Xiong, Y.; Tu, C.X. Method to Control Unsteady Force of Submarine Propeller Based on the Control of Horseshoe Vortex. J. Ship Res. 2012, 56, 12–22. [Google Scholar]
- Liu, Z.H.; Xiong, Y.; Tu, C.X. Numerical Simulation and Control of Horseshoe Vortex Around an Appendage-Body Junction. J. Fluids Struct. 2011, 27, 23–42. [Google Scholar]
- Ding, Z.Y.; Gong, S.Q.; Wang, Z.L.; Wang, X.Z.; Feng, D.K. Comparison of hydrodynamic performance of submarine hull rudder and bow rudder. Ship Sci. Technol. 2017, 39, 22–28. [Google Scholar]
- Wu, F.L.; Wu, X.G.; Ma, Y.Y.; Li, Z. Numerical study on the influence of submarine command platform enclosure on resistance and wake field. Ocean Eng. 2009, 27, 95–103. [Google Scholar]
- Liu, Z.Y.; Lin, X.P.; Zhou, Z.H. Study on the influence of submarine command station position on hydrodynamic force. J. Nav. Eng. Univ. 2006, 6, 34–37. [Google Scholar]
- Huang, Z.Y. Technical Summary Report on Optimal Shape of Submarine Command Console Enclosure; Science and Technology Report of China; Shipbuilding Research Center: Wuxi, China, 2003. [Google Scholar]
- Gorski, J.; Coleman, R.M. Use of RANS Calculations in the Design of a Submarine Sail. In Proceedings of the RTO AVT Symposium, Paris, France, 22–26 April 2002. [Google Scholar]
- Rais-Rohani, M.; Lokits, J. Reinforcement layout and sizing optimization of composite submarine sail structures. Struct. Multidiscip. Optim. 2007, 34, 75–90. [Google Scholar] [CrossRef]
- Toxopeus, S.; Kuin, R.; Kerkvliet, M.; Hoeijmakers, H.; Nienhuis, B. Improvement of Resistance and Wake Field of an Underwater Vehicle by Optimizing the Fin-Body Junction Flow with CFD. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8 June 2014. [Google Scholar]
- Wang, Z.B.; Yao, H.Z.; Zhang, N. Computational study on the influence of command console enclosure on submarine wake. Ship Mech. 2009, 13, 196–202. [Google Scholar]
- Liu, L.J.; Xu, Y. Numerical simulation of the effect of sand dune enclosure on submarine flow field. J. Ordnance Equip. Eng. 2014, 11, 1–4. [Google Scholar]
- Liu, Z.H.; Xiong, Y.; Ye, Q. Model experiment and numerical simulation of the hydrodynamic performance of a conformal rudder. J. Harbin Eng. Univ. 2018, 39, 658–663. [Google Scholar]
- Zhang, Y.; Wu, D. Research on Formation Mechanism and Suppression Method of Surface Force Caused by Pump Jet Propeller. In Proceedings of the Fluids Engineering Division Summer Meeting, Wuxi, China, 1 October 2021. [Google Scholar]
- Su, Z.; Shi, S.; Huang, X.; Rao, Z.; Hua, H. Effects of the duct on the vibro-acoustic characteristics of the pump-jet–shaft–submarine system under pump-jet excitation. Ocean Eng. 2022, 254, 111327. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, J.; Huang, B.; Zhang, D.; Wu, D. Suppression method for exciting force of pump jet propellers based on sinusoidal unevenly spaced rotor blades. Ocean Eng. 2022, 262, 112198. [Google Scholar] [CrossRef]
- Wu, X.; Wang, D.; Wei, Y.; Jin, S.B.; Zhu, H.; Hu, P.F.; Sun, F.X. Prediction and parameter analysis of pump jet broadband unsteady excitation force. J. Natl. Univ. Def. Technol. 2023, 45, 7. [Google Scholar]
- Spalart, P.R.; Allmaras, S.R. A one equation turbulence model for aerodynamic flows. In Proceedings of the A/AA92-0439, A1AA 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 14–17 January 1992. [Google Scholar]
- Spalart, P.R. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach. In Proceedings of the First AFOSR International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997. [Google Scholar]
- Patil, V.S.; Bano, F.; Kurahatti, R.V.; Patil, A.Y.; Raju, G.U.; Afzal, A.; Saleel, C.A. A study of sound pressure level (SPL) inside the truck cabin for new acoustic materials: An experimental and FEA approach. Alex. Eng. J. 2021, 60, 5949–5976. [Google Scholar] [CrossRef]
- Dhaduti, S.C.; Sarganachari, S.G.; Patil, A.Y.; Yunus Khan, T.M. Prediction of injection molding parameters for symmetric spur gear. J. Mol. Model. 2020, 26, 1–12. [Google Scholar] [CrossRef]
- Nikitin, N.V.; Nicoud, F.; Wasistho, B.; Squires, K.D.; Spalart, P.R. An approach to wall modeling in large-eddy simulations. Phys. Fluids 2000, 12, 1629–1632. [Google Scholar] [CrossRef]
- Li, M.J.; Wang, M.X.; Wang, L.; Liu, Z.H. Experiment and numerical simulation of denoising fillets of stern appendages on underwater vehicle. J. Ship Mech. 2016, 20, 1345–1354. [Google Scholar]
- He, Y.; Wang, G. Propeller Exciting Force; Shanghai Jiao Tong University Press: Shanghai, China, 1984. [Google Scholar]
- Wang, C.; Sun, S.; Li, L.; Ye, L. Numerical prediction analysis of propeller bearing force for full-scale hull-propeller-rudder system. Int. J. Nav. Archit. Ocean Eng. 2016, 8, 589–601. [Google Scholar] [CrossRef]
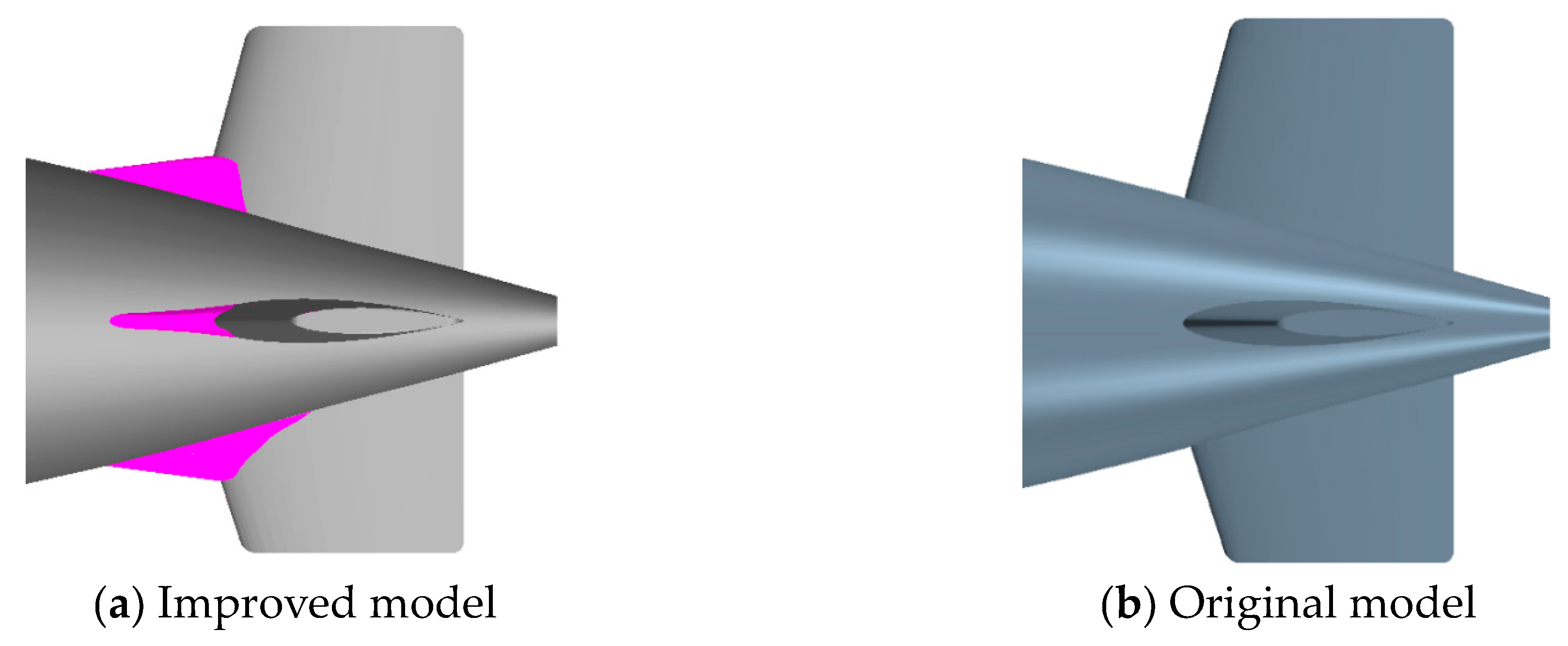
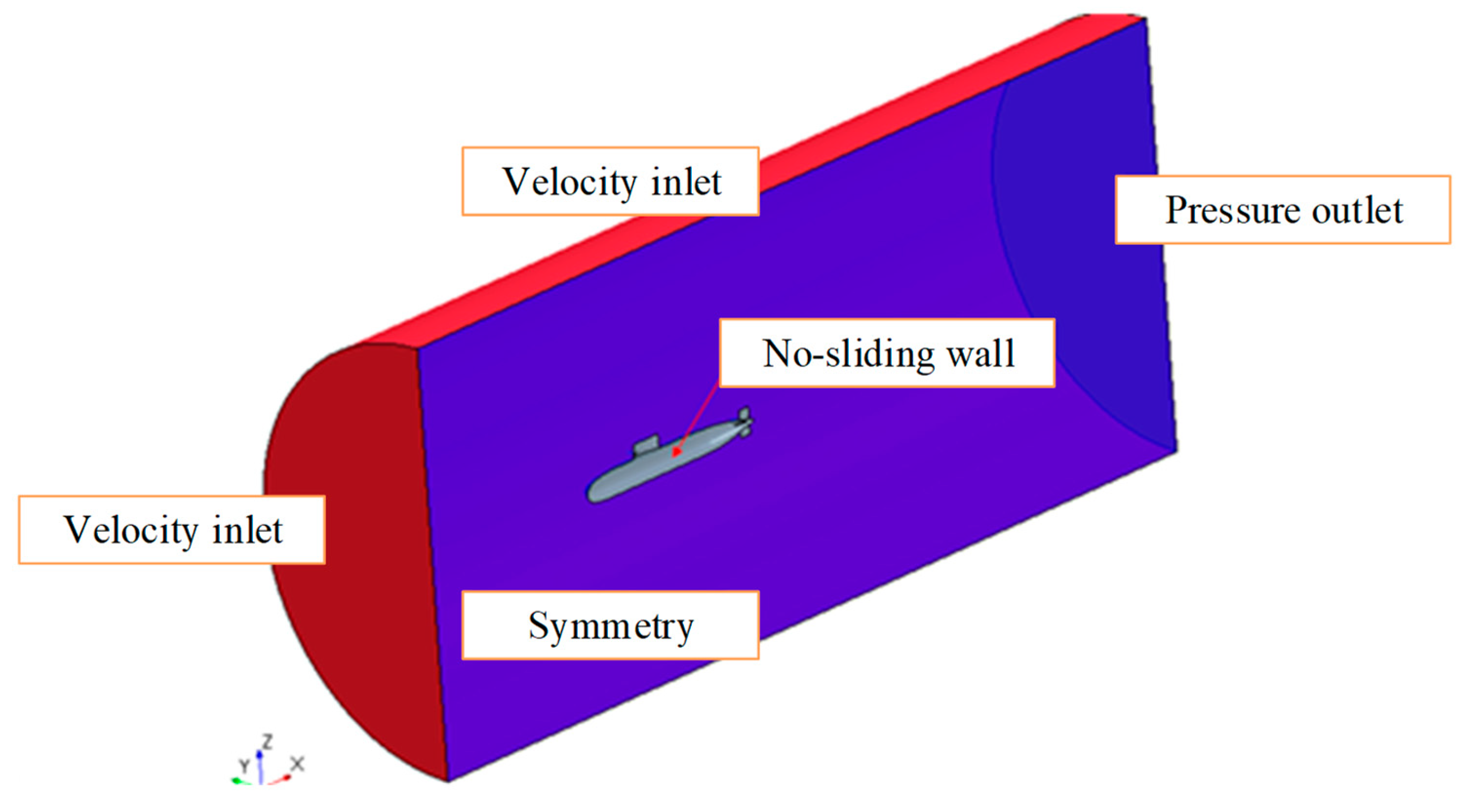

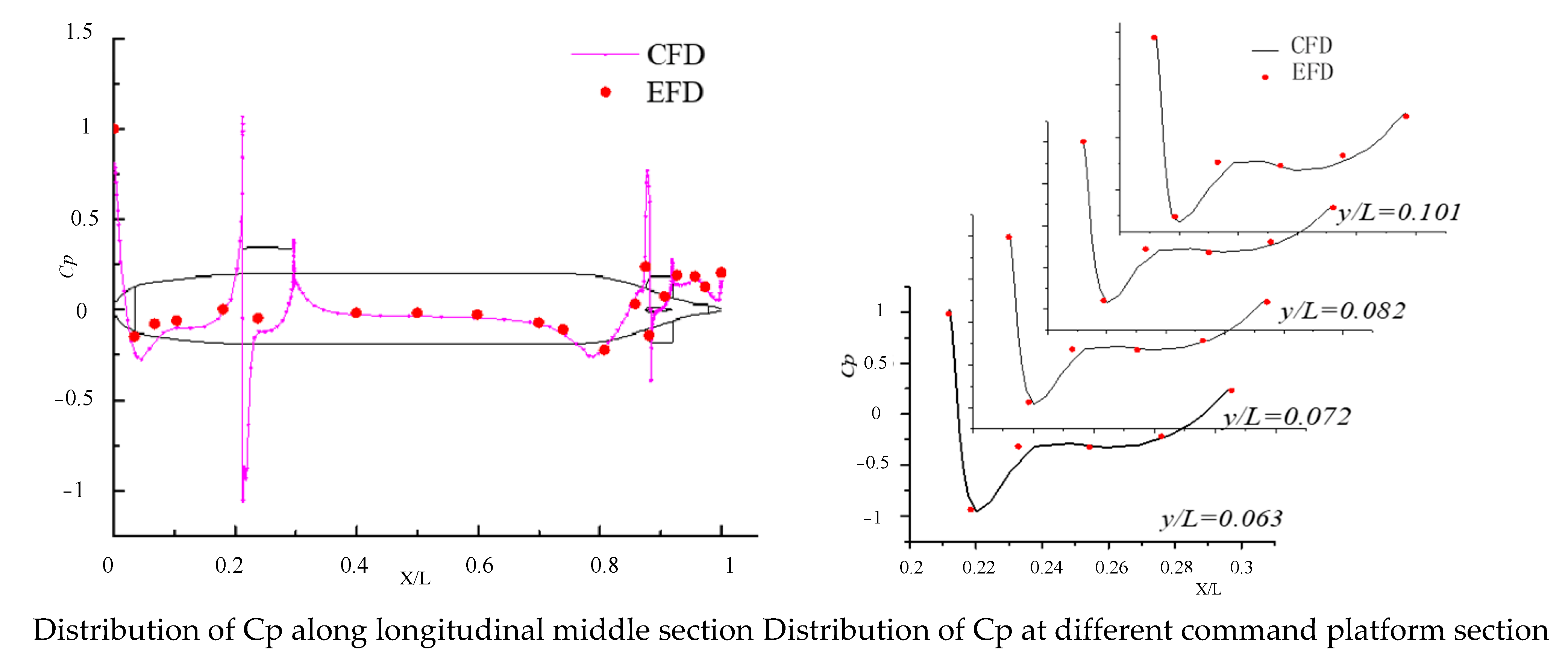
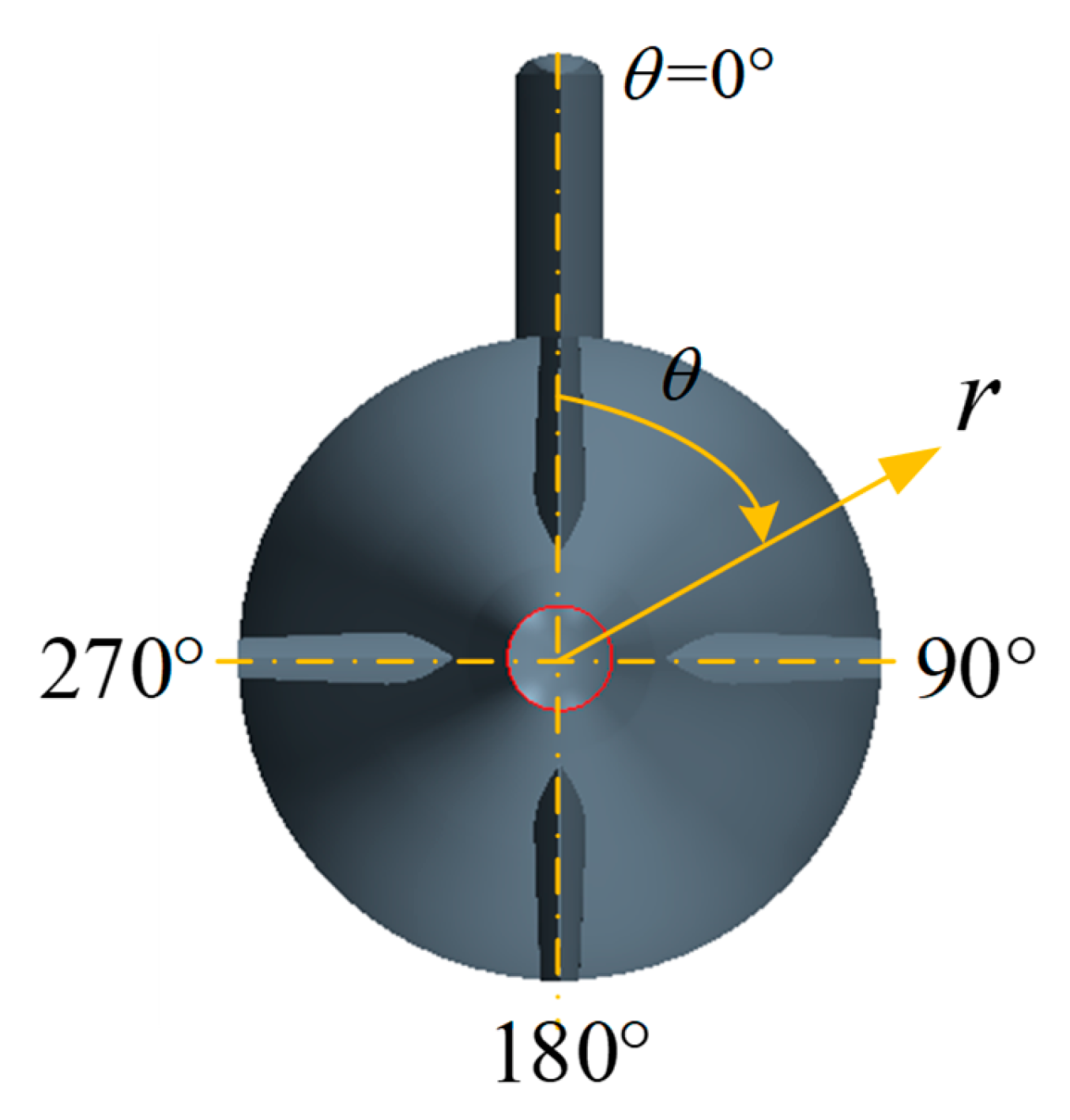
 | |
| Submarine length with full appendages L | 4.356 m |
| Maximum hull diameter Dmax | 0.508 m |
| Sail length | 0.368 m |
| Tail section of airfoil | NACA0020 |
| Scale ratio | 1:24 |
 | geometric parameters | DTMB4383 |
| Diameter (D/m) | 0.305 | |
| Number of blades, Z | 5 | |
| Hub diameter ratio, dh/D | 0.2 | |
| Area ratio, AE/A0 | 0.725 |
| Original Model | Improved Model | ||
|---|---|---|---|
| Resistance Calculation | Self-Propulsion Calculation | Resistance Calculation | Self-Propulsion Calculation |
| Without propeller | With propeller | Without propeller | With propeller |
| Mesh | Grid Number | CFD | EFD | Error |
|---|---|---|---|---|
| Fine | 5.12 M | 106.5 | 102.3 | 4.11% |
| Medium | 3.85 M | 107.3 | 102.3 | 4.89% |
| Corse | 2.25 M | 112.6 | 102.3 | 10.1% |
| Force | — | BPF | 2BPF | 3BPF | Time-Average |
|---|---|---|---|---|---|
| KTx × 104 | Improved | 312 | 8.19 | 6.36 | 1932 |
| Original | 722 | 7.41 | 5.61 | 1926 | |
| KTy × 104 | Improved | 78 | 6.21 | 16.80 | 963 |
| Original | 96 | 5.15 | 0.00 | 825 | |
| KTz × 104 | Improved | 67 | 6.24 | 5.33 | 716 |
| Original | 86 | 5.13 | 1.54 | 521 |
| Moment | — | BPF | 2BPF | 3BPF | Time-Average |
|---|---|---|---|---|---|
| 10KQx × 104 | Improved | 512 | 13.44 | 10.05 | 4086 |
| Original | 1018 | 12.36 | 11.33 | 4063 | |
| 10KQy × 104 | Improved | 632 | 24.15 | 13.31 | 762 |
| Original | 628 | 23.22 | 15.27 | 636 | |
| 10KQz × 104 | Improved | 1148 | 15.21 | 11.69 | 714 |
| Original | 1434 | 19.83 | 17.65 | 447 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Cai, W.; Ren, N.; Sun, S. The Effect of the Fillets on Submarine Wake Field and Propeller Unsteady Bearing Force. J. Mar. Sci. Eng. 2023, 11, 727. https://doi.org/10.3390/jmse11040727
Li X, Cai W, Ren N, Sun S. The Effect of the Fillets on Submarine Wake Field and Propeller Unsteady Bearing Force. Journal of Marine Science and Engineering. 2023; 11(4):727. https://doi.org/10.3390/jmse11040727
Chicago/Turabian StyleLi, Xiang, Wenyu Cai, Nianxin Ren, and Shuai Sun. 2023. "The Effect of the Fillets on Submarine Wake Field and Propeller Unsteady Bearing Force" Journal of Marine Science and Engineering 11, no. 4: 727. https://doi.org/10.3390/jmse11040727
APA StyleLi, X., Cai, W., Ren, N., & Sun, S. (2023). The Effect of the Fillets on Submarine Wake Field and Propeller Unsteady Bearing Force. Journal of Marine Science and Engineering, 11(4), 727. https://doi.org/10.3390/jmse11040727





