Experiment and Simulation of the Shape and Stored Gas Characteristics of the Flexible Spherical Airbag for Underwater Compressed Air Energy Storage
Abstract
:1. Introduction
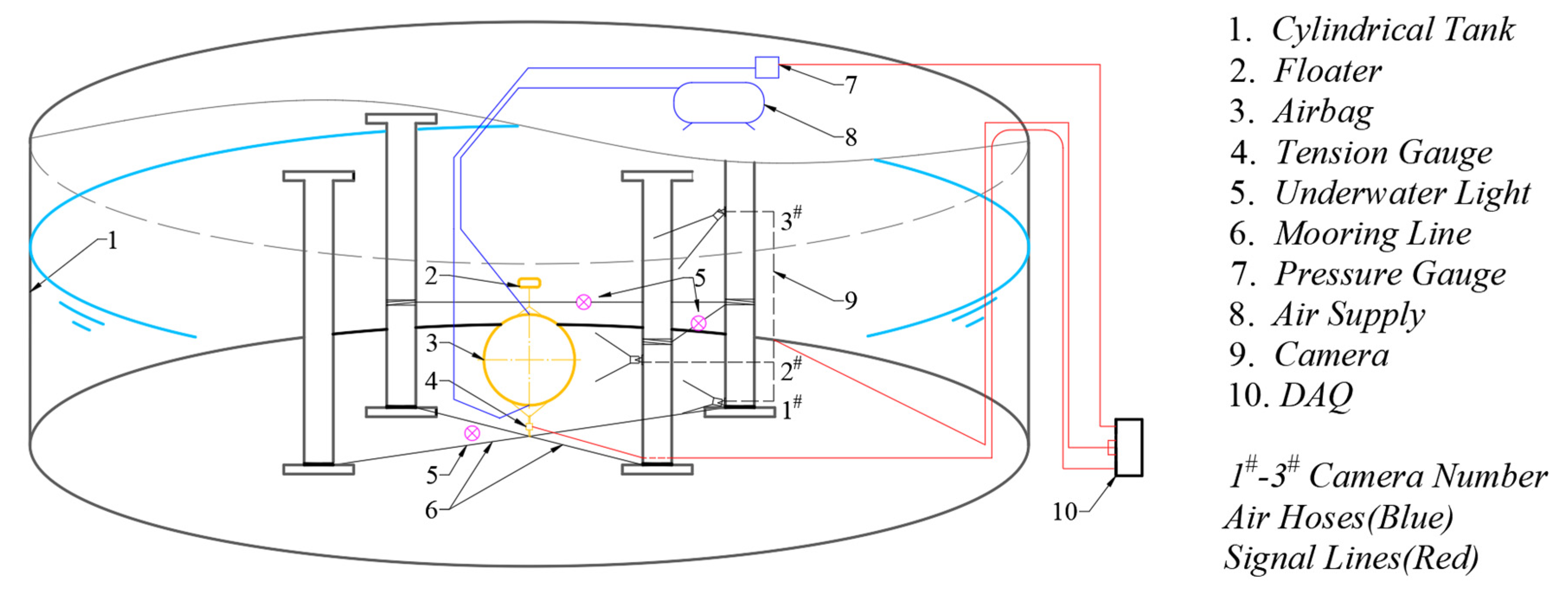
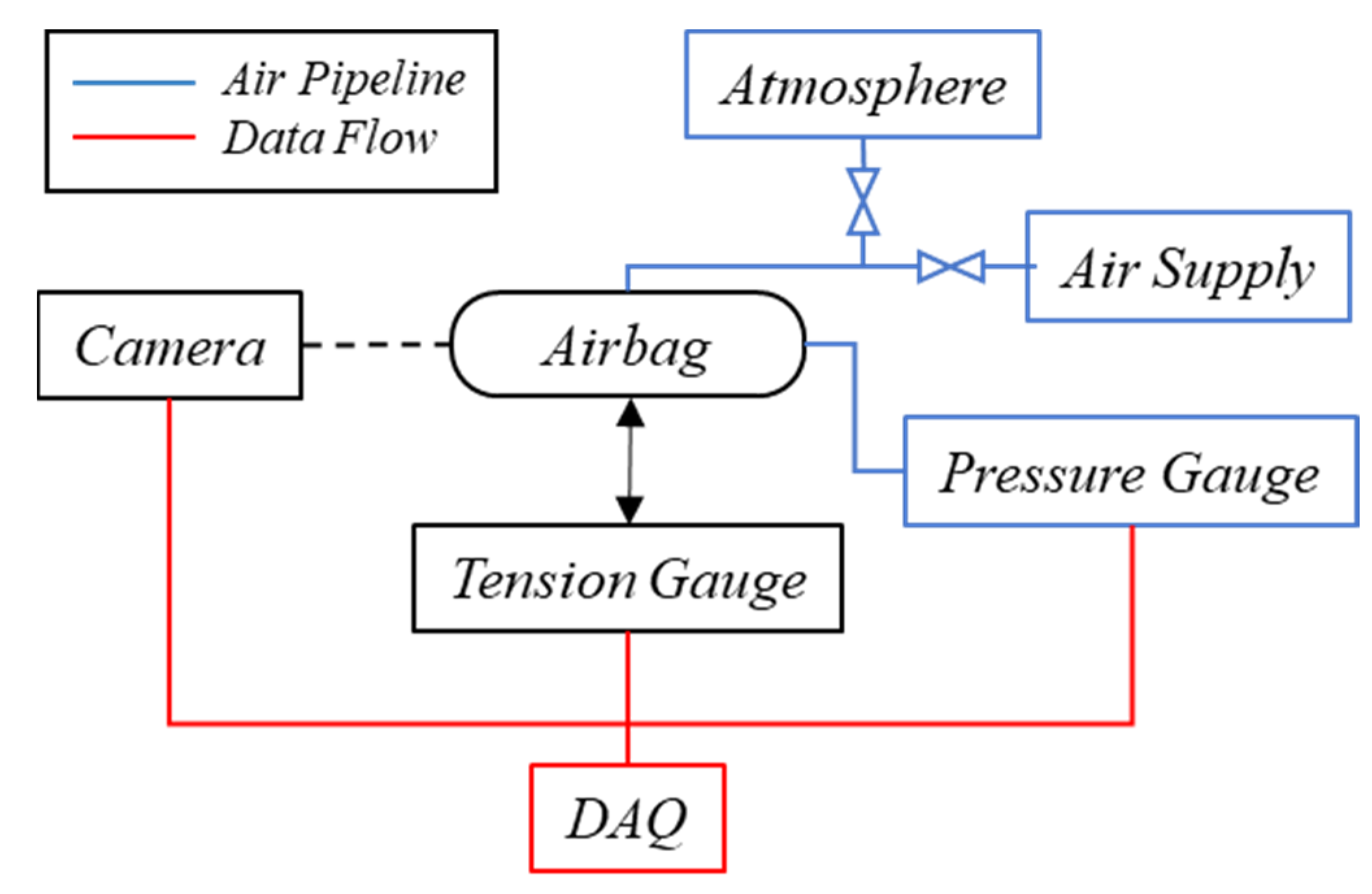
2. Experiment Design
2.1. Model Design
2.2. Test Scheme
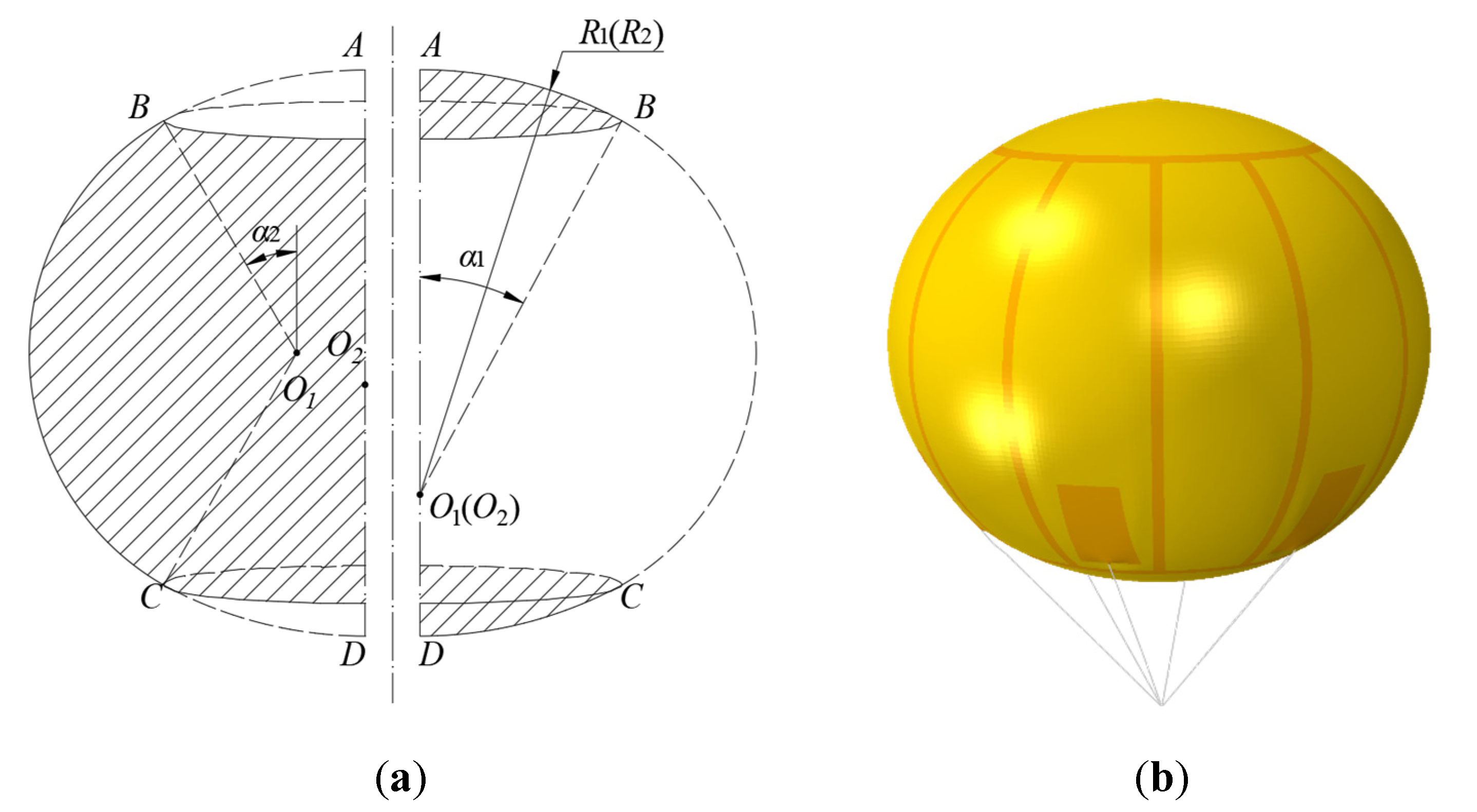
3. Numerical Model
3.1. FE Model
3.2. Verification and Validation
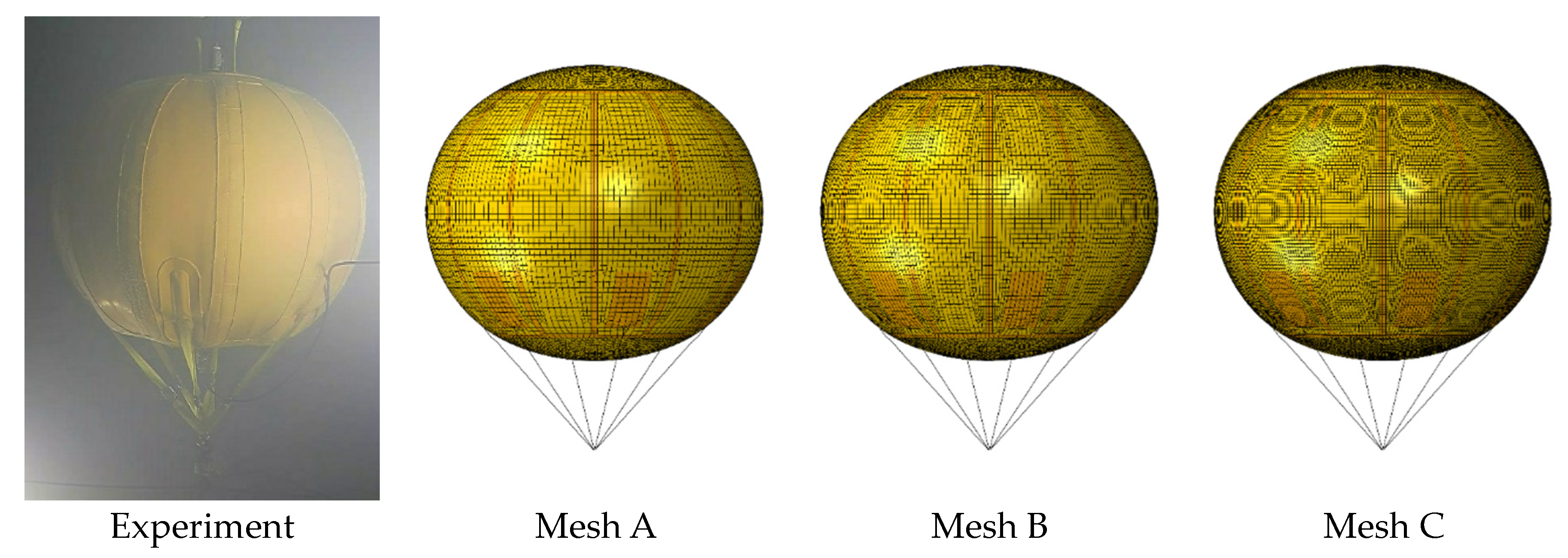
3.2.1. Mesh
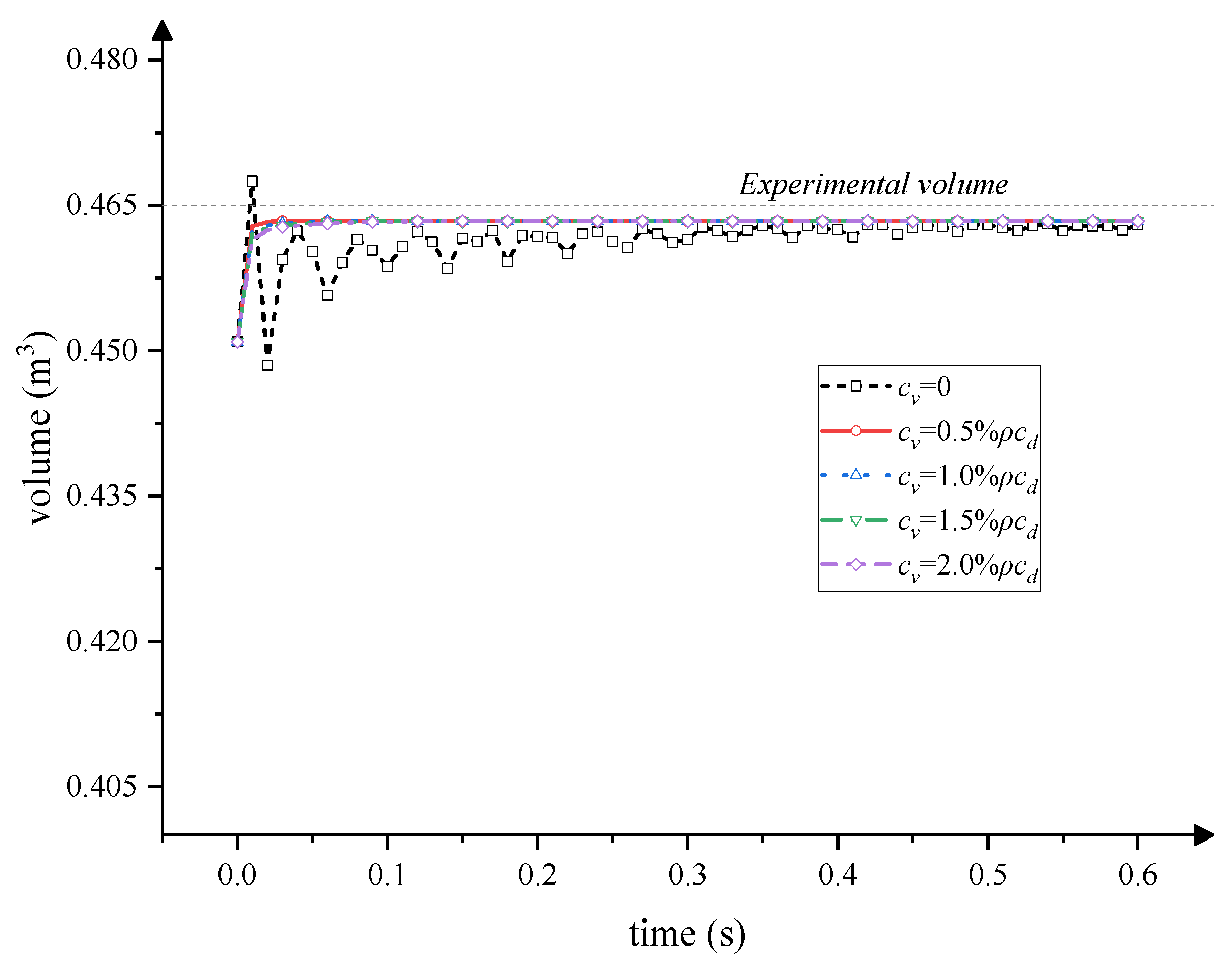
3.2.2. Viscous Pressure
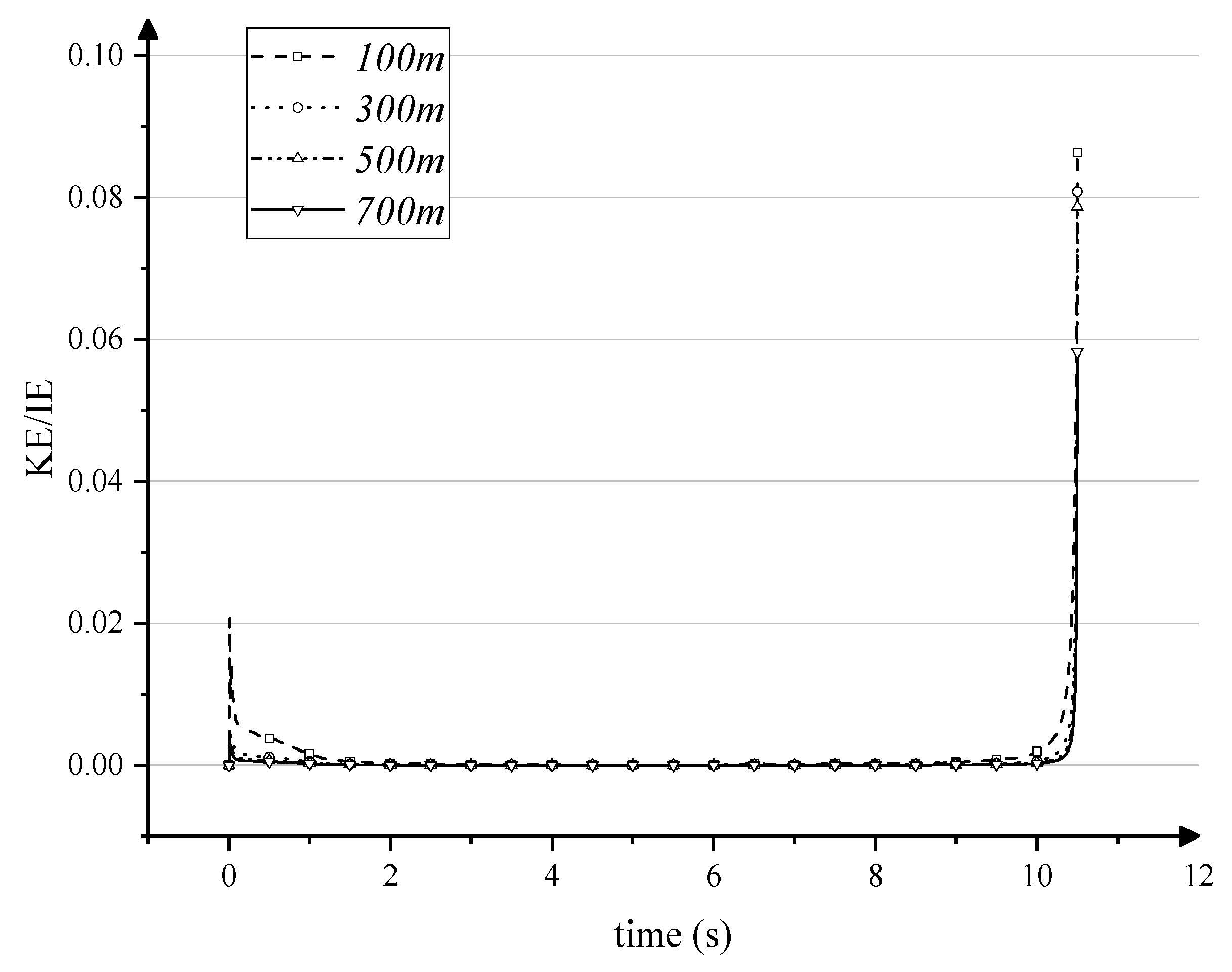
3.2.3. Mass Scaling Factor
4. Results
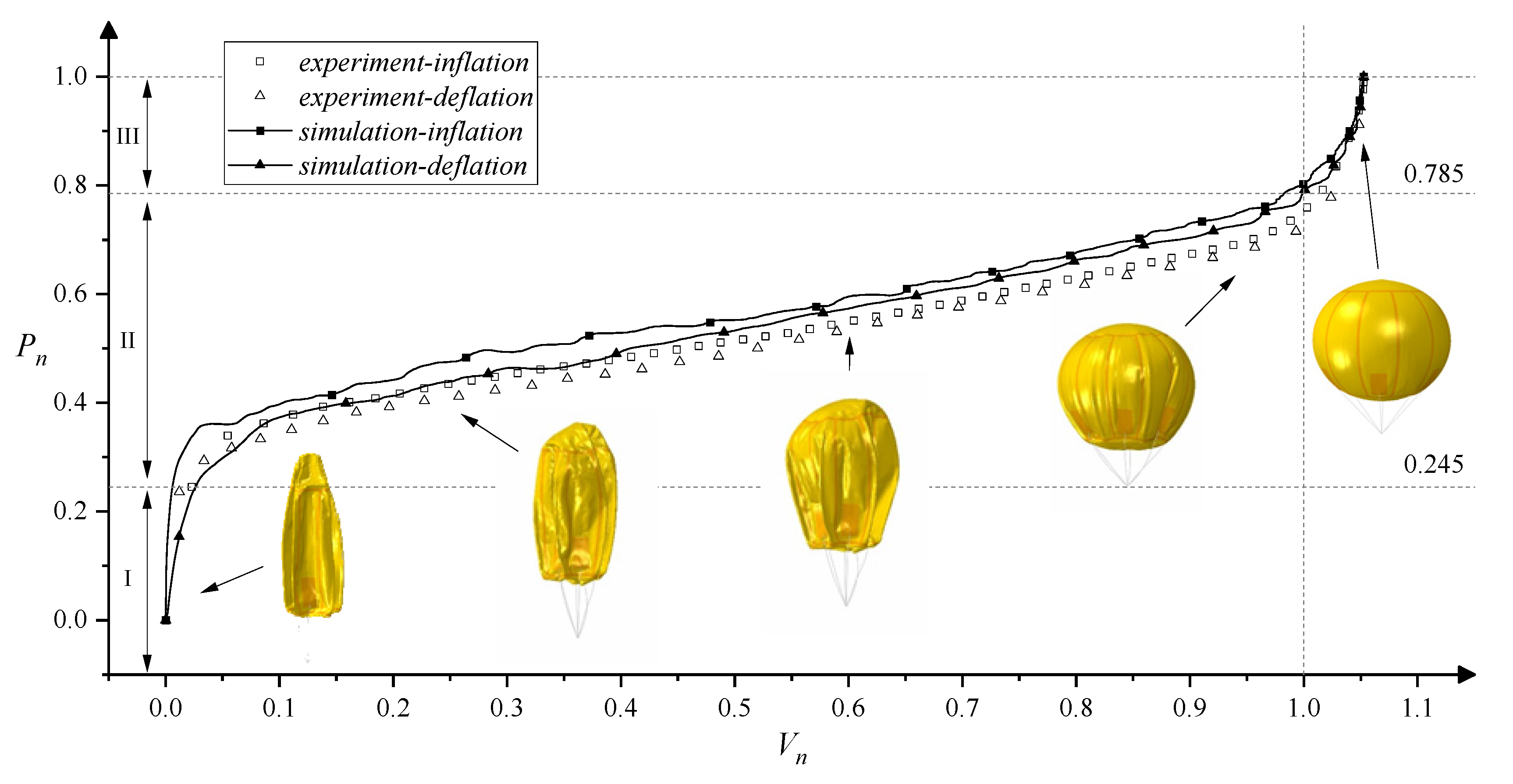
4.1. 1 m Model
4.1.1. Pressure
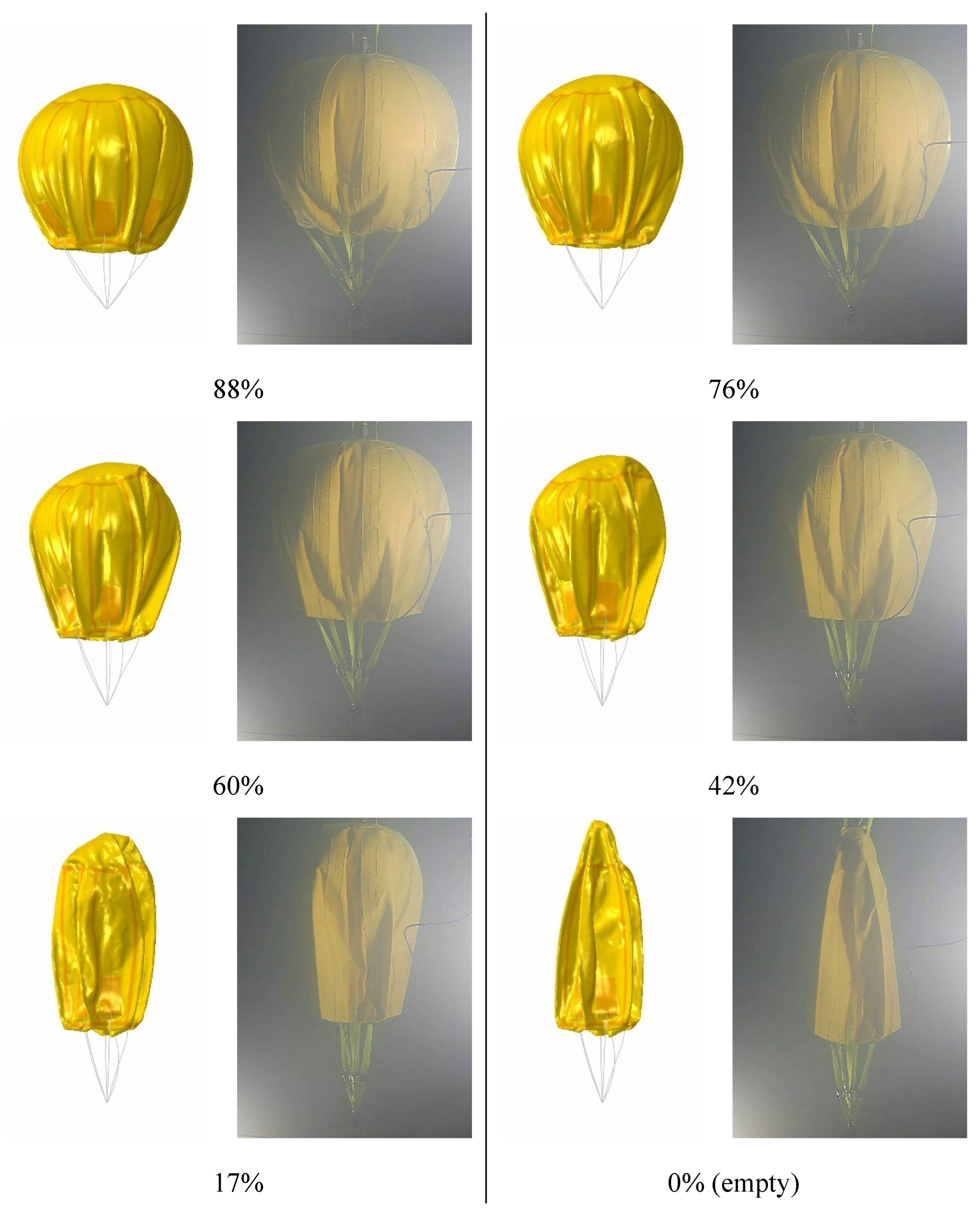
4.1.2. Deformation
4.2. 4 m Model
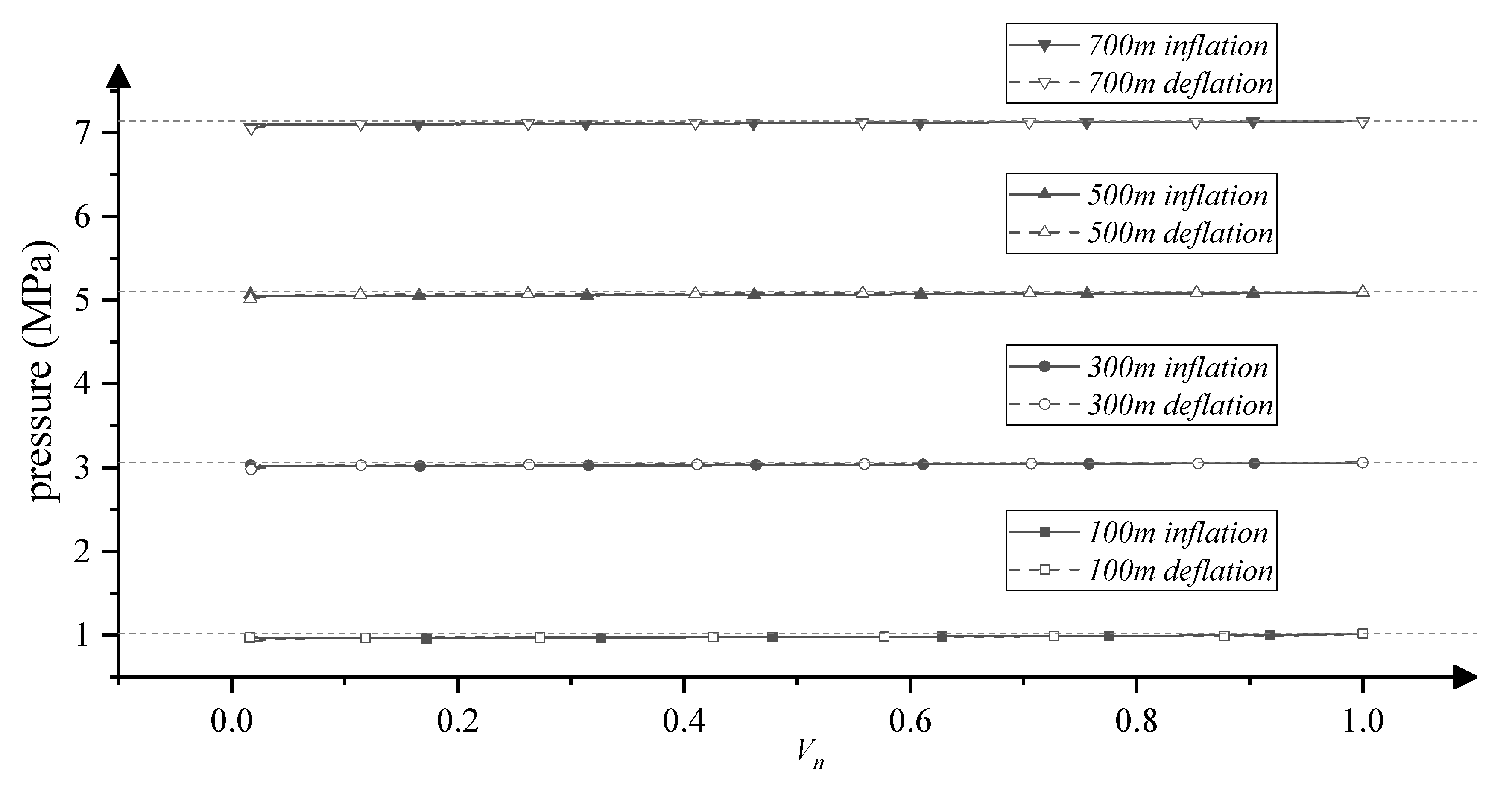
4.2.1. Pressure
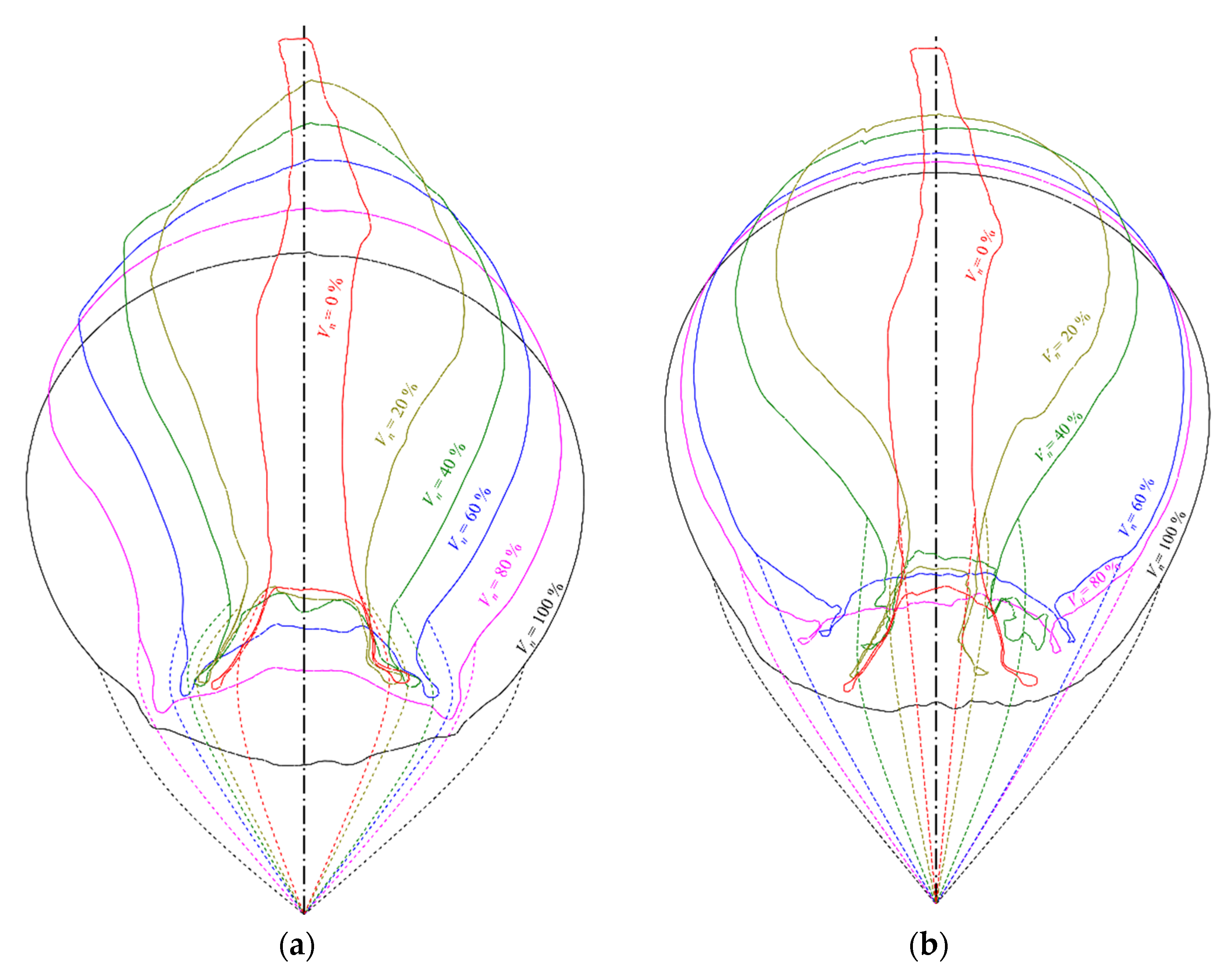
4.2.2. Deformation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Q.; Guo, X.; Qing, Q.; Gong, J. Dynamic deflation assessment of an air inflated membrane structure. Thin-Walled Struct. 2015, 94, 446–456. [Google Scholar] [CrossRef]
- Roekens, J.; De Laet, L.; Mollaert, M.; Luchsinger, R. Experimental and numerical investigation of a tensairity arch. Thin-Walled Struct. 2016, 105, 112–120. [Google Scholar] [CrossRef]
- Sosa, E.M.; Thompson, G.J.; Barbero, E.J. Experimental investigation of initial deployment of inflatable structures for sealing of rail tunnels. Tunn. Undergr. Space Technol. 2017, 69, 37–51. [Google Scholar] [CrossRef]
- Pecora, I.; Sosa, E.M.; Thompson, G.J.; Barbero, E.J. FE simulation of ceiling deployment of a large-scale inflatable structure for tunnel sealing. Thin-Walled Struct. 2019, 140, 272–293. [Google Scholar] [CrossRef]
- Pimm, A.; Garvey, S.D. Underwater Compressed Air Energy Storage. In Storing Energy; Elsevier: Amsterdam, The Netherlands, 2016; pp. 135–154. [Google Scholar] [CrossRef]
- Seymour, R.J. Ocean energy on-demand using underocean compressed air storage. In Proceedings of the ASME 2007 26th International Conference on Offshore Mechanics and Arctic Engineering, San Diego, CA, USA, 10–15 June 2007; American Society of Mechanical Engineers Digital Collection: Philadelphia, PA, USA. [Google Scholar] [CrossRef]
- Swinfen-Styles, L.; Garvey, S.D.; Giddings, D. Combining Wind-Driven Air Compression with Underwater Compressed Air Energy Storage. In Proceedings of the 2019 Offshore Energy and Storage Summit (OSES), Brest, France, 13–12 July 2019. [Google Scholar] [CrossRef]
- Debille, A.; Simon, C.; Loisel, R.; Guyomarc’H, D.; Neu, T.; Lemiale, L. Underwater CAES assessment: Economic and engineering references for energy mix sizing in islands grids. In Proceedings of the 2019 Offshore Energy and Storage Summit (OSES), Brest, France, 13–12 July 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Tiano, F.A.; Rizzo, G. Use of an Under-Water Compressed Air Energy Storage (UWCAES) to Fully Power the Sicily Region (Italy) With Renewable Energy: A Case Study. Front. Mech. Eng. 2021, 7, 641995. [Google Scholar] [CrossRef]
- Xiao, J.; Gabr, M.; Rahman, M. Preliminary Structural Design of OCAES Vessel. In ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering; American Society of Mechanical Engineers Digital Collection: Philadelphia, PA, USA, 2014. [Google Scholar] [CrossRef]
- Lim, S.D.; Mazzoleni, A.P.; Park, J.-K.; Ro, P.I.; Quinlan, B. Conceptual design of ocean compressed air energy storage system. Mar. Technol. Soc. J. 2013, 47, 70–81. [Google Scholar] [CrossRef]
- Lim, S.D. Ocean Compressed Air Energy Storage Integrated with Offshore Renewable Energy Sources. 2013. Available online: https://repository.lib.ncsu.edu/bitstream/handle/1840.16/8878/etd.pdf?sequence=2 (accessed on 1 December 2022).
- Xu, W.; Garvey, S.D.; Ren, T.; Hu, Y. Dynamics of dissolution for underwater compressed air energy storage. In Proceedings of the 2019 Offshore Energy and Storage Summit (OSES), Brest, France, 13–12 July 2019. [Google Scholar] [CrossRef]
- Zhou, G.; Li, C.; Zhang, D.; Liu, D.; Zhou, X.; Zhan, J. Overview of Underwater Transmission Characteristics of Oceanic LiDAR. In IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing; IEEE: Piscataway, NJ, USA, 2021; Volume 14, pp. 8144–8159. [Google Scholar] [CrossRef]
- Li, R.; Zhang, H.; Chen, Z.; Yu, N.; Kong, W.; Li, T.; Wang, E.; Wu, X.; Liu, Y. Denoising method of ground-penetrating radar signal based on independent component analysis with multifractal spectrum. Measurement 2022, 192, 110886. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, F.; Yin, S.; Wallace, C.D.; Soltanian, M.R.; Dai, Z.; Ritzi, R.W.; Ma, Z.; Zhan, C.; Lü, X. Application of upscaling methods for fluid flow and mass transport in multi-scale heterogeneous media: A critical review. Appl. Energy 2021, 303, 117603. [Google Scholar] [CrossRef]
- Wang, Z.; Ting, D.S.K.; Carriveau, R.; Xiong, W.; Wang, Z. Design and thermodynamic analysis of a multi-level underwater compressed air energy storage system. J. Energy Storage 2016, 5, 203–211. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, X.; Yang, S.; Hooman, K.; Yang, X. Assessment evaluation of a trigeneration system incorporated with an underwater compressed air energy storage. Appl. Energy 2021, 303, 117648. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Carriveau, R.; Ting, D.S.-K.; McGillis, A. Conventional and advanced exergy analysis of a grid connected underwater compressed air energy storage facility. Appl. Energy 2019, 242, 1198–1208. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Carriveau, R.; Ting, D.S.K.; McGillis, A.; Young, D. Transient Thermodynamic Assessment of the World’s First Grid Connected UWCAES Facility by Exergy Analysis. In Proceedings of the 2019 Offshore Energy and Storage Summit (OSES), Brest, France, 10–12 July 2019. [Google Scholar]
- Pimm, A.; Garvey, S. Analysis of flexible fabric structures for large-scale subsea compressed air energy storage. J. Physics Conf. Ser. 2009, 181. [Google Scholar] [CrossRef]
- Pimm, A.; Garvey, S.D.; Drew, R.J. Shape and cost analysis of pressurized fabric structures for subsea compressed air energy storage. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 1027–1043. [Google Scholar] [CrossRef]
- Pimm, A.J. Analysis of Flexible Fabric Structures; The University of Nottingham: Nottingham, UK, 2011. [Google Scholar]
- Jong, M.D. Commercial grid scaling of Energy Bags for underwater compressed air energy storage. Int. J. Environ. Stud. 2014, 71, 804–811. [Google Scholar] [CrossRef]
- Mas, J.; Rezola, J.M. Tubular design for underwater compressed air energy storage. J. Energy Storage 2016, 8, 27–34. [Google Scholar] [CrossRef]
- Wang, Z.; Ting, D.S.-K.; Carriveau, R.; Xiong, W.; Wang, Z. Numerical and experimental investigation of flow around a balloon-shaped bluff body. Sustain. Energy Technol. Assess. 2019, 35, 80–88. [Google Scholar] [CrossRef]
- Vasel-Be-Hagh, A.; Carriveau, R.; Ting, D.-K. Numerical simulation of flow past an underwater energy storage balloon. Comput. Fluids 2013, 88, 272–286. [Google Scholar] [CrossRef]
- Vasel-Be-Hagh, A. Hydrodynamics of Accumulators of Compressed Air for an UWCAES Plant; University of Windsor: Windsor, ON, Canada, 2015. [Google Scholar]
- Vasel-Be-Hagh, A.; Carriveau, R.; Ting, D.S.-K. Flow past an accumulator unit of an underwater energy storage system: Three touching balloons in a floral configuration. J. Mar. Sci. Appl. 2014, 13, 467–476. [Google Scholar] [CrossRef]
- Vasel-Be-Hagh, A.; Carriveau, R.; Ting, D.-K. Flow over submerged energy storage balloons in closely and widely spaced floral configurations. Ocean Eng. 2015, 95, 59–77. [Google Scholar] [CrossRef]
- Pimm, A.J.; Garvey, S.D.; de Jong, M. Design and testing of Energy Bags for underwater compressed air energy storage. Energy 2014, 66, 496–508. [Google Scholar] [CrossRef]
- Cheung, B.; Cao, N.; Carriveau, R.; Ting, D. Distensible air accumulators as a means of adiabatic underwater compressed air energy storage. Int. J. Environ. Stud. 2012, 69, 566–577. [Google Scholar] [CrossRef]
- Dassault Systèmes Simulia Corp. Abaqus User’s Manual, Documentation Collection Version 6.14-2; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2021. [Google Scholar]
- Mao, L.; Liu, Q.; Nie, K.; Wang, G. Temperature prediction model of gas wells for deep-water production in South China Sea. J. Nat. Gas Sci. Eng. 2016, 36, 708–718. [Google Scholar] [CrossRef]





| Parameter | 1/4 Model | Prototype | Unit |
|---|---|---|---|
| Diameter | 1 | 4 | m |
| Height (including harness) | 1.57 | 6.5 | m |
| Volume | 0.465 | 30 | m3 |
| Dry Weight | 9.37 | 210 | kg |
| Rated Pressure (relative pressure) | 20 | 7000 | kPa |
| Water Depth (bottom) | 1.60 | 700 | m |
| Material | PVC-coated polyester | ||
| Material Thickness | 1.3 | mm | |
| Material Density | 1.35 | g/cm3 | |
| Material Young’s Modulus | 120 | MPa | |
| Material Poisson’s Ratio | 0.3 | ||
| Averaged Element Size | Mesh Number | Stress at the Top Point | Stress Error | |
|---|---|---|---|---|
| Mesh A | 0.018 | 11,833 | 2.99 × 106 | 3.68% |
| Mesh B | 0.014 | 19,782 | 3.02 × 106 | 2.16% |
| Mesh C | 0.010 | 37,835 | 3.04 × 106 | 2.03% |
| Theoretical stress | 3.10 × 106 | |||
| Percentage of | Volume (m3) | Error |
|---|---|---|
| 0 | 0.46295 | −0.44% |
| 0.5% | 0.46335 | −0.35% |
| 1.0% | 0.46334 | −0.36% |
| 1.5% | 0.46334 | −0.36% |
| 2.0% | 0.46334 | −0.36% |
| Experimental volume | 0.465 |
| Expected Time Scaling | MSF | Peak KE/IE Ratio | Computational Time (h) | Height (m) | Height Error |
|---|---|---|---|---|---|
| 1 | 1 | 0.25% | 69.8 | 1.153 | 4.81% |
| 1/10 | 100 | 4.66% | 8.60 | 1.141 | 3.72% |
| 1/20 | 400 | 8.58% | 5.53 | 1.051 | −4.45% |
| Experimental model height | 1.10 | ||||
| Depth (m) | Temperature (K) | Rated Pressure (MPa) | Stored Energy (kW·h) | Specific Heat (kJ/kg·K) | Density (kg/m3) |
|---|---|---|---|---|---|
| 100 | 287.50 | 1.02 | 8.3 | 1.020 | 12.40 |
| 300 | 284.94 | 3.06 | 25.0 | 1.052 | 37.58 |
| 500 | 281.87 | 5.10 | 41.7 | 1.082 | 62.88 |
| 700 | 279.65 | 7.14 | 58.3 | 1.107 | 87.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Sun, K.; Wang, X.; Lu, C.; Ma, G.; Long, K. Experiment and Simulation of the Shape and Stored Gas Characteristics of the Flexible Spherical Airbag for Underwater Compressed Air Energy Storage. J. Mar. Sci. Eng. 2023, 11, 774. https://doi.org/10.3390/jmse11040774
Liu M, Sun K, Wang X, Lu C, Ma G, Long K. Experiment and Simulation of the Shape and Stored Gas Characteristics of the Flexible Spherical Airbag for Underwater Compressed Air Energy Storage. Journal of Marine Science and Engineering. 2023; 11(4):774. https://doi.org/10.3390/jmse11040774
Chicago/Turabian StyleLiu, Mingyao, Ke Sun, Xudong Wang, Changbo Lu, Gang Ma, and Kai Long. 2023. "Experiment and Simulation of the Shape and Stored Gas Characteristics of the Flexible Spherical Airbag for Underwater Compressed Air Energy Storage" Journal of Marine Science and Engineering 11, no. 4: 774. https://doi.org/10.3390/jmse11040774
APA StyleLiu, M., Sun, K., Wang, X., Lu, C., Ma, G., & Long, K. (2023). Experiment and Simulation of the Shape and Stored Gas Characteristics of the Flexible Spherical Airbag for Underwater Compressed Air Energy Storage. Journal of Marine Science and Engineering, 11(4), 774. https://doi.org/10.3390/jmse11040774







