Investigation on Load Characteristics of Hinged Connector for a Large Floating Structure Model under Wave Actions
Abstract
:1. Introduction
2. The Experimental Setup and Conditions
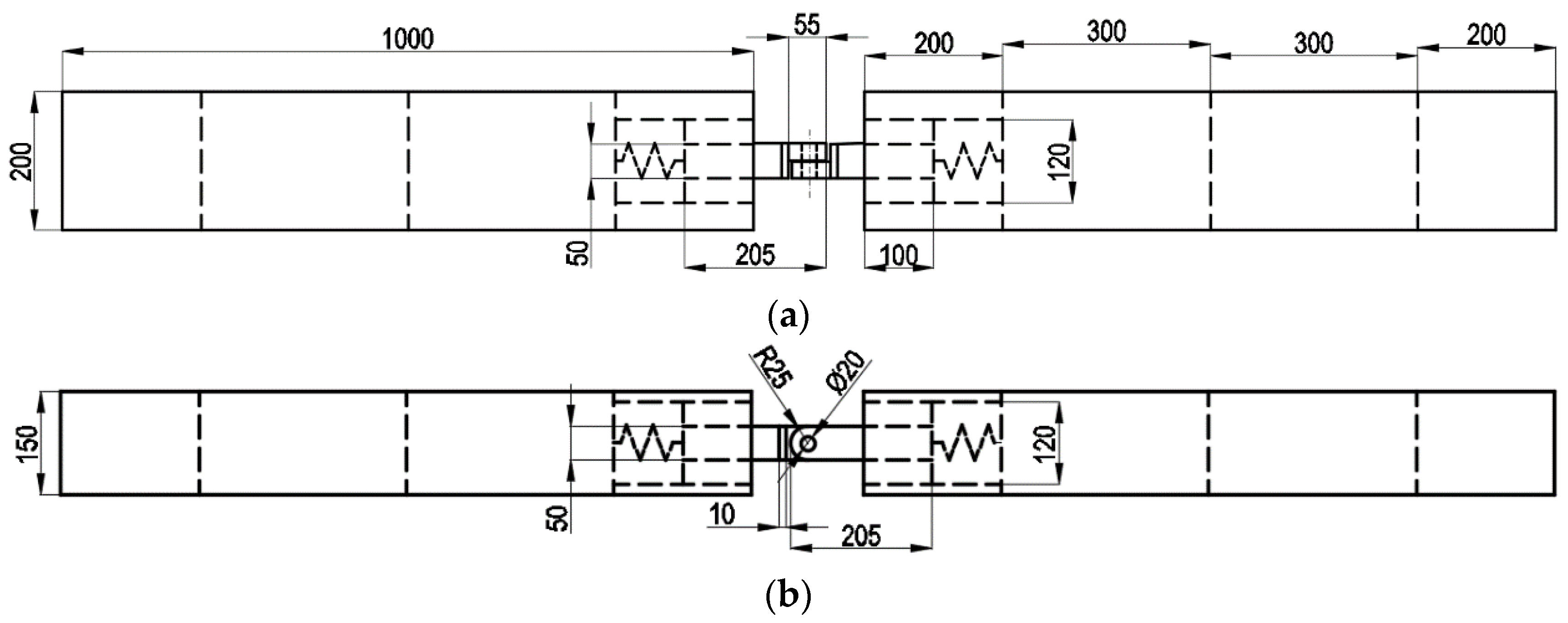
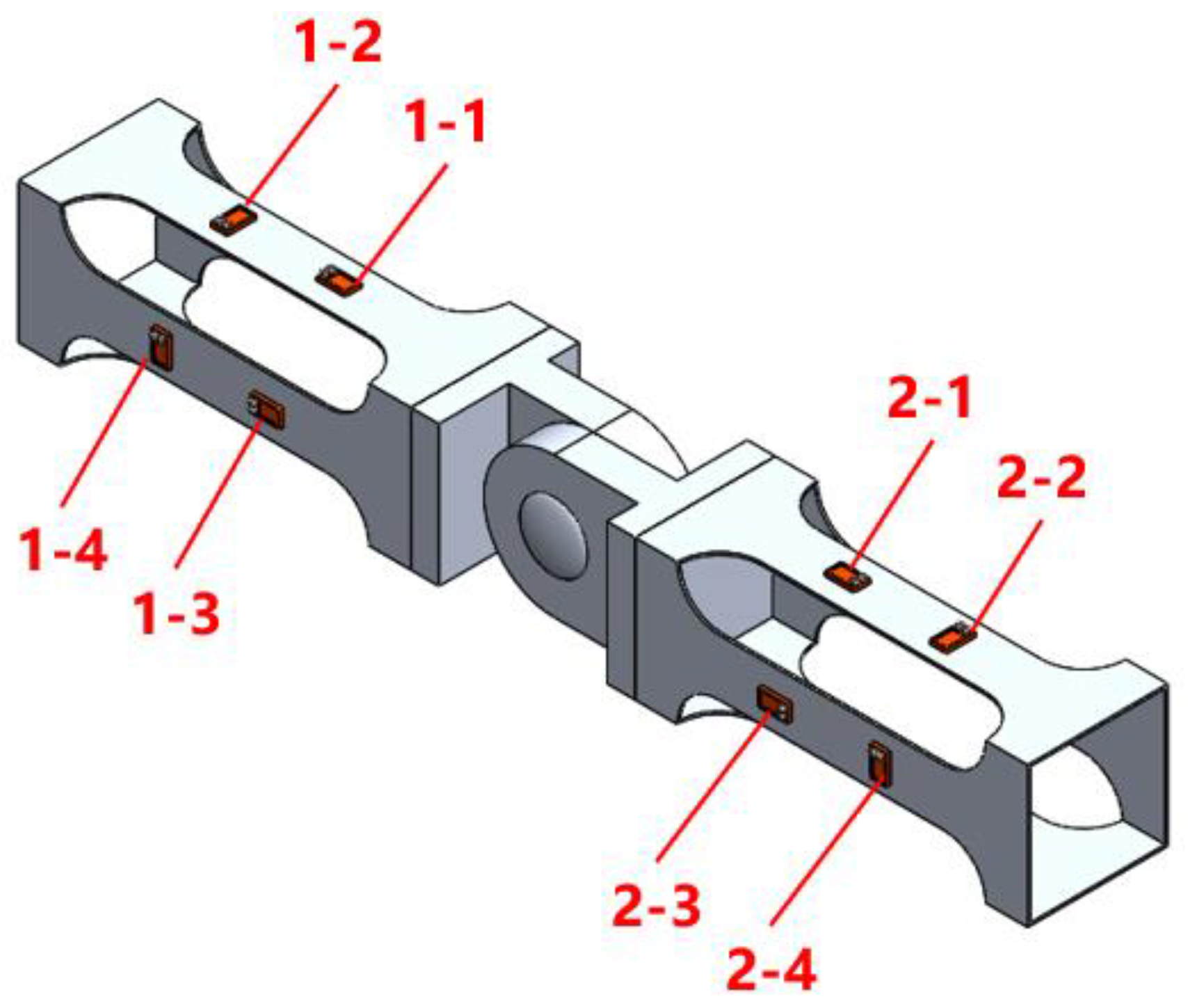
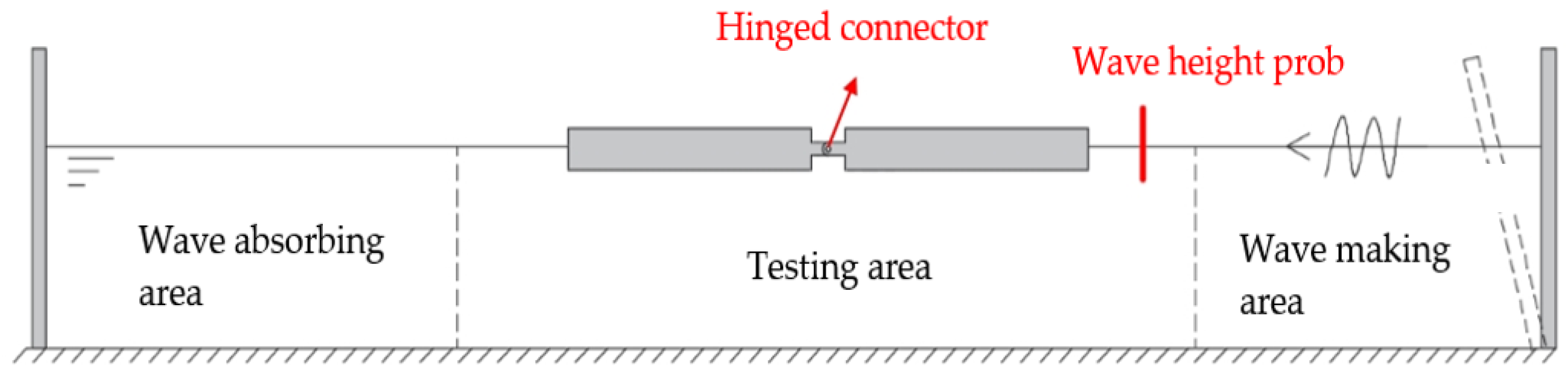
2.1. Physical Model and Experimental Facility
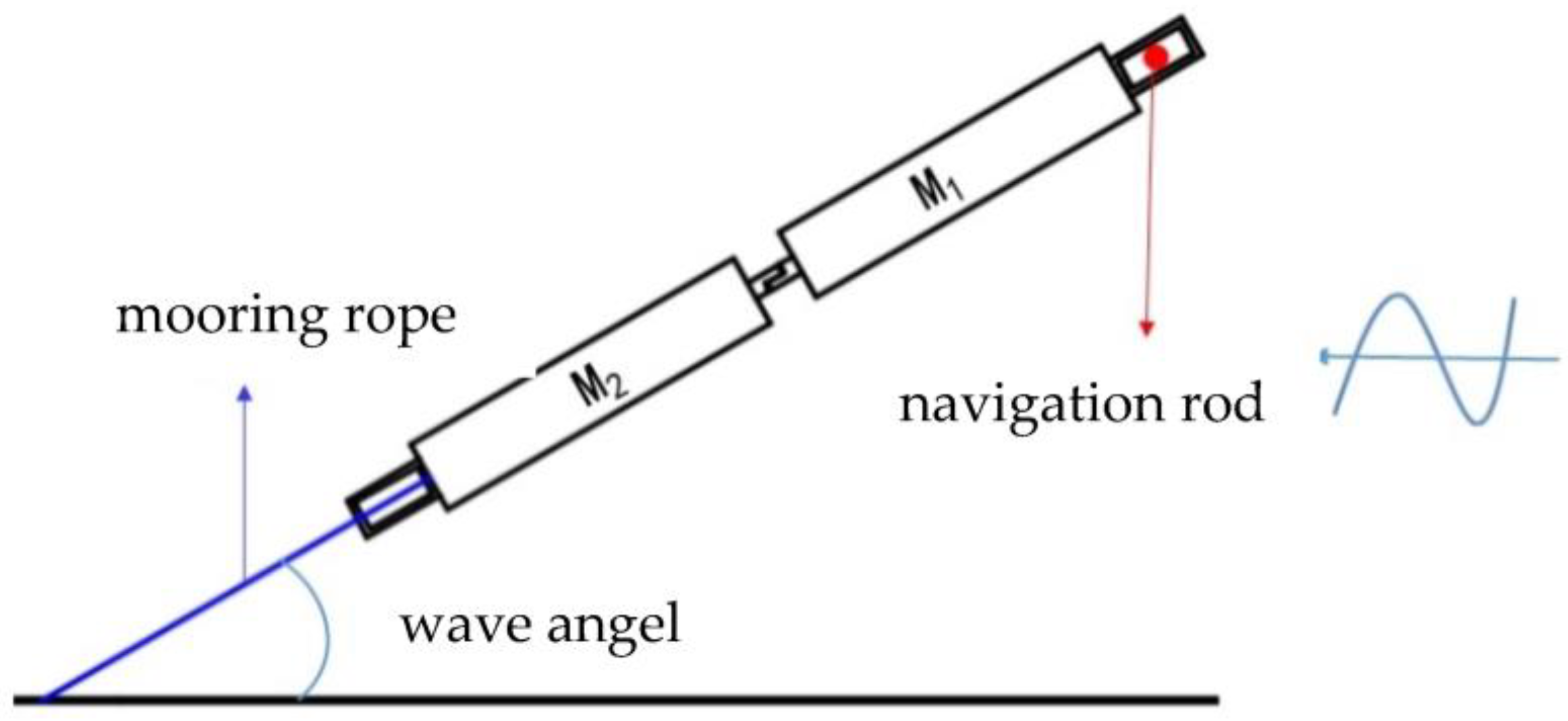
2.2. Mooring System
2.3. Test Conditions
3. Numerical Model and Simulation
3.1. Numerical Simulation Method
3.2. Numerical Model
4. Results and Discussion
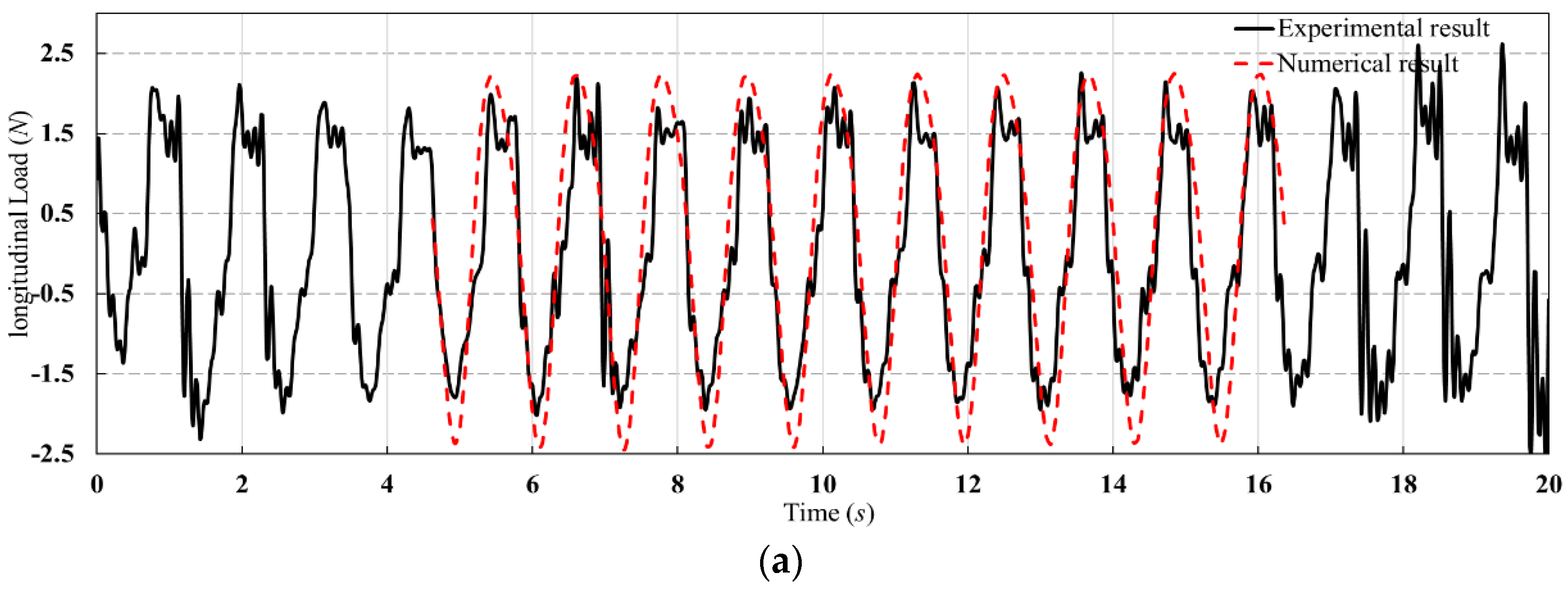
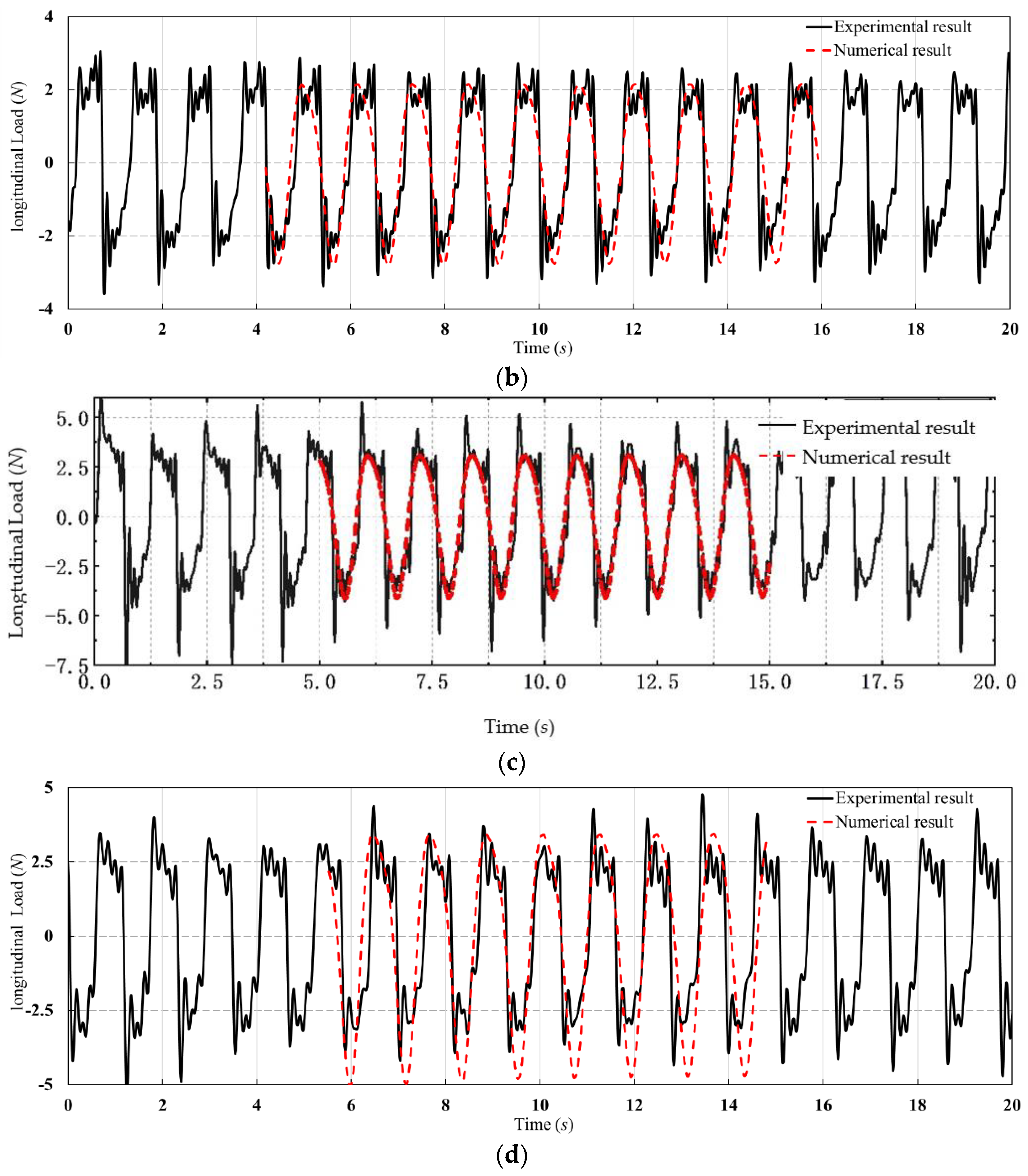
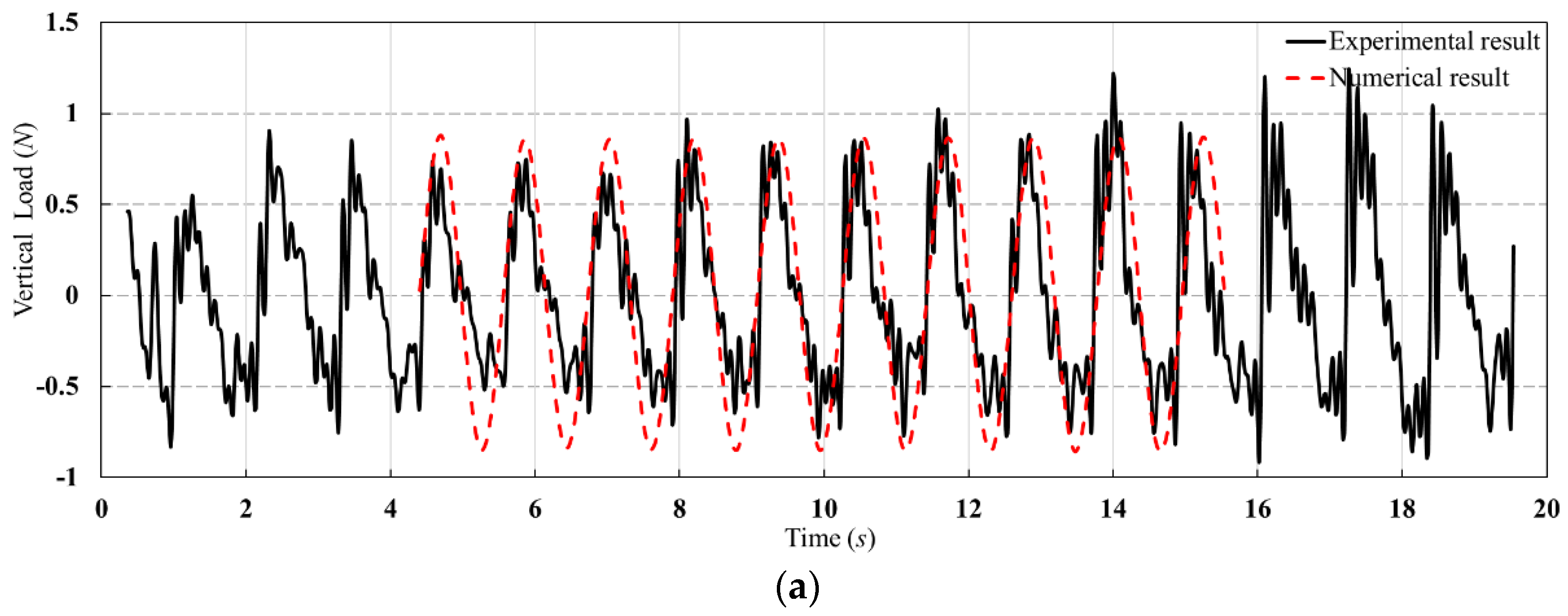
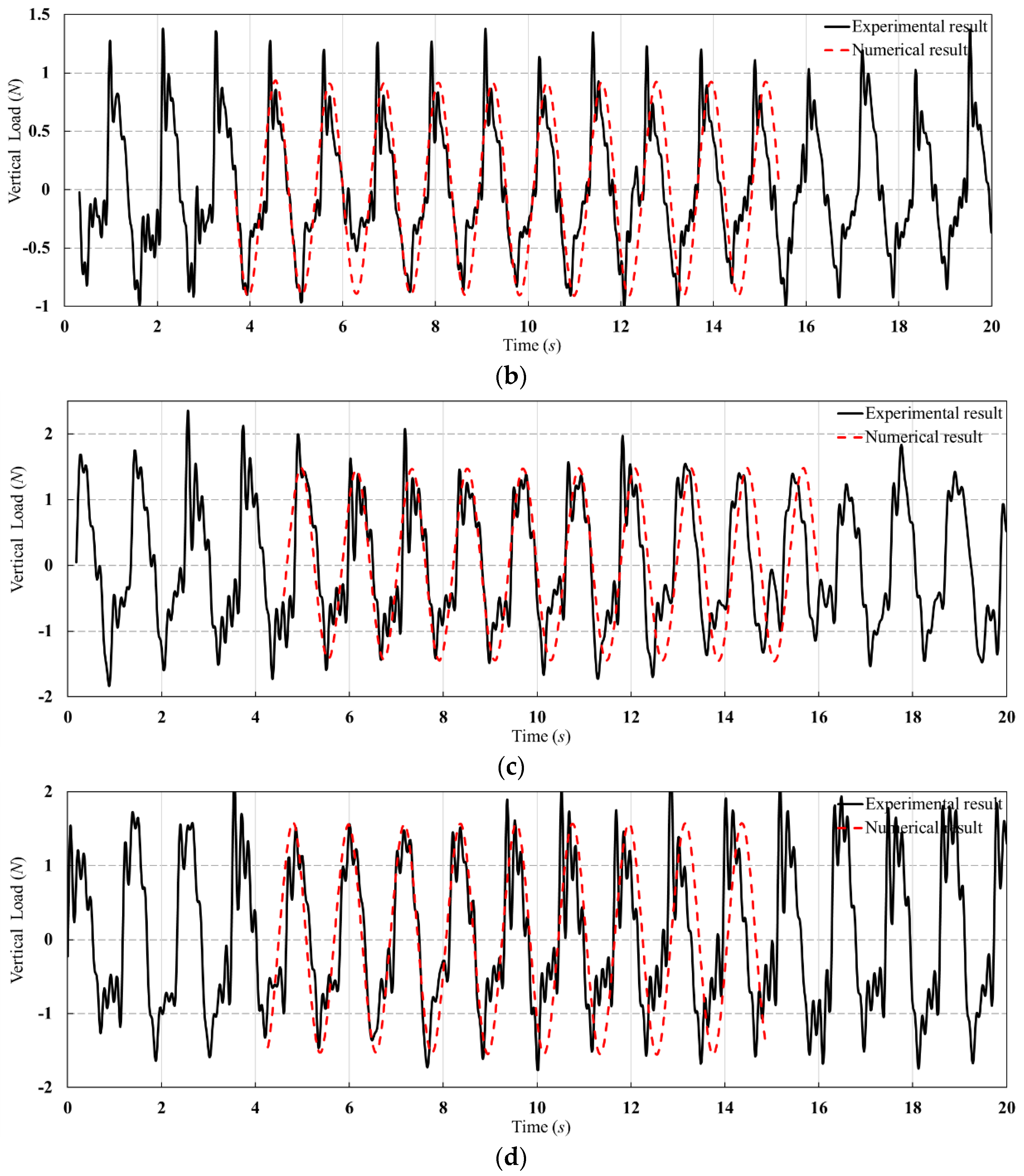
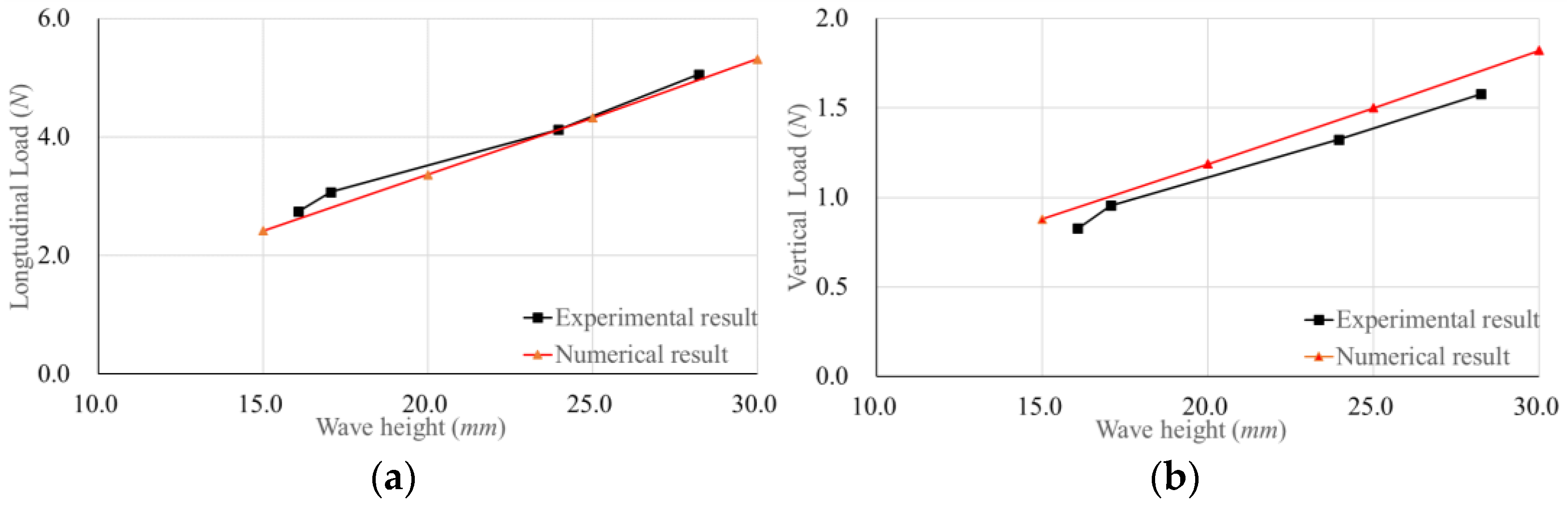
4.1. Influence of Wave Height on Load of Hinged Connector
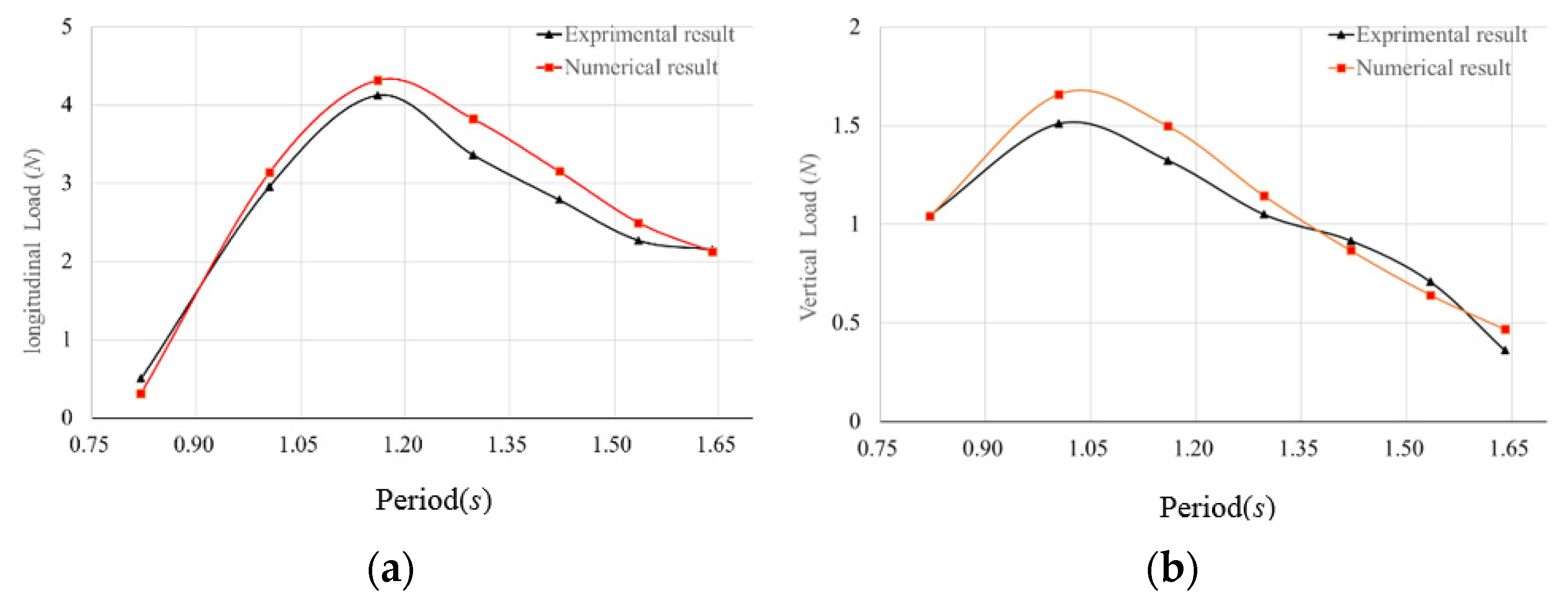
4.2. Influence of Wave Period on the Load of Hinged Connector
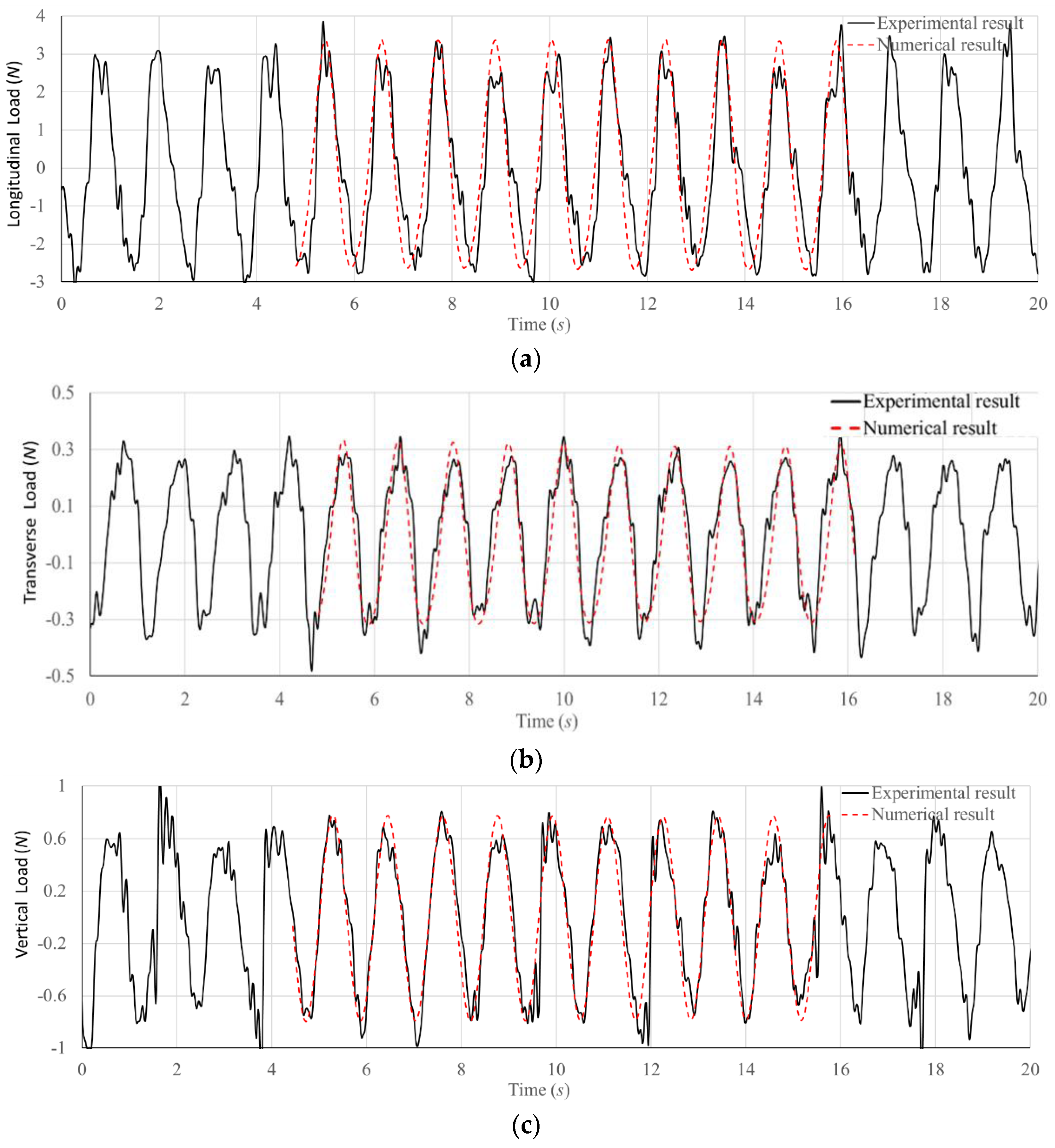
4.3. Influence of Wave Direction Angle on the Load of Hinged Connector
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Remmers, G.; Zueck, R.; Palo, P.; Taylor, R. Mobile offshore base. In Proceedings of the 1998 8th International Offshore and Polar Engineering Conference, Part 1 (of 4), Montreal, QC, Canada, 24–29 May 1998. [Google Scholar]
- Yoshida, K. Developments and research on VLFS in Japan. In Proceedings of the Second International Work Shop on Very Large Floating Structures, Hayama, Japan, 25–28 November 1996; p. 4522. [Google Scholar]
- Riggs, H.R.; Ertekin, R.C.; Mills, T.R.J. Impact of connector stiffness on the response of a multi-module mobile offshore base. In Proceedings of the International Offshore and Polar Engineer Conference, Montreal, QC, Canada, 24–29 May 1998; ISOPE: Mountain View, CA, USA, 1998; Volume 1, pp. 200–207. [Google Scholar]
- Suzuki, H. Safety target of very large floating structure used as a floating airport. Mar. Struct. 2001, 14, 103–113. [Google Scholar] [CrossRef]
- Suzuki, H.; Harada, H.; Natsume, T.; Maeda, K.; Iijima, K.; Hayashi, T. Technical Challenge on VLFS in JapanAfter Mega-Float Project. In Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017; p. V009T12A013. [Google Scholar]
- Suzuki, H. Overview of Megafloat: Concept, design criteria, analysis, and design. Mar. Struct. 2005, 18, 111–132. [Google Scholar] [CrossRef]
- Riggs, H.R.; Ertekin, R.C. Approximate methods for dynamic response of multi-module floating structures. Mar. Struct. 1993, 6, 117–141. [Google Scholar] [CrossRef]
- Pathak, M. Effects of Wave Length, Water Depth, Aspect Ratio and SlopigSeabed on Hydroelastic Response of VLFS; National University of Singapore: Singapore, 2014. [Google Scholar]
- Spry, S.; Hedrick, K. A Centralized Control Strategy for a Mobile Offshore Base. In Proceedings of the American Control Conference, San Diego, CA, USA, 2–4 June 1999. [Google Scholar]
- Zueck, R.; Taylor, R.; Palo, P. Assessment of Technology for Mobile Offshore Base. In Proceedings of the International Offshore and Polar Engineering Conference, Seattle, DC, USA, 28 May–2 June 2000. [Google Scholar]
- Palo, P.A.; Taylor, R.; Brackett, R.; Zueck, R. Contributions to offshore engineering from the mobile offshore base program. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Rio de Janeiro, Brazil, 3–8 June 2001. [Google Scholar]
- Girard, A.R.; de Sousa, J.B.; Hedrick, J.K. Dynamic Positioning Concepts and Strategies for the Mobile Offshore Base. In Proceedings of the IEEE Intelligent Transportation Systems Conference, Oakland, CA, USA, 25–29 August 2001. [Google Scholar]
- Rognaas, G.; Xu, J.; Lindseth, S.; Rosendahl, F. Mobile offshore base concepts Concrete hull and steel topsides. Mar. Struct. 2001, 14, 5–23. [Google Scholar] [CrossRef]
- Drummen, I.; Olbert, G. Conceptual design of a modular floating multi-purpose island. Front. Mar. Sci. 2021, 8, 615222. [Google Scholar] [CrossRef]
- McAllister, K.R. Mobile Offshore Base-An Overview of Recent Research. In Proceedings of the International Workshop On Very Large Floating Structures, Hayama, Japan, 25–28 November 1996; pp. 69–76. [Google Scholar]
- Wang, C.M.; Tay, Z.Y. Very large floating structures: Applications, research and development. Procedia Eng. 2011, 14, 62–72. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.J.; Li, R.P.; Shu, Z. Technical problems in the conceptual design of very large floating structures. Ocean. Eng. 2001, 19, 1–6. (In Chinese) [Google Scholar]
- Wung, C.C.; Manetas, M.; Ying, J. Hydrodynamic computational tools validation against mobile offshore base model testing. In Proceedings of the Third International Workshop on Very Large Floating Structure, Honolulu, HI, USA, 22–24 September 1999; Volume 2, pp. 538–545. [Google Scholar]
- Lv, H.; Yang, J.; Zhang, C. Experimental study of multi-rigid body for semi-submersible super-large floating body. Ship Eng. 2004, 5, 33–37. [Google Scholar]
- Ding, W.; Yu, L.; Li, R.P.; Yao, M.W. Dynamic response experiment of connector for mobile offshore base. Ocean. Eng. 2005, 23, 11–15. [Google Scholar]
- Wu, Y.S.; Gu, X.K.; Liu, S.X.; Tian, C.; Wang, X.F.; Cheng, X.M.; Qi, E.R. Advances of basic research on the responses and safety of very large floating structures in complicated environment. China Basic Sci. 2017, 19, 28–44. (In Chinese) [Google Scholar]
- Cui, W.C.; Wu, Y.S.; Li, R.P. Recent researches on dynamic performances of very large floating structures. J. Ship Mech. 2001, 5, 73–81. (In Chinese) [Google Scholar]
- Riggs, H.R.; Ertekin, R.C.; Mills, T.R.J. Characteristics of the wave response of Mobile Offshore Base. In Proceedings of the 18th International Conference on Offshore Mechanics and Arctic Engineering, St. Johns, NL, Canada, 11–16 July 1999; pp. 1–9. [Google Scholar]
- Zhang, X. Study on Configuration and Load of Multi-Module Very Large Floating Body. Ph.D. Thesis, China Ship Research Institute, Wuxi, China, 2018. [Google Scholar]
- Wang, W. Design and Load Analysis of Multi-Body Super Large Floating Structure Connectors. Ph.D. Thesis, Jiangsu University of Science and Technology, Zhenjiang, China, 2014. [Google Scholar]




| Main Parameter | Value |
|---|---|
| Length | 1000 mm |
| Width | 200 mm |
| Height | 150 mm |
| Draft | 80 mm |
| Displacement | 16 kg |
| No. | Wave Direction ° | Wave Height m | Wave Length/One Module | Period s |
|---|---|---|---|---|
| Height-1 | 0 | 0.015 | 2 | 1.160 |
| Height-2 | 0 | 0.020 | 2 | 1.160 |
| Height-3 | 0 | 0.025 | 2 | 1.160 |
| Height-4 | 0 | 0.030 | 2 | 1.160 |
| Length-1 | 0 | 0.025 | 1 | 0.820 |
| Length-2 | 0 | 0.025 | 1.5 | 1.005 |
| Length-3 | 0 | 0.025 | 2 | 1.160 |
| Length-4 | 0 | 0.025 | 2.5 | 1.297 |
| Length-5 | 0 | 0.025 | 3 | 1.421 |
| Length-6 | 0 | 0.025 | 3.5 | 1.535 |
| Length-7 | 0 | 0.025 | 4 | 1.641 |
| Direction-1 | 0 | 0.025 | 2 | 1.160 |
| Direction-2 | 15 | 0.025 | 2 | 1.160 |
| Direction-3 | 30 | 0.025 | 2 | 1.160 |
| Direction-4 | 45 | 0.025 | 2 | 1.160 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Liu, W.; Wu, H. Investigation on Load Characteristics of Hinged Connector for a Large Floating Structure Model under Wave Actions. J. Mar. Sci. Eng. 2023, 11, 786. https://doi.org/10.3390/jmse11040786
Song X, Liu W, Wu H. Investigation on Load Characteristics of Hinged Connector for a Large Floating Structure Model under Wave Actions. Journal of Marine Science and Engineering. 2023; 11(4):786. https://doi.org/10.3390/jmse11040786
Chicago/Turabian StyleSong, Xuemin, Weiqin Liu, and Hao Wu. 2023. "Investigation on Load Characteristics of Hinged Connector for a Large Floating Structure Model under Wave Actions" Journal of Marine Science and Engineering 11, no. 4: 786. https://doi.org/10.3390/jmse11040786
APA StyleSong, X., Liu, W., & Wu, H. (2023). Investigation on Load Characteristics of Hinged Connector for a Large Floating Structure Model under Wave Actions. Journal of Marine Science and Engineering, 11(4), 786. https://doi.org/10.3390/jmse11040786






