Numerical Simulation of Nonlinear Wave Propagation from Deep to Shallow Water
Abstract
:1. Introduction
2. Governing Equations
2.1. Nonlinear Water Wave Equations
2.2. and
2.2.1.
2.2.2.
2.3. Treatment of the Surface Gradient Term
2.4. Conservative Form of the Governing Equations
3. Numerical Scheme
3.1. Compact Form of the Governing Equations
3.2. Spatial Discretization
3.3. Time Integration
3.4. Boundary Conditions
4. Numerical Simulation of Wave Propagation in Waters of Uniform Depth
4.1. Numerical Simulation of Monochromatic Wave Propagation
4.2. Numerical Simulation of Bichromatic Wave Propagation
5. Numerical Simulation in the Wave Flume with an Uneven Bottom
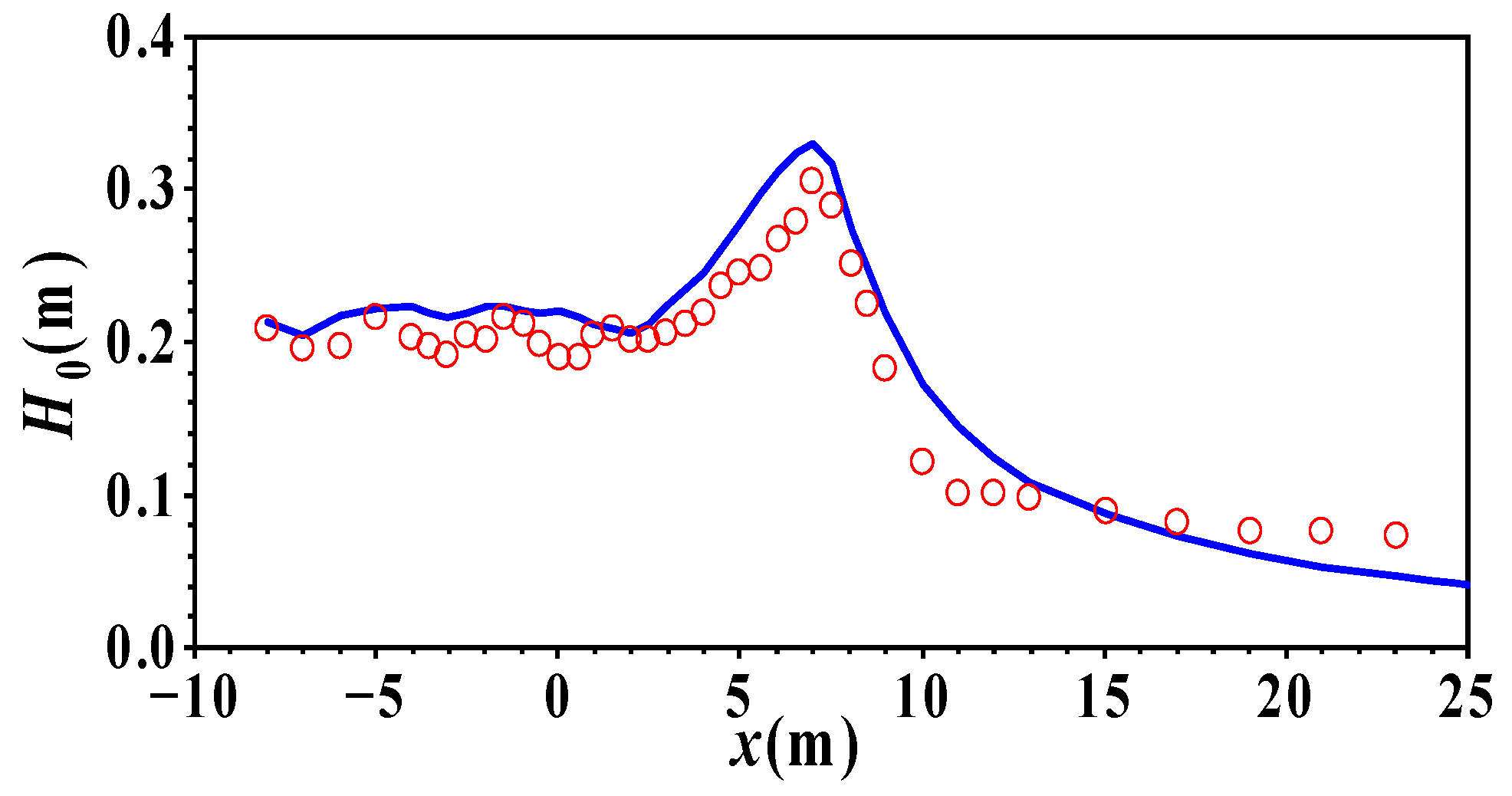
5.1. Wave Propagation over a Submerged Bar
5.2. Numerical Simulation of Wave Propagation on Slopes
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peregrine, D.H. Long waves on a beach. J. Fluid Mech. 1967, 27, 815–827. [Google Scholar] [CrossRef]
- Madsen, P.A.; Murray, R.; Sørensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Coast. Eng. 1991, 15, 371–388. [Google Scholar] [CrossRef]
- Nwogu, O. Alternative form of Boussinesq equations for nearshore wave propagation. J. Waterw. Port Coast. Ocean Eng. 1993, 119, 618–638. [Google Scholar] [CrossRef]
- Wei, G.; Kirby, J.T.; Grilli, S.T.; Subramanya, R. A fully nonlinear Boussinesq model for surface waves. Part 1. Highly nonlinear unsteady waves. J. Fluid Mech. 1995, 294, 71–92. [Google Scholar] [CrossRef]
- Hong, G.W. High order models of nonlinear and dispersive wave in water of varying depth with arbitrary slopping bottom. China Ocean Eng. 1997, 11, 243–260. [Google Scholar]
- Zhang, H.S.; Zhou, H.W.; Hong, G.W. A set of high order nonlinear Boussinesq-type equations and its numerical verification. Chin. J. Hydrodyn. Ser. A 2011, 26, 265–277. (In Chinese) [Google Scholar]
- Berkhoff, J.C.W. Computation of combined refraction-diffraction. In Proceedings of the 13th Confference on Coastal Engineering, Vancouver, BC, Canada, 10–14 July 1972; pp. 471–490. [Google Scholar]
- Hong, G.W. Mathematical models for combined refraction-diffraction of waves on non-uniform current and depth. China Ocean Eng. 1996, 10, 433–454. [Google Scholar]
- Panchang, V.G.; Wei, G.; Pearce, B.R.; Briggs, M.J. Numerical simulation of irregular wave propagation over shoal. J. Waterw. Port Coast. Ocean Eng. 1990, 116, 324–340. [Google Scholar] [CrossRef]
- Kirby, J.T.; Dalrymple, R.A. An approximate model for nonlinear dispersion in monochromatic wave propagation models. Coast. Eng. 1986, 9, 545–561. [Google Scholar] [CrossRef]
- Tsai, C.P.; Chen, H.B.; Hsu, J.R.C. Second-order time-dependent mild-slope equation for wave transformation. Math. Probl. Eng. 2014, 2014, 341385. [Google Scholar] [CrossRef]
- Kim, I.C.; Kaihatu, J.M. A consistent nonlinear mild-slope equation model. Coast. Eng. 2021, 170, 104006. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Ouellet, Y. A new kind of nonlinear mild-slope equation for combined refraction-diffraction of multifrequency waves. Coast. Eng. 1997, 31, 3–36. [Google Scholar] [CrossRef]
- Wu, Z.; Hong, G.W.; Zhang, H.S.; Zhang, Y. Numerical model and application of fully dispersive nonlinear wave. In Proceedings of the 14th China Marine (Shore) Engineering Symposium, Hohhot, China, 5 August 2009; pp. 460–469. (In Chinese). [Google Scholar]
- Li, B. Wave equations for regular and irregular water wave propagation. J. Waterw. Port Coast. Ocean Eng. 2008, 134, 121–142. [Google Scholar] [CrossRef]
- Li, B. A mathematical model for weakly nonlinear water wave propagation. Wave Motion 2010, 47, 265–278. [Google Scholar] [CrossRef]
- Hong, G.W.; Zhang, H.S.; Feng, W.B. Numerical simulation of nonlinear three-dimensional waves in water of arbitrary varying topography. China Ocean. Eng. 1998, 12, 383–404. [Google Scholar]
- Zhang, H.S.; Zhao, H.J.; Ding, P.X.; Miao, G.P. On the modeling of wave propagation on non-uniform currents and depth. Ocean Eng. 2007, 34, 1393–1404. [Google Scholar] [CrossRef]
- Fang, K.Z.; Zou, Z.L. Boussinesq-type equations for nonlinear evolution of wave trains. Wave Motion 2010, 47, 12–32. [Google Scholar] [CrossRef]
- Zhao, M.; Teng, B.; Cheng, L. A new form of generalized Boussinesq equations for varying water depth. Ocean Eng. 2004, 31, 2047–2072. [Google Scholar] [CrossRef]
- Liu, S.; Sun, Z.; Li, J. An unstructured FEM model based on Boussinesq equations and its application to the calculation of multidirectional wave run-up in a cylinder group. Appl. Math. Model. 2012, 36, 4146–4164. [Google Scholar] [CrossRef]
- Kirby, J.T.; Wei, G.; Chen, Q.; Kennedy, A.B.; Dalrymple, R.A. FUNWAVE 1.0: Fully Nonlinear Boussinesq Wave Model-Documentation and User’s Manual; Research Report NO. CACR-98-06; University of Delaware: Newark, NJ, USA, 1998. [Google Scholar]
- Walkley, M.; Berzins, M. A finite element method for the two-dimensional extended Boussinesq equations. Int. J. Numer. Methods Fluids 2002, 39, 865–885. [Google Scholar] [CrossRef]
- Erduran, K.S.; Ilic, S.; Kutija, V. Hybrid finite-volume finite-difference scheme for the solution of Boussinesq equations. Int. J. Numer. Methods Fluids 2005, 49, 1213–1232. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Part 2. A slowly-varying bathymetry. Coast. Eng. 1992, 18, 183–204. [Google Scholar] [CrossRef]
- Yamamoto, S.; Daiguji, H. Higher-order-accurate upwind schemes for solving the compressible Euler and Navier-Stokes equations. Comput. Fluids 1993, 22, 259–270. [Google Scholar] [CrossRef]
- Frazão, S.S.; Zech, Y. Undular bores and secondary waves-experiments and hybrid finite-volume modelling. J. Hydraul. Res. 2002, 40, 33–43. [Google Scholar] [CrossRef]
- Tonelli, M.; Petti, M. Hybrid finite volume-finite difference scheme for 2DH improved Boussinesq equations. Coast. Eng. 2009, 56, 609–620. [Google Scholar] [CrossRef]
- Roeber, V.; Cheung, K.F.; Kobayashi, M.H. Shock-capturing Boussinesq-type model for nearshore wave processes. Coast. Eng. 2010, 57, 407–423. [Google Scholar] [CrossRef]
- Shi, F.Y.; Kirby, J.T.; Harris, J.C.; Geiman, J.D.; Grilli, S.T. A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation. Ocean Model. 2012, 43, 36–51. [Google Scholar] [CrossRef]
- Choi, Y.K.; Shi, F.Y.; Malej, M.; Smith, J.M. Performance of various shock-capturing-type reconstruction schemes in the Boussinesq wave model, FUNWAVE-TVD. Ocean Model. 2018, 131, 86–100. [Google Scholar] [CrossRef]
- Kennedy, A.B.; Chen, Q.; Kirby, J.T.; Dalrymple, R.A. Boussinesq modeling of wave transformation, breaking, and runup. I: 1D. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 39–47. [Google Scholar] [CrossRef]
- Kim, D.H.; Lynett, P.J.; Socolofsky, S.A. A depth-integrated model for weakly dispersive, turbulent, and rotational fluid flows. Ocean Model. 2009, 27, 198–214. [Google Scholar] [CrossRef]
- Yao, Y.; Huang, Z.H.; Monismith, S.G.; Lo, E.Y.M. 1DH Boussinesq modeling of wave transformation over fringing reefs. Ocean Eng. 2012, 47, 30–42. [Google Scholar] [CrossRef]
- Zhao, D.H.; Shen, H.W.; Lai, J.S.; Tabios, G.Q., III. Approximate Riemann solvers in FVM for 2D hydraulic shock wave modeling. J. Hydraul. Eng. 1996, 122, 692–702. [Google Scholar] [CrossRef]
- Rogers, B.; Fujihara, M.; Borthwick, A.G.L. Adaptive Q-tree Godunov-type scheme for shallow water equations. Int. J. Numer. Methods Fluids 2001, 35, 247–280. [Google Scholar] [CrossRef]
- Rogers, B.D.; Borthwick, A.G.L.; Taylor, P.H. Mathematical balancing of flux gradient and source terms prior to using Roe’s approximate Riemann solver. J. Comput. Phys. 2003, 192, 422–451. [Google Scholar] [CrossRef]
- Hong, G.W. On the nonlinear interactions among gravity surface waves. Acta Oceanol. 1980, 2, 158–180. (In Chinese) [Google Scholar]
- Shiach, J.B.; Mingham, C.G. A temporally second-order accurate Godunov-type scheme for solving the extended Boussinesq equations. Coast. Eng. 2009, 56, 32–45. [Google Scholar] [CrossRef]
- Larsen, J.; Dancy, H. Open boundaries in short wave simulations—A new approach. Coast. Eng. 1983, 7, 285–297. [Google Scholar] [CrossRef]
- Luth, H.R.; Klopman, G.; Kitou, N. Kinematics of Waves Breaking Partially on an Offshore Bar: LDV Measurements of Waves with and without a Net Onshore Current; Report H-1573, Delft Hydraulics; IOP Publishing Ltd.: Delft, The Netherlands, 1994; Volume 40. [Google Scholar]
- Tsai, C.P.; Chen, H.B.; Hwung, H.H.; Huang, M.J. Examination of empirical formulas for wave shoaling and breaking on steep slopes. Ocean Eng. 2005, 3, 469–483. [Google Scholar] [CrossRef]

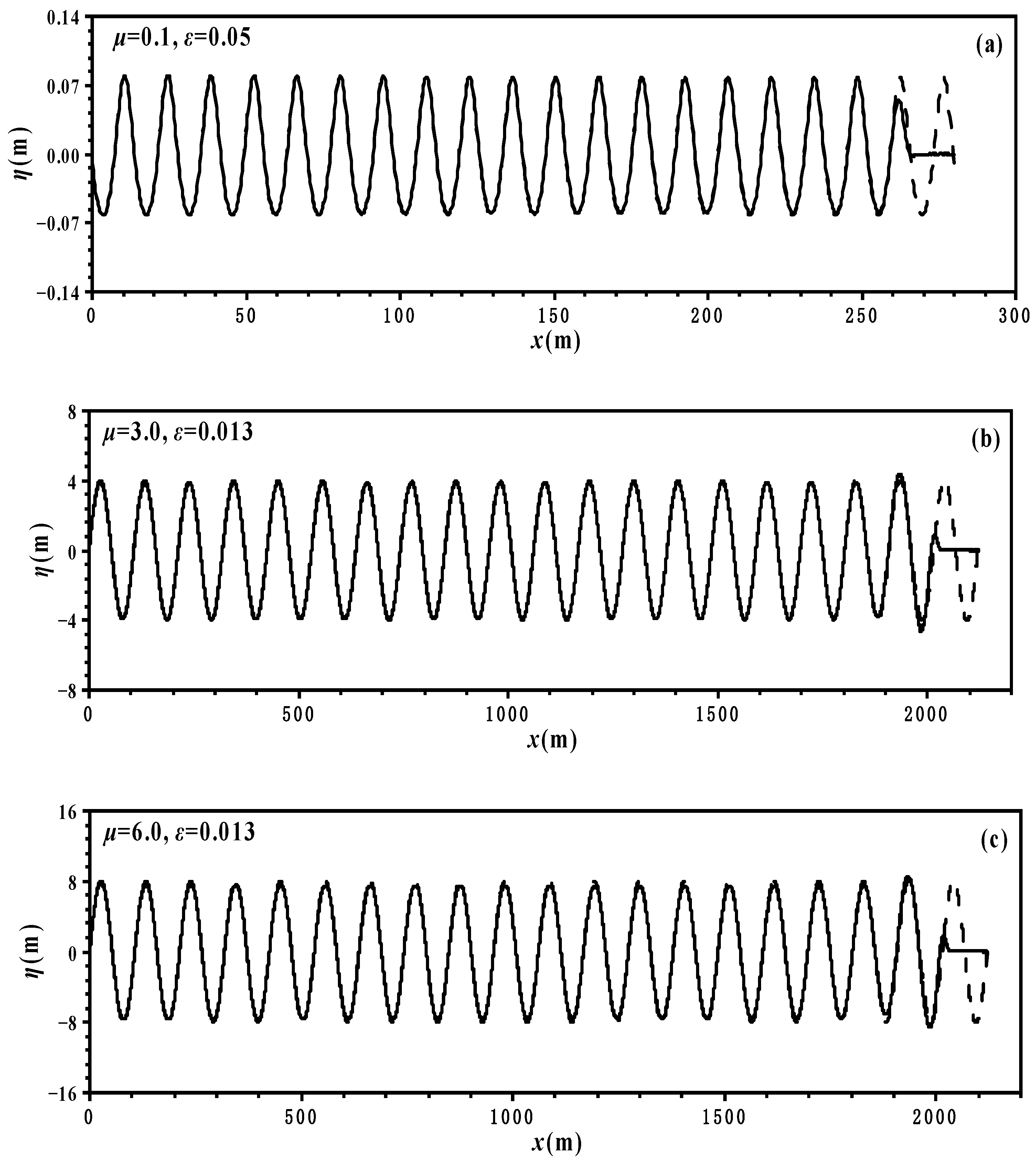



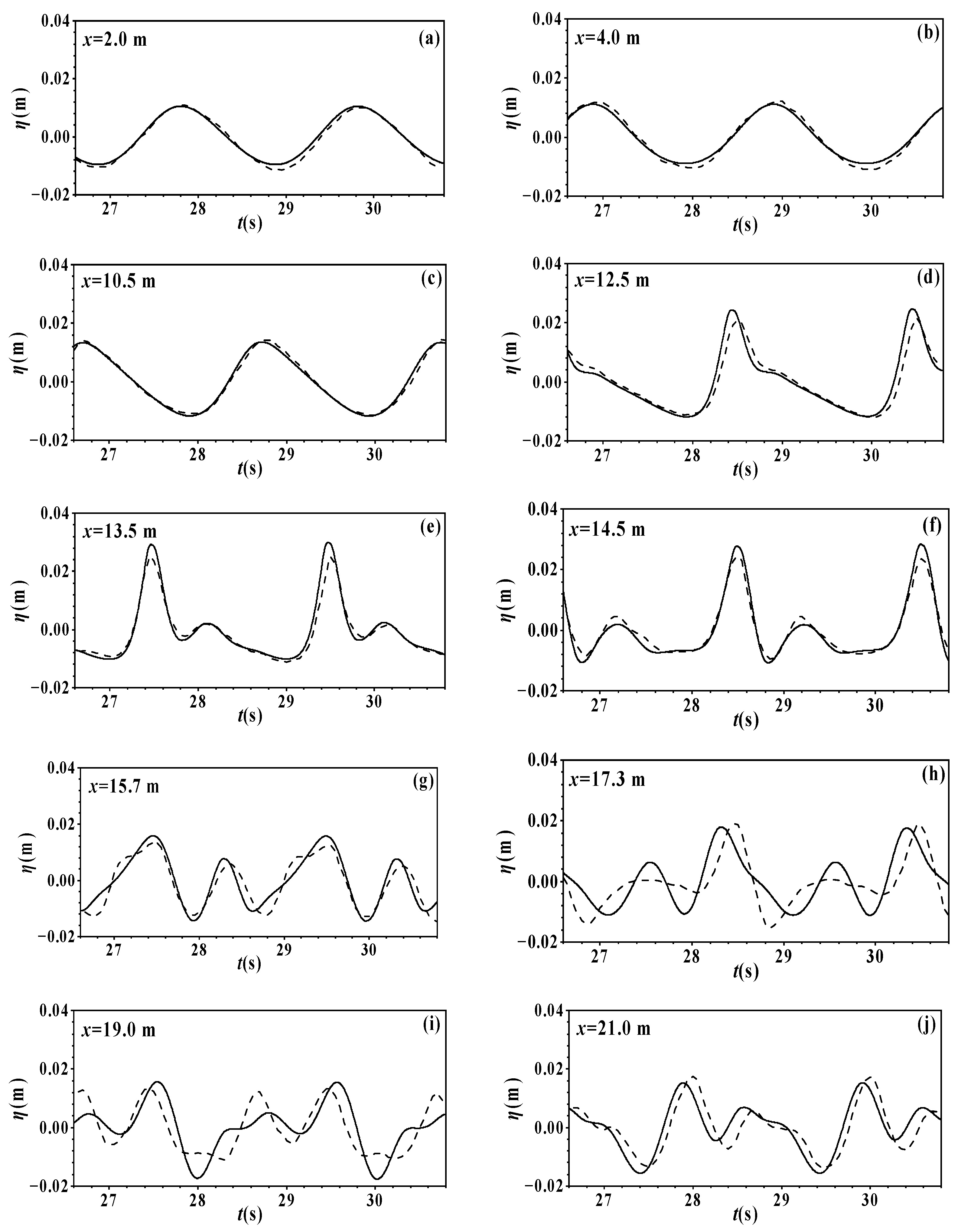
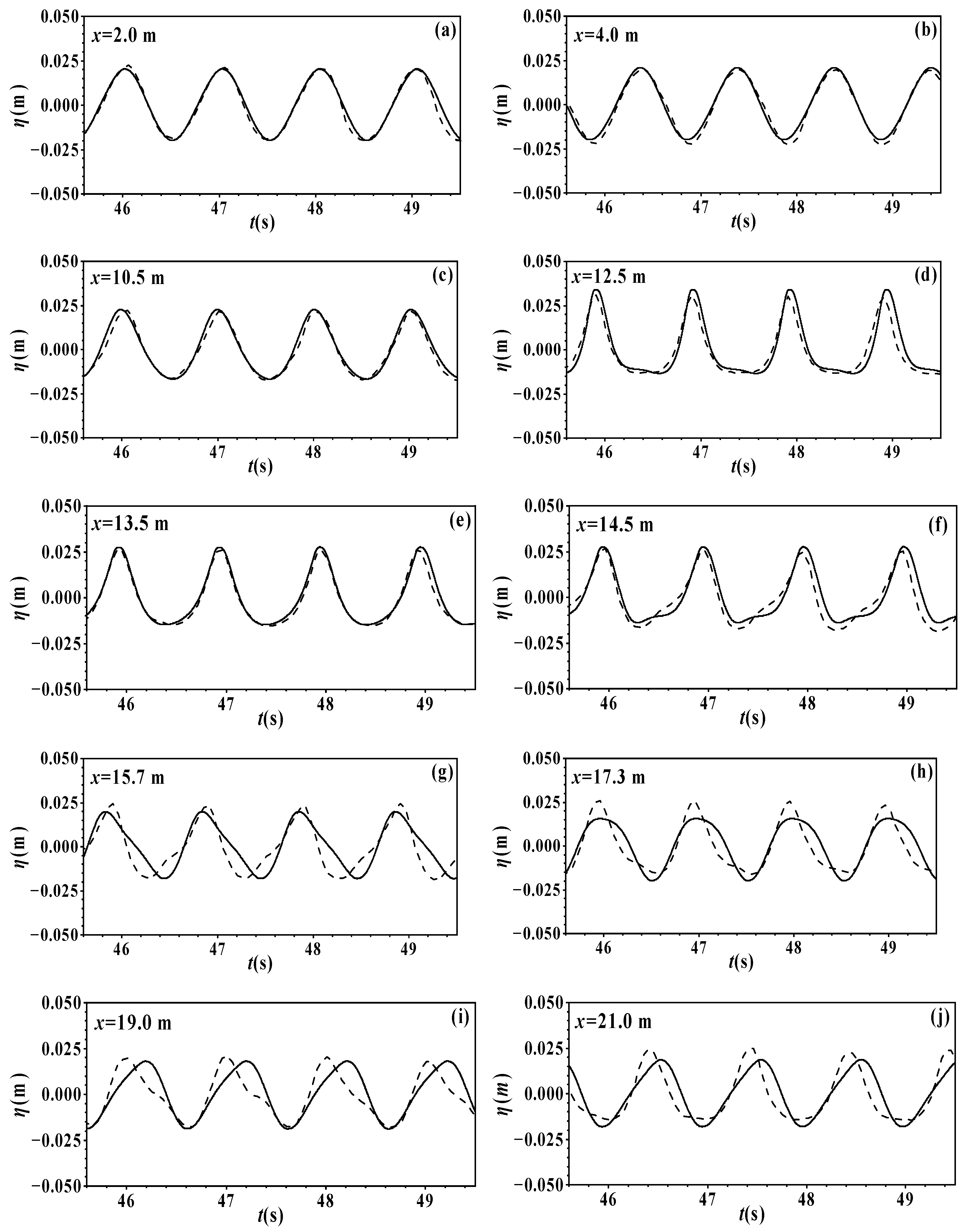
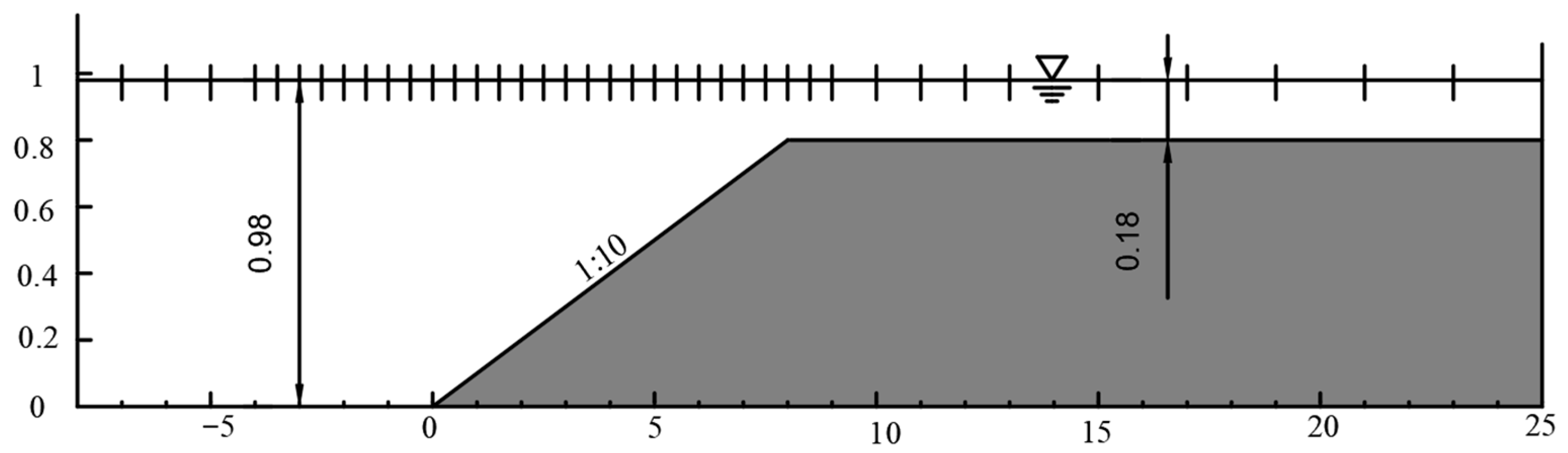
| Cases | h (m) | A (m) | H0 (m) | μ | ε | H0/h | H0/L | T (s) | L (m) |
|---|---|---|---|---|---|---|---|---|---|
| Ⅰ | 1.4 | 0.07 | 0.14 | 0.1 | 0.05 | 0.1 | 0.01 | 4.0 | 14.0 |
| II | 318.0 | 4.0 | 8.0 | 3.0 | 0.013 | 0.025 | 0.075 | 8.24 | 106.0 |
| III | 636.0 | 8.0 | 16.0 | 6.0 | 0.013 | 0.025 | 0.151 | 12.978 | 106.0 |
| Cases | Incident Wave 1 | Incident Wave 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| A | 7.0 | 0.02 | 21.62 | 0.046 | 14.0 | 0.002 | 43.70 | 0.023 |
| B1 | 2.0 | 0.01 | 3.88 | 0.12 | 2.5 | 0.01 | 5.0 | 0.09 |
| B2 | 1.02 | 0.02 | 1.51 | 0.265 | 2.15 | 0.02 | 4.01 | 0.1 |
| C | 0.6 | 0.004 | 0.56 | 0.71 | 0.6 | 0.003 | 0.56 | 0.71 |
| Cases | I | II |
|---|---|---|
| H0 (m) | 0.02 | 0.041 |
| T (s) | 2.02 | 1.01 |
| μ | 0.107 | 0.269 |
| ε | 0.025 | 0.051 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, P.-B.; Zhang, Z.-H.; Zhang, H.-S.; Zhao, X.-Y. Numerical Simulation of Nonlinear Wave Propagation from Deep to Shallow Water. J. Mar. Sci. Eng. 2023, 11, 1003. https://doi.org/10.3390/jmse11051003
Zheng P-B, Zhang Z-H, Zhang H-S, Zhao X-Y. Numerical Simulation of Nonlinear Wave Propagation from Deep to Shallow Water. Journal of Marine Science and Engineering. 2023; 11(5):1003. https://doi.org/10.3390/jmse11051003
Chicago/Turabian StyleZheng, Peng-Bo, Zhou-Hao Zhang, Hong-Sheng Zhang, and Xue-Yi Zhao. 2023. "Numerical Simulation of Nonlinear Wave Propagation from Deep to Shallow Water" Journal of Marine Science and Engineering 11, no. 5: 1003. https://doi.org/10.3390/jmse11051003






