Sensitivity Analysis of Forecasting Performance for ST6 Parameterization in High-Resolution Wave Model Based on WAVEWATCH III
Abstract
:1. Introduction
2. Methodology
2.1. ST6 Source Term
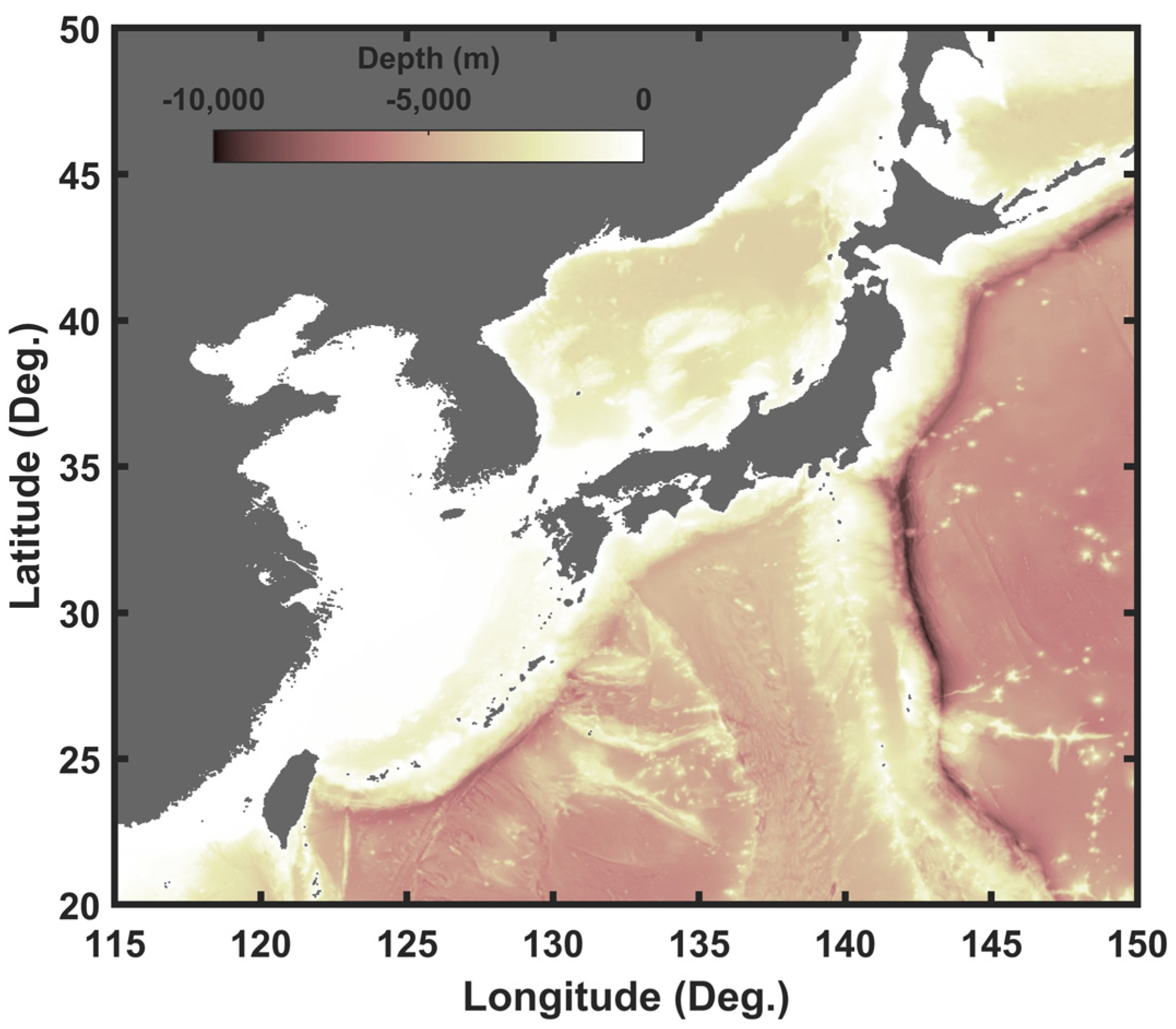
2.2. Numerical Model Set-Up
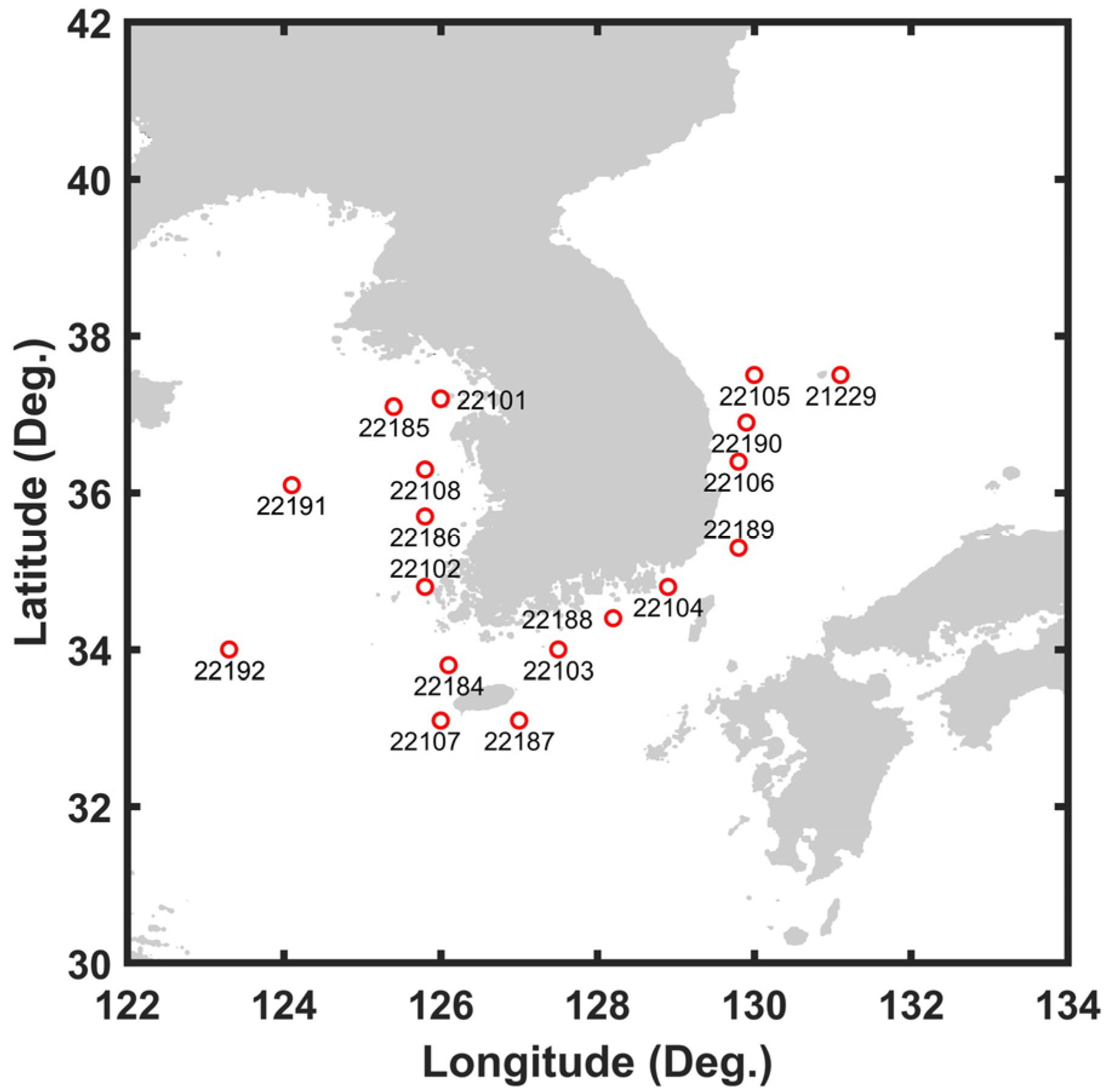
2.3. Observation Data
2.4. Validation Method
3. Results
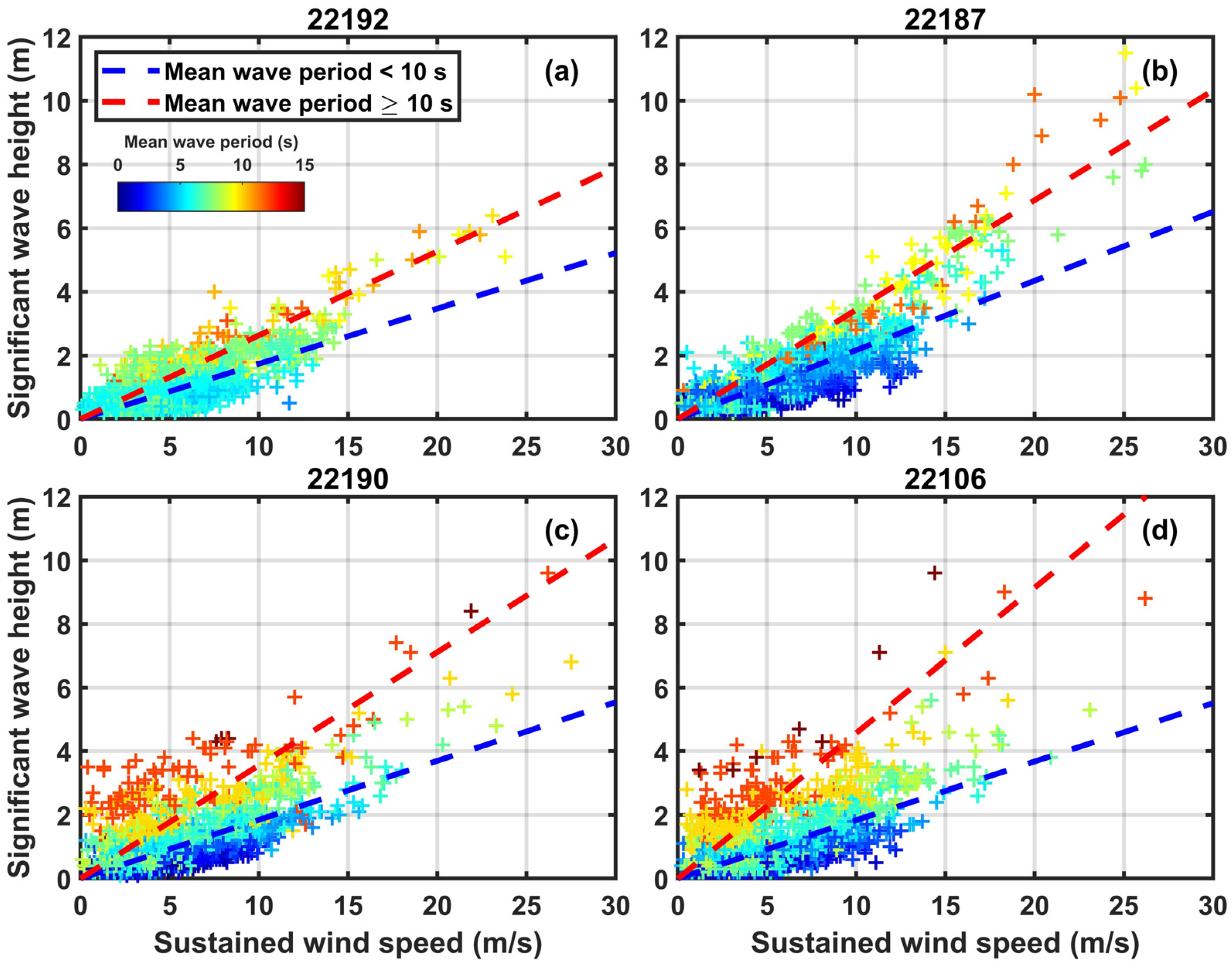
3.1. Analysis of the Relationship between Observed Offshore Wind and Significant Wave Height
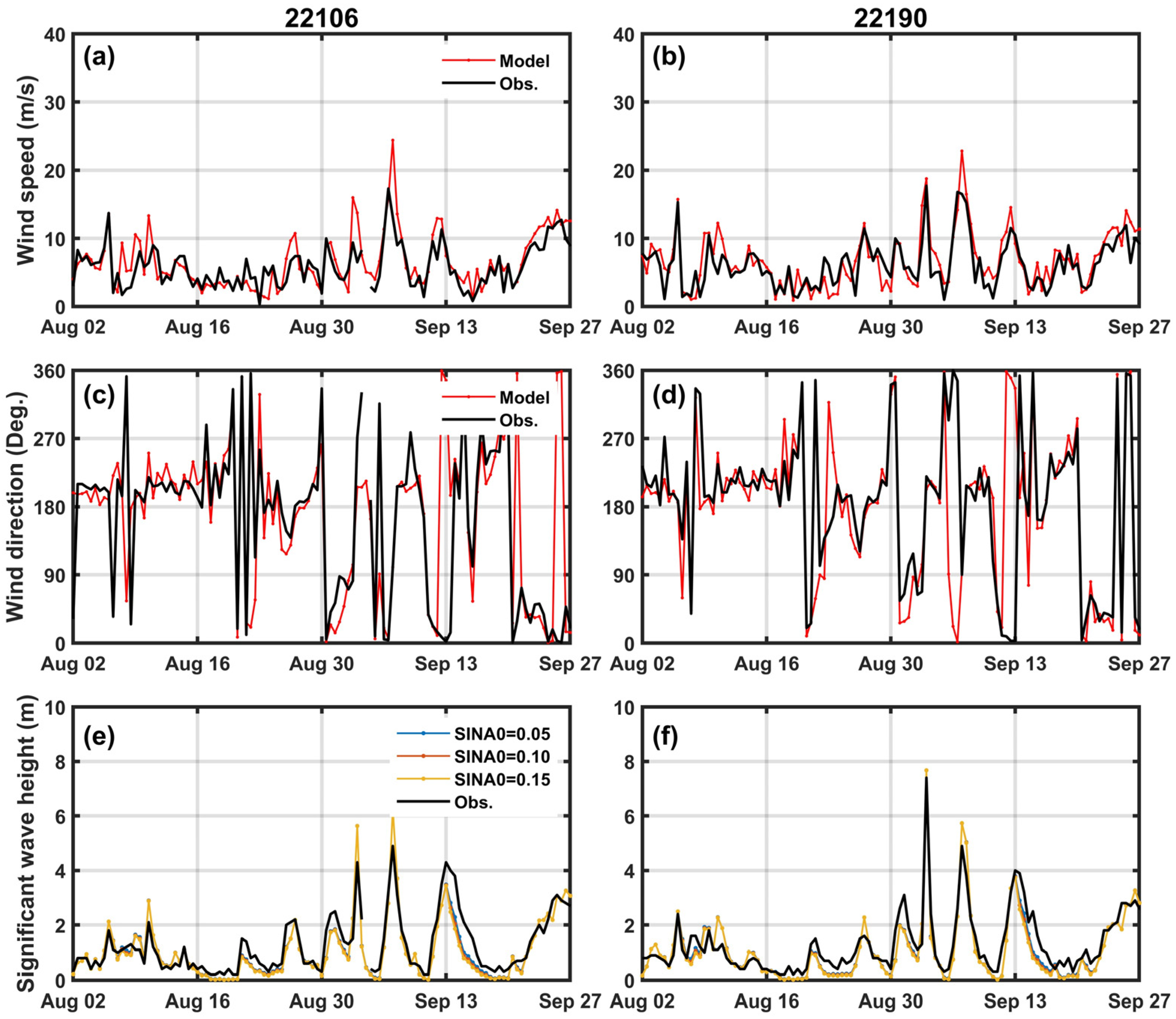
3.2. Validation of Offshore Wind Model Forecasting Data
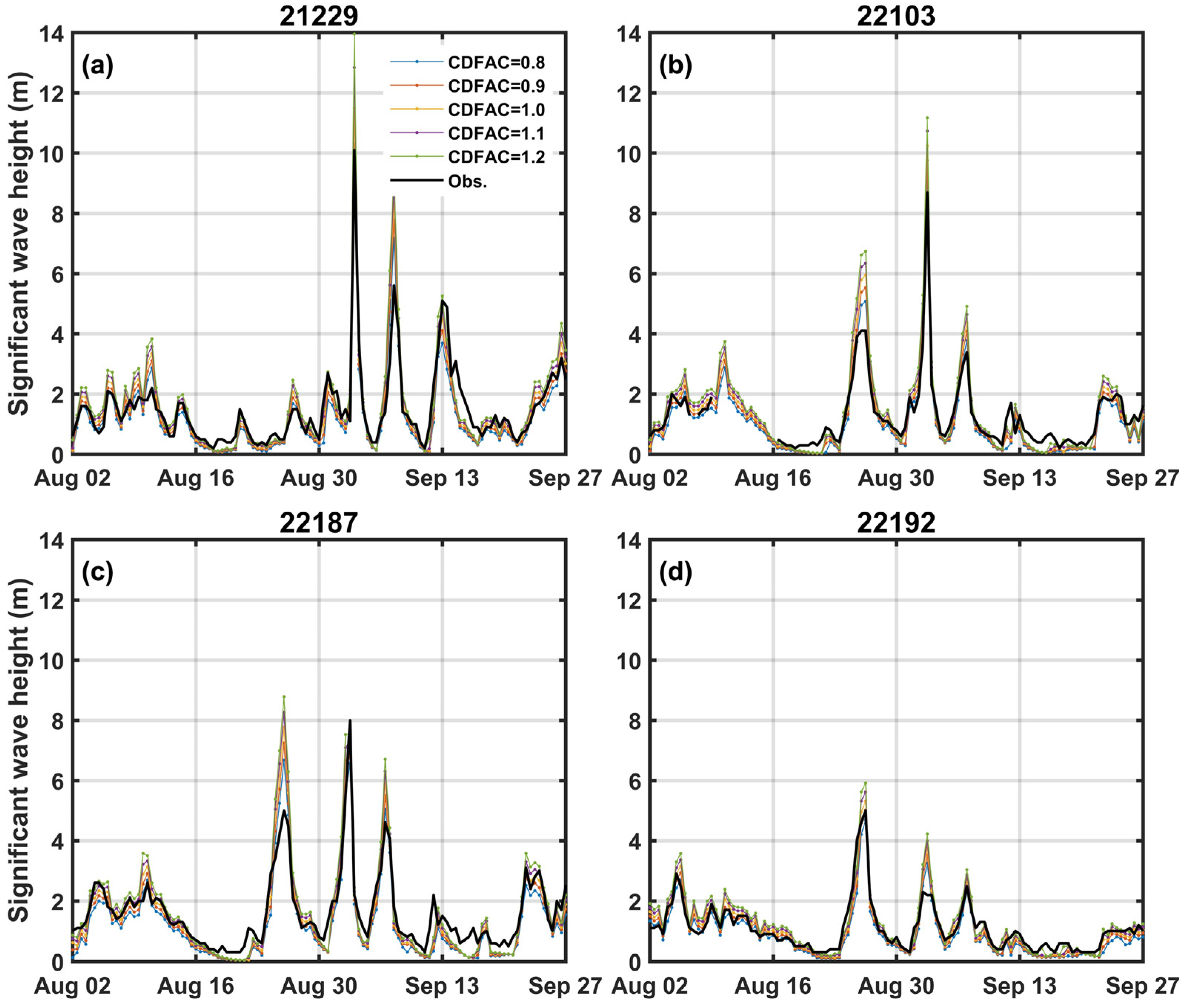
3.3. Wave Model Sensitivity Numerical Simulation Results
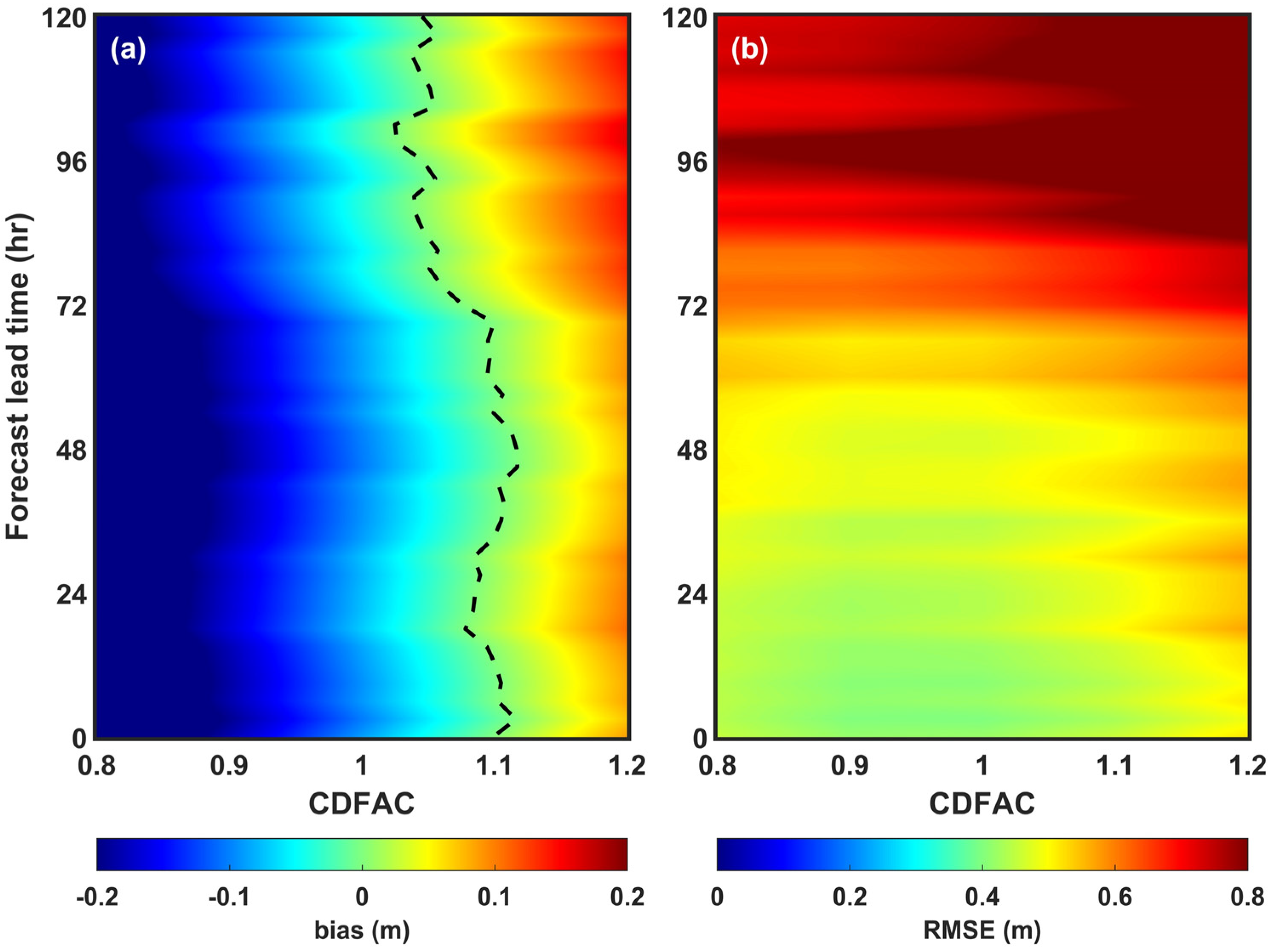
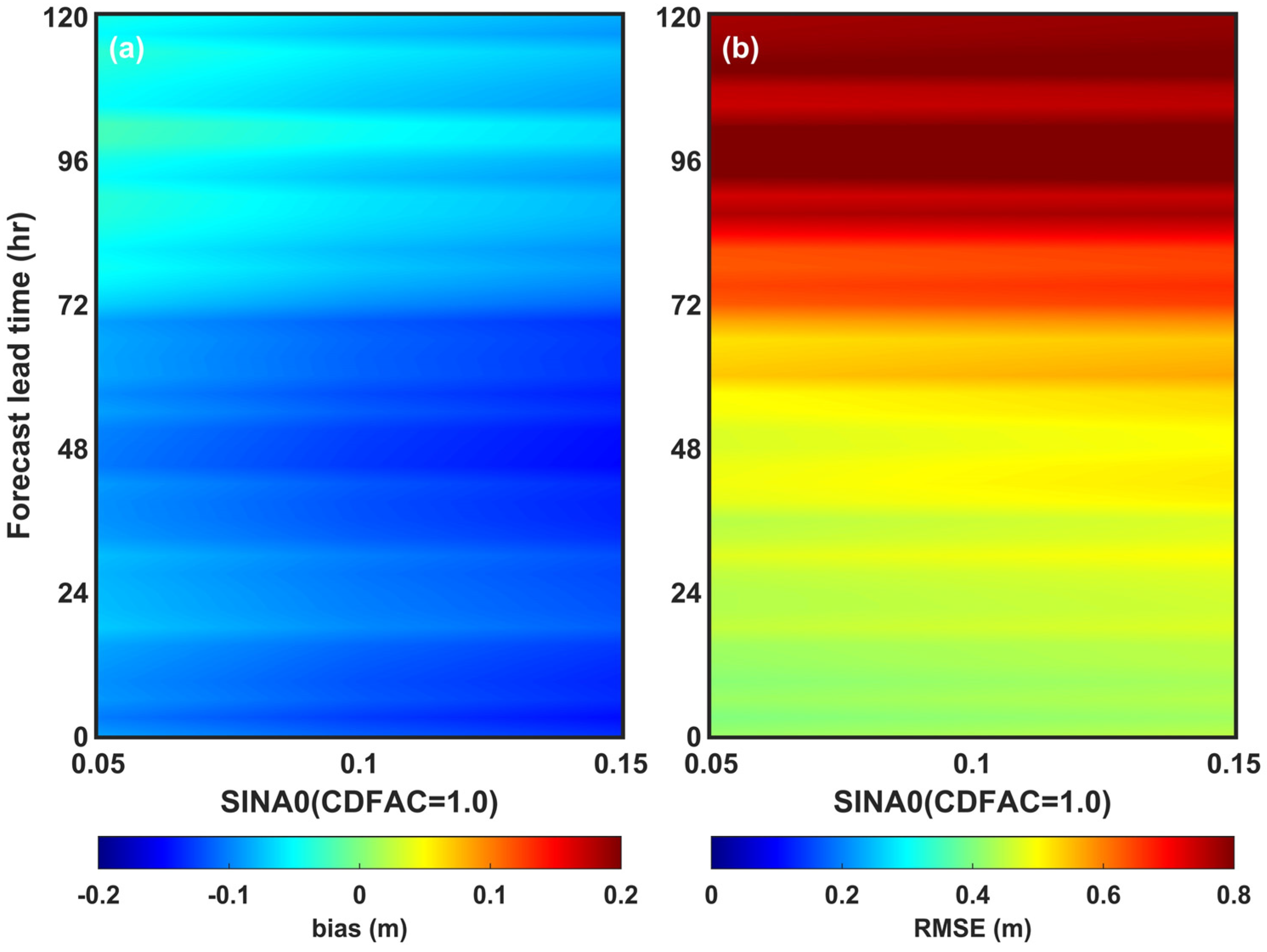
3.4. Impact on Forecasting Performance According to Changes in Wave Model Physical Variables
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Komen, G.J.; Hasselmann, S.; Hasselmann, K. On the Existence of a Fully Developed Wind-Sea Spectrum. J. Phys. Oceanogr. 1984, 14, 1271–1285. [Google Scholar] [CrossRef]
- Tolman, H.L.; Chalikov, D. Source terms in a third-generation wind-wave model. J. Phys. Oceanogr. 1996, 26, 2497–2518. [Google Scholar] [CrossRef]
- Tolman, H.L. Distributed-memory concepts in the wave model WAVEWATCH III. Parallel Comput. 2002, 28, 35–52. [Google Scholar] [CrossRef]
- Ardhuin, F.; Rogers, E.; Babanin, A.V.; Filipot, J.-F.; Magne, R.; Roland, A.; van der Westhuysen, A.; Queffeulou, P.; Lefevre, J.-M.; Aouf, L.; et al. Semiempirical Dissipation Source Functions for Ocean Waves. Part I: Definition, Calibration, and Validation. J. Phys. Oceanogr. 2010, 40, 1917–1941. [Google Scholar] [CrossRef]
- Tsagareli, K.N.; Babanin, A.V.; Walker, D.J.; Young, I.R. Numerical Investigation of Spectral Evolution of Wind Waves. Part I: Wind-Input Source Function. J. Phys. Oceanogr. 2010, 40, 656–666. [Google Scholar] [CrossRef]
- Rogers, W.E.; Babanin, A.V.; Wang, D.W. Observation consistent input and whitecapping dissipation in a model for wind-generated surface waves: Description and simple calculations. J. Atmos. Ocean. Technol. 2012, 29, 1329–1346. [Google Scholar] [CrossRef]
- Ardhuin, F.; Roland, A. The Development of Spectral Wave Models: Coastal and Coupled Aspects. In Proceedings of the 7th International Conference on Coastal Dynamics, Arcachon, France, 23–26 June 2013; Bonneton, P., Garlan, T., Eds.; University of Bordeaux: Bordeaux, France, 2013; pp. 25–38. [Google Scholar]
- Zieger, S.; Babanin, A.V.; Rogers, W.E.; Young, I.R. Observation-based source terms in the third-generation wave model WAVEWATCH. Ocean Model. 2015, 96, 2–25. [Google Scholar] [CrossRef]
- Liu, Q.; Rogers, W.E.; Babanin, A.V.; Young, I.R.; Romero, L.; Zieger, S.; Qiao, F.; Guan, C. Observation-based source terms in the third-generation wave model WAVEWATCH III: Updates and verification. J. Phys. Oceanogr. 2019, 49, 489–517. [Google Scholar] [CrossRef]
- Fan, Y.; Lin, S.J.; Held, I.M.; Yu, Z.; Tolman, H.L. Global ocean surface wave simulation using a coupled atmosphere-wave model. J. Clim. 2012, 25, 6233–6252. [Google Scholar] [CrossRef]
- Chen, S.S.; Zhao, W.; Donelan, M.A.; Tolman, H.L. Directional wind-wave coupling in fully coupled atmosphere-wave-ocean models: Results from CBLAST-Hurricane. J. Atmos. Sci. 2013, 70, 3198–3215. [Google Scholar] [CrossRef]
- Moghimi, S.; Van der Westhuysen, A.; Abdolali, A.; Myers, E.; Vinogradov, S.; Ma, Z.; Liu, F.; Mehra, A.; Kurkowski, N. Development of an ESMF based flexible coupling application of ADCIRC and WAVEWATCH III for high fidelity coastal inundation studies. J. Mar. Sci. Eng. 2020, 8, 308. [Google Scholar] [CrossRef]
- Ortiz-Royero, J.C.; Mercado-Irizarry, A. An intercomparison of Swan and Wavewatch III models with data from NDBC-NOAA Buoys at Oceanic scales. Coast. Eng. J. 2008, 50, 47–73. [Google Scholar] [CrossRef]
- Montoya, R.D.; Osorio Arias, A.; Ortiz Royero, J.C.; Ocampo-Torres, F.J. A wave parameters and directional spectrum analysis for extreme winds. Ocean Eng. 2013, 67, 100–118. [Google Scholar] [CrossRef]
- Barbariol, F.; Alves, J.-H.G.M.; Benetazzo, A.; Bergamasco, F.; Bertotti, L.; Carniel, S.; Cavaleri, L.; Chao, Y.Y.; Chawla, A.; Ricchi, A.; et al. Numerical modeling of space-time wave extremes using WAVEWATCH III. Ocean Dynam. 2017, 67, 535–549. [Google Scholar] [CrossRef]
- Abdolali, A.; Roland, A.; van der Westhuysen, A.; Meixner, J.; Chawla, A.; Hesser, T.J.; Smith, J.M.; Sikiric, M.D. Large-scale hurricane modeling using domain decomposition parallelization and implicit scheme implemented in WAVEWATCH III wave model. Coast. Eng. 2020, 157, 103656. [Google Scholar] [CrossRef]
- Abdolali, A.; van der Westhuysen, A.; Ma, Z.; Mehra, A.; Roland, A.; Moghimi, S. Evaluating the accuracy and uncertainty of atmospheric and wave model hindcasts during severe events using model ensembles. Ocean Dyn. 2021, 71, 217–235. [Google Scholar] [CrossRef]
- Ris, R.C.; Holthuijsen, L.H.; Booij, N. A third-generation wave model for coastal regions: 2. Verification. J. Geophys. Res. 1999, 104, 7667–7681. [Google Scholar] [CrossRef]
- Bi, F.; Song, J.; Wu, K.; Xu, Y. Evaluation of the simulation capability of the Wavewatch III model for Pacific Ocean wave. Acta Oceanol. Sin. 2015, 34, 43–57. [Google Scholar] [CrossRef]
- Zieger, S.; Vinoth, J.; Young, I.R. Joint calibration of multiplatform altimeter measurements of wind speed and wave height over the past 20 years. J. Atmos. Ocean. Technol. 2009, 26, 2549–2564. [Google Scholar] [CrossRef]
- Ponce de León, S.; Bettencourt, J.H. Composite analysis of North Atlantic extra-tropical cyclone waves from satellite altimetry observations. Adv. Space Res. 2021, 68, 762–772. [Google Scholar] [CrossRef]
- Liu, Q.; Babanin, A.V.; Guan, C.; Zieger, S.; Sun, J.; Jia, Y. Calibration and validation of HY-2 altimeter wave height. J. Atmos. Ocean. Technol. 2016, 33, 919–936. [Google Scholar] [CrossRef]
- Campos, R.M.; Alves, J.H.G.M.; Soares, C.G.; Guimaraes, L.G.; Parente, C.E. Extreme wind-wave modeling and analysis in the south Atlantic ocean. Ocean Model. 2018, 124, 75–93. [Google Scholar] [CrossRef]
- Hasselmann, S.; Hasselmann, K.; Allender, J.H.; Barnett, T.P. Computations and parameterizations of the nonlinear energy transfer in a gravity-wave specturm. Part II: Parameterizations of the nonlinear energy transfer for application in wave models. J. Phys. Oceanogr. 1985, 15, 1378–1392. [Google Scholar] [CrossRef]
- Van Vledder, G.P. The WRT method for the computation of non-linear four-wave interactions in discrete spectral wave models. Coast. Eng. 2006, 53, 223–242. [Google Scholar] [CrossRef]
- WAVEWATCH III Development Group, User Manual and System Documentation of WAVEWATCH III Version 6.07. Techn., 333. Available online: https://github.com/NOAA-EMC/WW3/wiki/files/manual.pdf (accessed on 25 January 2023).
- Stopa, J.E. Wind forcing calibration and wave hindcast comparison using multiple reanalysis and merged satellite wind datasets. Ocean Model. 2018, 127, 55–69. [Google Scholar] [CrossRef]
- Campos, R.M.; D’Agostini, A.; Franca, B.R.L.; Damiao, A.L.A.; Soares, C.G. Implementation of a multi-grid operational wave forecast in the South Atlantic Ocean. Ocean Eng. 2022, 243, 110173. [Google Scholar] [CrossRef]
- Moon, I.J.; Ginnis, I.; Hara, T.; Thomas, B. Physics-based parameterization of air-sea momentum flux at high wind speeds and its impact on hurricane intensity predictions. Mon. Weather Rev. 2006, 135, 2869–2878. [Google Scholar] [CrossRef]
- Babanin, A.V.; Banner, M.L.; Young, I.R.; Donelan, M.A. Wave-follower field measurements of the wind-input spectral function. Part III: Parameterization of the wind-input enhancement due to wave breaking. J. Phys. Oceanogr. 2007, 37, 2764–2775. [Google Scholar] [CrossRef]
- Waters, J.; Wyatt, L.R.; Wolf, J.; Hines, A. Data assimilation of partitioned HF radar wave data into Wavewatch III. Ocean Model. 2013, 72, 17–31. [Google Scholar] [CrossRef]
- Qi, P.; Cao, L. Establishment and tests of EnOI assimilation module for WAVEWATCH III. Chin. J. Ocean. Limnol. 2015, 33, 1295–1308. [Google Scholar] [CrossRef]
- Li, J.; Zhang, S. Mitigation of model bias influences on wave data assimilation with multiple assimilation systems using WaveWatch III v5.16 and SWAN v41.20. Geosci. Model Dev. 2020, 13, 1035–1054. [Google Scholar] [CrossRef]
- Li, J.-G. Propagation of ocean surface waves on a spherical multiple-cell grid. J. Comput. Phys. 2012, 231, 8262–8277. [Google Scholar] [CrossRef]
- Amrutha, M.M.; Kumar, V.S.; Sandhya, K.G.; Nair, T.B.; Rathod, J.L. Wave hindcast studies using SWAN nested in WAVEWATCH III—Comparison with measured nearshore buoy data off Karwar, eastern Arabian Sea. Ocean Eng. 2016, 119, 114–124. [Google Scholar] [CrossRef]
- Kuznetsova, A.; Baydakov, G.; Papko, V.; Kandaurov, A.; Vdovin, M.; Sergeev, D.; Troitskaya, Y. Adjusting of Wind Input Source Term in WAVEWATCH III Model for the Middle-Sized Water Body on the Basis of the Field Experiment. Adv. Meteorol. 2016, 2016, 8539127. [Google Scholar] [CrossRef]
- Kazeminezhad, M.H.; Siadatmousavi, S.M. Performance evaluation of WAVEWATCH III model in the Persian Gulf using different wind resources. Ocean Dynam. 2017, 67, 839–855. [Google Scholar] [CrossRef]
- Siadatmousavi, S.M.; Jose, F.; da Silva, G.M. Sensitivity of a third generation wave model to wind and boundary condition sources and model physics: A case study from the South Atlantic Ocean off Brazil coast. Comput. Geosci. 2016, 90, 57–65. [Google Scholar] [CrossRef]
- Fernández, L.; Calvino, C.; Dias, F. Sensitivity analysis of wind input parametrizations in the WAVEWATCH III spectral wave model using the ST6 source term package for Ireland. Appl. Ocean Res. 2021, 115, 102826. [Google Scholar] [CrossRef]
- Kalourazi, M.Y.; Siadatmousavi, S.M.; Yeganeh-Bakhtiary, A.; Jose, F. WAVEWATCH-III source terms evaluation for optimizing hurricane wave modeling: A case study of Hurricane Ivan. Oceanologia 2021, 63, 194–213. [Google Scholar] [CrossRef]
- Roh, M.; La, N.R.; Oh, S.M.; Kang, K.R.; Oh, Y.J.; Kim, H.S. Verification of forecast performance of a rapid refresh wave model based on wind-wave interaction effect. J. Mar. Sci. Eng. 2021, 9, 1230. [Google Scholar] [CrossRef]
- Beyramzadeh, M.; Siadatmousavi, S.M.; Derkani, M.H. Calibration and skill assessment of two input and dissipation parameterizations in WAVEWATCH-III model forced with ERA5 winds with application to Persian Gulf and Gulf of Oman. Ocean Eng. 2021, 219, 108445. [Google Scholar] [CrossRef]
- Shao, W.; Yu, W.; Jiang, X.; Shi, J.; Wei, Y.; Ji, Q. Analysis of Wave Distributions Using the WAVEWATCH-III Model in the Arctic Ocean. J. Ocean Univ. China 2022, 21, 15–27. [Google Scholar] [CrossRef]
- Hwang, P.A. A note on the ocean surface roughness spectrum. J. Atmos. Ocean. Technol. 2011, 28, 436–443. [Google Scholar] [CrossRef]
- WMO. Guide to Wave Analysis and Forecasting, 3rd ed.; World Meteorological Organization (WMO): Geneva, Switzerland, 2018; p. 131. [Google Scholar]


| Name | Description |
|---|---|
| Model | WAVEWATCH III ver.6.07 |
| Co-ordinate | Spherical co-ordinate |
| Domain | 20° N~50° N, 115° E~150° E |
| Resolution | (1051 × 901) |
| Forecast time | +120 h (3 hourly cycle) |
| Initial condition | 12 h forecast from the previous run |
| Boundary condition | Global wave model with data assimilation |
| Forcing data | Global Data Assimilation and Prediction System Korea Integrate Model (12 km L91) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roh, M.; Oh, S.-M.; Chang, P.-H.; Kang, H.-S.; Kim, H.-S. Sensitivity Analysis of Forecasting Performance for ST6 Parameterization in High-Resolution Wave Model Based on WAVEWATCH III. J. Mar. Sci. Eng. 2023, 11, 1038. https://doi.org/10.3390/jmse11051038
Roh M, Oh S-M, Chang P-H, Kang H-S, Kim H-S. Sensitivity Analysis of Forecasting Performance for ST6 Parameterization in High-Resolution Wave Model Based on WAVEWATCH III. Journal of Marine Science and Engineering. 2023; 11(5):1038. https://doi.org/10.3390/jmse11051038
Chicago/Turabian StyleRoh, Min, Sang-Myeong Oh, Pil-Hun Chang, Hyun-Suk Kang, and Hyung-Suk Kim. 2023. "Sensitivity Analysis of Forecasting Performance for ST6 Parameterization in High-Resolution Wave Model Based on WAVEWATCH III" Journal of Marine Science and Engineering 11, no. 5: 1038. https://doi.org/10.3390/jmse11051038
APA StyleRoh, M., Oh, S.-M., Chang, P.-H., Kang, H.-S., & Kim, H.-S. (2023). Sensitivity Analysis of Forecasting Performance for ST6 Parameterization in High-Resolution Wave Model Based on WAVEWATCH III. Journal of Marine Science and Engineering, 11(5), 1038. https://doi.org/10.3390/jmse11051038







