Ship Intrusion Collision Risk Model Based on a Dynamic Elliptical Domain
Abstract
1. Introduction
2. AIS Data-Driven Dynamic Elliptical Ship Domain
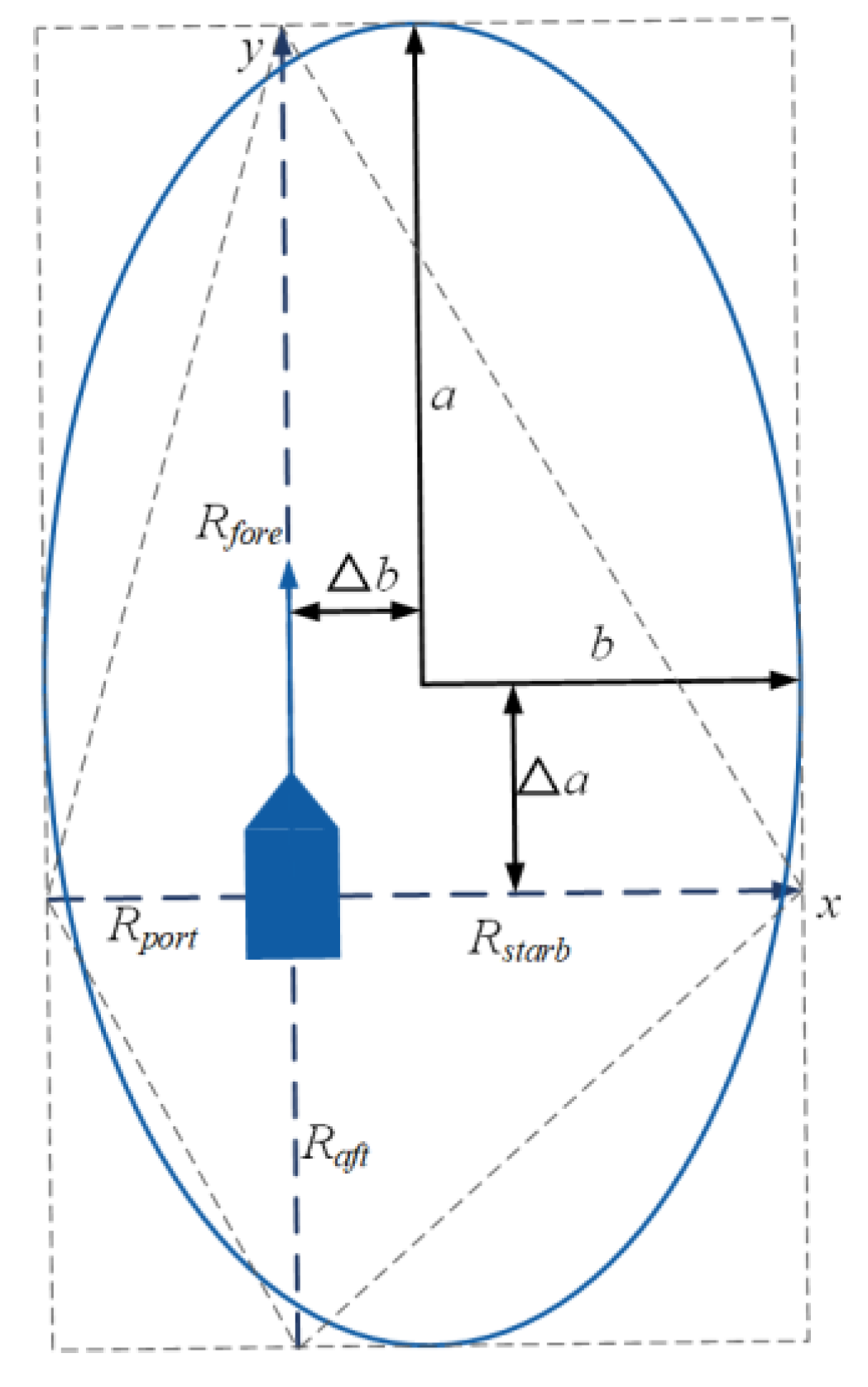
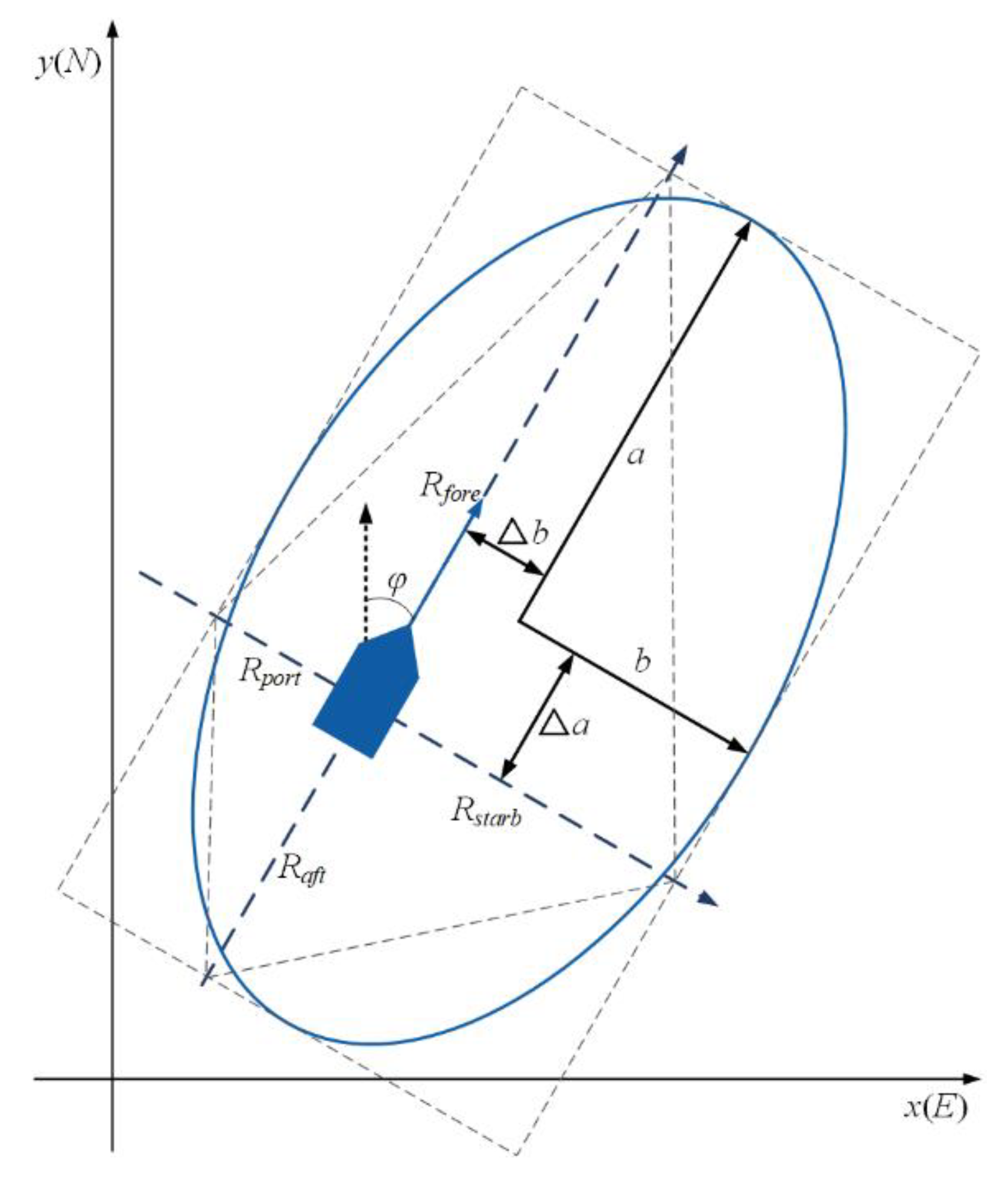
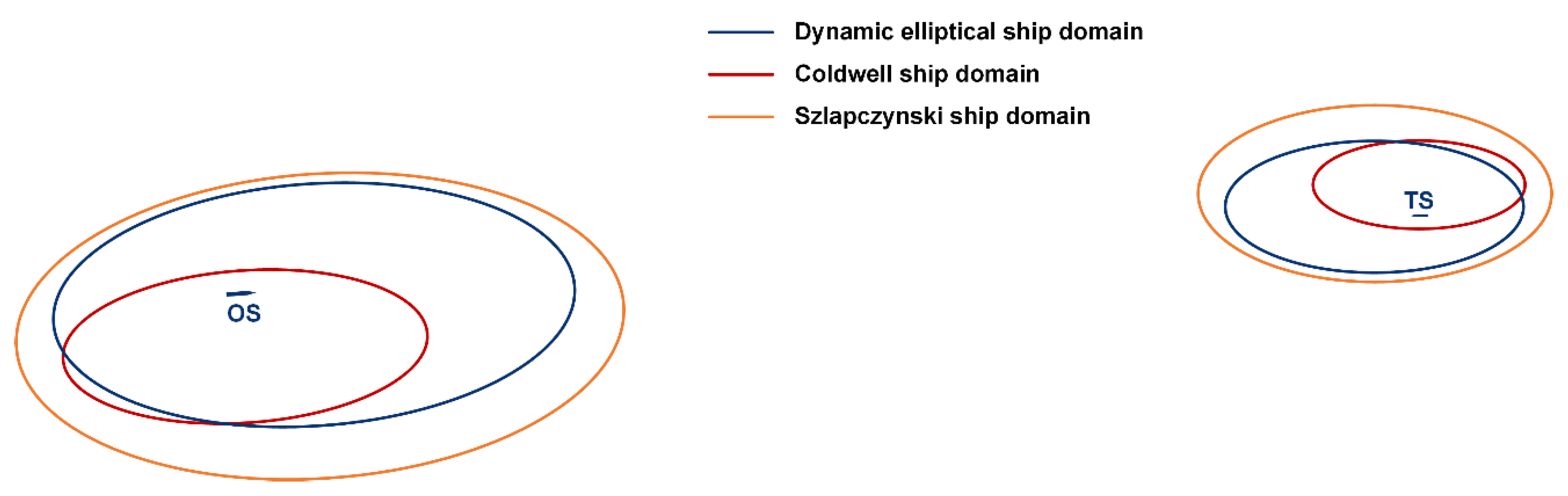
2.1. Dynamic Elliptical Ship Domain
2.2. Incorporation of AIS Data
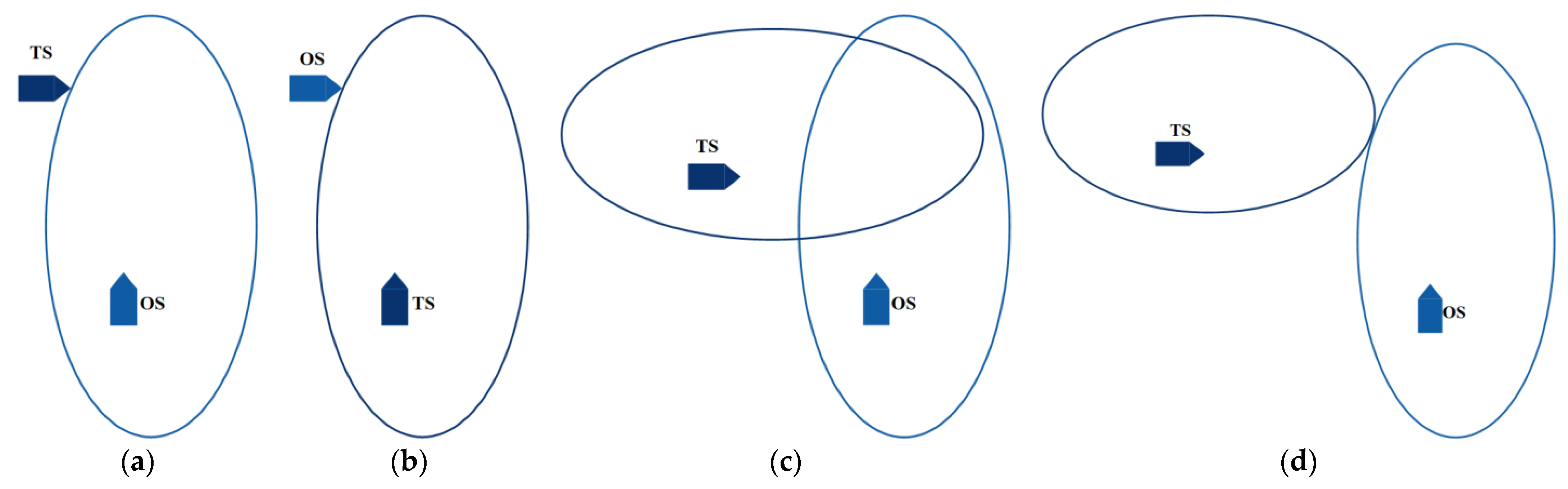
2.3. Domain-Based Safety Criteria
- The OS domain should not be invaded by the TS;
- The TS domain should not be invaded by the OS;
- Neither the OS nor TS should invade each other’s domain;
- The OS and TS domains should not overlap.
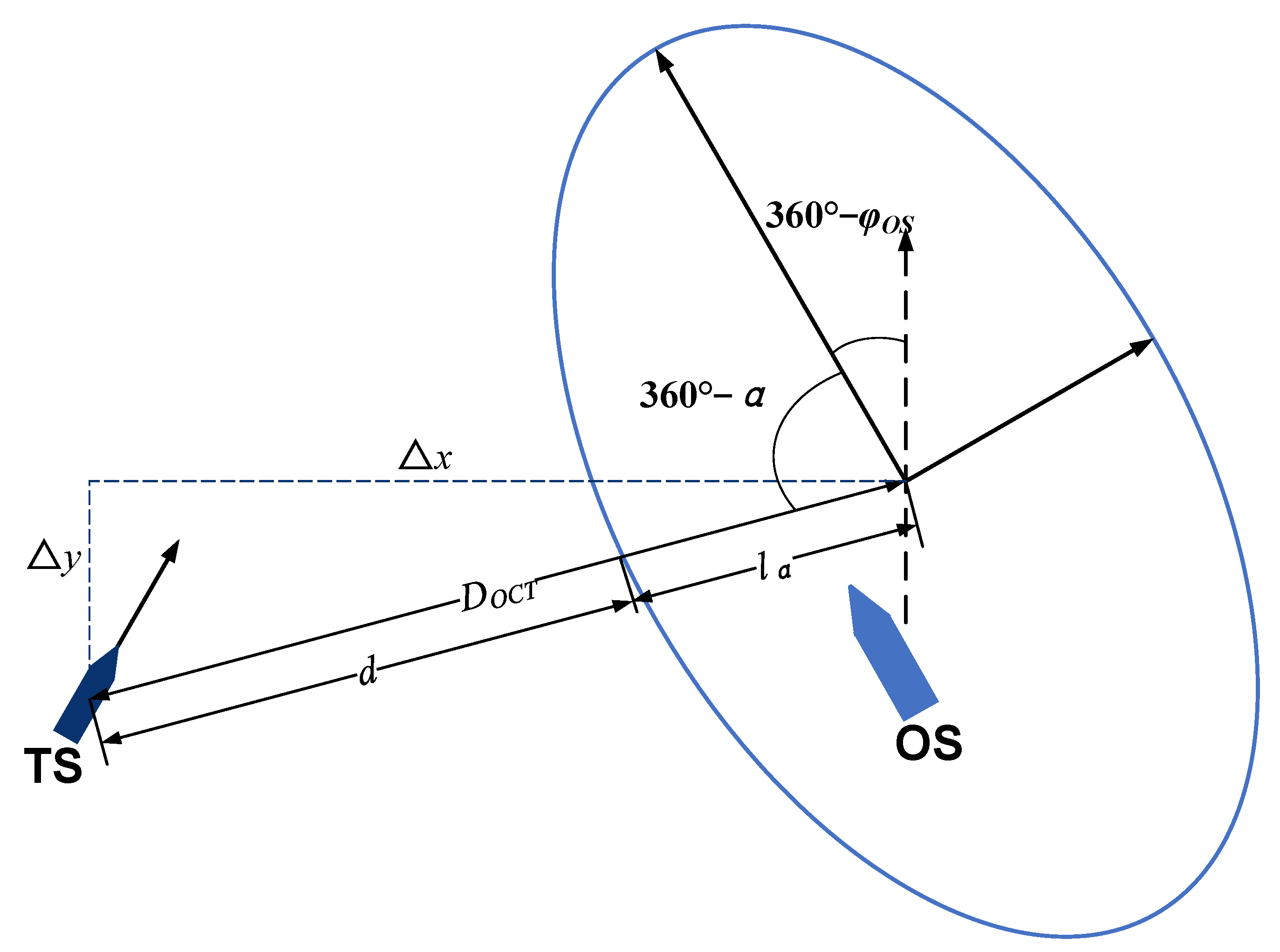
2.4. Calculation of Domain Parameters
3. Ship Intrusion Collision Risk Model
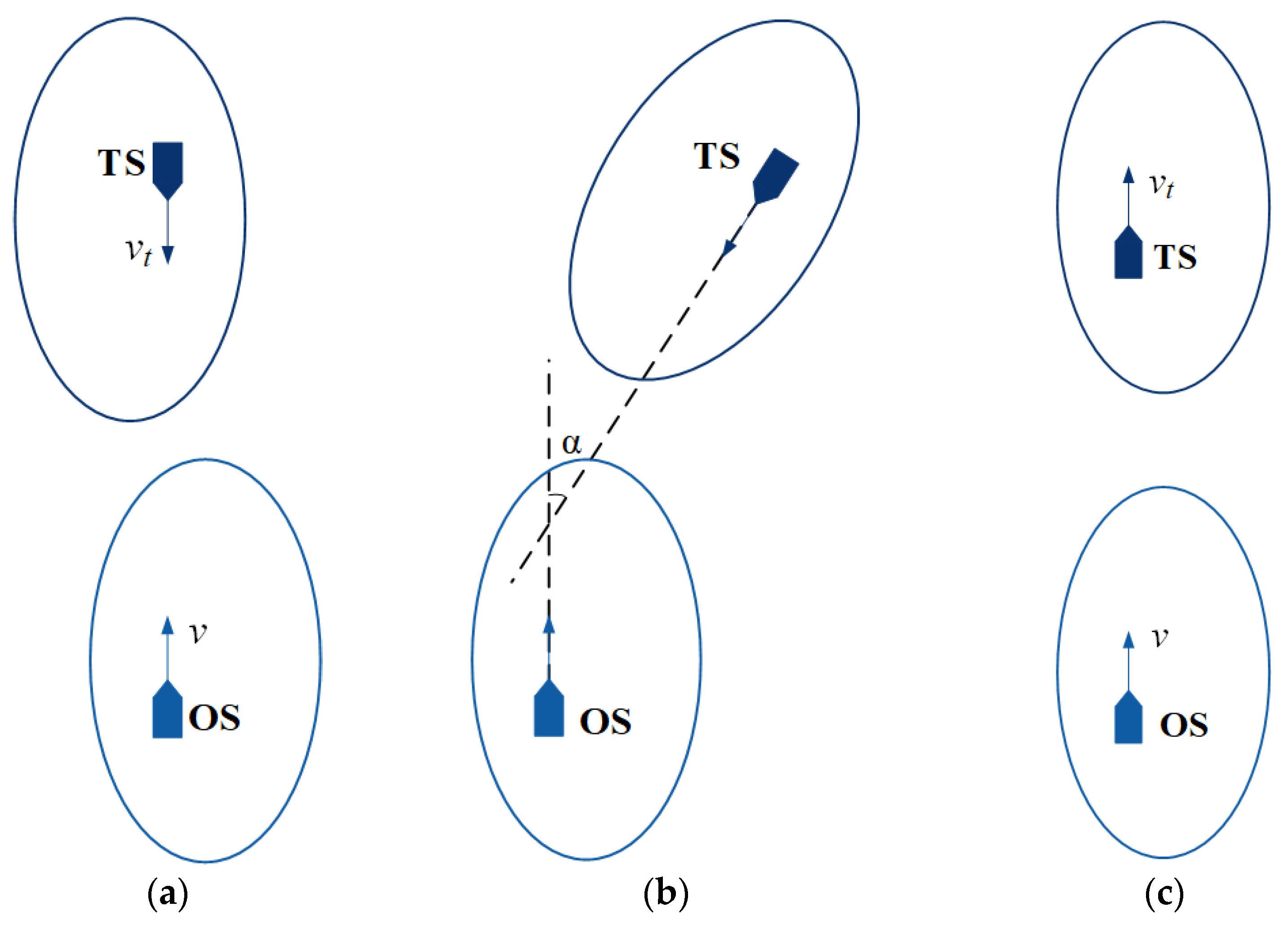
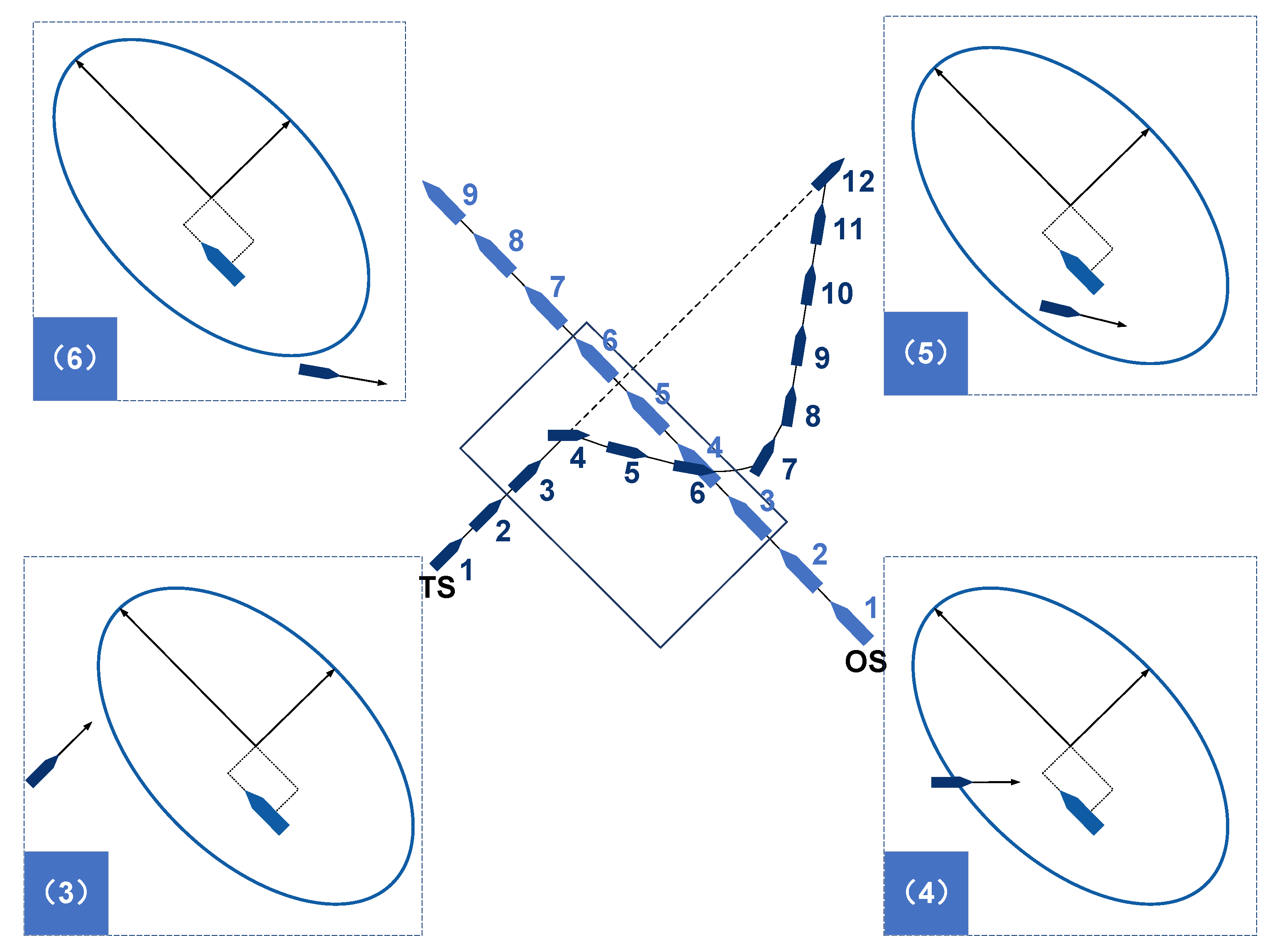
3.1. Ship Intrusion Collision Risk
- The TS is outside the OS domain: the TS is sailing toward the OS domain (Figure 6(3)), so .
- The TS is within the OS domain: the TS enters the OS domain, reaches the maximum degree of intrusion, and sails out of the domain (Figure 6(4,5)), so .
- The TS is outside the ship domain: the TS is leaving the OS domain (Figure 6(6)), so .
3.2. Parameter Calculation
4. Simulation of Model
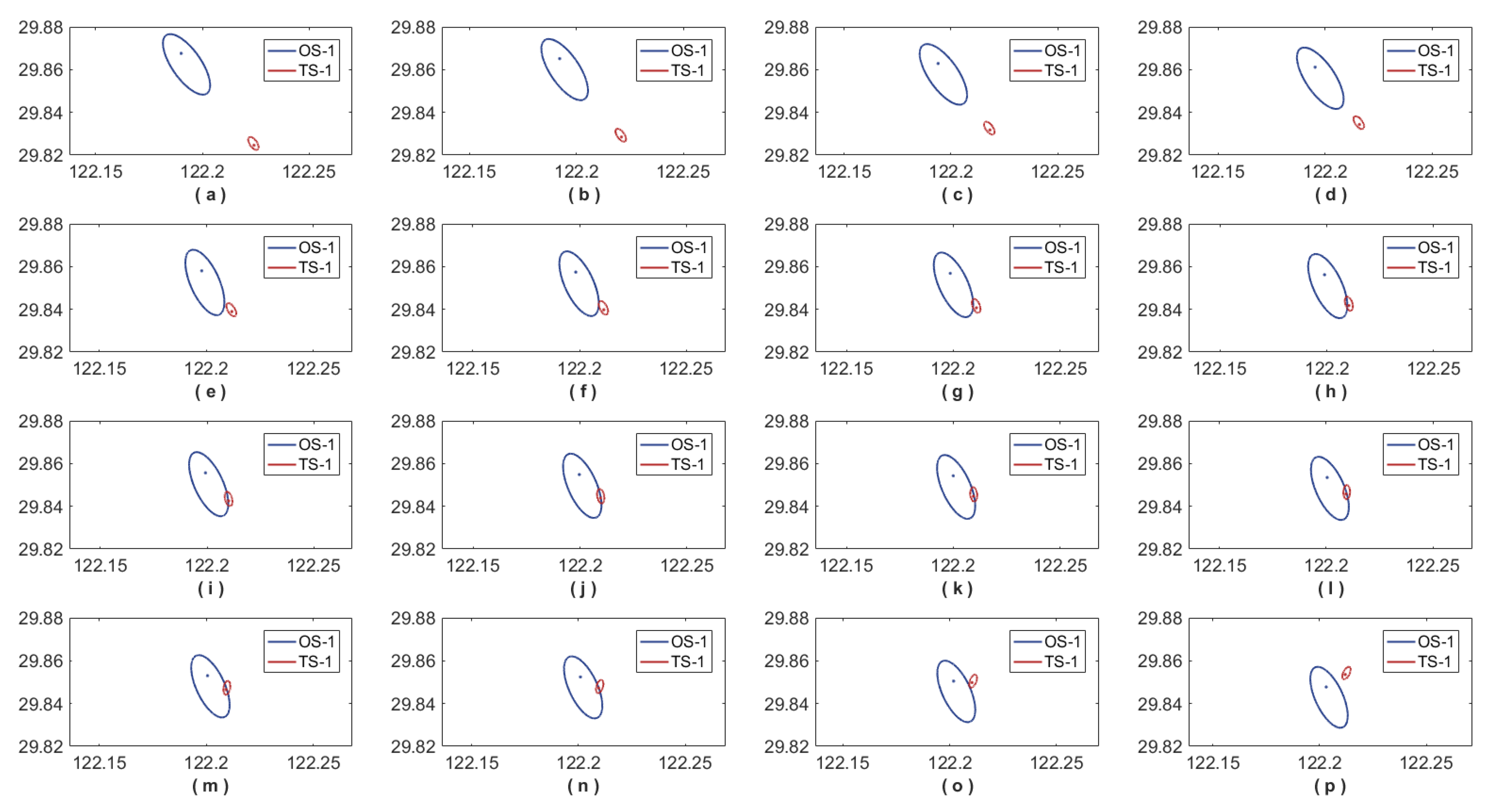
4.1. Head-On Encounter Situation
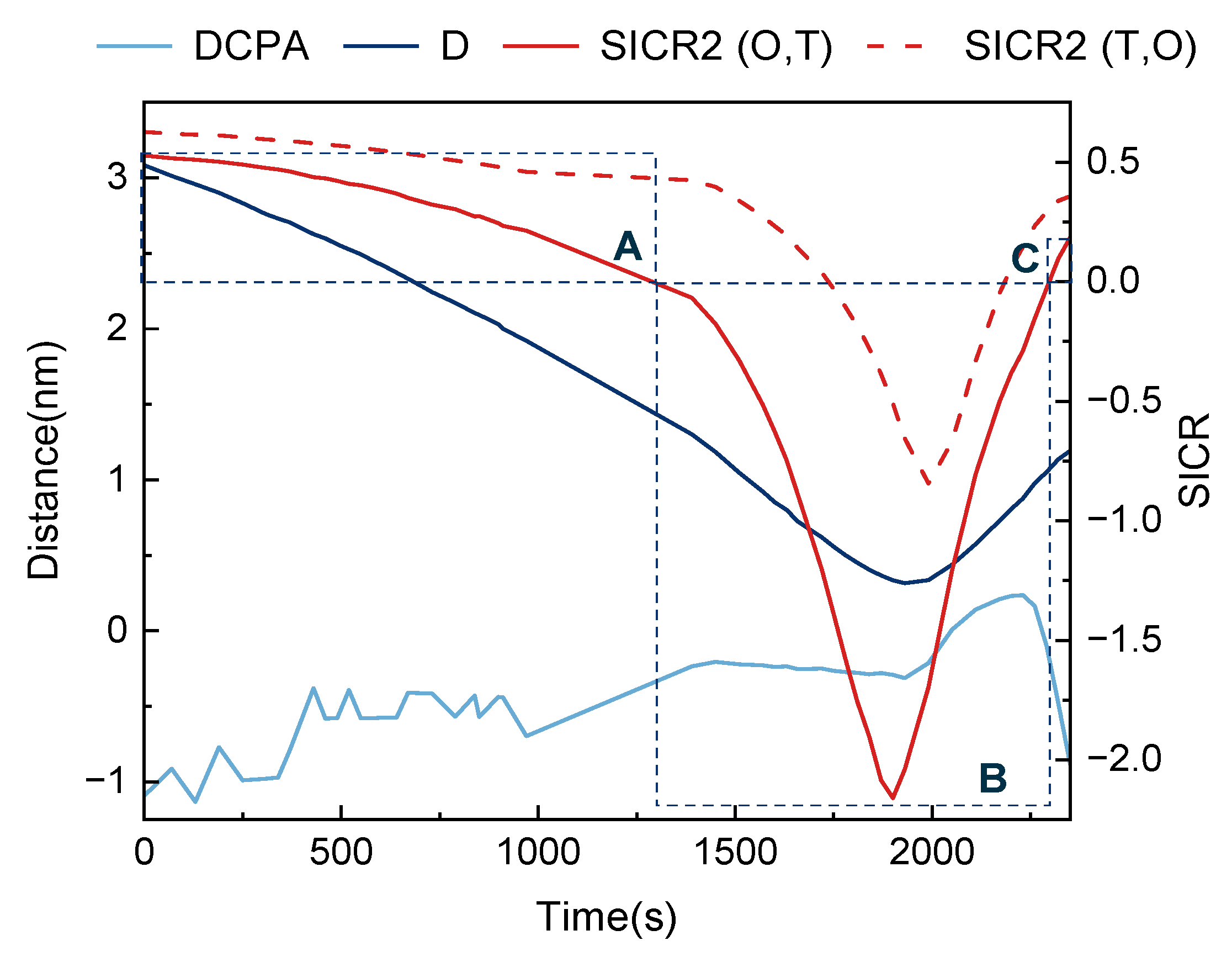
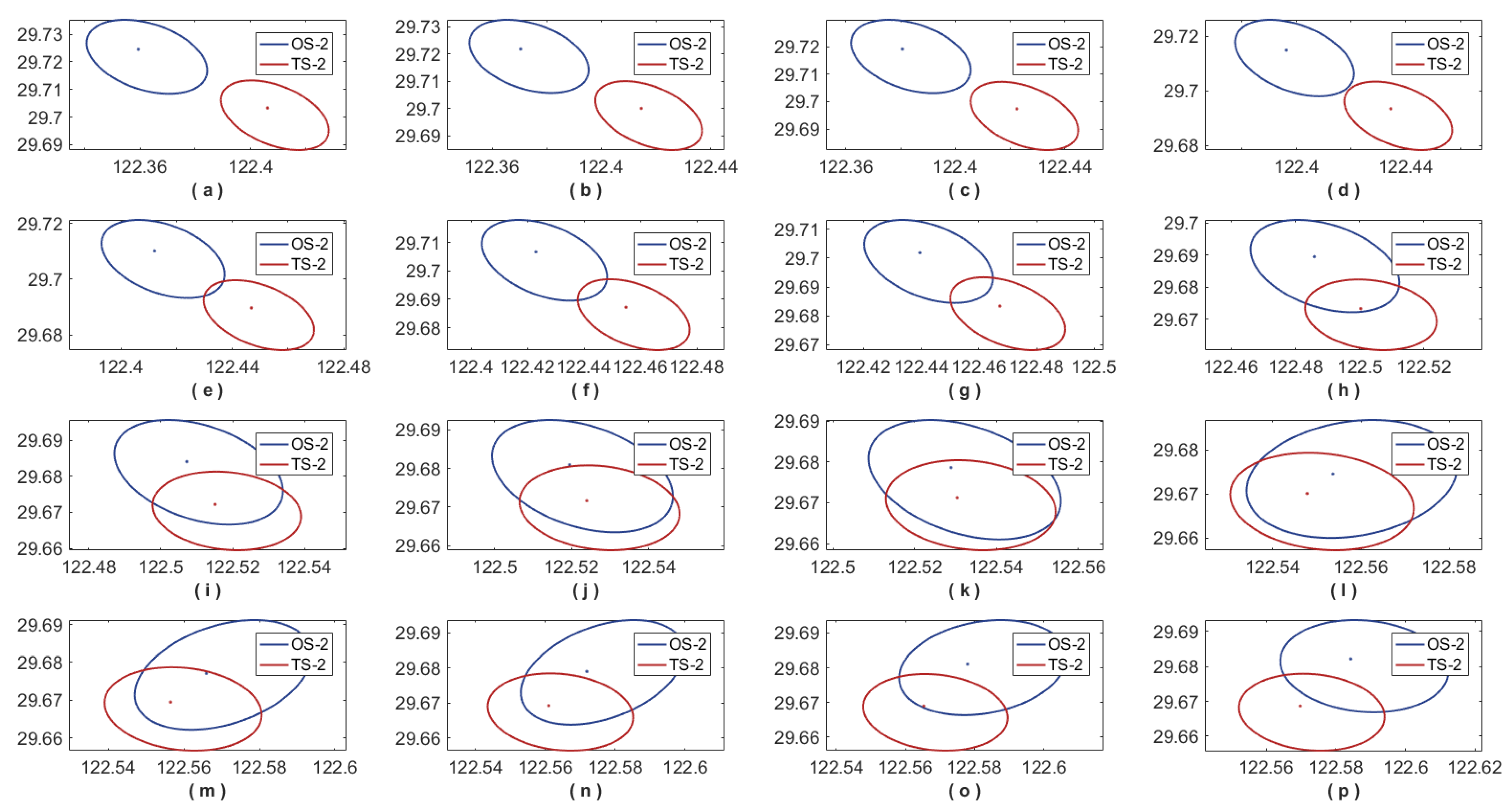
4.2. Overtaking Encounter Situation
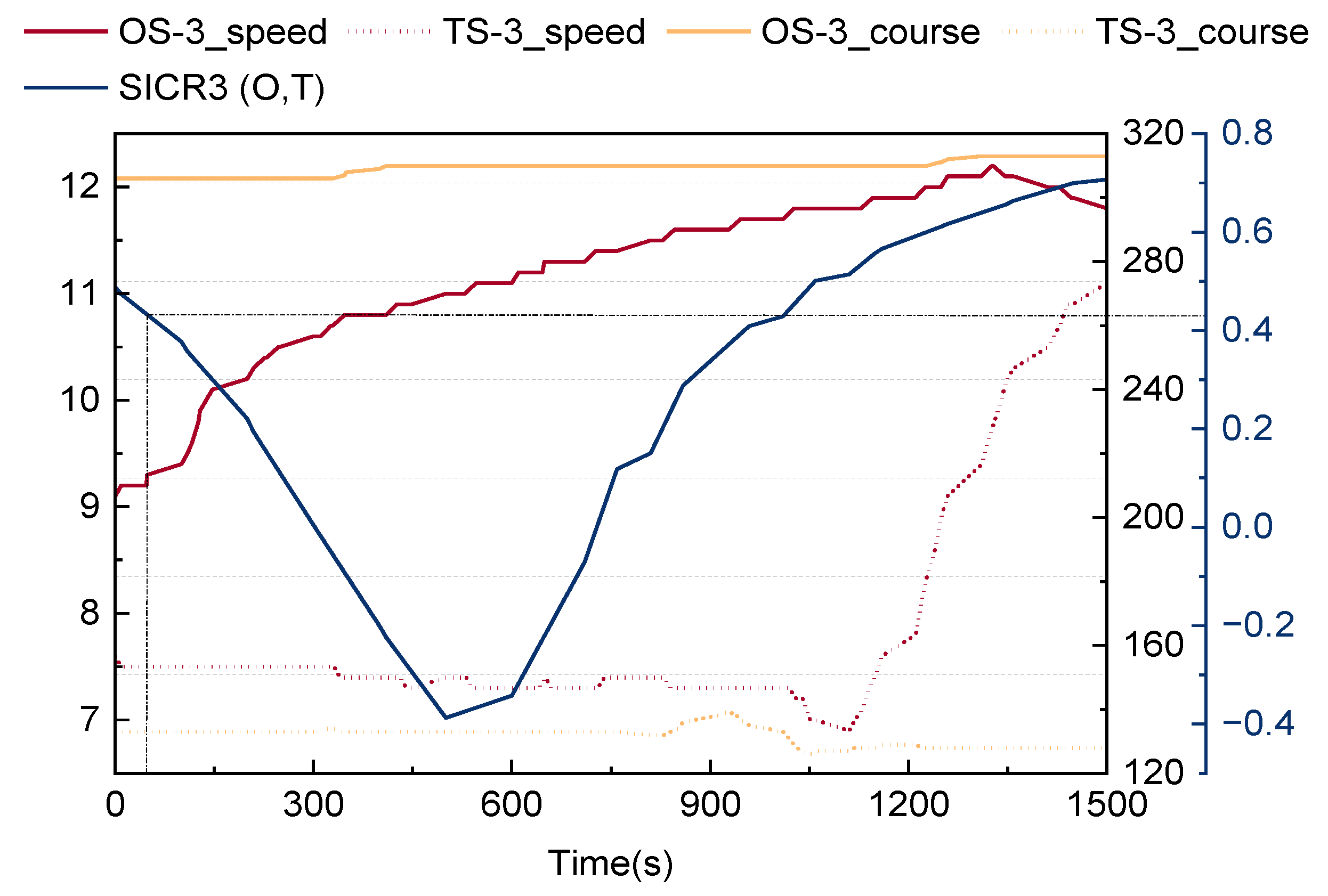
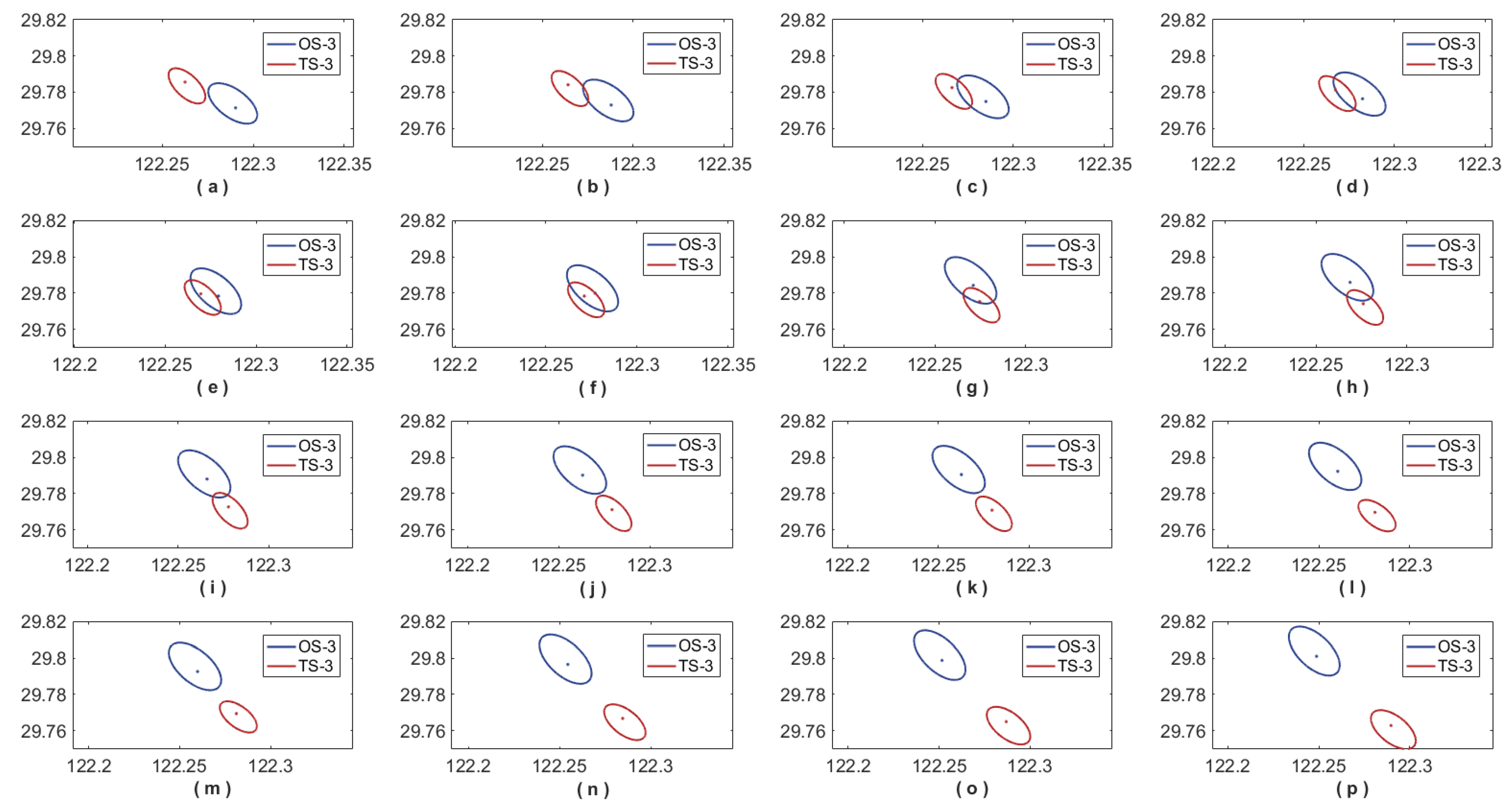
4.3. Crossing Encounter Situation
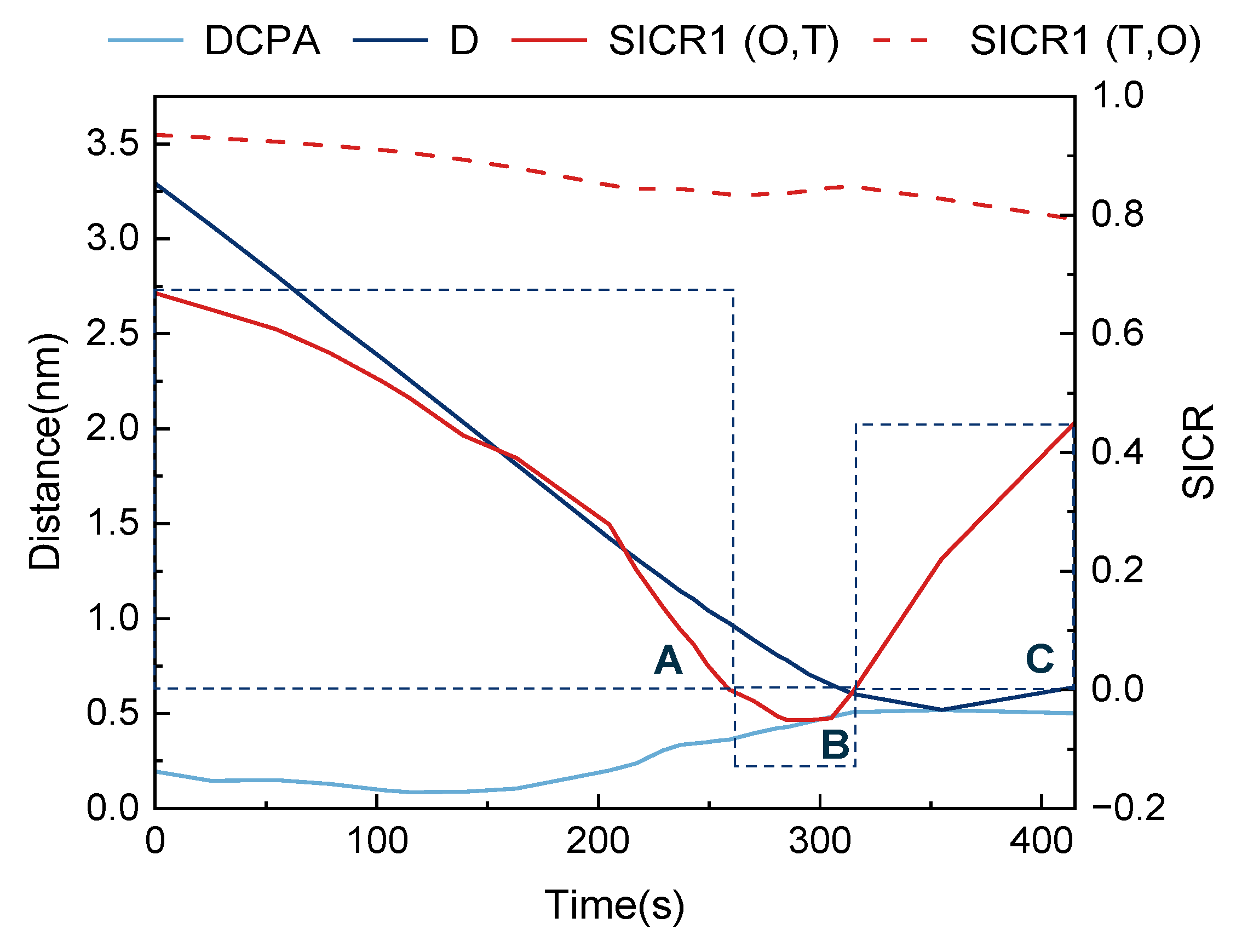
4.4. Case Simulation Discussion
5. Conclusions
- Utilizing AIS data to optimize the dynamic elliptical ship domain meets the needs of algorithm calculation and visual display, which is convenient for rapid application in navigation collision avoidance practice.
- The proposed SICR is more reasonable than the previous CRI because it is based on a dynamic elliptical ship domain driven by AIS data, and it fully considers the ship speed and maneuverability.
- The SICR values of two ships in an encounter situation may differ because their differing maneuverability and speed affect the sizes of their individual domains, which in turn affect the safe distance. In this case, the smaller value between SICR (O, T) and SICR (T, O) at a given time can be used to measure the collision risk.
- The SICR model can accurately detect the collision risk, and it can facilitate early warning of a collision risk. The simulation results indicated that ships can collaborate to avoid collisions at a minimum SICR of 0.5–0.6, and collision avoidance actions are most effective at SICR values of 0.3–0.5.
- During the transmission of AIS data, the ship position is inevitably affected by wind, waves, and currents. This generates offsets in the speed and position of the ship, which introduces some error in the SICR calculation.
- Existing ship track prediction models have low prediction accuracy and a lack of real-time prediction capability. We are developing an online multioutput least squares support vector machine (SM-OMLSSVR) ship track prediction model based on AIS data and a selection mechanism. The AIS data of TSs with a potential collision risk are obtained in real time, and the TS track is predicted to assist the OS with evaluating the collision risk.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| AIS | Automatic Identification System |
| COLREGs | International Regulations for Preventing Collisions at Sea |
| CRI | Collision Risk Index |
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
| DCPA | Distance at the closest point of approach |
| IMO | International Maritime Organization |
| MMSI | Maritime Mobile Service Identity |
| OS | Own ship |
| OS-1 | Own ship in the head-on situation |
| OS-2 | Own ship in the overtaking situation |
| OS-3 | Own ship in the crossing situation |
| SICR | Ship Intrusion Collision Risk |
| SICR (O, T) | Ship Intrusion Collision Risk of the TS entering the OS domain |
| SICR (T, O) | Ship Intrusion Collision Risk of the OS entering the TS domain |
| SICR1 (O, T) | Ship Intrusion Collision Risk of the TS entering the OS domain in the head-on situation |
| SICR1 (T, O) | Ship Intrusion Collision Risk of the OS entering the TS domain in the head-on situation |
| SICR2 (O, T) | Ship Intrusion Collision Risk of the TS entering the OS domain in the overtaking situation |
| SICR2 (T, O) | Ship Intrusion Collision Risk of the OS entering the TS domain in the overtaking situation |
| SICR3 (O, T) | Ship Intrusion Collision Risk of the TS entering the OS domain in the crossing situation |
| SICR3 (T, O) | Ship Intrusion Collision Risk of the OS entering the TS domain in the crossing situation |
| SM-OMLSSVR | Online Multioutput Least Squares Support Vector Machine based on Selection Mechanism |
| TCPA | Time at the closest point of approach |
| TS | Target Ship |
| TS-1 | Target Ship in the head-on situation |
| TS-2 | Target Ship in the overtaking situation |
| TS-3 | Target Ship in the crossing situation |
References
- International Maritime Organization. Review of Maritime Transport 2019; IMO: London, UK, 2019. [Google Scholar]
- Agency EMS. European Maritime Safety Report 2022; Publications Office of the European Union: Luxembourg, 2022. [Google Scholar]
- Rong, H.; Teixeira, A.P.; Soares, C.G. Spatial correlation analysis of near ship collision hotspots with local maritime traffic characteristics. Reliab. Eng. Syst. Saf. 2021, 209, 107463. [Google Scholar] [CrossRef]
- Yuhong, L.; Hongbo, C.; Yanling, H. A Risk-Degree Model of Collision Based on Fuzzy Theory. Navig. China 1998, 2, 25–31. [Google Scholar]
- Shu, W.; Meng-Hong, Y.U. Development of Collision Avoidance System by Using Expert System and Search Algorithm. Ship Ence Technol. 2007, 48, 197–212. [Google Scholar]
- Zhen, R.; Riveiro, M.; Jin, Y. A novel analytic framework of real-time multi-vessel collision risk assessment for maritime traffic surveillance. Ocean Eng. 2017, 145, 492–501. [Google Scholar] [CrossRef]
- Chen, P.; Li, M.; Mou, J. A Velocity Obstacle-Based Real-Time Regional Ship Collision Risk Analysis Method. J. Mar Sci Eng 2021, 9, 428. [Google Scholar] [CrossRef]
- Huang, Y.; van Gelder, P.H.A.J. Collision risk measure for triggering evasive actions of maritime autonomous surface ships. Safety Sci. 2020, 127, 104708. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, Y. A Field Theory-Based Novel Algorithm for Navigational Hazard Index. J. Mar. Sci. Eng. 2023, 11, 178. [Google Scholar] [CrossRef]
- Fujii, Y.; Shiobara, R. The Analysis of Traffic Accidents. J. Navig. 1971, 24, 534–543. [Google Scholar] [CrossRef]
- Szlapczynski, R.; Szlapczynska, J. Review of ship safety domains: Models and applications. Ocean Eng. 2017, 145, 277–289. [Google Scholar] [CrossRef]
- Goodwin, E.M. A Statistical Study of Ship Domains. J. Navig. 1975, 28, 328–344. [Google Scholar] [CrossRef]
- Coldwell, T.G. Marine Traffic Behaviour in Restricted Waters. J. Navig. 1983, 36, 430–444. [Google Scholar] [CrossRef]
- Hansen, M.G.; Jensen, T.K.; Lehn-Schiøler, T.; Melchild, K.; Rasmussen, F.M.; Ennemark, F. Empirical Ship Domain based on AIS Data. J. Navig. 2013, 66, 931–940. [Google Scholar] [CrossRef]
- Iperen, E.V. Classifying Ship Encounters to Monitor Traffic Safety on the North Sea from AIS Data. Transnav Int. J. Mar. Navig. Saf. Sea Transp. 2015, 9, 51–58. [Google Scholar] [CrossRef]
- Sun, L. The Research on Mathematic Models of Decision-Making in Ship Collision Avoidance. Ph.D. Thesis, Dalian Maritime University, Dalian, China, 2000. [Google Scholar]
- Liu, S. The Research of the Inland River Channel Transit Capacity Where Ship Is Crowed. Master’s Thesis, Dalian Maritime University, Dalian, China, 2002. [Google Scholar]
- Pietrzykowski, Z.; Uriasz, J. The Ship Domain—A Criterion of Navigational Safety Assessment in an Open Sea Area. J. Navig. 2009, 62, 93–108. [Google Scholar] [CrossRef]
- Pietrzykowski, Z. Ship’s Fuzzy Domain: A Criterion for Navigational Safety in Narrow Fairways. J. Navig. 2008, 61, 499–514. [Google Scholar] [CrossRef]
- Zhu, X.; Xu, H.; Lin, J. Domain and Its Model Based on Neural Networks. J. Navig. 2001, 54, 97–103. [Google Scholar] [CrossRef]
- Wang, N. An intelligent spatial collision risk based on the quaternion ship domain. J. Navig. 2010, 63, 733–749. [Google Scholar] [CrossRef]
- Wang, N. A novel analytical framework for dynamic quaternion ship domains. J. Navig. 2013, 66, 265–281. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Huo, R.; Mao, W. A real-time ship collision risk perception model derived from domain-based approach parameters. Ocean Eng. 2022, 265, 112554. [Google Scholar] [CrossRef]
- Szlapczynski, R.; Szlapczynska, J. An analysis of domain-based ship collision risk parameters. Ocean Eng. 2016, 126, 47–56. [Google Scholar] [CrossRef]
- Liu, J.; Shi, G.; Zhu, K. A novel ship collision risk evaluation algorithm based on the maximum interval of two ship domains and the violation degree of two ship domains. Ocean Eng. 2022, 255, 111431. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, D.; Zhang, J.; Zhang, M.; Soares, C.G. A novel real-time collision risk awareness method based on velocity obstacle considering uncertainties in ship dynamics. Ocean Eng. 2020, 220, 108436. [Google Scholar] [CrossRef]
- Li, W.; Zhong, L.; Xu, Y.; Shi, G. Collision Risk Index Calculation Based on an Improved Ship Domain Model. J. Mar. Sci. Eng. 2022, 10, 2016. [Google Scholar] [CrossRef]
- Smierzchalski, R.; Michalewicz, Z. Modeling of ship trajectory in collision situations by an evolutionary algorithm. IEEE Trans. Evolut. Comput. 2000, 4, 227–241. [Google Scholar] [CrossRef]
- Wielgosz, M.; Pietrzykowski, Z. Ship domain in the restricted area—Analysis of the influence of ship speed on the shape and size of the domain. Chin. J. Clin. Neurosurg. 2012, 36, 514. [Google Scholar] [CrossRef]
- Wang, Y.; Chin, H.C. An Empirically-Calibrated Ship Domain as a Safety Criterion for Navigation in Confined Waters. J. Navig. 2016, 69, 257–276. [Google Scholar] [CrossRef]
- Zhou, D.; Zheng, Z. Dynamic Fuzzy Ship Domain Considering the Factors of Own Ship and Other Ships. J. Navig. 2019, 72, 467–482. [Google Scholar] [CrossRef]
- Pietrzykowski, Z.; Wielgosz, M. Effective ship domain—Impact of ship size and speed. Ocean Eng. 2021, 219, 108423. [Google Scholar] [CrossRef]
- Kijima, K.; Furukawa, Y. Automatic collision avoidance system using the concept of blocking area. IFAC Proc. Vol. 2003, 36, 223–228. [Google Scholar] [CrossRef]
- Pallotta, G.; Vespe, M.; Bryan, K. Vessel Pattern Knowledge Discovery from AIS Data: A Framework for Anomaly Detection and Route Prediction. Entropy 2013, 15, 2218–2245. [Google Scholar] [CrossRef]
- Aarsæther, K.G.; Moan, T. Estimating navigation patterns from AIS. J. Navig. 2009, 62, 587–607. [Google Scholar] [CrossRef]
- Zhang, W.; Goerlandt, F.; Kujala, P.; Wang, Y. An advanced method for detecting possible near miss ship collisions from AIS data. Ocean Eng. 2016, 124, 141–156. [Google Scholar] [CrossRef]





| Type | Reference | Influencing Factors |
|---|---|---|
| Static domain models | [10] | OS size, TS size, Weather conditions |
| [12] | Weather conditions, COLREGs | |
| [13] | OS size, Encounter situations, COLREGs | |
| [18] | OS size, speed, and maneuverability; Weather conditions; Traffic conditions | |
| [24] | OS size | |
| Dynamic domain models | [28] | OS speed and maneuverability |
| [29] | OS size and speed | |
| [30] | OS size and speed, TS size and speed, COLREGs | |
| [27] | OS size, speed, and maneuverability; TS size, speed, and maneuverability; Encounter situations; COLREGs | |
| Fuzzy boundary domain models | [21,22] | OS size, speed, and maneuverability; Weather conditions; COLREGs |
| [31] | Distance of TSs to OS in different directions | |
| [32] | OS size, speed, and maneuverability; Encounter situations; Weather conditions; Traffic conditions |
| Parameters | YUPENG (OS) | YUKUN (TS) |
|---|---|---|
| MMSI | 412212110 | 412701000 |
| Length overall (m) | 199.8 | 116 |
| Breadth (m) | 27.8 | 18 |
| Depth (m) | 15.5 | 8.35 |
| Displacement (T) | 22,036.7 | 5735.5 |
| Design draft (m) | 10.3 | 5.4 |
| Name | Ship Position (Relative to Nautical Miles) | Course (°) | Speed (kn) |
|---|---|---|---|
| YUPENG (OS) | (−5.7, −0.26) | 086 | 17 |
| YUKUN (TS) | (−1.5, 0) | 270 | 15 |
| MMSI | Ship Position | Course (°) | Speed (kn) | Length (m) | |
|---|---|---|---|---|---|
| OS-1 | 210302000 | (29°52.056′ N, 122°11.406′ E) | 145 | 12.2 | 225 |
| TS-1 | 355384000 | (29°49.476′ N, 122°13.451′ E) | 325 | 19.1 | 45 |
| MMSI | Ship Position | Course (°) | Speed (kn) | Length (m) | |
|---|---|---|---|---|---|
| OS-2 | 209251000 | (29°43.474′ N, 122°21.564′ E) | 108 | 16.9 | 337 |
| TS-2 | 235069077 | (29°41.199′ N, 122°24.372′ E) | 112 | 13.3 | 340 |
| MMSI | Ship Position | Course (°) | Speed (kn) | Length (m) | |
|---|---|---|---|---|---|
| OS-3 | 219080000 | (29°46.283′ N, 122°17.418′ E) | 306 | 9.1 | 300 |
| TS-3 | 355384000 | (29°47.133′ N, 122°15.747′ E) | 133 | 7.6 | 260 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Zhong, L.; Liu, Y.; Shi, G. Ship Intrusion Collision Risk Model Based on a Dynamic Elliptical Domain. J. Mar. Sci. Eng. 2023, 11, 1122. https://doi.org/10.3390/jmse11061122
Li W, Zhong L, Liu Y, Shi G. Ship Intrusion Collision Risk Model Based on a Dynamic Elliptical Domain. Journal of Marine Science and Engineering. 2023; 11(6):1122. https://doi.org/10.3390/jmse11061122
Chicago/Turabian StyleLi, Weifeng, Lufeng Zhong, Yaochen Liu, and Guoyou Shi. 2023. "Ship Intrusion Collision Risk Model Based on a Dynamic Elliptical Domain" Journal of Marine Science and Engineering 11, no. 6: 1122. https://doi.org/10.3390/jmse11061122
APA StyleLi, W., Zhong, L., Liu, Y., & Shi, G. (2023). Ship Intrusion Collision Risk Model Based on a Dynamic Elliptical Domain. Journal of Marine Science and Engineering, 11(6), 1122. https://doi.org/10.3390/jmse11061122





