Comprehensive Analysis of the Impact of the Icing of Wind Turbine Blades on Power Loss in Cold Regions
Abstract
1. Introduction
2. Numerical Simulation
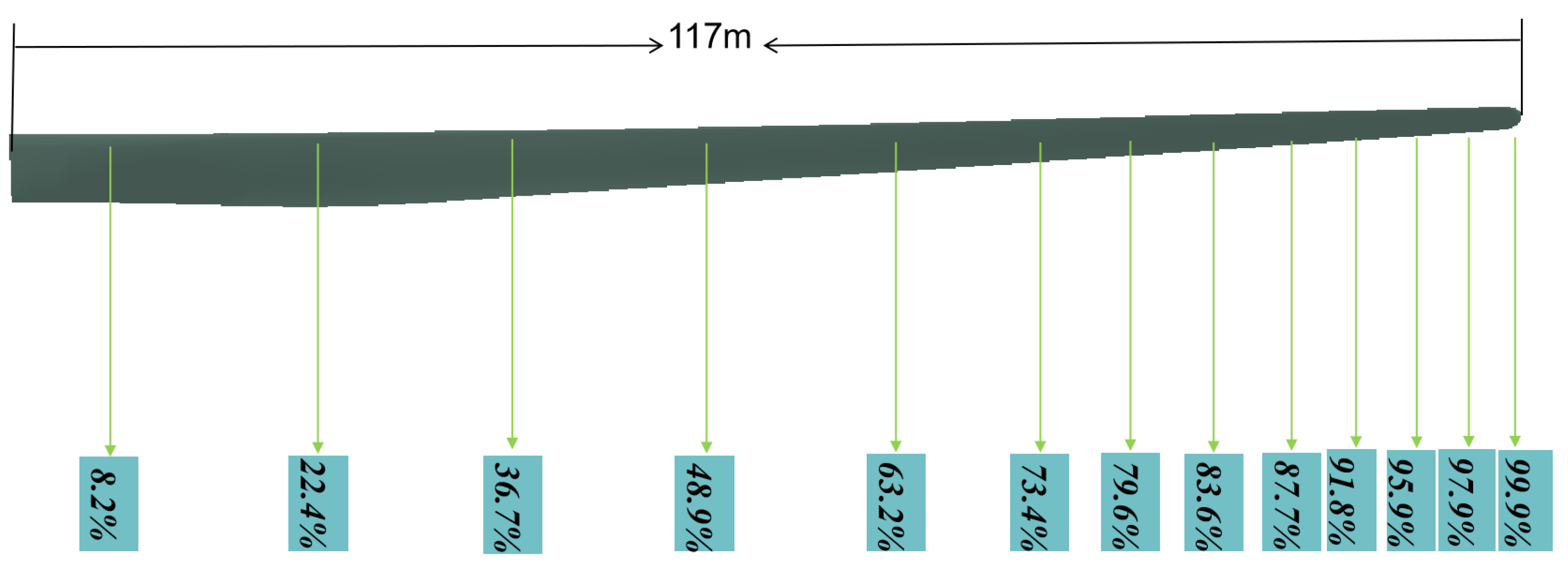
2.1. Wind Turbine Model
2.2. Numerical Model
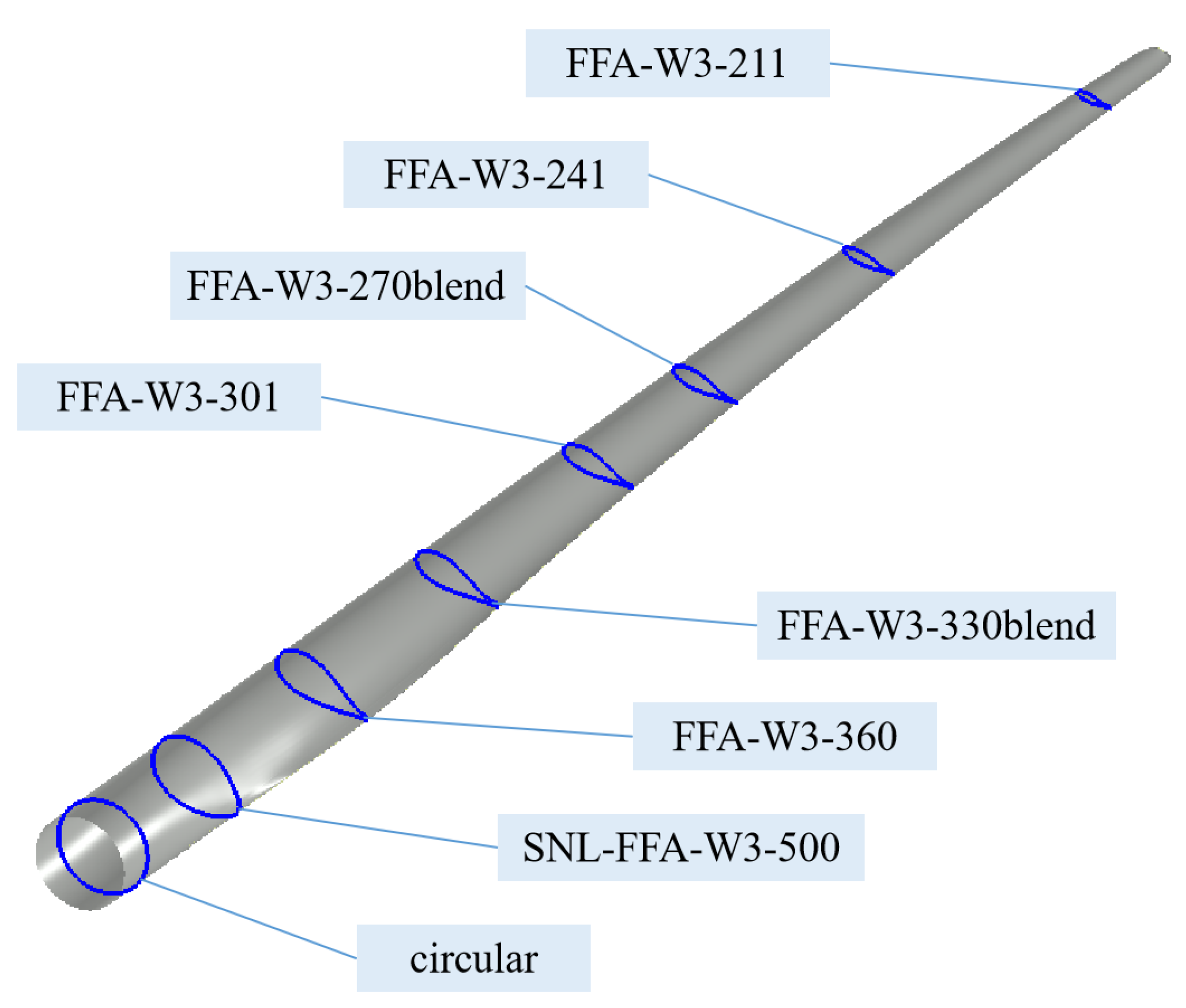
2.2.1. Icing Section Selection
2.2.2. Icing Calculation Model
2.2.3. Environmental Parameter
3. Theoretical Method
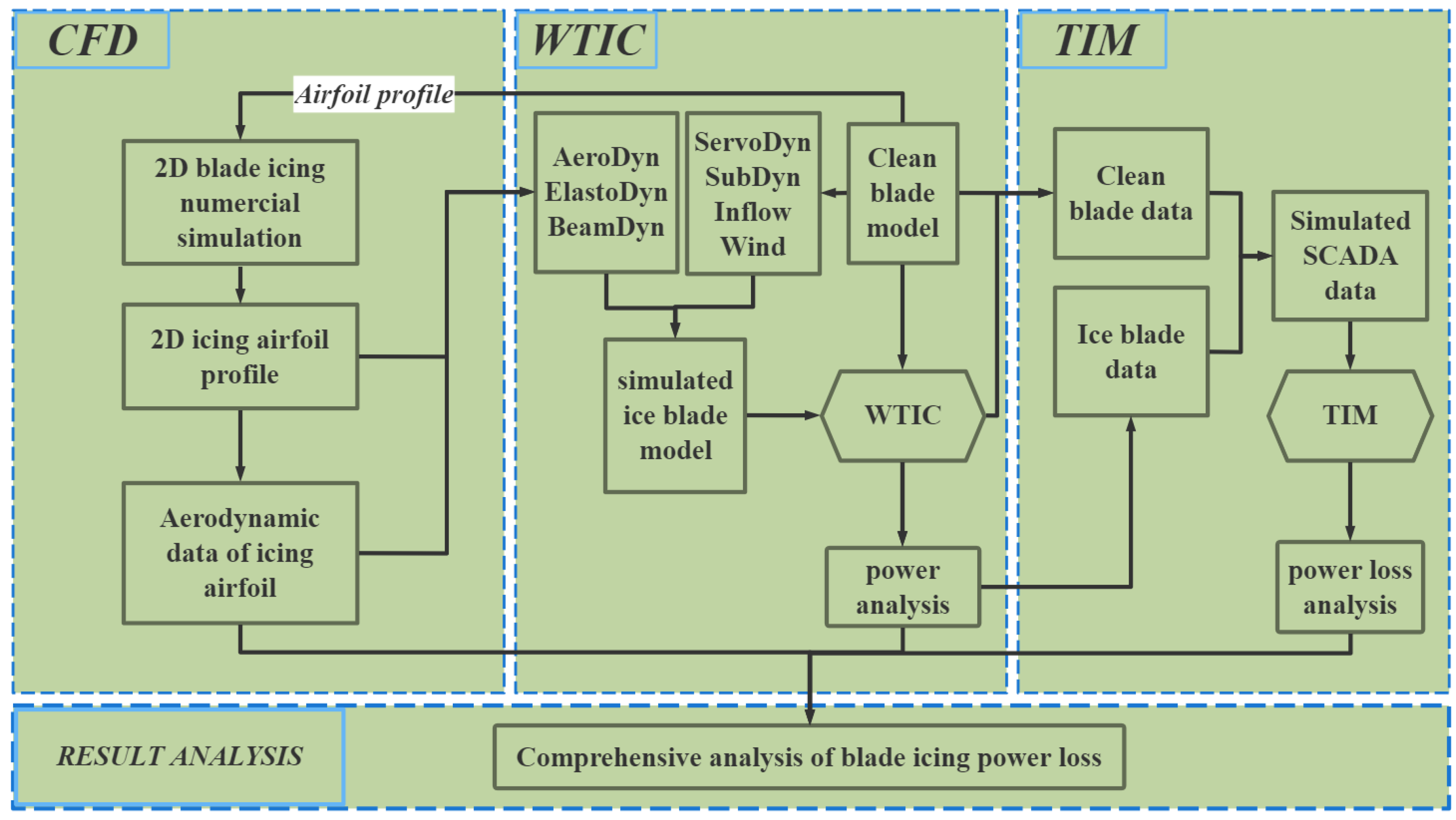
3.1. Method and Procedure
3.2. The Icing Growth Model
3.2.1. Motion Models of Air and Water Droplets
3.2.2. Icing Model
3.3. Wind Turbine Integrated Calculation Method
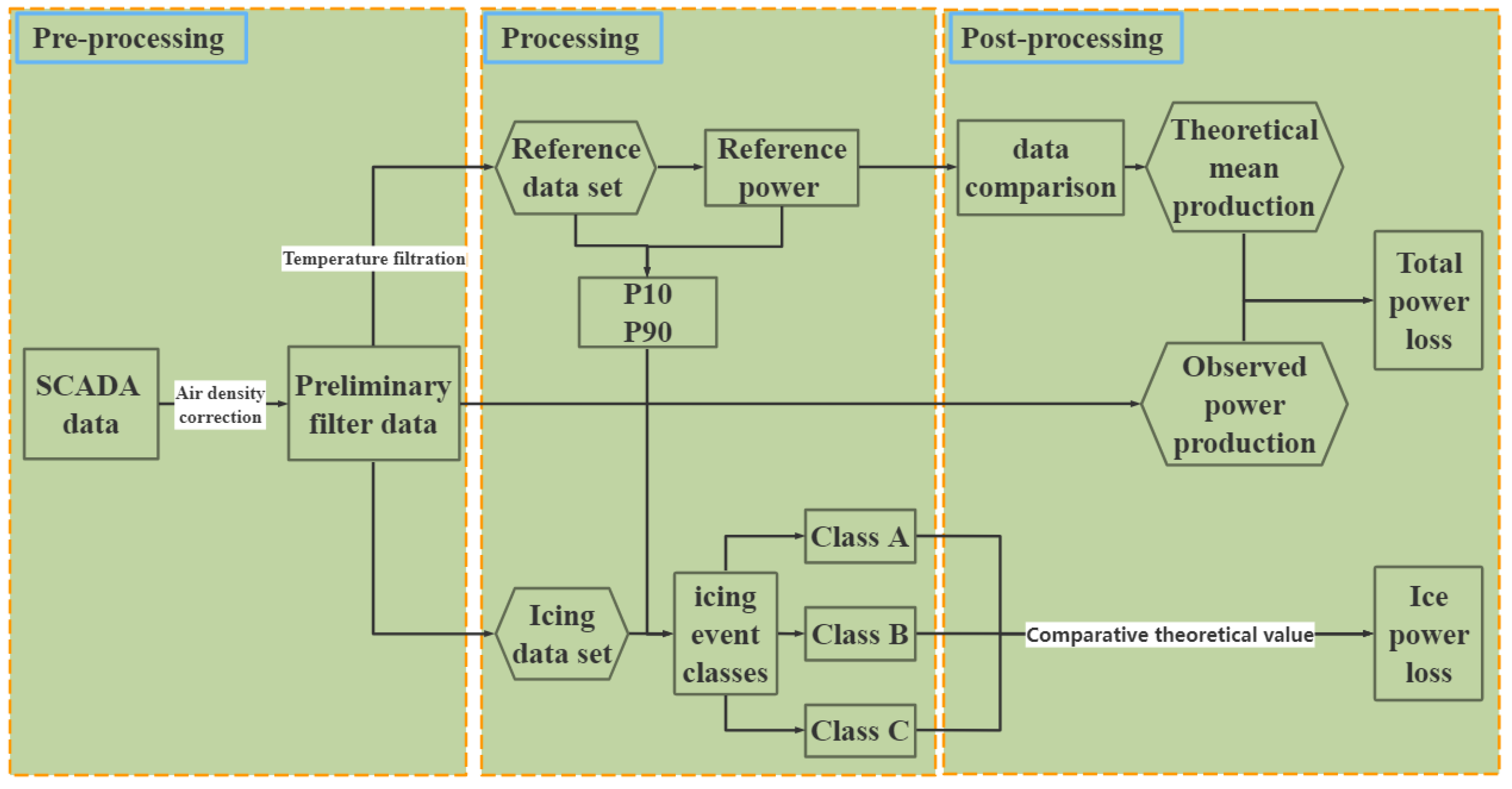
3.4. ILM-Power Loss Computing Theory
4. Result and Discussion
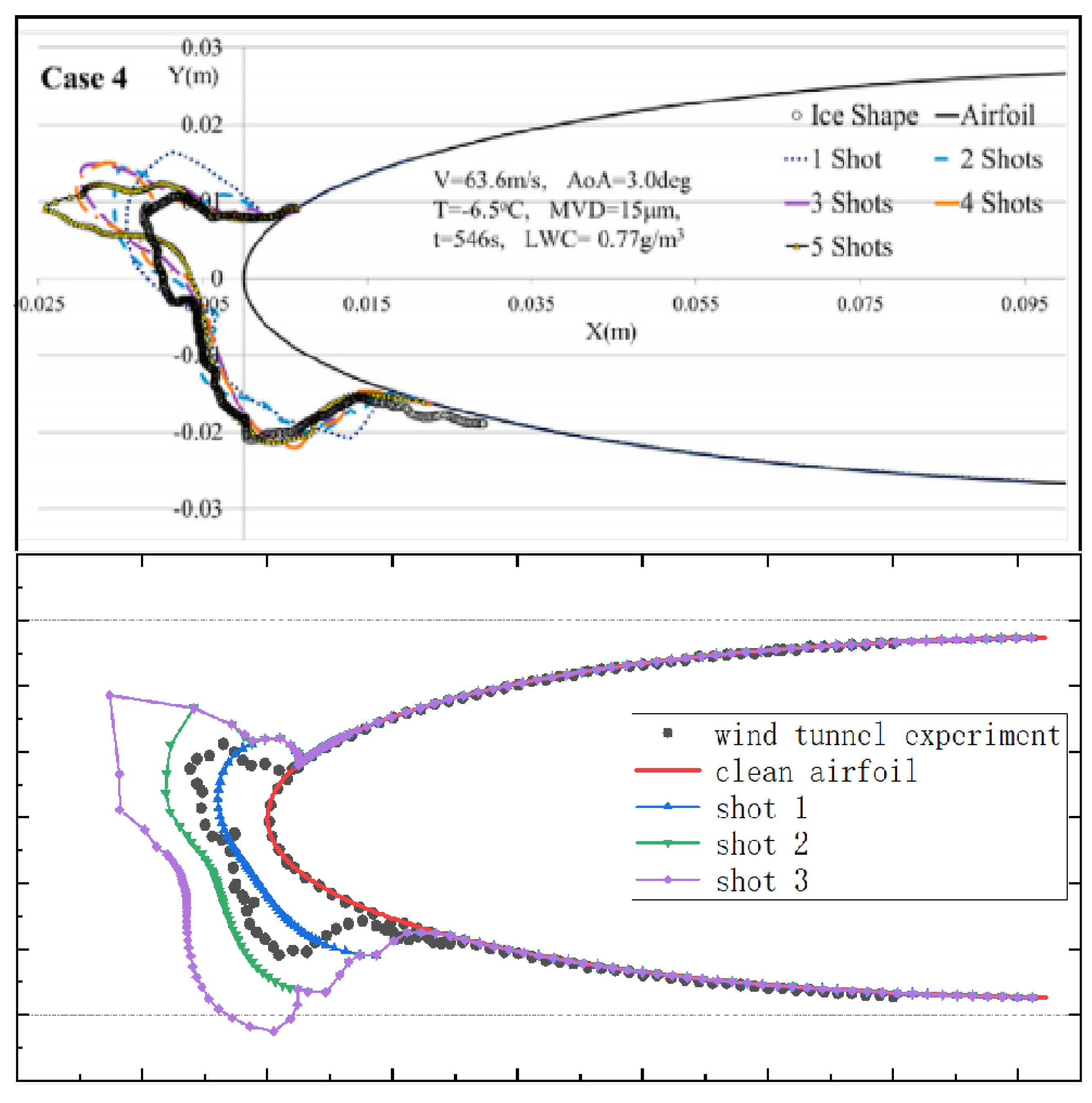
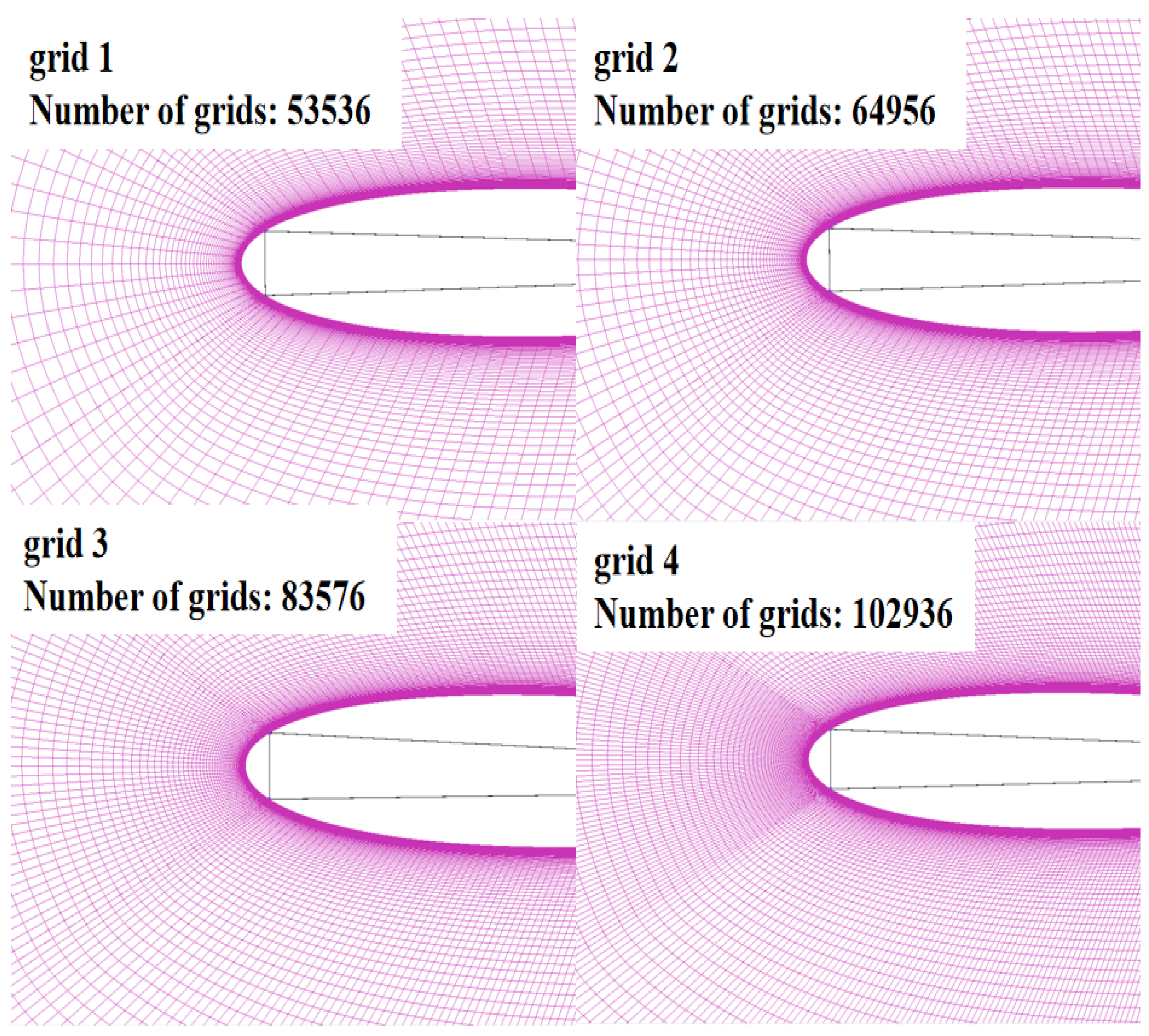
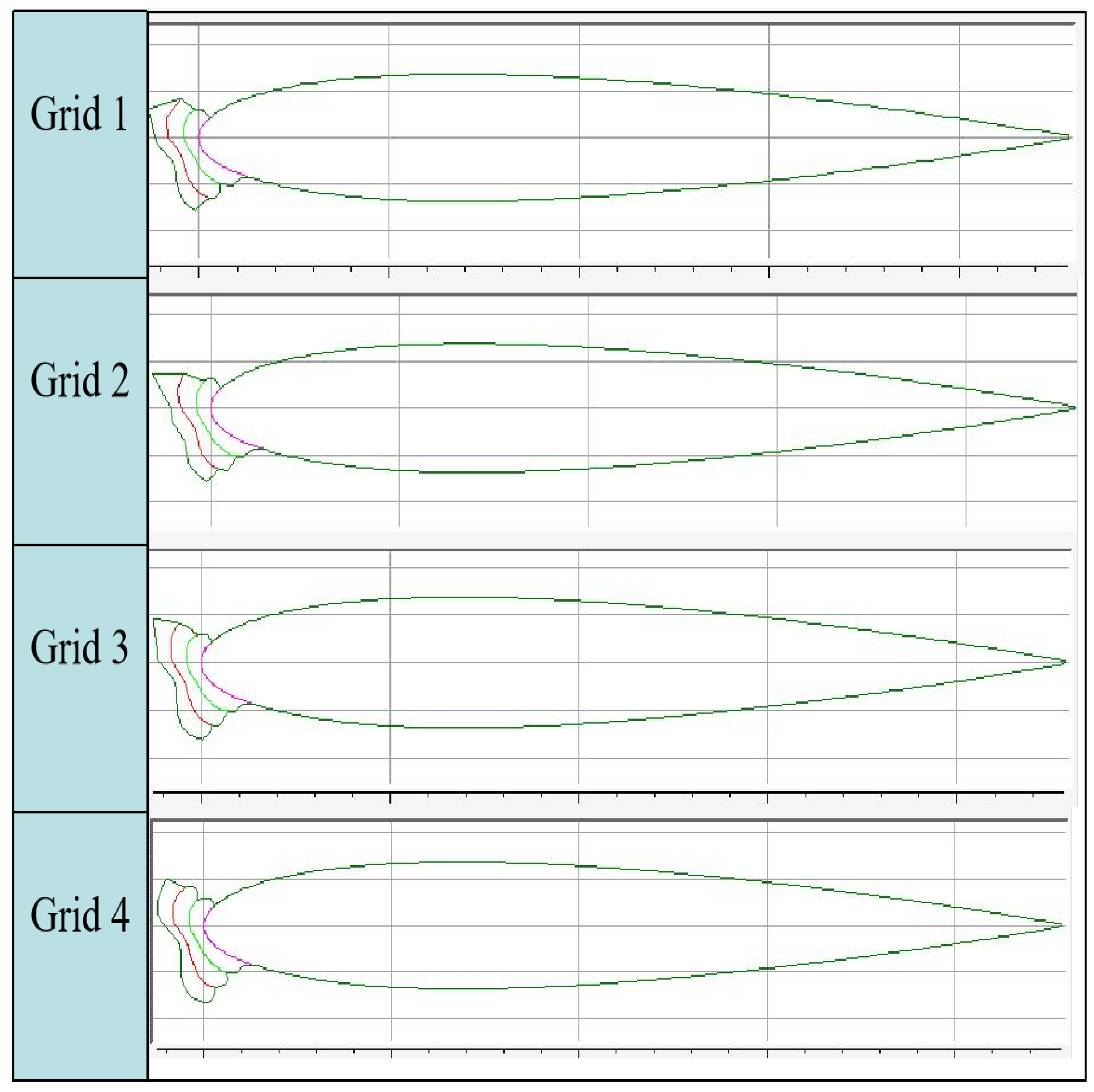
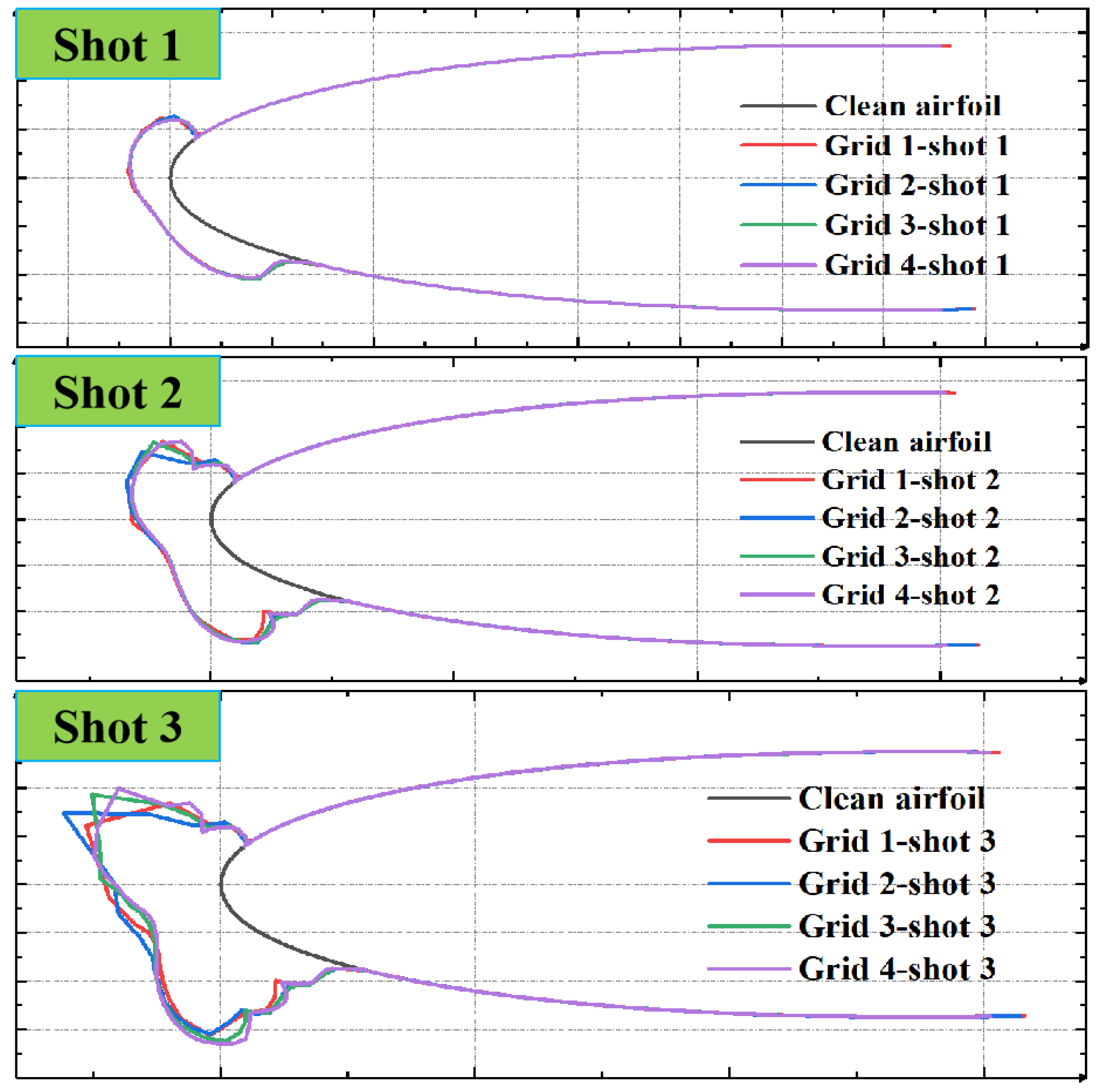
4.1. Grid Convergence Analysis
4.2. Icing Discussion
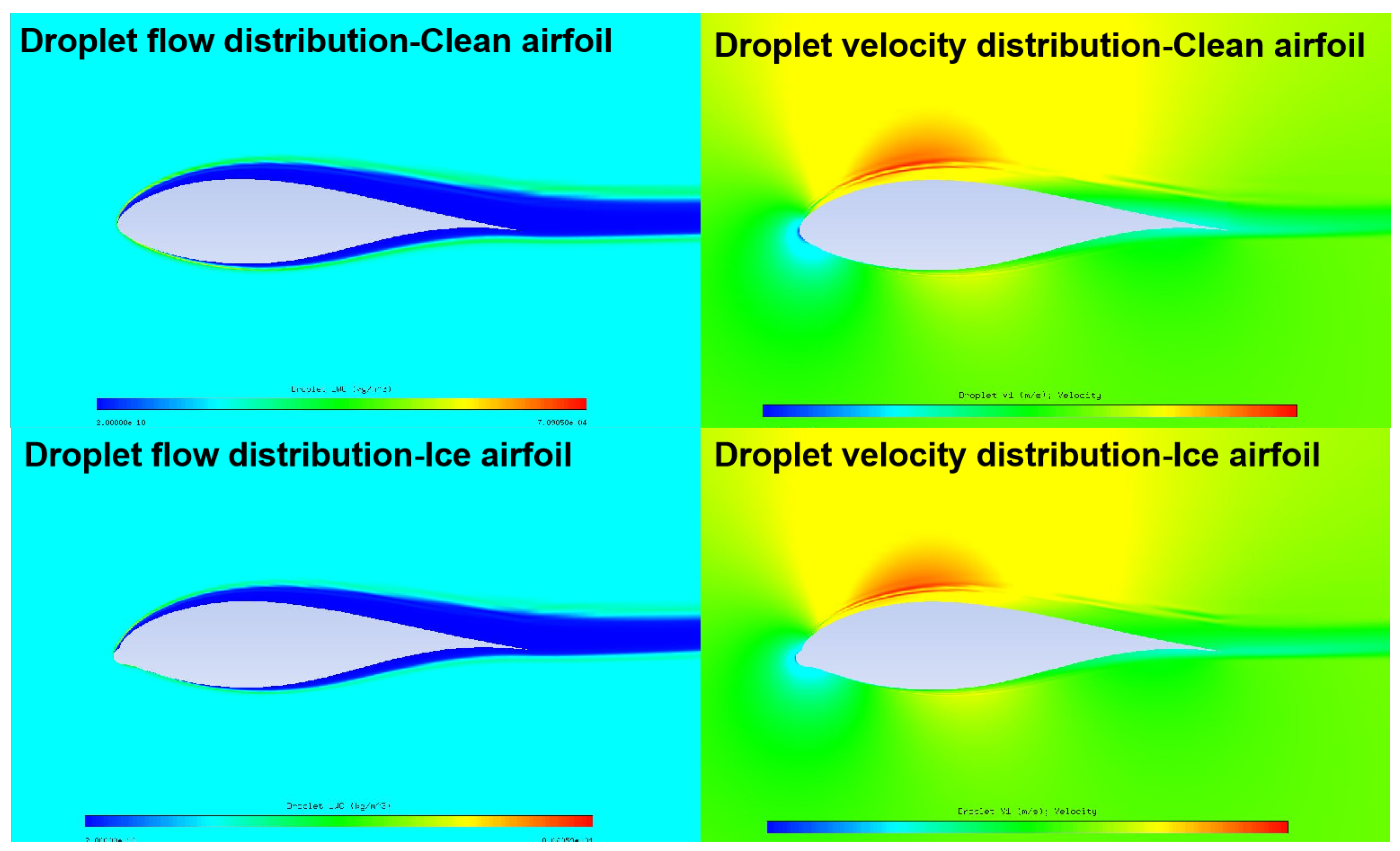
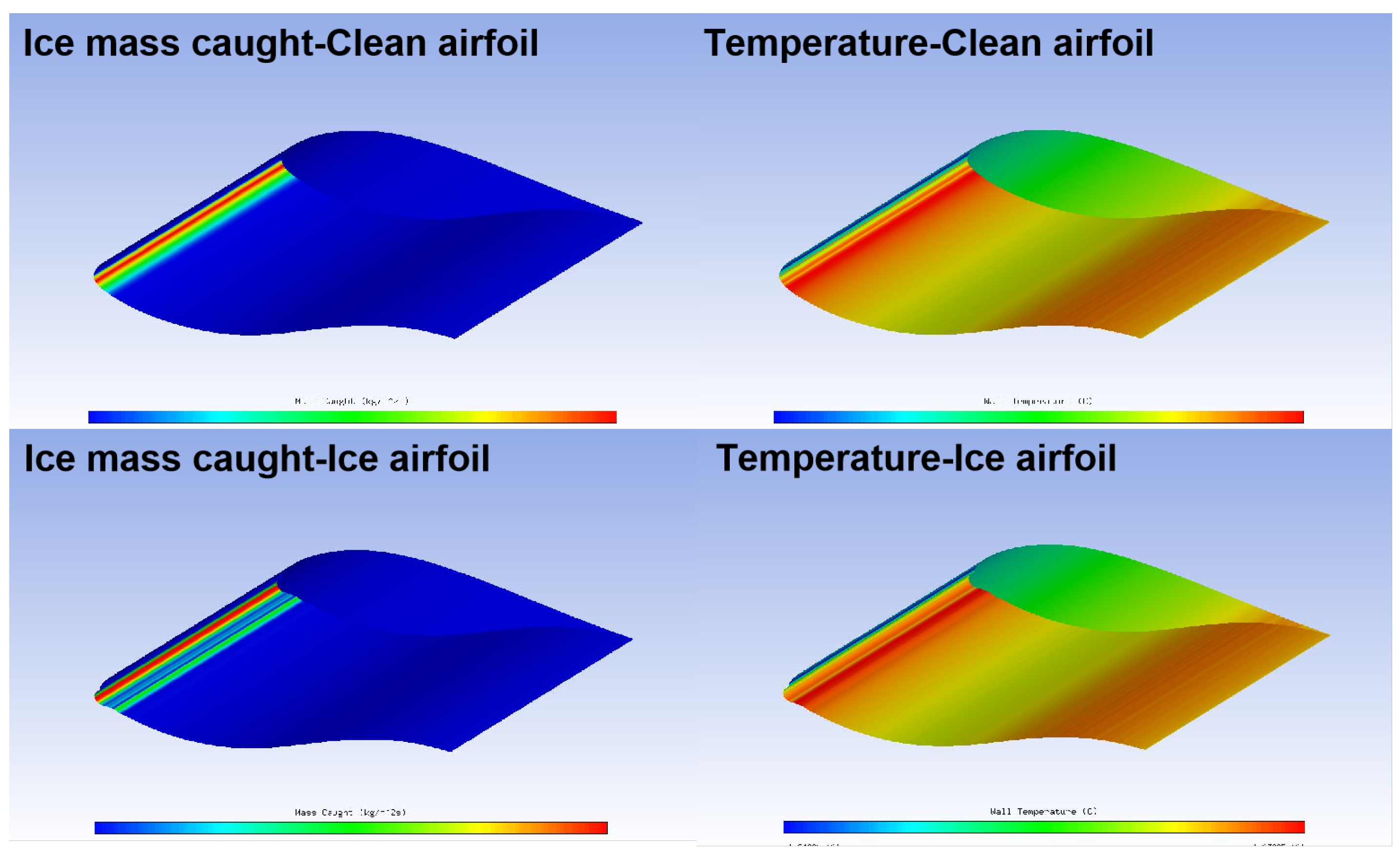
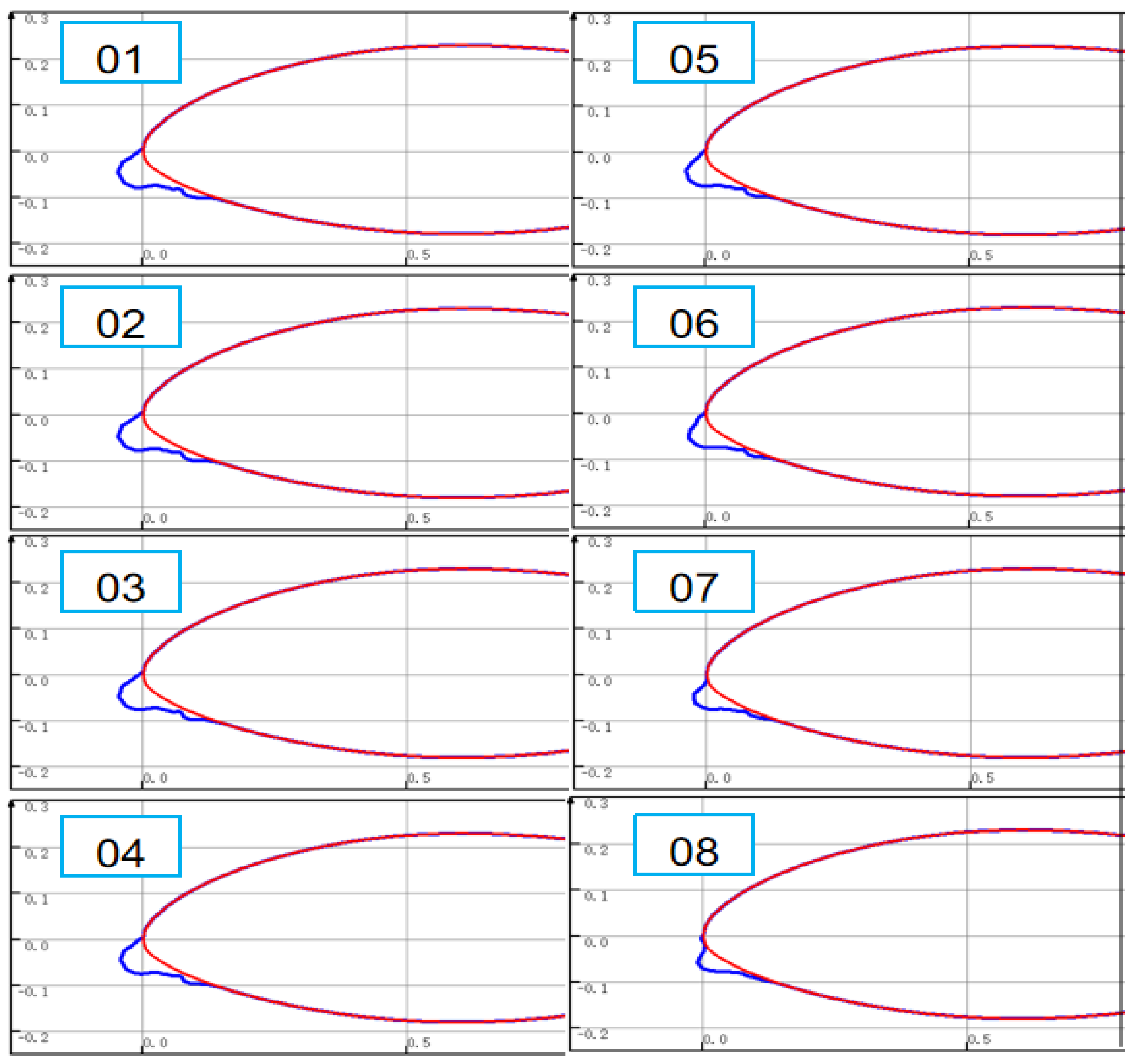
4.2.1. Ice Accumulation Process
4.2.2. Icing Effect
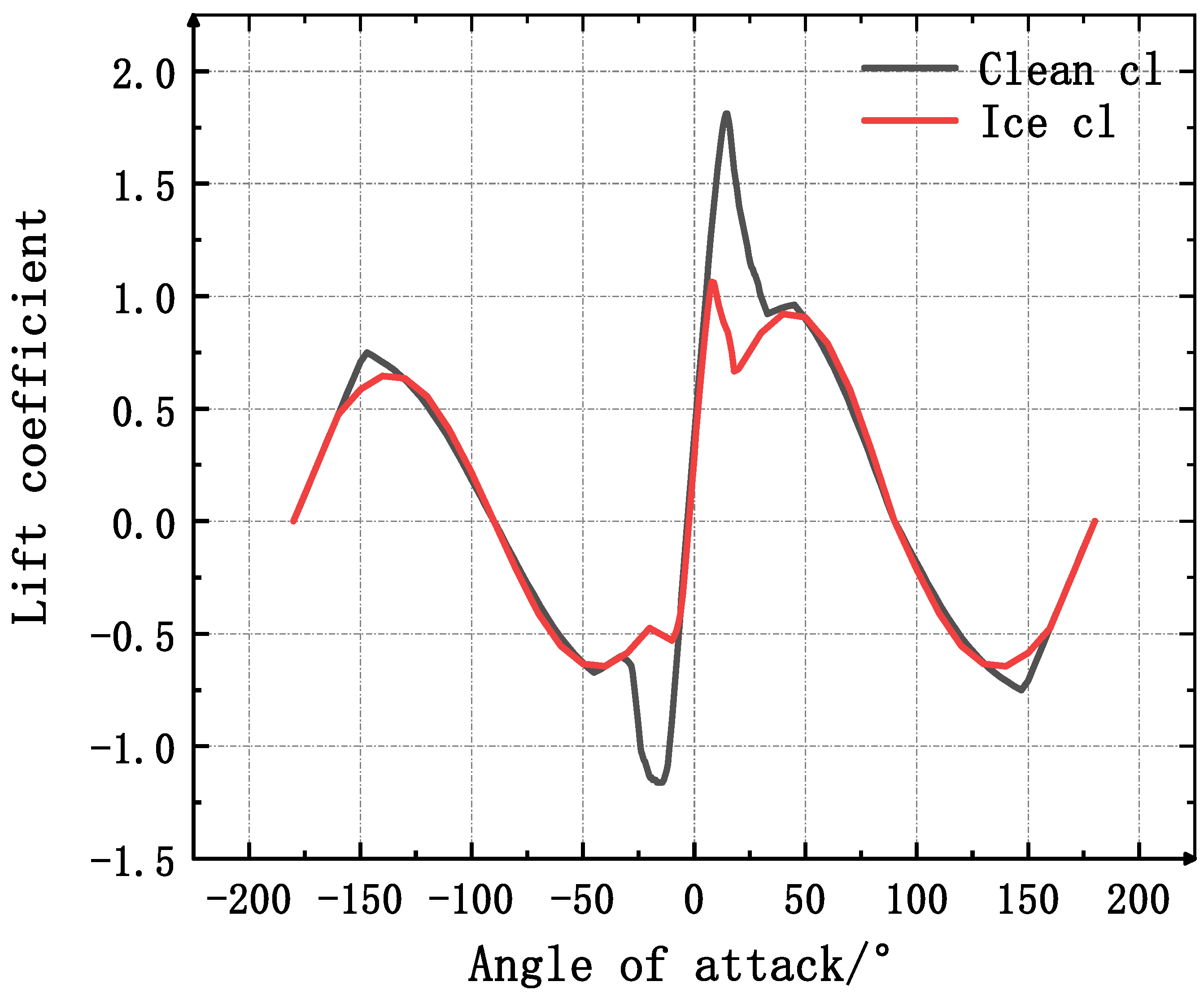
4.2.3. Aerodynamic Characteristic Discussion
4.3. Power Discussion
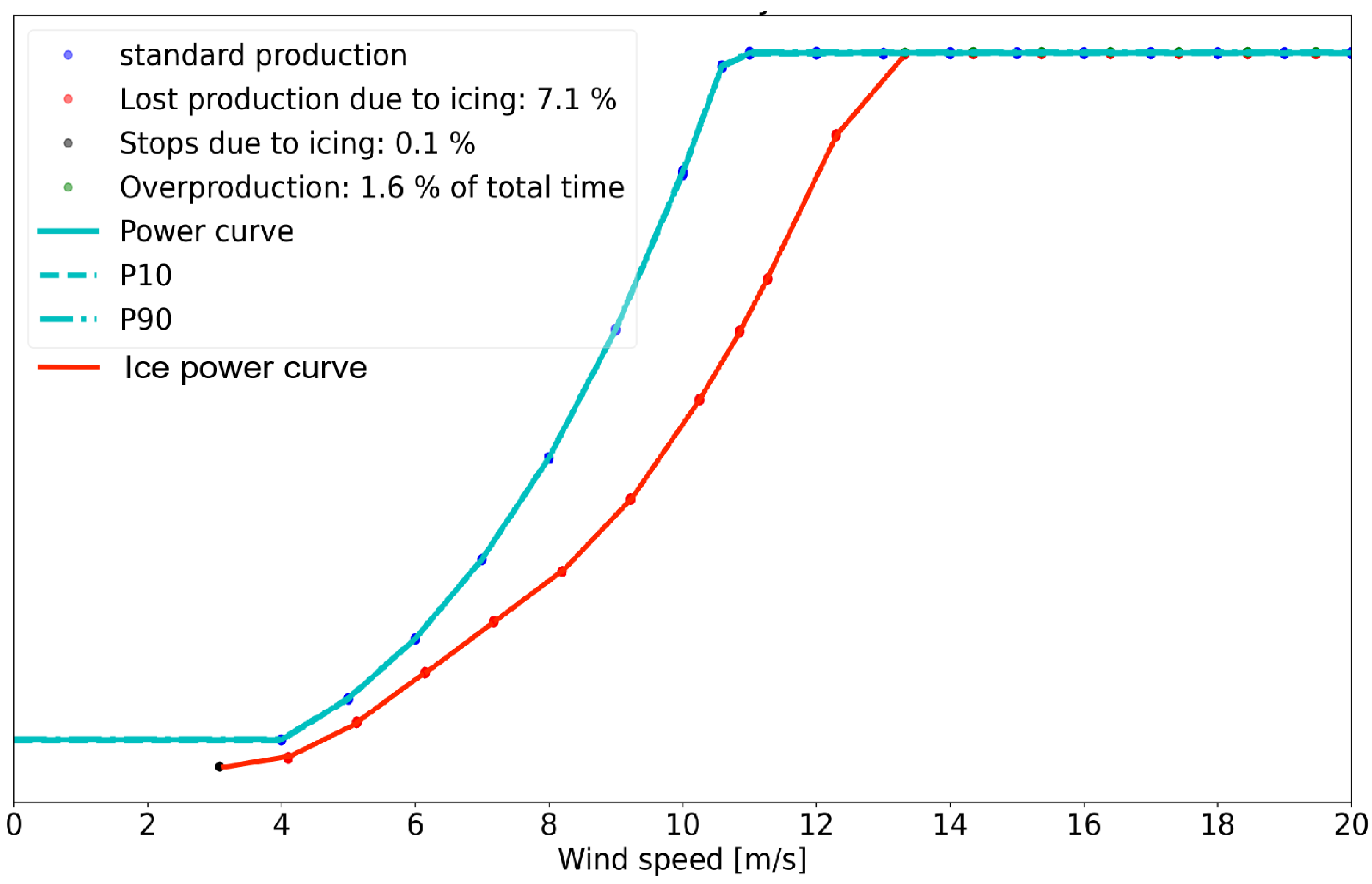
4.3.1. WTIC Result
4.3.2. ILM-Power Loss Discussion
5. Conclusions
- It was found that the air flow will move around the airfoil after colliding with it. Icing is mainly distributed at the droplet impact site at the leading edge of the airfoil, and the trailing edge will produce slight icing. The icing is most obvious at the blade tip and the icing significantly decreases towards the blade root.
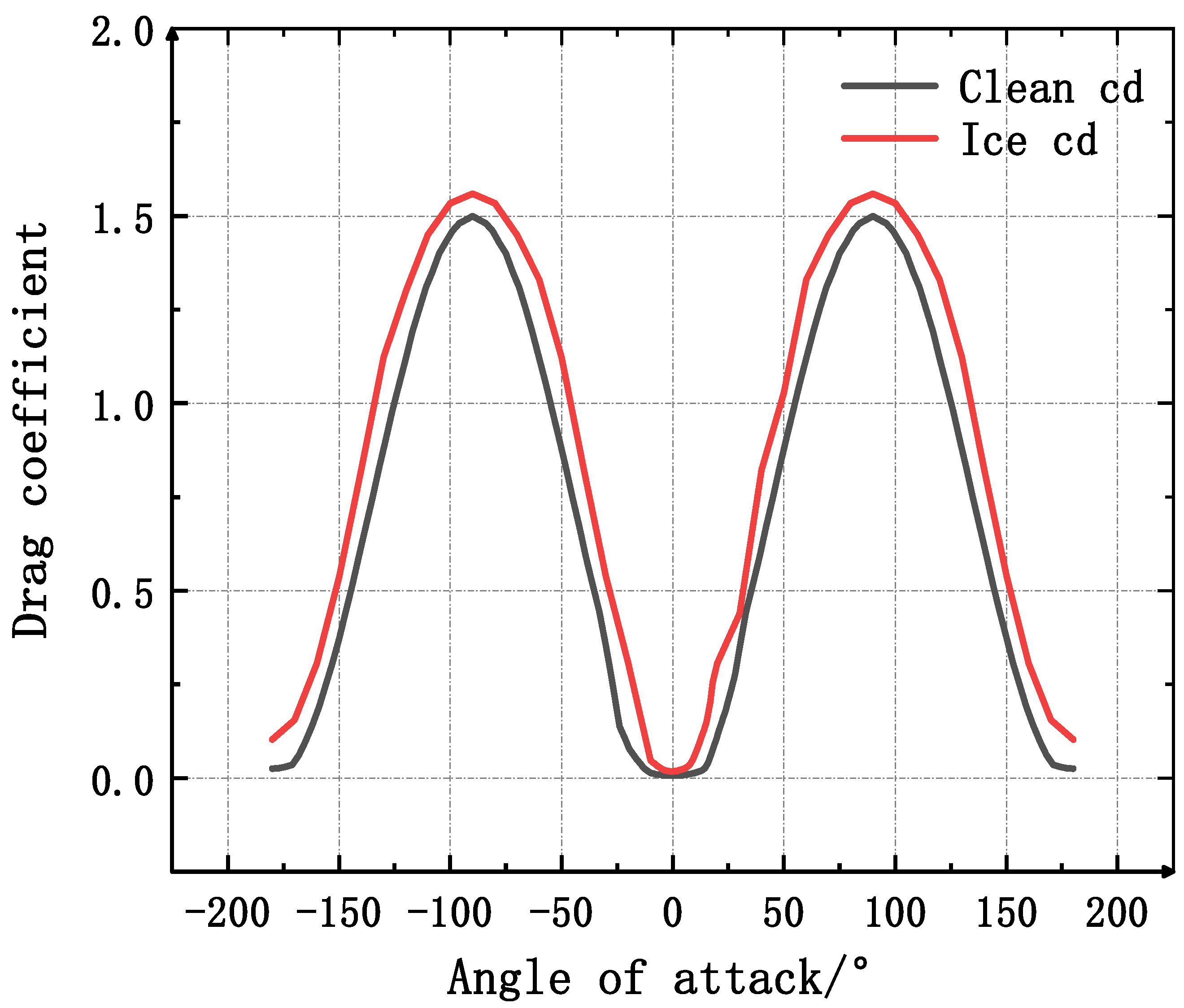
- It was found that the lift coefficient and drag coefficient change obviously before and after the airfoil icing at the tip. When the angle-of-attack is 0°, the lift coefficient decreases by 24.32%, the drag coefficient increases by 165.47%, the maximum lift coefficient decreases by 41.19%, and the maximum drag coefficient increases by 4.67%. Blade icing caused the stall Angle to push from 14.8° forward to 8°.
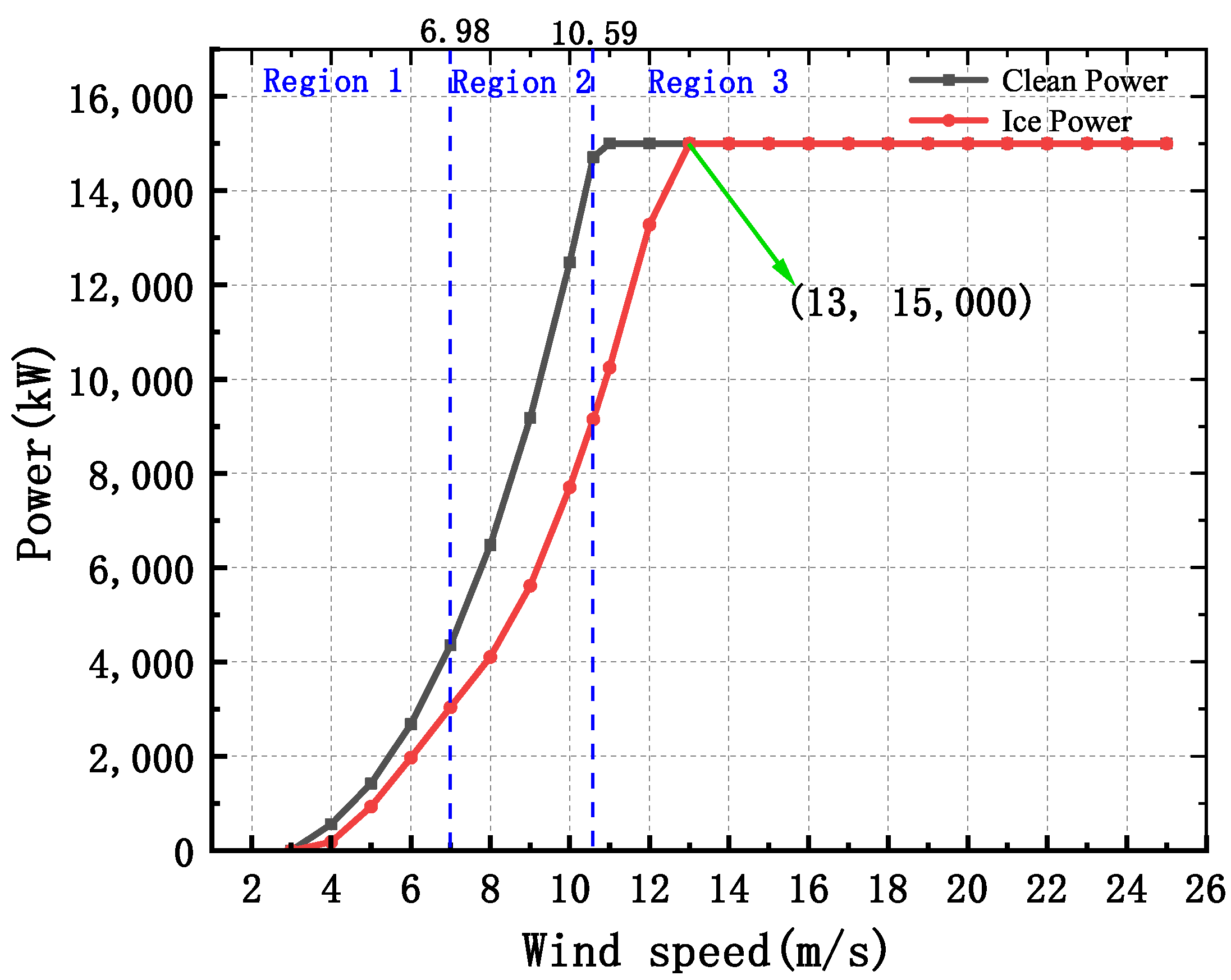
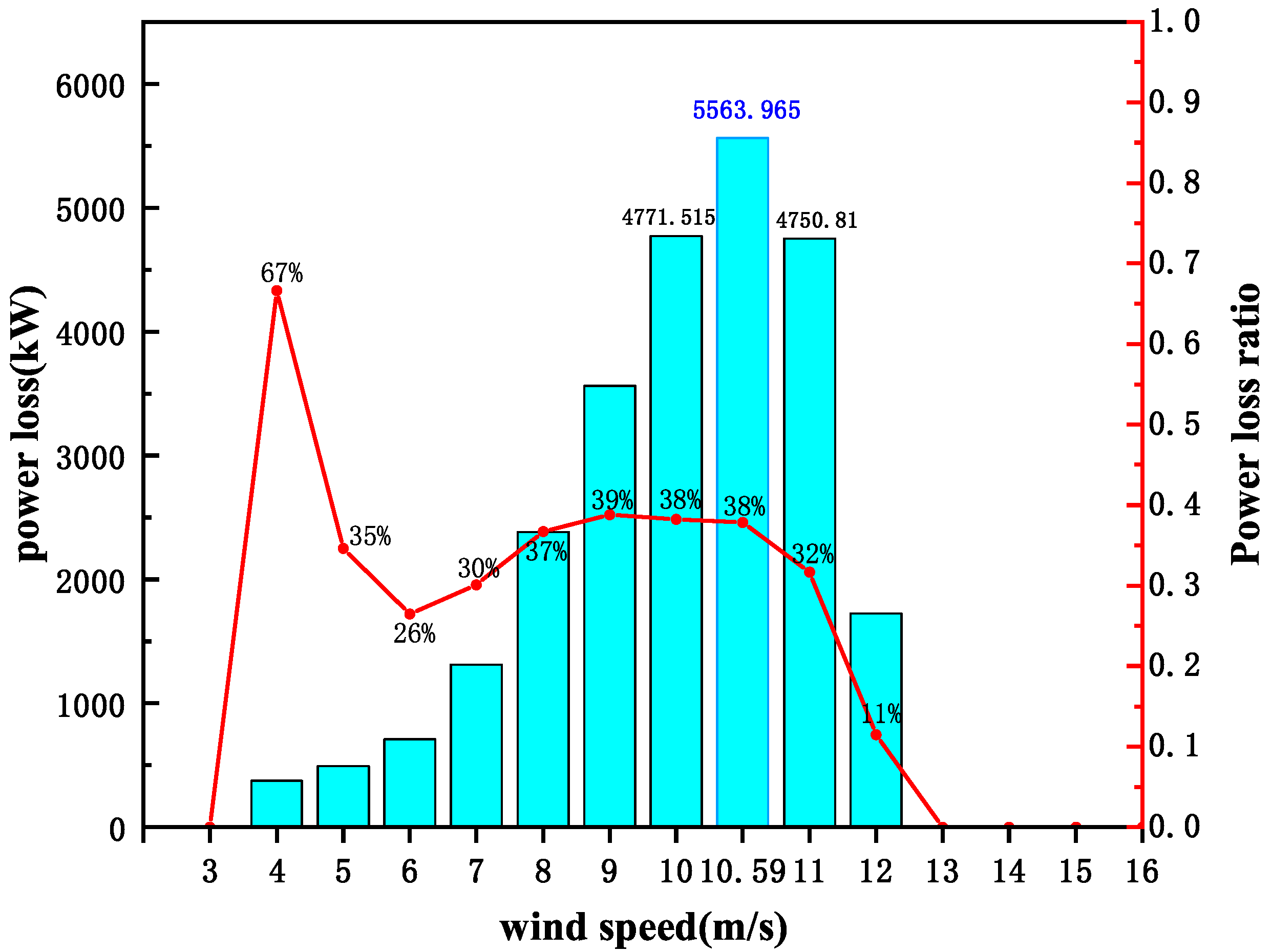
- The integrated analysis of wind turbine power found that icing causes the rated wind speed of the wind turbine to be delayed from 10.59 m/s to 13 m/s. When the wind speed is less than 13 m/s, the output power decreases under the same wind speed conditions. The average hourly power generation under rated wind speed decreases by 5563.965 kW, and the output power decreases by 38%. Secondly, icing causes the power loss of the Region 2 wind turbine in the optimization stage to reach 37.48%.
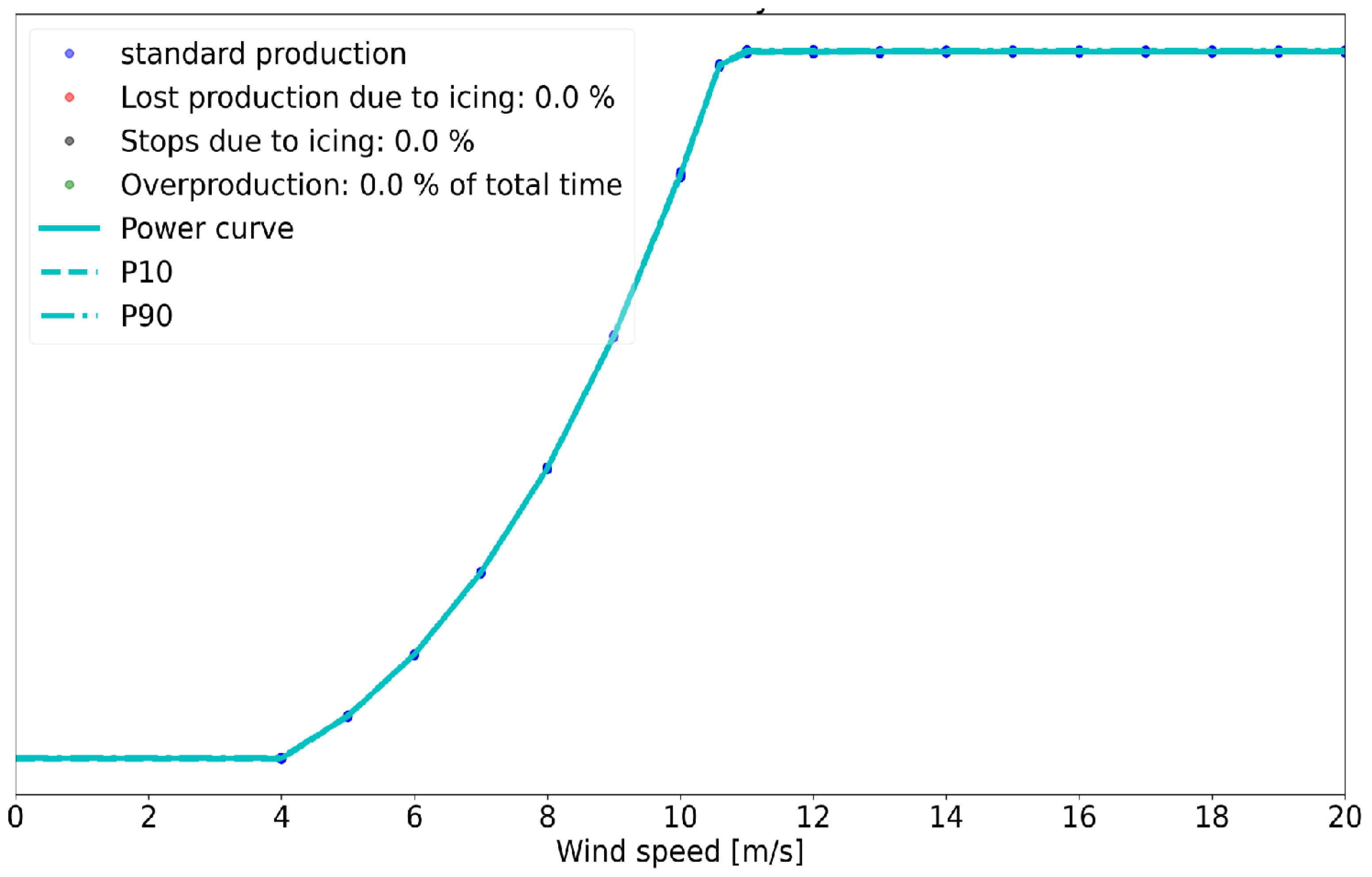
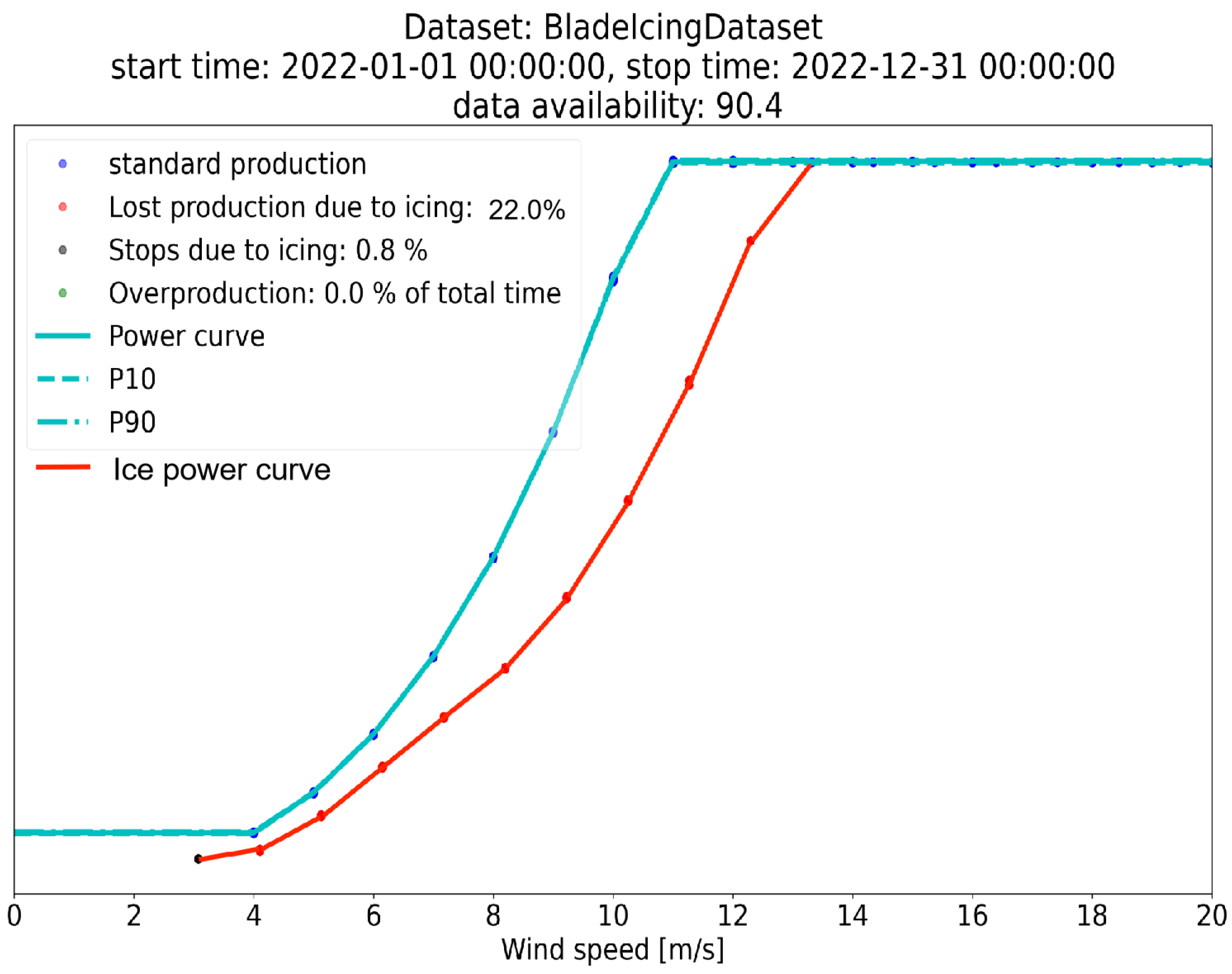
- Through ILM analysis, it was found that, under the condition of wind resources with equal spacing from 3 m/s to 20 m/s, the power loss caused by icing accounts for 14.60%, which is close to the power loss of 12.65% in the integrated analysis of wind turbines. By calculating the annual power loss caused by icing, it was found that the power loss caused by blade icing accounts for 22.0%, and the annual loss is 7,810,870.3 kWh. The degree of icing simulated in this study was small. The amount of icing will increase under more complex environmental loads and more serious power loss will be caused.
Author Contributions
Funding
Conflicts of Interest
References
- Gao, L.; Tao, T.; Liu, Y.; Hu, H. A field study of ice accretion and its effects on the power production of utility-scale wind turbines. Renew. Energy 2021, 167, 917–928. [Google Scholar] [CrossRef]
- Struk, P.M.; King, M.C.; Bartkus, T.P.; Tsao, J.C.; Fuleki, D.; Neuteboom, M.; Chalmers, J. Ice Crystal Icing Physics Study using a NACA 0012 Airfoil at the National Research Council of Canada’s Research Altitude Test Facility. In Proceedings of the 2018 Atmospheric and Space Environments Conference, Atlanta, GA, USA, 25–29 June 2018; p. 4224. [Google Scholar]
- Kraj, A.; Bibeau, E. Phases of icing on wind turbine blades characterized by ice accumulation. Renew. Energy 2010, 35, 966–972. [Google Scholar] [CrossRef]
- Han, Y.; Palacios, J.; Schmitz, S. Scaled ice accretion experiments on a rotating wind turbine blade. J. Wind. Eng. Ind. Aerodyn. 2012, 109, 55–67. [Google Scholar] [CrossRef]
- Barber, S.; Wang, Y.; Jafari, S.; Chokani, N. The Impact of Ice Formation on Wind Turbine Performance and Aerodynamics. J. Sol. Energy Eng. 2011, 133. [Google Scholar] [CrossRef]
- Maissan, J.F. Wind Power Development in Sub-Arctic Conditions With Severe Rime Icing. North. Rev. 2002. [Google Scholar]
- Etemaddar, M.; Hansen, M.O.L.; Moan, T. Wind turbine aerodynamic response under atmospheric icing conditions. Wind Energy 2014, 17, 241–265. [Google Scholar] [CrossRef]
- Yirtici, O.; Tuncer, I.H. Aerodynamic shape optimization of wind turbine blades for minimizing power production losses due to icing. Cold Reg. Sci. Technol. 2021, 185, 103250. [Google Scholar] [CrossRef]
- Xie, C.; Zhou, L.; Ding, S.; Liu, R.; Zheng, S. Experimental and numerical investigation on self-propulsion performance of polar merchant ship in brash ice channel. Ocean. Eng. 2023, 269, 113424. [Google Scholar]
- Rissanen, S.; Lehtomäki, V.; Wennerkoski, J.; Wadham-Gagnon, M.; Sandel, K. Modelling load and vibrations due to iced turbine operation. Wind Eng. 2016, 40, 293–303. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, B.; Wang, G.; Yu, D.; Han, X.; Zhang, D. Effect of ice coating on aerodynamic performance of offshore wind turbine blades. Ship Eng. 2022, 44, 166–171. [Google Scholar]
- Yirtici, O.; Tuncer, I.H.; Ozgen, S. Ice Accretion Prediction on Wind Turbines and Consequent Power Losses. J. Phys. Conf. Ser. 2016, 753, 022022. [Google Scholar] [CrossRef][Green Version]
- Yirtici, O.; Ozgen, S.; Tuncer, I.H. Predictions of ice formations on wind turbine blades and power production losses due to icing. Wind Energy 2008, 22, 945–958. [Google Scholar] [CrossRef]
- Yirtici, O.; Cengiz, K.; Ozgen, S.; Tuncer, I.H. Aerodynamic validation studies on the performance analysis of iced wind turbine blades. Comput. Fluids 2019, 192, 104271. [Google Scholar] [CrossRef]
- Homola, M.C.; Virk, M.S.; Nicklasson, P.J.; Sundsbø, P.A. Performance losses due to ice accretion for a 5 MW wind turbine. Wind Energy 2012, 15, 379–389. [Google Scholar] [CrossRef]
- Lamraoui, F.; Fortin, G.; Benoit, R.; Perron, J.; Masson, C. Atmospheric icing impact on wind turbine production. Cold Reg. Sci. Technol. 2014, 100, 36–49. [Google Scholar] [CrossRef]
- Chen, Z.; Wei, L.; Li, Z.; Liu, K.; Ding, M. Characteristics of sea fog in the Arctic Ocean floating ice region in summer 2017. Mar. Forecast. 2019, 36, 77–78. [Google Scholar]
- Iuliano, E.; Mingione, G.; Petrosino, F.; Hervy, F. Eulerian Modeling of Large Droplet Physics Toward Realistic Aircraft Icing Simulation. J. Aircr. 2011, 48, 1621–1632. [Google Scholar] [CrossRef]
- Jin, J.Y.; Virk, M.S.; Hu, Q.; Jiang, X. Study of Ice Accretion on Horizontal Axis Wind Turbine Blade Using 2D and 3D Numerical Approach. IEEE Access 2020, 8, 166236. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, drops, and particles. Dry. Technol 1978, 11, 263–264. [Google Scholar]
- Jonkman, J.; Buhl, M. New Developments for the NWTC’s FAST Aeroelastic HAWT Simulator. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004. [Google Scholar]
- Chuang, Z.; Li, C.; Liu, S.; Li, X.; Li, Z.; Zhou, L. Numerical analysis of blade icing influence on the dynamic response of an integrated offshore wind turbine. Ocean Eng. 2022, 257, 111593. [Google Scholar] [CrossRef]
- IEA Wind Task 19, T19IceLossMethod: Method for Estimating Icing Losses from Wind Turbine SCADA Data. 2019. Available online: https://github.com/IEAWind-Task19/T19IceLossMethod (accessed on 15 November 2019).
- IEA. Wind TCP Task 19: Available Technologies for Wind Energy in Cold Climates. Available online: https://iea-wind.org/task19/t19-publications/ (accessed on 15 November 2019).
- Wang, Q.; Yi, X.; Liu, Y.; Ren, J.; Li, W.; Wang, Q.; Lai, Q. Simulation and analysis of wind turbine ice accretion under yaw condition via an Improved Multi-Shot Icing Computational Model. Renew. Energy 2020, 162, 1854–1873. [Google Scholar] [CrossRef]






| Parameter | Value | Units |
|---|---|---|
| Rated Power | 15 | MW |
| Rotor diameter | 240 | m |
| Hub height | 150 | m |
| Blade length | 117 | m |
| Root diameter | 5.2 | m |
| Cut-in wind speed | 3 | m/s |
| Optimized wind speed | 6.98 | m/s |
| Rated wind speed | 10.59 | m/s |
| Cut-out wind speed | 25 | m/s |
| Maximum tip speed | 95 | m/s |
| Minimum rotational speed | 5 | rmp |
| Rated rotational speed | 7.5 | rmp |
| Parameter | Value | Units |
|---|---|---|
| Temperature | −15∼0 | °C |
| Wind speed | ⩽13 | m·s |
| LWC | 0.04∼0.20 | g·m |
| MVD | 4∼20 | m |
| Air density | 1.293 | kg·m |
| Air viscosity | ms |
| Parameter | Value | Units |
|---|---|---|
| Temperature | −6.5 | |
| Wind speed | 63.6 | m·s |
| LWC | 0.77 | g·m |
| MVD | 15 | m |
| Ice accumulation time | 546 | s |
| Angle of attack | 3.0 | deg |
| Characteristic length | 0.4572 | m |
| Project | Value | Units |
|---|---|---|
| Theoretical mean production | 44,034,161.0 | kWh |
| Observed power production | 35,554,436.2 | kWh |
| Icing during production | 3506.7 | h |
| Power loss ratio | 22.0% | - |
| Power loss due to icing | 7,810,870.3 | kWh |
| Downtime due to icing | 349,742.5 | kWh |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chuang, Z.; Yi, H.; Chang, X.; Liu, H.; Zhang, H.; Xia, L. Comprehensive Analysis of the Impact of the Icing of Wind Turbine Blades on Power Loss in Cold Regions. J. Mar. Sci. Eng. 2023, 11, 1125. https://doi.org/10.3390/jmse11061125
Chuang Z, Yi H, Chang X, Liu H, Zhang H, Xia L. Comprehensive Analysis of the Impact of the Icing of Wind Turbine Blades on Power Loss in Cold Regions. Journal of Marine Science and Engineering. 2023; 11(6):1125. https://doi.org/10.3390/jmse11061125
Chicago/Turabian StyleChuang, Zhenju, Hui Yi, Xin Chang, Hongxiang Liu, Haidian Zhang, and Lulin Xia. 2023. "Comprehensive Analysis of the Impact of the Icing of Wind Turbine Blades on Power Loss in Cold Regions" Journal of Marine Science and Engineering 11, no. 6: 1125. https://doi.org/10.3390/jmse11061125
APA StyleChuang, Z., Yi, H., Chang, X., Liu, H., Zhang, H., & Xia, L. (2023). Comprehensive Analysis of the Impact of the Icing of Wind Turbine Blades on Power Loss in Cold Regions. Journal of Marine Science and Engineering, 11(6), 1125. https://doi.org/10.3390/jmse11061125





