A Location-Allocation Model with Obstacle and Capacity Constraints for the Layout Optimization of a Subsea Transmission Network with Line-Shaped Conduction Structures
Abstract
1. Introduction
1.1. Background
1.2. Related Work
- (1)
- Production requirements and the avoidance of subsea obstacles are both integrated into the MILP model quantitatively, making the description of the layout closer to practical situations.
- (2)
- A “global to local” search process based on the Delaunay triangulation method is constructed to solve the model, instead of the orthogonal grid method, which reduces the number of service center candidates, which is an effective way to find the optimal solution with high efficiency.
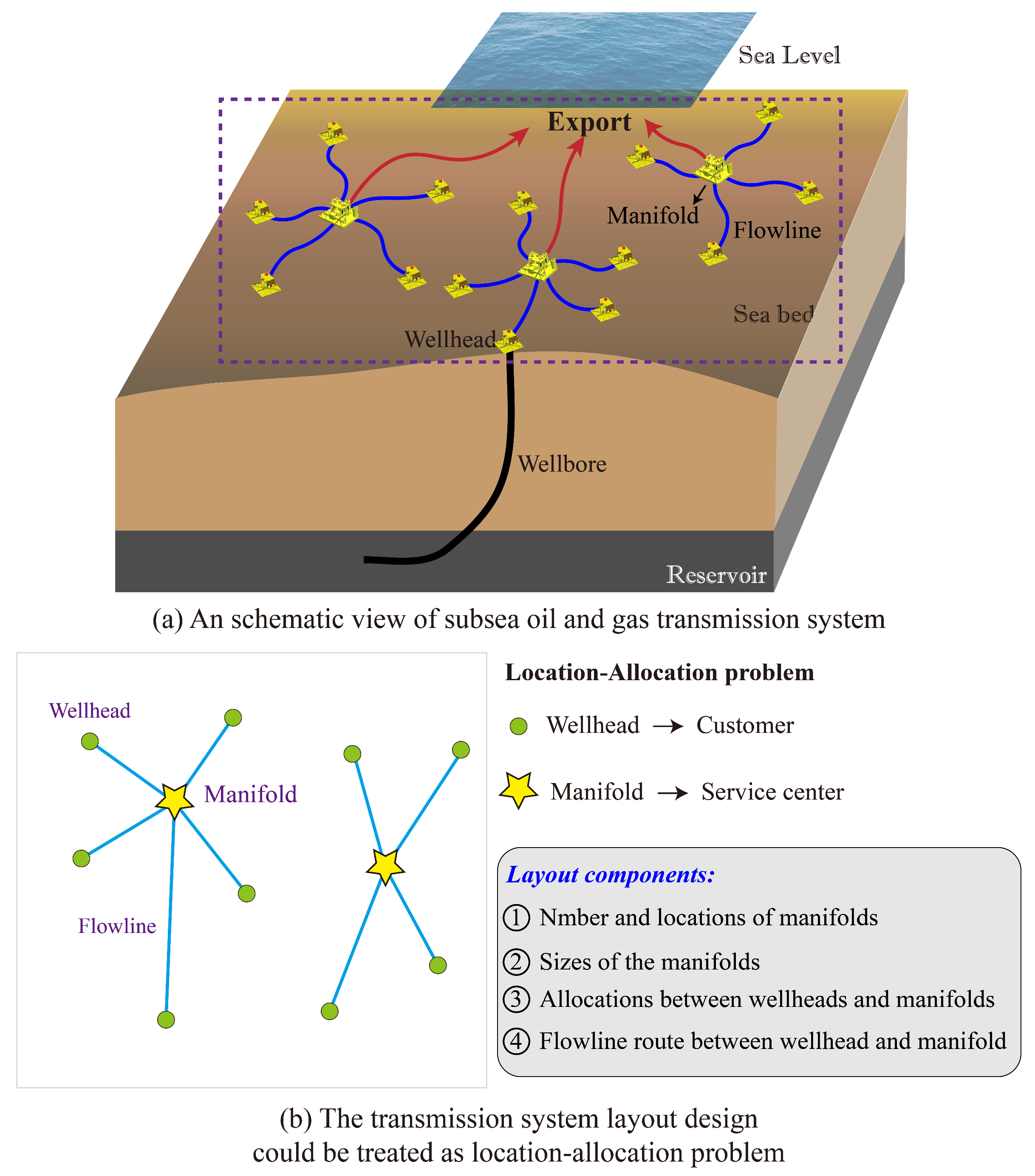
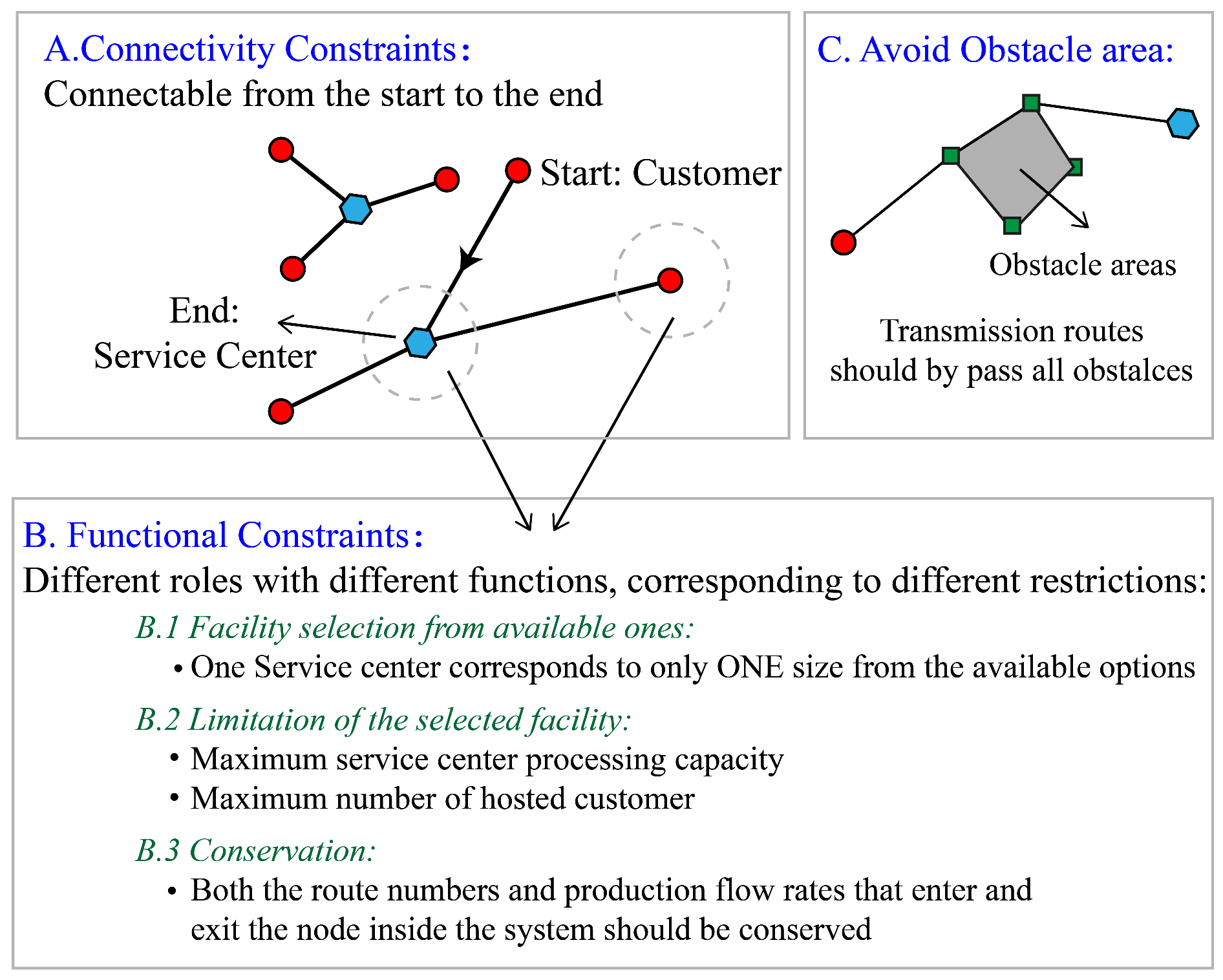
2. Problem Statement and Basic Assumptions
2.1. Assumptions
- (1)
- A lot of studies have worked on undulating seabeds, considering that, in deep sea areas, the variation in the seabed elevation is much smaller compared with the horizontal scale of the seabed area [41]. As a result, all customers, services centers, and obstacles are assumed to be located on a horizontal plane, and the undulating landscape is not considered.
- (2)
- The scales of the customers and service centers are neglected (width, length, and height), because they are much smaller compared with the distances among these agencies. All customers and services centers are assumed to be nodes.
- (3)
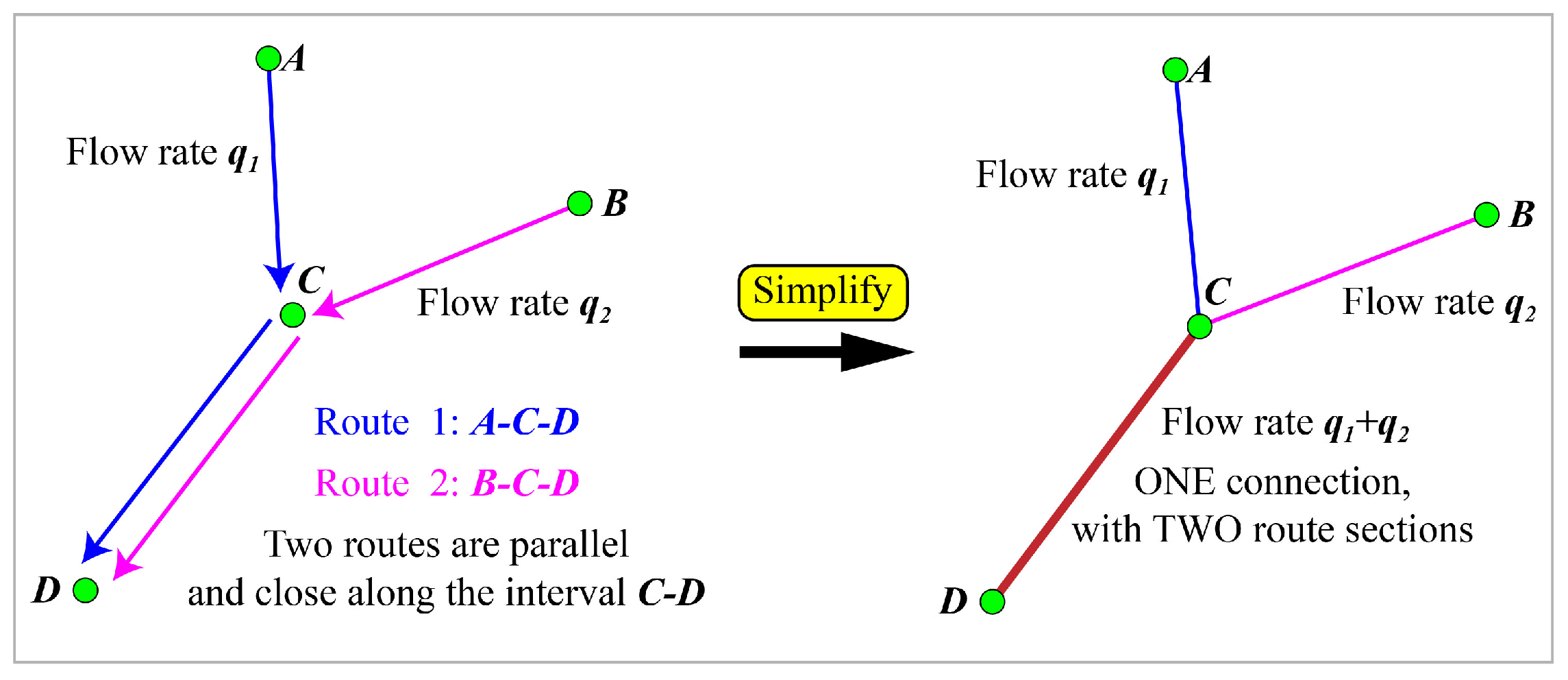
- It is possible that multiple transportation routes are parallel or close to each other in some parts, as shown in the left part of Figure 3. In this work, these parallel parts are assumed to be overlapped and share the same interval, which rarely affects the total route length, as shown in the right part of Figure 3. Therefore, for the overlapped interval, the transportation flow rate equals the summation of the rates of different routes, and the number of route sections equals the number of routes passing through.
- (4)
- The transportation routes are assumed to be uniform and can always satisfy the needs of the flow, which means that, in this work, we do not include the route size selection, and the cost of the route is only related to the route length.
2.2. Problem Descriptions
- ➀
- Find the positions of the service centers;
- ➁
- Select the size and capacity of the service centers from the available options;
- ➂
- Determine the allocation between the customers and the service centers; in other words, determine which service center each customer should be connected to;
- ➃
- Design the transportation routes between each customer and the corresponding service centers while considering the avoidance of obstacles distributed inside the target region;
3. Mathematical Modeling
3.1. Parameter Definitions
- (1)
- The number of customers is , and the x and y coordinates are , where indicates the production rate of the customer, and , denotes this node set.
- (2)
- The obstacle areas are treated as convex polygons, and all vertices’ coordinates are provided. The total number of obstacle area vertices is , and denotes this node set;
- (3)
- The candidates of the service center positions. Coordinates indicate the service center candidates. The total number of candidates is , and denotes this node set;
- (4)
- There are different types of service centers for selection. The total number of available types is . For the type, represents the maximum number of transportation routes it can host, and represents its production processing capacity. denotes the corresponding cost;
- (5)
- The cost of the transportation route per unit length is ;
- (6)
- All related nodes are gathered by order, forming a integrated node set represented by , , and denotes the element number. Obviously, .
3.2. Decision Variables
- (1)
- Binary variables , where indicates that the service center candidate is selected; otherwise, , . This decision variable set represents task ➀ defined in Section 2.
- (2)
- Binary variables , where indicates that the service center uses the type from the available options; otherwise, . , . This decision variable set represents task ➀ defined in Section 2.
- (3)
- Binary variables , where , indicates that node i and node j are connected; otherwise, . . This decision variable set represents task ➂ defined in Section 2.
- (4)
- Non-negative integer variables , representing the number of route sections between node i and node j. . The decision variables are set considering the situation where there might be more than one route that passes through two consecutive nodes i and j, as illustrated in Figure 3.
- (5)
- Continuous non-negative variables , denoting the total weight on the section between node i and j. . Decision variables and together represent task ➃ defined in Section 2.
3.3. Objective Function
3.4. Constraints
3.5. Short Summary of the Mathematical Model
4. Solution Strategy
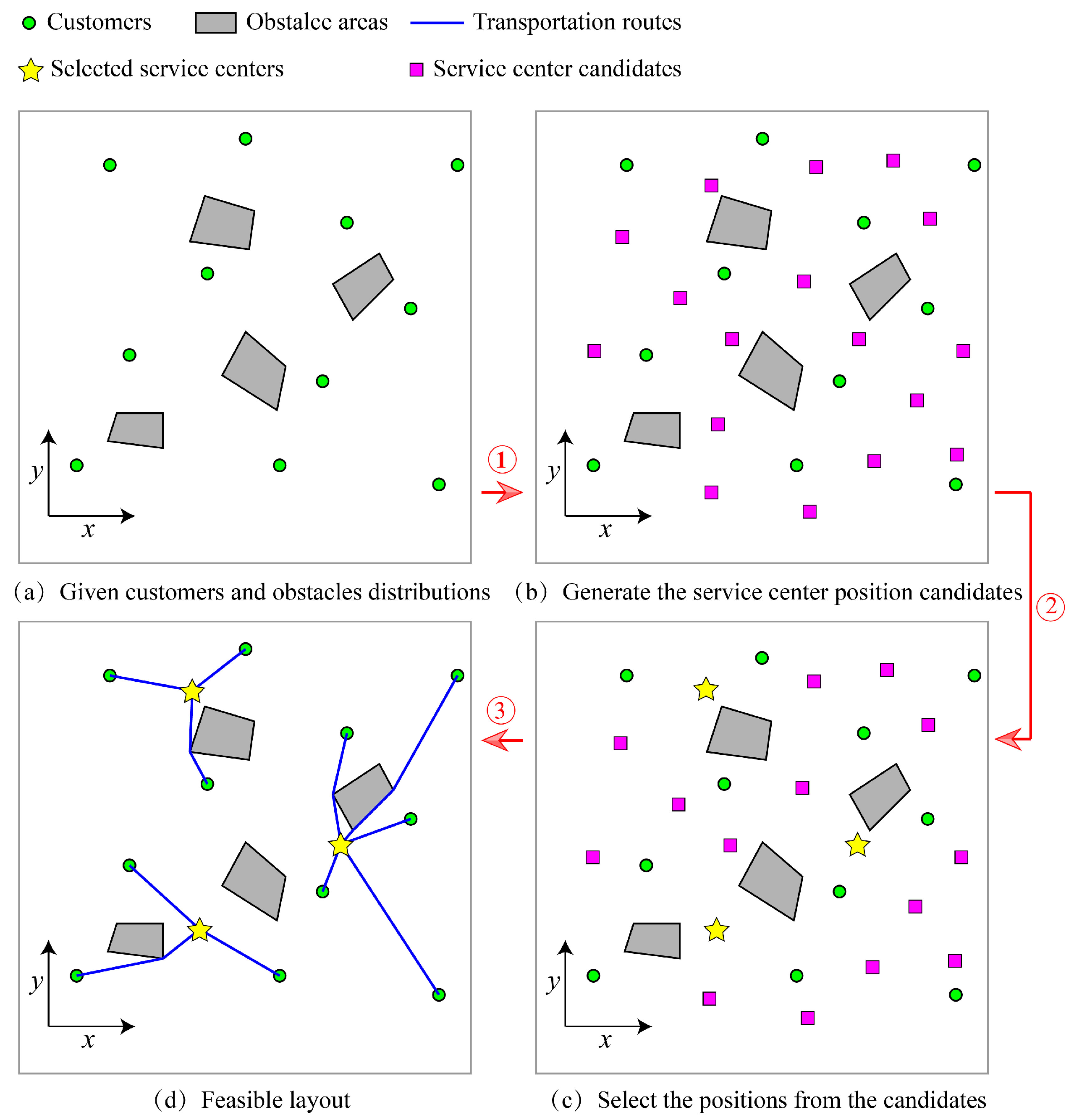
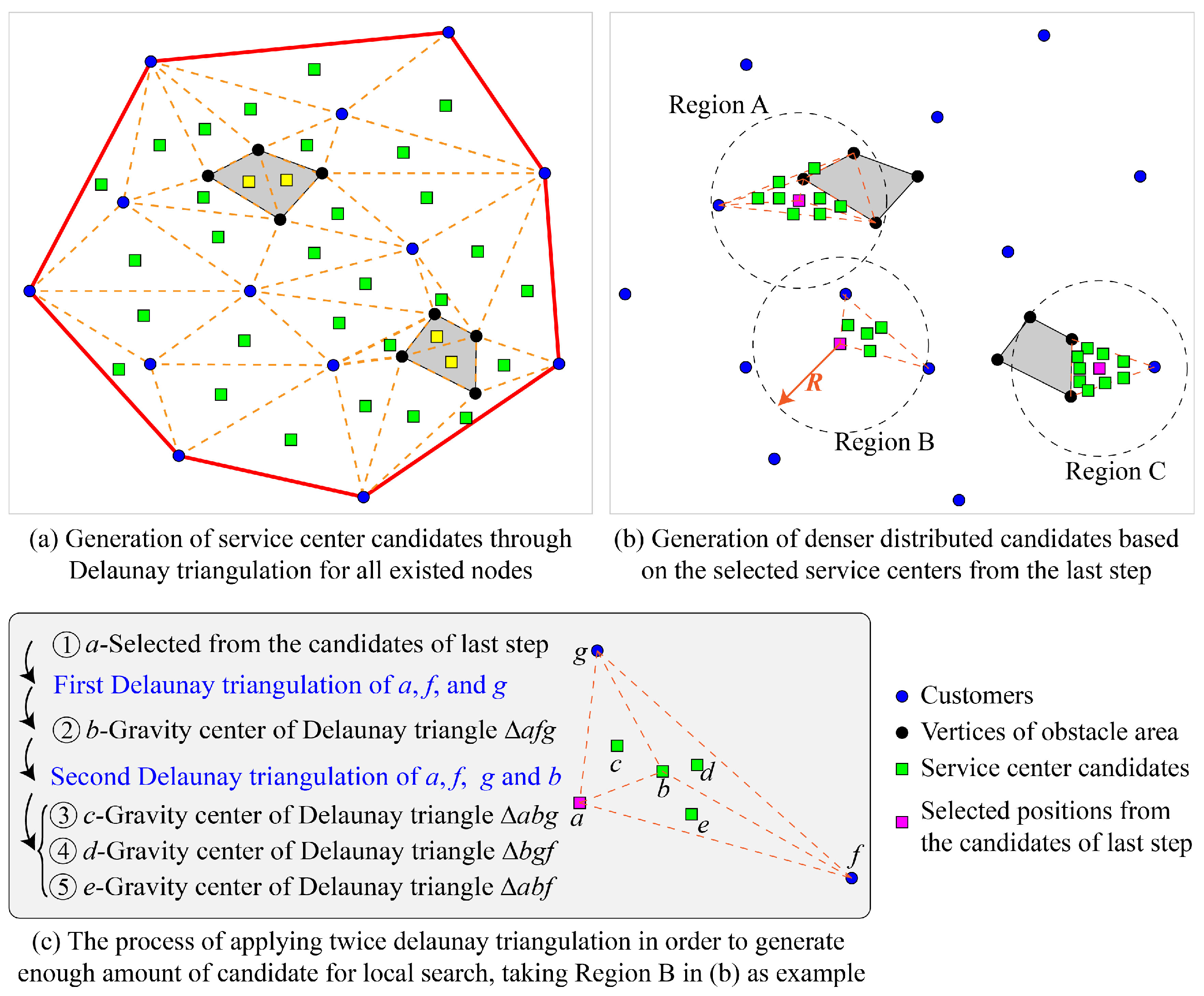
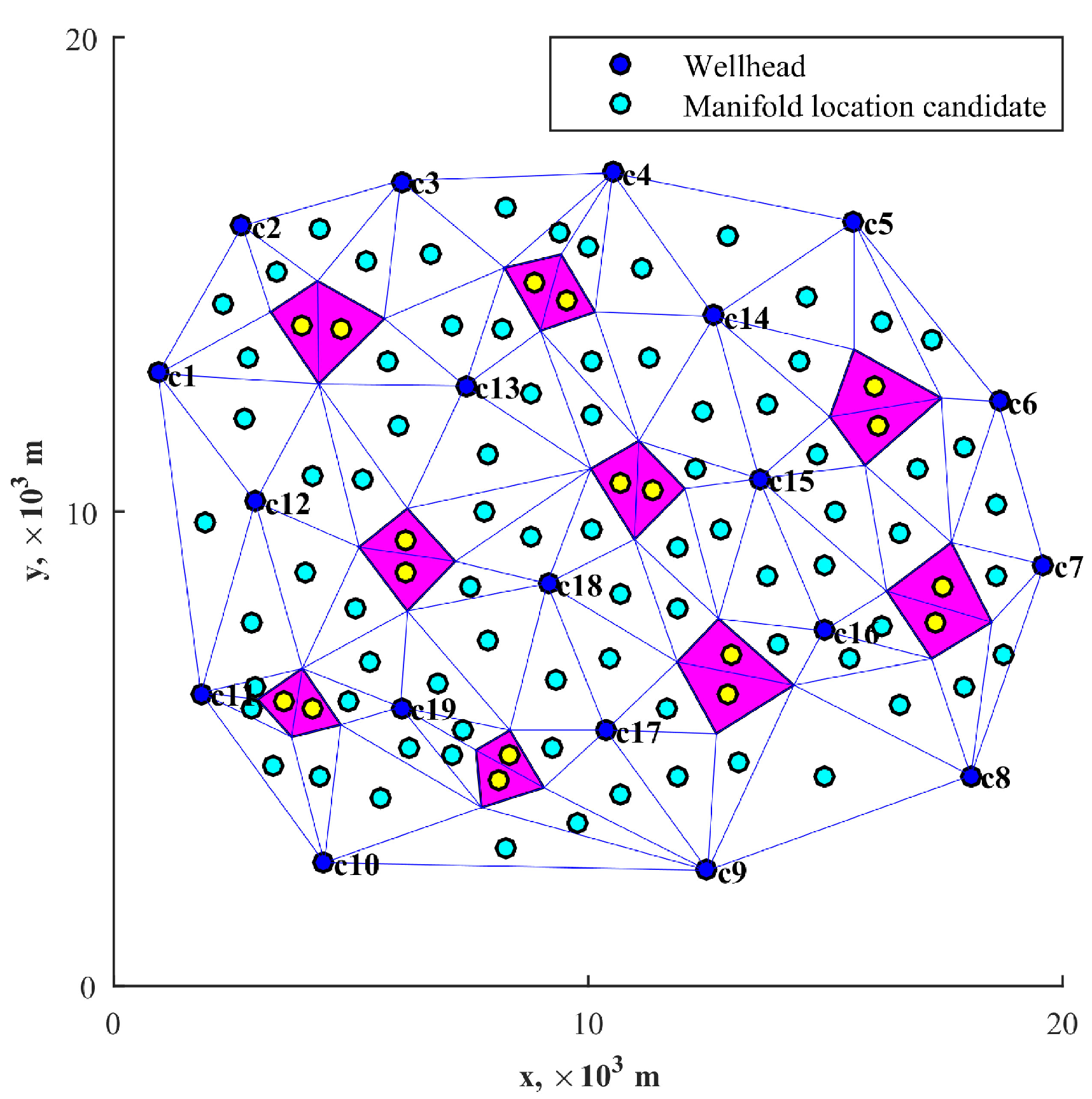
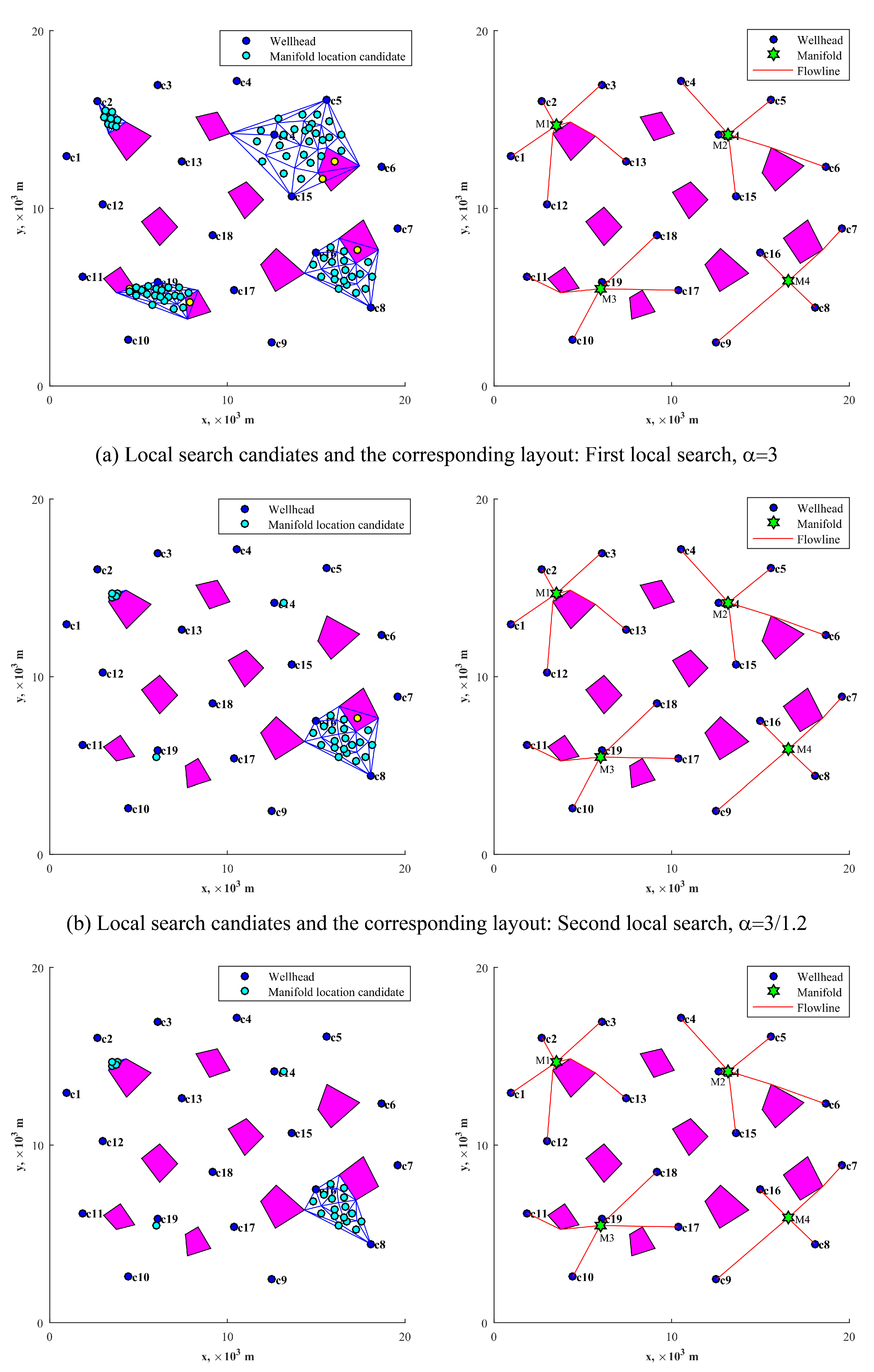
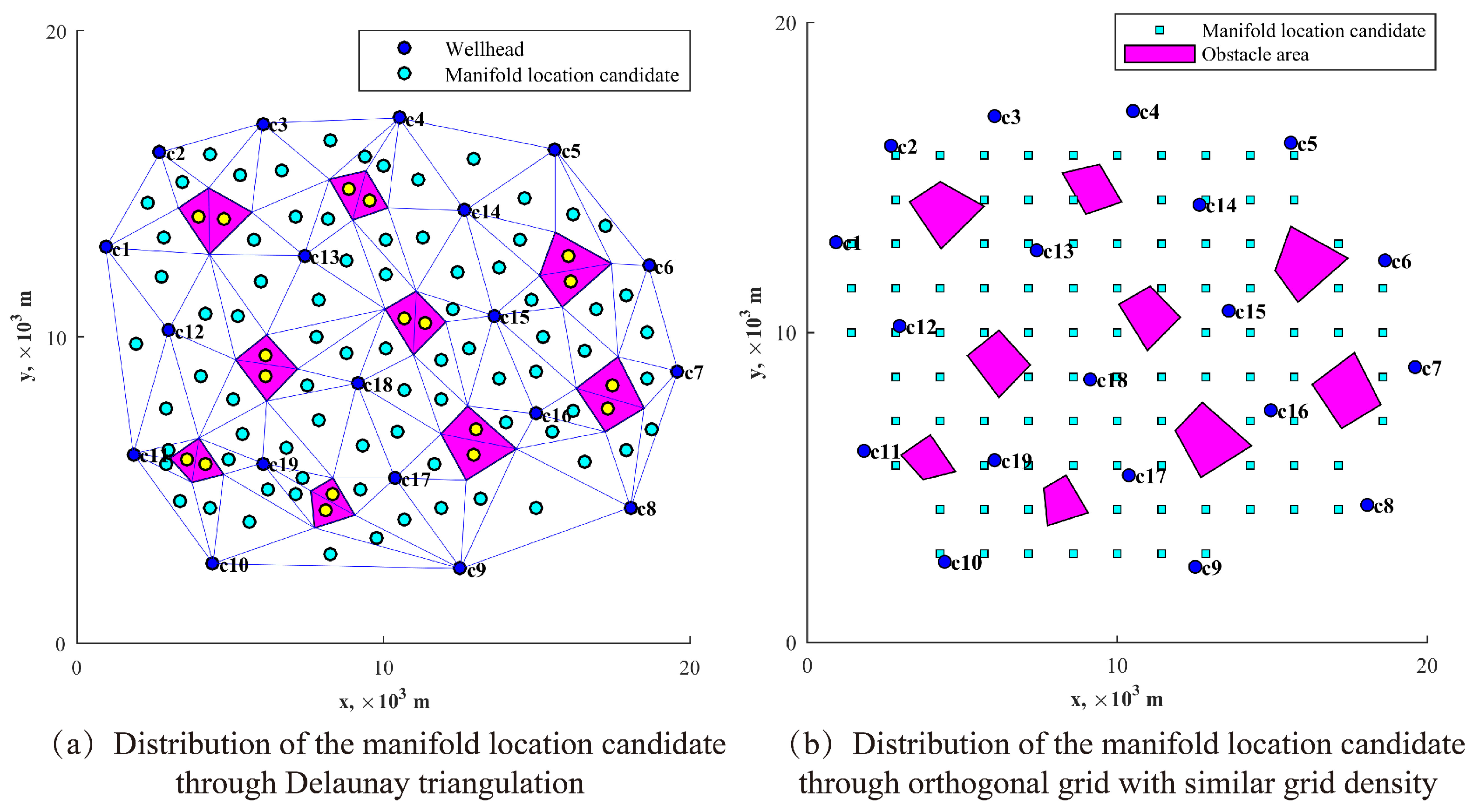
- Step 1: Delaunay triangulation is applied to the original node set, which includes the customer nodes and the vertices of the obstacle regions. Delaunay triangulation (also known as Delone triangulation) for a given set of discrete points in a plane is a triangulation such that no point is inside the circumcircle of any triangle [43]. The gravity centers of all Delaunay triangles, except for the ones inside the obstacles, are set as the service center candidates. Delaunay triangulation helps to make “uniformly” divisions of the target area, so that the distribution of the candidates is moderate, neither too dense (which might result in larger calculation consumption) nor too sparse (which might not bring a good solution), presenting the “global search” characteristics, as shown in Figure 7a. With these candidates, the proposed model can be solved through some linear programming solvers, such as CPLEX, GUROBI, etc. CPLEX is used in this work.
- Step 2: Centered at each obtained service center, the circle with a given radius R includes some of the existed nodes, which are collected and used to generate new candidates for the service centers. Delaunay triangulation is applied twice in order to provide denser candidates, as shown in Figure 7b,c. For each service center, the searching radius R comes from a given factor and the minimum distance towards the other nodes. The factor is reduced proportionally after each step of local searching, thus resulting in a reduction in the search radius, as shown by Equation (23).This treatment generates candidates in a limited region which is closed to the service center positions obtained in the last step, presenting the “local search” characteristics, which helps to find more accurate service center positions. The updated MILP model results in a set of updated service center positions.
- Step 3: Reduce the given radius R proportionally, and repeat Step2 until the obtained service center positions do not change, thus achieving the final service center positions as well as the corresponding layout.
5. Case Studies
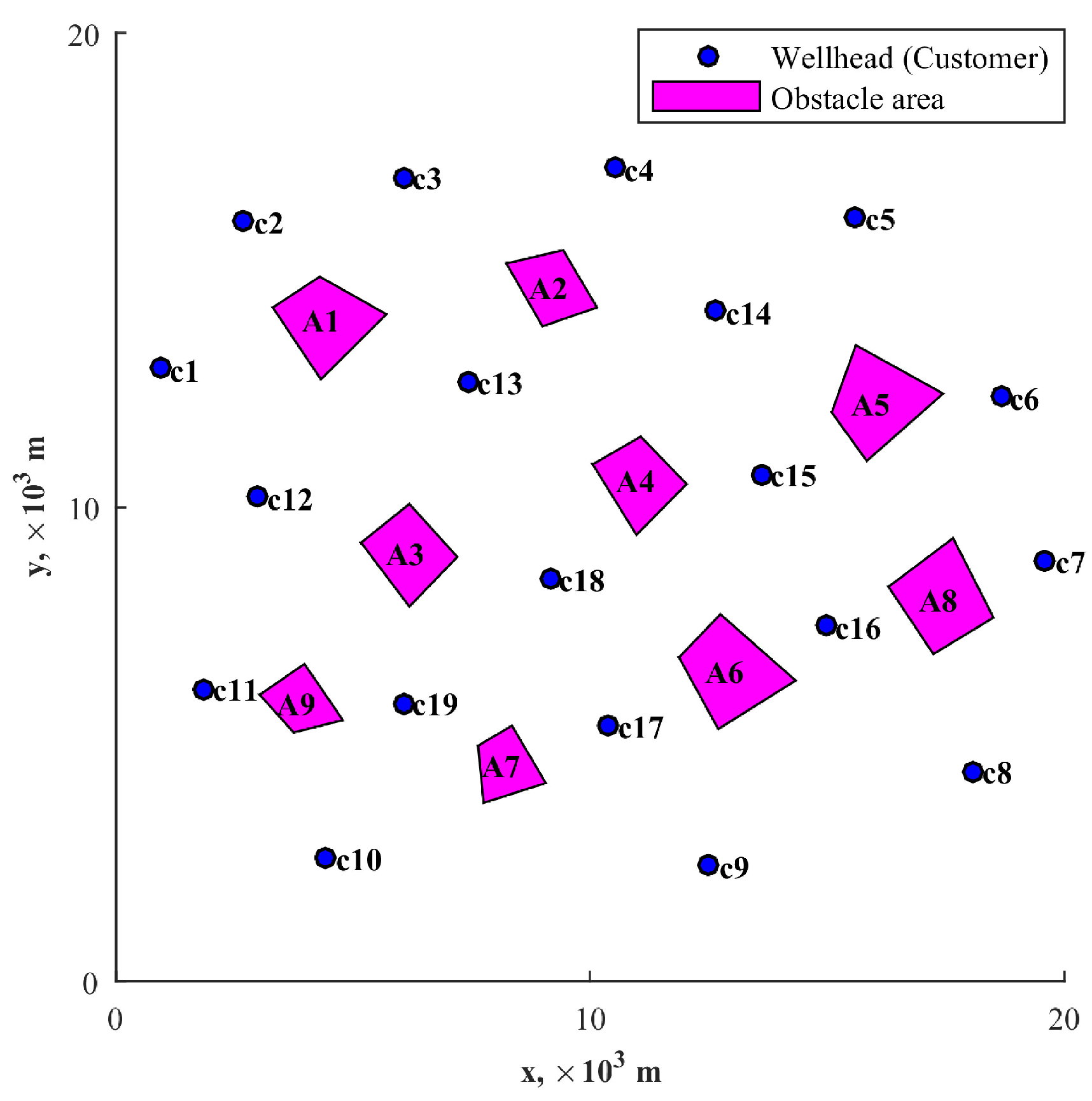
5.1. Input Information
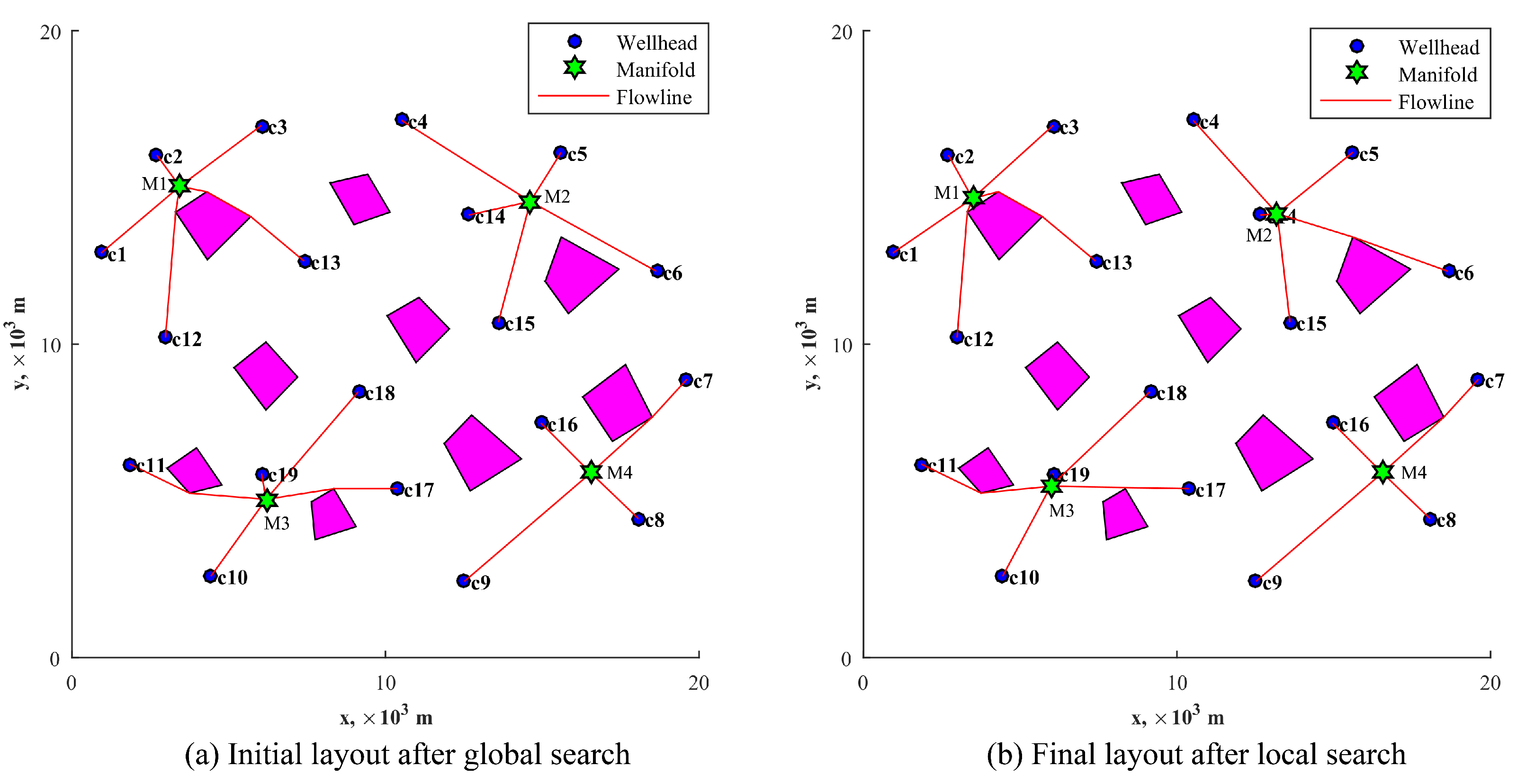
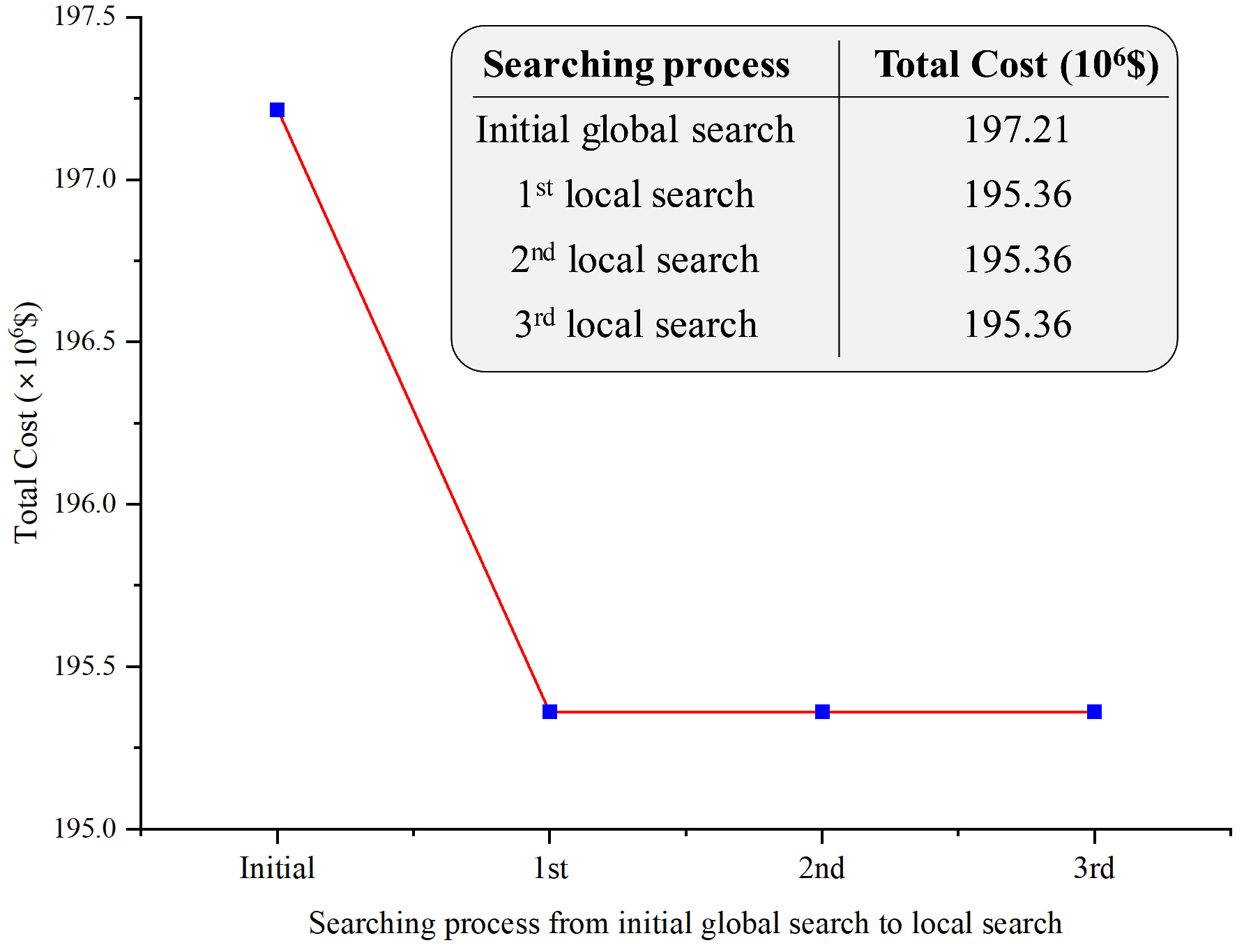
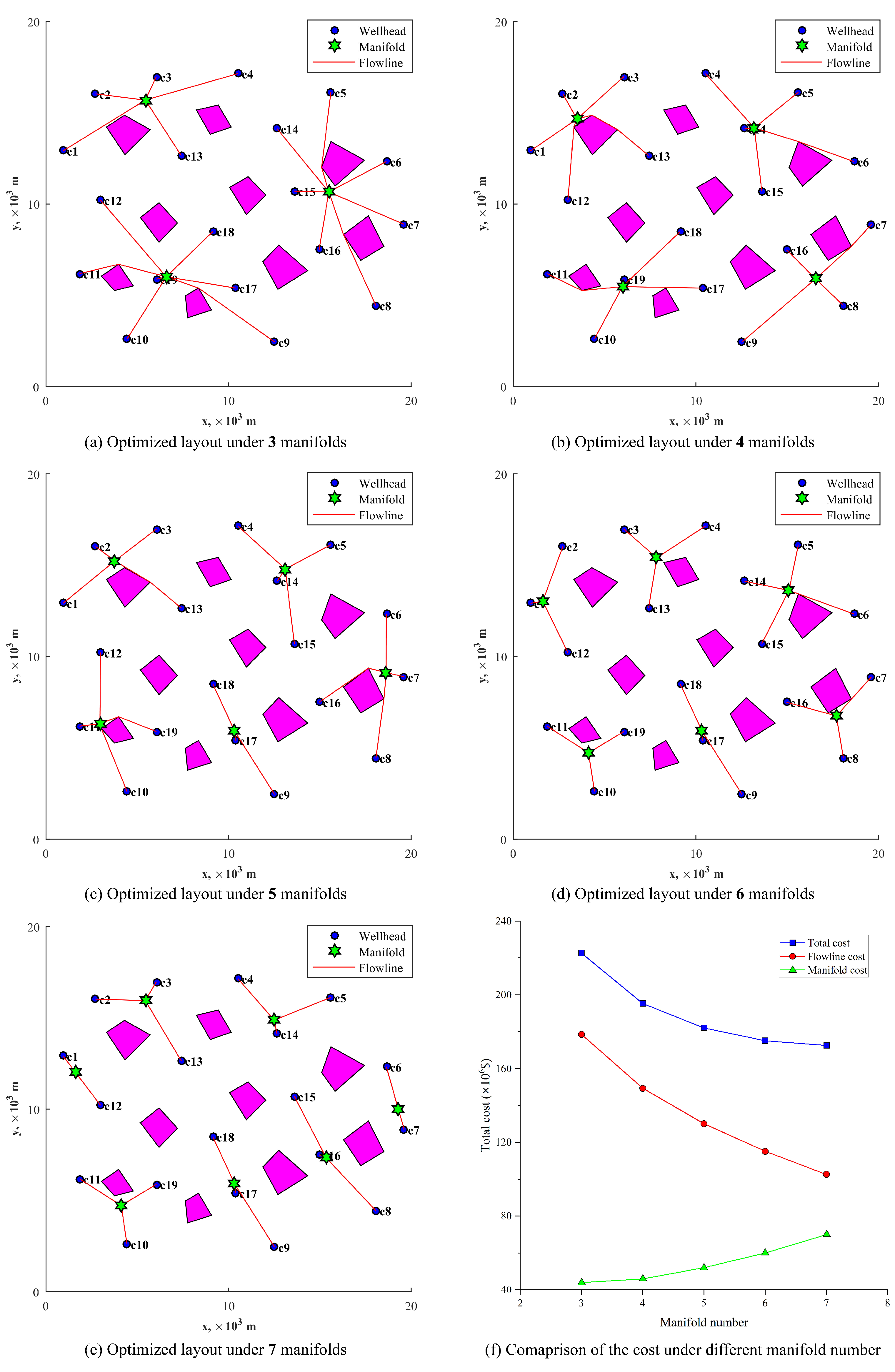
5.2. Optimization Results
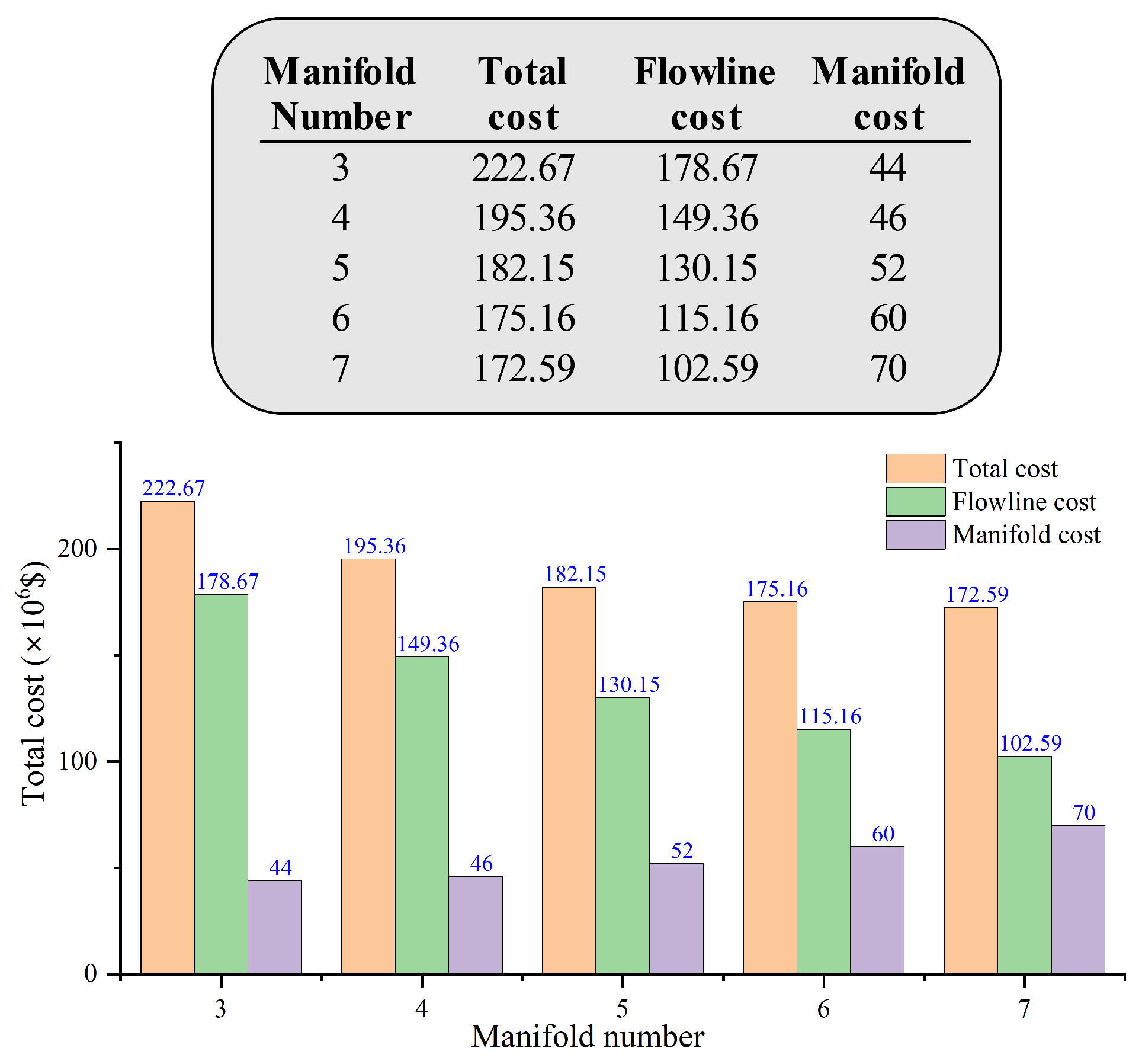
5.3. Effect of Manifold Number
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buckley, K.; Uehara, R. Subsea Concept Alternatives for Brazilian Pre-Salt Fields. In Proceedings of the Offshore Technology Conference Brasil, Rio de Janeiro, Brazil, 24–26 October 2017. [Google Scholar] [CrossRef]
- Froese, G.; Ku, S.Y.; Kheirabadi, A.C.; Nagamune, R. Optimal layout design of floating offshore wind farms. Renew. Energy 2022, 190, 94–102. [Google Scholar] [CrossRef]
- Almedallah, M.K.; Walsh, S.D. Integrated well-path and surface-facility optimization for shallow-water oil and gas field developments. J. Pet. Sci. Eng. 2019, 174, 859–871. [Google Scholar] [CrossRef]
- Cocimano, R. KM3NeT deep-sea cabled network: The star-like layout. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2013, 725, 223–226. [Google Scholar] [CrossRef]
- Liu, H.; Gjersvik, T.B.; Faanes, A. Subsea field layout optimization (part II)–the location-allocation problem of manifolds. J. Pet. Sci. Eng. 2022, 208, 109273. [Google Scholar] [CrossRef]
- Cooper, L. Location-Allocation Problems. Oper. Res. 1963, 11, 331–343. [Google Scholar] [CrossRef]
- Chu, P.C.; Beasley, J.E. A genetic algorithm for the generalised assignment problem. J. Oper. Res. Soc. 1997, 48, 804–809. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Hekmatfar, M.; Fahimnia, B.; Kazemzadeh, N. Hierarchical facility location problem: Models, classifications, techniques, and applications. Comput. Ind. Eng. 2014, 68, 104–117. [Google Scholar] [CrossRef]
- Şahin, G.; Süral, H.; Meral, S. Locational analysis for regionalization of Turkish Red Crescent blood services. Comput. Oper. Res. 2007, 34, 692–704. [Google Scholar] [CrossRef]
- Shariff, S.; Moin, N.H.; Omar, M. Location allocation modeling for healthcare facility planning in Malaysia. Comput. Ind. Eng. 2012, 62, 1000–1010. [Google Scholar] [CrossRef]
- Mestre, A.M.; Oliveira, M.D.; Barbosa-Póvoa, A.P. Location-allocation approaches for hospital network planning under uncertainty. Eur. J. Oper. Res. 2014, 240, 791–806. [Google Scholar] [CrossRef]
- Cicek, C.T.; Gultekin, H.; Tavli, B. The location-allocation problem of drone base stations. Comput. Oper. Res. 2019, 111, 155–176. [Google Scholar] [CrossRef]
- Feng, Y.; Liu, Y.K.; Chen, Y. Distributionally robust location–allocation models of distribution centers for fresh products with uncertain demands. Expert Syst. Appl. 2022, 209, 118180. [Google Scholar] [CrossRef]
- Fahmy, S.A.; Zaki, A.M.; Gaber, Y.H. Optimal locations and flow allocations for aggregation hubs in supply chain networks of perishable products. Socio-Econ. Plan. Sci. 2022, 86, 101500. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J. A task allocation algorithm for a swarm of unmanned aerial vehicles based on bionic wolf pack method. Knowl.-Based Syst. 2022, 250, 109072. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Jia, D.; Zhou, Y. A Bi-level programming for union battery swapping stations location-routing problem under joint distribution and cost allocation. Energy 2023, 272, 127152. [Google Scholar] [CrossRef]
- Devine, M.D.; Lesso, W.G. Models for the Minimum Cost Development of Offshore Oil Fields. Manag. Sci. 1972, 18, 378–387. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, M.; Xu, M.; Wang, D.; Feng, W. A mathematical model for subsea wells partition in the layout of cluster manifolds. Appl. Ocean Res. 2012, 36, 26–35. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, M.; Feng, J.; Mao, D.; Xu, M.; Estefen, S.F. Modeling for the optimization of layout scenarios of cluster manifolds with pipeline end manifolds. Appl. Ocean Res. 2014, 46, 94–103. [Google Scholar] [CrossRef]
- Liu, H.; Gjersvik, T.B.; Faanes, A. Subsea field layout optimization (part III) — the location-allocation problem of drilling sites. J. Pet. Sci. Eng. 2022, 208, 109336. [Google Scholar] [CrossRef]
- Fischetti, M.; Pisinger, D. Optimizing wind farm cable routing considering power losses. Eur. J. Oper. Res. 2018, 270, 917–930. [Google Scholar] [CrossRef]
- Liu, Y.; Fu, Y.; Huang, L.L.; Ren, Z.X.; Jia, F. Optimization of offshore grid planning considering onshore network expansions. Renew. Energy 2022, 181, 91–104. [Google Scholar] [CrossRef]
- Kim, S.; Kang, S.; Lee, J.H. Optimal design of offshore wind power farm in high resolution using geographical information system. Comput. Chem. Eng. 2023, 174, 108253. [Google Scholar] [CrossRef]
- Ramshani, M.; Ostrowski, J.; Zhang, K.; Li, X. Two level uncapacitated facility location problem with disruptions. Comput. Ind. Eng. 2019, 137, 106089. [Google Scholar] [CrossRef]
- Kratica, J.; Dugošija, D.; Savić, A. A new mixed integer linear programming model for the multi level uncapacitated facility location problem. Appl. Math. Model. 2014, 38, 2118–2129. [Google Scholar] [CrossRef]
- Gokbayrak, K.; Kocaman, A.S. A distance-limited continuous location-allocation problem for spatial planning of decentralized systems. Comput. Oper. Res. 2017, 88, 15–29. [Google Scholar] [CrossRef]
- Rodrigues, H.W.L.; Prata, B.A.; Bonates, T.O. Integrated optimization model for location and sizing of offshore platforms and location of oil wells. J. Pet. Sci. Eng. 2016, 145, 734–741. [Google Scholar] [CrossRef]
- Silva, L.M.; Guedes Soares, C. Oilfield development system optimization under reservoir production uncertainty. Ocean Eng. 2021, 225, 108758. [Google Scholar] [CrossRef]
- Nash, I. Arctic Development of the Canadian Beaufort Sea, Geohazards and Export Route Options. In Proceedings of the OTC Arctic Technology Conference, Copenhagen, Denmark, 23–25 March 2015. [Google Scholar] [CrossRef]
- Hong, C.; Estefen, S.F.; Lourenço, M.I.; Wang, Y. A nonlinear constrained optimization model for subsea pipe route selection on an undulating seabed with multiple obstacles. Ocean Eng. 2019, 186, 106088. [Google Scholar] [CrossRef]
- Zhang, H.; Liang, Y.; Ma, J.; Qian, C.; Yan, X. An MILP method for optimal offshore oilfield gathering system. Ocean Eng. 2017, 141, 25–34. [Google Scholar] [CrossRef]
- Wu, Y.; Xia, T.; Wang, Y.; Zhang, H.; Feng, X.; Song, X.; Shibasaki, R. A synchronization methodology for 3D offshore wind farm layout optimization with multi-type wind turbines and obstacle-avoiding cable network. Renew. Energy 2022, 185, 302–320. [Google Scholar] [CrossRef]
- Hong, C.; Estefen, S.F.; Wang, Y.; Lourenço, M.I. Mixed-integer nonlinear programming model for layout design of subsea satellite well system in deep water oil field. Autom. Constr. 2021, 123, 103524. [Google Scholar] [CrossRef]
- Mikolajková, M.; Haikarainen, C.; Saxén, H.; Pettersson, F. Optimization of a natural gas distribution network with potential future extensions. Energy 2017, 125, 848–859. [Google Scholar] [CrossRef]
- Mikolajková, M.; Saxén, H.; Pettersson, F. Linearization of an MINLP model and its application to gas distribution optimization. Energy 2018, 146, 156–168. [Google Scholar] [CrossRef]
- Gong, D.; Gen, M.; Xu, W.; Yamazaki, G. Hybrid evolutionary method for obstacle location-allocation. Comput. Ind. Eng. 1995, 29, 525–530. [Google Scholar] [CrossRef]
- Gong, D.; Gen, M.; Yamazaki, G.; Xu, W. Planar Location-allocation with Obstacles Problem. 1996 IEEE Int. Conf. Syst. Man Cybernetics. Inf. Intell. Syst. 1996, 4, 2671–2676. [Google Scholar]
- Hong, C.; Estefen, S.F.; Wang, Y.; Lourenço, M.I. An integrated optimization model for the layout design of a subsea production system. Appl. Ocean Res. 2018, 77, 1–13. [Google Scholar] [CrossRef]
- Dutta, R.N.; Ghosh, S.C. Mobility aware resource allocation for millimeter-wave D2D communications in presence of obstacles. Comput. Commun. 2023, 200, 54–65. [Google Scholar] [CrossRef]
- Lerch, M.; De-Prada-Gil, M.; Molins, C. A metaheuristic optimization model for the inter-array layout planning of floating offshore wind farms. Int. J. Electr. Power Energy Syst. 2021, 131, 107128. [Google Scholar] [CrossRef]
- Saint-Marcoux, J.; Legras, J. Impact on Risers and Flowlines Design of the FPSO Mooring in Deepwater and Ultra Deepwater. In Proceedings of the OTC Offshore Technology Conference, Houston, TX, USA, 5–8 May 2014. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Sastry, S.P. A 2D advancing-front Delaunay mesh refinement algorithm. Comput. Geom. Theory Appl. 2021, 97, 101772. [Google Scholar] [CrossRef]

| Well No. | x-y Cord (m) | Flow Rate (/day) | Well No. | x-y Cord (m) | Flow Rate (/day) |
|---|---|---|---|---|---|
| 1 | (935.43, 12,909.21) | 918.06 | 11 | (1835.43, 6180.3) | 1238.62 |
| 2 | (2710.67, 16,027.38) | 1407.18 | 12 | (2983.15, 10,208.46) | 1679.16 |
| 3 | (6046.48, 16,979.12) | 1368.48 | 13 | (7404.75, 12,650.4) | 1438.21 |
| 4 | (10,513.49, 17,141.91) | 1332.25 | 14 | (12,656.17, 14,119.75) | 1665.35 |
| 5 | (15,603.91, 16,119.22) | 1006.12 | 15 | (13,601.6, 10,696.85) | 1622.74 |
| 6 | (18,642.47, 12,324.81) | 1236.42 | 16 | (14,959.86, 7486.84) | 1855.76 |
| 7 | (19,612.66, 8881.05) | 1138.85 | 17 | (10,377.25, 5391.36) | 1317.39 |
| 8 | (18,068.61, 4435.45) | 1226.73 | 18 | (9134.58, 8484.49) | 1513.62 |
| 9 | (12,519.93, 2435.98) | 1100.93 | 19 | (6046.48, 5879.75) | 1110.49 |
| 10 | (4436.37, 2598.78) | 1177.61 |
| Obstacle No. | Vertices’ Coordinates (m) | Obstacle No. | Vertices’ Coordinates (m) |
|---|---|---|---|
| A1 | (3309.3, 14,211.58) | A6 | (11,875.89, 6831.48) |
| (4296.01, 14,862.76) | (12,747, 7741.47) | ||
| (5703.82, 14,069.65) | (14,336.46, 6343.09) | ||
| (4320.78, 12,696.32) | (12,701.59, 5320.4) | ||
| A2 | (8234.57, 15,142.44) | A7 | (7635.95, 4969.76) |
| (9431.83, 15,422.12) | (8350.17, 5391.36) | ||
| (10,146.06, 14,211.58) | (9064.4, 4180.82) | ||
| (8994.21, 13,815.02) | (7751.54, 3763.4) | ||
| A3 | (5171.24, 9252.55) | A8 | (16,293.36, 8321.69) |
| (6186.85, 10,066.54) | (17,655.76, 9348.56) | ||
| (7198.33, 8952.01) | (18,506.23, 7670.51) | ||
| (6186.85, 7904.27) | (17,238.78, 6902.44) | ||
| A4 | (10,055.23, 10,905.56) | A9 | (3032.69, 6042.55) |
| (11,066.71, 11,489.96) | (3973.99, 6693.73) | ||
| (12,036.9, 10,488.14) | (4783.17, 5508.24) | ||
| (10,975.88, 9415.35) | (3746.92, 5249.44) | ||
| A5 | (15,096.1, 11,999.22) | ||
| (15,603.91, 13,418.47) | |||
| (17,445.21, 12,395.77) | |||
| (15,835.1, 10,976.53) |
| Slot Number | Processing Capacity (bbl/day) | Price ( USD) |
|---|---|---|
| 4 | 35,000 | 10 |
| 6 | 50,000 | 12 |
| 8 | 65,000 | 16 |
| 10 | 80,000 | 20 |
| Items | Initial Layout from Global Search | Final Layout from Local Search | |
|---|---|---|---|
| Manifold types and locations | M1 | 6 slots, (3438.66, 15,033.91) | 6 slots (3476.43, 14,649.41) |
| M2 | 6 slots, (14,621.33, 14,552.48) | 6 slots, (13,194.25, 14164.58) | |
| M3 | 6 slots, (6193.73, 5050.46) | 6 slots, (5971.56, 5469.9) | |
| M4 | 4 slots, (16,547.95, 5893.66) | 4 slots, (16,547.95, 5893.66) | |
| Cost of manifolds ( $) | 46 | 46 | |
| Cost of flowlines ( $) | 151.21 | 149.36 | |
| Total cost ( $) | 197.21 | 195.36 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, C.; Wang, Y.; Estefen, S.F. A Location-Allocation Model with Obstacle and Capacity Constraints for the Layout Optimization of a Subsea Transmission Network with Line-Shaped Conduction Structures. J. Mar. Sci. Eng. 2023, 11, 1171. https://doi.org/10.3390/jmse11061171
Hong C, Wang Y, Estefen SF. A Location-Allocation Model with Obstacle and Capacity Constraints for the Layout Optimization of a Subsea Transmission Network with Line-Shaped Conduction Structures. Journal of Marine Science and Engineering. 2023; 11(6):1171. https://doi.org/10.3390/jmse11061171
Chicago/Turabian StyleHong, Cheng, Yuxi Wang, and Segen F. Estefen. 2023. "A Location-Allocation Model with Obstacle and Capacity Constraints for the Layout Optimization of a Subsea Transmission Network with Line-Shaped Conduction Structures" Journal of Marine Science and Engineering 11, no. 6: 1171. https://doi.org/10.3390/jmse11061171
APA StyleHong, C., Wang, Y., & Estefen, S. F. (2023). A Location-Allocation Model with Obstacle and Capacity Constraints for the Layout Optimization of a Subsea Transmission Network with Line-Shaped Conduction Structures. Journal of Marine Science and Engineering, 11(6), 1171. https://doi.org/10.3390/jmse11061171






