Numerical Investigation on Cavitation Vortex Dynamics of a Centrifugal Pump Based on Vorticity Transport Method
Abstract
:1. Introduction
2. Numerical Method
2.1. Governing Equations
2.2. Turbulence Model
2.3. Zwart Cavitation Model
2.4. Pump Model, Mesh, and Boundary Setup
3. Results and Discussion
3.1. Pump Performance Testing
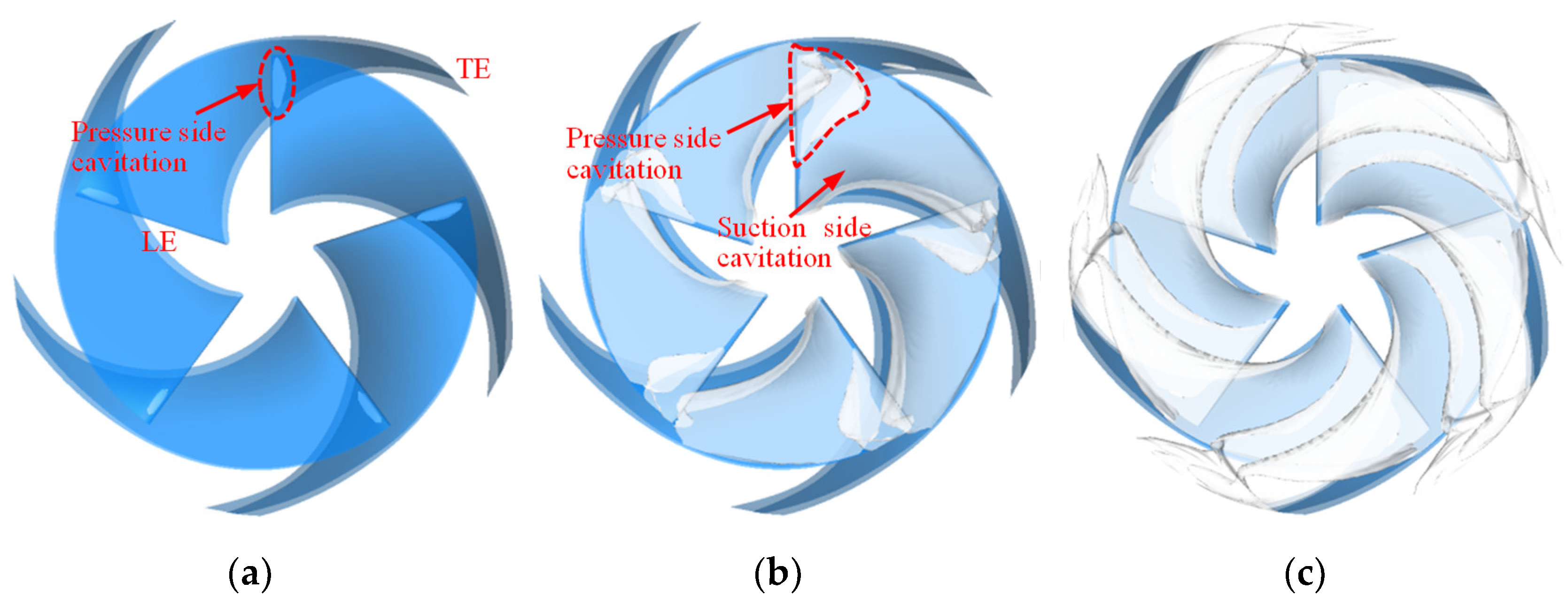
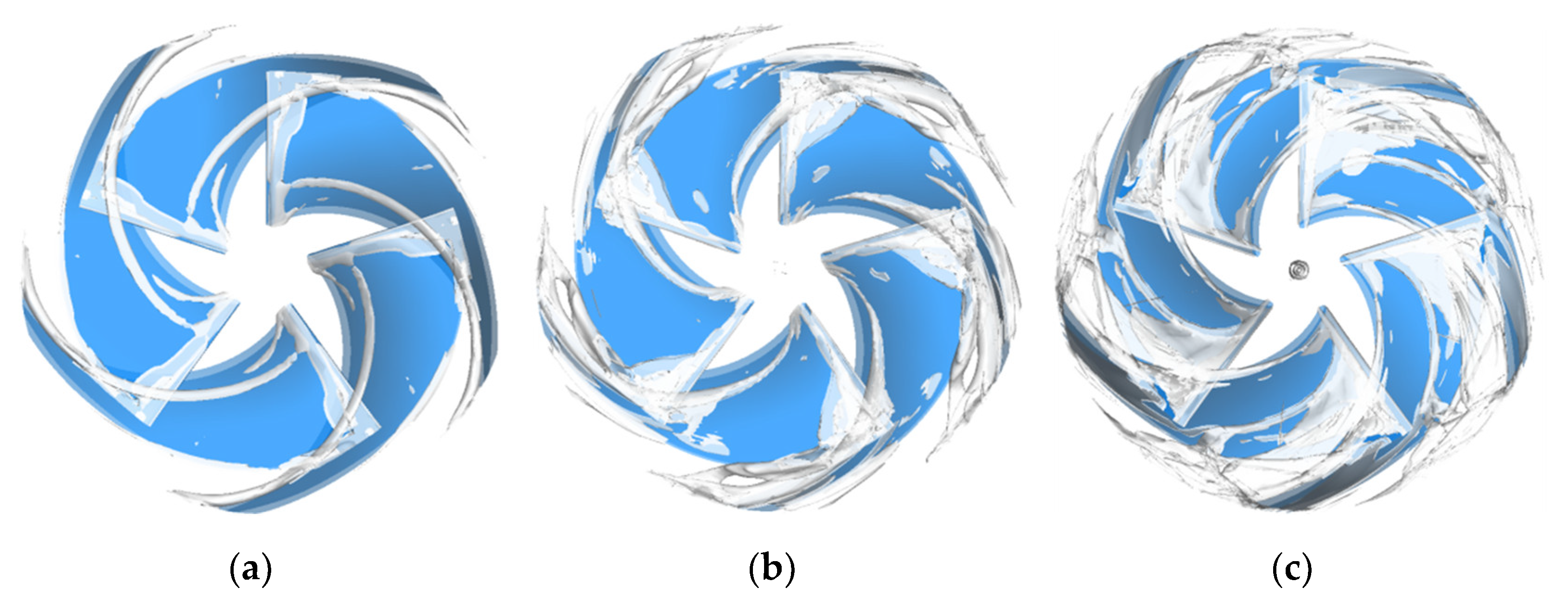
3.2. Cavitation Performance Analysis
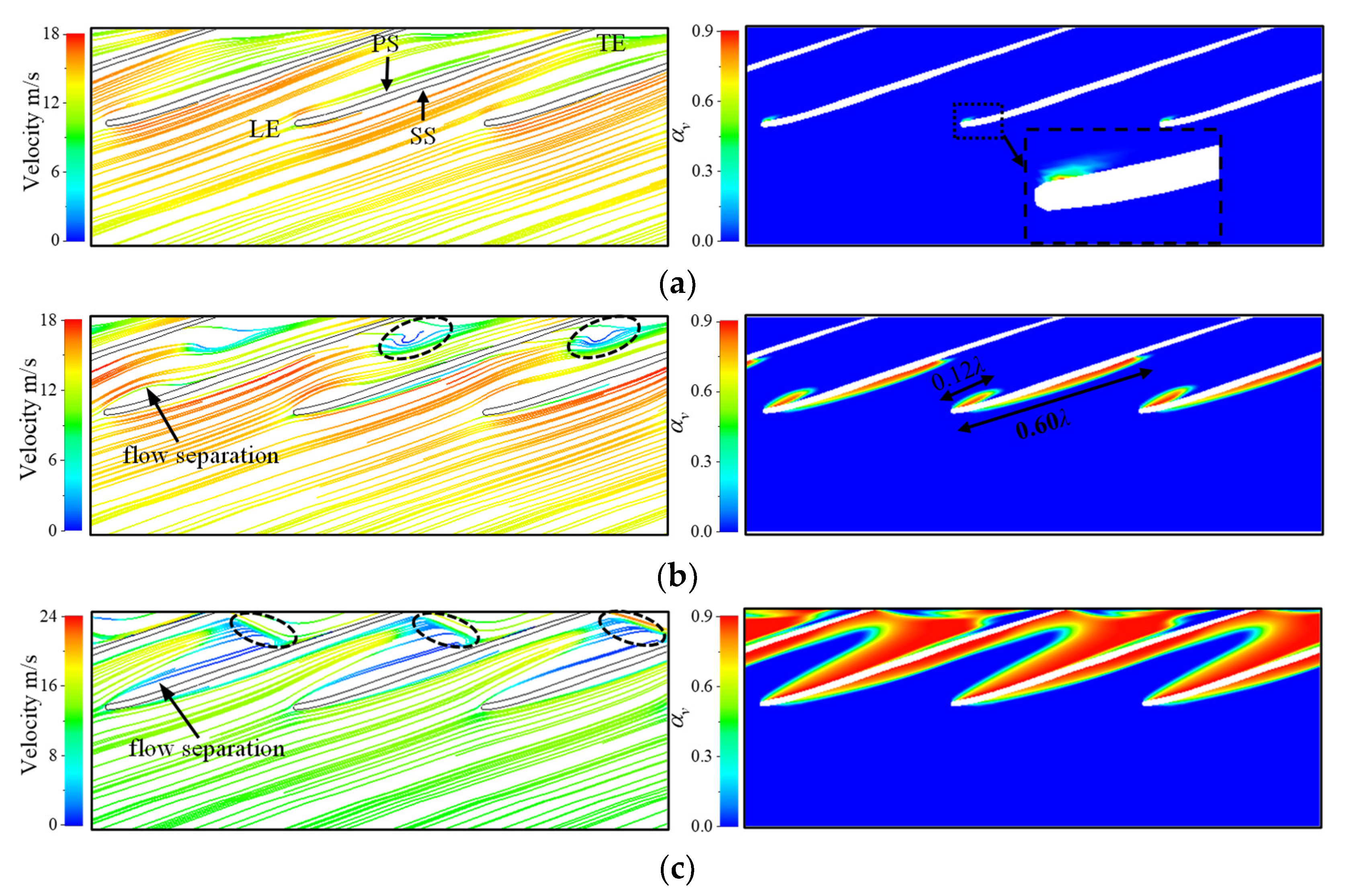
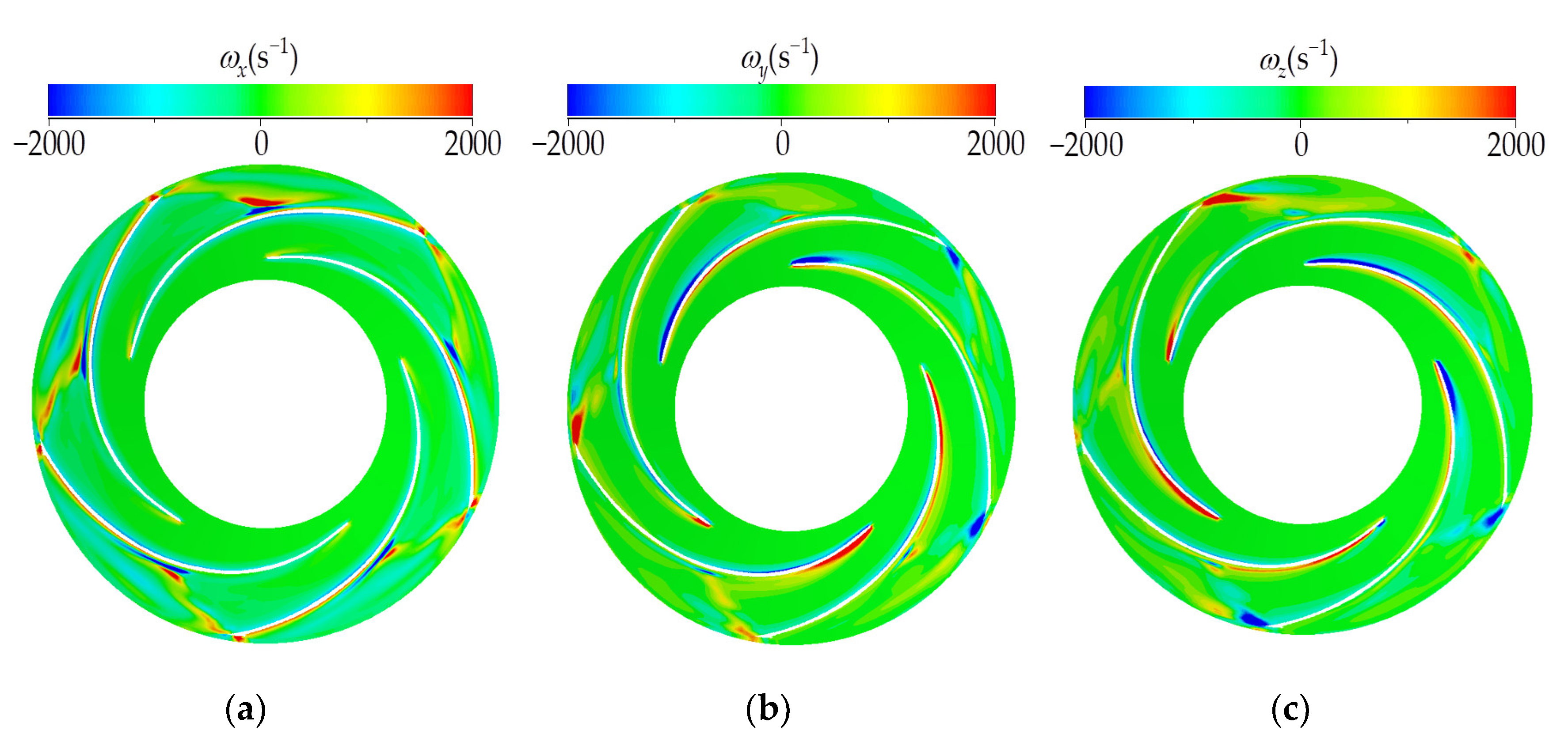
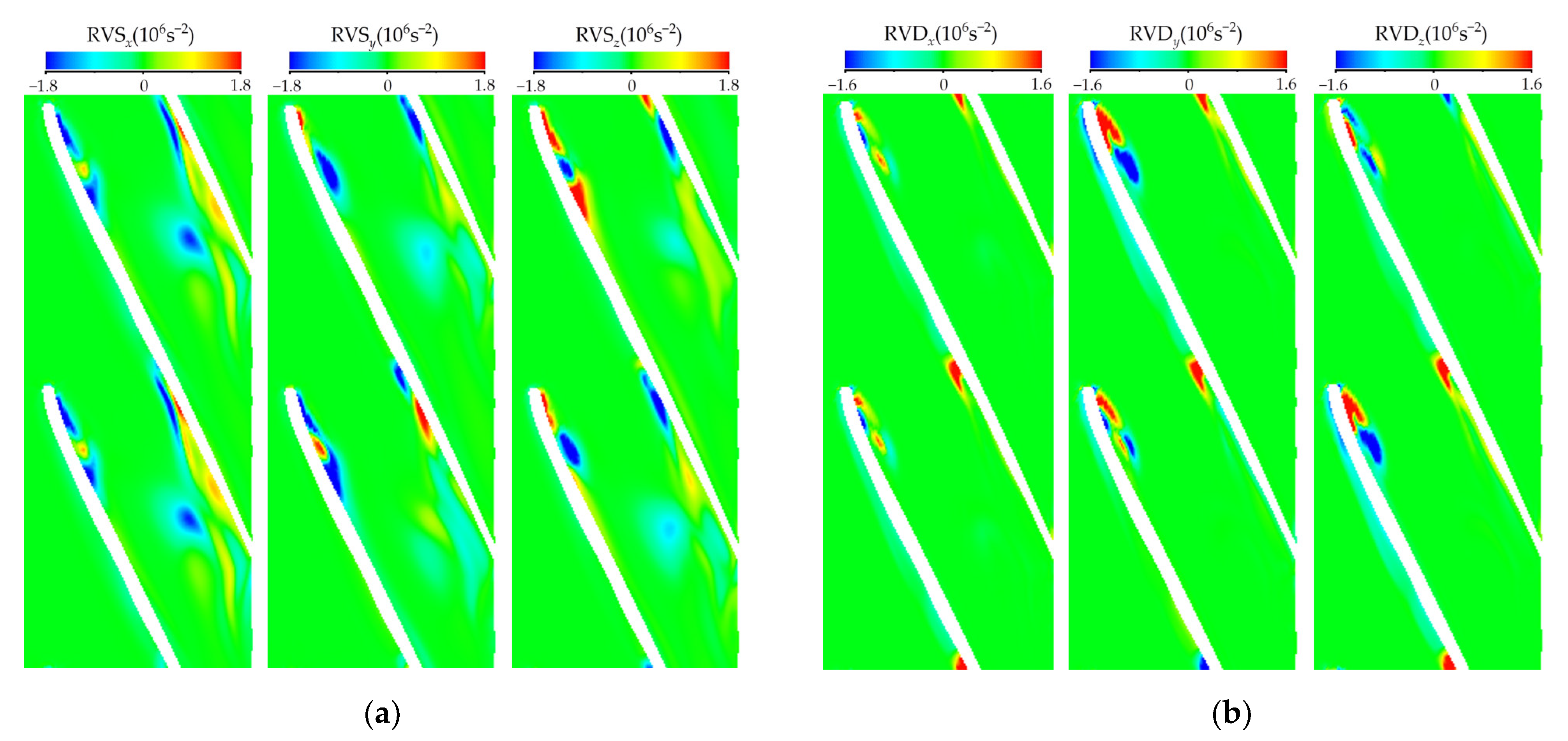
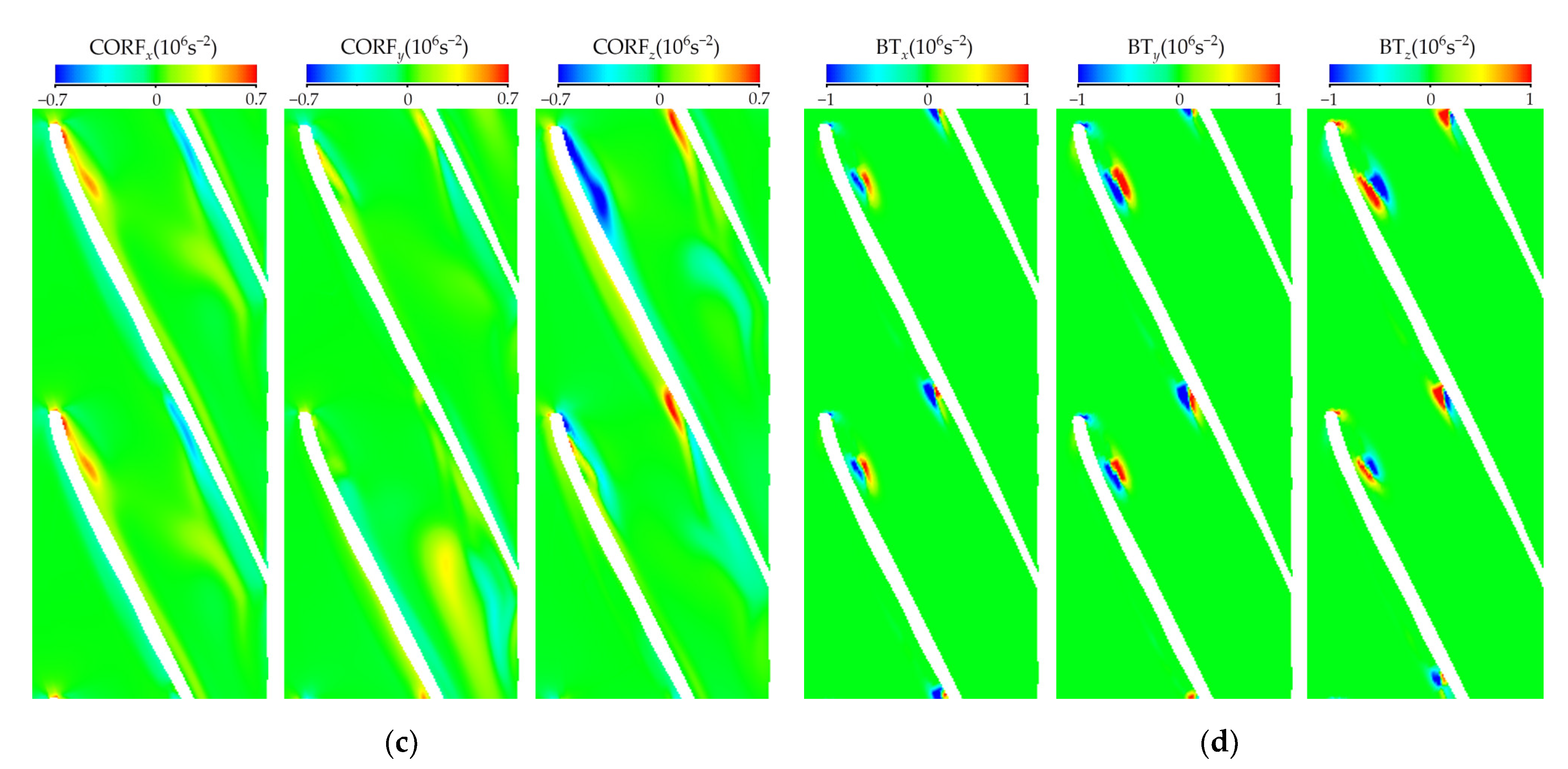
3.3. Cavitation Vortex Dynamics Analysis
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| σc | Critical cavitation number |
| σ | Cavitation number |
| N | Impeller blades number |
| D1 | Inlet pipe diameter, m |
| D2 | Outlet pipe diameter, m |
| Q | Flow discharge, m3/h |
| Qopt | Optimum flow rate, m3/h |
| H | Head, m |
| ns | Specific speed |
| n | Rotating speed, r/min |
| η | Efficiency, % |
| ρm | Mixture density, kg/m3 |
| ui | Velocity in the i direction, m/s |
| fi | Body force term in the i direction |
| µm | Mixture viscosity |
| μt | Mixture turbulent eddy viscosity |
| p | Mixture pressure, Pa |
| δ | Turbulent kinetic energy |
| αv | Vapor volume fraction, |
| μl | Dynamic viscosity of liquid |
| l | Subscript that represents the liquid phase |
| v | Subscript that represents the vapor phase |
| k | Turbulent kinetic energy in Equation (5) |
| ω | Turbulent dissipation rate |
| S | Strain rate dimension |
| F2 | Experience coefficient |
| Evaporation term | |
| Condensation term | |
| Fe | Empirical coefficients for the mass transfer term |
| Fc | Empirical coefficients for the mass transfer term |
| rnu | Volume fraction of the nucleation site |
| RB | Bubble size, m |
| Pin | Pump inlet pressure, Pa |
| Pva | Saturated vapor pressure of the liquid, Pa |
| ρ | Liquid density, |
| U2 | Circumferential velocity of the impeller outlet, m/s |
| wx | Vorticity in the x direction with the Q criterion, s−1 |
| Relative vorticity | |
| Relative velocity | |
| Rotational angular velocity in Equation (16), rad/s | |
| Kinematic viscosity. | |
| LE | Leading edge |
| TE | Trailing edge |
| PS | Pressure side |
| SS | Suction side |
| RVS | Relative vortex stretching |
| RVD | Relative vortex dilation |
| CORF | Coriolis force |
| BT | Baroclinic torque |
| VISD | Viscos diffusion |
References
- Huang, R.; Zhang, Z.; Zhang, W.; Mou, J.; Zhou, P.; Wang, Y. Energy performance prediction of the centrifugal pumps by using a hybrid neural network. Energy 2020, 213, 119005. [Google Scholar] [CrossRef]
- Pei, J.; Yuan, S.; Yuan, J. Numerical analysis of periodic flow unsteadiness in a single-blade centrifugal pump. Sci. China Tech. Sci. 2013, 56, 212–221. [Google Scholar] [CrossRef]
- Li, X.; Chen, B.; Luo, X.; Zhu, Z. Effects of flow pattern on hydraulic performance and energy conversion characterisation in a centrifugal pump. Renew. Energy 2020, 151, 475–487. [Google Scholar] [CrossRef]
- Sun, H.; Luo, Y.; Yuan, S.; Yin, J. Hilbert spectrum analysis of unsteady characteristics in centrifugal pump operation under cavitation status. Ann. Nucl. Energy 2018, 114, 607–615. [Google Scholar] [CrossRef]
- Medvitz, R.; Kunz, R.; Boger, D.; Lindau, J.; Yocum, A.; Pauley, L. Performance Analysis of Cavitating Flow in Centrifugal Pumps Using Multiphase CFD. J. Fluids Eng. 2002, 124, 377–383. [Google Scholar] [CrossRef]
- Rakibuzzaman, M.; Kim, K.; Suh, S. Numerical and experimental investigation of cavitation flows in a multistage centrifugal pump. J. Mech. Sci. Technol. 2018, 32, 1071–1078. [Google Scholar] [CrossRef]
- Mousmoulis, G.; Karlsen-Davies, N.; Aggidis, G.; Anagnostopoulos, I.; Papantonis, D. Experimental analysis of cavitation in a centrifugal pump using acoustic emission, vibration measurements and flow visualization. Eur. J. Mech. B/Fluids 2019, 75, 300–311. [Google Scholar] [CrossRef] [Green Version]
- Ramirez, R.; Avila, E.; Lopez, L.; Bula, A.; Forero, J. CFD characterization and optimization of the cavitation phenomenon in dredging centrifugal pumps. Alex. Eng. J. 2020, 59, 291–309. [Google Scholar] [CrossRef]
- Friedrichs, J.; Kosyna, G. Rotating Cavitation in a Centrifugal Pump Impeller of Low Specific Speed. J. Fluids Eng. 2002, 124, 356–362. [Google Scholar] [CrossRef]
- Bachert, R.; Stoffel, B.; Dular, M. Unsteady Cavitation at the Tongue of the Volute of a Centrifugal Pump. J. Fluids Eng. 2010, 132, 061301. [Google Scholar] [CrossRef]
- Christopher, S.; Kumaraswamy, S. Identification of Critical Net Positive Suction Head from Noise and Vibration in a Radial Flow Pump for Different Leading Edge Profiles of the Vane. J. Fluids Eng. 2013, 135, 121301. [Google Scholar] [CrossRef]
- Tan, L.; Zhu, B.; Wang, Y.; Cao, S.; Gui, S. Numerical study on characteristics of unsteady flow in a centrifugal pump volute at partial load condition. Eng. Comput. 2015, 32, 1549–1566. [Google Scholar] [CrossRef]
- Zhu, D.; Tao, R.; Xiao, R. Anti-Cavitation Design of the Symmetric Leading-Edge Shape of Mixed-Flow Pump Impeller Blades. Symmetry 2019, 11, 46. [Google Scholar] [CrossRef] [Green Version]
- Zuhra, S.; Khan, N.S.; Islam, S. Magnetohydrodynamic second—Grade nanofluid flow containing nanoparticles and gyrotactic microorganisms. Comp. Appl. Math. 2018, 37, 6332–6358. [Google Scholar] [CrossRef]
- Khan, N.S. Bioconvection in Second Grade Nanofluid Flow Containing Nanoparticles and Gyrotactic Microorganisms. Braz. J. Phys. 2018, 48, 227–241. [Google Scholar] [CrossRef]
- Tan, L.; Zhu, B.; Cao, S.; Wang, Y.; Wang, B. Numerical simulation of unsteady cavitation flow in a centrifugal pump at off-design conditions. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 1994–2006. [Google Scholar]
- Wang, Y.; Liu, H.; Yuan, S.; Tan, M.; Kai, W. Experimental testing on cavitation vibration and noise of centrifugal pumps under off-design conditions. Trans. Chin. Soc. Agric. Eng. 2012, 28, 35–38. [Google Scholar]
- Liu, H.; Liu, D.; Wang, Y.; Wu, X.; Zhuang, S. Applicative evaluation of three cavitating models on cavitating flow calculation in centrifugal pump. Trans. Chin. Soc. Agric. Eng. 2012, 28, 54–59. [Google Scholar]
- Tan, L.; Zhu, B.; Cao, S.; Wang, Y. Cavitation flow simulation for a centrifugal pump at a low flow rate. China Sci. Bull. 2013, 58, 949–952. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Yuan, S.; Pan, Z.; Yuan, J.; Fu, Y. Numerical simulation of leading—Edge cavitation within the whole flow passage of a centrifugal pump. Sci. Chin. Tech. Sci. 2013, 56, 2156–2162. [Google Scholar] [CrossRef]
- Tao, R.; Xiao, R.; Wang, Z. Influence of Blade Leading-Edge Shape on Cavitation in a Centrifugal Pump Impeller. Energies 2018, 11, 2588. [Google Scholar] [CrossRef]
- Fu, Y.; Yuan, J.; Yuan, S.; Giovanni, P.; d’Agostino, L.; Huang, P.; Li, X. Numerical and Experimental Analysis of Flow Phenomena in a Centrifugal Pump Operating Under Low Flow Rates. J. Fluids Eng. 2015, 137, 011102. [Google Scholar] [CrossRef]
- Kang, D.; Yonezawa, K.; Horiguchi, H.; Kawata, Y.; Tsujimoto, Y. Cause of Cavitation Instabilities in Three Dimensional Inducer. Int. J. Fluid Mach. Syst. 2009, 2, 206–214. [Google Scholar] [CrossRef] [Green Version]
- Tani, N.; Yamanishi, N.; Tsujimoto, Y. Influence of Flow Coefficient and Flow Structure on Rotational Cavitation in Inducer. J. Fluids Eng. 2012, 134, 021302. [Google Scholar] [CrossRef]
- Zhang, D.; Shi, L.; Shi, W.; Zhao, R.; Wang, H. Numerical analysis of unsteady tip leakage vortex cavitation cloud and unstable suction-side-perpendicular cavitating vortices in an axial flow pump. Int. J. Mult. Flow 2015, 77, 244–259. [Google Scholar] [CrossRef]
- Huang, R.; Ji, B.; Luo, X.W.; Zhai, Z.H.; Zhou, J. Numerical investigation of cavitation-vortex interaction in a mixed-flow waterjet pump. J. Mech. Sci. Technol. 2015, 29, 3707–3716. [Google Scholar] [CrossRef]
- Zwart, P.; Gerber, A.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the 5th International Conference on Multiphase Flow, Yokohama, Japan, 30 May–3 June 2004. [Google Scholar]
- Menter, F. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Com. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Bardina, J.; Huang, P.; Coakley, T. Turbulence Modeling Validation, Testing, and Development; NASA Technical Memorandum: Washington, DC, USA, 1997.
- Reboud, J.; Stutz, B.; Coutier-Delgosha, O. Two-Phase Flow Structure of Cavitation: Experiment and Modelling of Unsteady Effects. In Proceedings of the Third International Symposium on Cavitation, Grenoble, France, 7–10 April 1998. [Google Scholar]
- Shen, X.; Zhang, D.; Xu, B.; Ye, C.; Shi, W. Experimental and numerical investigation of tip leakage vortex cavitation in an axial flow pump under design and off-design conditions. Proc. Inst. Mech. Eng. Part A J. Power Energy 2020, 235, 70–80. [Google Scholar] [CrossRef]
- Coutier-Delgosha, O.; Fortes-Patella, R.; Reboud, J. Evaluation of the Turbulence Model Influence on the Numerical Simulations of Unsteady Cavitation. J. Fluids Eng. 2003, 125, 38–45. [Google Scholar] [CrossRef] [Green Version]
- Coutier-Delgosha, O.; Courtot, Y.; Joussellin, F.; Reboud, J. Numerical simulation of the unsteady cavitation behavior of an inducer blade cascade. AIAAJ 2012, 42, 560–569. [Google Scholar] [CrossRef] [Green Version]
- Leroux, J.; Coutier-Delgosha, O.; Astolfi, J. A joint experimental and numerical study of mechanisms associated to instability of partial cavitation on two-dimensional hydrofoil. Phys. Fluids 2005, 17, 052101. [Google Scholar] [CrossRef] [Green Version]
- Dular, M.; Bachert, R.; Stoffel, B.; Širok, B. Experimental evaluation of numerical simulation of cavitating flow around hydrofoil. Eur. J. Mech. B/Fluids. 2005, 24, 522–538. [Google Scholar] [CrossRef]
- Liu, J.; Liu, S.; Wu, Y.; Jiao, L.; Wang, L.; Sun, Y. Numerical investigation of the hump characteristic of a pump–turbine based on an improved cavitation model. Com. Fluids 2012, 68, 105–111. [Google Scholar] [CrossRef]
- Mejri, I.; Bakir, F.; Rey, R.; Belamri, T. Comparison of Computational Results Obtained from a Homogeneous Cavitation Model With Experimental Investigations of Three Inducers. J. Fluids Eng. 2006, 128, 1308–1323. [Google Scholar] [CrossRef]
- Ji, B.; Luo, X.; Peng, X.; Wu, Y.; Xu, H. Numerical analysis of cavitation evolution and excited pressure fluctuation around a propeller in non-uniform wake. Int. J. Mult. Flow 2012, 43, 13–21. [Google Scholar] [CrossRef]
- Seo, J.; Lele, S. Numerical investigation of cloud cavitation and cavitation noise on a hydrofoil section. In Proceedings of the 7th International Symposium on Cavitation, Ann Arbor, MI, USA, 17–22 August 2009. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R.B. Ten years of industrial experience with the SST turbulence model. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Lu, J.; Yuan, S.; Siva, P.; Yuan, J.; Ren, X.; Zhou, B. The characteristics investigation under the unsteady cavitation condition in a centrifugal pump. J. Mech. Sci. Technol. 2017, 31, 1213–1222. [Google Scholar] [CrossRef]
- Coutier-Delgosha, O.; Fortes-Patella, R.; Reboud, J.; Hofmann, M.; Stoffel, B. Experimental and Numerical Studies in a Centrifugal Pump with Two-Dimensional Curved Blades in Cavitating Condition. J. Fluids Eng. 2003, 125, 970–978. [Google Scholar] [CrossRef] [Green Version]
- Otsuka, S.; Tsujimoto, Y.; Kamijo, K.; Furuya, O. Frequency Dependence of Mass Flow Gain Factor and Cavitation Compliance of Cavitating Inducers. J. Fluids Eng. 1996, 118, 400–408. [Google Scholar] [CrossRef]
- Hunt, J.; Wray, A.; Moin, P. Eddies, Stream, and Convergence Zones in Turbulent Flows. In Proceedings of the Summer Program in Center for Turbulence Research, Stanford, CA, USA, November 1988; pp. 193–208. [Google Scholar]
- Liu, Y.; Tan, L. Tip clearance on pressure fluctuation intensity and vortex characteristic of a mixed flow pump as turbine at pump mode. Renew. Energy 2018, 129, 606–615. [Google Scholar] [CrossRef]
- Yang, L.; Guo, Z.; Cai, P.; Wang, B. Study of the Magnitude Analysis of Coriolis Force in Hydrocyclone. Fluid Mach. 2015, 43, 21–27. [Google Scholar]
- Wang, Y.; Zhang, M.; Chen, T.; Huang, B. Unsteady cavitating flow of liquid hydrogen around the ogive body. J. Aero. Power 2018, 33, 1845–1854. [Google Scholar]
- Ji, B.; Luo, X.; Arndt, R.; Wu, Y. Numerical simulation of three-dimensional cavitation shedding dynamics with special emphasis on cavitation–vortex interaction. Ocean Eng. 2014, 87, 64–77. [Google Scholar] [CrossRef]
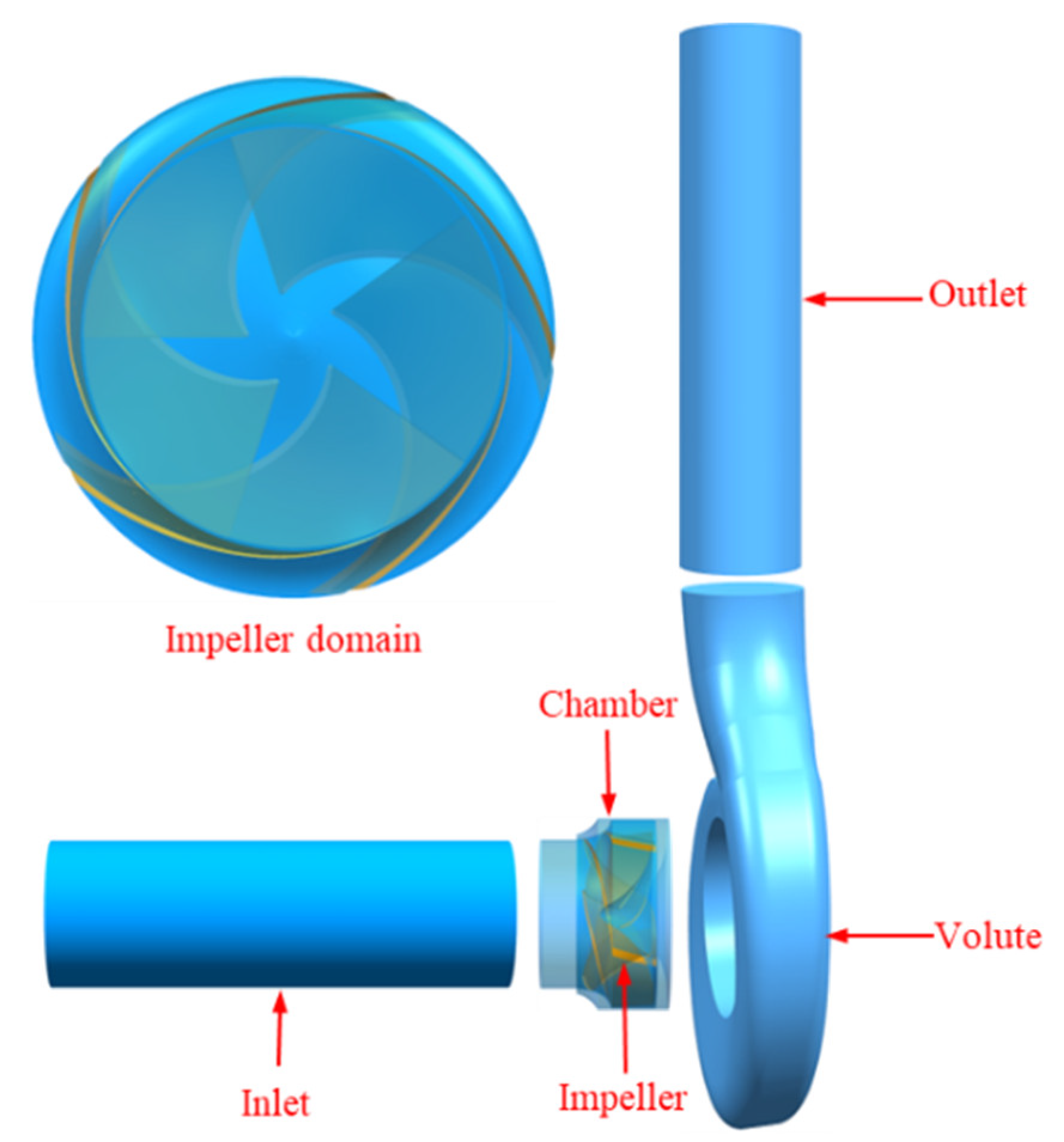
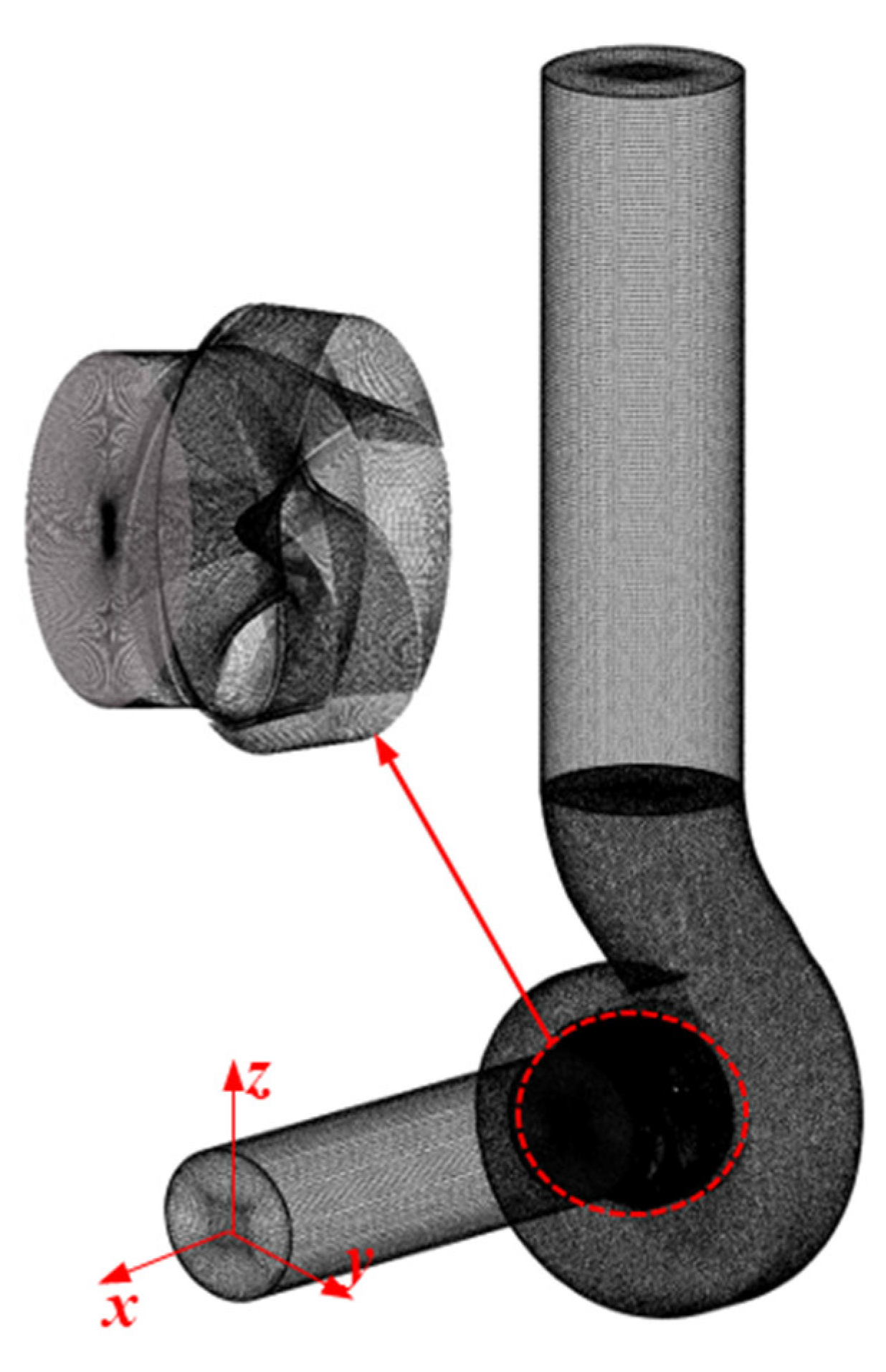

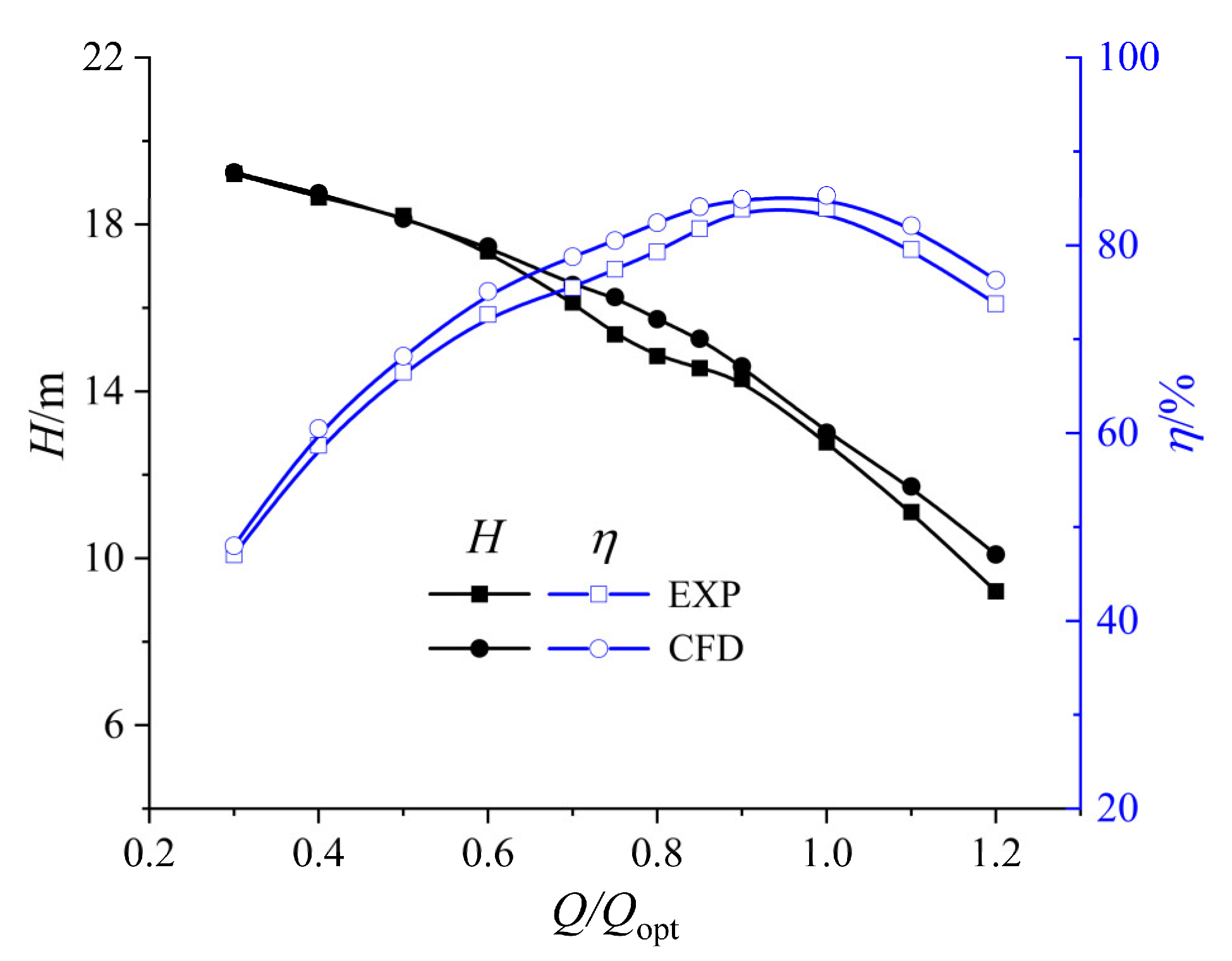

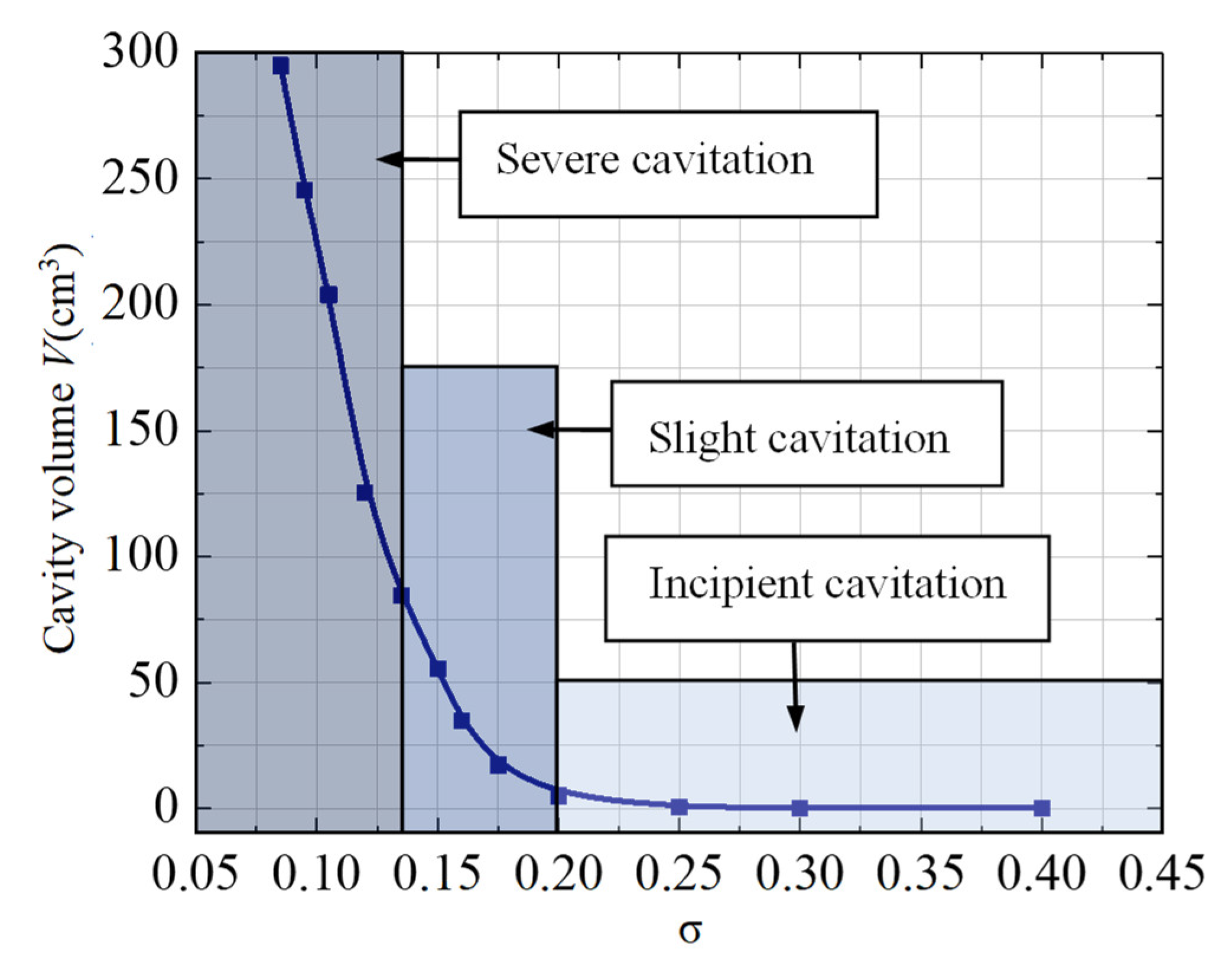


| Parameters | Value | Unit |
|---|---|---|
| Impeller blades number [N] | 5 | - |
| Inlet pipe diameter [D1] | 0.270 | m |
| Outlet pipe diameter [D2] | 0.250 | m |
| Optimum flow rate [Qopt] | 550 | m3/h |
| Head [H] | 12.40 | m |
| Specific speed [ns] | 320 | - |
| Rotating speed [n] | 1480 | r/min |
| Test Cases | Mesh Nodes | Convergence Precision | Head (m) |
|---|---|---|---|
| Case 1 | 2,534,884 | 10−5 | 12.63 |
| Case 2 | 3,548,873 | 10−5 | 12.52 |
| Case 3 | 5,068,372 | 10−5 | 12.51 |
| Case 4 | 6,955,720 | 10−5 | 12.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Q.; Shen, X.; Zhao, X.; Yang, G.; Zhang, D. Numerical Investigation on Cavitation Vortex Dynamics of a Centrifugal Pump Based on Vorticity Transport Method. J. Mar. Sci. Eng. 2023, 11, 1424. https://doi.org/10.3390/jmse11071424
Meng Q, Shen X, Zhao X, Yang G, Zhang D. Numerical Investigation on Cavitation Vortex Dynamics of a Centrifugal Pump Based on Vorticity Transport Method. Journal of Marine Science and Engineering. 2023; 11(7):1424. https://doi.org/10.3390/jmse11071424
Chicago/Turabian StyleMeng, Qinghui, Xi Shen, Xutao Zhao, Gang Yang, and Desheng Zhang. 2023. "Numerical Investigation on Cavitation Vortex Dynamics of a Centrifugal Pump Based on Vorticity Transport Method" Journal of Marine Science and Engineering 11, no. 7: 1424. https://doi.org/10.3390/jmse11071424
APA StyleMeng, Q., Shen, X., Zhao, X., Yang, G., & Zhang, D. (2023). Numerical Investigation on Cavitation Vortex Dynamics of a Centrifugal Pump Based on Vorticity Transport Method. Journal of Marine Science and Engineering, 11(7), 1424. https://doi.org/10.3390/jmse11071424







