Numerical Investigation of Uplift Failure Mode and Capacity Estimation for Deep Helical Anchors in Sand
Abstract
:1. Introduction
- (1)
- The direct observations of rupture surfaces are limited, especially for the multi-helix anchors. Some observations on the rupture surface of single-helix or circular plate anchors in sand have been reported, but they mostly came from 1 g small-scale model tests. This may produce differences between the observed rupture surface and the actual state due to the low stress level, especially for deep anchors. Therefore, it is necessary to further study the failure mode of deep helical anchors, which is essential for the estimation of the uplift capacity.
- (2)
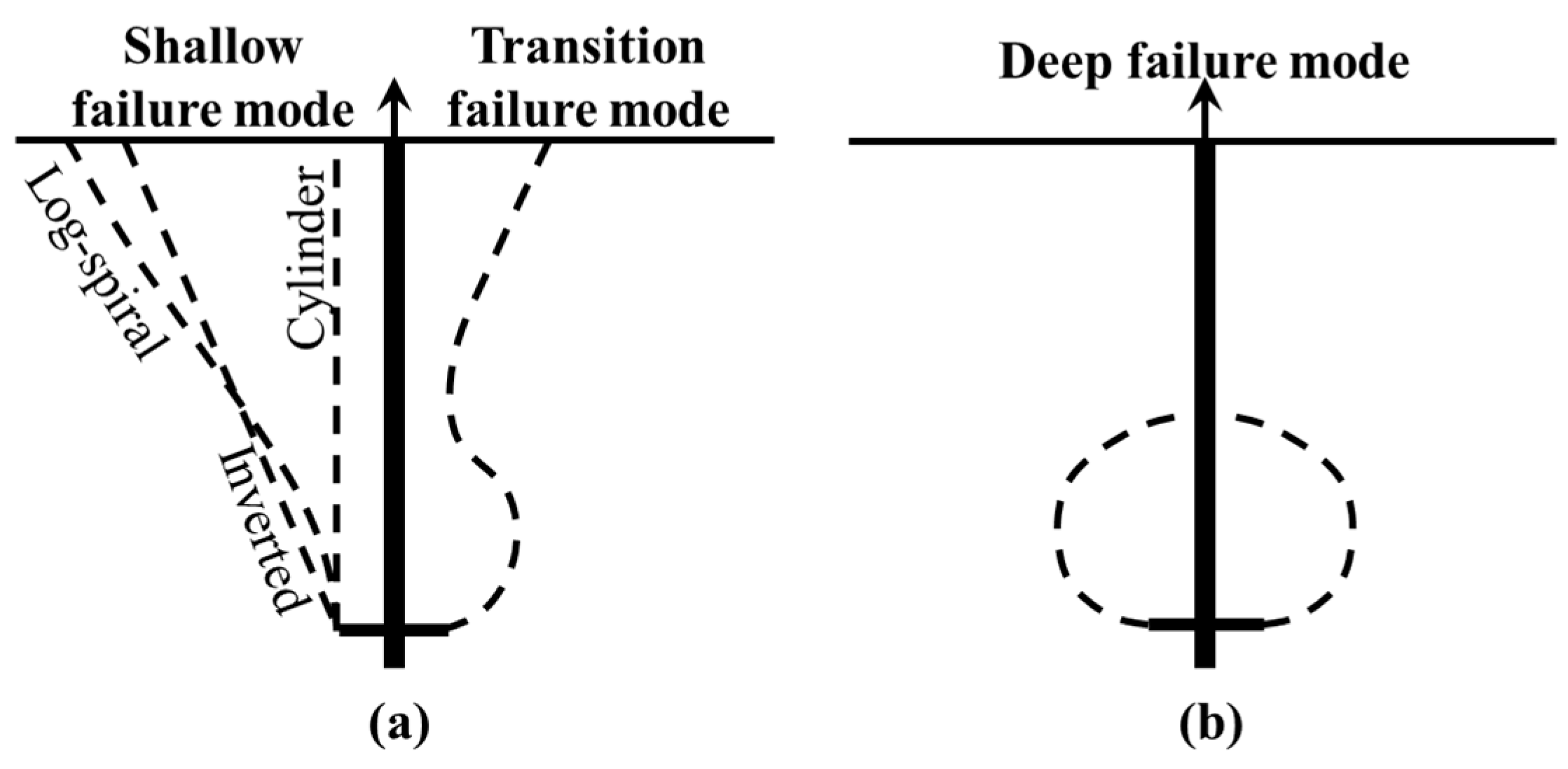
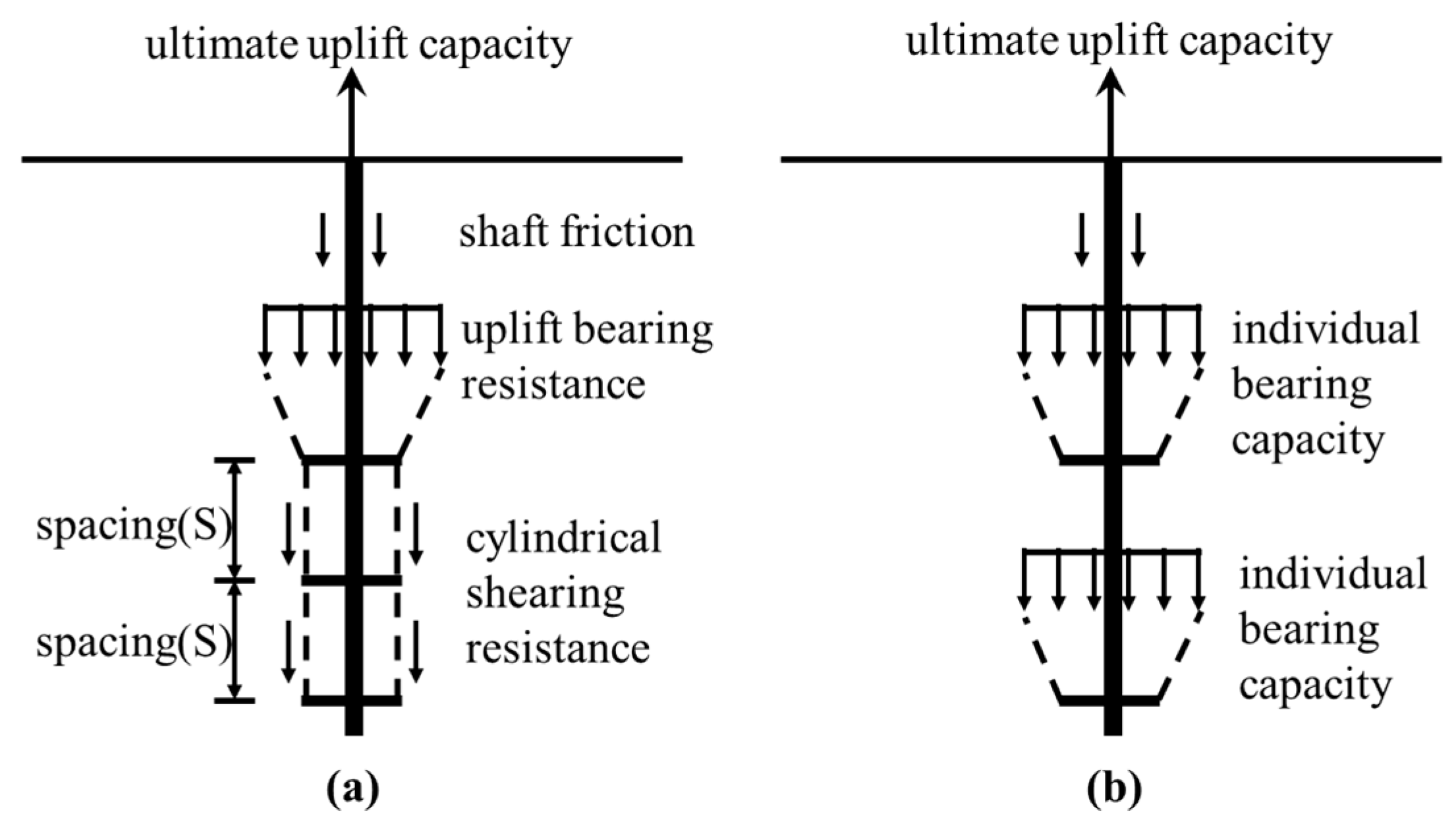
- The estimation of uplift capacity for multi-helix anchors with transition helix spacing based on the two recognized failure modes (Figure 2) is inconsistent. That is, when the helix spacing is transition spacing, the uplift capacity calculated by the individual bearing method is higher than that calculated by the cylindrical shear method.
2. FEM Model and Validation
2.1. FEM Model
2.2. Influence of Pullout Rate and Mesh Density
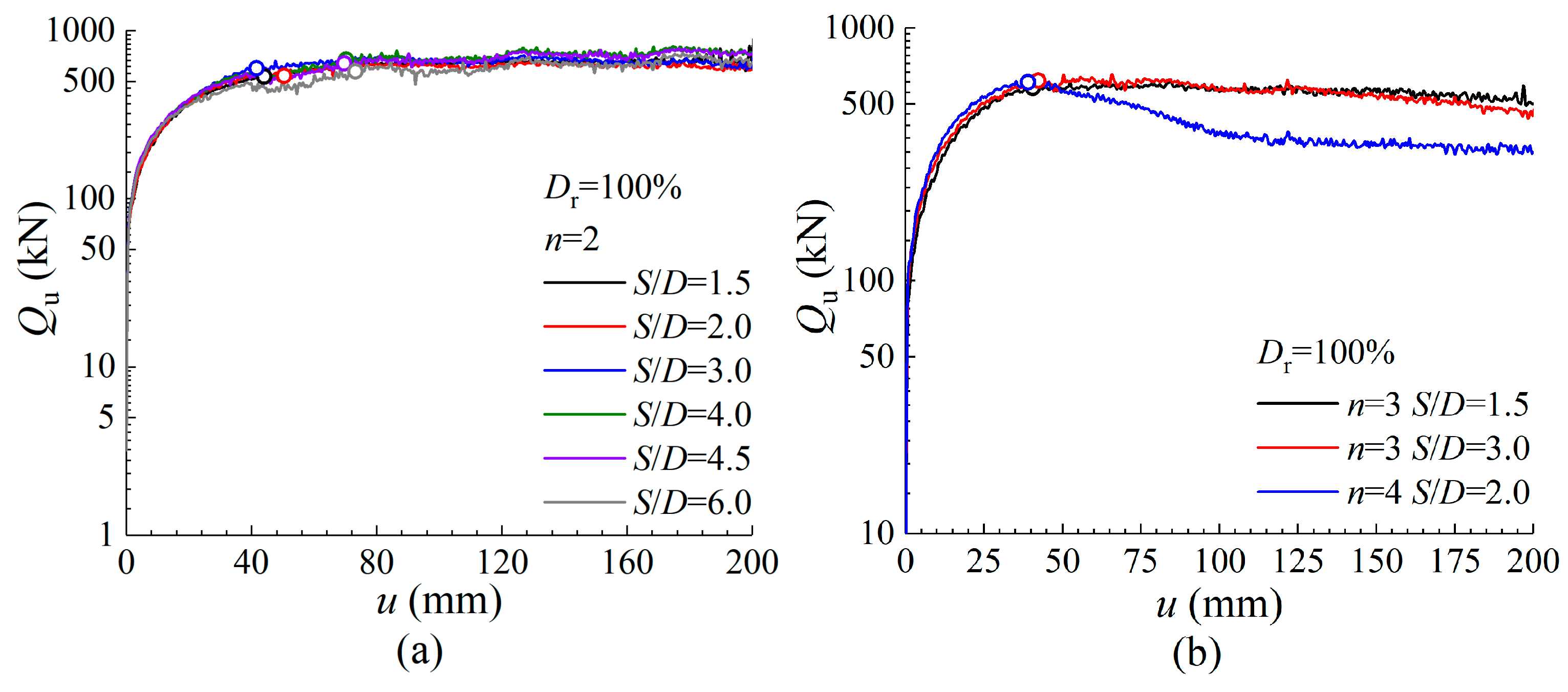
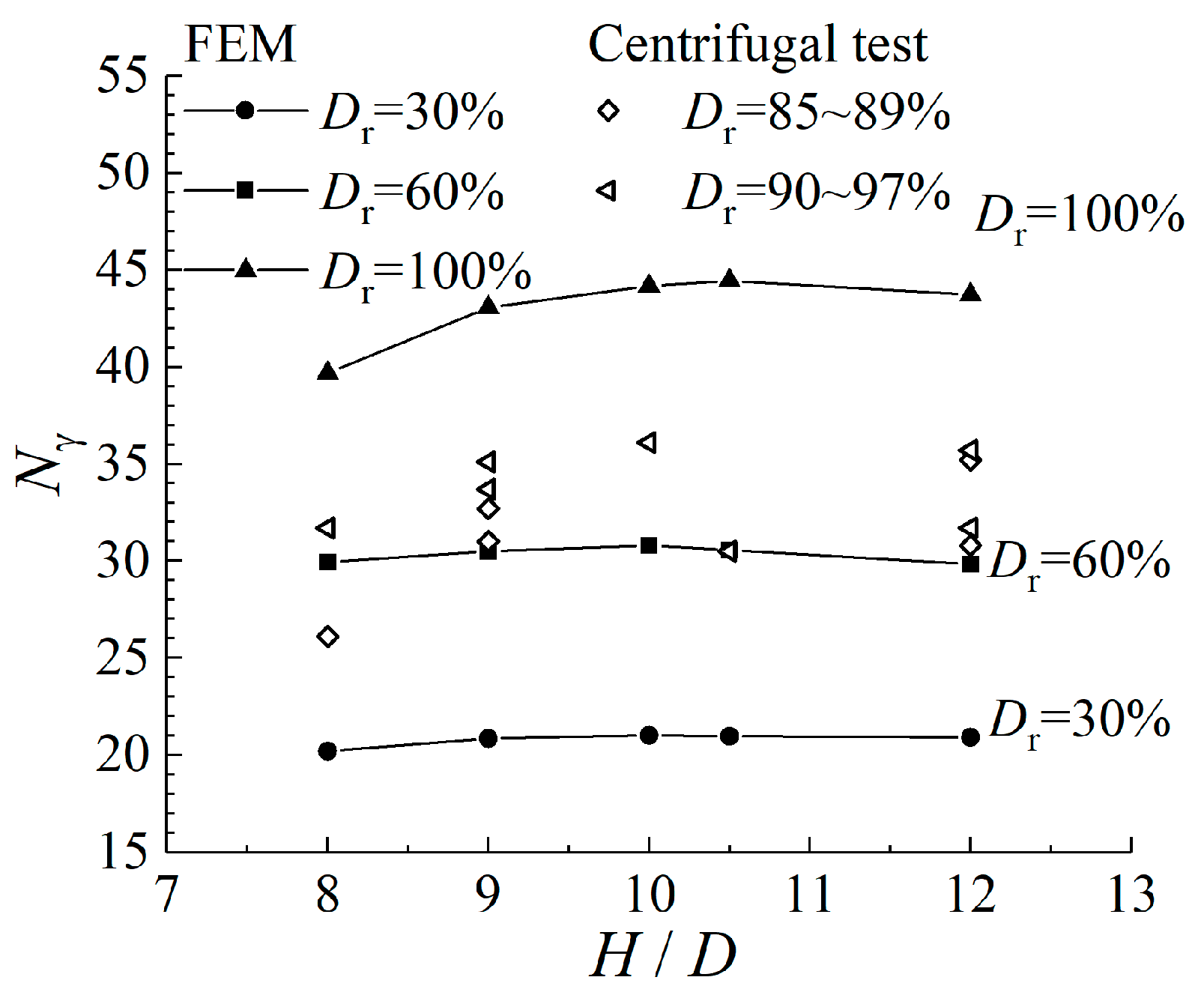
2.3. Determination and Verification of Uplift Capacity
3. Uplift Failure Mode
3.1. Process of Soil Strength Mobilization
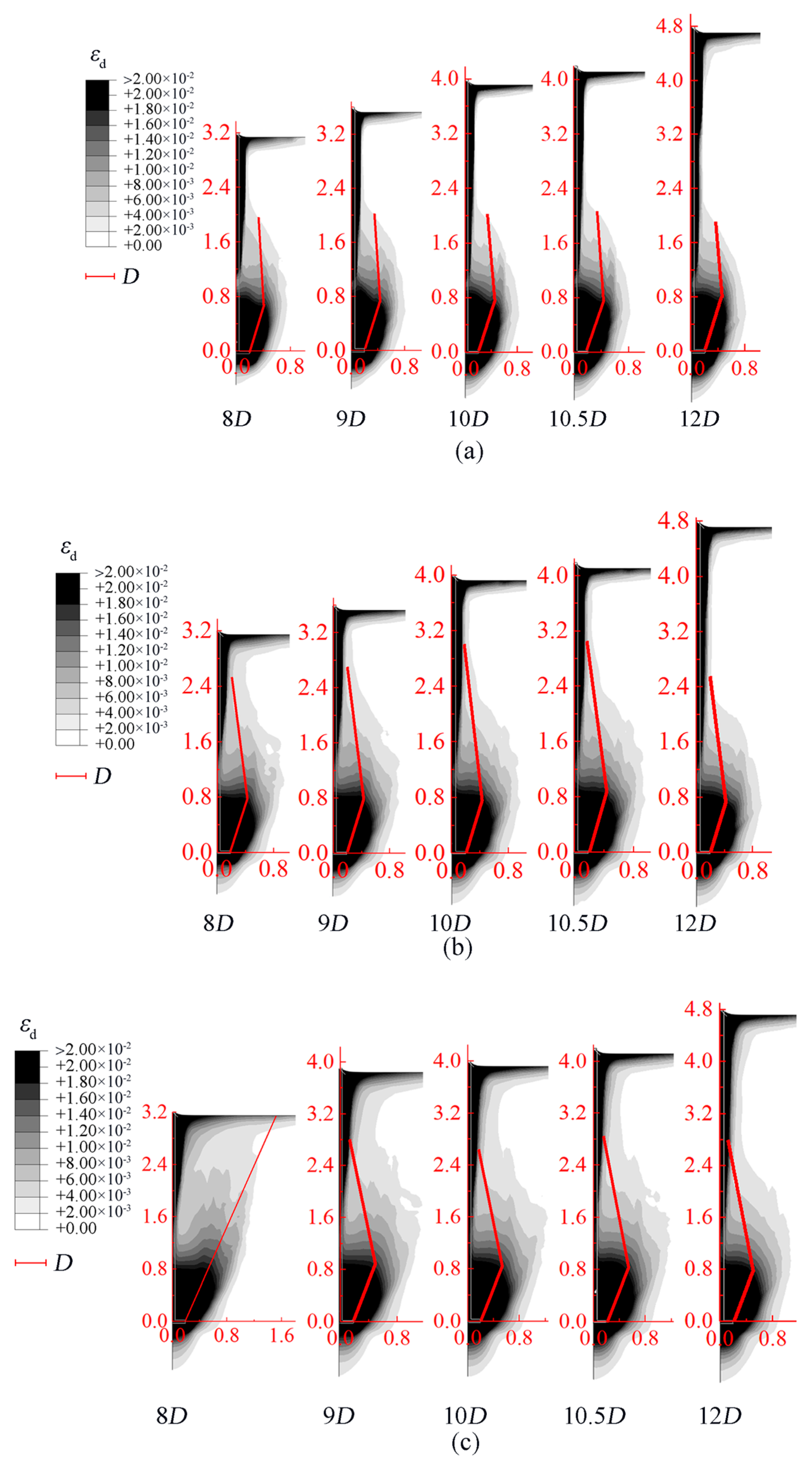
3.2. Deep Failure Behavior of Single-Helix Anchors
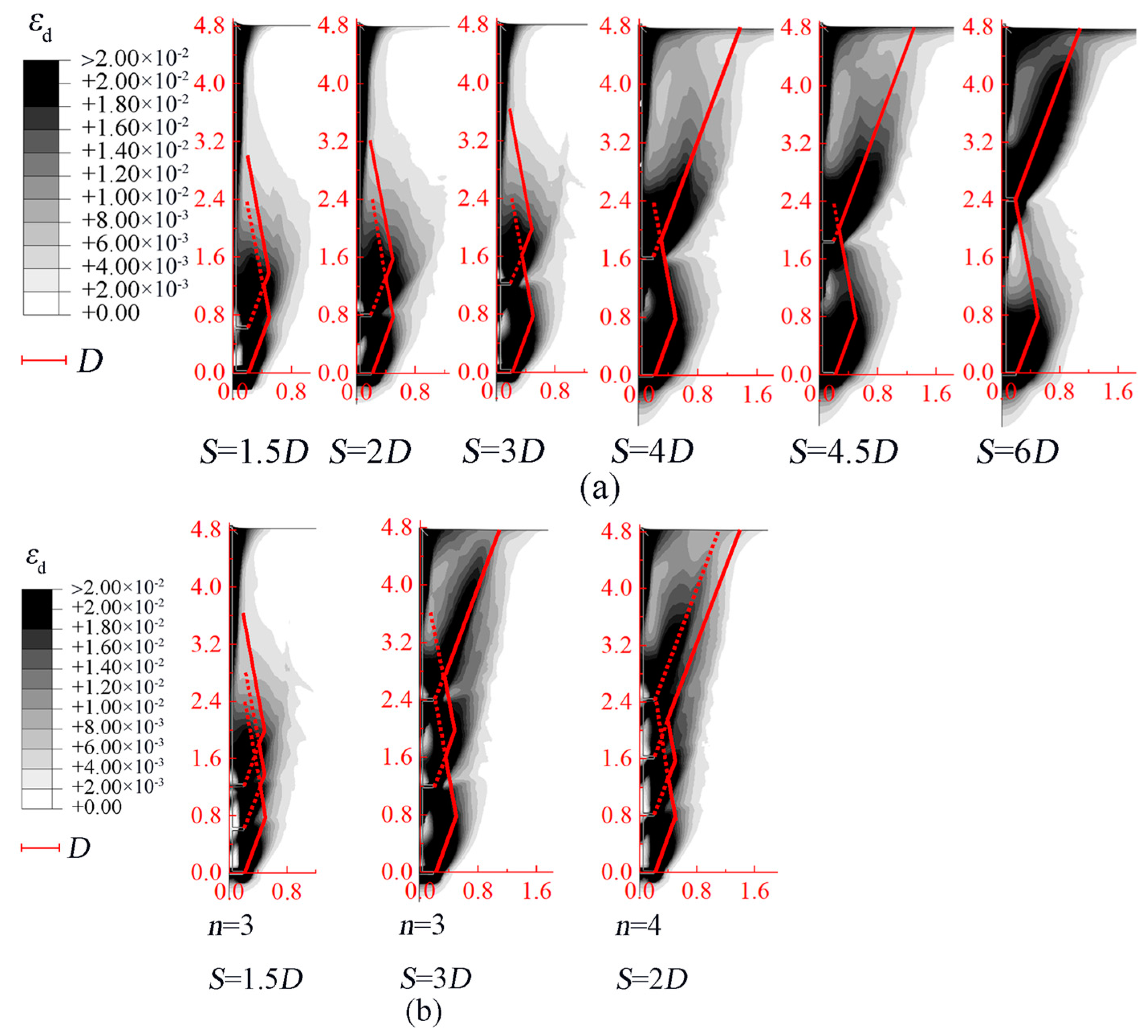
3.3. Deep Failure Behavior of Multi-Helix Anchors
4. Estimation of Uplift Capacity
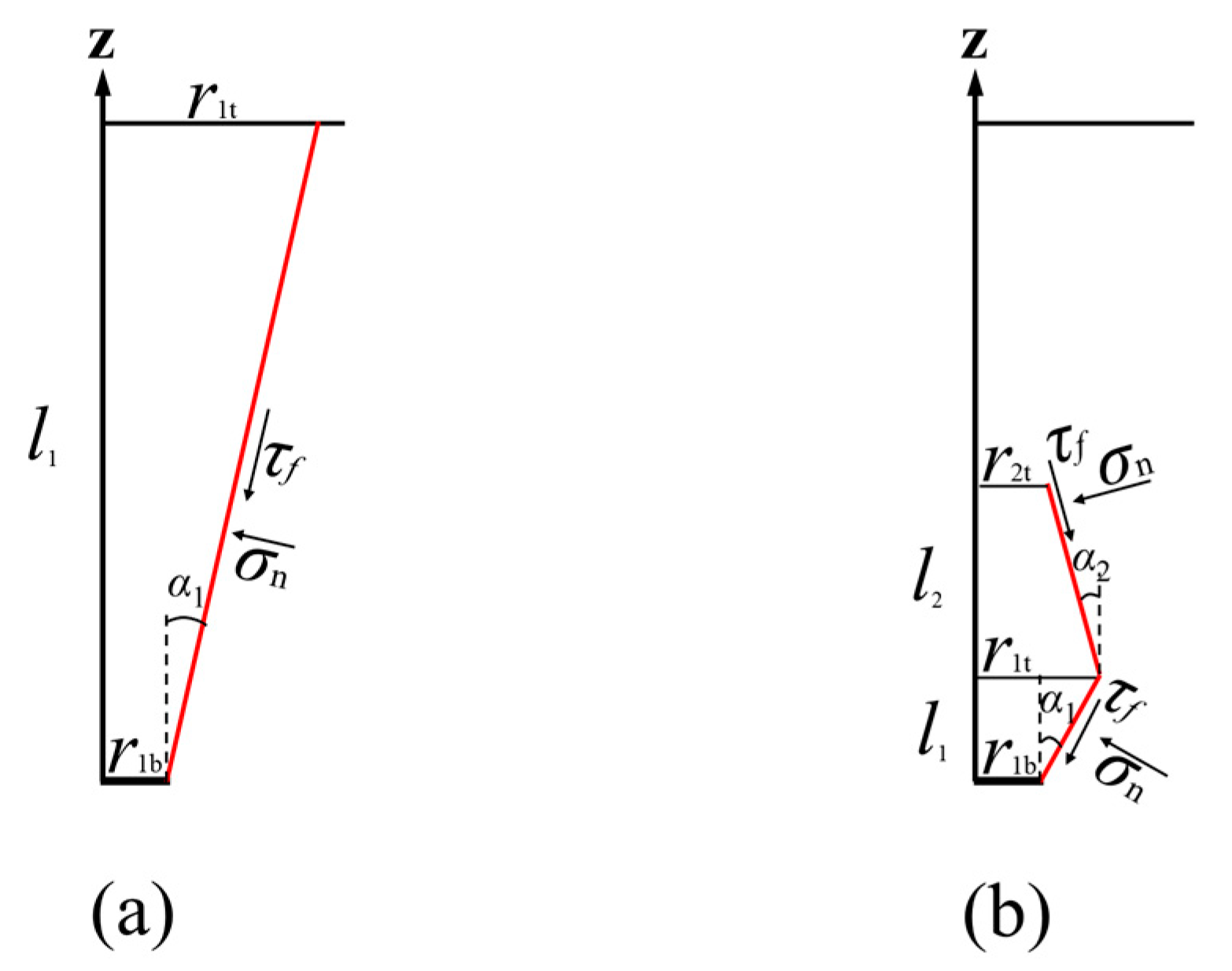
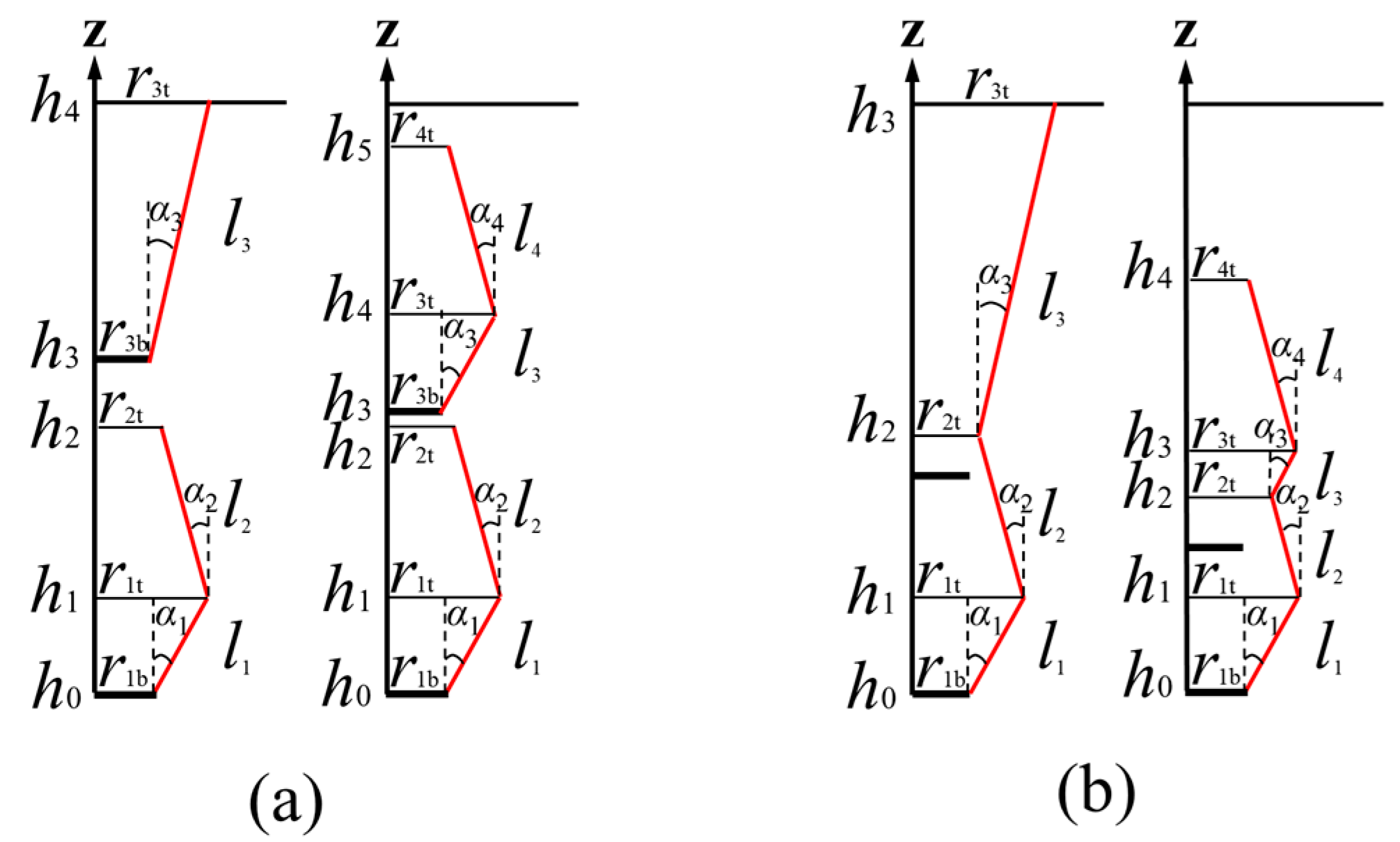
4.1. Simplified Rupture Surfaces
4.2. A Unified Calculation Method
4.3. Lateral Earth Pressure Coefficient
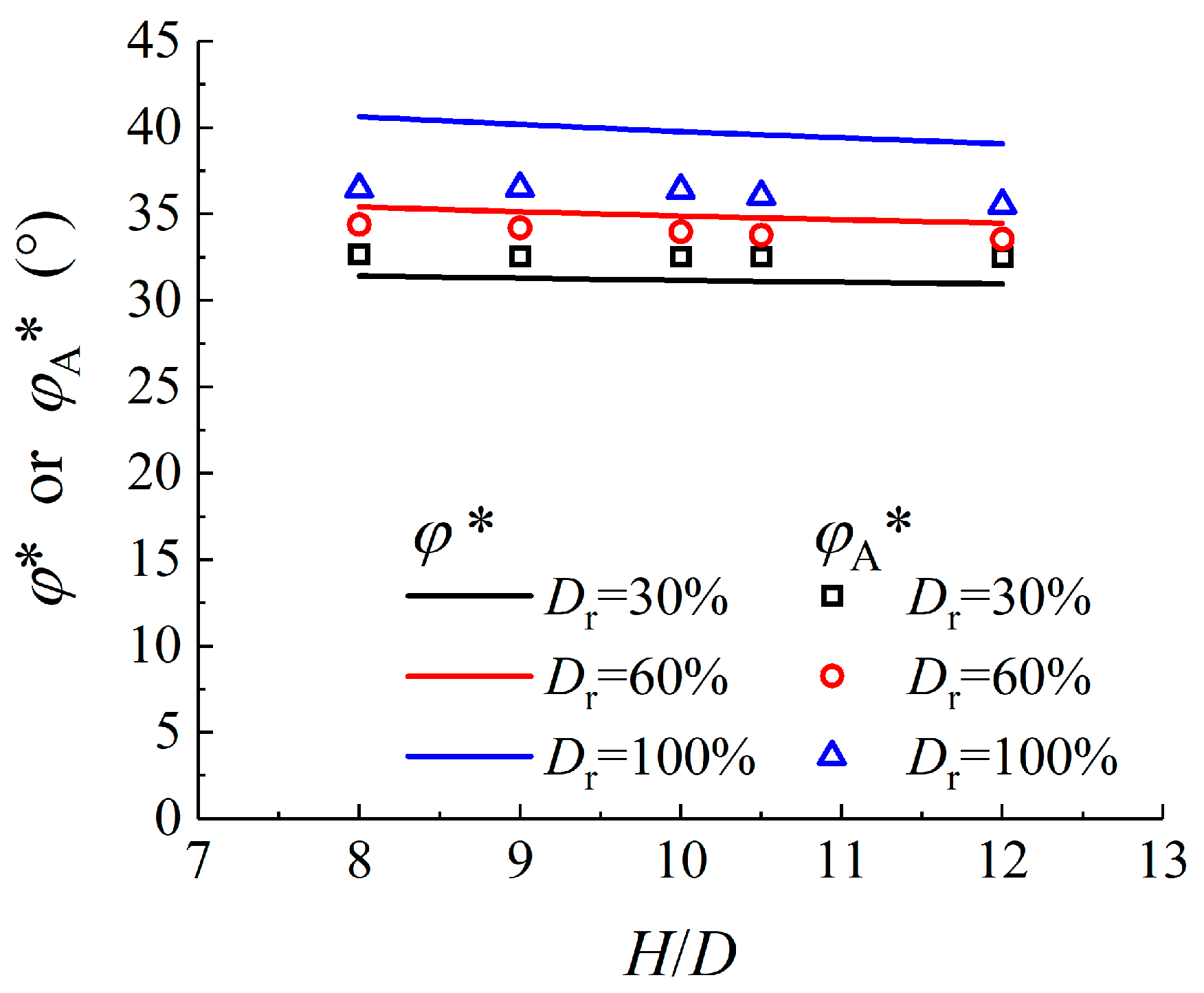
4.4. Average Internal Friction Angle
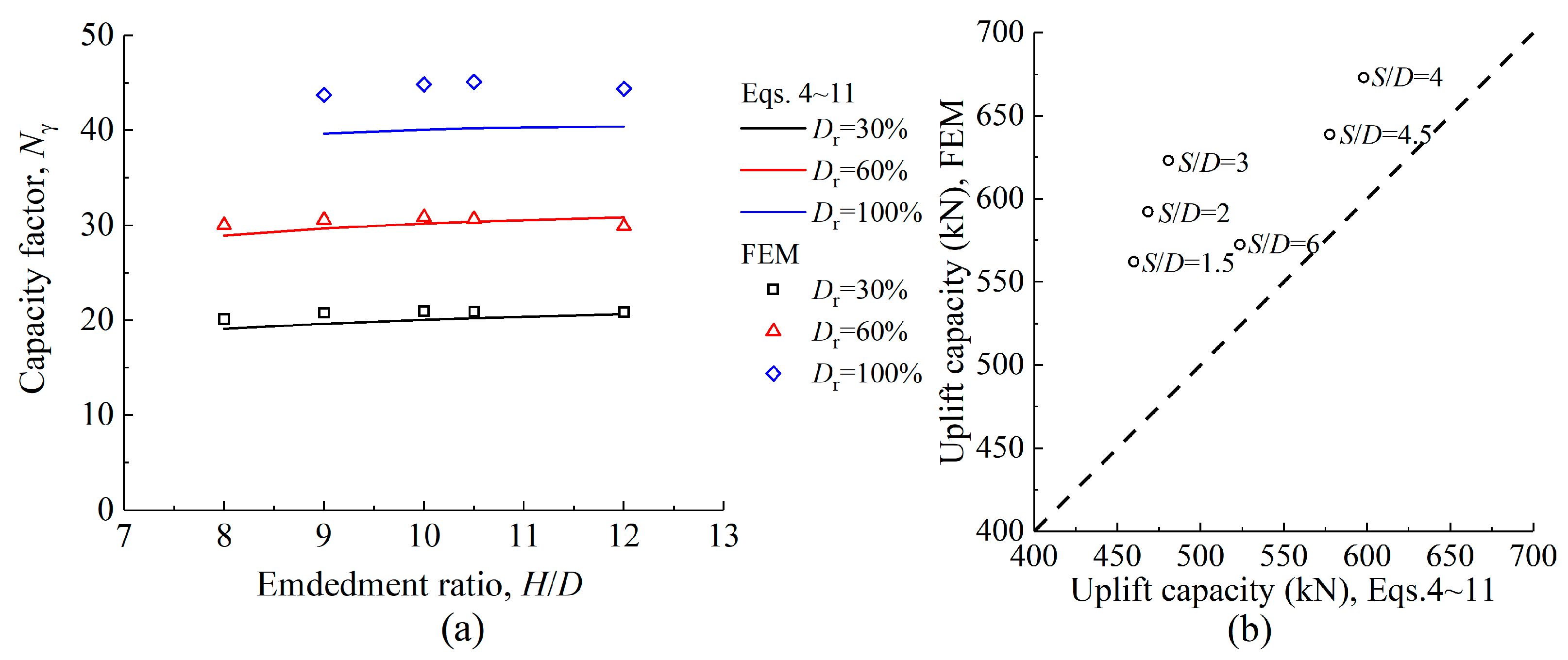
4.5. Comparison with Results
- (1)
- Comparison with the FEM results
- (2)
- Comparison between Equations (9) and (10)
- (3)
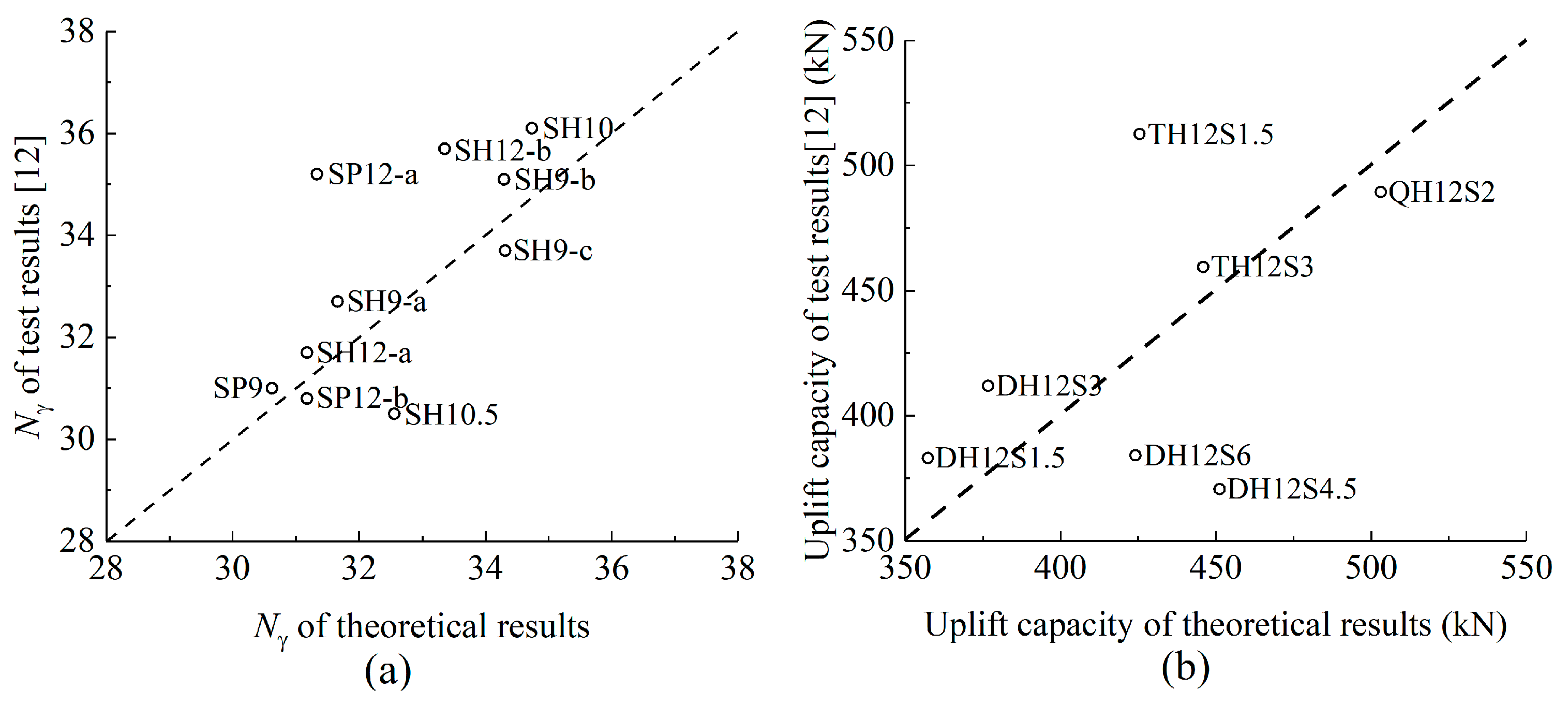
- Comparison with the test results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameters | Definition |
|---|---|
| D | Helix diameter |
| t | Helix thickness |
| H | Embedment |
| S | Helix spacing |
| ΔB | Minimum element size |
| Dr | Density |
| φ0 | Initial internal friction angle |
| φcr | Critical internal friction angle |
| φp | Peak internal friction angle |
| ψp | Peak dilatancy angle |
| σ3 | Confining pressure |
| Critical equivalent plastic strain | |
| Peak equivalent plastic strain | |
| E | Young’s modulus |
| v | Poisson’s ratio |
| Nγ | Uplift capacity factors |
| γ’ | Soil effective unit weight |
| A | Plate area |
| Qu | Ultimate uplift capacity |
| uf | Failure displacement |
| z | Vertical distance from the lowermost plate |
| zp | Vertical distance of the peak value point from the plate |
| α | Inclination between the simplified rupture plane and the vertical direction |
| σn | Normal stress |
| K0 | Initial lateral pressure coefficient |
| Ku | Lateral earth pressure coefficient |
| Kn | Lateral earth pressure coefficient proposed by Hao [12] |
| Ku,peak | Peak lateral earth pressure coefficient |
| φ* | Internal friction angle of the equivalent associated plastic MC model |
| φ*A | Average internal friction angle |
| W | Soil weight |
| li | Vertical height of the ith rupture surface |
| rib, rit | Bottom and top radii, respectively |
References
- Hao, D.; Che, J.; Chen, R.; Zhang, X.; Yuan, C.; Chen, X. Experimental Investigation on Behavior of Single-Helix Anchor in Sand Subjected to Uplift Cyclic Loading. J. Mar. Sci. Eng. 2022, 10, 1338. [Google Scholar] [CrossRef]
- Lin, Y.; Xiao, J.; Le, C.; Zhang, P.; Chen, Q.; Ding, H. Bearing Characteristics of Helical Pile Foundations for Offshore Wind Turbines in Sandy Soil. J. Mar. Sci. Eng. 2022, 10, 889. [Google Scholar] [CrossRef]
- Meyerhof, G.; Adams, J. The ultimate uplift capacity of foundations. Can. Geotech. J. 1968, 5, 225–244. [Google Scholar] [CrossRef]
- Mitsch, M.P.; Clemence, S.P. The uplift capacity of helix anchors in sand. In Proceedings of the Uplift Behavior of Anchor Foundations in Soil, New York, NY, USA, 24 October 1985; pp. 26–47. [Google Scholar]
- Murray, E.; Geddes, J.D. Uplift of anchor plates in sand. J. Geotech. Eng. 1987, 113, 202–215. [Google Scholar] [CrossRef]
- Ghaly, A.; Hanna, A.; Ranjan, G.; Hanna, M. Helical anchors in dry and submerged sand subjected to surcharge. J. Geotech. Eng. 1991, 117, 1463–1470. [Google Scholar] [CrossRef]
- Giampa, J.R.; Bradshaw, A.S.; Schneider, J.A. Influence of dilation angle on drained shallow circular anchor uplift capacity. Int. J. Geomech. 2017, 17, 04016056. [Google Scholar] [CrossRef]
- Cerfontaine, B.; Knappett, J.A.; Brown, M.J.; Bradshaw, A.S. Effect of soil deformability on the failure mechanism of shallow plate or screw anchors in sand. Comput. Geotech. 2019, 109, 34–45. [Google Scholar] [CrossRef] [Green Version]
- Ghaly, A.; Hanna, A. Ultimate pullout resistance of single vertical anchors. Can. Geotech. J. 1994, 31, 661–672. [Google Scholar] [CrossRef]
- Saeedy, H.S. Stability of circular vertical earth anchors. Can. Geotech. J. 1987, 24, 452–456. [Google Scholar] [CrossRef]
- Al Hakeem, N.; Aubeny, C. Numerical investigation of uplift behavior of circular plate anchors in uniform sand. J. Geotech. Geoenvironmental Eng. 2019, 145, 04019039. [Google Scholar] [CrossRef]
- Hao, D.; Wang, D.; O’Loughlin, C.D.; Gaudin, C. Tensile monotonic capacity of helical anchors in sand: Interaction between helices. Can. Geotech. J. 2019, 56, 1534–1543. [Google Scholar] [CrossRef]
- Ghaly, A.; Hanna, A.; Hanna, M. Uplift behavior of screw anchors in sand. I: Dry sand. J. Geotech. Eng. 1991, 117, 773–793. [Google Scholar] [CrossRef]
- Ilamparuthi, K.; Dickin, E.; Muthukrisnaiah, K. Experimental investigation of the uplift behaviour of circular plate anchors embedded in sand. Can. Geotech. J. 2002, 39, 648–664. [Google Scholar] [CrossRef]
- Tappenden, K.M.; Sego, D.C. Predicting the axial capacity of screw piles installed in Canadian soils. In Proceedings of the Canadian Geotechnical Society (CGS), OttawaGeo2007 Conference, Ottawa, ON, Canada, 21–24 October 2007; pp. 1608–1615. [Google Scholar]
- Schiavon, J.; Tsuha, C.; Esquivel, E. Experimental stress analysis in helical pile foundations by the photoelastic method. In ICPMG2014–Physical Modelling in Geotechnics Proceedings of the 8th International Conference on Physical Modelling in Geotechnics, Perth, Australia, 14–17 January 2014; CRC Press: Boca Raton, FL, USA, 2014; pp. 757–762. [Google Scholar]
- Girout, R.; Blanc, M.; Dias, D.; Thorel, L. Numerical analysis of a geosynthetic-reinforced piled load transfer platform–validation on centrifuge test. Geotext. Geomembr. 2014, 42, 525–539. [Google Scholar] [CrossRef]
- Motamedinia, H.; Hataf, N.; Habibagahi, G. A study on failure surface of helical anchors in sand by PIV/DIC technique. Int. J. Civ. Eng. 2019, 17, 1813–1827. [Google Scholar] [CrossRef]
- Salehzadeh, H.; Nuri, H.; Rafsanjani, A.A.H. Failure Mechanism of Helical Anchors in Sand by Centrifuge Modeling and PIV. Int. J. Geomech. 2022, 22, 04022111. [Google Scholar] [CrossRef]
- Das, B.M.; Shukla, S.K. Earth Anchors; J. Ross Publishing: Plantation, FL, USA, 2013. [Google Scholar]
- Zhang, D.J.Y. Predicting Capacity of Helical Screw Piles in Alberta Soils. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 1999. [Google Scholar]
- Clemence, S.P.; Pepe, F. Measurement of lateral stress around multihelix anchors in sand. Geotech. Test. J. 1984, 7, 145–152. [Google Scholar]
- Chance. Technical Design Manual Edition 4; Intech Anchoring Systems: Caseyville, IL, USA, 2019. [Google Scholar]
- Lutenegger, A.J. Behavior of multi-helix screw anchors in sand. In Proceedings of the 14th Pan-American Conference on Soil Mechanics and Geotechnical Engineering, Toronto, ON, Canada, 2–6 October 2011. [Google Scholar]
- Council, I.C. International Building Code (IBC); ICC: Washington, DC, USA, 2015. [Google Scholar]
- Society, C.G. Canadian Foundation Engineering Manual, 4th ed.; Canadian Geotechnical Society: Saskatoon, SK, Canada, 2006; p. 488. [Google Scholar]
- Kurian, N.P.; Shah, S.J. Studies on the behaviour of screw piles by the finite element method. Can. Geotech. J. 2009, 46, 627–638. [Google Scholar] [CrossRef]
- Nasr, M. Performance-based design for helical piles. In Contemporary Topics in Deep Foundations; ASCE: Lawrence, KS, USA, 2009; pp. 496–503. [Google Scholar]
- Salhi, L.; Nait-Rabah, O.; Deyrat, C.; Roos, C. Numerical modeling of single helical pile behavior under compressive loading in sand. EJGE 2013, 18, 4319–4338. [Google Scholar]
- Gavin, K.; Doherty, P.; Tolooiyan, A. Field investigation of the axial resistance of helical piles in dense sand. Can. Geotech. J. 2014, 51, 1343–1354. [Google Scholar] [CrossRef]
- Mittal, S.; Mukherjee, S. Behaviour of group of helical screw anchors under compressive loads. Geotech. Geol. Eng. 2015, 33, 575–592. [Google Scholar] [CrossRef]
- Spagnoli, G.; Gavin, K. Helical piles as a novel foundation system for offshore piled facilities. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 9–12 November 2015. [Google Scholar]
- Akl, S.A.; Elhami, O.M.; Abu-keifa, M.A. Lateral performance of helical piles as foundations for offshore wind farms. In Geo-Chicago 2016; ASCE: Lawrence, KS, USA, 2016; pp. 449–458. [Google Scholar]
- Fahmy, A.; El Naggar, M. Cyclic lateral performance of helical tapered piles in silty sand. DFI J.-J. Deep. Found. Inst. 2016, 10, 111–124. [Google Scholar] [CrossRef]
- George, B.E.; Banerjee, S.; Gandhi, S.R. Numerical analysis of helical piles in cohesionless soil. Int. J. Geotech. Eng. 2017, 14, 361–375. [Google Scholar] [CrossRef]
- Afzalian, M.; Medhi, B.; Eun, J.; Medhi, T. Retrofitting Uplift Capacity of Telecommunication Tower Foundation with Helical Piles in Dense Granular Soils. In Proceedings of the Geo-Congress 2020: Foundations, Soil Improvement, and Erosion, Minneapolis, MN, USA, 25–28 February 2020; pp. 239–245. [Google Scholar]
- Alwalan, M.; El Naggar, M. Finite element analysis of helical piles subjected to axial impact loading. Comput. Geotech. 2020, 123, 103597. [Google Scholar] [CrossRef]
- Cerfontaine, B.; Knappett, J.A.; Brown, M.J.; Davidson, C.S.; Al-Baghdadi, T.; Sharif, Y.U.; Brennan, A.; Augarde, C.; Coombs, W.M.; Wang, L. A finite element approach for determining the full load–displacement relationship of axially loaded shallow screw anchors, incorporating installation effects. Can. Geotech. J. 2021, 58, 565–582. [Google Scholar] [CrossRef]
- Ho, H.M.; Malik, A.A.; Kuwano, J.; Rashid, H.M.A. Influence of helix bending deflection on the load transfer mechanism of screw piles in sand: Experimental and numerical investigations. Soils Found. 2021, 61, 874–885. [Google Scholar] [CrossRef]
- Nowkandeh, M.J.; Choobbasti, A.J. Numerical study of single helical piles and helical pile groups under compressive loading in cohesive and cohesionless soils. Bull. Eng. Geol. Environ. 2021, 80, 4001–4023. [Google Scholar] [CrossRef]
- Konkol, J. Numerical solutions for large deformation problems in geotechnical engineering. PhD Interdiscip. J. 2014, 49–55. [Google Scholar]
- Qiu, G.; Henke, S.; Grabe, J. Application of a Coupled Eulerian–Lagrangian approach on geomechanical problems involving large deformations. Comput. Geotech. 2011, 38, 30–39. [Google Scholar] [CrossRef]
- Chen, Z.; Tho, K.K.; Leung, C.F.; Chow, Y.K. Influence of overburden pressure and soil rigidity on uplift behavior of square plate anchor in uniform clay. Comput. Geotech. 2013, 52, 71–81. [Google Scholar] [CrossRef]
- Qiu, G.; Henke, S.; Grabe, J. Applications of Coupled Eulerian-Lagrangian method to geotechnical problems with large deformations. In Proceedings of the SIMULIA Customer Conference, London, UK, 18–21 May 2009; pp. 420–435. [Google Scholar]
- Wood, D.M.; Belkheir, K. Strain softening and state parameter for sand modelling. Géotechnique 1994, 44, 335–339. [Google Scholar] [CrossRef]
- Cheng, P.; Liu, Y.; Li, Y.P.; Yi, J.T. A large deformation finite element analysis of uplift behaviour for helical anchor in spatially variable clay. Comput. Geotech. 2022, 141, 104542. [Google Scholar] [CrossRef]
- Cheng, P.; Guo, J.; Yao, K.; Chen, X. Numerical investigation on pullout capacity of helical piles under combined loading in spatially random clay. Mar. Georesources Geotechnol. 2022, 1–14. [Google Scholar] [CrossRef]
- Popa, H.; Batali, L. Using Finite Element Method in geotechnical design. Soil constitutive laws and calibration of the parameters. Retaining wall case study. WSEAS Trans. Appl. Theor. Mech. 2010, 5, 177–186. [Google Scholar]
- Chen, R.; Fu, S.; Hao, D.; Shi, D. Scale effects of uplift capacity of circular anchors in dense sand. Chin. J. Geotech. Eng. 2019, 41, 78–85. [Google Scholar]
- Chow, S.H.; Roy, A.; Herduin, M.; Heins, E.; King, L.; Bienen, B.; O’Loughlin, C.; Gaudin, C.; Cassidy, M. Characterisation of UWA Superfine Silica Sand; The University of Western Australia: Crawley, Australia, 2019. [Google Scholar]
- Pei, H.; Wang, D.; Liu, Q. Numerical study of relationships between the cone resistances and footing bearing capacities in silica and calcareous sands. Comput. Geotech. 2023, 155, 105220. [Google Scholar] [CrossRef]
- Hsu, S.; Liao, H. Uplift behaviour of cylindrical anchors in sand. Can. Geotech. J. 1998, 35, 70–80. [Google Scholar] [CrossRef]
- Bolton, M. The strength and dilatancy of sands. Geotechnique 1986, 36, 65–78. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Liu, M.; Zhu, Z. Sand deformation around an uplift plate anchor. J. Geotech. Geoenvironmental Eng. 2012, 138, 728–737. [Google Scholar] [CrossRef]
- Shi, D.; Yang, Y.; Deng, Y.; Xue, J. DEM modelling of screw pile penetration in loose granular assemblies considering the effect of drilling velocity ratio. Granul. Matter 2019, 21, 74. [Google Scholar] [CrossRef]
- Nazir, R.; Chuan, H.S.; Niroumand, H.; Kassim, K.A. Performance of single vertical helical anchor embedded in dry sand. Measurement 2014, 49, 42–51. [Google Scholar] [CrossRef]
- Srinivasan, V.; Ghosh, P.; Santhoshkumar, G. Experimental and Numerical Analysis of Interacting Circular Plate Anchors Embedded in Homogeneous and Layered Cohesionless Soil. Int. J. Civ. Eng. 2020, 18, 231–244. [Google Scholar] [CrossRef]
- Drescher, A.; Detournay, E. Limit load in translational failure mechanisms for associative and non-associative materials. Géotechnique 1993, 43, 443–456. [Google Scholar] [CrossRef]
- Davis, E. Theories of plasticity and the failure of soil masses. In Soil Mechanics: Selected Topics; Springer: Berlin/Heidelberg, Germany, 1969. [Google Scholar]
- Vermeer, P. The orientation of shear bands in biaxial tests. Geotechnique 1990, 40, 223–236. [Google Scholar] [CrossRef]
- Chen, X.; Wang, D.; Yu, Y.; Lyu, Y. A modified Davis approach for geotechnical stability analysis involving non-associated soil plasticity. Géotechnique 2020, 70, 1109–1119. [Google Scholar] [CrossRef]

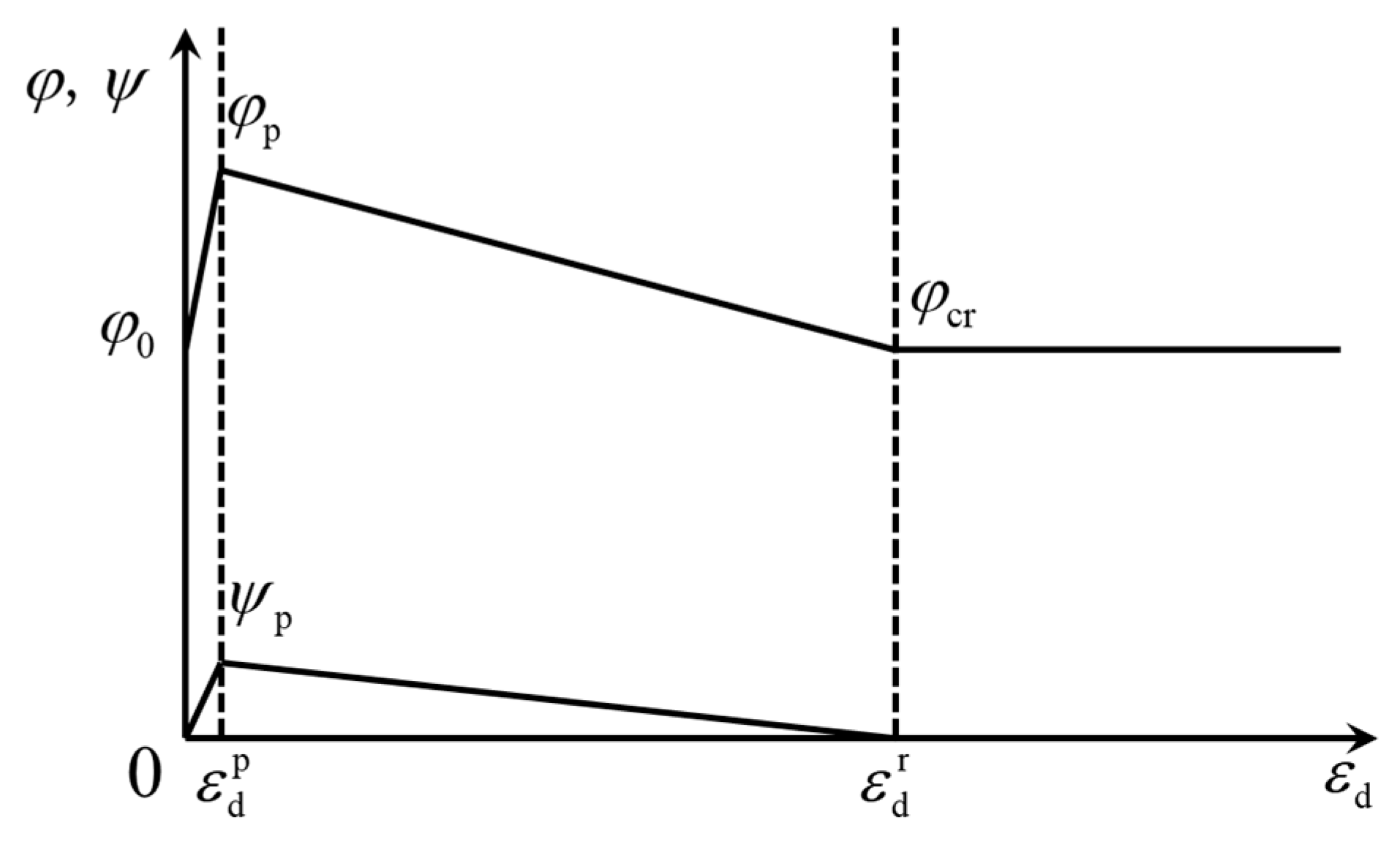




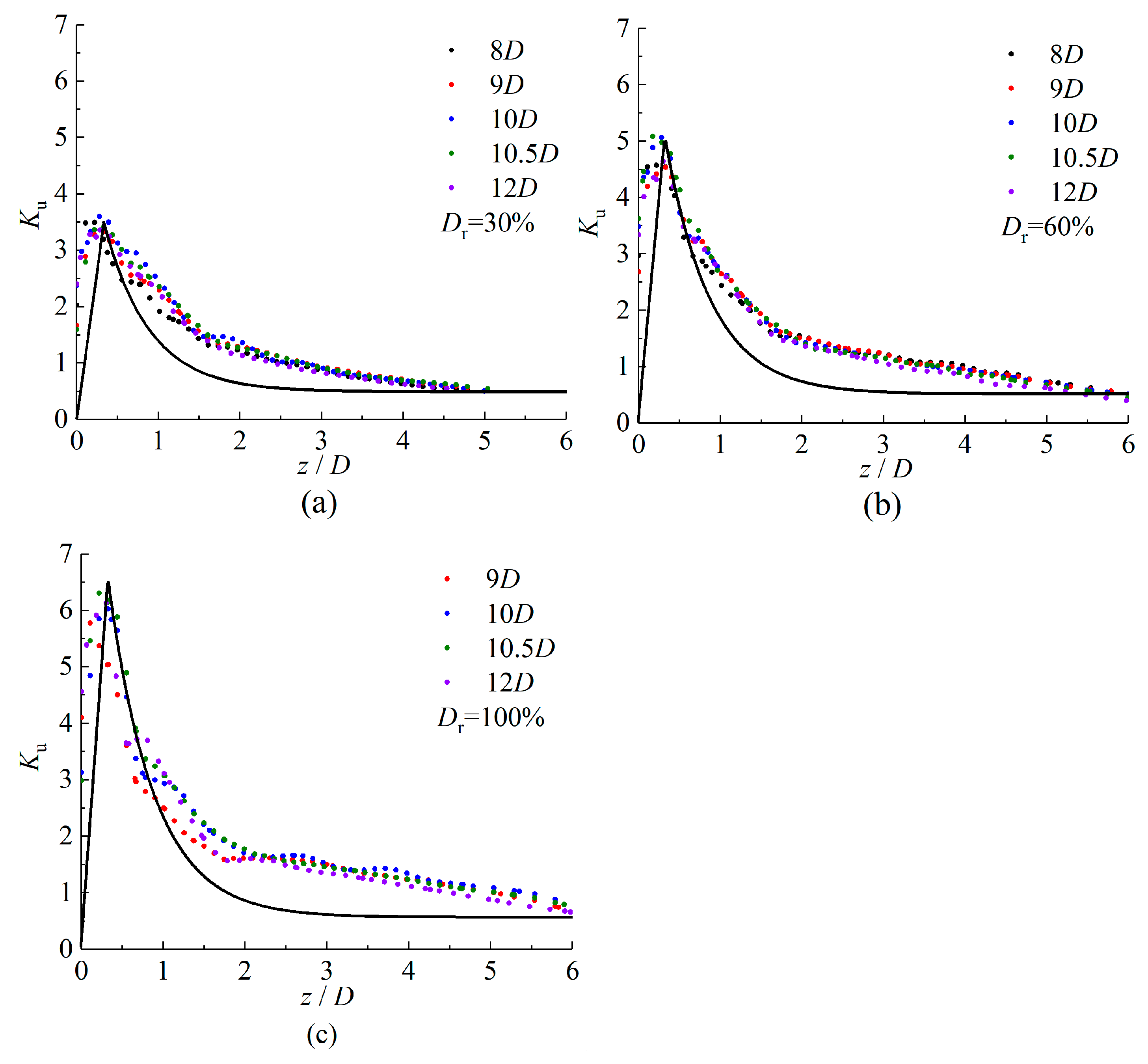


| Dr | 30% | 60% | 100% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| H/D | E (MPa) | φp (°) | ψp (°) | E (MPa) | φp (°) | ψp (°) | E (MPa) | φp (°) | ψp (°) |
| 8 | 24.27 | 34.77 | 7.54 | 35.47 | 38.31 | 12.26 | 50.4 | 42.9 | 23.8 |
| 9 | 25.64 | 34.65 | 7.3 | 37.48 | 38.07 | 11.86 | 53.26 | 42.5 | 23 |
| 10 | 26.94 | 34.54 | 7.08 | 39.38 | 37.86 | 11.5 | 55.96 | 42.14 | 22.28 |
| 10.5 | 27.57 | 34.49 | 6.98 | 40.29 | 37.76 | 11.34 | 57.25 | 41.98 | 21.95 |
| 12 | 29.35 | 34.36 | 6.71 | 42.89 | 37.49 | 10.89 | 60.95 | 41.52 | 21.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, C.; Hao, D.; Chen, R.; Zhang, N. Numerical Investigation of Uplift Failure Mode and Capacity Estimation for Deep Helical Anchors in Sand. J. Mar. Sci. Eng. 2023, 11, 1547. https://doi.org/10.3390/jmse11081547
Yuan C, Hao D, Chen R, Zhang N. Numerical Investigation of Uplift Failure Mode and Capacity Estimation for Deep Helical Anchors in Sand. Journal of Marine Science and Engineering. 2023; 11(8):1547. https://doi.org/10.3390/jmse11081547
Chicago/Turabian StyleYuan, Chi, Dongxue Hao, Rong Chen, and Ning Zhang. 2023. "Numerical Investigation of Uplift Failure Mode and Capacity Estimation for Deep Helical Anchors in Sand" Journal of Marine Science and Engineering 11, no. 8: 1547. https://doi.org/10.3390/jmse11081547
APA StyleYuan, C., Hao, D., Chen, R., & Zhang, N. (2023). Numerical Investigation of Uplift Failure Mode and Capacity Estimation for Deep Helical Anchors in Sand. Journal of Marine Science and Engineering, 11(8), 1547. https://doi.org/10.3390/jmse11081547






