FEM-SPH Numerical Simulation of Impact Loading on Floating Laminates
Abstract
:1. Introduction
2. Materials and Methods
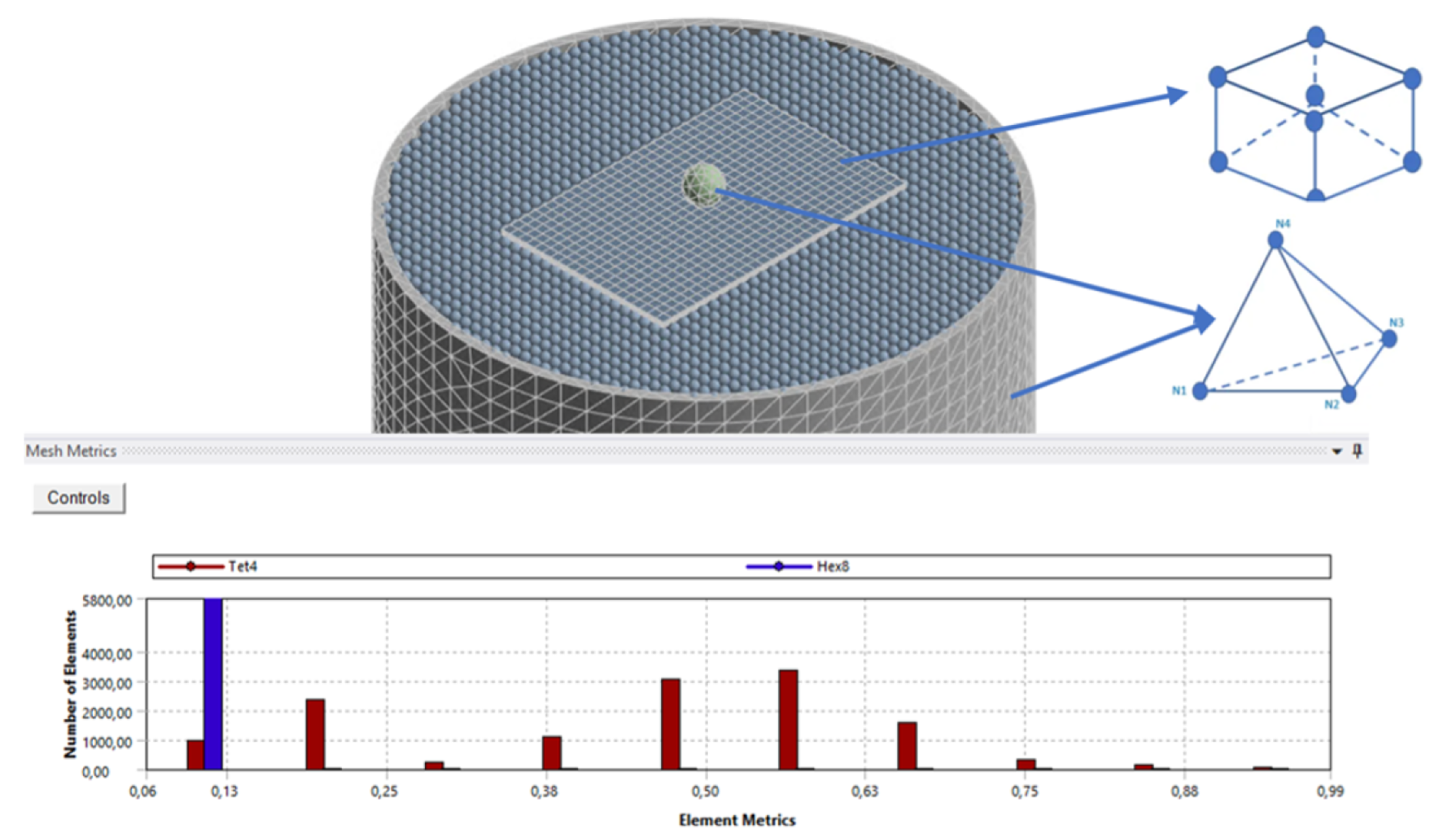
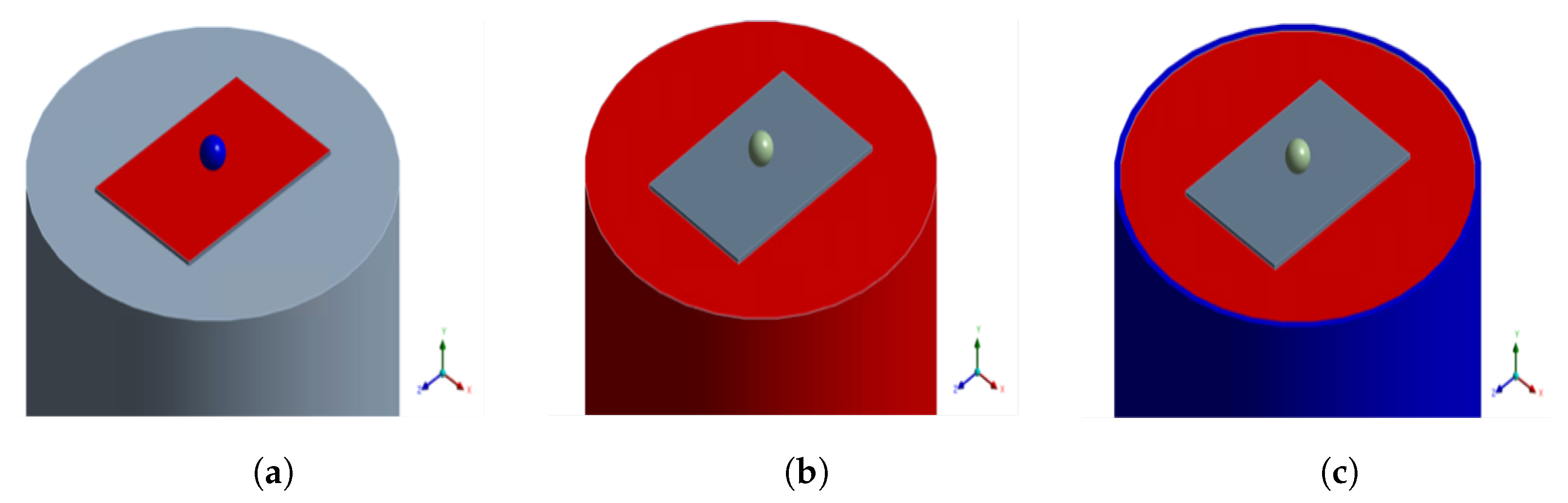
2.1. Geometry Model and Discretization
2.2. The SPH and FEM Methods
2.3. Contacts in a Coupled FEM-SPH
- One-way vs. two-way contact that we used. In one-way contacts, only the slave nodes are checked for penetration, while in two-way contacts masters and slaves are reversed, and contact is checked both ways.
- Automatic vs. non-automatic contact, where automatic in the name indicates an improved algorithm invoked to compute contact. Automatic contacts are non-oriented and can detect penetration coming from either side of the shell element. Always take into account shell thickness; it is more robust.
- Contact algorithm, penalty or constraint. In the case of the penalty algorithm, a slave node penetrates the master segment. This penetration is detected, and the penetration depth (DP) is calculated. This “penalty” force is applied on the slave node . The effect is to project the node back up to the surface of the master segment. A reaction force is applied to the master segment nodes, so the total force on the master nodes equals the applied slave node force. Both a normal and a friction force penalty force are applied to the slave node.
2.4. Material Mathematical Models
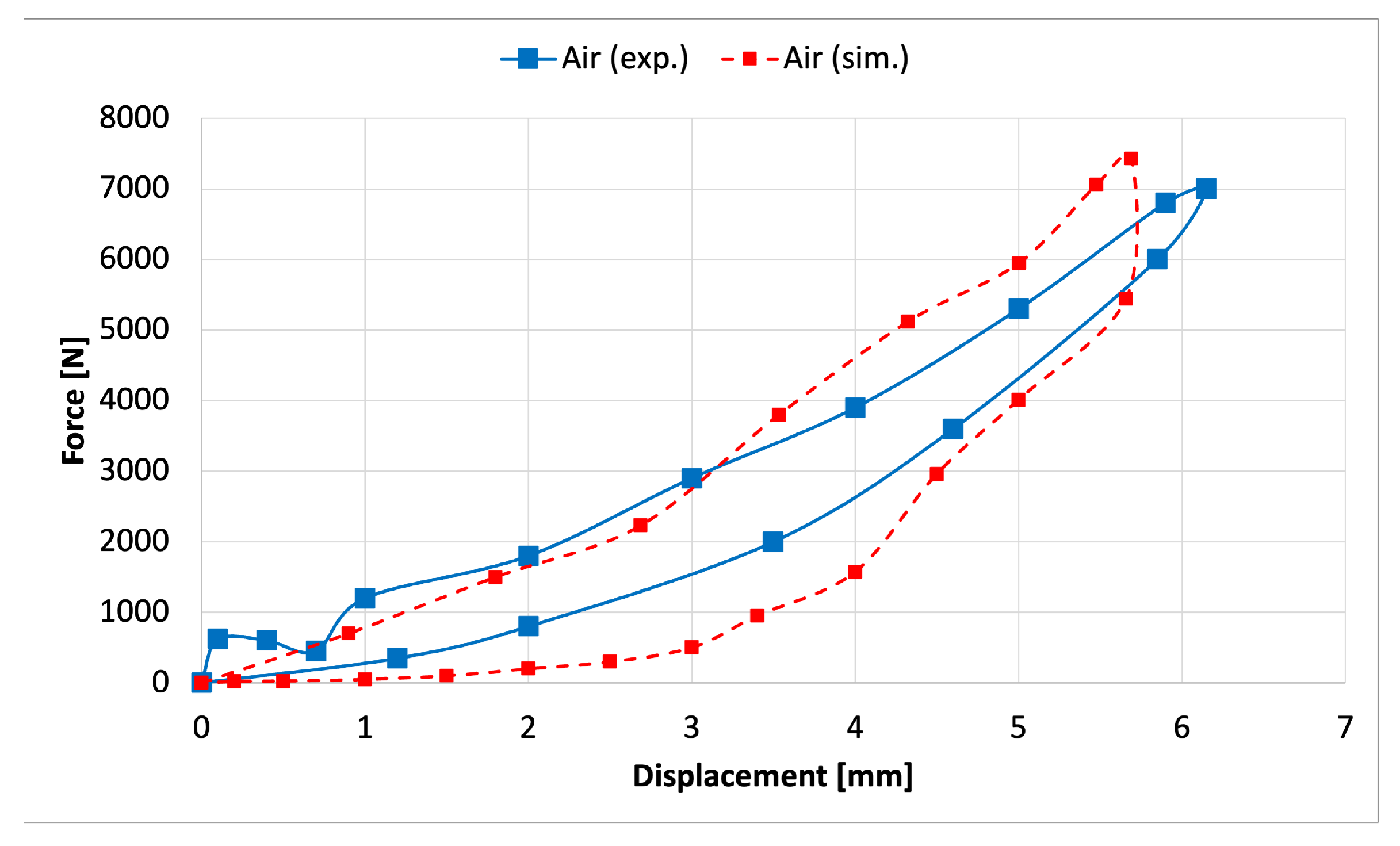
3. Results
4. Discussion
5. Conclusions
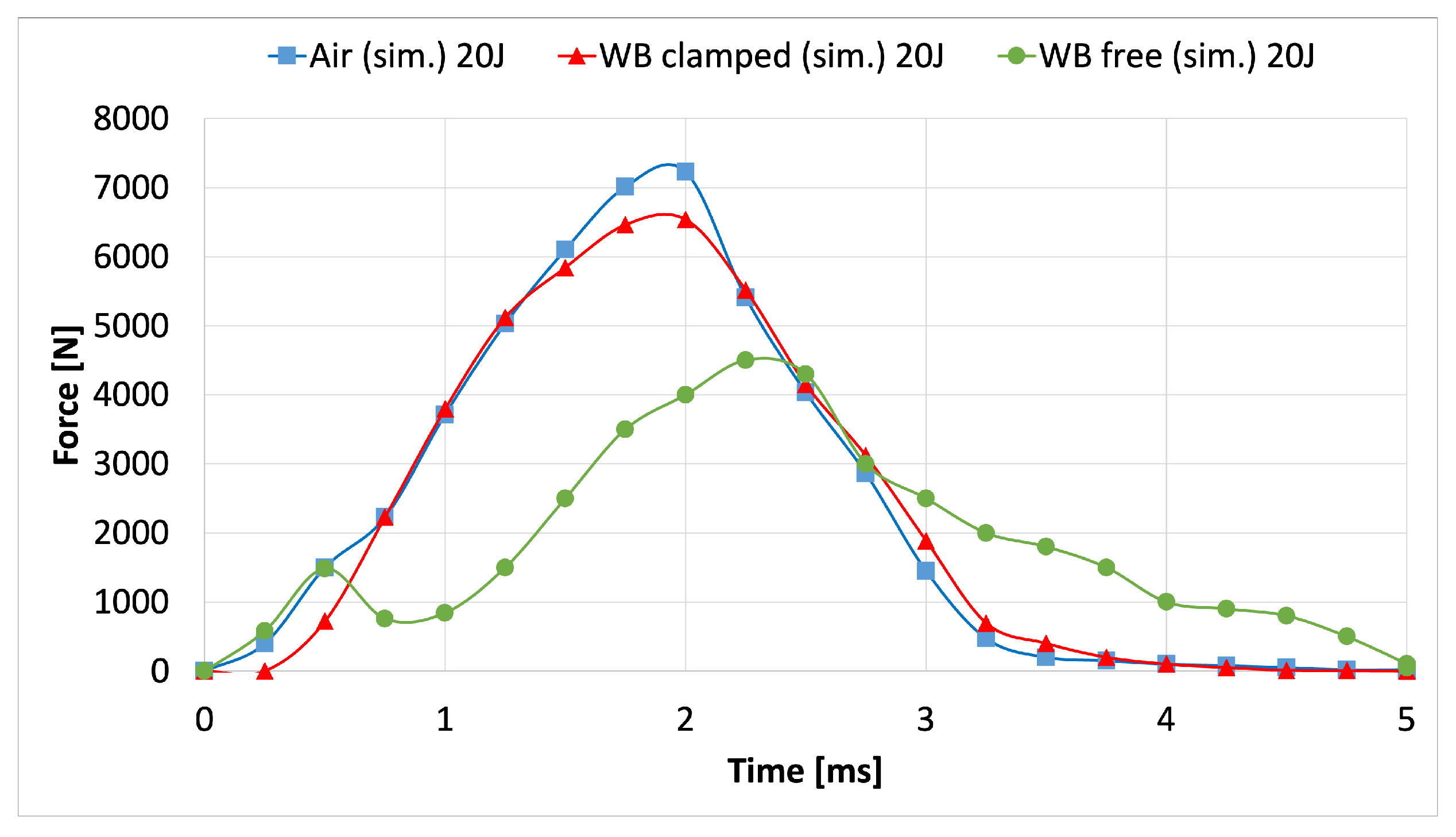
- The fluid–structure interaction significantly influences the dynamic response of a composite panel in good agreement with the literature’s experimental data;
- The absorbed energy is higher in the floating and water-backed clamped conditions due to the quota transferred to the water, thus resulting in lower damage to the laminates with respect to the air-backed clamped condition;
- Damage calculation by using *MAT054 element is not straightforward and does not include delamination.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| SPH | Smoothed-Particle Hydrodynamics |
| BEM | Boundary Element Method |
| DIC | Digital Image Correlation |
| MOM | Moving Object Method |
| PIV | Particle Image Velocimetry |
| FSI | Fluid–Structure Interaction |
Appendix A. SPH Basics
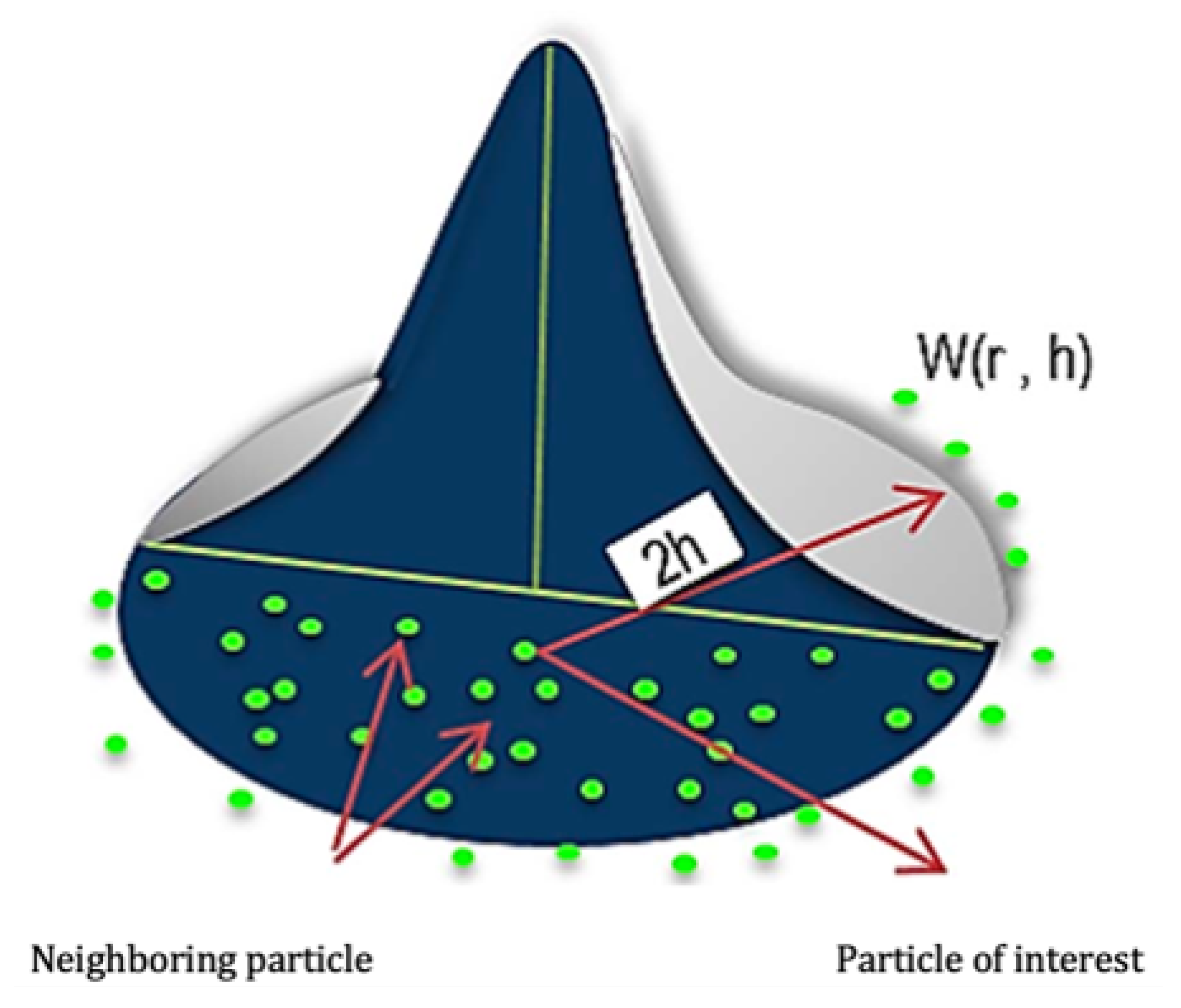
Appendix B. Input Parameters for the MAT054 Element
| Property | Value | Units |
|---|---|---|
| Stress limit, tau 1 | 0 | Pa |
| Strain limit, gamma 1 | 0 | mm |
| Shear Modulus ab direction, Gab | GPa | |
| Shear Modulus be direction, Gbc | GPa | |
| Shear Modulus ca direction, Gca | GPa | |
| Factor to determine the minimum stress limit after stress maximum (fiber tension), slimt1 | ||
| Factor to determine the minimum stress limit after stress maximum (fiber compression), slimc1 | 1 | |
| Factor to determine the minimum stress limit after stress maximum (matrix tension), slimt2 | ||
| Factor to determine the minimum stress limit after stress maximum (matrix compression), slimc2 | 1 | |
| Factor to determine the minimum stress limit after stress maximum (shear), slims | 1 | |
| Time Step for automatic element deletion, tsize | 0 | s |
| Maximum Effective strain for element layer failure, erods | 0 | mm |
| Softening Reduction factor for strength in the crashfront, soft | 0 | |
| Plastic Failure Strain for element deletion, epsf | 0 | mm |
| Final Rupture Transverse Shear Strain, epsr | 0 | mm |
| Transverse Shear Maximum Damage, tsmd | 0 | |
| X Coordinate of point p, xp | 0 | mm |
| Y Coordinate of point p, yp | 0 | mm |
| Z Coordinate of point p, zp | 0 | mm |
| Component 1 of vector a, A1 | 0 | |
| Component 2 of vector a, A2 | 0 | |
| Component 3 of vector a, A3 | 0 | |
| Poisson’s ratio ca, pcra | 0 | |
| Poisson’s ratio cb, pcrb | 0 | |
| Component 1 of vector V, V1 | 0 | |
| Component 2 of vector v, V2 | 1 | |
| Component 3 of vector v, V3 | 0 | |
| Component 1 of vector d, D1 | 0 | |
| Component 2 of vector d, D2 | 0 | |
| Component 3 of vector d, D3 | 0 | |
| Material Angle in degrees, beta | 0 | |
| Strain at longitudinal compressive strength a-axis, e11c | mm | |
| Strain at longitudinal tensile strength a-axis., e11t | mm | |
| Strain at transverse compressive strength b-axis, e22c | mm | |
| Strain at transverse tensile strength b-axis, e22t | mm | |
| Engineering shear strain at shear strength ab plane, gms | mm |
References
- Rubino, F.; Nisticò, A.; Tucci, F.; Carlone, P. Marine Application of Fiber Reinforced Composites: A Review. J. Mar. Sci. Eng. 2020, 8, 26. [Google Scholar] [CrossRef] [Green Version]
- Crupi, V.; Epasto, G.; Napolitano, F.; Palomba, G.; Papa, I.; Russo, P. Green Composites for Maritime Engineering: A Review. J. Mar. Sci. Eng. 2023, 11, 599. [Google Scholar] [CrossRef]
- Abrate, S. Impact on Composite Structures; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar] [CrossRef]
- Saghafi, H.; Minak, G.; Zucchelli, A.; Brugo, T.M.; Heidary, H. Comparing various toughening mechanisms occurred in nanomodified laminates under impact loading. Compos. Part B Eng. 2019, 174, 106964. [Google Scholar] [CrossRef]
- Sutherland, L.S. A review of impact testing on marine composite materials: Part I—Marine impacts on marine composites. Compos. Struct. 2018, 188, 197–208. [Google Scholar] [CrossRef]
- Poodts, E.; Panciroli, R.; Minak, G. Design rules for composite sandwich wakeboards. Compos. Part B Eng. 2013, 44, 628–638. [Google Scholar] [CrossRef]
- Panciroli, R.; Abrate, S.; Minak, G.; Zucchelli, A. Hydroelasticity in water-entry problems: Comparison between experimental and SPH results. Compos. Struct. 2012, 94, 532–539. [Google Scholar] [CrossRef]
- Panciroli, R.; Abrate, S.; Minak, G. Dynamic response of flexible wedges entering the water. Compos. Struct. 2013, 99, 163–171. [Google Scholar] [CrossRef]
- Panciroli, R.; Ubertini, S.; Minak, G.; Jannelli, E. Experiments on the Dynamics of Flexible Cylindrical Shells Impacting on a Water Surface. Exp. Mech. 2015, 55, 1537–1550. [Google Scholar] [CrossRef]
- Panciroli, R.; Pagliaroli, T.; Minak, G. On Air-Cavity Formation during Water Entry of Flexible Wedges. J. Mar. Sci. Eng. 2018, 6, 155. [Google Scholar] [CrossRef] [Green Version]
- Fragassa, C.; Topalovic, M.; Pavlovic, A.; Vulovic, S. Dealing with the Effect of Air in Fluid Structure Interaction by Coupled SPH-FEM Methods. Materials 2019, 12, 1162. [Google Scholar] [CrossRef] [Green Version]
- Korobkin, A. Unsteady Hydroelasticity of Floating Plates. J. Fluids Struct. 2000, 14, 971–991. [Google Scholar] [CrossRef]
- Kashiwagi, M. A Time-domain mode-expansion method for calculating transient elastic responses of a pontoon-type VLFS. J. Mar. Sci. Technol. 2000, 5, 89–100. [Google Scholar] [CrossRef]
- Shams, A.; Lopresto, V.; Porfiri, M. Impact Loading on Marine Panels: Modeling the Effect of Water Backing. Procedia Eng. 2016, 167, 18–22. [Google Scholar] [CrossRef]
- Yoon, J.S.; Lee, P.S. Towards hydro-elastoplastic analysis of floating plate structures. J. Fluids Struct. 2017, 71, 164–182. [Google Scholar] [CrossRef]
- Shams, A.; Lopresto, V.; Porfiri, M. Modeling fluid-structure interactions during impact loading of water-backed panels. Compos. Struct. 2017, 171, 576–590. [Google Scholar] [CrossRef]
- Zhang, P.; Porfiri, M. A combined digital image correlation/particle image velocimetry study of water-backed impact. Compos. Struct. 2019, 224, 111010. [Google Scholar] [CrossRef]
- Lopresto, V.; Langella, A.; Papa, I. Interaction of Water with Carbon Fiber Reinforced Polymer Laminates under Dynamic Loading Conditions. J. Mater. Eng. Perform. 2019, 28, 3220–3227. [Google Scholar] [CrossRef]
- Nguyen, X.V.; Luong, V.H.; Cao, T.N.T.; Lieu, X.Q.; Nguyen, T.B. Hydroelastic responses of floating composite plates under moving loads using a hybrid moving element-boundary element method. Adv. Struct. Eng. 2020, 23, 2759–2775. [Google Scholar] [CrossRef]
- Khabakhpasheva, T.I.; Korobkin, A.A. Blunt body impact onto viscoelastic floating ice plate with a soft layer on its upper surface. Phys. Fluids 2021, 33, 062105. [Google Scholar] [CrossRef]
- Achor, C.H.; Kwon, Y.W.; Didoszak, J.M.; Crow, N.E.; Hardman, D.J. Study of air-backed and water-backed carbon fiber composite plates subjected to underwater shock loading. Compos. Struct. 2022, 300, 116147. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, W.; Hao, H.; Dong, Y.; Huang, Z. Numerical prediction of blast fragmentation of reinforced concrete slab using ALE-FEM-SPH coupling method. Finite Elem. Anal. Des. 2023, 220, 103948. [Google Scholar] [CrossRef]
- Karmakar, S.; Shaw, A. Response of R.C. plates under blast loading using FEM-SPH coupled method. Eng. Fail. Anal. 2021, 125, 105409. [Google Scholar] [CrossRef]
- Slimane, S.A.; Slimane, A.; Guelailia, A.; Boudjemai, A.; Kebdani, S.; Smahat, A.; Mouloud, D. Hypervelocity impact on honeycomb structure reinforced with bi-layer ceramic/aluminum facesheets used for spacecraft shielding. Mech. Adv. Mater. Struct. 2022, 29, 4487–4505. [Google Scholar] [CrossRef]
- Feng, Y.; Li, H.; Ong, M.C.; Wang, W. Numerical investigation of collision between massive ice floe and marine structure using coupled SPH-FEM method. Ships Offshore Struct. 2023, 18, 380–390. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, Y.; Huang, T.; Cai, W. SPH-FEM simulation of impacted composite laminates with different layups. Aerosp. Sci. Technol. 2019, 95, 105469. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, Y.; Huang, T. Bird-Strike Resistance of Composite Laminates with Different Materials. Materials 2020, 13, 129. [Google Scholar] [CrossRef] [Green Version]
- Hasanpour, A.; Istrati, D.; Buckle, I. Coupled SPH–FEM Modeling of Tsunami-Borne Large Debris Flow and Impact on Coastal Structures. J. Mar. Sci. Eng. 2021, 9, 1068. [Google Scholar] [CrossRef]
- Xu, J.; Wang, J. Interaction Methods for the SPH Parts (Multiphase Flows, Solid Bodies) in LS-DYNA®. In Proceedings of the 13th International LS-DYNA Users Conference, Dearborn, DE, USA, 8–10 June 2014. [Google Scholar]
- Liu, M.B.; Liu, G.R.; Lam, K.Y.; Zong, Z. Smoothed-particle hydrodynamics for numerical simulation of underwater explosion. Comput. Mech. 2003, 30, 106–118. [Google Scholar] [CrossRef]
- Fourtakas, G.; Stansby, P.; Rogers, B.; Lind, S. An Eulerian–Lagrangian incompressible SPH formulation (ELI-SPH) connected with a sharp interface. Comput. Methods Appl. Mech. Eng. 2018, 329, 532–552. [Google Scholar] [CrossRef]
- Hu, D.; Long, T.; Xiao, Y.; Han, X.; Gu, Y. Fluid–structure interaction analysis by coupled FE–SPH model based on a novel searching algorithm. Comput. Methods Appl. Mech. Eng. 2014, 276, 266–286. [Google Scholar] [CrossRef] [Green Version]
- Monaghan, J. Simulating Free Surface Flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Gabreil, E.; Wu, H.; Chen, C.; Li, J.; Rubinato, M.; Zheng, X.; Shao, S. Three-dimensional smoothed particle hydrodynamics modeling of near-shore current flows over rough topographic surface. Front. Mar. Sci. 2022, 9, 935098. [Google Scholar] [CrossRef]
- Mir, A.; Luo, X.; Sun, J. The investigation of influence of tool wear on ductile to brittle transition in single point diamond turning of silicon. Wear 2016, 364–365, 233–243. [Google Scholar] [CrossRef] [Green Version]
- Andersson, M.; Liedberg, P. Crash Behavior of Composite Structures—A CAE Benchmarking Study. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2014. [Google Scholar]
- Feraboli, P.; Wade, B.; Deleo, F.; Rassaian, M.; Higgins, M.; Byar, A. LS-DYNA MAT54 modeling of the axial crushing of a composite tape sinusoidal specimen. Compos. Part A Appl. Sci. Manuf. 2011, 42, 1809–1825. [Google Scholar] [CrossRef]
- Berk, B.; Karakuzu, R.; Icten, B.M.; Arıkan, V.; Arman, Y.; Atas, C.; Goren, A. An experimental and numerical investigation on low velocity impact behavior of composite plates. J. Compos. Mater. 2016, 50, 3551–3559. [Google Scholar]
- Hosseinzadeh, R.; Shokrieh, M.M.; Lessard, L. Damage behavior of fiber reinforced composite plates subjected to drop weight impacts. Compos. Sci. Technol. 2006, 66, 61–68. [Google Scholar] [CrossRef]
- Maio, L.; Monaco, E.; Ricci, F.; Lecce, L. Simulation of low velocity impact on composite laminates with progressive failure analysis. Compos. Struct. 2013, 103, 75–85. [Google Scholar] [CrossRef]
- Tomblin, J.; Sherraden, J.; Seneviratne, W.; Raju, K.S. Advanced General Aviation Transport Experiments A-Basis and B-Basis Design Allowables for Epoxy-Based Prepreg TORAY T700SC-12K-50C/#2510 Plain Weave Fabric, AGATE-WP3.3-033051-131; National Institute for Aviation Research, Wichita State University: Wichita, KS, USA, 2002. [Google Scholar]
- T700SC 12K/2510 Plain Weave Fabric. In Composite Materials Handbook (CMH-17); Rev. G. [Chapter 4.2.38]; Wichita State University: Wichita, KS, USA, 2018; Volume 2.
- Vannucchi de Camargo, F.; Pavlovic, A.; Schenal, E.C.; Fragassa, C. Explicit Stacked-Shell Modelling of Aged Basalt Fiber Reinforced Composites to Low-Velocity Impact. Compos. Struct. 2021, 256, 113017. [Google Scholar] [CrossRef]
- Feraboli, P.; Wade, B. Simulating Laminated Composite Materials Using LS-DYNA Material Model MAT54: Single-Element Investigation. In Federal Aviation Administration Technical Report; National Technical Information Services (NTIS): Springfield, VA, USA, 2015. [Google Scholar]
- Sory, D.R.; Areias, A.; Overby, D.; Proud, W. Novel method to dynamically load cells in 3D-hydrogels culture for blast injury studies. AIP Conf. Proc. 2017, 1793, 140003. [Google Scholar] [CrossRef] [Green Version]
- Hinrichsen, R.; Moshier, M.; Kurtz, A. High Velocity Impacts of Man Portable Air Defense Systems (MANPADS) on Selected Targets. In Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Springs, CA, USA, 19–22 April 2004. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, J.; Li, X.; Zhang, C. Numerical Study of the damage behavior of carbon fiber/glass fiber hybrid composite laminates under low-velocity impact. Fibers Polym. 2020, 21, 2873–2887. [Google Scholar] [CrossRef]





| Property | Symbol | LS-DYNA Parameter | Experimental Value |
|---|---|---|---|
| Density | RO | kg/m | |
| Young Modulus (1) | EA | 127 GPa | |
| Young Modulus (2) | EB/EC | GPa | |
| Shear Modulus | GAB | GPa | |
| Major Poisson’s ratio | / | ||
| Minor Poisson’s ratio | PRBA | ||
| Strength in tension (1) | XT | GPa | |
| Strength in compression (1) | XC | GPa | |
| Strength in tension (2) | YT | MPa | |
| Strength in compression (2) | YC | 199 MPa | |
| Shear strength | SC | 154 MPa |
| Variable | Units | Experimental | Numerical | Difference |
|---|---|---|---|---|
| Air-backed clamped | ||||
| Max Displacement | mm | |||
| Max Force | kN | |||
| Absorbed Energy | J | |||
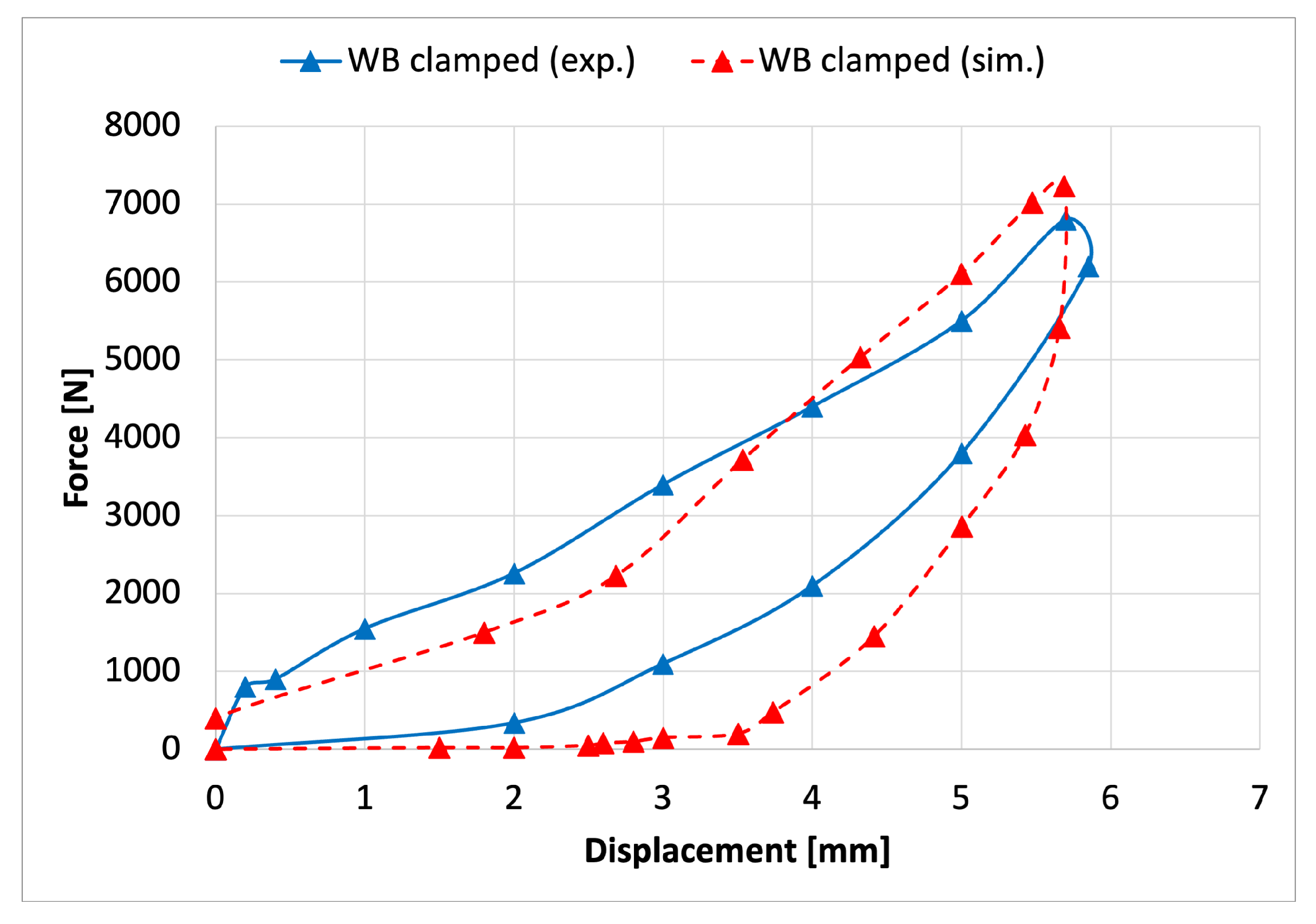
| Water-backed clamped | ||||
| Max Displacement | mm | |||
| Max Force | kN | |||
| Absorbed Energy | J | |||
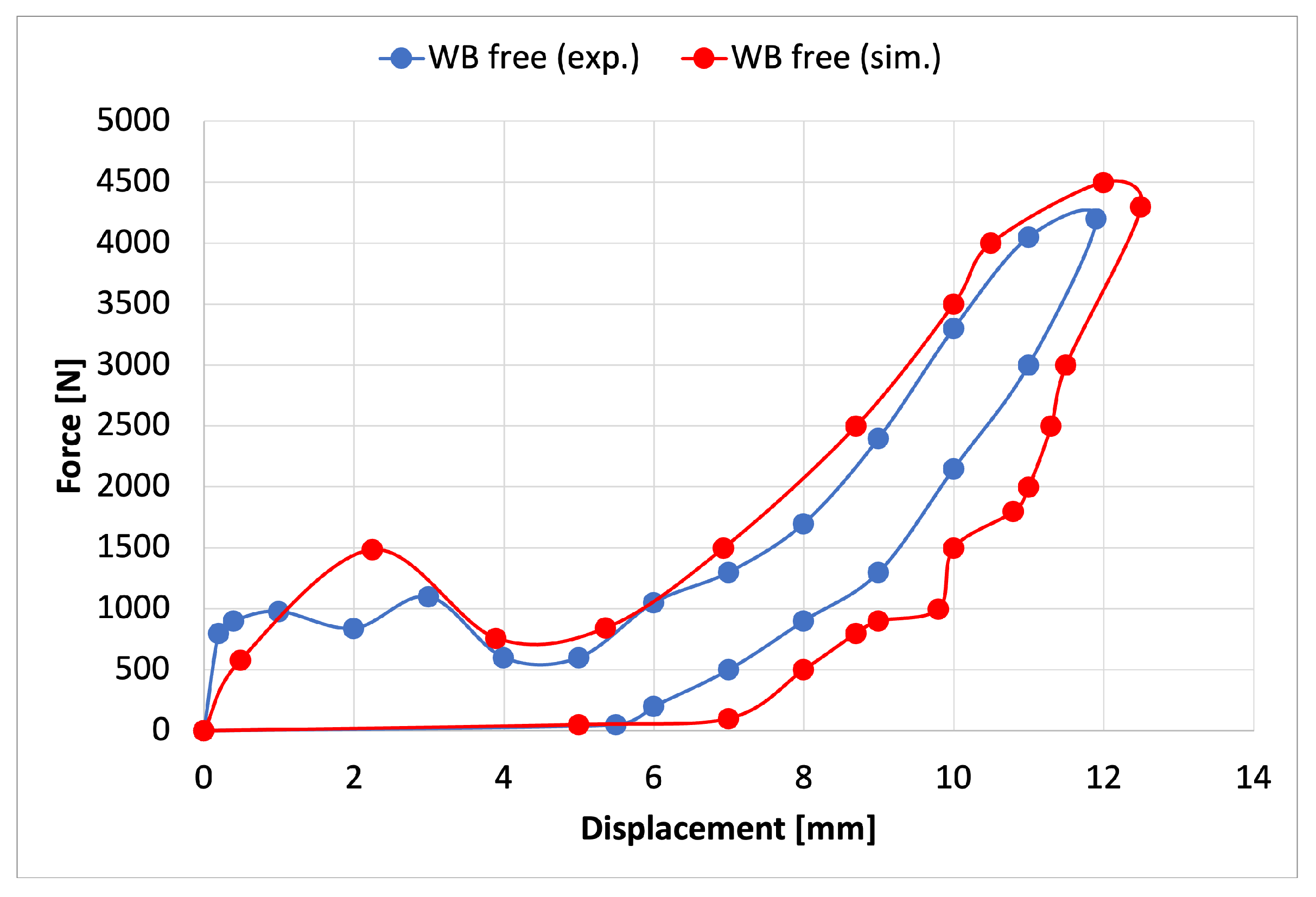
| Floating | ||||
| Max Displacement | mm | |||
| Max Force | kN | |||
| Absorbed Energy | J | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavlović, A.; Minak, G. FEM-SPH Numerical Simulation of Impact Loading on Floating Laminates. J. Mar. Sci. Eng. 2023, 11, 1590. https://doi.org/10.3390/jmse11081590
Pavlović A, Minak G. FEM-SPH Numerical Simulation of Impact Loading on Floating Laminates. Journal of Marine Science and Engineering. 2023; 11(8):1590. https://doi.org/10.3390/jmse11081590
Chicago/Turabian StylePavlović, Ana, and Giangiacomo Minak. 2023. "FEM-SPH Numerical Simulation of Impact Loading on Floating Laminates" Journal of Marine Science and Engineering 11, no. 8: 1590. https://doi.org/10.3390/jmse11081590
APA StylePavlović, A., & Minak, G. (2023). FEM-SPH Numerical Simulation of Impact Loading on Floating Laminates. Journal of Marine Science and Engineering, 11(8), 1590. https://doi.org/10.3390/jmse11081590








