Visual-Aided Shared Control of Semi-Autonomous Underwater Vehicle for Efficient Underwater Grasping

Abstract

Human intelligence has the advantage for making high-level decisions in the remote control of underwater vehicles, while autonomous control is superior for accurate and fast close-range pose adjustment. Combining the advantages of both remote and autonomous control, this paper proposes a visual-aided shared-control method for a semi-autonomous underwater vehicle (sAUV) to conduct flexible, efficient and stable underwater grasping. The proposed method utilizes an arbitration mechanism to assign the authority weights of the human command and the automatic controller according to the attraction field (AF) generated by the target objects. The AF intensity is adjusted by understanding the human intention, and the remote-operation command is fused with a visual servo controller. The shared controller is designed based on the kinematic and dynamic models, and model parameter uncertainties are also addressed. Efficient and stable control performance is validated by both simulation and experiment. Faster and accurate dynamic positioning in front of the target object is achieved using the shared-control method. Compared to the pure remote operation mode, the shared-control mode significantly reduces the average time consumption on grasping tasks for both skilled and unskilled operators.

1. Introduction

Unmanned underwater vehicles (UUVs) are essential tools for underwater observation tasks [1,2]. They can be commonly categorized according to their autonomy levels, from remotely operated vehicles (ROVs) of limited autonomy to autonomous underwater vehicles (AUVs) of high autonomy [3,4,5]. Most AUVs can only be adopted in some simple tasks such as observation, exploration or monitoring, and more complex tasks such as underwater grasping and manipulation can hardly be performed without human interventions [6]. Such tasks rely on the UUVs equipped with manipulators [7,8,9], which are mostly remotely operated since human intelligence is indispensable in understanding complicated mission requirements and controlling multi-degrees of freedom (DOFs) motion.

The harsh underwater environment creates many difficulties for the application of perception and positioning sensors. Some common robot sensors are unavailable in the underwater environment, and some underwater sensors are bulky and expensive, which strongly limits the autonomy capability of AUVs. For example, robust underwater velocity and position measurement across a wide range rely heavily on acoustic devices [10,11]. The water turbidity and lack of visible reference objects and features also limit the application of vision-based positioning and perception methods [12,13,14]. In many cases, AUVs are specifically tailored for certain types of underwater missions [15,16]. Structures, electronic devices and autonomy programs have to be specially designed according to the mission requirements, which limits their applicability to a wider range of occasions.

With intervention or remote control by human operators, the ROVs are generally more versatile in underwater explorations and manipulation [17]. Low-cost and miniaturized ROVs are becoming more popular in ocean explorations to serve as alternatives for the expensive AUVs. Humans can make decisions and undertake operations with minor sensor information to conduct complex underwater missions. New control methods are also increasingly investigated, and practical issues such as communication rate [18] and winch performance [19] are also considered in the ROV control problems.

However, the performance of an ROV is highly relevant to the human operator’s skills. Furthermore, prolonged concentrated work is not only physically demanding, but also has a high risk of accidents. Therefore, shared autonomy approaches have been proposed in the literature to leverage the capabilities of autonomous systems to complement the skills of human operators [20]. Human intelligence is superior in making intelligent and flexible high-level decisions, dealing with unexpected events, and comprehending the varying and unconstructed environment., while machine autonomy has the advantage of high stability, accuracy and fast responses [21,22].

Many attempts have been made to apply shared-control algorithms to land robots [23,24,25], but the shared control of UUVs has still not been fully investigated. A shared autonomy approach for a low-cost sAUV is developed in [20]. It contains a variable level assistant control mode with an online estimation of user skill level and a planner which generates paths that avoid tether entanglement of the sAUV. The method reduces the training requirements and attentional burden required for underwater inspection tasks, but the accurate control of close-range object grasping tasks has not been fully discussed. An ROV teleoperation via human body motion mapping is proposed in [26], where the ROV hydrodynamic forces are converted into haptic feedback, and the human body motions are modeled and mapped into the gesture controls. The control precision is improved and mental load is reduced, but automatic control has not yet been fused into the system to form a shared-control scheme.

In order to improve the working efficiency and reduce the operational burden on humans in underwater grasping tasks, this paper develops a practical visual-aided shared-control method for a low-cost prototype sAUV. The primary contributions of this paper are three-fold.

• The proposed method takes full advantage of human command in the high-level guidance, and the visual servo autonomy in the close-range dynamic positioning, to construct a stable, flexible and efficient shared controller for underwater grasping tasks.
• A variable AF of the target objects is proposed, whose field intensity is adjusted by the human intention extracted from the remote commands. An arbitration mechanism is then adopted to assign authority weights to the human command and the automatic controller according to the AF intensity.
• The shared controller is realized based on the reference velocity fusion in the kinematic level, which is then tracked by the dynamic controller considering model parameter uncertainties. Both the simulation and experiment demonstrate an obvious increase in the grasping efficiency and stability.

The rest of this paper is organized as follows. Section 2 introduces the hardware construction and modeling of the prototype sAUV. Section 3 introduces the detailed design procedure of the shared controller, including both the adjustable AF concept and the model-based dynamic controller considering model uncertainties. Section 4 provides the simulation and experiment results, and Section 5 concludes the paper.

2. System Construction and Modeling

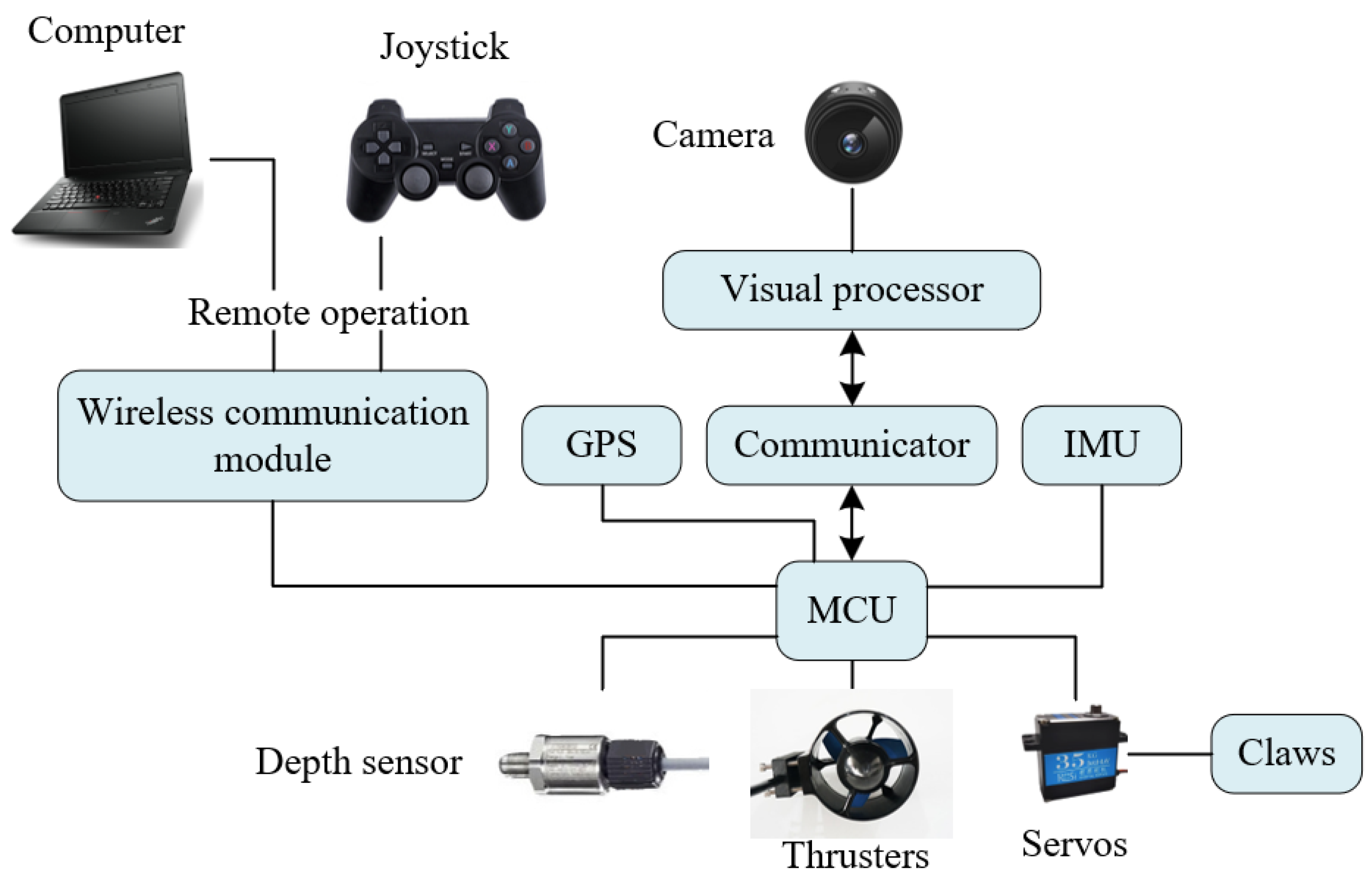
2.1. System Construction

The prototype miniaturized sAUV is shown in Figure 1, and its functional diagram is illustrated in Figure 2. The prototype is approximately 0.7 m in length including the claws, 0.35 m in width, and 0.25 m in height, which is miniaturized and low-cost. It is equipped with six thrusters to provide five-DOF motion for dexterous underwater grasping tasks. Nevertheless, it is passively stable in roll and pitch unless a special pose adjustment is required. The sAUV is wirelessly controlled and capable of three control modes: full autonomy, remote control and shared control. It can receive remote-control signals from a joystick and an onshore computer.

Figure 1. Structure of the prototype sAUV: (a) Side view with claws; (b) Top view without claws.

Figure 2. Functional diagram of the sAUV.

Due to budget and weight limits, acoustic devices are not applied in this prototype version. The sAUV utilizes a forward-looking camera for observation and object searching. The real-time visual program is taken charge of by an independent visual processor. All the other sensors and modules are connected to a microcontroller unit (MCU), which is the central brain of the electrical system. The inertial measurement unit (IMU) provides Euler angles in the north-east-down (NED) earth coordinate. The wireless communication module takes charge of the mutual communication between the sAUV and the external operators, including the joystick and the onshore computer. High-speed communication is established between the MCU and the visual processor to conduct the shared autonomous control algorithm. When the visual measurement is available, the joystick provides the reference velocities and poses as remote commands, otherwise, the translational motions are directly controlled by the input thrust forces. The control modes are switched according to different task requirements.

2.2. Kinematic Model

Kinematic and dynamic models of the sAUV were established following the classic model introduced by T.I Fossen [27]. The positions and poses are denoted in the NED frame, and the sAUV velocities are denoted in the body-fixed coordinate frame (B-frame). The schematic of the kinematic model is shown in Figure 3.

Figure 3. Schematic of the kinematic model.

The six-DOF kinematic model is written as:

$$\dot{\eta }=\mathbf{J}(\eta )v,$$

(1)

where $\eta ={\eta }_1+{\eta }_2$ is the position and Euler angle vector in the NED frame, and v is the velocity vector in the B-frame. Given that the sAUV is passively stable in roll and pitch, a decoupled four-DOF motion on the horizontal plane along with an independent vertical motion is adopted, which gives a simplified kinematic model as:

$$\begin{array}{l}\dot{x}=u\cos \psi -v\sin \psi ,\\ \dot{y}=u\sin \psi +v\cos \psi ,\\ \dot{z}=w,\\ \dot{\psi }=r.\end{array}$$

(2)

The automatic visual servo control is performed when the target object is recognized by the camera fixed on the front of the sAUV. The rotation matrix from the B-frame to the camera-fixed coordinate frame (C-frame) is given by:

$$R_B^C=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right].$$

(3)

The center position $P_i^C$ of an object in the C-frame is:

$$P_i^C=R_B^C{R}^{-1}\left({\eta }_2\right)\left(P_i-{\eta }_1\right),$$

(4)

where ${\eta }_1=\left(x,y,z\right)$, ${\eta }_2=\left(\varphi ,\theta ,\psi \right)$, $R$ denotes the rotation matrix of the current pose, and $P_i=\left(P_{ix},P_{iy},P_{iz}\right)$ is the object position in the NED frame. A position-based visual error function is utilized for the convenience of the controller design. Assuming that the object is expected to be located at $P_t^C=\left(P_{tu}^C,P_{tv}^C,P_{tw}^C\right)$ in the C-frame in a grasping task, the visual error is then defined as:

$$\begin{array}{ll}\hfill e_v& =P_t^C-P_i^C\hfill \\ & =P_t^C-R_B^C{R}^{-1}\left({\eta }_2\right)\left(P_i-{\eta }_1\right).\hfill \end{array}$$

(5)

The visual error in (5) can be directly obtained from the image captured by the camera. Given that the sAUV is self-stabilized in pitch and roll, which gives $\varphi =\theta =0$, the expansion form of (5) then becomes:

$$e_v=\left[\begin{array}{c}{e}_u\\ \begin{array}{l}{e}_v\\ e_w\end{array}\end{array}\right]=\left[\begin{array}{l}-\sin \psi \left(x-P_{ix}\right)+\cos \psi \left(y-P_{iy}\right)\hfill \\ z-P_{iz}\hfill \\ \cos \psi \left(x-P_{ix}\right)+\sin \psi \left(y-P_{iy}\right)\hfill \end{array}\right]+\left[\begin{array}{c}{P}_{tu}^C\\ \begin{array}{l}{P}_{tv}^C\\ P_{tw}^C\end{array}\end{array}\right].$$

(6)

Using the kinematic model in (2), the time derivative of (6) can be written as:

$${\dot{e}}_v=\left[\begin{array}{c}{\dot{e}}_u\\ \begin{array}{l}{\dot{e}}_v\\ {\dot{e}}_w\end{array}\end{array}\right]=\left[\begin{array}{l}v-(e_w-P_{tw}^C)r\hfill \\ w\hfill \\ u+(e_u-P_{tu}^C)r\hfill \end{array}\right].$$

(7)

For most of the object-grasping tasks, an object can be grabbed from an arbitrary direction when the translational visual error is eliminated using appropriate motion control. Hence, only the translation component of the visual error is considered in this paper, and the Euler angles are measured by the IMU and are independently controlled. Equation (7) is equivalent to the kinematic model but is more straightforward for the visual servo controller design.

2.3. Dynamic Model

The system dynamics in the grasping task are acquired from the six-DOF dynamic model [27]:

$$M\dot{v}+C(v)\mathbf{v}+\mathbf{D}(v)\mathbf{v}+\mathbf{G}(\eta )\mathbf{\eta }=\mathbf{\tau },$$

(8)

where M, C, D, and G are the mass, Coriolis-centripetal, damping, and restoring force terms, respectively, and M = M_A + M_RB. τ contains the input forces and torques. Since the sAUV is self-stabilized in pitch and roll, a decoupled four-DOF dynamic can be utilized by simplifying (8). The high-order terms and nonlinear terms in the viscous hydrodynamic force can also be neglected in the low-speed motion, which gives:

$$\begin{array}{l}{m}_u\dot{u}-m_{v}vr+d_{u}u={\tau }_u,\\ m_v\dot{v}+m_{u}ur+d_{v}v={\tau }_v,\\ m_w\dot{w}+d_{w}w={\tau }_w,\\ m_r\dot{v}-m_{uv}uv+d_{r}v={\tau }_r,\end{array}$$

(9)

The shared controller in the next section is designed based on the kinematic model in (2) and (7), and the dynamic model in (9).

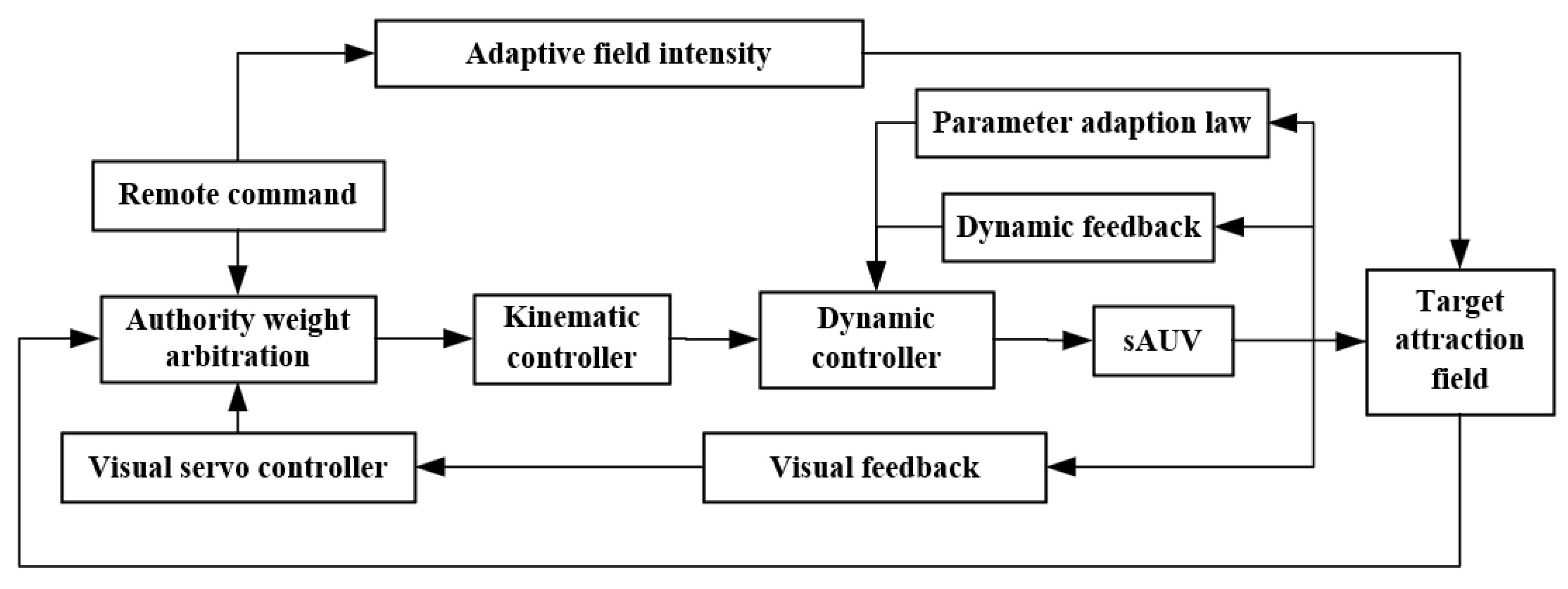
3. Shared Controller Design

The control performances for pure ROVs are closely related to the operating skills of the human operators. Similar to the athletic skills of human beings, the remote operation skill needs extended training, and is also highly related to the natural ability of the operator. Still, precise and delicate operations can be challenging and physically consuming even for skilled operators.

Aiming to mitigate the dependency of grasping task performance on the individual operators, this paper proposes a shared-control algorithm for the sAUV, which provides more convenient, efficient and accurate pose adjustment during the tasks. The controller is designed based on an adjustable AF concept. The general control diagram is illustrated in Figure 4.

Figure 4. Diagram of the shared controller.

3.1. Shared Control Based on Attraction Field

A visual servo controller at the kinematic level was first designed according to the visual error model in (6) to automatically eliminate the visual error. A Lyapunov function was selected as:

$$V_k(e_v,\psi )=\frac{1}{2}\left(e_u{}^2+e_v{}^2+e_w{}^2+{\tilde{\psi }}^2\right),$$

(10)

where $\tilde{\psi }=\psi -{\psi }_d$ is the yaw angle error. The time derivative of (10) is:

$$\begin{array}{l}{\dot{V}}_k=e_u{\dot{e}}_u+e_v{\dot{e}}_v+e_w{\dot{e}}_w+\tilde{\psi }r\\ =e_u\left(v-(e_w-P_{tw})r\right)+e_{v}w+e_w\left(u+(e_u-P_{tu})r\right)+\tilde{\psi }r.\end{array}$$

(11)

The kinematic control law was selected as;

$$\begin{array}{l}\begin{array}{l}u=-\left(e_u-P_{tu}\right)r-k_u{e}_w,\hfill \\ v=\left(e_w-P_{tw}\right)r-k_v{e}_u,\hfill \\ w=-k_w{e}_v,\hfill \end{array}\\ r=-k_r\tilde{\psi }.\end{array}$$

(12)

Bringing (12) into (11), the time derivative of the kinematic Lyapunov function becomes:

$${\dot{V}}_k=-k_u{e}_w{}^2-k_v{e}_u{}^2-k_w{e}_v{}^2-k_r{\tilde{\psi }}^2<0,$$

(13)

which indicates that $\left(e_u,e_v,e_w,\tilde{\psi }\right)$ exponentially converges to zero as t→∞.

The automatic visual servo on the kinematic level addresses the control problem in the absence of human intervention. However, the remote command from the human operator must be taken into consideration in the shared-control approach. The concept of attraction field (AF) is then introduced as the basis of the shared controller.

The concept of AF is inspired by the potential field commonly utilized in obstacle avoidance problems, where the obstacles are regarded as sphere or ellipsoidal sets, and the robotics are prohibited from entering these sets [28]. However, in the proposed grasping problem, the target objects are regarded as sources that generate AFs to attract the sAUV, as illustrated in Figure 5. For a detected object Q_i (i = 1, 2, … n) at P_i, its AF intensity A_i at an arbitrary point P in the field can be described by:

$$A_i=\frac{K_A}{\sqrt{e_u{}^2+e_v{}^2+e_w{}^2+\delta }}{q}_i,\left(P\in {\Omega }_i\right)$$

(14)

where K_A is the attraction coefficient which can be adjusted by human intention, ${\Omega }_i$ is the effective range of the AF, q_i is the importance factor of the object, and $\delta$ is a small positive constant.

Figure 5. Concept of the attraction field in object grasping.

When the sAUV recognizes a single target object, it is naturally attracted by the AF generated by the object within the effective range. When n ≥ 2 objects simultaneously appear in the camera view, which are denoted by {Q_i} (i = 1, 2, …, n), all the potential AF intensities at the current position at time T caused by {Q_i} are calculated as $\left\{A_{T,i}\right\}$(i = 1, 2, …, n). As only one of the objects is expected to be grasped at each time, the resultant active AF at time T belongs to only one of these fields. The resultant AF is selected using the following criterion.

• Assuming that the active AF at the last sample time T − 1 comes from Q_i and has an intensity of $A_{T,i}$ at the current time T. If the current AF with the largest intensity $A_{T,1}$ satisfies:

  $$\begin{array}{l}{A}_{T,1}-A_{T,i}\ge \left(1+H_s\right)A_{T,i},\\ A_{T,1}=\max \{A_{T,1},A_{T,2},\dots ,A_{T,n}\},\end{array}$$

  (15)

  where (1 + H_s) > 1 is the threshold ratio, the AF at time T is then switched to A_T,1, and the corresponding source object is Q₁ also selected.
• Otherwise, the resultant AF is still calculated using the object Q_i at time T.

The above criterion is a straightforward strategy with a hysteresis characteristic. It can be simply interpreted as that the resultant AF only changes when the current largest intensity is much larger than the resultant AF in the last moment. This hysteresis characteristic avoids unstable and frequent changes between different AFs.

Based on the AF concept, the shared-control strategy at the kinematic level is designed to minimize the conflict between automatic control and human intentions. When executing a grasping task, the arbitrator determines the reference control signal to make a combination of the remote operation input u_c,T and the visual servo reference velocity $u_{v,T}$ at time T. The authority weight of the shared controller is determined according to the AF field intensity, which is given by:

$$u_{o,T}=\tanh \left(A_{T,i}\right)u_{v,T}+\left(1-\tanh \left(A_{T,i}\right)\right)u_{c,T},$$

(16)

where A_T,i is calculated by (14).

The AF attraction coefficient K_A in (14) is then utilized to adjust the attraction strength according to the human intention. Assuming that the control input at time T is decomposed in the three orthogonal directions in the B-frame as $u_{c,T}=\left(u_{c,T},v_{c,T},w_{c,T}\right)$, the reference velocity given by the automatic visual servo controller is $u_{v,T}=\left(u_{v,T},v_{v,T},w_{v,T}\right)$. The deviation degree between $u_{v,T}$ and $u_{c,T}$ is then defined as:

$$D_{\chi ,T}=\sqrt{\left|{\chi }_{c,T}\right|\left|{\chi }_{c,T}-{\chi }_{v,T}\right|},\left(\chi =u,v,w\right).$$

(17)

The deviation degree defined by (17) reflects the human intention of taking more or less control of the sAUV. A larger value of $\left|{\chi }_{c,T}\right|\left(\chi =u,v,w\right)$ indicates a stronger intention from the operator to take more control of the system, and a larger value of $\left|{\chi }_{c,T}-{\chi }_{v,T}\right|\left(\chi =u,v,w\right)$ indicates a stronger divergence from the human operator with the automatic controller.

At each sample time T, the derivative of the attraction coefficient is calculated according to the largest deviation, which is given by:

$$\begin{array}{l}\frac{d{K}_A}{dt}=\{\begin{array}{l}-\left|\Delta K_{A1}\right|,{\overline{D}}_{\chi ,T}>D_{TH1},\\ \left|\Delta K_{A2}\right|,{\overline{D}}_{\chi ,T}<D_{TH2},\\ 0,\mathrm{otherwise},\end{array}\\ {\overline{D}}_{\chi ,T}=\max \left\{D_{u,T},D_{v,T},D_{w,T}\right\},\\ K_A\in [0,K_{A,\max }],\end{array}$$

(18)

where D_TH1 > 0 is the AF decreasing threshold, D_TH2 > 0 is the AF recovery threshold, and $K_{A,\max }$ is the upper bound of the coefficient. When the AF needs to be switched using Equation (15), the newly updated AF intensity is also calculated using the current coefficient K_A.

Using the coefficient updated by (18), the AF intensity can be adjusted smoothly by interpreting the remote command. When the operator provides a remote command that is very different from the attraction on purpose, the AF intensity quickly decreases within a couple of seconds to transfer the control authority to the operator. When the human intention is coincident with the visual control or has a moderate deviation, the AF intensity gradually recovers, which means that the operator needs help from the automatic controller to perform accurate control.

3.2. Dynamic Controller

In the inner loop, the dynamic controller is designed to track the shared-control reference velocities. The controller in (16) is extended to the dynamic case by taking the kinematic controllers as virtual control laws. Let α_u, α_v, α_w and α_r be the virtual control laws, introducing the control errors:

$$\begin{array}{l}{z}_u=u-{\alpha }_u,\\ z_v=v-{\alpha }_v,\\ z_w=w-{\alpha }_w,\\ z_r=r-{\alpha }_r.\end{array}$$

(19)

Given that the exact values of the dynamic model parameters are inaccessible in reality, the parameter uncertainties are considered in the model-based dynamic controllers. According to the models in (8), all the parameters to be estimated are concatenated in a vector denoted by:

$$\theta ={\left(m_u,m_v,d_u,{m^{\prime }}_v,{m^{\prime }}_u,d_v,m_w,d_w,m_r,m_{uv},d_r\right)}^{\mathrm{T}}.$$

(20)

Let $\widehat{\mathsf{\theta }}$ be the estimation of $\mathsf{\theta }$, define the parameter estimation error as $\stackrel{\mathrm{~}}{\mathsf{\theta }}=\mathsf{\theta }-\widehat{\mathsf{\theta }}$. Combining the virtual control errors and the parameter estimation errors, a Lyapunov function is chosen as:

$$V_d(z,\tilde{\theta })=\frac{1}{2}\left(m_u{z}_u{}^2+m_v{z}_v{}^2+m_w{z}_w{}^2+m_r{z}_r{}^2+{\tilde{\theta }}^{\mathrm{T}}{\mathsf{\Gamma }}^{-1}\tilde{\theta }\right).$$

(21)

The time derivative of V_d is:

$$\begin{array}{ll}\hfill {\dot{V}}_d& =m_u{z}_u{\dot{z}}_u+m_v{z}_v{\dot{z}}_v+m_w{z}_w{\dot{z}}_w+m_r{z}_r{\dot{z}}_r-{\tilde{\theta }}^{\mathrm{T}}{\mathsf{\Gamma }}^{-1}\dot{\widehat{\theta }}\hfill \\ & =z_u\left({\tau }_u-m_u{\dot{\alpha }}_u+m_{v}vr-d_{u}u\right)+z_v\left({\tau }_v-m_v{\dot{\alpha }}_v-m_{u}ur-d_{v}v\right)\hfill \\ & +z_w\left({\tau }_w-m_w{\dot{\alpha }}_w-d_{w}w\right)+z_r\left({\tau }_r-m_r{\dot{\alpha }}_r+m_{uv}uv-d_{r}r\right)-{\tilde{\theta }}^{\mathrm{T}}{\mathsf{\Gamma }}^{-1}\dot{\widehat{\theta }}.\hfill \end{array}$$

(22)

Choosing the control law at the dynamic level:

$$\begin{array}{l}{\tau }_u={\widehat{m}}_u{\dot{\alpha }}_u-{\widehat{m}}_{v}vr+{\widehat{d}}_{u}u-k_{\tau u}{z}_u,\\ {\tau }_p={{\widehat{m}}^{\prime }}_v{\dot{\alpha }}_v+{{\widehat{m}}^{\prime }}_{u}ur+d_{v}v-k_{\tau v}{z}_v,\\ {\tau }_w={\widehat{m}}_w{\dot{\alpha }}_w+{\widehat{d}}_{w}w-k_{\tau w}{z}_w,\\ {\tau }_r={\widehat{m}}_r{\dot{\alpha }}_r-{\widehat{m}}_{uv}uv+{\widehat{d}}_{r}r-k_{\tau r}{z}_r.\end{array}$$

(23)

Bringing (23) into (22) yields:

$${\dot{V}}_d=-k_{\tau u}{z}_u^2-k_{\tau v}{z}_v^2-k_{\tau w}{z}_w^2-k_{\tau r}{z}_r^2+{\tilde{\theta }}^{\mathrm{T}}\left(\Phi -{\mathsf{\Gamma }}^{-1}\dot{\widehat{\theta }}\right),$$

(24)

where:

$$\Phi ={\left(-z_u{\dot{\alpha }}_u,-z_{u}vr,-z_u{u}_r,-z_v{\dot{\alpha }}_v,z_{v}ur,-z_{v}v,z_w{\dot{\alpha }}_w,-z_{w}w,z_r{\dot{\alpha }}_r,z_{r}uv,-z_{r}r\right)}^T.$$

(25)

Then applying the adaptive law:

$$\dot{\widehat{\theta }}=\Gamma \Phi .$$

(26)

where $\mathsf{\Gamma }$ is a positive diagonal matrix. Applying (23) and (26) into (22) yields:

$${\dot{V}}_d=-k_{\tau u}{z}_u^2-k_{\tau v}{z}_v^2-k_{\tau w}{z}_w^2-k_{\tau r}{z}_r^2<0,$$

(27)

which indicates that $\left(z_u,z_v,z_w,z_r\right)$ converges to zero as $t\to \infty$.

The above dynamic guarantees a convergence of the visual and yaw angle error in the automatic control mode. However, the reference velocities in the shared-control mode are partially provided by the human operator, and thus do not always make the visual error converge to zero as $t\to \infty$. In such cases, the virtual control laws in (19) are synthesized by the shared controller expressed in (16), while the dynamic controller still tracks the reference velocities. In general, the designed dynamic control law in (23) guarantees a successful tracking of the reference velocities in both the automatic and shared-control modes.

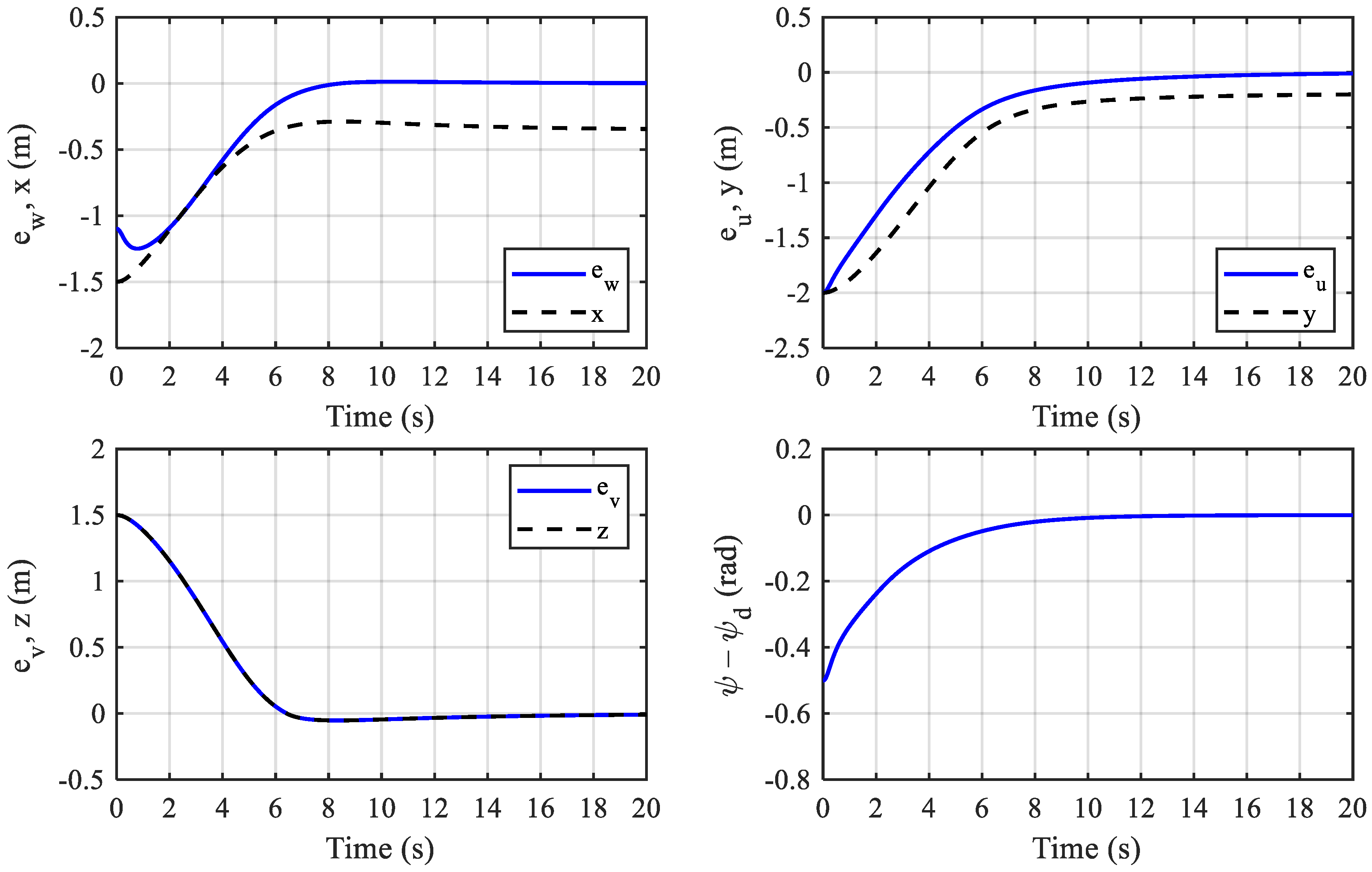
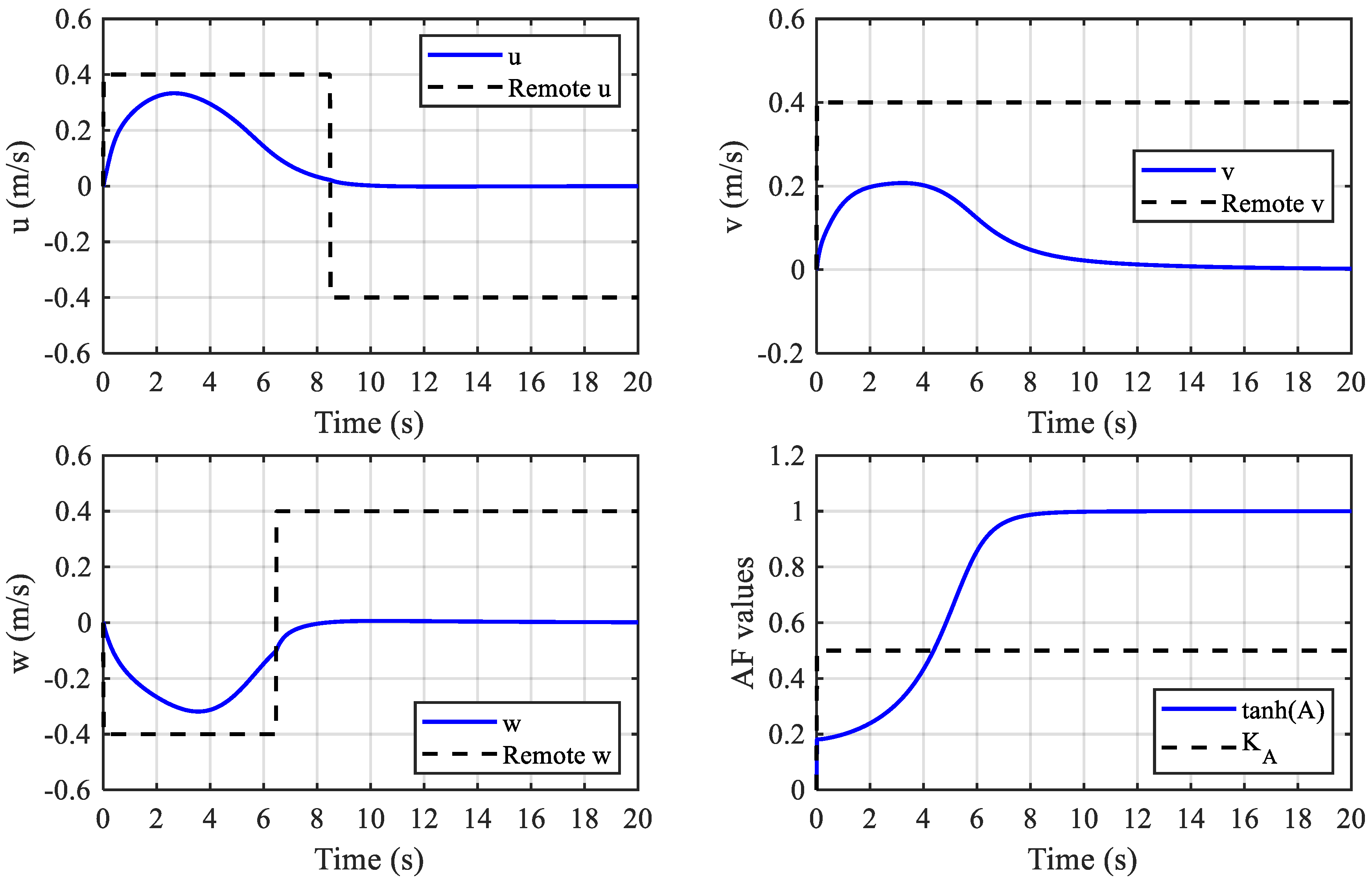
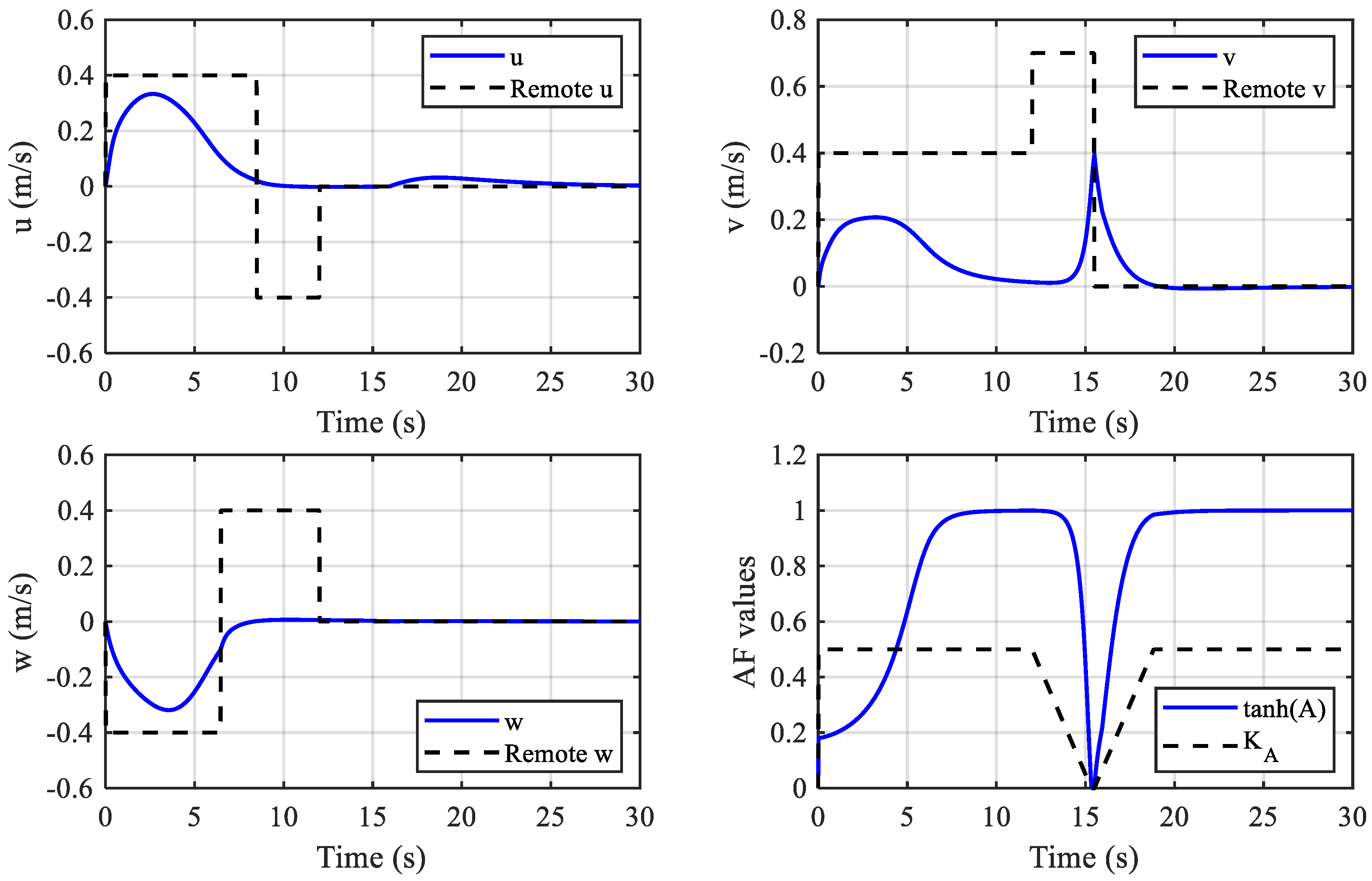
4. Simulation and Experiment

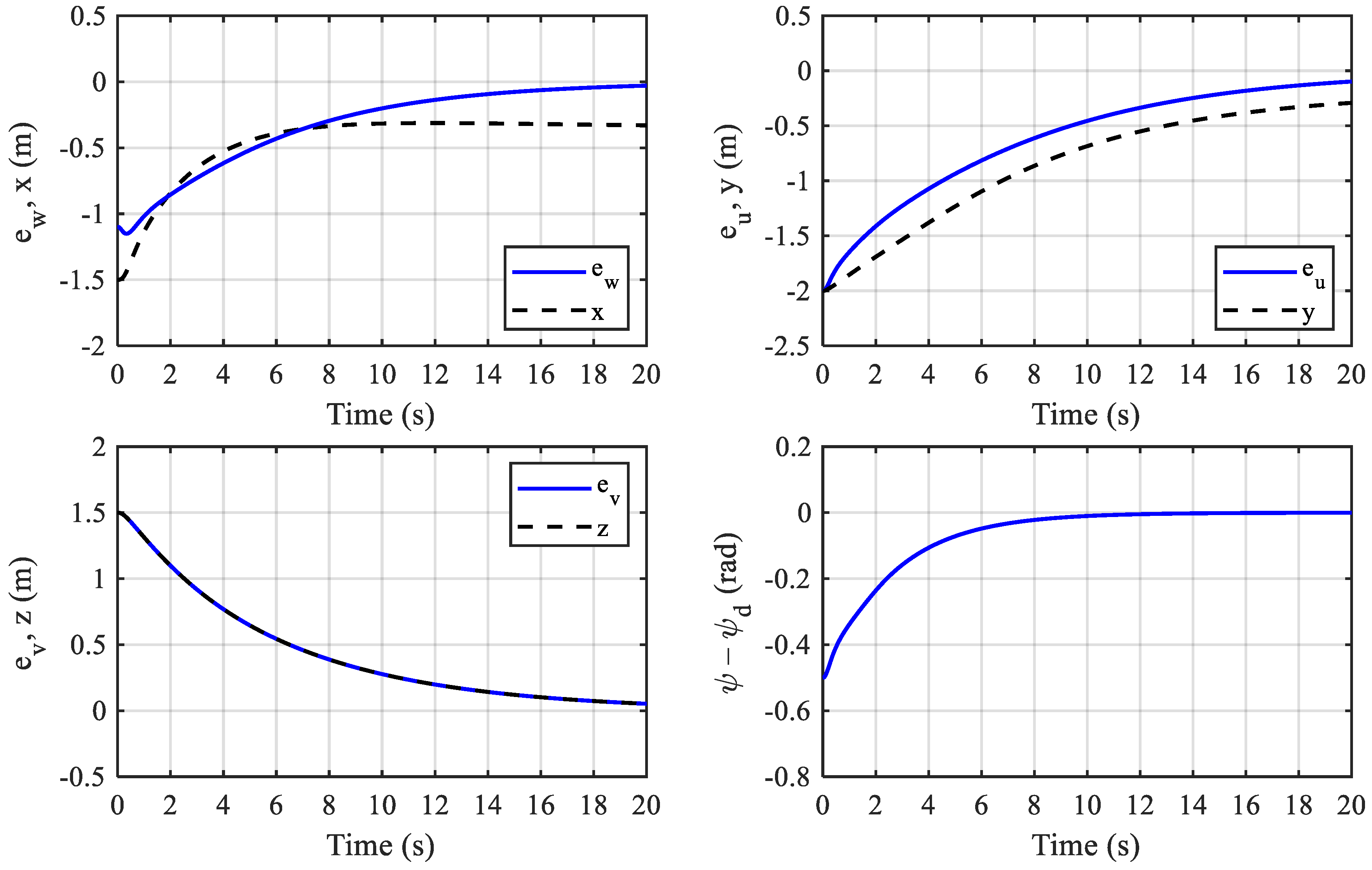
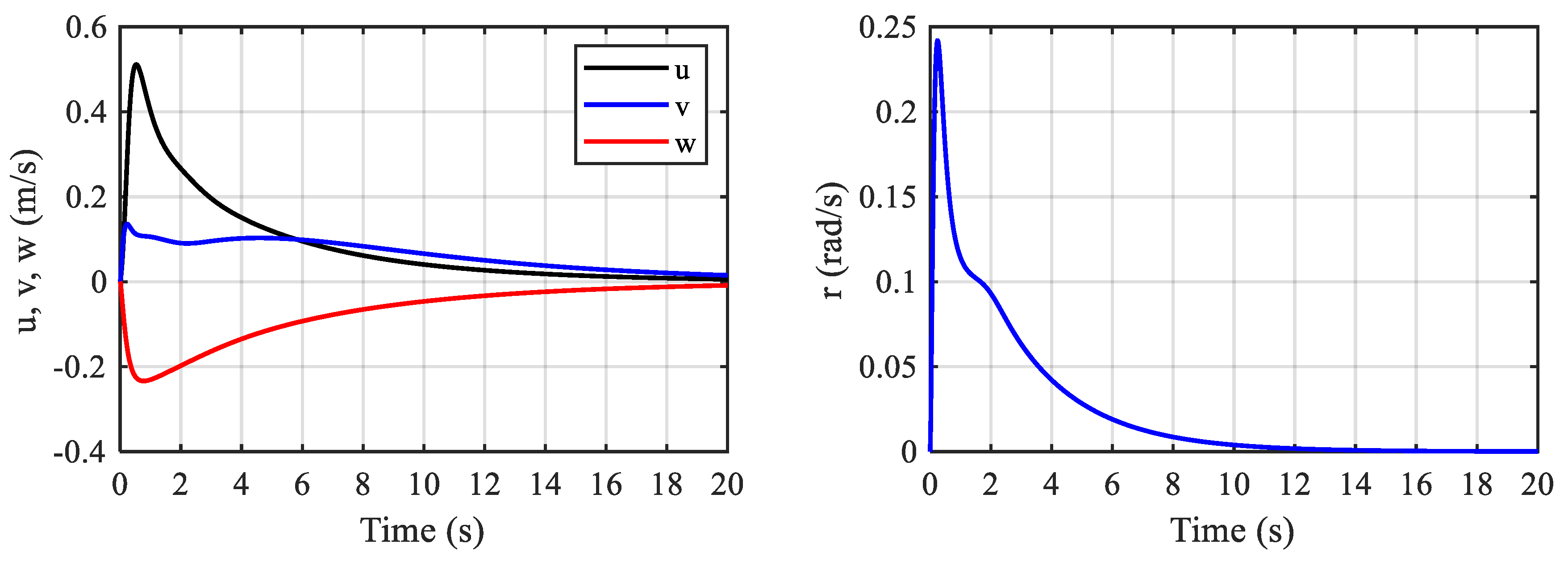
4.1. Simulation

Simulation is conducted using MATLAB based on an approximate model of the sAUV. The model parameters applied in the simulation are set as M = diag(21, 23, 25, 1.3, 2.1, 1.8), D_A = diag(12, 18, 20, 1.5, 2.5, 2.4), and $G(\eta )\eta$ is neglected due to the passive stability in roll and pitch. The initial model parameter estimations in the controller are chosen to have at least 50% errors. The controller gains are k_u = k_v = k_w = 0.2, k_u = 0.4, k_τu = k_τv = k_τw = 20, k_τr = 10. $\mathsf{\Gamma }=100\times diag{(1,1,\dots ,1)}_{11}$. The importance factors for all the objects are chosen to be q_i = 1, and $\delta =0.01$. The initial position of the sAUV is set at P₀ = (−1.5, −2, 1.5), ψ₀ = 0 and ψ_d = 0.5.

The simulation is conducted on three basic operating tasks, including automatic visual servo, shared control with unskilled control, and shared control with target switch. These three task units are basic issues that need to be addressed during the whole underwater grasping task, which also reveal the major advantages of the proposed shared controller.

The fully automatic visual servo performance is an important foundation for the shared-control mode and is thus firstly validated in the simulation. In the first task, the sAUV is expected to perform dynamic positioning in front of the target with a desired yaw angle using the visual servo technique. The NED coordinate position of the target object is set at P_t = (0, 0, 0), and the target C-frame position is set at $P_t^C$ = (0, 0, 0.4). The simulation results are shown in Figure 6 and Figure 7.

Figure 6. Pose and visual errors in the automatic control task.

Figure 7. Translational and rotational velocities in the automatic control task.

It can be observed from Figure 6 that the visual errors all converge smoothly within the period. Due to the existence of the non-zero desired yaw angle ψ, only the errors e_v and z are coincident. Figure 7 shows the translational and yaw velocities during the pose-adjusting process. The velocities change smoothly and gradually decrease as the sAUV approaches the target. The maximum translational velocities are near 0.4 m/s, and the maximum yaw velocity is about 0.25 rad/s, which are reasonable values for the prototype.

The second task is set to mimic a common situation when the remote command is provided by an unskilled operator. The operator is supposed to have normal observation ability, but very poor operation skills, so that the enhanced assistant and corrective ability of the shared-control strategy can be fully revealed. The unskilled operator can recognize the rough deviation direction of the sAUV from the target object, and intends to approach and grasp it with rough speed control. Specifically, the operator provides constant reference velocities with correct directions when the position deviation is recognizable, but cannot adjust the velocity magnitudes according to the deviation distance. Similar to the previous task, the target object is set at $P_t$ = (0, 0, 0), and the target C-frame position is $P_t^C$ = (0, 0, 0.4). The corresponding results are shown in Figure 8 and Figure 9.

Figure 8. Pose and visual errors in the shared-control task.

Figure 9. Velocities and AF values in the shared-control task.

Compared to Figure 6, the results in Figure 8 show a much faster convergence of the visual errors due to the remote-control signals provided to approach the target object. Figure 9 compares the actual velocities with the remote-control velocities. Before the first 6 to 8 seconds, the visual errors are large, and the operator provides 0.4 m/s constant translational velocities to control to eliminate the errors. These remote-control signals at the beginning are regarded as correct and helpful signals to accelerate the convergence of the visual errors.

When each translational error becomes small, the corresponding remote-control signals of u and w changes to the opposite direction, and all the large remote-control velocities are regarded as wrong commands from the unskilled operator. However, as the AF intensity increases when the sAUV approaches the target, the overall velocities are mainly determined by the automatic controller. The harmful disturbances of the rough remote commands are thus eliminated according to the shared controller described in (16). Consequently, the results of the second task demonstrate that the shared-control strategy can successfully help to improve the control performance of an unskilled operator.

The third task is set to evaluate the target switching performance on occasions where the operator wants to pick target objects far from the current candidate objects. The distraction candidates near the target object are not expected to be picked up immediately but generate disturbance AF during the switching process before the correct target is reached. During the switching process, the operator first provides constant reference velocity towards the candidate target at $P_{t1}$ = (0, 0, 0). When the sAUV is attracted by the candidate target, the operator gives a large escape velocity to v towards the correct target at P_t2 = (0, 0.5, 0). The target C-frame position is $P_t^C$ = (0, 0, 0.4) for both the candidate and correct targets. The corresponding results are shown in Figure 10 and Figure 11.

Figure 10. Pose and visual errors in the target switching task.

Figure 11. Velocities and AF values in the target switching task.

The visual error and yaw angle curves in Figure 10 show a rapid and smooth target switch process. There are obvious abrupt changes in the visual errors of e_w and e_u, but the position coordinates x and y change smoothly, because the visual errors are re-calculated when the active AF is switched from the candidate target to the correct target. Similar rapid changes in the velocities u and v also occur in Figure 11.

Notice that the operator gives a remote-control signal only to the velocity v after 12 s to switch the target. When the reference velocity deviation of (17) in any one of the directions exceeds the threshold value, the attraction coefficient K_A rapidly reduces, and results in a rather low AF intensity near 15 s, as shown in Figure 11. The operator thus has high authority to control the sAUV to quickly switch the target until the reference velocity deviation goes beneath the recovery threshold. The low AF intensity time is also flexibly controlled by the operator. In general, the results demonstrate a good target switching performance using the proposed shared-control strategy.

4.2. Experiment

An object-grasping experiment is conducted on the prototype sAUV in a water pool. Due to the limited depth of the pool, the sAUV performs a three-DOF planar motion on the water which is still enough to verify the shared-control performance. Four plastic balls in two different colors are attached on one side of the pool to serve as target objects, as shown in Figure 12. The sAUV first follows a desired path before stopping in front of the target objects and then grasps two of the objects according to different task requirements. In task one, the sAUV is required to grasp any two of the objects despite their colors. In task two, the sAUV is required to grasp two green objects without damaging the red ones. Obviously, task two requires a more skillful remote operation.

Figure 12. Water pool experiment. (a) The sAUV and target objects. (b) Shared control for object grasping.

The grasping task is conducted by both a skilled and an unskilled operator, with a pure remote control and a shared-control mode. The tasks are conducted several times and the results are recorded statistically to demonstrate the general efficiency improvement using the shared-control algorithm. Specifically, each task is repeated 10 times in each mode by an operator, and the average times are recorded and compared in Figure 13a,b.

Figure 13. Comparison of the operating time in the experiment. (a) Operating time for different tasks and operators. (b) Visual servo time reduction percentage with the shared-control mode.

Figure 13a shows that the shared-control strategy generally reduces the averaging operation time for both operators. The time saving is moderate for the skilled operator, because the pure remote-control performance of the skilled operator is closer to the automatic system than the unskilled operator. The time saving for the unskilled operator is more significant, because the shared-control strategy effectively corrects the inappropriate commands given by the operator, and provides greater help on the precise pose adjustment before grasping. The time-saving effect for task two is also more significant for both of the operators, because the shared control is more helpful when the manual operation complexity increases.

Figure 13b compares the time proportion of the visual servo process in the grasping experiment, which is the total time needed to stop in front of each object before grasping. This process is regarded as the most challenging process for an unskilled operator. The time-saving effect has a similar trend to Figure 13a, but is more significant for the visual servo process. Owing to the help of the shared controller, the time needed for the unskilled operator in the visual servo process of task two is drastically reduced by nearly 40%. Besides the time-saving effect, both of the operators also report a much more easy and relaxed operating feeling with the shared-control mode. In conclusion, the proposed shared-control method significantly improves the efficiency of conducting the grasping tasks.

5. Conclusions

A visual-aided shared-control method is proposed and validated in this paper to improve the underwater grasping efficiency of the sAUV. The control algorithm utilizes the variable AF to adjust the authority weights of the human command and the automatic controller, and takes full advantage of human intelligence for decision-making and the automatic system for precise control. Compared to pure-remote operation, the proposed shared controller significantly improves the efficiency of underwater grasping tasks and reduces the operation skill required for the operators.

The proposed method provides a valuable reference for controlling various kinds of underwater vehicles. Future work will proceed with algorithm improvements to consider practical issues in underwater environments, including measurement noise, water turbidity, communication delays and other environmental disturbances. Experiments will also be conducted with more complex tasks. The proposed method is believed to have great potential in real applications of underwater exploration and manipulation.