Tide-Induced Upwelling and Its Three-Dimensional Balance of the Vertical Component of Vorticity in the Wider Area of the Bohai Strait
Abstract
1. Introduction
2. Data and Methods
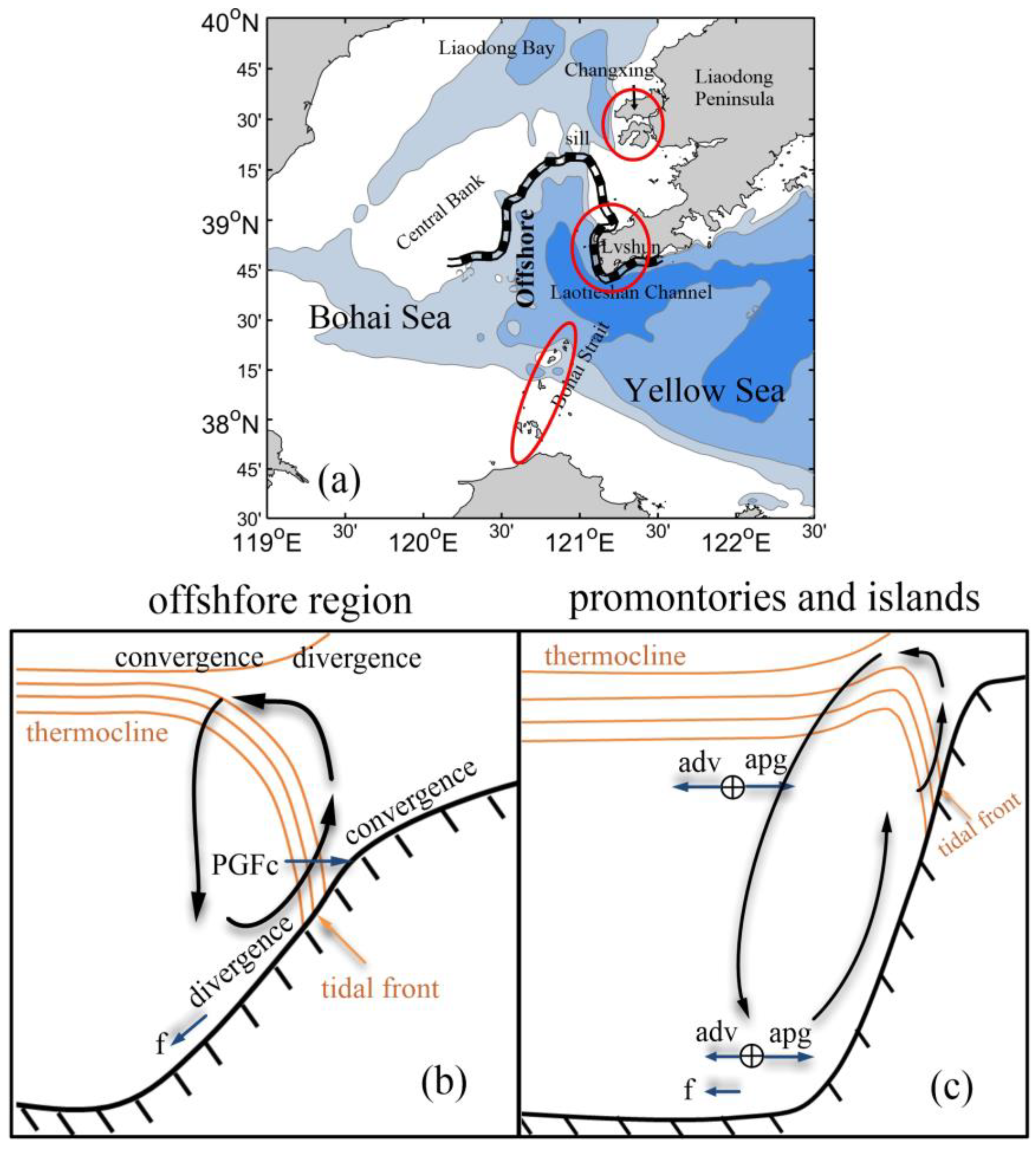
2.1. Study Area
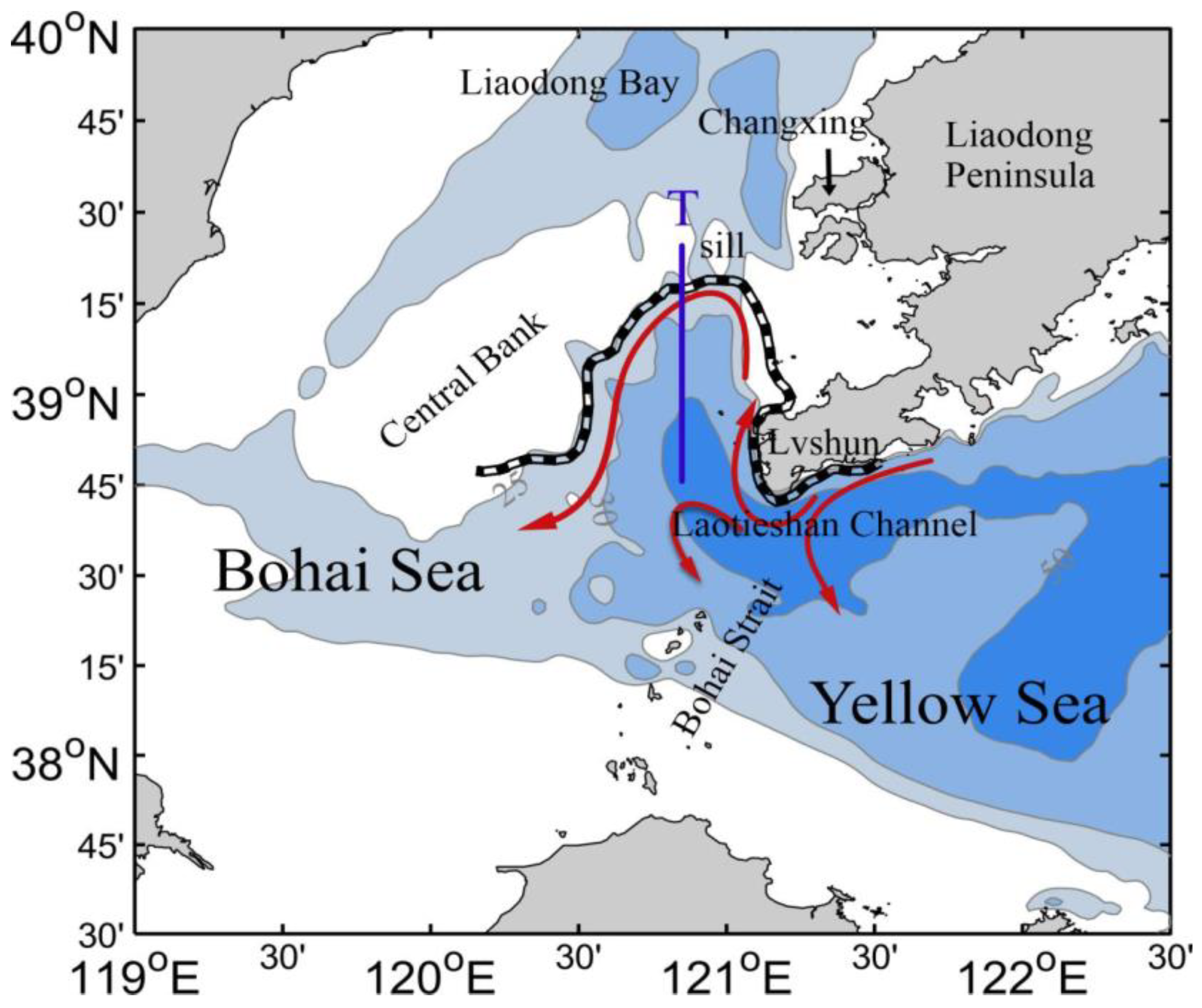
2.2. Ocean Model
2.2.1. Model Configurations
2.2.2. Model Experiments
2.3. MODIS Data
2.4. 3D Balance of the Vertical Component of Vorticity
3. Results
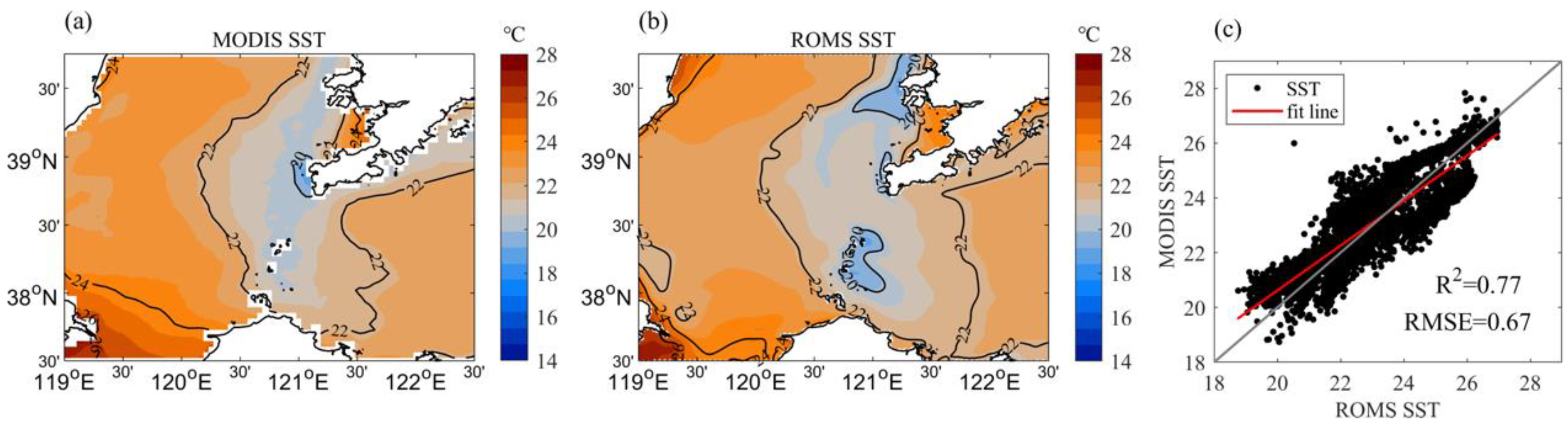
3.1. Model Validation
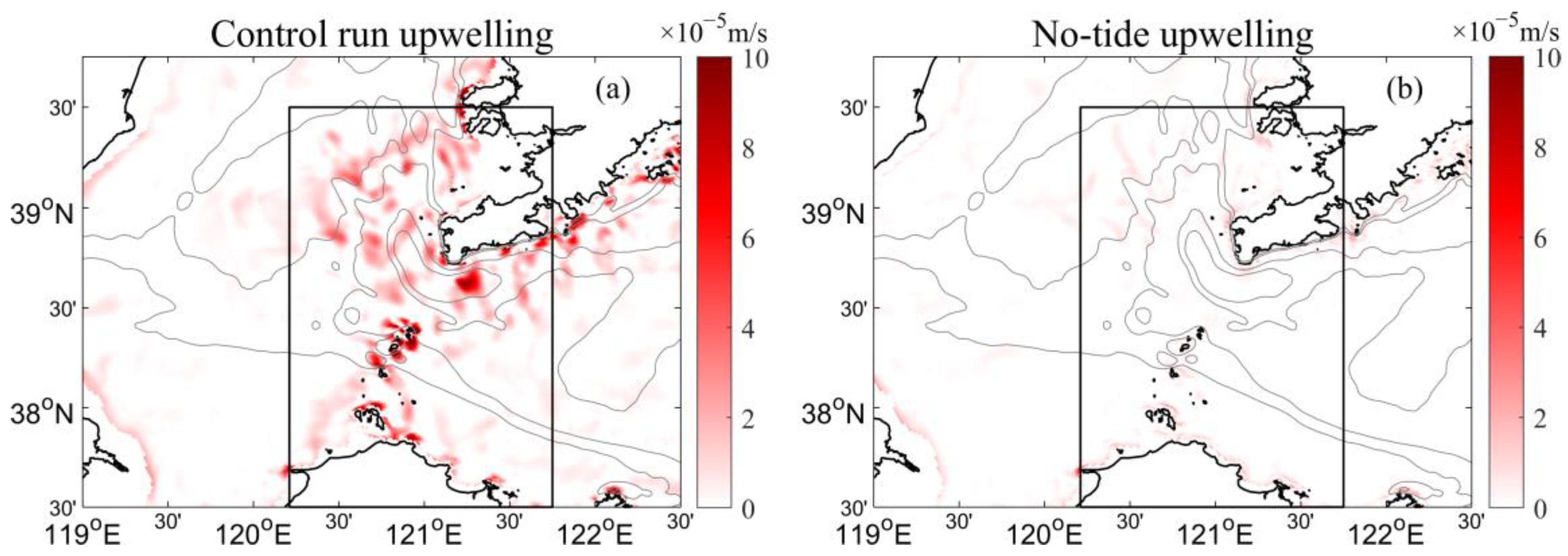
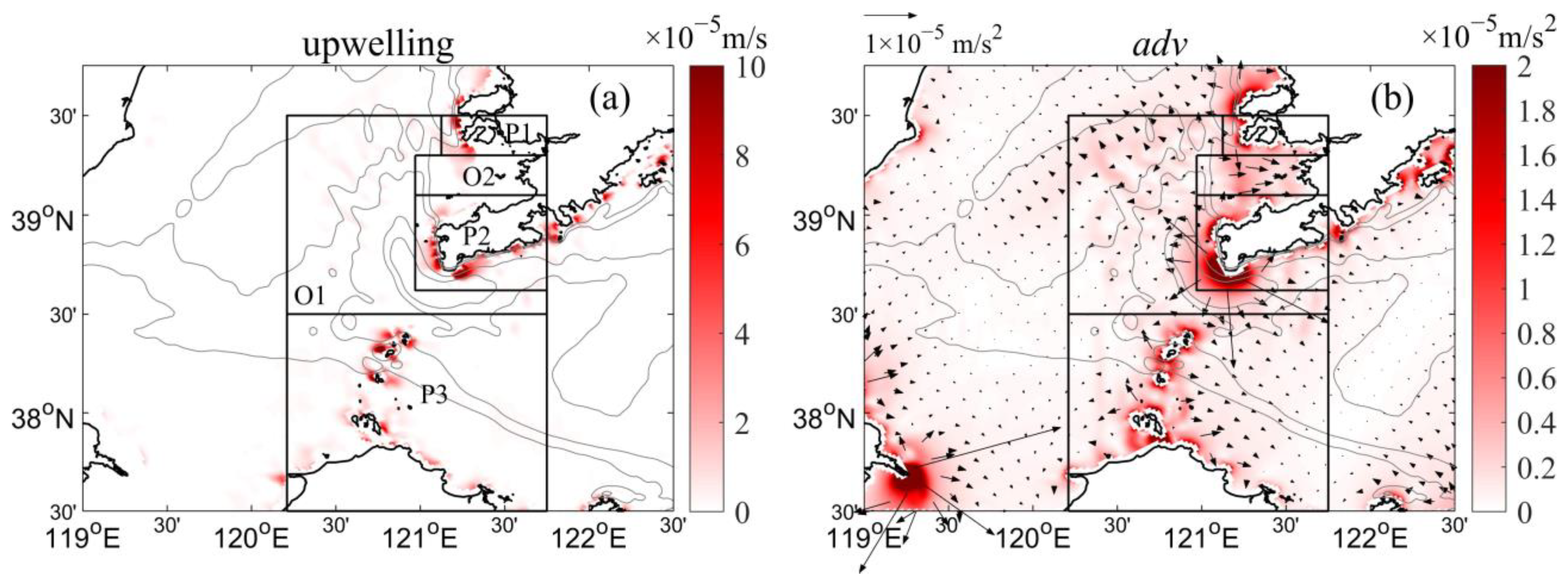
3.2. Tide-Induced Upwelling Near the Bohai Strait
3.3. Mechanism of the Tidal Effect on the Upwelling
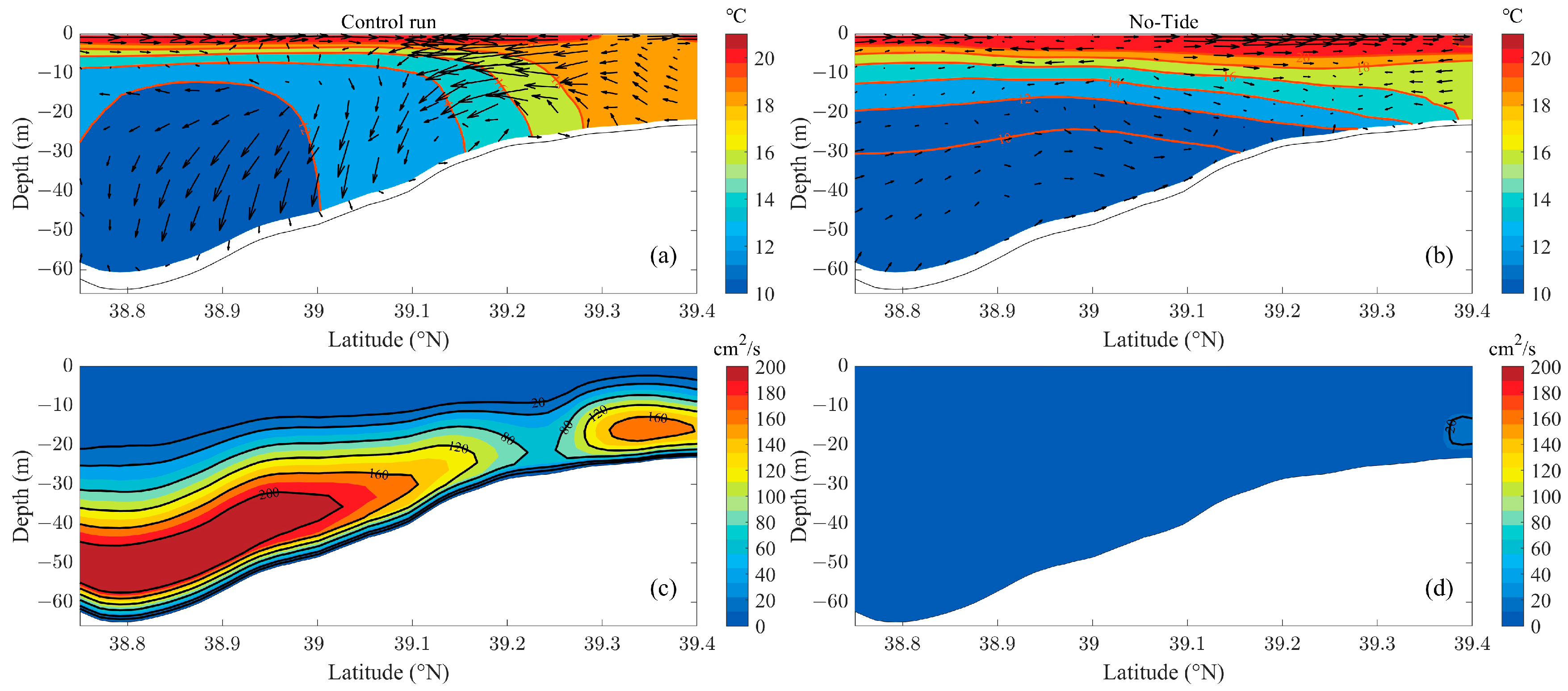
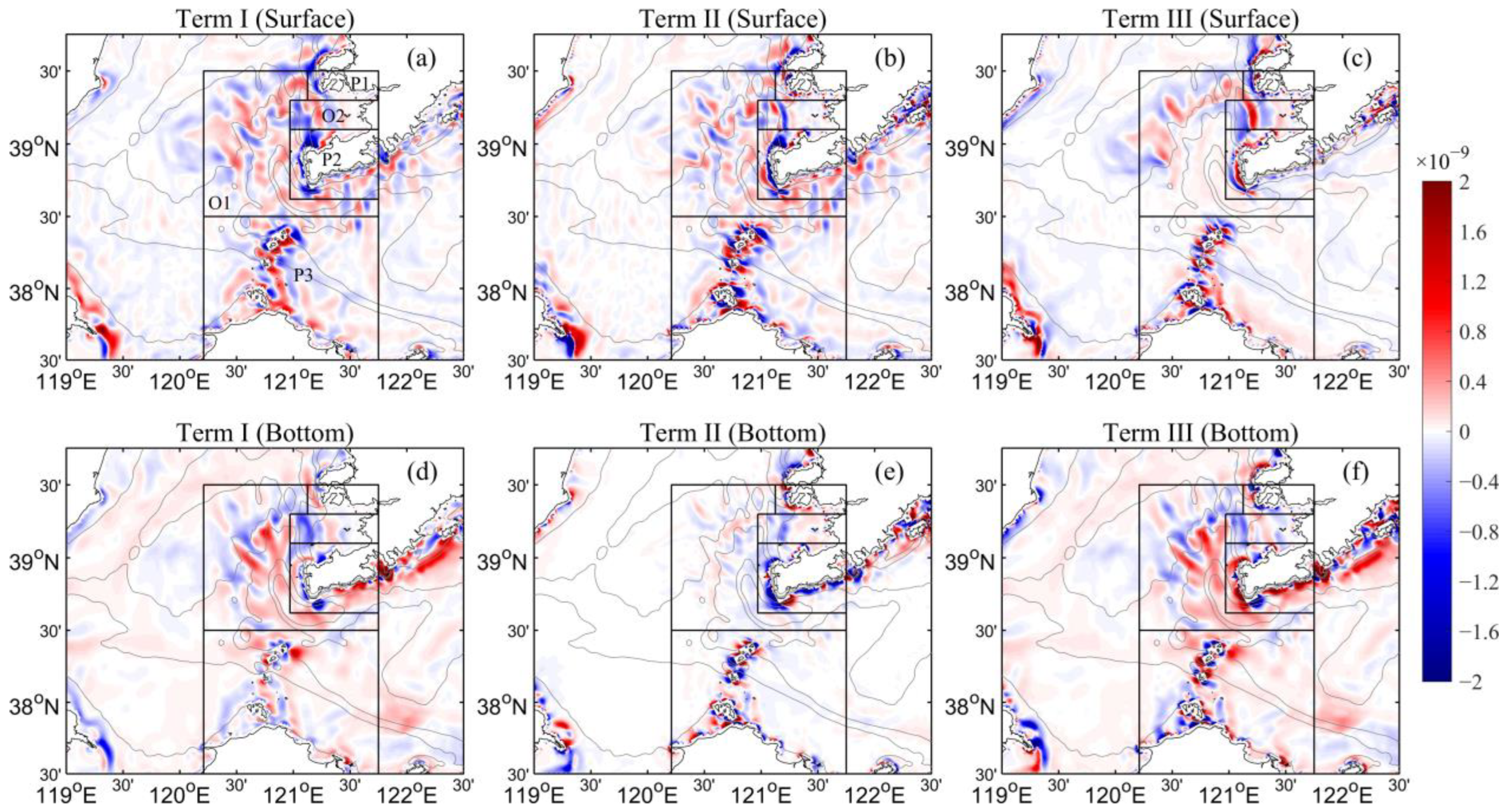
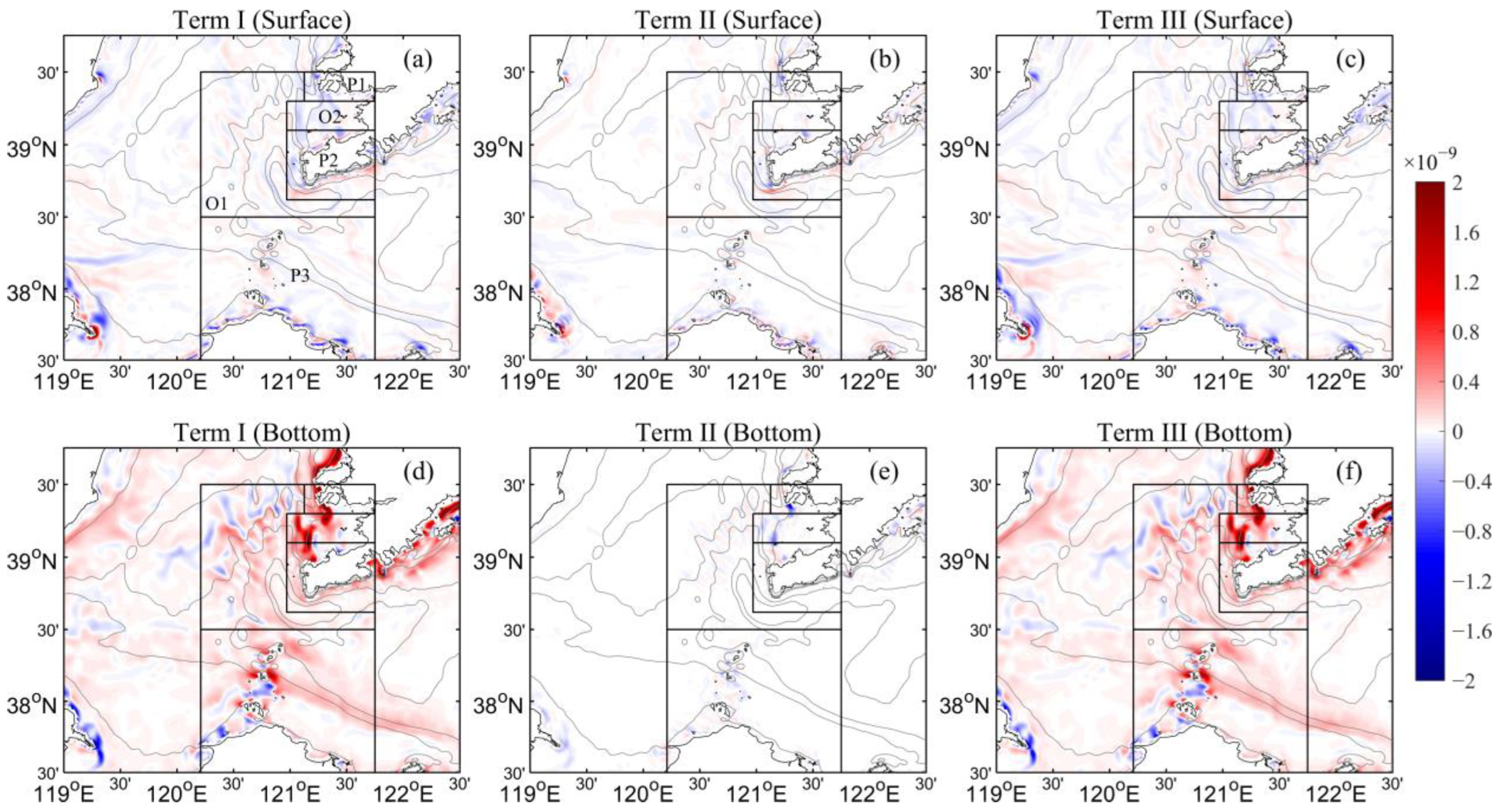
3.3.1. Upwelling and Balance of the Vertical Component of Vorticity off Promontories and Small Islands
3.3.2. Upwelling and Balance of the Vertical Component of Vorticity in the Offshore Region
4. Discussion
4.1. Tidal Nonlinear Effect
4.2. Upwelling Induced by Barotropic and Baroclinic Tides
4.3. Mechanism of the Tide-Induced Upwelling off Promontories
4.4. Model Implications and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Joint, I.; Rees, A.P.; Woodward, E.M.S. Primary Production and Nutrient Assimilation in the Iberian Upwelling in August 1998. Prog. Oceanogr. 2001, 51, 303–320. [Google Scholar] [CrossRef]
- Escribano, R.; Schneider, W. The Structure and Functioning of the Coastal Upwelling System off Central/Southern Chile. Prog. Oceanogr. 2007, 75, 343–347. [Google Scholar] [CrossRef]
- Song, X.; Lai, Z.; Ji, R.; Chen, C.; Zhang, J.; Huang, L.; Yin, J.; Wang, Y.; Lian, S.; Zhu, X. Summertime Primary Production in Northwest South China Sea: Interaction of Coastal Eddy, Upwelling and Biological Processes. Cont. Shelf Res. 2012, 48, 110–121. [Google Scholar] [CrossRef]
- Hu, J.; Wang, X.H. Progress On Upwelling Studies in the China Seas. Rev. Geophys. 2016, 54, 653–673. [Google Scholar] [CrossRef]
- Fréon, P.; Barange, M.; Arístegui, J. Eastern Boundary Upwelling Ecosystems: Integrative and Comparative Approaches. Prog. Oceanogr. 2009, 83, 1–14. [Google Scholar] [CrossRef]
- Benazzouz, A.; Mordane, S.; Orbi, A.; Chagdali, M.; Hilmi, K.; Atillah, A.; Lluís Pelegrí, J.; Hervé, D. An Improved Coastal Upwelling Index From Sea Surface Temperature Using Satellite-Based Approach—The Case of the Canary Current Upwelling System. Cont. Shelf Res. 2014, 81, 38–54. [Google Scholar] [CrossRef]
- McGregor, H.V.; Dima, M.; Fischer, H.W.; Mulitza, S. Rapid 20th-Century Increase in Coastal Upwelling off Northwest Africa. Science 2007, 315, 637–639. [Google Scholar] [CrossRef]
- Xie, S.; Xie, Q.; Wang, D.; Liu, W.T. Summer Upwelling in the South China Sea and its Role in Regional Climate Variations. J. Geophys. Res. Oceans 2003, 108, 3261. [Google Scholar] [CrossRef]
- Dippner, J.W.; Nguyen, K.V.; Hein, H.; Ohde, T.; Loick, N. Monsoon-Induced Upwelling Off the Vietnamese Coast. Ocean Dynam. 2007, 57, 46–62. [Google Scholar] [CrossRef]
- Wang, D.; Wang, H.; Li, M.; Liu, G.; Wu, X. Role of Ekman Transport Versus Ekman Pumping in Driving Summer Upwelling in the South China Sea. J. Ocean Univ. China 2013, 12, 355–365. [Google Scholar] [CrossRef]
- Gan, J.; San Ho, H.; Liang, L. Dynamics of Intensified Downwelling Circulation over a Widened Shelf in the Northeastern South China Sea. J. Phys. Oceanogr. 2013, 43, 80–94. [Google Scholar] [CrossRef]
- Benthuysen, J.; Thomas, L.N.; Lentz, S.J. Rapid Generation of Upwelling at a Shelf Break Caused by Buoyancy Shutdown. J. Phys. Oceanogr. 2015, 45, 294–312. [Google Scholar] [CrossRef]
- Liu, Z.; Gan, J. Modeling Study of Variable Upwelling Circulation in the East China Sea: Response to a Coastal Promontory. J. Phys. Oceanogr. 2014, 44, 1078–1094. [Google Scholar] [CrossRef]
- Liu, Z.; Gan, J. Upwelling Induced by the Frictional Stress Curl and Vertical Squeezing of the Vortex Tube over a Submerged Valley in the East China Sea. J. Geophys. Res. Oceans 2015, 120, 2571–2587. [Google Scholar] [CrossRef]
- Lü, X.; Qiao, F.; Xia, C.; Zhu, J.; Yuan, Y. Upwelling Off Yangtze River Estuary in Summer. J. Geophys. Res. 2006, 111, C11S08. [Google Scholar] [CrossRef]
- Lü, X.; Qiao, F.; Xia, C.; Wang, G.; Yuan, Y. Upwelling and Surface Cold Patches in the Yellow Sea in Summer: Effects of Tidal Mixing on the Vertical Circulation. Cont. Shelf Res. 2010, 30, 620–632. [Google Scholar] [CrossRef]
- Gu, Y.; Pan, J.; Lin, H. Remote Sensing Observation and Numerical Modeling of an Upwelling Jet in Guangdong Coastal Water. J. Geophys. Res. Oceans 2012, 117, C08019. [Google Scholar] [CrossRef]
- Gan, J.; Wang, J.; Liang, L.; Li, L.; Guo, X. A Modeling Study of the Formation, Maintenance, and Relaxation of Upwelling Circulation on the Northeastern South China Sea Shelf. Deep Sea Res. Part II Top. Stud. Oceanogr. 2015, 117, 41–52. [Google Scholar] [CrossRef]
- Simpson, J.H.; Brown, J.; Matthews, J.; Allen, G. Tidal Straining, Density Currents, and Stirring in the Control of Estuarine Stratification. Estuaries 1990, 13, 125–132. [Google Scholar] [CrossRef]
- Visser, A.W.; Souza, A.J.; Hessner, K.; Simpson, J.H. The Effect of Stratification on Tidal Current Profiles in a Region of Freshwater Influence. Oceanol. Acta 1994, 17, 369–381. [Google Scholar]
- Simpson, J.H.; Souza, A.J. Semidiurnal Switching of Stratification in the Region of Freshwater Influence of the Rhine. J. Geophys. Res. Oceans 1995, 100, 7037–7044. [Google Scholar] [CrossRef]
- de Boer, G.J.; Pietrzak, J.D.; Winterwerp, J.C. SST Observations of Upwelling Induced by Tidal Straining in the Rhine ROFI. Cont. Shelf Res. 2009, 29, 263–277. [Google Scholar] [CrossRef]
- Lü, X.; Qiao, F.; Wang, G.; Xia, C.; Yuan, Y. Upwelling Off the West Coast of Hainan Island in Summer: Its Detection and Mechanisms. Geophys. Res. Lett. 2008, 35, L02604. [Google Scholar] [CrossRef]
- Li, Y.; Curchitser, E.N.; Wang, J.; Peng, S. Tidal Effects on the Surface Water Cooling Northeast of Hainan Island, South China Sea. J. Geophys. Res. Oceans 2020, 125, e2019JC016016. [Google Scholar] [CrossRef]
- Jing, Z.; Qi, Y.; Du, Y. Persistent Upwelling and Front over the Sulu Ridge and their Variations. J. Geophys. Res. Oceans 2012, 117, C11011. [Google Scholar] [CrossRef]
- Gregory Lough, R.; Manning, J.P. Tidal-Front Entrainment and Retention of Fish Larvae on the Southern Flank of Georges Bank. Deep Sea Res. Part II Top. Stud. Oceanogr. 2001, 48, 631–644. [Google Scholar] [CrossRef]
- Simpson, J.H.; Hunter, J.R. Fronts in the Irish Sea. Nature 1974, 250, 404–406. [Google Scholar] [CrossRef]
- Garrett, C.J.R.; Loucks, H. Upwelling along the Yarmouth Shore of Nova Scotia. J. Fish. Res. Board Can. 1976, 33, 116–117. [Google Scholar] [CrossRef]
- Xia, Z.; Guo, B. Cold Water and Upwelling around the Tips of Shandong Peninsula and Liaodong Peninsula. J. Oceanogr. Huanghai Bohai Seas 1983, 1, 13–19. [Google Scholar]
- Guo, B.; Xia, Z. An Analytical Model of Upwelling Induced by Tidal Current around the Peninsula. Acta Oceanol. Sin. 1986, 8, 272–282. [Google Scholar]
- Lee, H.J.; Chao, S.Y.; Fan, K.L.; Kuo, T.Y. Tide-Induced Eddies and Upwelling in a Semi-Enclosed Basin: Nan Wan. Estuar. Coast. Shelf Sci. 1999, 49, 775–787. [Google Scholar] [CrossRef][Green Version]
- Hsu, P.; Lee, H.; Zheng, Q.; Lai, J.; Su, F.; Ho, C. Tide-Induced Periodic Sea Surface Temperature Drops in the Coral Reef Area of Nanwan Bay, Southern Taiwan. J. Geophys. Res. Oceans 2020, 125, e2019JC015226. [Google Scholar] [CrossRef]
- Liu, D.; Lv, T.; Lin, L.; Wei, Q. Review of Fronts and its Ecological Effects in the Shelf Sea of China. Adv. Mar. Sci. 2022, 40, 725–741. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, F.; Meng, Q.; Zeng, D.; Yan, T.; Zhang, W. How Do Topography and Thermal Front Influence the Water Transport from the Northern Laotieshan Channel to the Bohai Sea Interior in Summer? Deep Sea Res. Part II Top. Stud. Oceanogr. 2023, 208, 105261. [Google Scholar] [CrossRef]
- Zhang, R.; Song, J.; Polonsky, A.B.; Wang, L.; Guo, J.; Fu, Y.; Zhao, Q.; Zhang, R. The Spring–Neap Variability and Mechanisms of Long-Term Variations in the Upwelling at the Tip of Liaodong Peninsula, China. Reg. Stud. Mar. Sci. 2022, 55, 102574. [Google Scholar] [CrossRef]
- Meng, X.; Zhang, S. The Effect of Cold SST on Summer Atmosphere Boundary Layer and Sea Fog over the Yellow Sea. Period. Ocean. Univ. China 2012, 42, 16–23. [Google Scholar]
- Chen, R.; Wu, X.; Liu, B.; Wang, Y. Spatiotemporal Distribution of Fishing Grounds in the Bohai Sea and its Adjacent Waters Based on AIS. Mar. Fish. 2022, 44, 780–789. [Google Scholar] [CrossRef]
- Zang, K.; Zhang, G.; Zhao, H.; Xu, X.; Zheng, N.; Wang, J.; Zhang, G. Multiple Factors Dominate the Distribution of Methane and its Sea-To-Air Flux in the Bohai Sea in Summer and Autumn of 2014. Mar. Pollut. Bull. 2020, 154, 111049. [Google Scholar] [CrossRef] [PubMed]
- Yan, T. Features and Classification of Coastal Upwellings off China. Mar. Sci. Bull. 1991, 10, 16–26. [Google Scholar]
- Liu, S.; Zhao, Q.; Wang, Y.; Zhang, Y. Long-Term Variation of Upwelling at the Tip of Liaodong Peninsula: Features and Factors. Oceanol. Limnol. Sin. 2020, 51, 31–39. [Google Scholar] [CrossRef]
- Liu, X.; Wang, D.; Su, J.; Chen, D.; Lian, T.; Dong, C.; Liu, T. On the Vorticity Balance over Steep Slopes: Kuroshio Intrusions Northeast of Taiwan. J. Phys. Oceanogr. 2020, 50, 2089–2104. [Google Scholar] [CrossRef]
- Moon, J.; Hirose, N.; Yoon, J. Comparison of Wind and Tidal Contributions to Seasonal Circulation of the Yellow Sea. J. Geophys. Res. 2009, 114, C08016. [Google Scholar] [CrossRef]
- Liu, Z.; Tang, Y.; Wang, K.; Xia, D.; Berne, S.; Marsset, T.; Bourillet, J.F. Tidal Dynamic Geomorphic System in the East Part of the Bohai Sea. J. Oceanogr. Huanghai Bohai Seas 1996, 14, 7–21. [Google Scholar]
- Bi, C.; Bao, X.; Ding, Y.; Zhang, C.; Wang, Y.; Shen, B.; Wan, K. Observed Characteristics of Tidal Currents and Mean Flow in the Northern Yellow Sea. J. Oceanol. Limnol. 2019, 37, 461–473. [Google Scholar] [CrossRef]
- Liu, H.; Pang, C.; Yang, D.; Liu, Z. Seasonal Variation in Material Exchange through the Bohai Strait. Cont. Shelf Res. 2021, 231, 104599. [Google Scholar] [CrossRef]
- Li, Y.; Wolanski, E.; Dai, Z.; Lambrechts, J.; Tang, C.; Zhang, H. Trapping of Plastics in Semi-Enclosed Seas: Insights from the Bohai Sea, China. Mar. Pollut. Bull. 2018, 137, 509–517. [Google Scholar] [CrossRef] [PubMed]
- Bowers, D.G.; Simpson, J.H. Mean Position of Tidal Fronts in European-shelf Seas. Cont. Shelf Res. 1987, 7, 35–44. [Google Scholar] [CrossRef]
- Liu, H.; Pan, W. Numerical Simulation of the Seasonal Variations of the Stratification and Tidal Front in the Bohai Sea. Adv. Water Sci. 2007, 18, 398–403. [Google Scholar]
- Haidvogel, D.B.; Arango, H.G.; Hedstrom, K.; Beckmann, A.; Malanotte-Rizzoli, P.; Shchepetkin, A.F. Model Evaluation Experiments in the North Atlantic Basin: Simulations in Nonlinear Terrain-following Coordinates. Dynam. Atmos. Oceans 2000, 32, 239–281. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient Inverse Modeling of Barotropic Ocean Tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Da Silva, A.M.; Young, C.C.; Levilus, S. Atlas of Surface Marine Data 1994, Vol. I: Algorithms and Procedures; NOAA Atlas NESDIS 6; NOAA: Washington, DC, USA, 1994.
- Warner, J.; Sherwood, C.; Arango, H.; Signell, R. Performance of Four Turbulence Closure Methods Implemented Using a Generic Length Scale Method. Ocean Model. 2005, 8, 81–113. [Google Scholar] [CrossRef]
- Sun, F.; Yu, F.; Si, G.; Wang, J.; Xu, A.; Pan, J.; Tang, Y. Characteristics and Influencing Factors of Frontal Upwelling in the Yellow Sea in Summer. Acta Oceanol. Sin. 2022, 41, 84–96. [Google Scholar] [CrossRef]
- Lü, X.; Qiao, F.; Xia, C.; Yuan, Y. Tidally Induced Upwelling off Yangtze River Estuary and in Zhejiang Coastal Waters in Summer. Sci. China Ser. D-Earth Sci. 2007, 50, 462–473. [Google Scholar] [CrossRef]
- Lin, X.; Xie, S.; Chen, X.; Xu, L. A Well-Mixed Warm Water Column in the Central Bohai Sea in Summer: Effects of Tidal and Surface Wave Mixing. J. Geophys. Res. 2006, 111, C11017. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Liu, X.; Zhou, F.; Chen, X.; Ye, R.; Chen, D. Tide-Induced Upwelling and Its Three-Dimensional Balance of the Vertical Component of Vorticity in the Wider Area of the Bohai Strait. J. Mar. Sci. Eng. 2023, 11, 1839. https://doi.org/10.3390/jmse11091839
Xu Y, Liu X, Zhou F, Chen X, Ye R, Chen D. Tide-Induced Upwelling and Its Three-Dimensional Balance of the Vertical Component of Vorticity in the Wider Area of the Bohai Strait. Journal of Marine Science and Engineering. 2023; 11(9):1839. https://doi.org/10.3390/jmse11091839
Chicago/Turabian StyleXu, Yinfeng, Xiaohui Liu, Feng Zhou, Xueen Chen, Ruijie Ye, and Dake Chen. 2023. "Tide-Induced Upwelling and Its Three-Dimensional Balance of the Vertical Component of Vorticity in the Wider Area of the Bohai Strait" Journal of Marine Science and Engineering 11, no. 9: 1839. https://doi.org/10.3390/jmse11091839
APA StyleXu, Y., Liu, X., Zhou, F., Chen, X., Ye, R., & Chen, D. (2023). Tide-Induced Upwelling and Its Three-Dimensional Balance of the Vertical Component of Vorticity in the Wider Area of the Bohai Strait. Journal of Marine Science and Engineering, 11(9), 1839. https://doi.org/10.3390/jmse11091839







