Global Path Planning for Autonomous Ship Navigation Considering the Practical Characteristics of the Port of Ulsan
Abstract
1. Introduction
1.1. Research Background
1.2. Contributions
- Global Route Planning for Autonomous Ships in Port Sea Areas: This study specifically focuses on global route planning in the Port of Ulsan sea area, Republic of Korea. We utilized public information on traffic lanes and anchorage areas [14], in conjunction with ENC data pertaining to coastlines and water depth, to model the navigable area for MASS. The improved A* algorithm, augmented with an additional cost function, is applied to differentiate between traffic lanes and anchorage areas. An additional cost function is integrated to facilitate right-side navigation in traffic lanes, and an algorithm suitable for smoothing is employed to create more realistic global path planning route.
- A New Approach to Managing and Finding Anchorage Areas: To manage unexpected port traffic congestion and berthing challenges, this study proposes modeling broad group anchorage areas into small and specific circular anchorages. This enables the automatic establishment of global path planning routes that include stopovers at anchorages.
- Path Planning Considering Ship Maneuverability: This study derives realistic paths that reflect the dynamic characteristics of a particular ship, specifically an autonomous testbed ship constructed by the KASS (Korea Autonomous Surface Ship) project [15], and the feasibility of the generated routes are validated through maneuvering simulations. The target ship applied in this study was simulated based on hydrodynamic coefficients of the autonomous testbed ship built by the KASS project. These simulations take into account the ship’s properties, engine speed, and steering, effectively integrating them into global route generation. This approach provides practical guidelines for the operation of autonomous ships within the Port of Ulsan by comparing the optimized routes of the improved A* algorithm, integrating ships’ dynamic properties into the route planning process.
2. Related Works
3. Materials and Methods
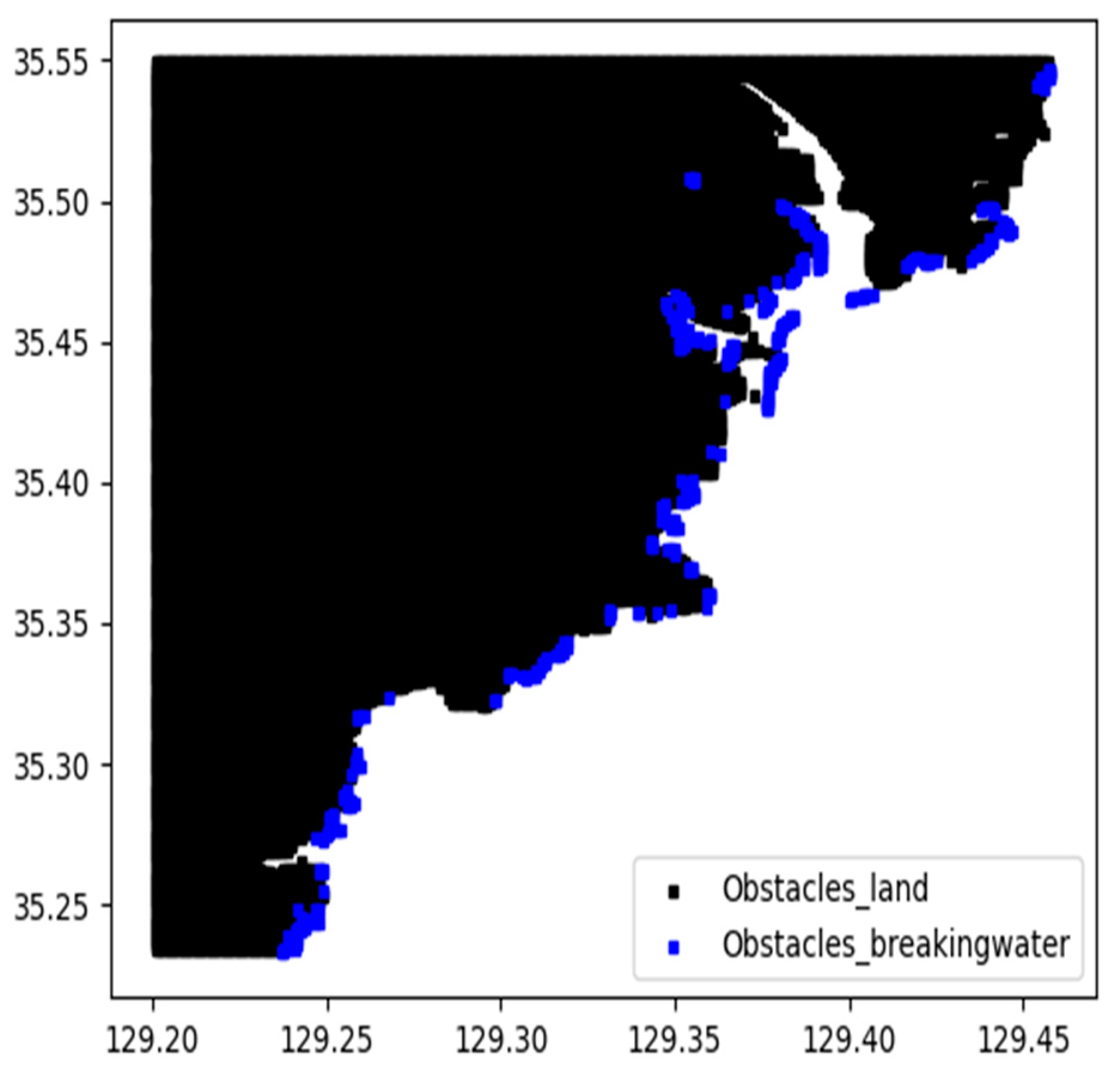
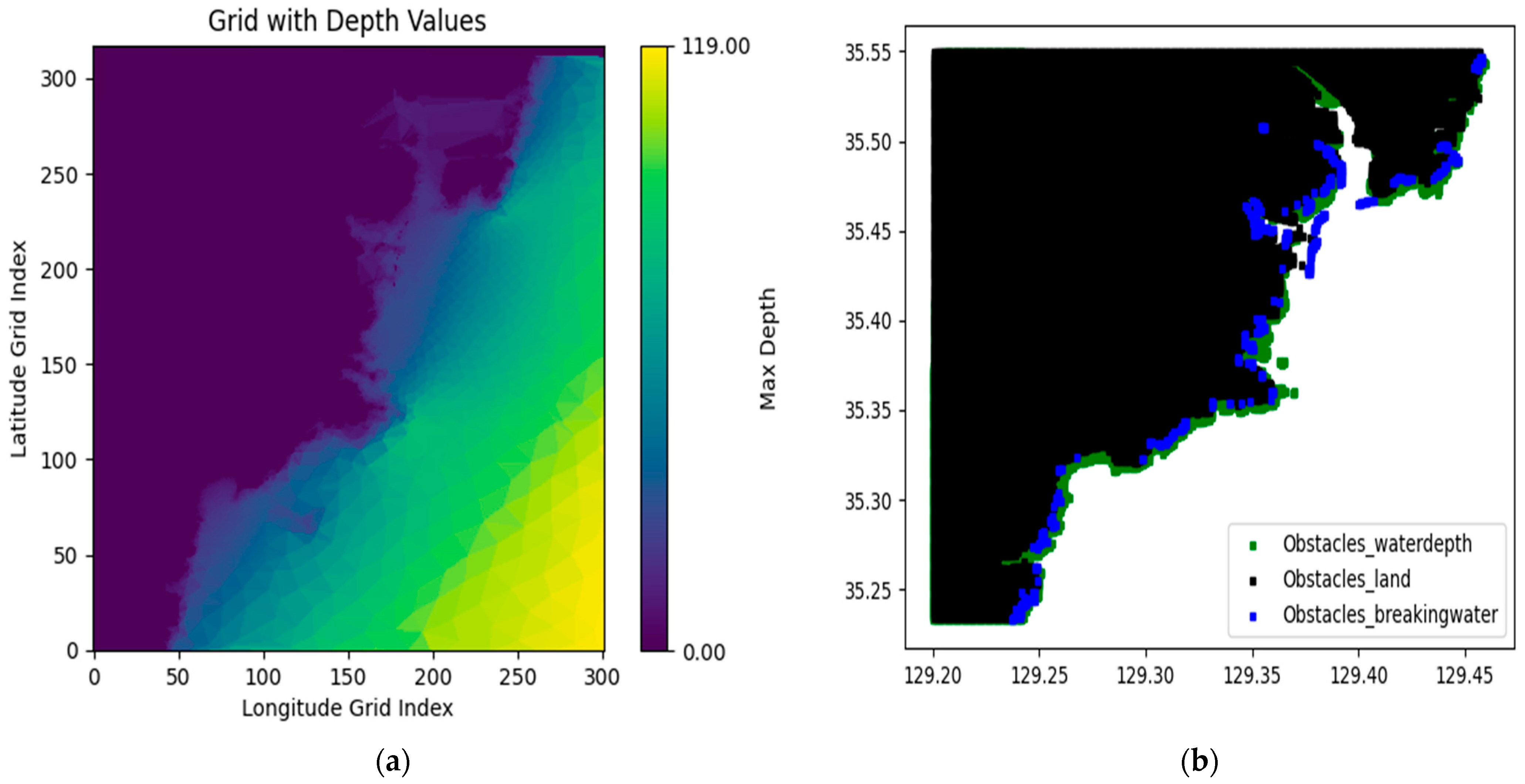
3.1. Grid Modeling of Port of Ulsan
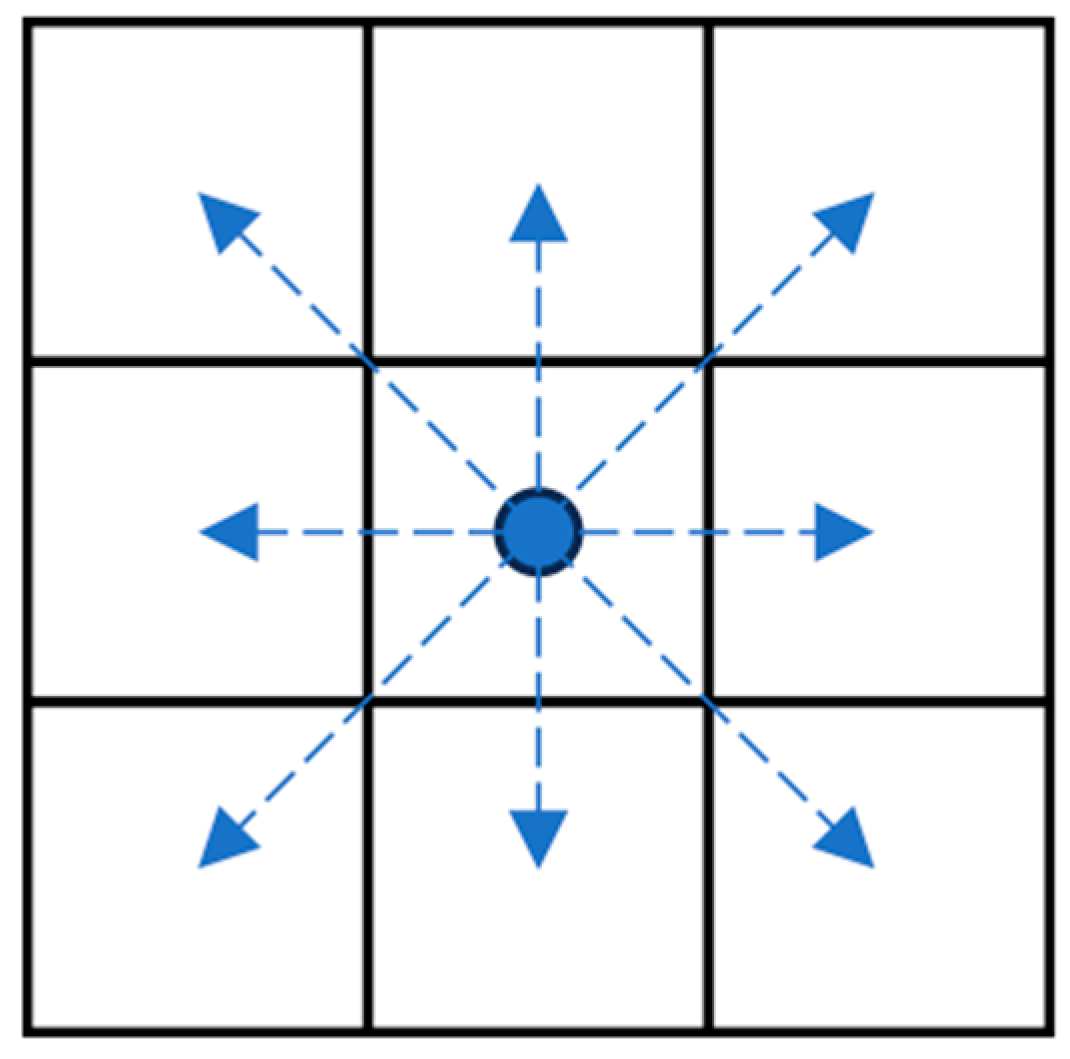
3.2. Global Path Planning Algorithms
3.3. Post-Processing Method for Route Optimization
3.4. Maneuvering Simulation
3.5. Analysis Procedure
4. Results and Discussion
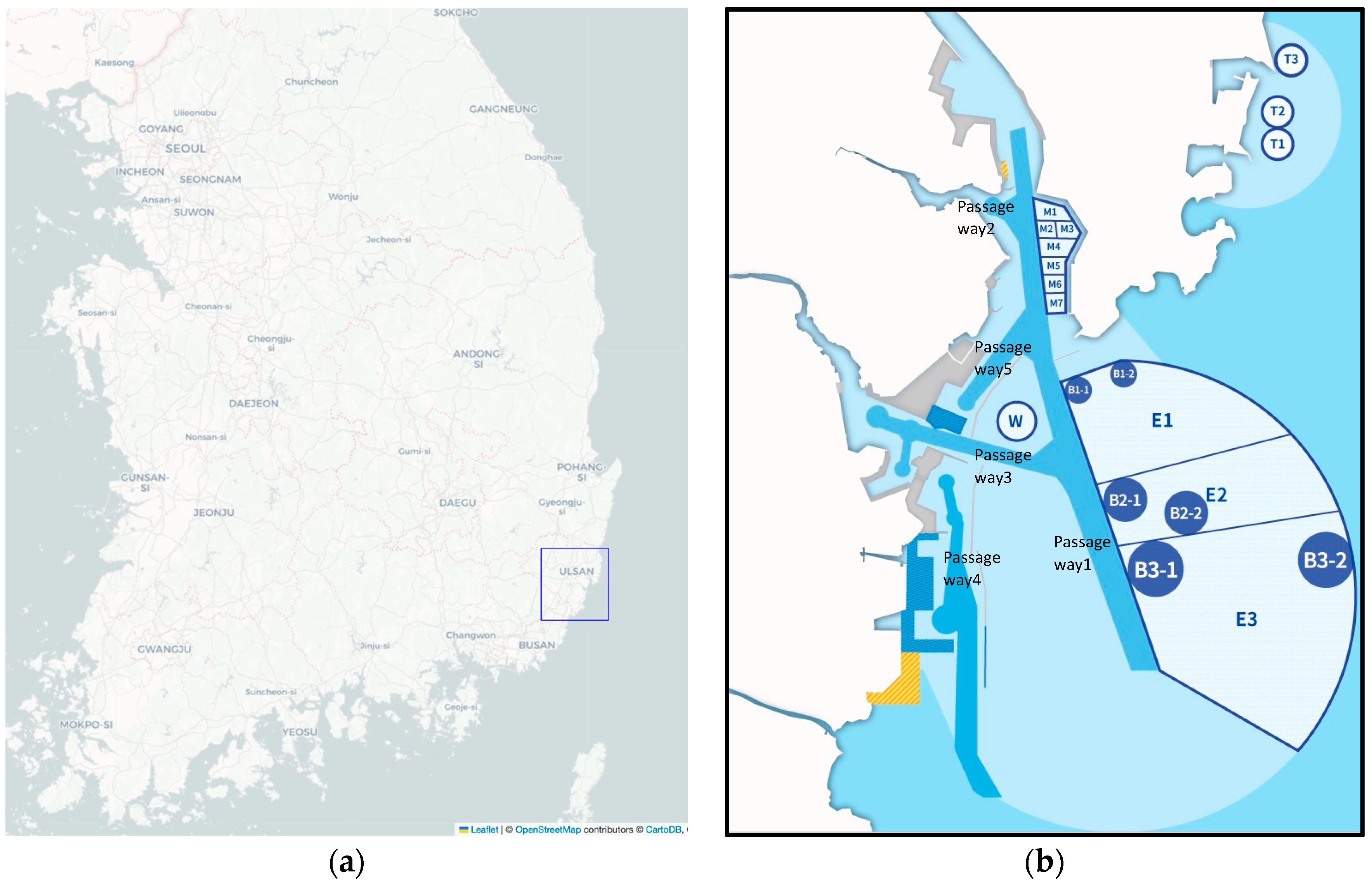
4.1. Port of Ulsan Sea Area Modeling
4.2. Modeling Characteristic Regions of the Port of Ulsan
4.3. Global Path Planning Results
4.3.1. Improved A* Algorithm
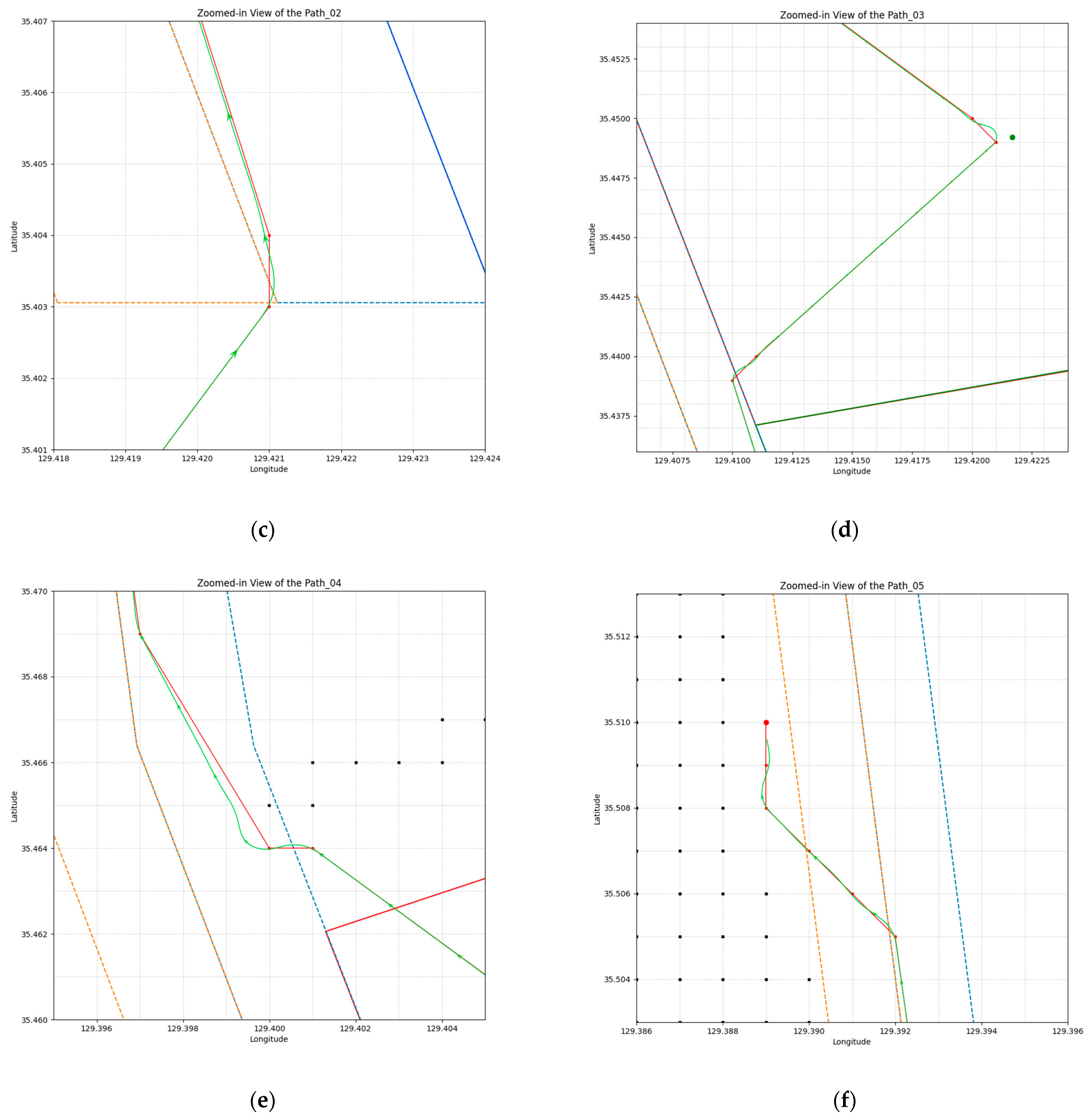
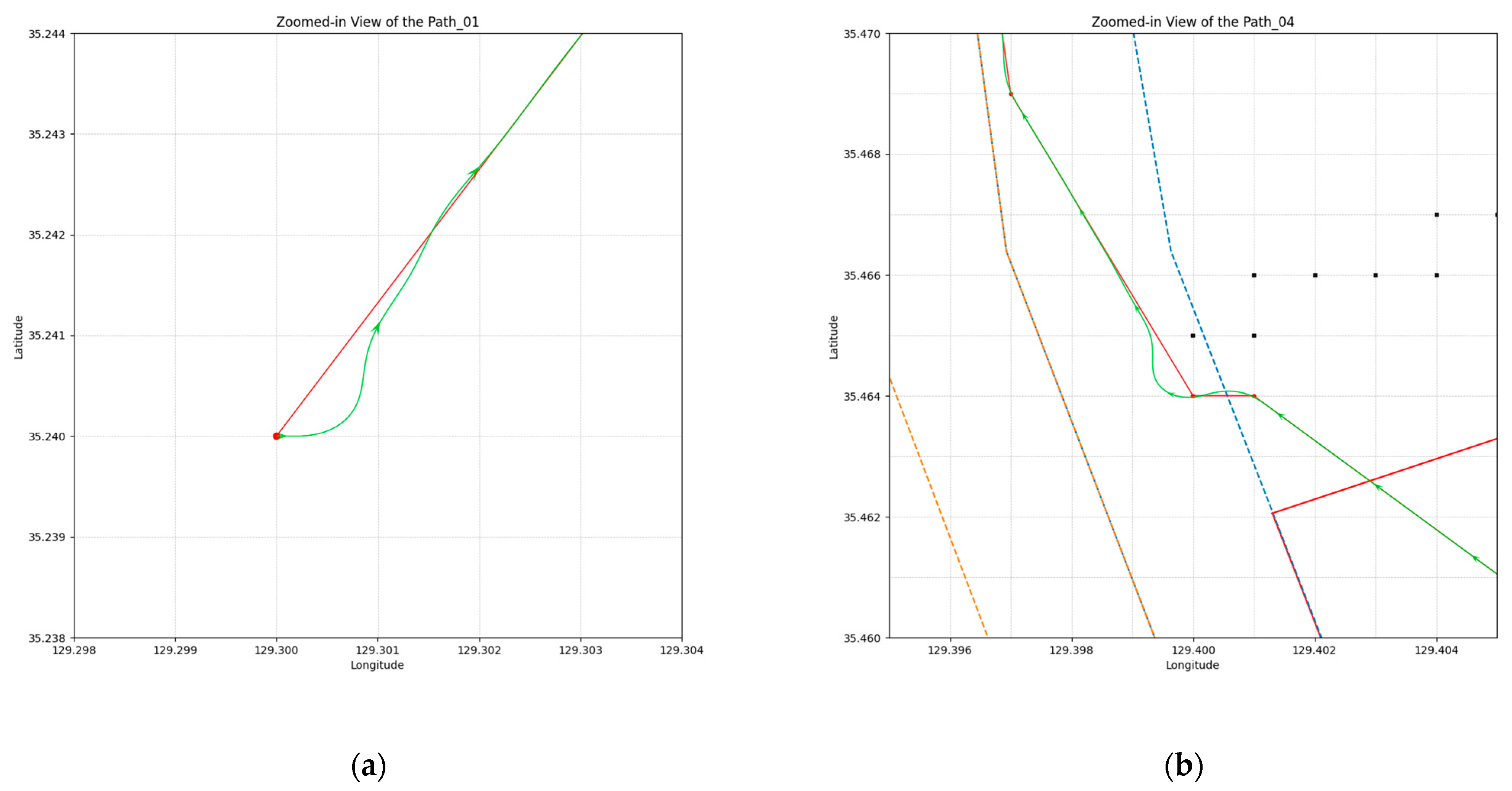
4.3.2. Smoothing the Global Path
4.4. Validation through Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| IMO | The International Maritime Organization |
| MASS | Maritime Autonomous Surface Ships |
| SOLAS | International Convention for the Safety of Life at Sea |
| COLREGs | Convention on the International Regulations for Preventing Collisions at Sea |
| VTS | Vessel Traffic Services |
| AIS | Automatic Identification System |
| KASS | Korea Autonomous Surface Ship |
| ENC | Electronic Navigational Chart |
| DTW | Dynamic Time Warping |
| DWT | Dead Weight Tonnage |
| MMG | Maneuvering Mathematical Group |
References
- Kim, S.; Yun, S.; You, Y. Eco-Friendly Speed Control Algorithm Development for Autonomous Vessel Route Planning. J. Mar. Sci. Eng. 2021, 9, 583. [Google Scholar] [CrossRef]
- Campbell, S.; Naeem, W.; Irwin, G.W. A Review on Improving the Autonomy of Unmanned Surface Vehicles through Intelligent Collision Avoidance Manoeuvres. Annu. Rev. Control 2012, 36, 267–283. [Google Scholar] [CrossRef]
- Perera, L.P.; Ferrari, V.; Santos, F.P.; Hinostroza, M.A.; Guedes Soares, C. Experimental Evaluations on Ship Autonomous Navigation and Collision Avoidance by Intelligent Guidance. IEEE J. Ocean. Eng. 2015, 40, 374–387. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y.; Yu, X.; Yuan, C. Unmanned Surface Vehicles: An Overview of Developments and Challenges. Annu. Rev. Control 2016, 41, 71–93. [Google Scholar] [CrossRef]
- Hu, L.; Naeem, W.; Rajabally, E.; Watson, G.; Mills, T.; Bhuiyan, Z.; Raeburn, C.; Salter, I.; Pekcan, C. A Multiobjective Optimization Approach for COLREGs-Compliant Path Planning of Autonomous Surface Vehicles Verified on Networked Bridge Simulators. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1167–1179. [Google Scholar] [CrossRef]
- EMSA Agency. Annual Overview of Marine Casualties and Incidents; European Maritime Safety Agency: Lisbon, Portugal, 2022. [Google Scholar]
- Kim, M.; Joung, T.H.; Jeong, B.; Park, H.S. Autonomous Shipping and Its Impact on Regulations, Technologies, and Industries. J. Int. Marit. Safety Environ. Aff. Shipp. 2020, 4, 17–25. [Google Scholar] [CrossRef]
- Guo, W.; Zhang, X.; Wang, J.; Feng, H.; Tengecha, N.A. Traffic Organization Service for Maritime Autonomous Surface Ships (MASS) with Different Degrees of Autonomy. J. Mar. Sci. Eng. 2022, 10, 1889. [Google Scholar] [CrossRef]
- Othman, A.; El Gazzar, S.; Knez, M. Investigating the Influences of Smart Port Practices and Technology Employment on Port Sustainable Performance: The Egypt Case. Sustainability 2022, 14, 14014. [Google Scholar] [CrossRef]
- Yoon, J.H.; Kim, D.H.; Yun, S.W.; Kim, H.J.; Kim, S. Enhancing Container Vessel Arrival Time Prediction through Past Voyage Route Modeling: A Case Study of Busan New Port. J. Mar. Sci. Eng. 2023, 11, 1234. [Google Scholar] [CrossRef]
- Di Ciaccio, F.; Menegazzo, P.; Troisi, S. Optimization of the maritime signaling system in the lagoon of venice. Sensors 2019, 19, 1216. [Google Scholar] [CrossRef]
- Ma, Y.; Chang, D.; Wang, H.; Tang, M. Optimal Shipping Path Algorithm Design for Coastal Port. Procedia Comput. Sci. 2019, 162, 375–382. [Google Scholar] [CrossRef]
- Yun, G.H.; Kim, B.Y.; Park, J.S.; Lee, Y.S. Enlargement of Harbour Limit and Anchorages According to the Development of New Ulsan Port. J. Navig. Port Res. 2010, 34, 487–492. [Google Scholar] [CrossRef]
- Ulsan Port Authority Website. Available online: https://upa.or.kr/contents.do?mId=001004005001000000 (accessed on 29 November 2023).
- Korea Autonomous Surface Ship Project. Available online: https://kassproject.org/en/main.php (accessed on 29 November 2023).
- Ozturk, U.; Cicek, K. Individual Collision Risk Assessment in Ship Navigation: A Systematic Literature Review. Ocean Eng. 2019, 180, 130–143. [Google Scholar] [CrossRef]
- Öztürk, Ü.; Akdağ, M.; Ayabakan, T. A Review of Path Planning Algorithms in Maritime Autonomous Surface Ships: Navigation Safety Perspective. Ocean Eng. 2022, 251, 111010. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A Note on Two Problems in Connexion with Graphs. In Edsger Wybe Dijkstra: His Life, Work, and Legacy; Association for Computing Machinery and Morgan & Claypool Publishers: New York, NY, USA, 2022; pp. 287–290. [Google Scholar]
- Liang, C.; Zhang, X.; Watanabe, Y.; Deng, Y. Autonomous Collision Avoidance of Unmanned Surface Vehicles Based on Improved A Star and Minimum Course Alteration Algorithms. Appl. Ocean Res. 2021, 113, 102755. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Tang, G.; Tang, C.; Claramunt, C.; Hu, X.; Zhou, P. Geometric A-Star Algorithm: An Improved A-Star Algorithm for AGV Path Planning in a Port Environment. IEEE Access 2021, 9, 59196–59210. [Google Scholar] [CrossRef]
- Casalino, G.; Turetta, A.; Simetti, E. A Three-Layered Architecture for Real Time Path Planning and Obstacle Avoidance for Surveillance USVs Operating in Harbour Fields. In Oceans 2009-Europe; IEEE: Piscataway, NJ, USA, 2009; pp. 1–8. [Google Scholar]
- Xie, L.; Xue, S.; Zhang, J.; Zhang, M.; Tian, W.; Haugen, S. A Path Planning Approach Based on Multi-Direction A* Algorithm for Ships Navigating Within Wind Farm Waters. Ocean Eng. 2019, 184, 311–322. [Google Scholar] [CrossRef]
- He, Q.; Hou, Z.; Zhu, X. A Novel Algorithm for Ship Route Planning Considering Motion Characteristics and ENC Vector Maps. J. Mar. Sci. Eng. 2023, 11, 1102. [Google Scholar] [CrossRef]
- Hu, S.; Tian, S.; Zhao, J.; Shen, R. Path Planning of an Unmanned Surface Vessel Based on the Improved A-Star and Dynamic Window Method. J. Mar. Sci. Eng. 2023, 11, 1060. [Google Scholar] [CrossRef]
- Zhang, L.; Mou, J.; Chen, P.; Li, M. Path Planning for Autonomous Ships: A Hybrid Approach Based on Improved APF and Modified VO Methods. J. Mar. Sci. Eng. 2021, 9, 761. [Google Scholar] [CrossRef]
- Xu, Y.; Guan, G.; Song, Q.; Jiang, C.; Wang, L. Heuristic and random search algorithm in optimization of route planning for Robot’s geomagnetic navigation. Comput. Commun. 2020, 154, 12–17. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, W.; Jiang, P.; Wan, C. An Improved Bald Eagle Search Algorithm for Global Path Planning of Unmanned Vessel in Complicated Waterways. J. Mar. Sci. Eng. 2023, 11, 118. [Google Scholar] [CrossRef]
- Braun, J.; Brito, T.; Lima, J.; Costa, P.; Costa, P.; Nakano, A. A Comparison of A* and RRT* Algorithms with Dynamic and Real Time Constraint Scenarios for Mobile Robots. In SIMULTECH 2019; Scitepress: Setúbal, Portugal, 2019; pp. 398–405. [Google Scholar]
- Son, J.; Kim, D.H.; Yun, S.W.; Kim, H.J.; Kim, S. The Development of Regional Vessel Traffic Congestion Forecasts Using Hybrid Data from an Automatic Identification System and a Port Management Information System. J. Mar. Sci. Eng. 2022, 10, 1956. [Google Scholar] [CrossRef]
- Dantas, J.L.; Theotokatos, G. A Framework for the Economic-Environmental Feasibility Assessment of Short-Sea Shipping Autonomous Vessels. Ocean Eng. 2023, 279, 114420. [Google Scholar] [CrossRef]
- Lee, S.W.; Jo, J.; Kim, S. Leveraging the 4th Industrial Revolution Technology for Sustainable Development of the Northern Sea Route (NSR)—The Case Study of Autonomous Vessel. Sustainability 2021, 13, 8211. [Google Scholar] [CrossRef]
- Zheng, J.; Sun, W.; Li, Y.; Hu, J. A Receding Horizon Navigation and Control System for Autonomous Merchant Ships: Reducing Fuel Costs and Carbon Emissions Under the Premise of Safety. J. Mar. Sci. Eng. 2023, 11, 127. [Google Scholar] [CrossRef]
- Hu, X.; Hu, K.; Tao, D.; Zhong, Y.; Han, Y. GIS-Data-Driven Efficient and Safe Path Planning for Autonomous Ships in Maritime Transportation. Electronics 2023, 12, 2206. [Google Scholar] [CrossRef]
- Zhen, R.; Gu, Q.; Shi, Z.; Suo, Y. An Improved A-Star Ship Path-Planning Algorithm Considering Current, Water Depth, and Traffic Separation Rules. J. Mar. Sci. Eng. 2023, 11, 1439. [Google Scholar] [CrossRef]
- Yasukawa, H.; Yoshimura, Y. Introduction of MMG Standard Method for Ship Maneuvering Predictions. J. Mar. Sci. Technol. 2015, 20, 37–52. [Google Scholar] [CrossRef]
- Yasukawa, H.; Zaky, M.; Yonemasu, I.; Miyake, R. Effect of engine output on maneuverability of a VLCC in still water and adverse weather conditions. J. Mar. Sci. Technol. 2017, 22, 574–586. [Google Scholar] [CrossRef]
- Vessel Traffic Service Center Website. Available online: https://www.kcg.go.kr/kcg/si/sub/info.do?page=2836&num=13&mi=2836 (accessed on 29 November 2023).
- Luo, Y.; Qin, Q.; Hu, Z.; Zhang, Y. Path Planning for Unmanned Delivery Robots Based on EWB-GWO Algorithm. Sensors 2023, 23, 1867. [Google Scholar] [CrossRef] [PubMed]
- Bresenham, J.E. Algorithm for Computer Control of a Digital Plotter. In Seminal Graphics: Pioneering Efforts That Shaped the Field; Association for Computing Machinery and Morgan & Claypool Publishers: New York, NY, USA, 1998; pp. 1–6. [Google Scholar]
- Myers, C.S.; Rabiner, L.R. A comparative study of several dynamic time-warping algorithms for connected-word recognition. Bell Syst. Tech. J. 1981, 60, 1389–1409. [Google Scholar] [CrossRef]
- Choi, W.; Cho, J.; Lee, S.; Jung, Y. Fast constrained dynamic time warping for similarity measure of time series data. IEEE Access 2020, 8, 222841–222858. [Google Scholar] [CrossRef]
- Tsou, M.C. Discovering Knowledge from AIS Database for Application in VTS. J. Navig. 2010, 63, 449–469. [Google Scholar] [CrossRef]
- Park, J.M.; Kim, S. Improvement Plans for Anchorage at Masan Port. J. Korean Soc. Mar. Environ. Saf. 2018, 24, 637–645. [Google Scholar] [CrossRef]
- Cao, L.; Wang, X.; Zhang, W.; Gao, L.; Xie, S.; Liu, Z. Research on Intelligent Detection Algorithm of the Single Anchored Mooring Area for Maritime Autonomous Surface Ships. Appl. Sci. 2022, 12, 6009. [Google Scholar] [CrossRef]
- Lee, Y.S. A Study on the Anchoring Safety Assessment of E-Group Anchorage in Ulsan Port. J. Korean Soc. Mar. Environ. Saf. 2014, 20, 172–178. [Google Scholar] [CrossRef][Green Version]
- Park, J.M. A Study on the Establishment of Design Criteria for Anchorage According to Port Characteristics. J. Korean Soc. Mar. Environ. Saf. 2017, 23, 279–286. [Google Scholar] [CrossRef]


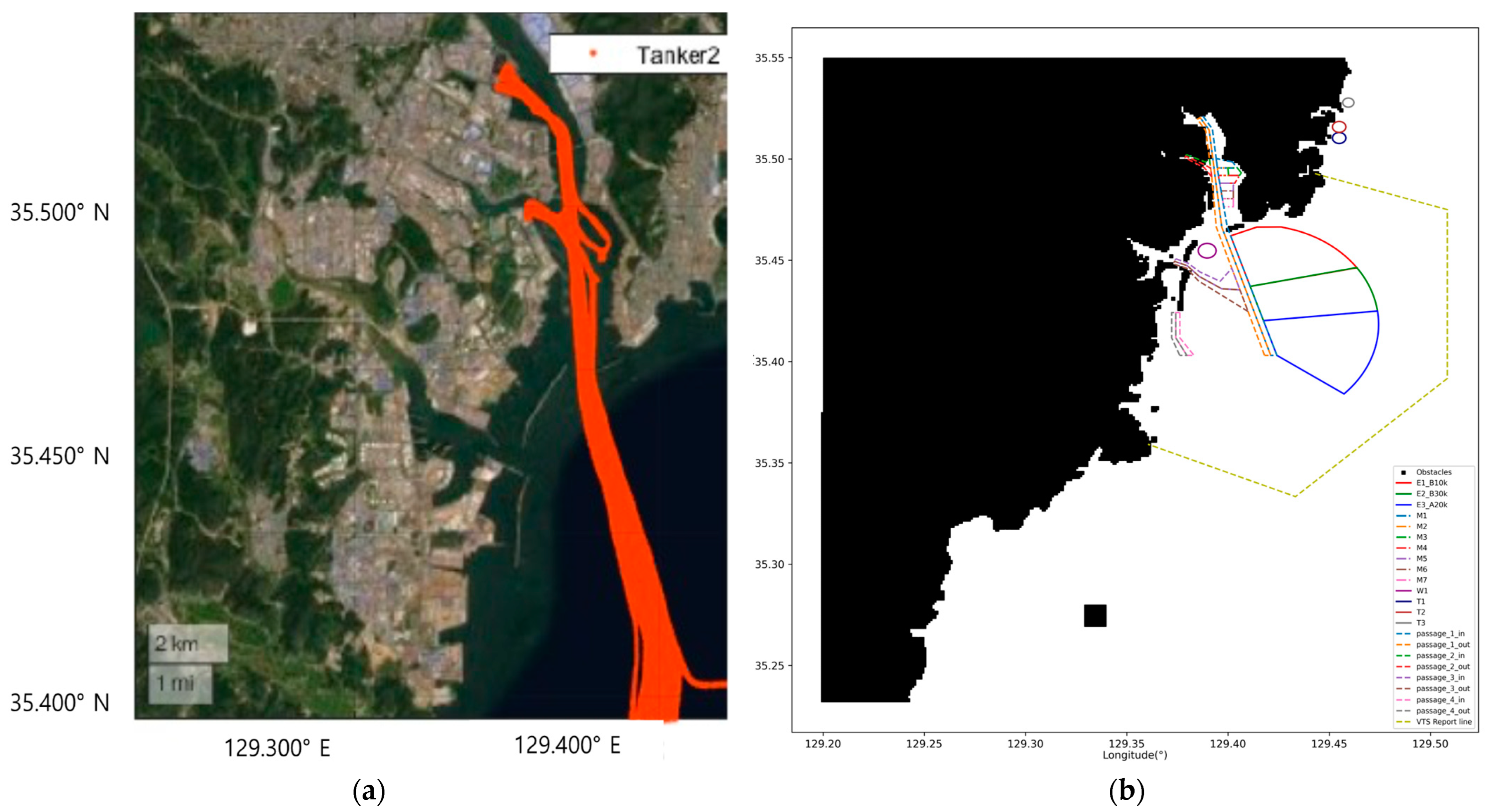
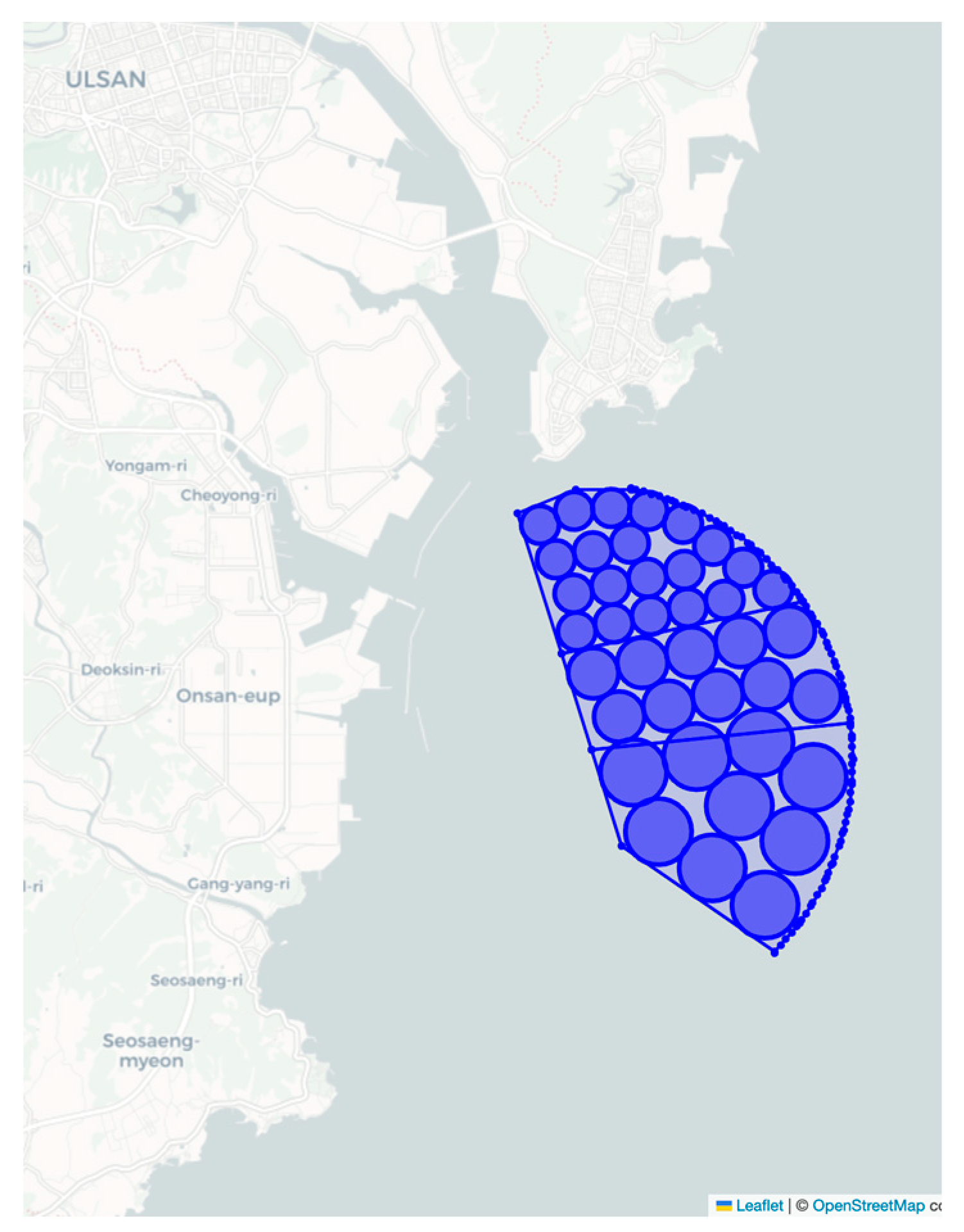
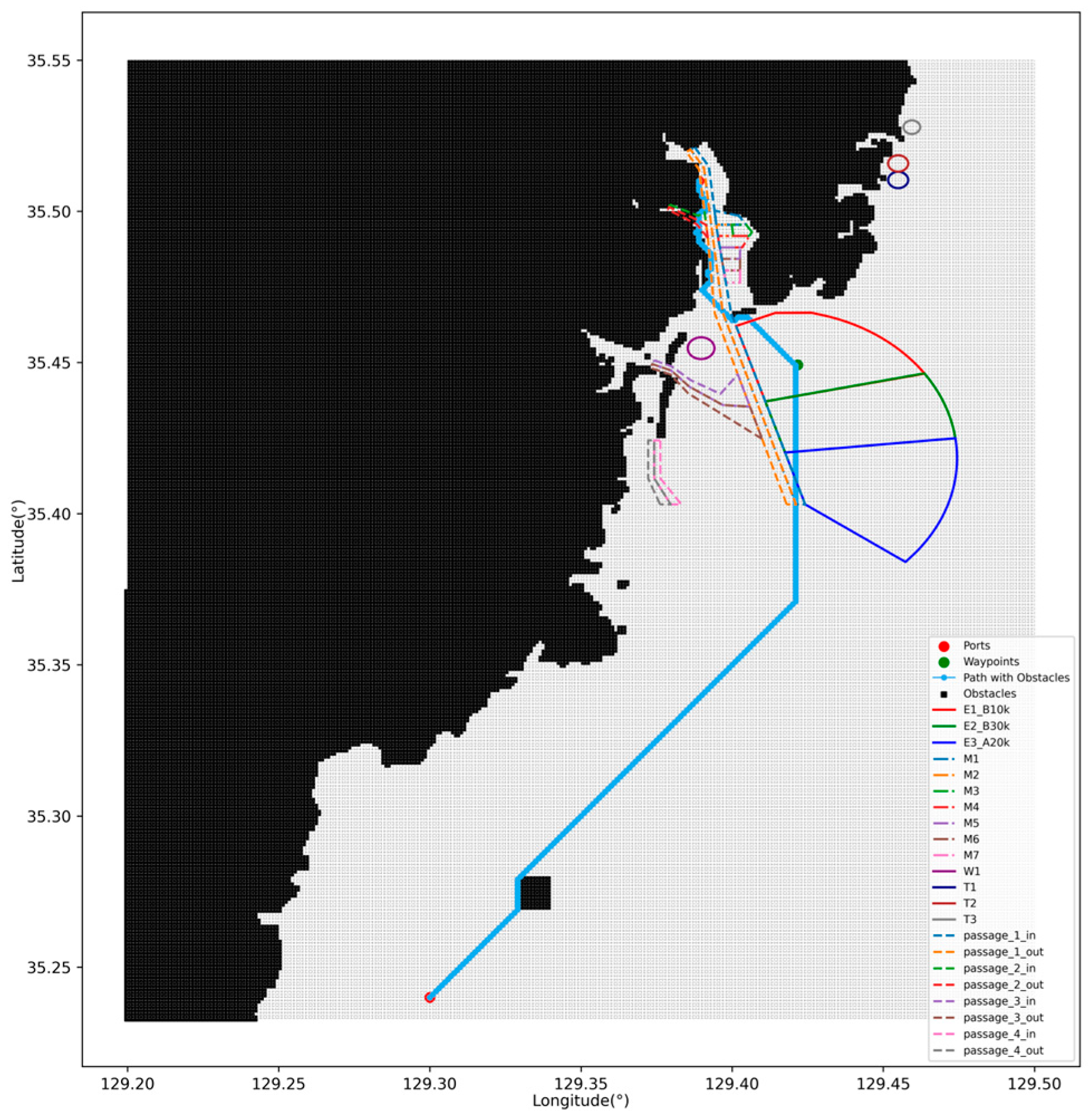

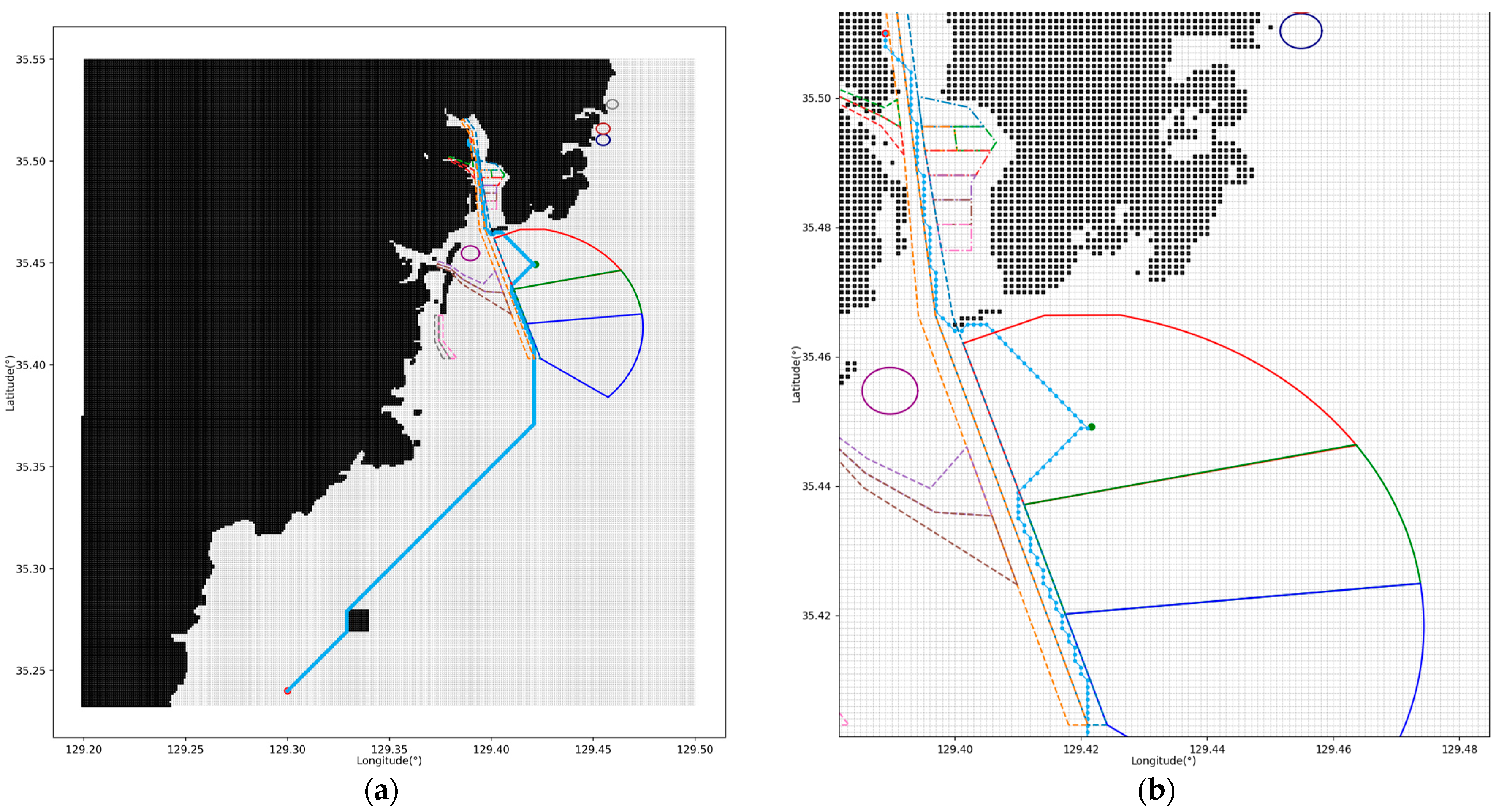

| Type | Anchorage Area | Allowed Displacement |
|---|---|---|
| Group anchorage | E1 | Up to 10,000 tons |
| E2 | Up to 30,000 tons | |
| E3 | Over 20,000 tons | |
| Circular anchorage | W1 | Up to 20,000 tons |
| T1/T2 | Up to 5000 tons | |
| T3 | Up to 2000 tons | |
| Bunkering exclusive | B1-1/B1-2 | Up to 10,000 tons |
| B2-1/B2-2 | Up to 30,000 tons | |
| B3-1 | Over 20,000 tons, Up to 50,000 tons | |
| B3-2 | Over 50,000 tons | |
| Small anchorage | M1~M7 | Below 2000 tons |
| DWT (ton) | Loa (m) | Breath (m) | Draft (m) | Water Depth (m) | Radius (m) |
|---|---|---|---|---|---|
| 3000 | 94 | 14.6 | 5.6 | E1, 40 | 334 |
| 5000 | 109 | 16.8 | 6.5 | E1, 40 | 349 |
| 10,000 | 127 | 20.8 | 7.9 | E1, 40 | 367 |
| 30,000 | 190 | 22.6 | 10.7 | E2, 50 | 490 |
| 50,000 | 215.4 | 32 | 12.3 | E3, 60 | 575.4 |
| 150,000 | 277.4 | 46 | 17 | E3, 60 | 637.4 |
| 300,000 | 333 | 58 | 22.5 | E3, 60 | 693 |
| E1_Circle_Anchorage | E2_Circle_Anchorage | E3_Circle_Anchorage | ||||
|---|---|---|---|---|---|---|
| Number | Latitude | Longitude | Latitude | Longitude | Latitude | Longitude |
| 1 | 35.4485 | 129.4571 | 35.4411 | 129.4607 | 35.4152 | 129.4658 |
| 2 | 35.4524 | 129.4506 | 35.4392 | 129.4500 | 35.4214 | 129.4542 |
| 3 | 35.4563 | 129.4440 | 35.4374 | 129.4393 | 35.4189 | 129.4405 |
| 4 | 35.4602 | 129.4375 | 35.4355 | 129.4286 | 35.4161 | 129.4267 |
| 5 | 35.4625 | 129.4299 | 35.4337 | 129.4180 | 35.4040 | 129.4618 |
| 6 | 35.4630 | 129.4219 | 35.4296 | 129.4664 | 35.4102 | 129.4497 |
| 7 | 35.4625 | 129.4138 | 35.4317 | 129.4558 | 35.4056 | 129.4321 |
| 8 | 35.4600 | 129.4064 | 35.4298 | 129.4450 | 35.3925 | 129.4553 |
| 9 | 35.4467 | 129.4465 | 35.4279 | 129.4343 | 35.3991 | 129.4438 |
| 10 | 35.4453 | 129.4385 | 35.4260 | 129.4236 | ||
| 11 | 35.4439 | 129.4304 | ||||
| 12 | 35.4425 | 129.4224 | ||||
| 13 | 35.4411 | 129.4144 | ||||
| 14 | 35.4520 | 129.4378 | ||||
| 15 | 35.4506 | 129.4297 | ||||
| 16 | 35.4492 | 129.4217 | ||||
| 17 | 35.4478 | 129.4136 | ||||
| 18 | 35.4567 | 129.4259 | ||||
| 19 | 35.4553 | 129.4179 | ||||
| 20 | 35.4539 | 129.4098 | ||||
| Route Names | Length (km) | Turns |
|---|---|---|
| Improved A* algorithm route | 36.188 | 43 |
| Smoothing algorithm route | 34.667 | 12 |
| Set | Comparing Routes | Waypoints: Maneuvering | Length of Smoothing Routes (km) | Length of Maneuvering Simulation Routes (km) | DTW Results (deg) |
|---|---|---|---|---|---|
| 1 | Smoothing routes with maneuvering (Figure 13) | 17 | 34.667 | 34.735 | 0.474 |
| 2 | Interpolated smoothing routes with maneuvering (Figure 14) | 147 | 34.667 | 34.751 | 0.141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yun, S.-W.; Kim, D.-H.; Kim, S.-W.; Kim, D.-J.; Kim, H.-J. Global Path Planning for Autonomous Ship Navigation Considering the Practical Characteristics of the Port of Ulsan. J. Mar. Sci. Eng. 2024, 12, 160. https://doi.org/10.3390/jmse12010160
Yun S-W, Kim D-H, Kim S-W, Kim D-J, Kim H-J. Global Path Planning for Autonomous Ship Navigation Considering the Practical Characteristics of the Port of Ulsan. Journal of Marine Science and Engineering. 2024; 12(1):160. https://doi.org/10.3390/jmse12010160
Chicago/Turabian StyleYun, Sang-Woong, Dong-Ham Kim, Se-Won Kim, Dong-Jin Kim, and Hye-Jin Kim. 2024. "Global Path Planning for Autonomous Ship Navigation Considering the Practical Characteristics of the Port of Ulsan" Journal of Marine Science and Engineering 12, no. 1: 160. https://doi.org/10.3390/jmse12010160
APA StyleYun, S.-W., Kim, D.-H., Kim, S.-W., Kim, D.-J., & Kim, H.-J. (2024). Global Path Planning for Autonomous Ship Navigation Considering the Practical Characteristics of the Port of Ulsan. Journal of Marine Science and Engineering, 12(1), 160. https://doi.org/10.3390/jmse12010160







