Peridynamic Simulation of the Penetration of an Ice Sheet by a Vertically Ascending Cylinder
Abstract
:1. Introduction
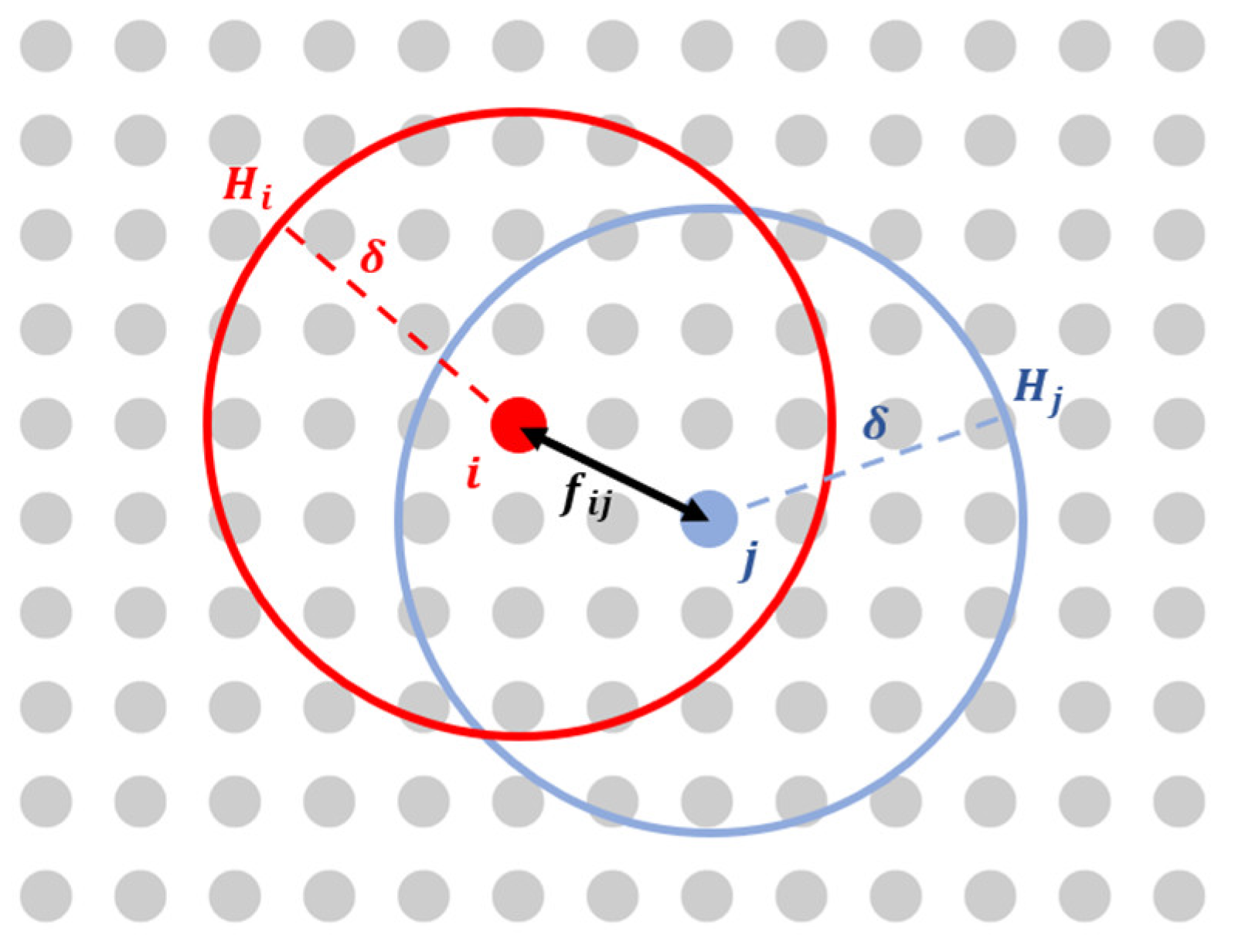
2. Peridynamic Framework
3. Numerical Implementation
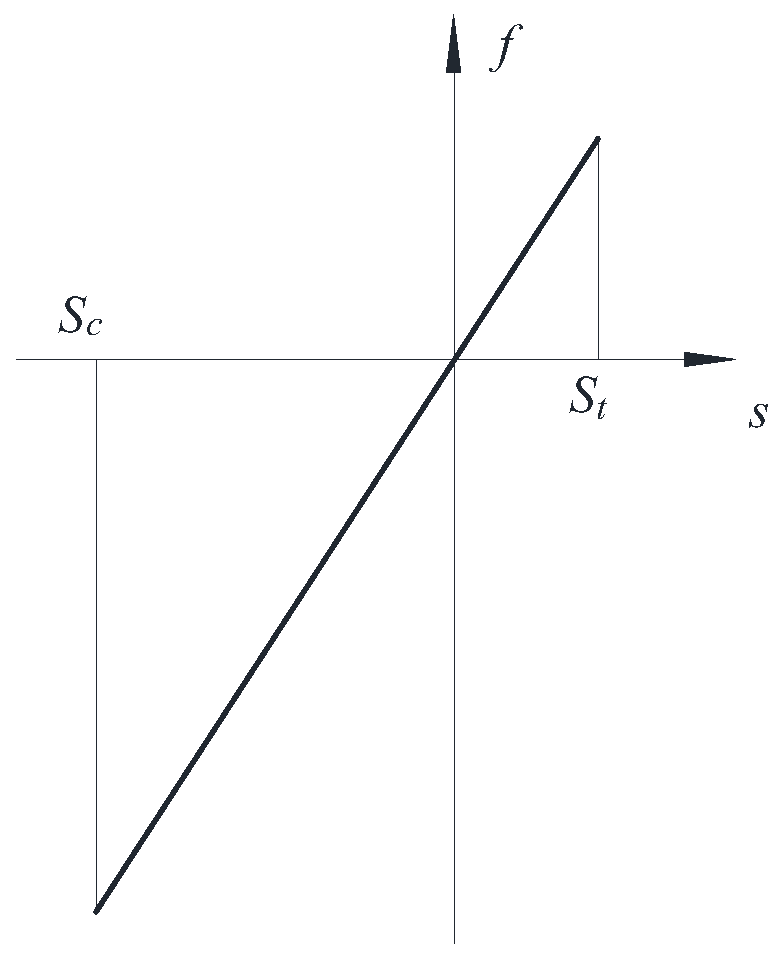
3.1. Constitutive Model of Ice
3.2. Contact Algorithm
3.3. Numerical Algorithm
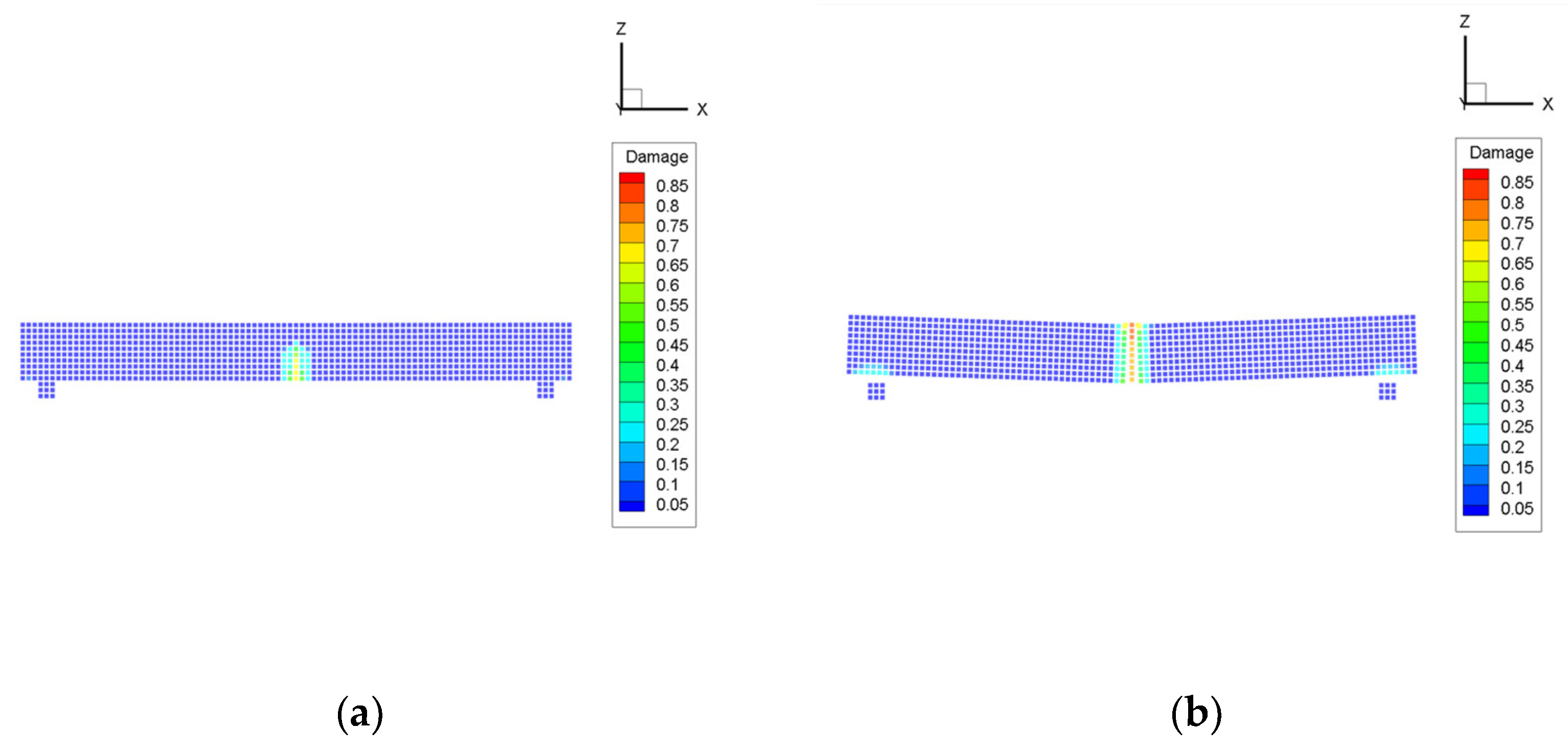
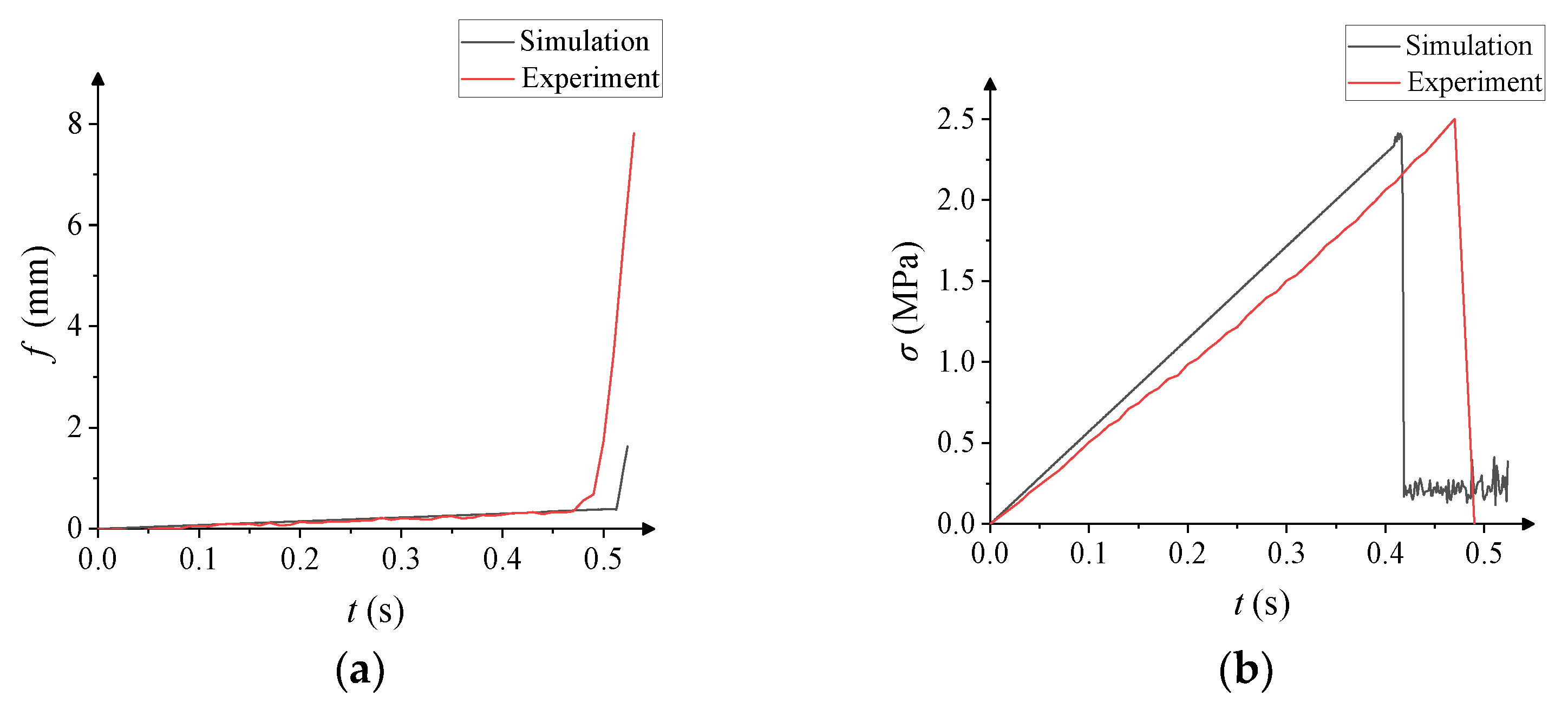
3.4. Numerical Validation
4. Numerical Result
5. Parametric Analysis
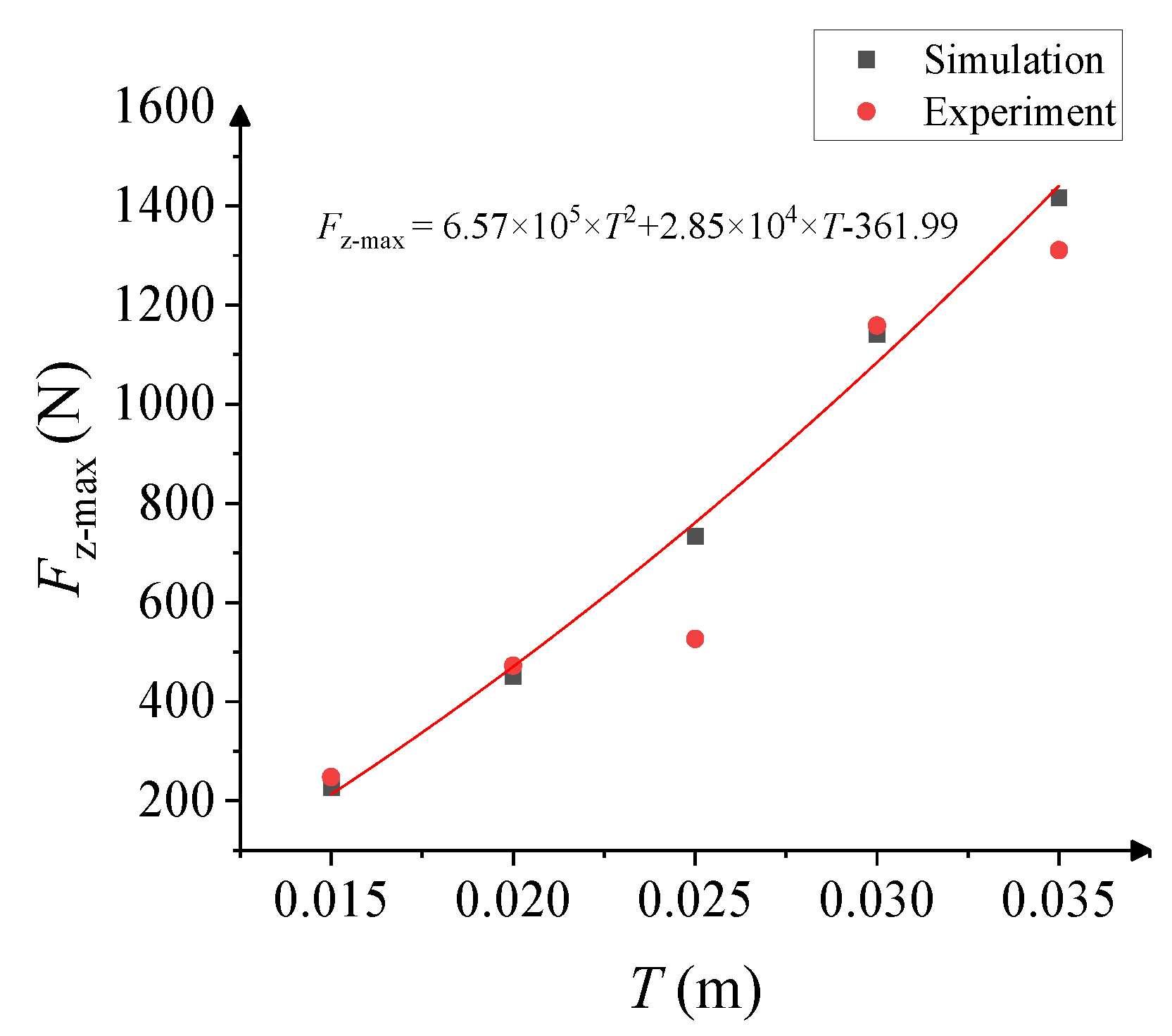
5.1. Ice Thickness
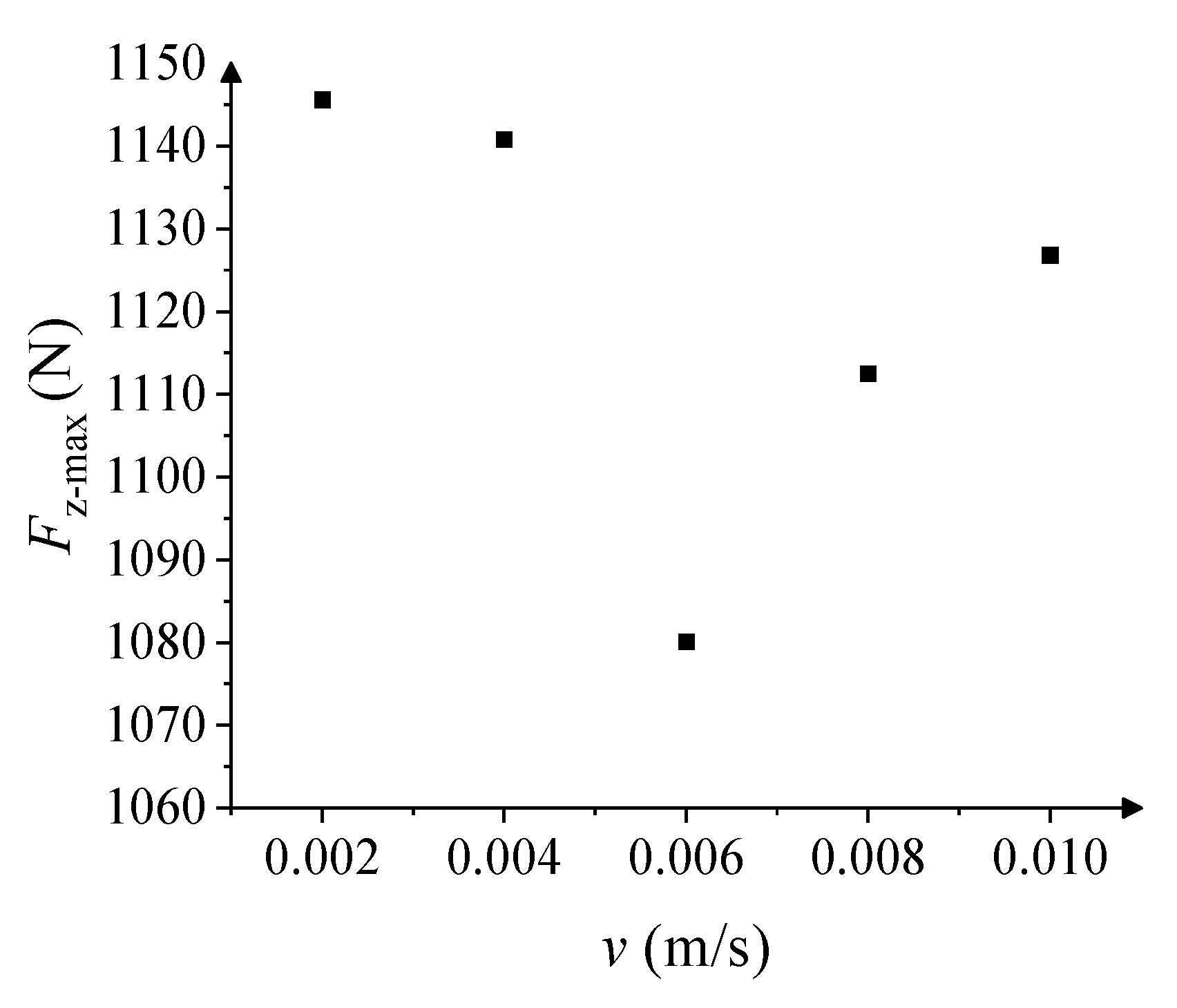
5.2. Impact Velocity
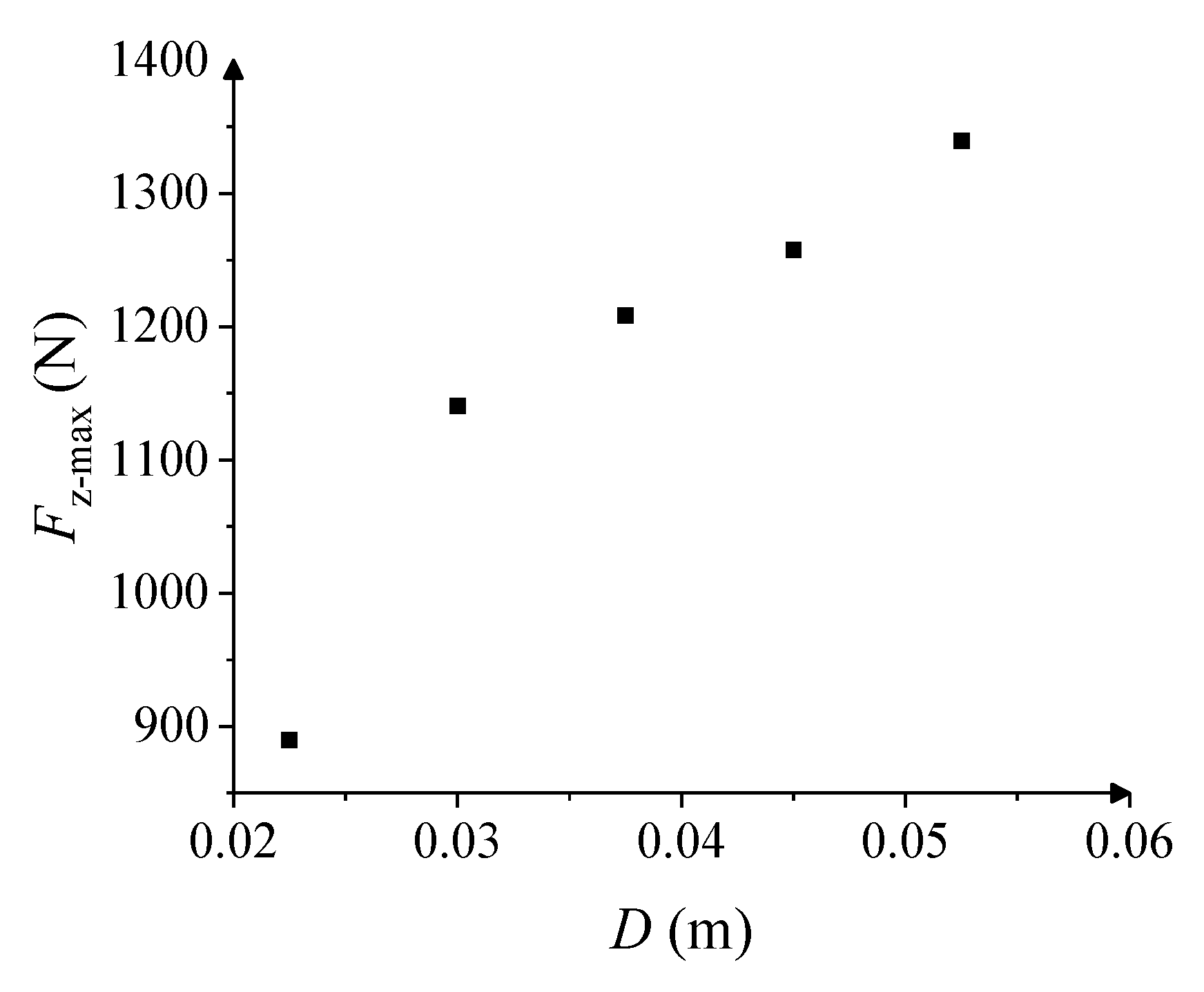
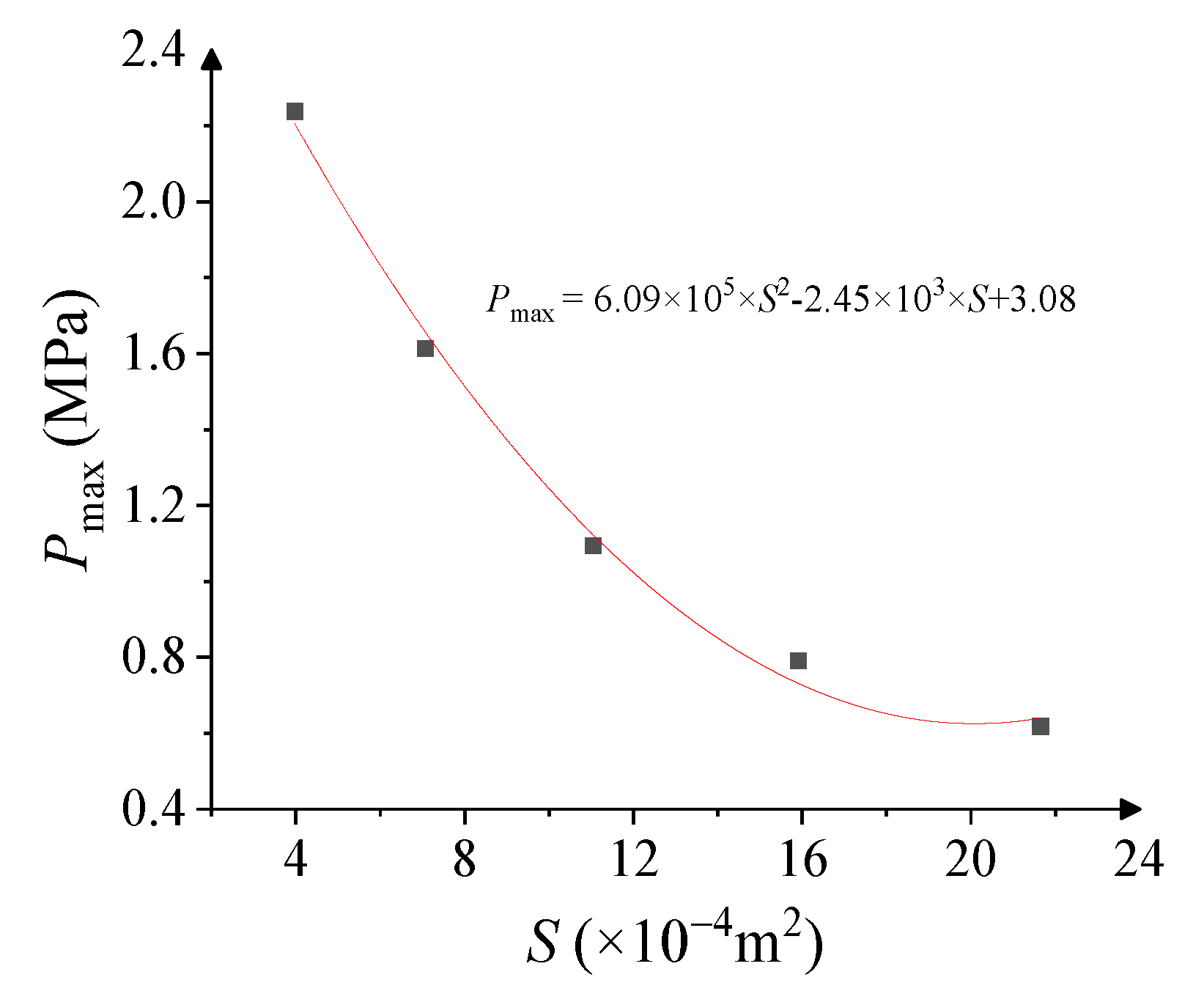
5.3. Cylinder Diameter
6. Conclusions
- (1)
- As the ice thickness increases, the cracks will change from only diagonal symmetry to complete symmetry, and the role of crushing as the cause of failure will be more prominent. The breakthrough load is positively related to the ice thickness, and the relationship can be fitted with a quadratic function.
- (2)
- If the impact velocity is within a certain range, there is no obvious difference in the crack distribution in the ice sheet. There might be an impact velocity within this range, and the structure will experience a minimal ice load when vertically penetrating the ice sheet with it.
- (3)
- As the cylinder diameter increases, the number of radial cracks in the ice sheet gradually decreases and gathers diagonally, and the breakthrough load gradually increases. The breakthrough pressure is inversely proportional to the contact area, and the relationship between the two can also be described using a quadratic function.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Masterson, D.M. State of the art of ice bearing capacity and ice construction. Cold Reg. Sci. Technol. 2009, 58, 99–112. [Google Scholar] [CrossRef]
- Sodhi, D.S. Vertical penetration of floating ice sheets. Int. J. Solids Struct. 1998, 35, 4275–4294. [Google Scholar] [CrossRef]
- Kerr, A.D. The bearing capacity of floating ice plates subjected to static or quasi-static loads. J. Glaciol. 1976, 17, 229–268. [Google Scholar]
- Kerr, A.D.; Palmer, W.T. The deformations and stresses in floating ice plates. Acta Mech. 1972, 15, 57–72. [Google Scholar] [CrossRef]
- Gold, L.W. Field study on the load bearing capacity of ice covers. Pulp Pap. Can. 1960, 61, 153–158. [Google Scholar]
- Gold, L.W. Use of ice covers for transportation. Can. Geotech. J. 1971, 8, 170–181. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Li, Y.N. Penetration fracture of sea ice plate: Simplified analysis and size effect. J. Eng. Mech. 1994, 120, 1304–1321. [Google Scholar] [CrossRef]
- Assur, A. Traffic over frozen or crusted surfaces. In Proceedings of the International Conference on the Mechanics of Soil-Vehicle Systems, Torino, Italy, 12–16 June 1961; pp. 913–923. [Google Scholar]
- Meyerhof, G.G. Bearing capacity of floating ice sheets. J. Eng. Mech. Div. 1960, 86, 113–145. [Google Scholar] [CrossRef]
- Coon, M.D.; Mohaghegh, M.M. Plastic Analysis of Coulomb Plates and Its Application to the Bearing Capacity of Sea Ice; Department of Atmospheric Sciences, University of Washington: Seattle, WA, USA, 1972. [Google Scholar]
- Sodhi, D.S. Breakthrough loads of floating ice sheets. J. Cold Reg. Eng. 1995, 9, 4–22. [Google Scholar] [CrossRef]
- Kheysin, D.Y. On the problem of the elastic-plastic bending of an ice cover. Tr. Arkticheskii Antarkt. Nauchno-Issledovatel’skii Inst. 1964, 267, 143–149. [Google Scholar]
- Garbaccio, D.H. Creep of Floating Ice Sheets, Computer Calculations; Science Engineering Associates Report; Defense Technical Information Center: Fort Belvoir, VA, USA, 1968. [Google Scholar]
- Panfilov, D.F. On the Determination of the Carrying Capacity of an Ice Cover for Loads of Long Duration; Corps of Engineers, US Army Cold Regions Research and Engineering Laboratory: Vicksburg, MS, USA, 1972. [Google Scholar]
- Frankenstein, G.E. Load Test Data for Lake Ice Sheets; Technical Report; Cold Regions Research and Engineering Laboratory (U.S.): Vicksburg, MS, USA, 1963. [Google Scholar]
- Lichtenberger, G.J.; Jones, J.W.; Stegall, R.D.; Zadow, D.W. Static Ice Loading Tests, Resolute Bay—Winter 1973/74; Report No. 7458-74-14; Sunoco Science and Technology: Richardson, TX, USA, 1974. [Google Scholar]
- Lichtenberger, G.J.; Stegall, R.D.; Braun, C.; Zadow, D.W. Vertical Load Bearing Capacity Tests of Natural Ice and of Artificial-Natural Ice Laminates, Resolute Bay, Winter 1974/75; Report No. 7481-75-2; Suntech: Richardson, TX, USA, 1975. [Google Scholar]
- Frederking, R.M.W.; Gold, L.W. The bearing capacity of ice covers under static loads. Can. J. Civ. Eng. 1976, 3, 288–293. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Kim, J.J.H. Size effect in penetration of sea ice plate with part-through cracks. I: Theory. J. Eng. Mech. 1998, 124, 1310–1315. [Google Scholar] [CrossRef]
- Beltaos, S. Bearing capacity of floating ice covers: Theory versus fact. In Proceeding of the 11th Workshop on River Ice: River Ice Processes within a Changing Environment, Ottawa, ON, Canada, 14–16 May 2001; pp. 14–16. [Google Scholar]
- Beltaos, S. A strain energy criterion for failure of floating ice sheets. Can. J. Civ. Eng. 1978, 5, 352–361. [Google Scholar] [CrossRef]
- Beltaos, S. Collapse of floating ice covers under vertical loads: Test data vs. theory. Cold Reg. Sci. Technol. 2002, 34, 191–207. [Google Scholar] [CrossRef]
- Wang, C.; Fang, Y.; Wang, C.H.; Zhu, G.Y.; Guo, C.Y. Experimental Study on Ice Vertical Penetration Rupture, Proceedings of the Chinse Society of Naval Architects and Marine Engineers; Academic Committee of Ship Mechanics—Testing Technology Group: Kunming, China, 28 July 2021; pp. 89–100. [Google Scholar]
- Wang, C.H.; Zhu, G.Y.; Wang, C.; Guo, C.Y.; Wang, J.A. Analysis of ice breaking under vertical loads and its influencing factors. J. Vib. Shock. 2022, 41, 11–19. [Google Scholar]
- Wang, C.H.; Wang, J.A.; Wang, C.; Guo, C.Y.; Zhu, G.Y. Research on vertical movement of cylindrical structure out of water and breaking through ice layer based on S-ALE method. Chin. J. Theor. Appl. Mech. 2021, 53, 3110–3123. [Google Scholar]
- Li, F.; Huang, L. A review of computational simulation methods for a ship advancing in broken ice. J. Mar. Sci. Eng. 2022, 10, 165. [Google Scholar] [CrossRef]
- Long, X.; Liu, S.; Ji, S. Discrete element modelling of relationship between ice breaking length and ice load on conical structure. Ocean Eng. 2020, 201, 107152. [Google Scholar] [CrossRef]
- Long, X.; Liu, L.; Liu, S.; Ji, S. Discrete element analysis of high-pressure zones of sea ice on vertical structures. J. Mar. Sci. Eng. 2021, 9, 348. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Silling, S.A.; Askari, E. A meshfree method based on the peridynamic model of solid mechanics. Comput. Struct. 2005, 83, 1526–1535. [Google Scholar] [CrossRef]
- Huang, D.; Zhang, Q.; Qiao, P.Z.; Shen, F. A review on peridynamics method and its applications. Adv. Mech. 2010, 40, 448–459. [Google Scholar]
- Vazic, B.; Oterkus, E.; Oterkus, S. Peridynamic approach for modelling ice-structure interactions. In Proceedings of the 7th International Conference on Marine Structures (MARSTRUCT 2019), Dubrovnik, Croatia, 6–8 May 2019; CRC Press: Boca Raton, FL, USA, 2019; p. 55. [Google Scholar]
- Song, Y.; Yan, J.L.; Li, S.F.; Kang, Z. Peridynamic modeling and simulation of ice craters by impact. Comput. Model. Eng. Sci. 2019, 121, 465–492. [Google Scholar] [CrossRef]
- Lu, W.; Li, M.Y.; Vazic, B.; Oterkus, S.; Wang, Q. Peridynamic modelling of fracture in polycrystalline ice. J. Mech. 2020, 36, 223–234. [Google Scholar] [CrossRef]
- Vazic, B.; Oterkus, E.; Oterkus, S. In-plane and out-of plane failure of an ice sheet using peridynamics. J. Mech. 2020, 36, 265–271. [Google Scholar] [CrossRef]
- Jia, B.; Ju, L.; Wang, Q. Numerical simulation of dynamic interaction between ice and wide vertical structure based on peridynamics. Comput. Model. Eng. Sci. 2019, 121, 501–522. [Google Scholar] [CrossRef]
- Liu, M.H.; Wang, Q.; Lu, W. Peridynamic simulation of brittle-ice crushed by a vertical structure. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 209–218. [Google Scholar] [CrossRef]
- Parks, M.L.; Seleson, P.; Plimpton, S.J.; Silling, S.A.; Lehoucq, R.B. Peridynamics with Lammps: A User Guide, v0. 3 Beta; Sandia Report (2011–8253); Sandia National Laboratories: Albuquerque, NM, USA, 2011. [Google Scholar]
- Wang, Q.; Wang, Y.; Zan, Y.F.; Lu, W.; Bai, X.L.; Guo, J. Peridynamics simulation of the fragmentation of ice cover by blast loads of an underwater explosion. J. Mar. Sci. Technol. 2018, 23, 52–66. [Google Scholar] [CrossRef]
- Madenci, E.; Oterkus, E. Peridynamic Theory and Its Applications; Springer: New York, NY, USA, 2017. [Google Scholar]
- Huang, D.; Lu, G.D.; Qiao, P.Y. An improved peridynamic approach for quasi-static elastic deformation and brittle fracture analysis. Int. J. Mech. Sci. 2015, 94–95, 111–122. [Google Scholar] [CrossRef]
- Timco, G.W.; Weeks, W.F. A review of the engineering properties of sea ice. Cold Reg. Sci. Technol. 2010, 60, 107–129. [Google Scholar] [CrossRef]
- Schulson, E.M. Brittle failure of ice. Eng. Fract. Mech. 2001, 68, 1839–1887. [Google Scholar] [CrossRef]
- Karr, D.; Das, S. Ice strength in brittle and ductile failure modes. J. Struct. Eng. 1983, 109, 2802–2811. [Google Scholar] [CrossRef]
- Lu, W. The Study of the Numerical Simulation Method of Peridynamic Based on the Bending Fracture of Sea Ice. Master’s Thesis, Harbin Engineering University, Harbin, China, 2017. [Google Scholar]

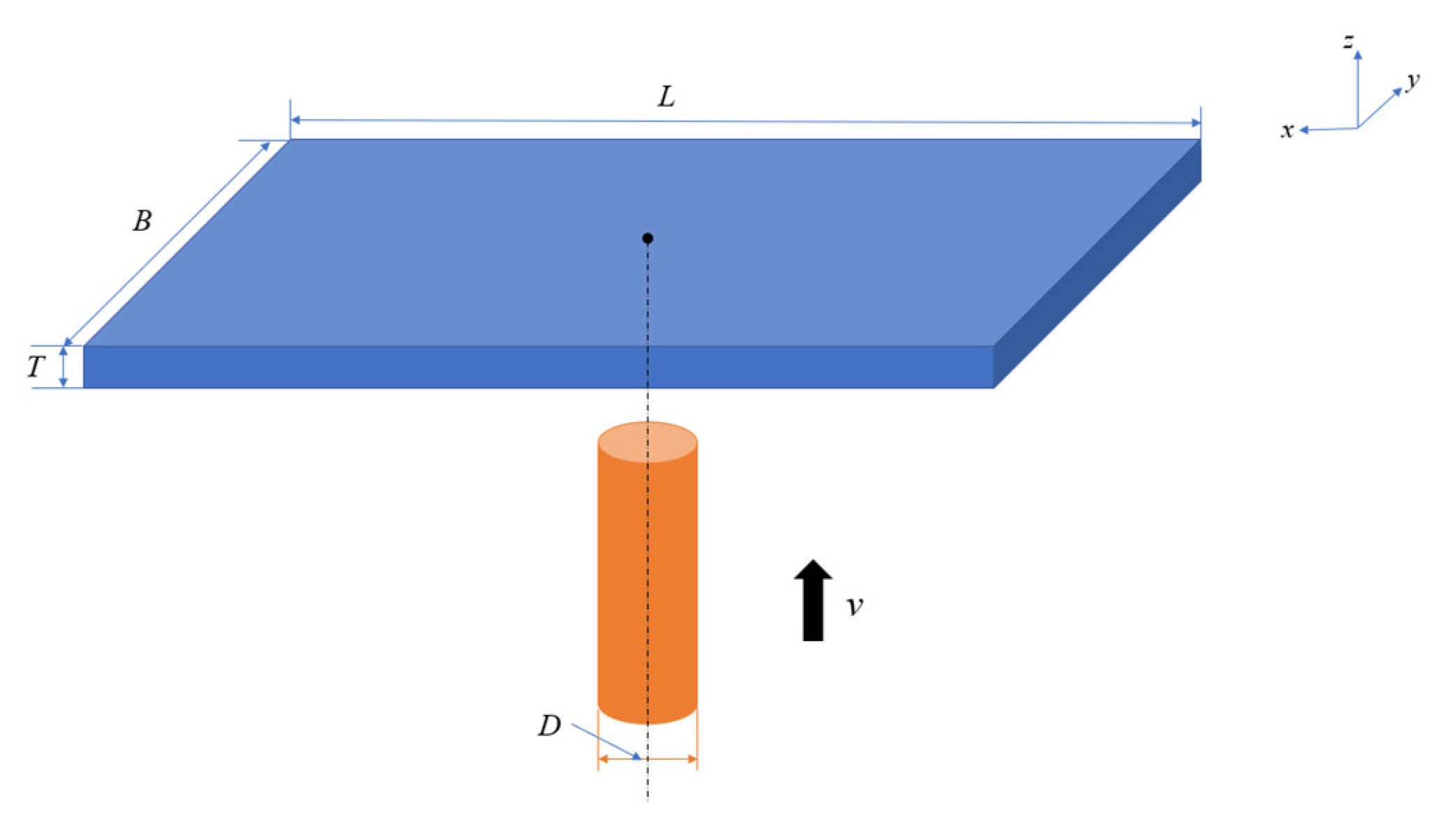
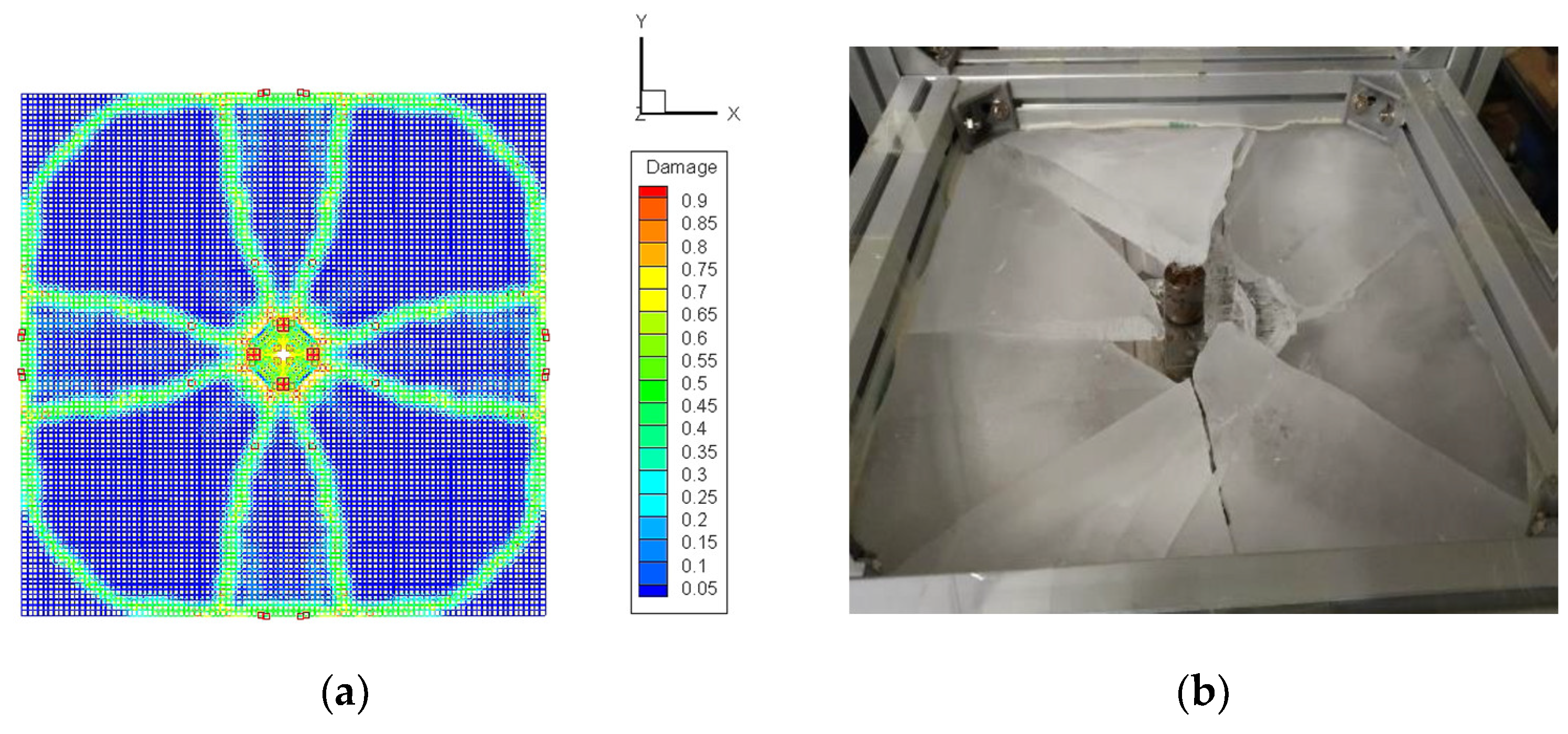
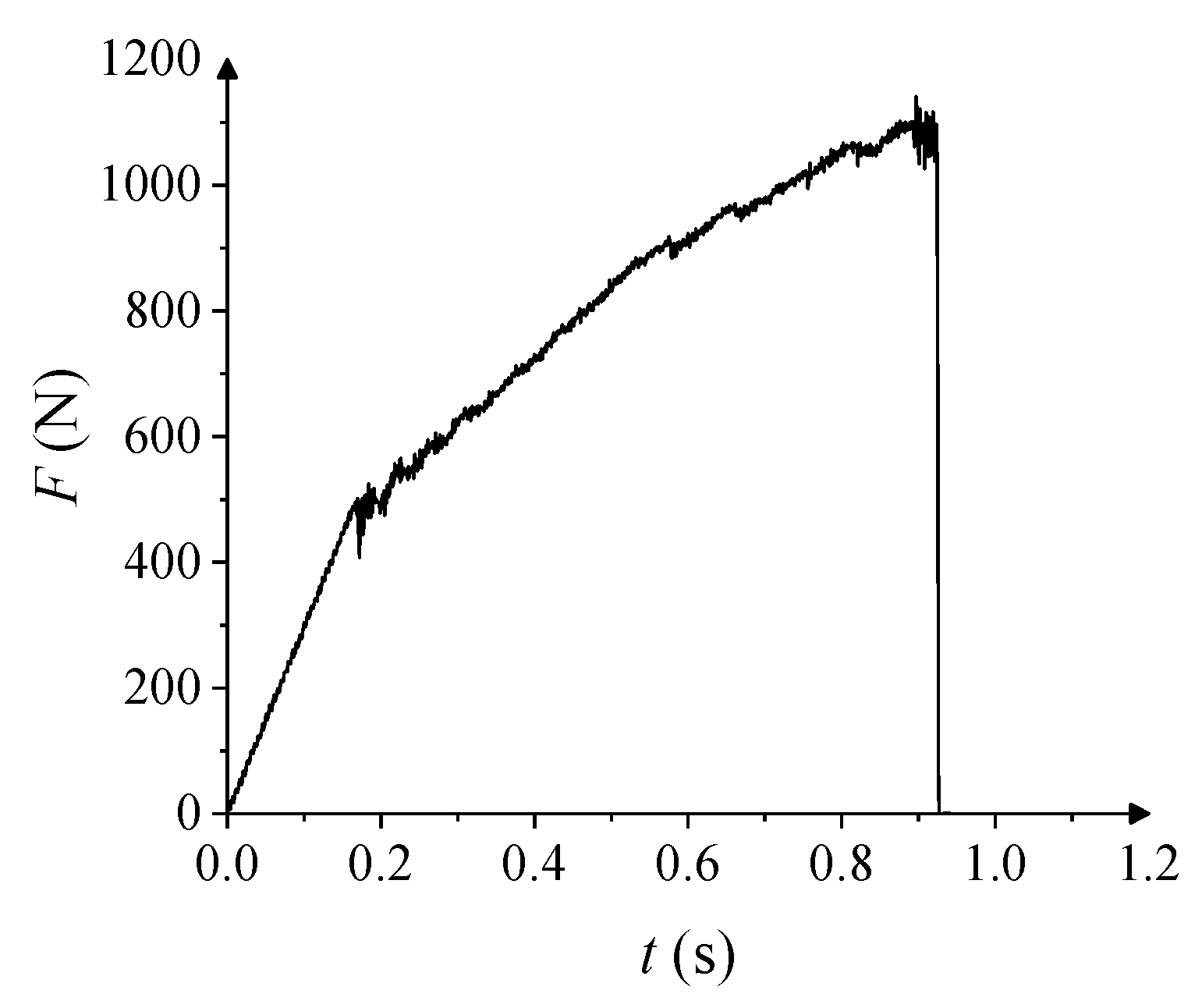
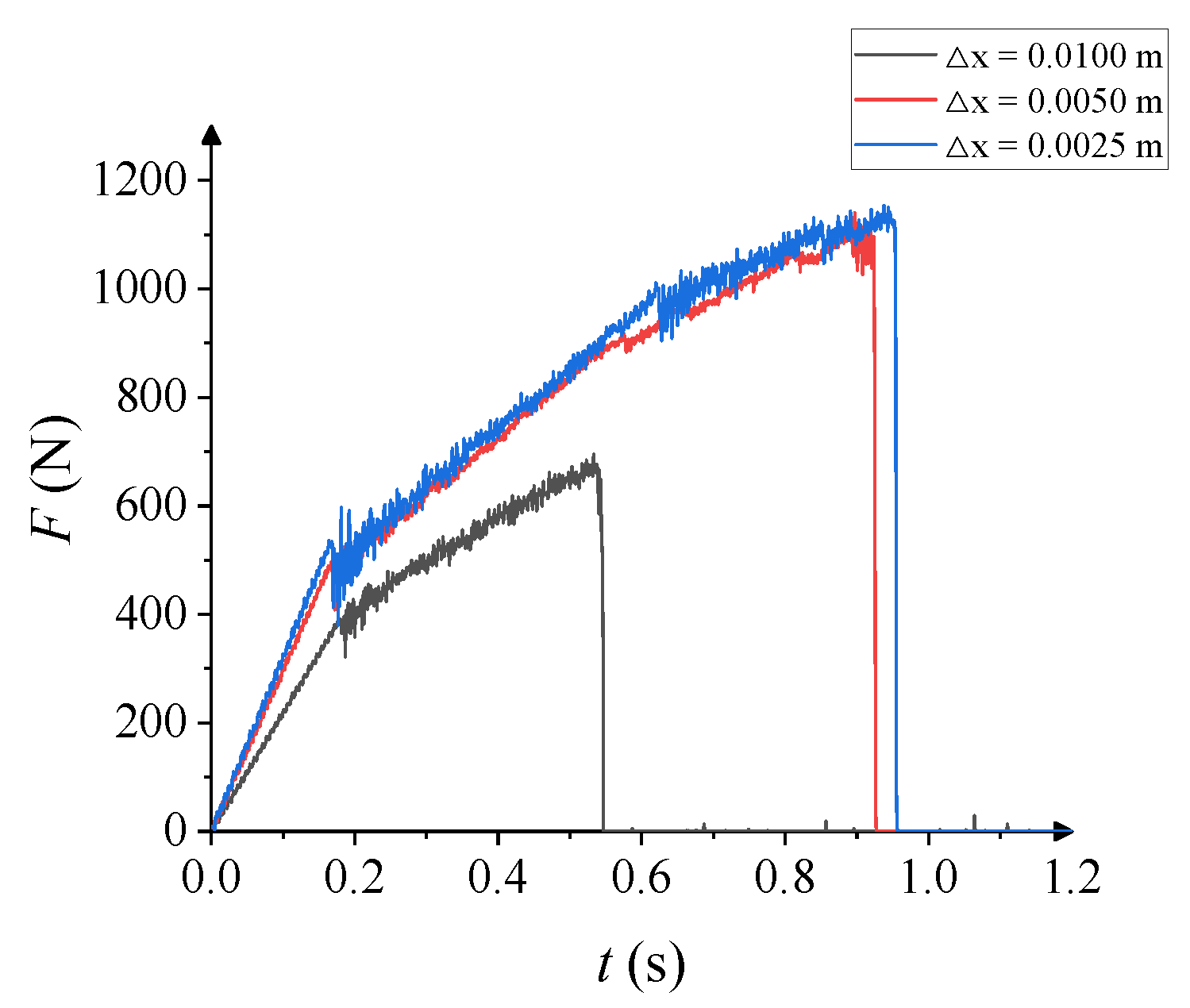
| Parameter | Value | |
|---|---|---|
| Size parameter | Length () | 0.65 m |
| Span between supports () | 0.60 m | |
| Height () | 0.07 m | |
| Width () | 0.07 m | |
| Material parameter | Elastic modulus () | 6.81 GPa |
| Density ( | 896.977 kg·m3 | |
| Poisson ratio | 1/3 |
| Test Results | Numerical Results | Error | |
|---|---|---|---|
| Rupture time (s) | 0.47 | 0.5125 | 9.04% |
| Maximum deflection (mm) | 0.35 | 0.3743 | 6.94% |
| Flexural strength (MPa) | 2.50 | 2.4103 | 3.59% |
| Parameter | Value | |
|---|---|---|
| Ice | Dimension (a × b) | 0.5 m × 0.5 m |
| Thickness (h) | 0.03 m | |
| Density () | 917 kg/m3 | |
| Elastic modulus (E) | 1.0 GPa | |
| Poisson ratio (υ) | 0.3 | |
| Compressive strength () | 2.41 MPa | |
| Rigid cylinder | Diameter (D) | 0.03 m |
| Height (h0) | 0.05 m | |
| Speed (v) | 0.004 m/s |
| Test Results | Numerical Results | Error | |
|---|---|---|---|
| Rupture time (s) | 1.093 | 0.926 | 15.28% |
| Breakthrough load (N) | 1158.45 | 1140.80 | 1.52% |
| Ice Thickness (m) | Impact Velocity (m/s) | Cylinder Diameter (m) | |
|---|---|---|---|
| 1 | 0.015 | 0.004 | 0.0300 |
| 0.020 | |||
| 0.025 | |||
| 0.030 | |||
| 0.035 | |||
| 2 | 0.030 | 0.002 | 0.0300 |
| 0.004 | |||
| 0.006 | |||
| 0.008 | |||
| 0.010 | |||
| 3 | 0.030 | 0.004 | 0.0225 |
| 0.0300 | |||
| 0.0375 | |||
| 0.0450 | |||
| 0.0525 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, B.; Wang, Q.; Ju, L.; Hu, C.; Zhao, R.; Han, D.; Pang, F. Peridynamic Simulation of the Penetration of an Ice Sheet by a Vertically Ascending Cylinder. J. Mar. Sci. Eng. 2024, 12, 188. https://doi.org/10.3390/jmse12010188
Jia B, Wang Q, Ju L, Hu C, Zhao R, Han D, Pang F. Peridynamic Simulation of the Penetration of an Ice Sheet by a Vertically Ascending Cylinder. Journal of Marine Science and Engineering. 2024; 12(1):188. https://doi.org/10.3390/jmse12010188
Chicago/Turabian StyleJia, Bin, Qing Wang, Lei Ju, Chenjun Hu, Rongsheng Zhao, Duanfeng Han, and Fuzhen Pang. 2024. "Peridynamic Simulation of the Penetration of an Ice Sheet by a Vertically Ascending Cylinder" Journal of Marine Science and Engineering 12, no. 1: 188. https://doi.org/10.3390/jmse12010188





