Experimental and Numerical Analysis of Ultimate Carrying Capacity of a Funnel Structure with Opening under Wind Pressure
Abstract
:1. Introduction
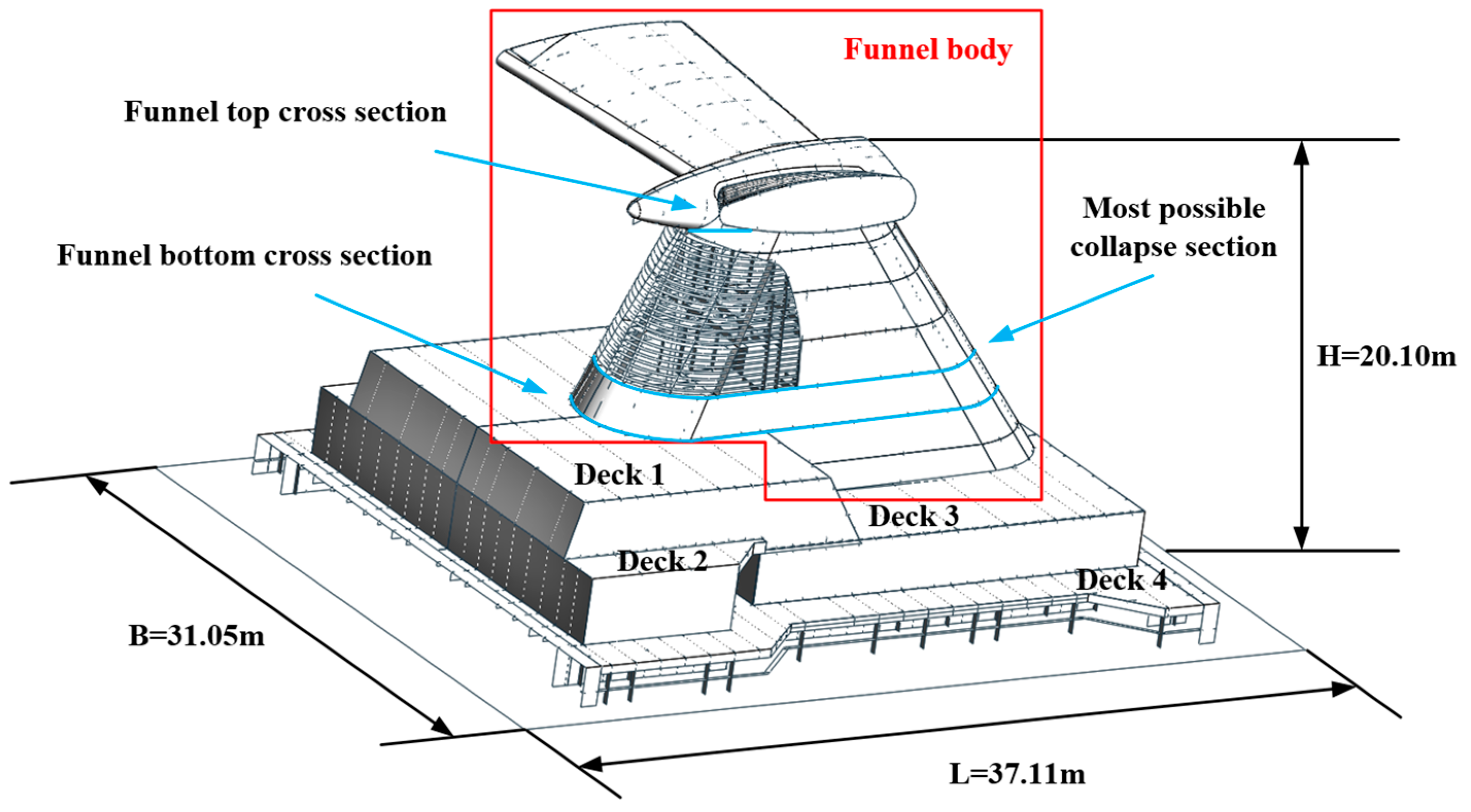
2. Scaled Experiment
2.1. Similarity Law
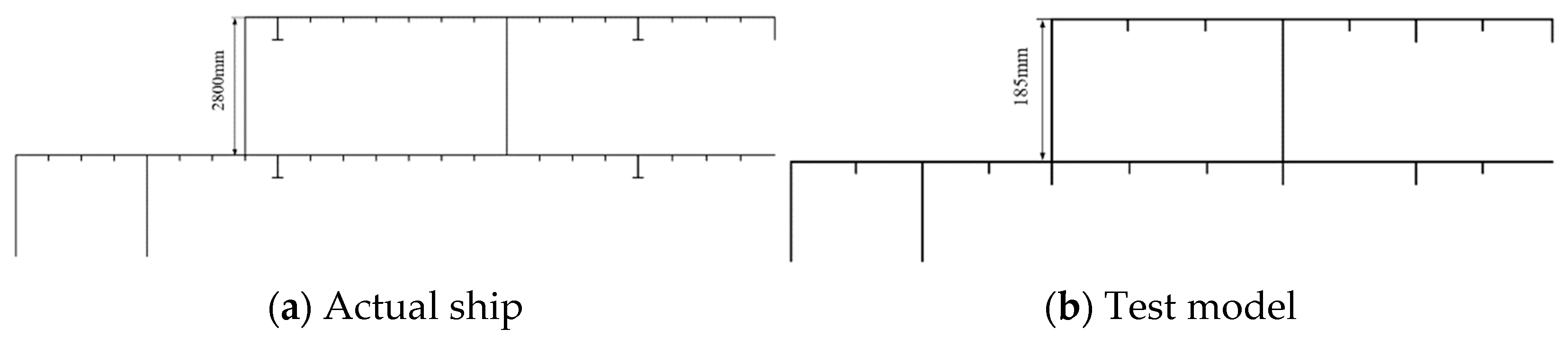
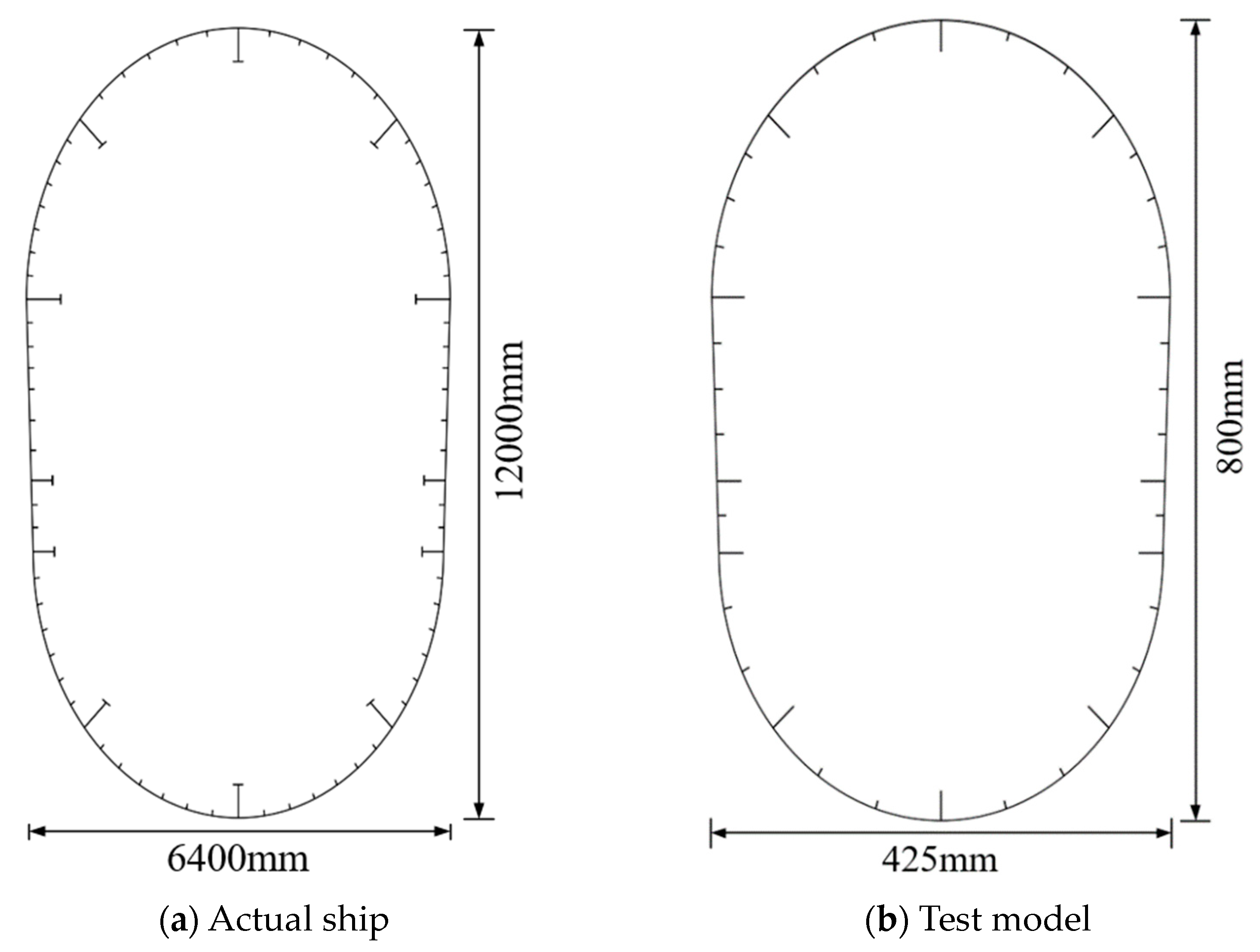
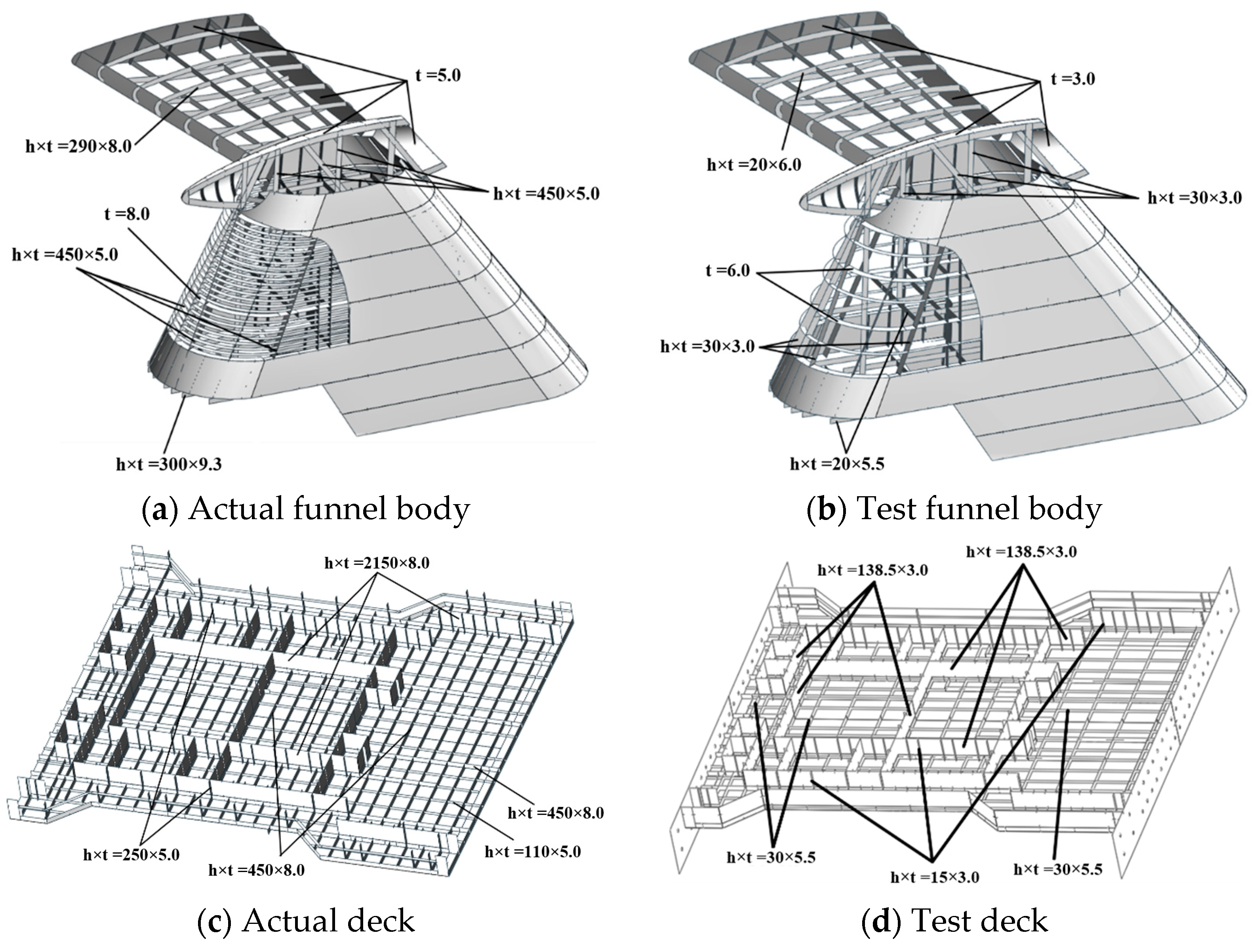
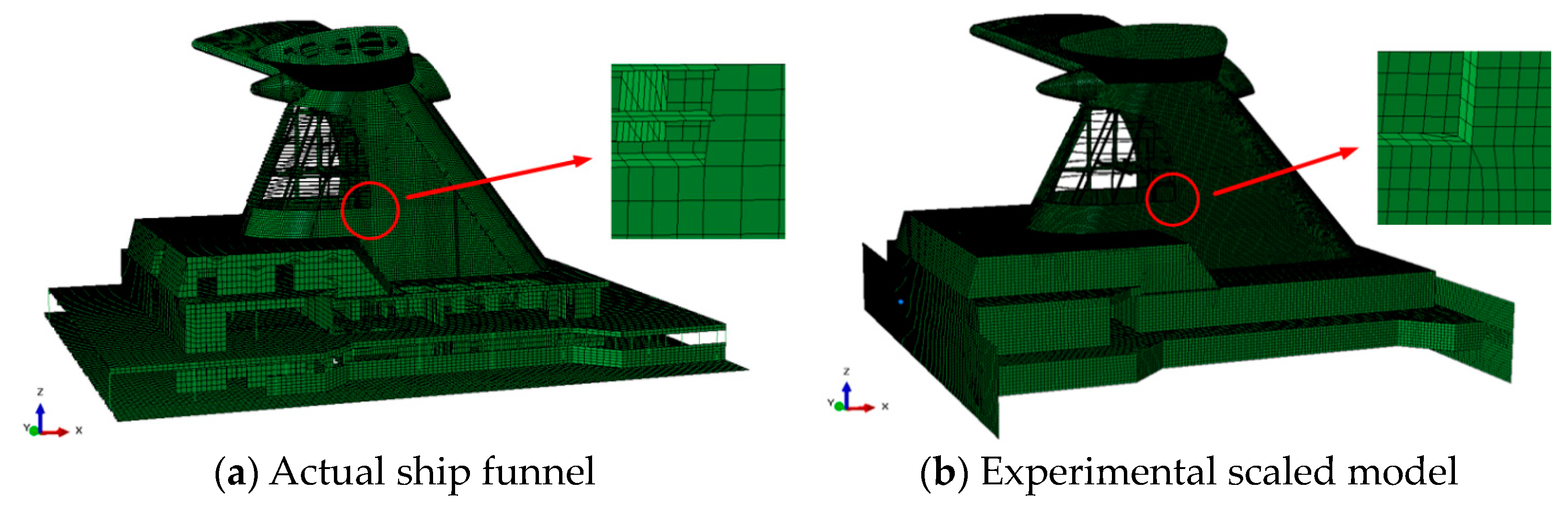
2.2. Model Design
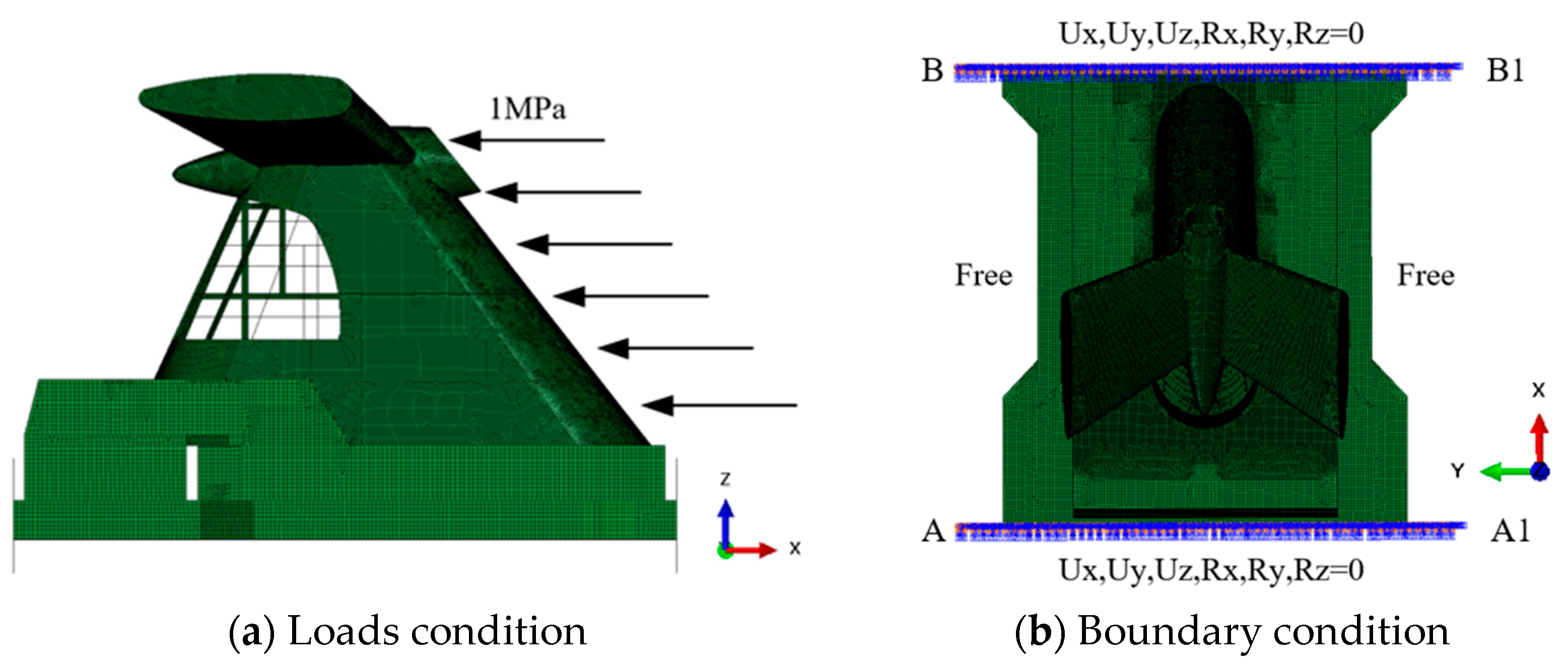
2.3. Experiment Setup
2.4. Tensile Test
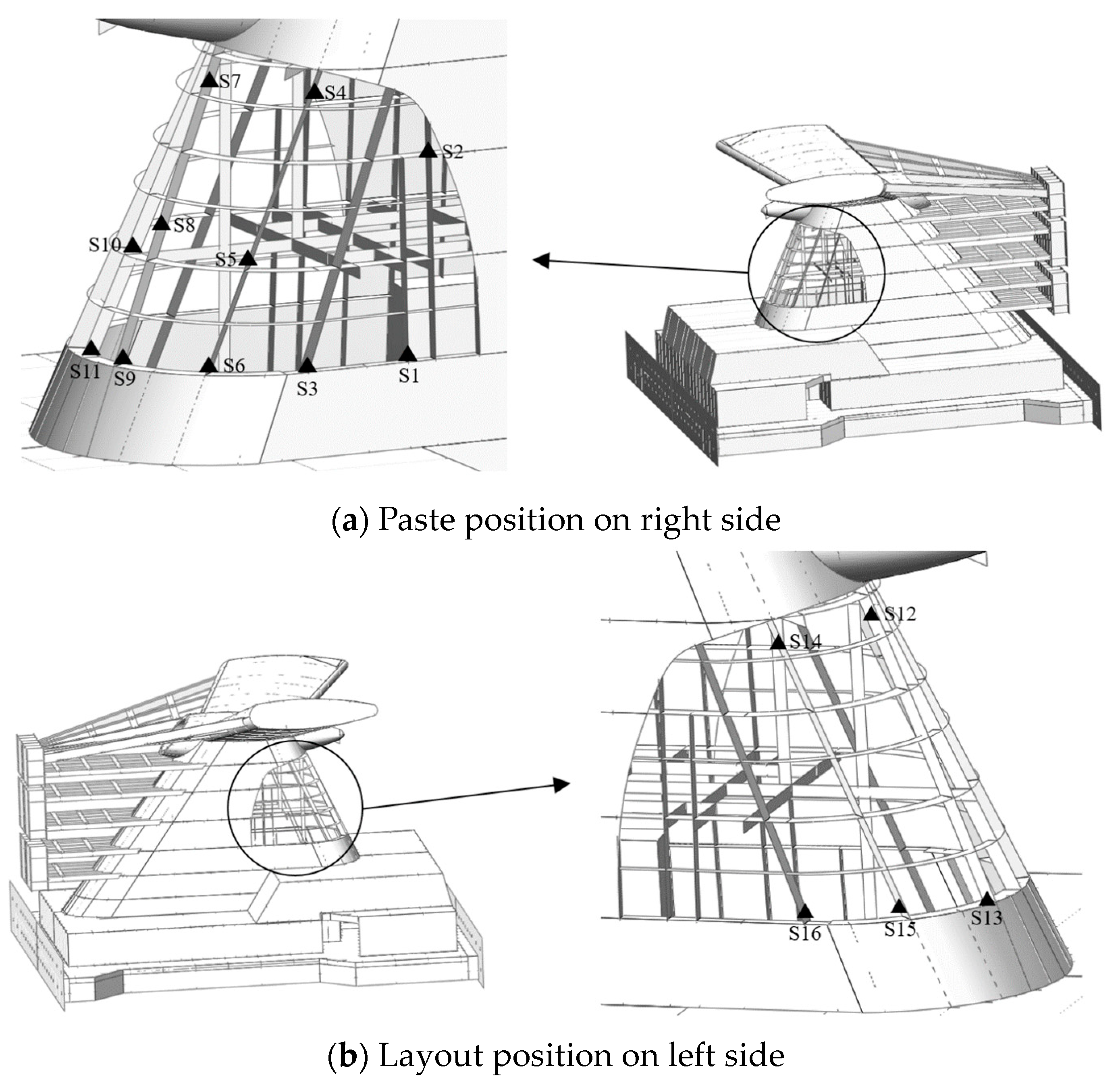
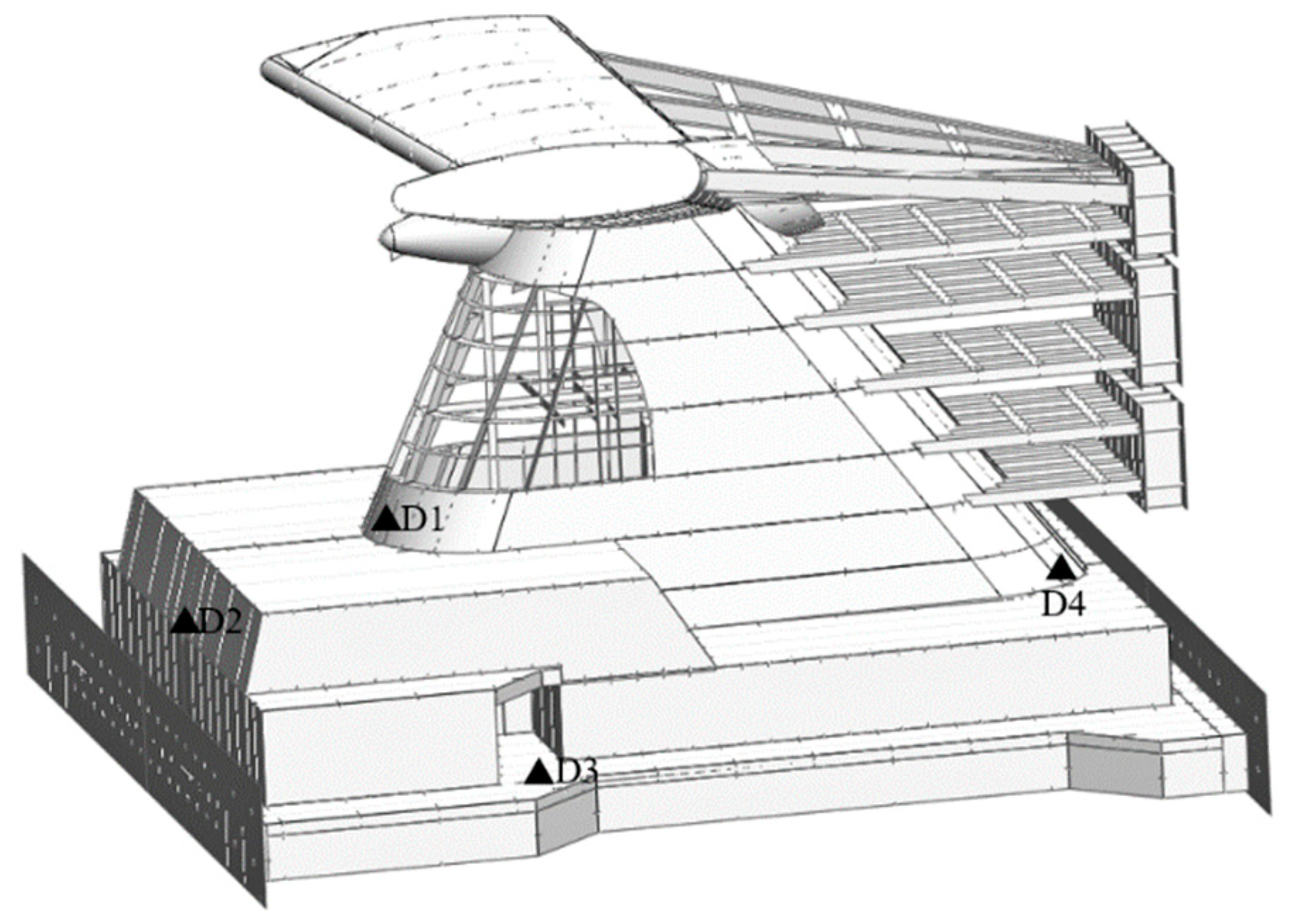
2.5. Measuring Device Setup
3. Experiment Results
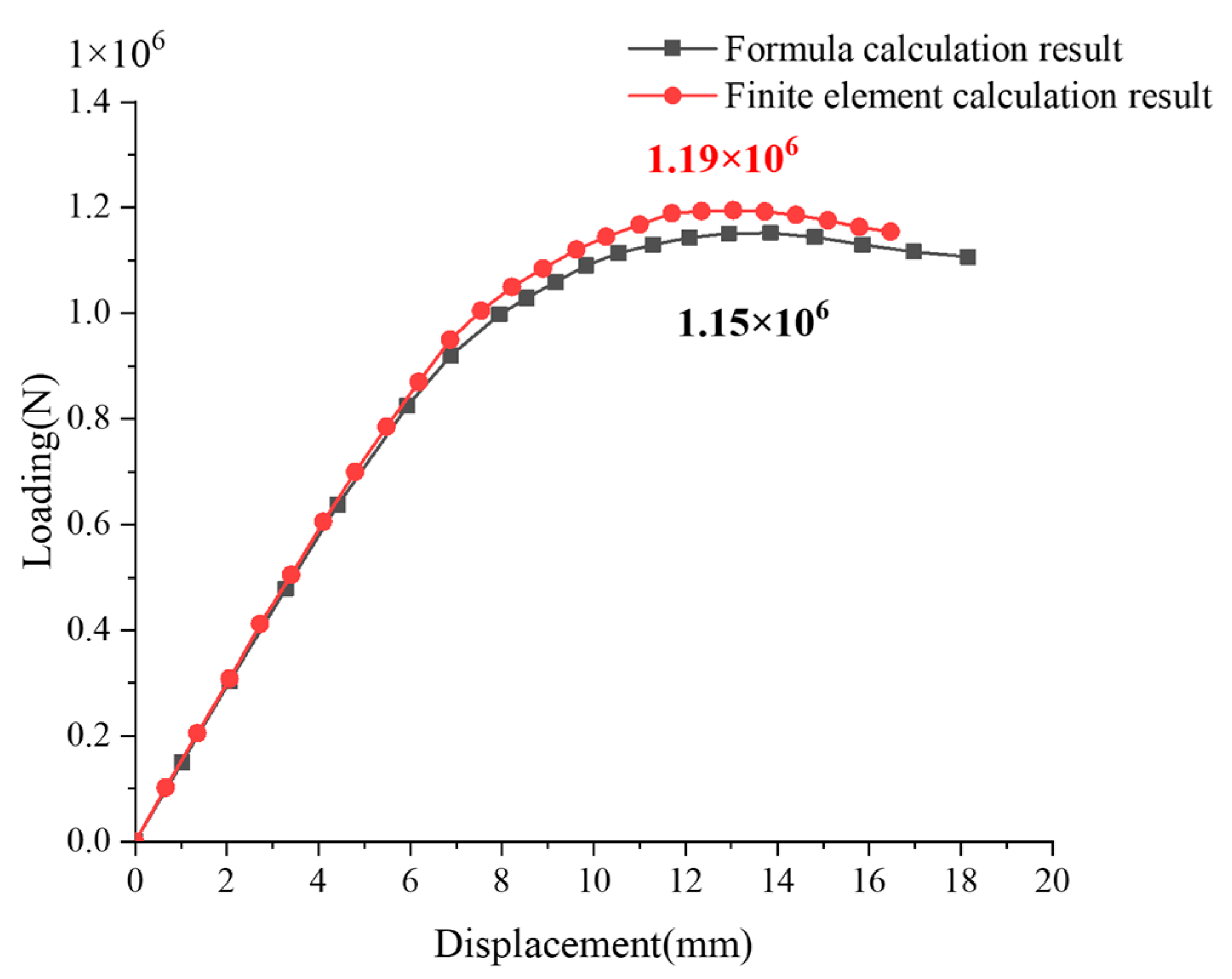
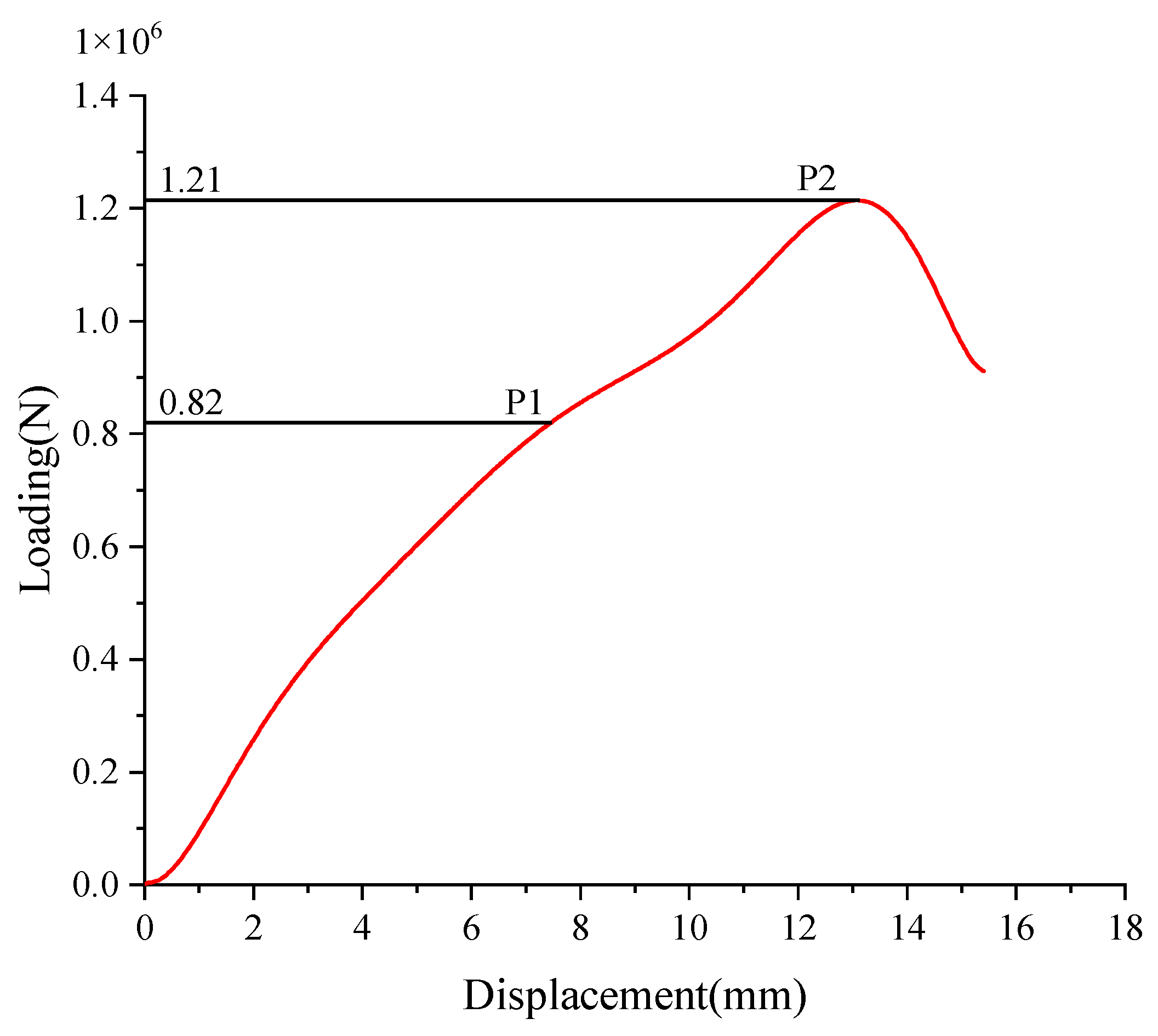
3.1. Load–Displacement Relationship
3.2. Collapse Mode
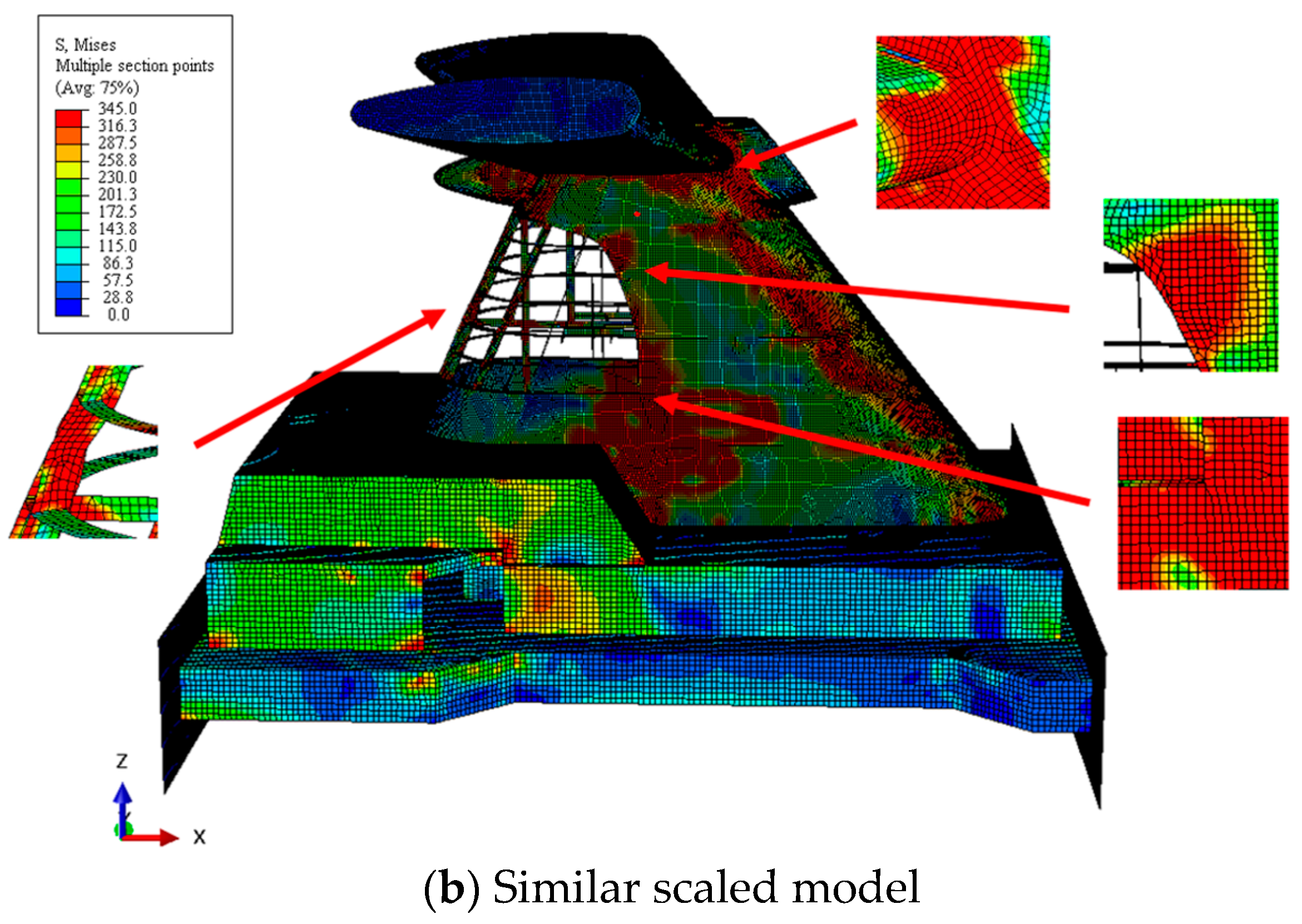
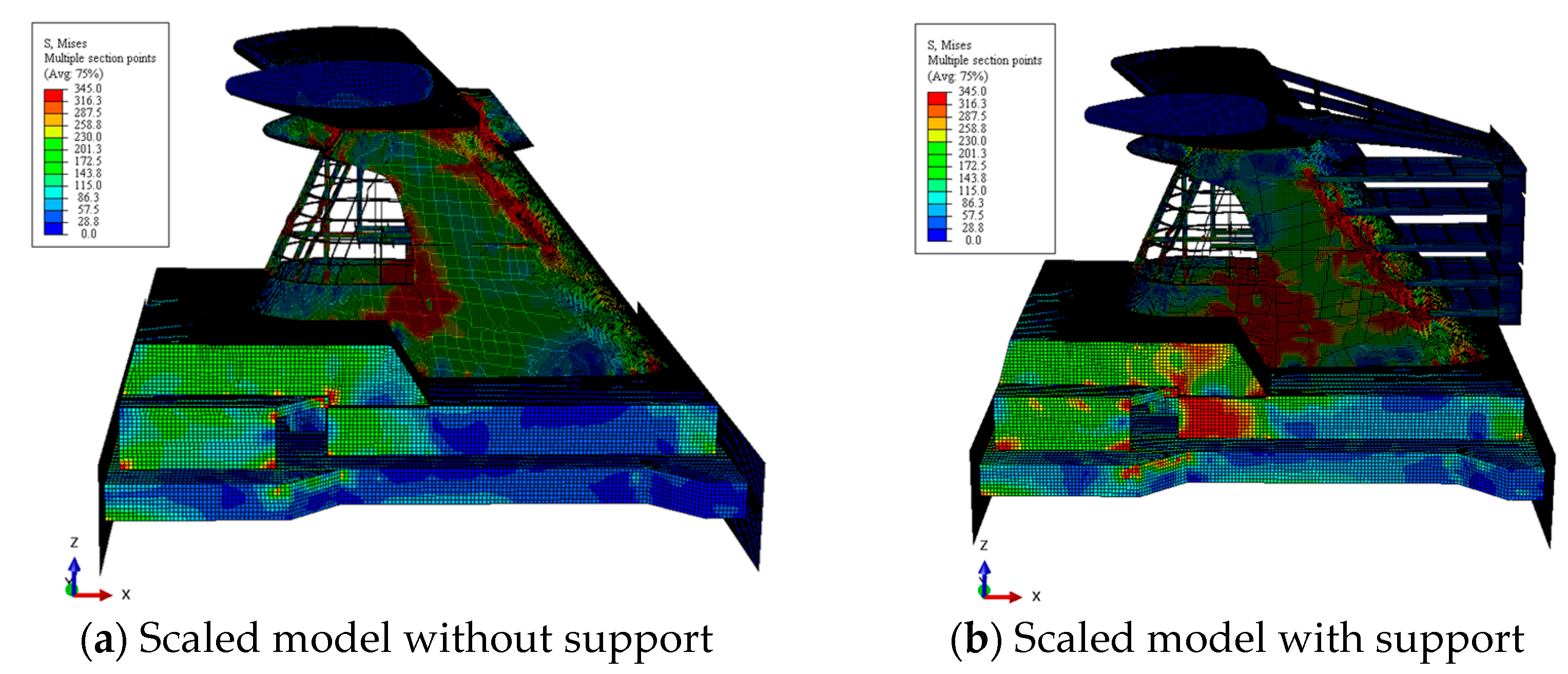
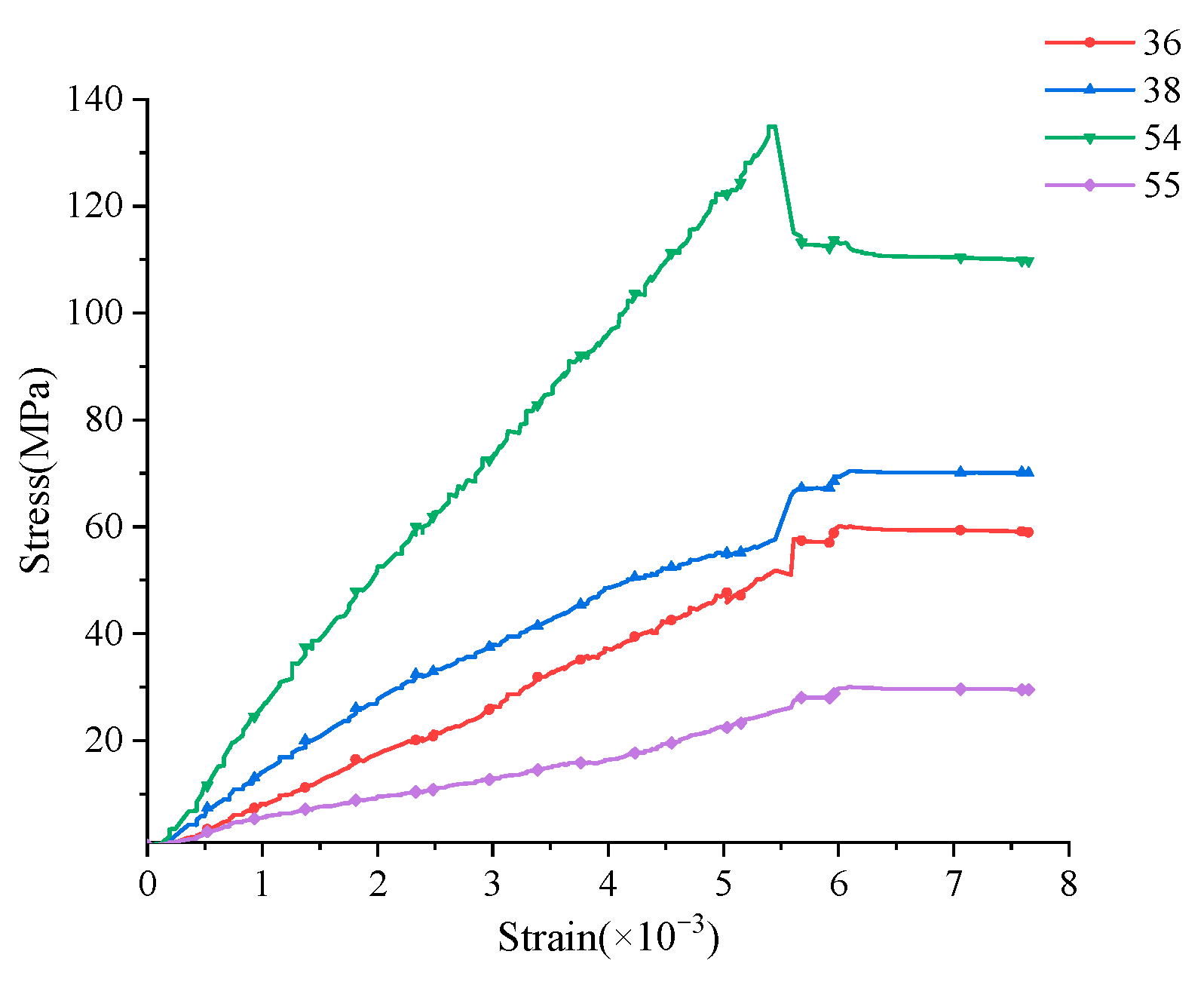
3.3. Stress Distribution
4. Comparison of the Experimental and Numerical Results
5. Discussion
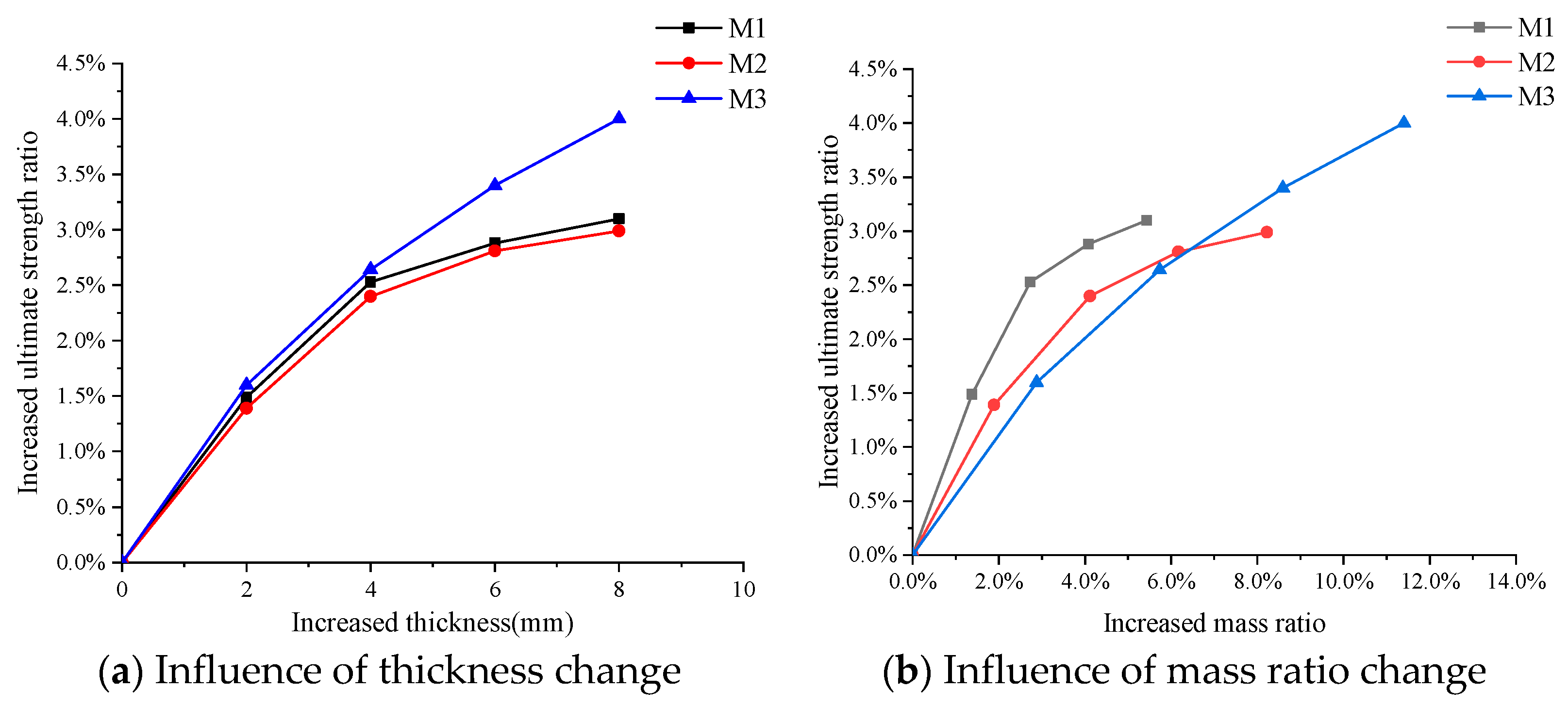
5.1. Effect of Reinforced Stiffeners
5.2. Effect of Member Thickness
5.3. Effect of the Large Opening
6. Conclusions
- (1)
- The designed testing device is valid to apply large wind loads, and the scaled model can accurately present the progressive collapse process of the ship funnel subjected to wind pressure, with an error of 3.5% for predicting the ultimate strength value. The collapse patterns of structures observed in the experiment coincide with those derived from numerical analysis.
- (2)
- The presence of a large opening significantly alters the collapse pattern of the funnel structure, reducing its ultimate strength by 29.2%. The buckling deformation primarily occurs at the opening’s corner, followed by the sudden collapse of the specimen due to plastic deformation at the opening cross-section. The funnel tends to lean backward like a cantilever beam under horizontal wind pressure. The plates and stiffeners near the opening are prone to buckling under compression, and the side plates facing the wind are subjected to tensile stress.
- (3)
- Reinforcing the members surrounding the aperture increases the bending stiffness of the opening section and finally enhances the funnel’s ultimate strength. Thickening the plate material is found to be more effective than merely increasing the thickness of internal stiffeners. The optimal approach for improving structural strength involves ensuring the open section has comparable stiffness to the closed ones, thereby shifting the buckling region to the structures far from the opening. This principle is crucial for the optimal design of structures with inevitable openings.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Janssen, W.D.; Blocken, B.; van Wijhe, H.J. CFD simulations of wind loads on a container ship: Validation and impact of geometrical simplifications. J. Wind. Eng. Ind. Aerodyn. 2017, 166, 106–116. [Google Scholar] [CrossRef]
- Bahatmaka, A.; Kim, D.; Prabowo, A. Numerical Investigation against Laboratory Experiment: An Overview of Damage and Wind Loads on Structural Design. Procedia Struct. Integr. 2020, 27, 6–13. [Google Scholar] [CrossRef]
- Chou, J.; Chiu, C.; Huang, I.; Chi, K.-N. Failure analysis of wind turbine blade under critical wind loads. Eng. Fail. Anal. 2013, 27, 99–118. [Google Scholar] [CrossRef]
- Ishihara, T.; Yamaguchi, A.; Takahara, K.; Mekaru, T.; Matsuura, S. An analysis of damaged wind turbines by typhoon maemi in 2003. In Proceedings of the Sixth Asia-Pacific Conference on Wind Engineering, Seoul, Republic of Korea, 12–14 September 2005. [Google Scholar]
- Bajic, D. Structural design of passenger cruise ships—An introduction to classification requirements. Ships Offsh Struct. 2015, 10, 232–238. [Google Scholar] [CrossRef]
- Jebsen, J.J.; Papakonstantinou, V.C. Evaluation of the Physical Risk of Ship Grounding. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1997. [Google Scholar]
- Wang, P.; Wang, F.; Chen, Z. Investigation on aerodynamic performance of luxury cruise ship. Ocean. Eng. 2020, 213, 107790. [Google Scholar] [CrossRef]
- Doan, V.T.; Liu, B.; Garbatov, Y.; Wu, W.; Guedes Soares, C. Strength assessment of aluminium and steel stiffened panels with openings on longitudinal girders. Ocean. Eng. 2020, 200, 107047. [Google Scholar] [CrossRef]
- Zhou, B.; Han, X.; Guo, W.; Liu, Y.; Tan, S.K. Numerical and experimental study on cutting access opening in ship structure. J. Ship Prod. Des. 2017, 33, 12–23. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, M.; Gao, Y.; Sun, Q. Investigations on shear capacity of steel plates with local opening. J. Constr. Steel Res. 2021, 179, 106518. [Google Scholar] [CrossRef]
- Liu, B.; Du, X.K.; Gan, J.; Ao, L.; Wu, W.; Soares, C.G. Experimental and numerical analysis of the ultimate compressive strength of double-deck structures with a large opening. Ships Offshore Struct. 2022, 17, 2788–2801. [Google Scholar] [CrossRef]
- Liu, B.; Gao, L.J.; Ao, L.; Wu, W. Experimental and numerical analysis of ultimate compressive strength of stiffened panel with openings. Ocean. Eng. 2021, 220, 108453. [Google Scholar] [CrossRef]
- Morshedsolouk, F.; Khedmati, M.R. An extension of coupled beam method and its application to study ship’s hull-superstructure interaction problems. Lat Am J Solids Struct. 2011, 8, 265–290. [Google Scholar] [CrossRef]
- Romanoff, J.; Remes, H.; Varsta, P.; Jelovica, J.; Klanac, A.; Niemelä, A.; Bralic, S.; Naar, H. Hull-superstructure interaction in optimised passenger ships. Ships Offshore Struct. 2012, 8, 612–620. [Google Scholar] [CrossRef]
- Yao, T.; Fujikubo, M.; Yanagihara, D.; Fujii, I.; Matsui, R.; Furui, N.; Kuwamura, Y. Buckling collapse strength of ship carrier under longitudinal bending (1st Report). J. Soc. Nav. Archit. Jpn. 2002, 191, 255–264. [Google Scholar] [CrossRef]
- Benson, S.; AbuBakar, A.; Dow, R.S. A comparison of computational methods to predict the progressive collapse behaviour of a damaged box girder. Eng. Struct. 2013, 48, 266–280. [Google Scholar] [CrossRef]
- Hirdaris, S.E.; Bai, W.; Dessi, D.; Ergin, A.; Gu, X.; Hermundstad, O.A.; Huijsmans, R.; Iijima, K.; Nielsen, U.; Parunov, J.; et al. Loads for use in the design of ships and offshore structures. Ocean. Eng. 2014, 78, 131–174. [Google Scholar] [CrossRef]
- Quispe, J.P.; Estefen, S.F.; de Souza, M.I.L.; Chujutalli, J.H.; Amante, D.D.A.M.; Gurova, T. Numerical and experimental analyses of ultimate longitudinal strength of a small-scale hull box girder. Mar. Struct. 2022, 85, 103273. [Google Scholar] [CrossRef]
- Pei, Z.Y.; Yuan, Q.N.; Ao, L.; Wu, W. A research on similarity law for combined ultimate bending and torsional strength. Ships Offshore Struct. 2023, 1–12. [Google Scholar] [CrossRef]
- Kulkarni, P.R.; Singh, S.N.; Seshadri, V. Parametric Studies of Exhaust Smoke–superstructure Interaction on a Naval Ship Using CFD. Comput Fluids. 2007, 36, 794–816. [Google Scholar] [CrossRef]
- Chen, Q.; Yin, Q.; Fan, A.; Sun, X.; Mou, X. Research on the calculation methods of wind load coefficients of inland cruise ship. In Proceedings of the 2015 International Conference on Transportation Information and Safety (ICTIS), Wuhan, China, 25–28 June 2015; pp. 871–876. [Google Scholar]
- Zhang, J.F.; Pei, H.; Li, J.; Ge, Y.J.; Zhao, L. Failure process and ultimate strength of RC hyperbolic cooling towers under equivalent static wind loads. Thin-Walled Struct. 2022, 176, 109307. [Google Scholar] [CrossRef]
- Bhatt, M.; Vasanwala, S.A. Ultimate Strength of RC Chimney Section under Monotonic Loading. J. Eng. Proj. Prod. Manag. 2022, 12, 217–223. [Google Scholar]
- Wang, C.; Wu, J.; Wang, D. Experimental and numerical investigations on the ultimate longitudinal strength of an ultra large container ship. Ocean. Eng. 2019, 192, 106546. [Google Scholar] [CrossRef]
- Zhang, S.; Khan, I. Buckling and ultimate capability of plates and stiffened panels in axial compression. Mar. Struct. 2009, 22, 791–808. [Google Scholar] [CrossRef]
- Dassault, S. Abaqus Analysis User’s Guide; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2014. [Google Scholar]
- Wang, Q.; Wang, C.; Wu, J.; Wang, D. Investigations on the torsional failure characteristics of the global hull girder with large deck openings. Ocean Eng. 2020, 198, 107007. [Google Scholar] [CrossRef]
- Jimenez-Martinez, M.; Varela-Soriano, J.; Carreón, J.; Torres-Cedillo, S.G. Waveform load analysis for fatigue in the printed PLA. Heliyon 2023, 9, e18480. [Google Scholar] [CrossRef]
- Hoang, T.; Duhamel, D.; Foret, G. Wave finite element method for waveguides and periodic structures subjected to arbitrary loads. Finite Elem. Anal. Des. 2020, 179, 103437. [Google Scholar] [CrossRef]
- Liang, Y.; Ren, X. Failure analysis and curvature-based failure criterion of super large cooling tower under strong equivalent static wind load. Eng. Fail. Anal. 2022, 142, 106801. [Google Scholar] [CrossRef]




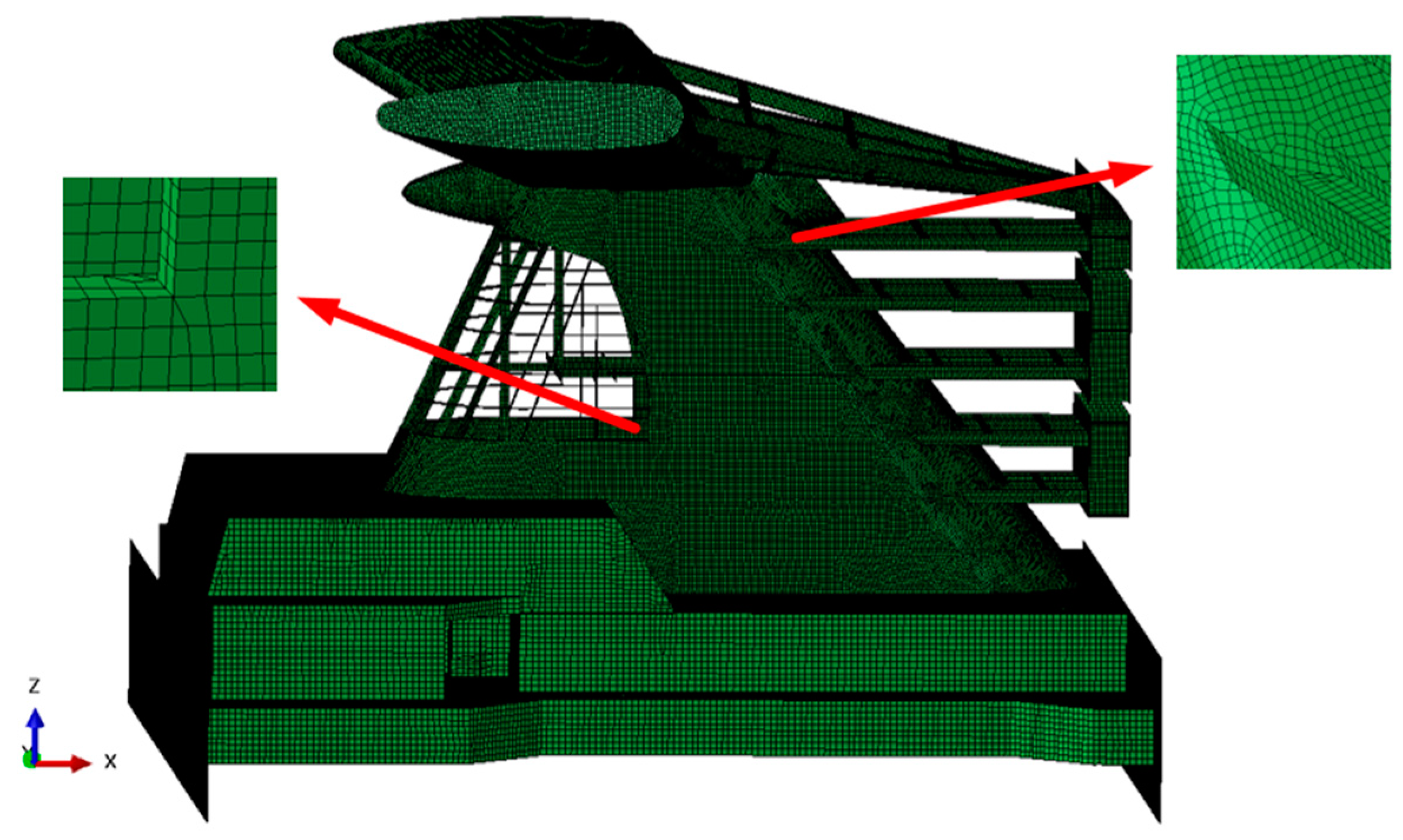

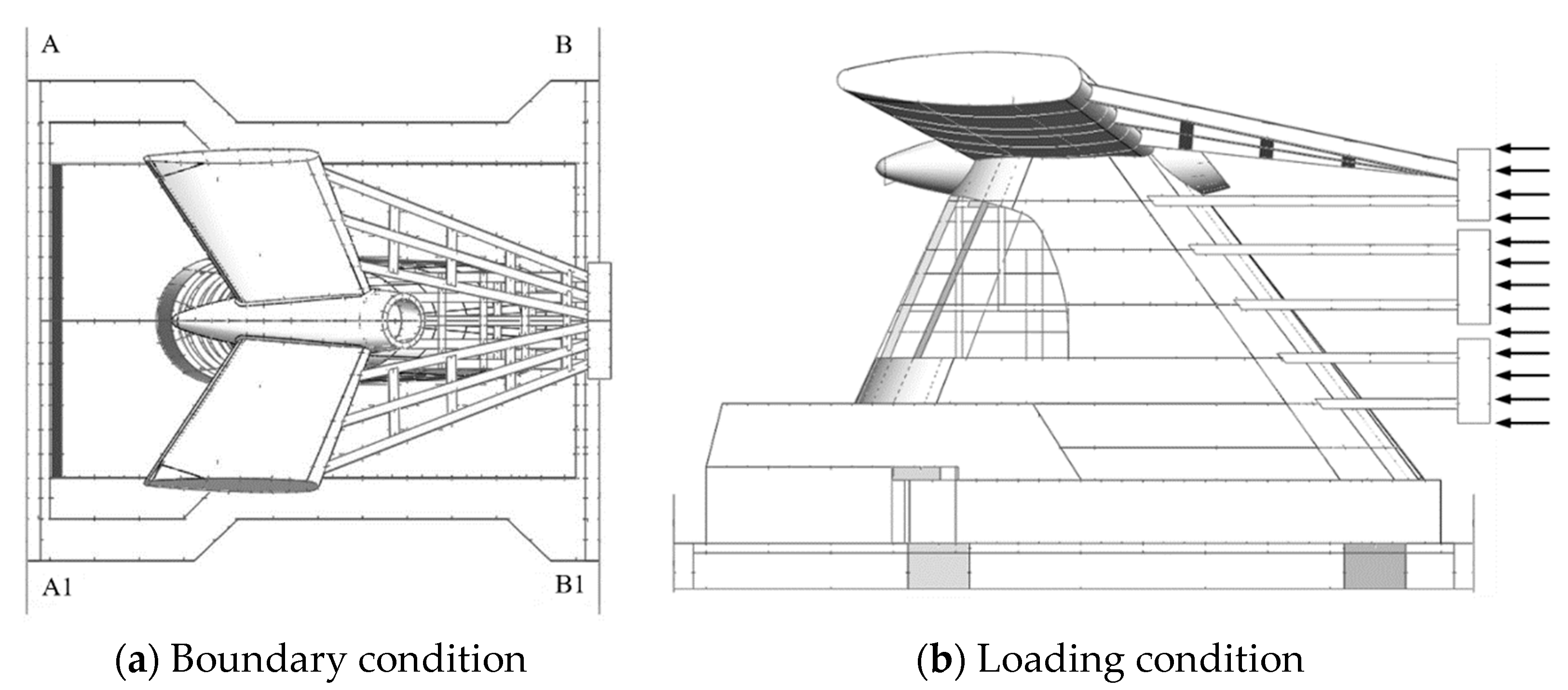


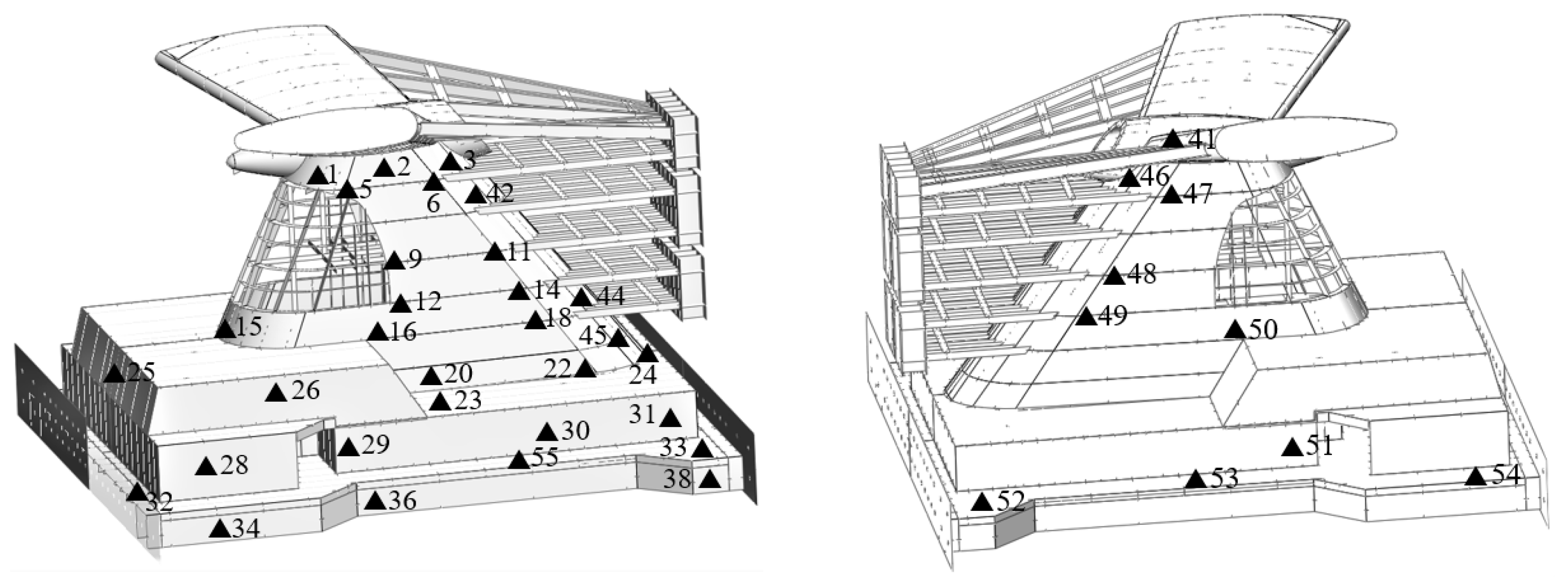







| Section | Parameters | Actual Ship | Similar Transformation | Model | Error |
|---|---|---|---|---|---|
| Deck 1 | Section area (mm2) | 93,519.3 | 3740.8 | 3904.5 | 4.4% |
| Position of neutral axis (mm) | 357.0 | 23.8 | 24.5 | 2.8% | |
| Inertia moment about neutral axis (mm4) | 5.2 × 1010 | 9.2 × 106 | 8.9 × 106 | 3.1% | |
| Deck 2 | Area (mm2) | 116,506.8 | 4660.3 | 4885.5 | 4.8% |
| Position of neutral axis (mm) | 311.4 | 20.8 | 20.5 | 1.2% | |
| Inertia moment about neutral axis (mm4) | 6.3 × 1010 | 1.1 × 106 | 1.1 × 106 | 0.4% | |
| Deck 3 | Section area (mm2) | 104,539.5 | 4181.6 | 4353.5 | 4.1% |
| Position of neutral axis (mm) | 451.1 | 30.1 | 30.4 | 1.1% | |
| Inertia moment about neutral axis (mm4) | 6.1 × 1010 | 1.1 × 106 | 1.1 × 106 | 4.6% | |
| Deck 4 | Section area (mm2) | 137,016.0 | 5480.6 | 5736.0 | 4.7% |
| Position of neutral axis (mm) | 202.5 | 13.5 | 13.6 | 0.5% | |
| Inertia moment about neutral axis (mm4) | 2.5 × 1010 | 4.5 × 106 | 4.4 × 106 | 0.8% | |
| Funnel bottom cross section | Section area (mm2) | 417,581.2 | 16,703.3 | 16,252.3 | 2.7% |
| Moment of inertia (mm4) | 4.6 × 1012 | 8.2 × 108 | 7.9 × 108 | 3.0% | |
| Funnel top cross section | Section area (mm2) | 202,448.3 | 8097.9 | 7807.7 | 3.6% |
| Moment of inertia (mm4) | 1.4 × 1012 | 2.4 × 108 | 2.5 × 108 | 5.1% |
| Members | (Formula) | (FEA) | ||
|---|---|---|---|---|
| The stiffened panel of deck1 | 2.23/2.01 | 0.87/0.88 | 0.62/0.64 | 0.64/0.65 |
| The stiffened panel of funnel body | 2.05/1.96 | 1.36/1.37 | 0.43/0.43 | 0.39/0.41 |
| Thickness | Yield Stress (MPa) |
|---|---|
| 3 mm | 335.4 |
| 4 mm | 348.6 |
| 5 mm | 359.4 |
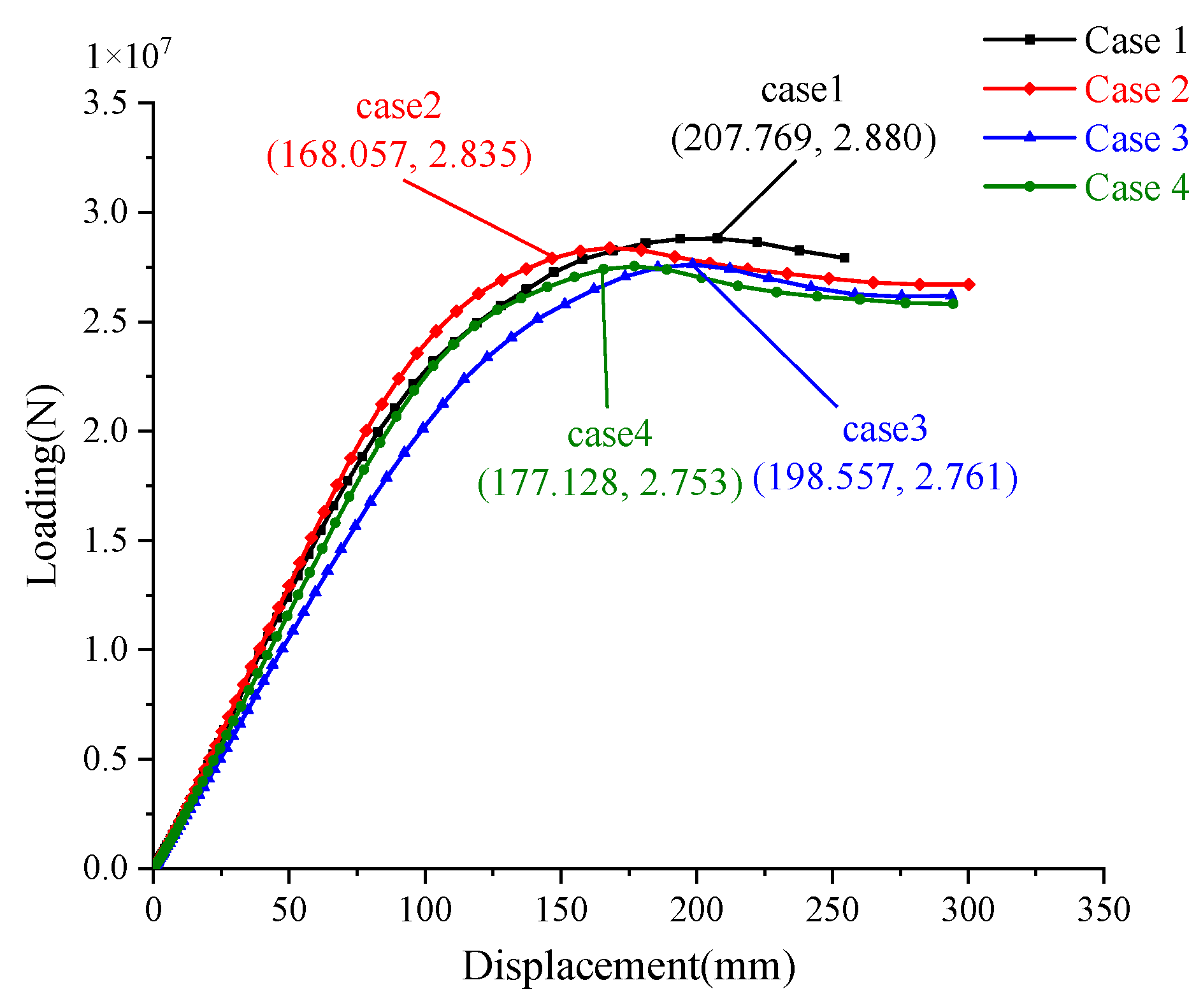
| Case | Reinforced Opening | Stiffener Thickness | Plate Thickness | Ultimate Strength |
|---|---|---|---|---|
| 1 | V + T | 10 mm | 5 mm | 2.880 × 107 N |
| 2 | V | 10 mm | 5 mm | 2.835 × 107 N |
| 3 | T | 10 mm | 5 mm | 2.761 × 107 N |
| 4 | 10 mm | 5 mm | 2.753 × 107 N | |
| 5 | V + T | 10 mm | 7 mm | 2.923 × 107 N |
| 6 | V + T | 10 mm | 9 mm | 2.953 × 107 N |
| 7 | V + T | 10 mm | 11 mm | 2.963 × 107 N |
| 8 | V + T | 10 mm | 13 mm | 2.969 × 107 N |
| 9 | V + T | 12 mm | 5 mm | 2.920 × 107 N |
| 10 | V + T | 14 mm | 5 mm | 2.949 × 107 N |
| 11 | V + T | 16 mm | 5 mm | 2.961 × 107 N |
| 12 | V + T | 18 mm | 5 mm | 2.966 × 107 N |
| 13 | V + T | 12 mm | 7 mm | 2.926 × 107 N |
| 14 | V + T | 14 mm | 9 mm | 2.956 × 107 N |
| 15 | V + T | 16 mm | 11 mm | 2.978 × 107 N |
| 16 | V + T | 18 mm | 13 mm | 2.996 × 107 N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ao, L.; Ding, Z.; Liu, B.; Pei, Z.; Tang, Q.; Wu, W. Experimental and Numerical Analysis of Ultimate Carrying Capacity of a Funnel Structure with Opening under Wind Pressure. J. Mar. Sci. Eng. 2024, 12, 41. https://doi.org/10.3390/jmse12010041
Ao L, Ding Z, Liu B, Pei Z, Tang Q, Wu W. Experimental and Numerical Analysis of Ultimate Carrying Capacity of a Funnel Structure with Opening under Wind Pressure. Journal of Marine Science and Engineering. 2024; 12(1):41. https://doi.org/10.3390/jmse12010041
Chicago/Turabian StyleAo, Lei, Ziqi Ding, Bin Liu, Zhiyong Pei, Qin Tang, and Weiguo Wu. 2024. "Experimental and Numerical Analysis of Ultimate Carrying Capacity of a Funnel Structure with Opening under Wind Pressure" Journal of Marine Science and Engineering 12, no. 1: 41. https://doi.org/10.3390/jmse12010041
APA StyleAo, L., Ding, Z., Liu, B., Pei, Z., Tang, Q., & Wu, W. (2024). Experimental and Numerical Analysis of Ultimate Carrying Capacity of a Funnel Structure with Opening under Wind Pressure. Journal of Marine Science and Engineering, 12(1), 41. https://doi.org/10.3390/jmse12010041








