Numerical Simulation of Icebreaking by Underwater-Explosion Bubbles and Compressed-Gas Bubbles Based on the ALE Method
Abstract
:1. Introduction
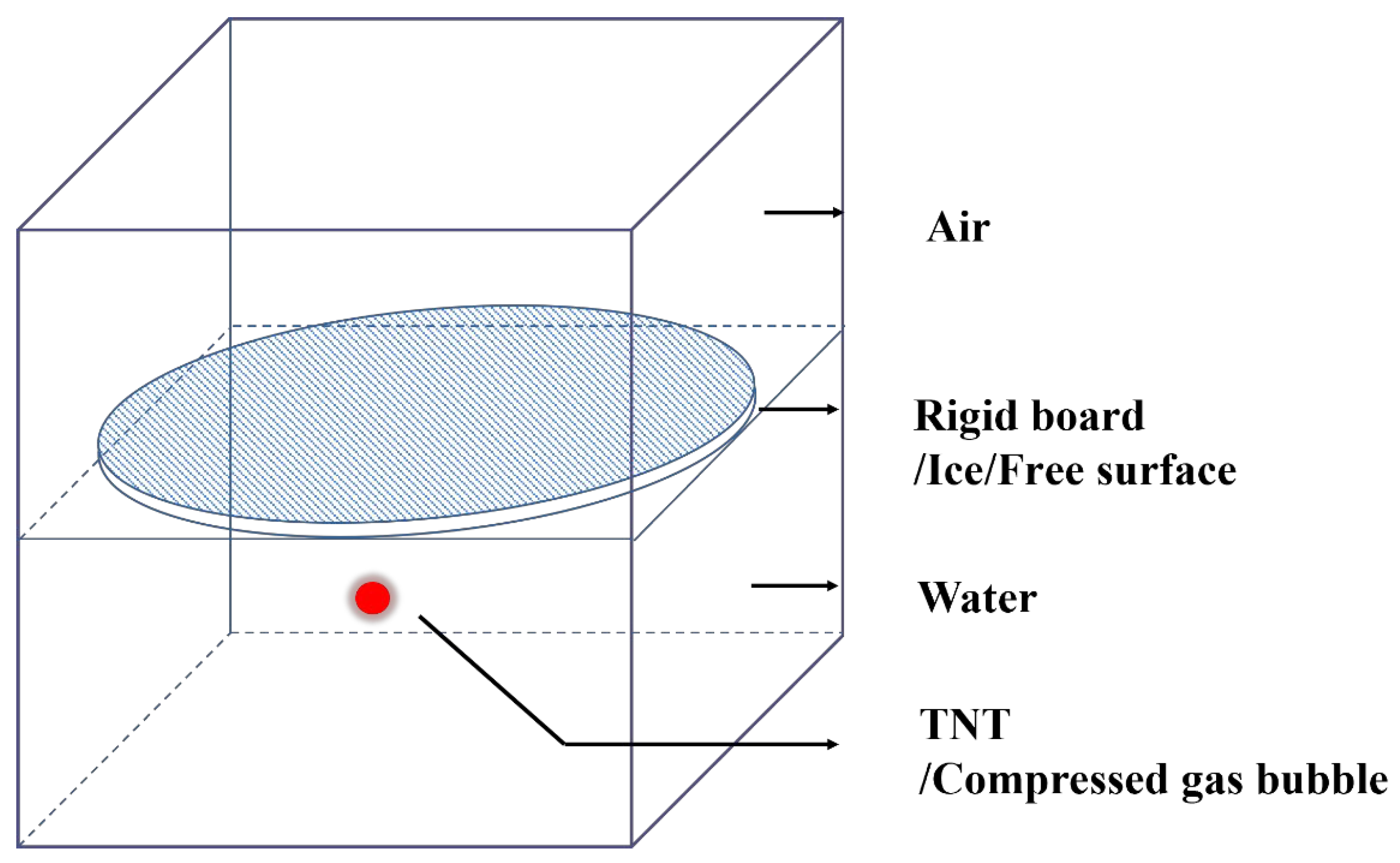
2. Numerical Models and Computational Modeling
2.1. ALE Methodology
2.2. Material Modeling
2.2.1. TNT
2.2.2. Air and Compressed Gas
2.2.3. Water
2.2.4. Ice
2.3. Validation of Numerical Methods
2.3.1. Mesh Independence
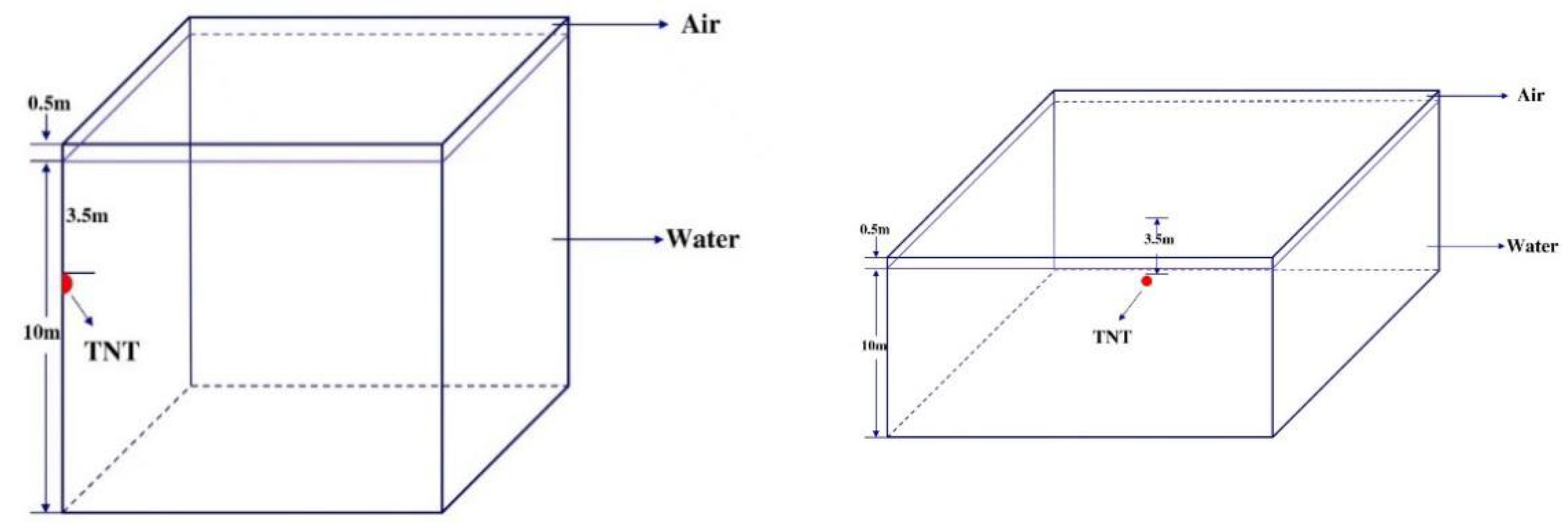
2.3.2. Validation of TNT Underwater Explosion Bubble Model
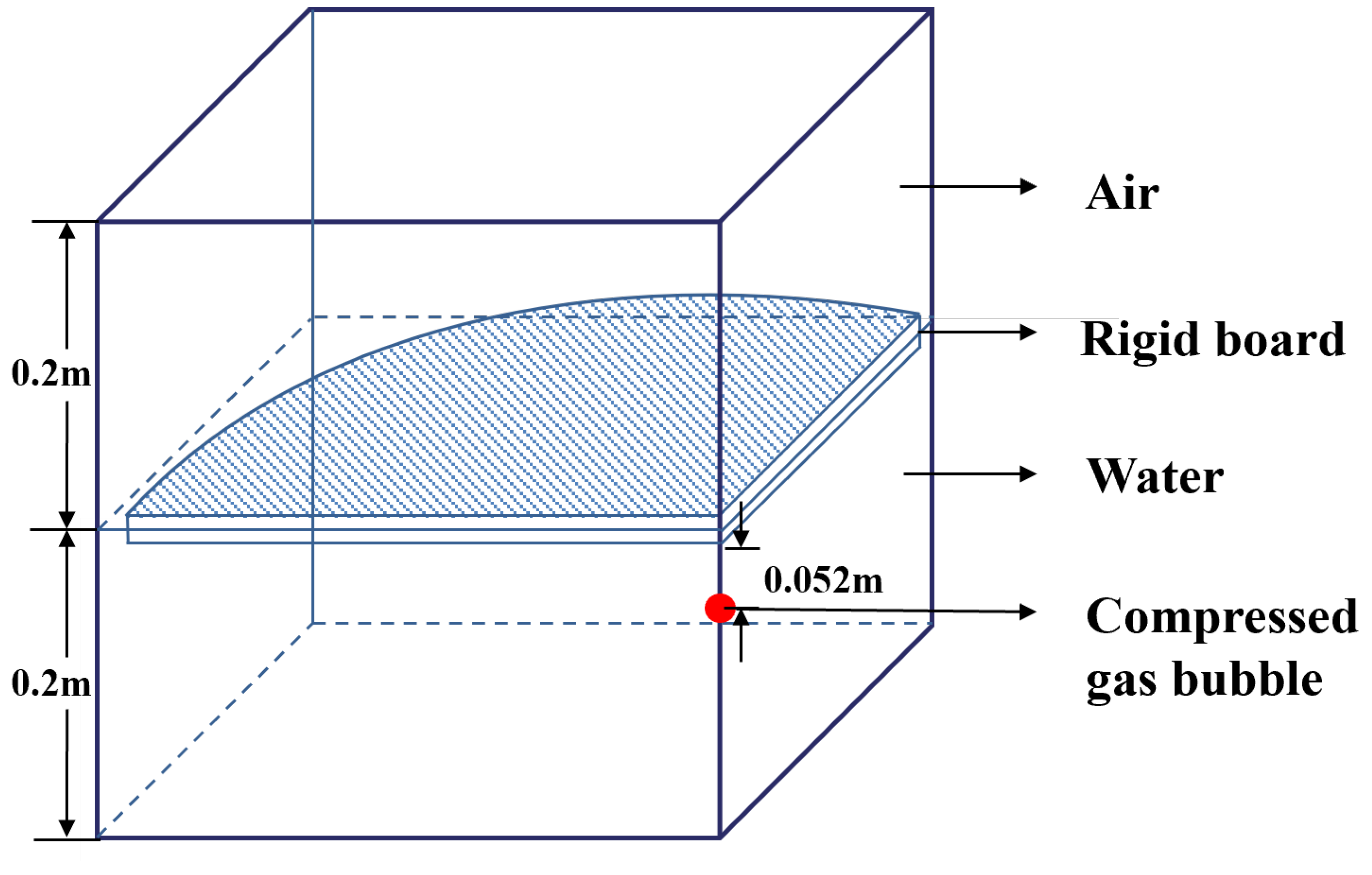
2.3.3. Validation of Compressed Gas Bubble Model
2.3.4. Validation of Compressed Gas Bubble-Ice Coupling Model
3. Numerical Simulation Results and Discussions
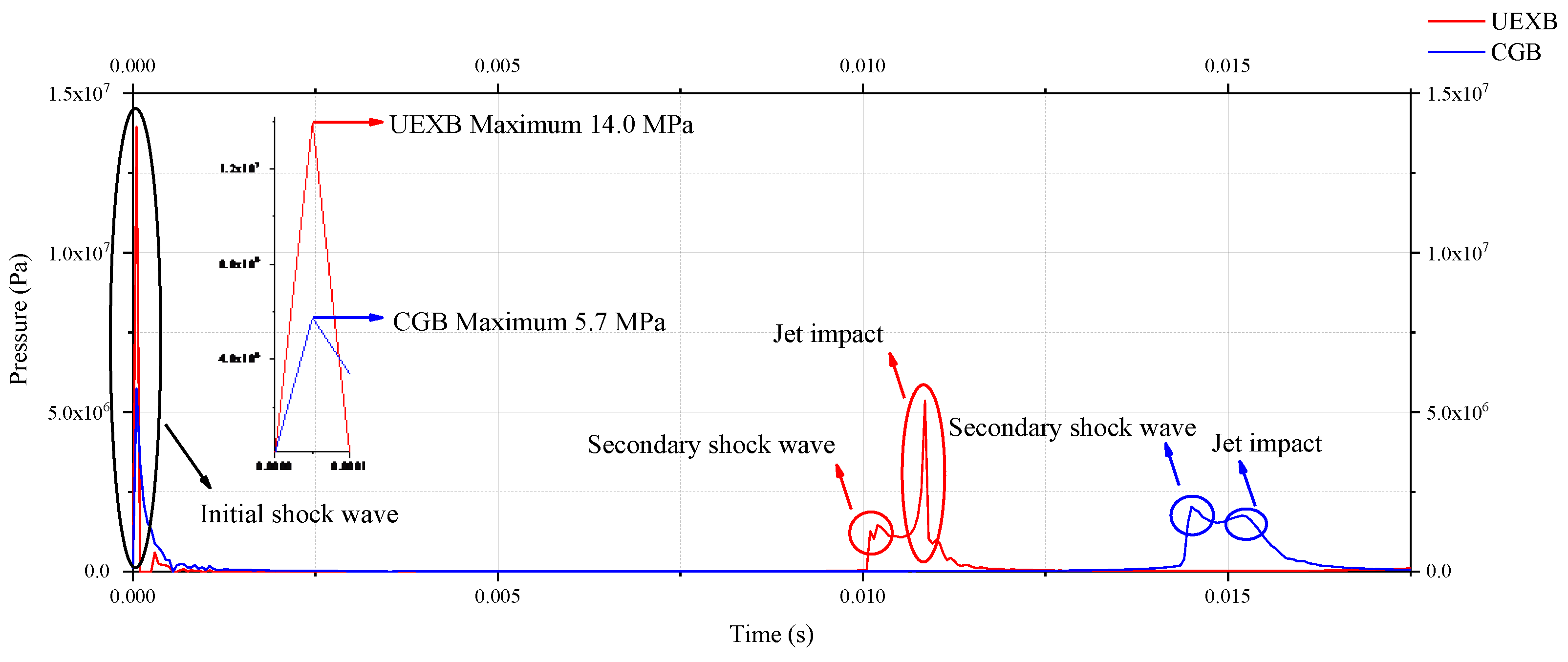
3.1. Characterization of the Compressed Gas Bubble and TNT Underwater Explosive Bubble
3.2. Damage to Ice by Compressed Gas Bubbles and TNT Underwater Explosion Bubbles
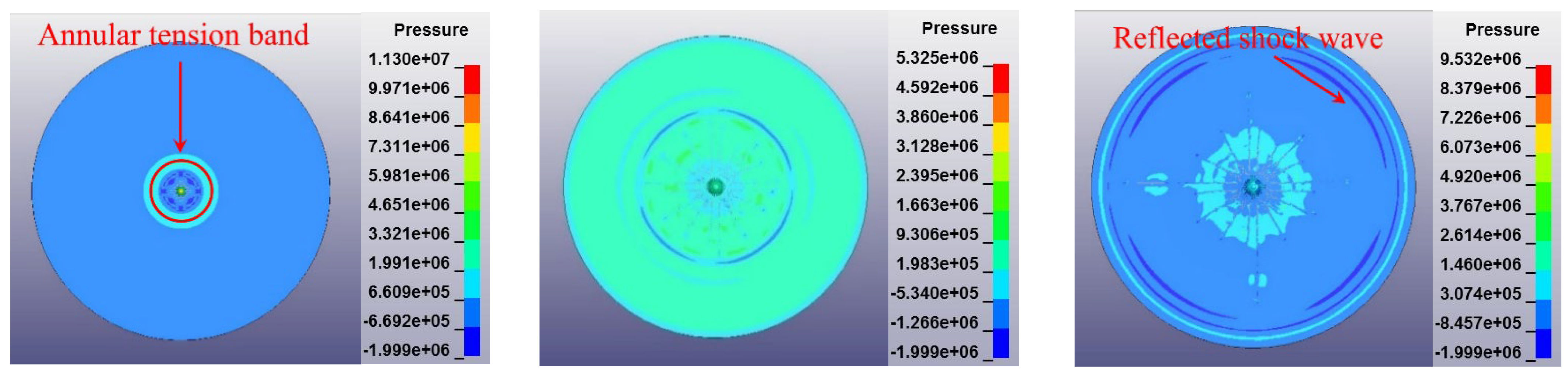
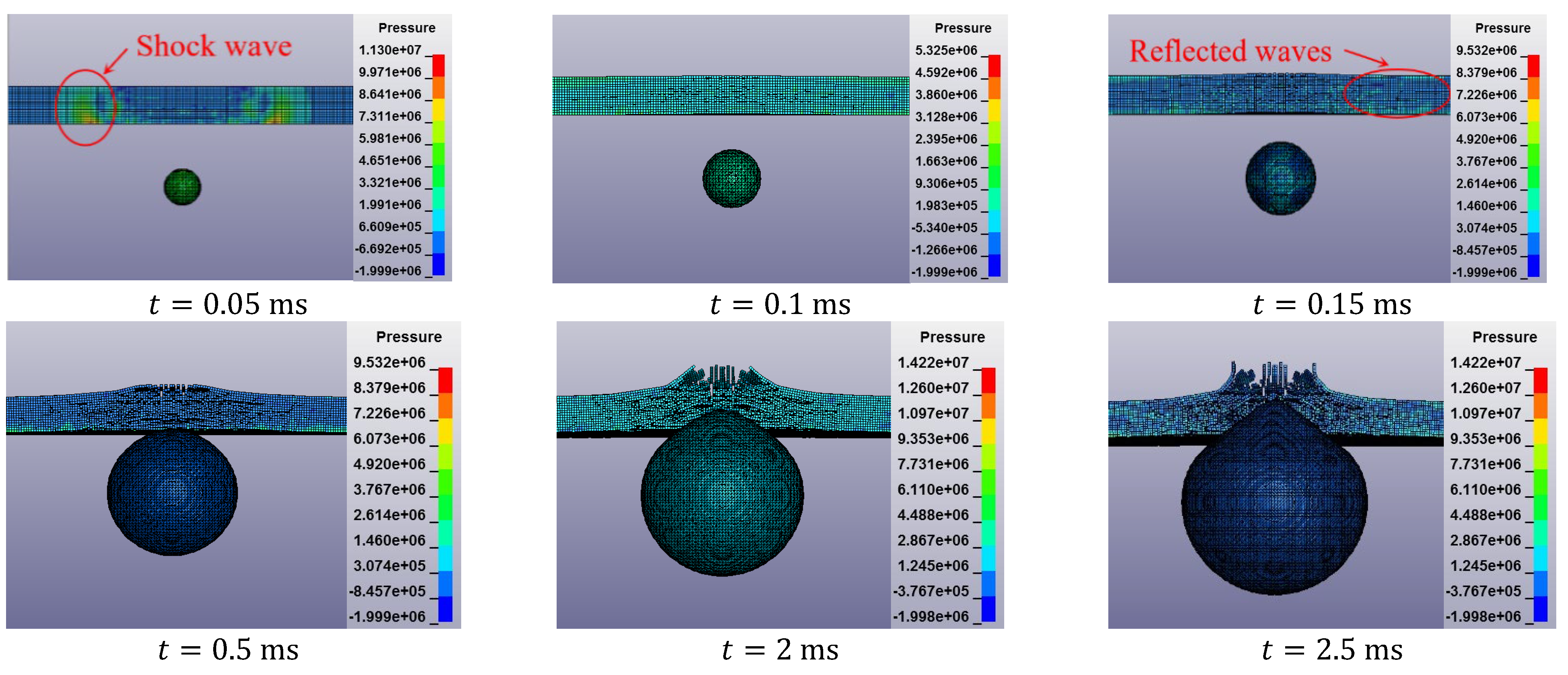
3.2.1. Damage to the Ice by TNT Underwater Explosion Bubbles
3.2.2. Damage to Ice by Compressed Gas Bubbles
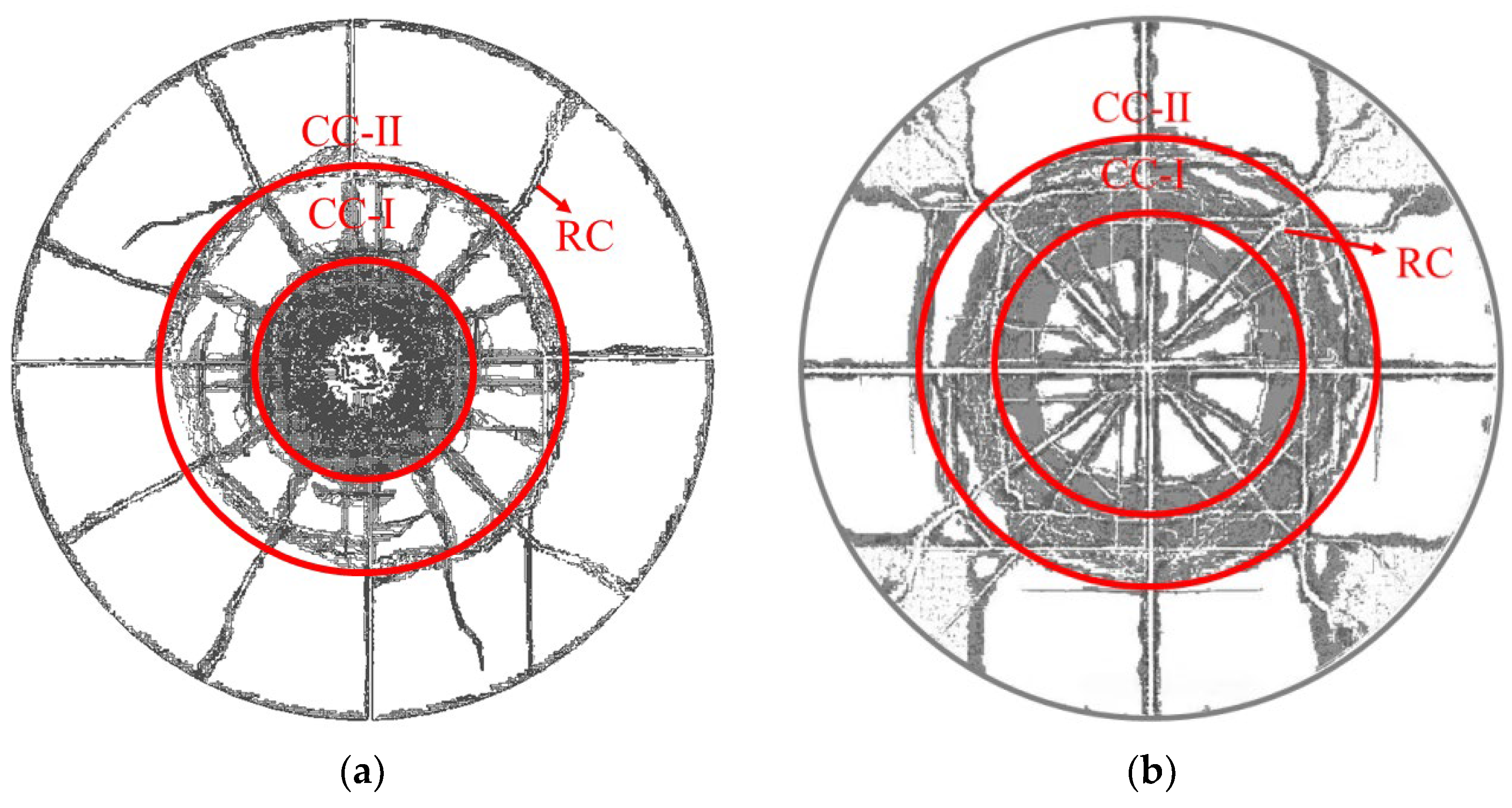
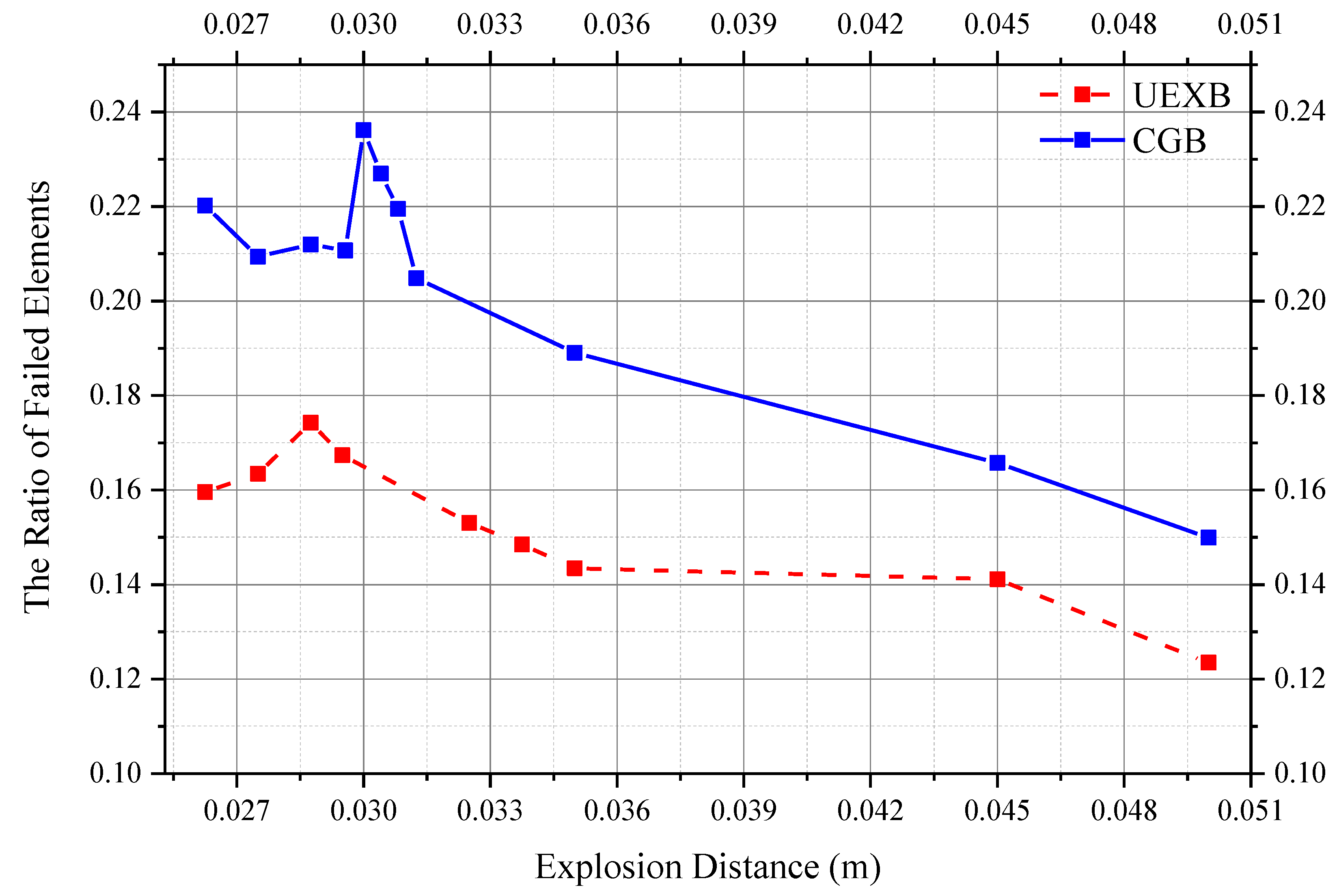
3.2.3. Comparison of Ice Damage by Two Bubble Sources
3.2.4. Optimum Standoff Distance
4. Conclusions
- (1)
- When the initial internal energies of the two bubbles are the same, the CGB has a larger maximum volume than the UEXB, and its period is longer. The UEXB generates a larger shockwave and dissipates more energy. Since this study focuses on near-wall conditions, under the same internal energy conditions, the UEXB’s collapse produces a higher peak jet velocity than the CGB, and the jet duration and secondary shockwave are both shorter than the CGB. This is related to the development of bubbles near the wall.
- (2)
- Due to the larger shockwave generated by the UEXB under the same energy conditions, the UEXB is more likely to create a hole in the ice sheet. The CGB causes a larger damaged area on the ice sheet, and its expansion process has a more pronounced effect on ice sheet damage, resulting in larger ice fragments compared to the UEXB. This is related to the different ways in which the UEXB and CGB damage the ice. Moreover, under the same energy conditions, the total number of failure elements caused by the CGB on the ice sheet is higher than that of the UEXB, indicating an overall better icebreaking effect for the CGB. Additionally, the CGB generates a smaller shockwave, making it a safer option for practical operational scenarios.
- (3)
- The choice of the optimal braking distance is an important issue in practical icebreaking applications. It involves many factors such as the nature of the ice, the characteristics of the bubbles, and boundary conditions. For the parameter of the blast distance discussed in this paper, a smaller blast distance does not necessarily guarantee better icebreaking effects. Further research on this issue will involve more parameters and considerations. For an ice plate with a radius of 0.19 m and a thickness of 0.15 m, the optimum standoff distance of the compressed gas bubble with 120 J is 0.03 m, and the optimum standoff distance of the TNT with 120 J is 0.02875 m.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
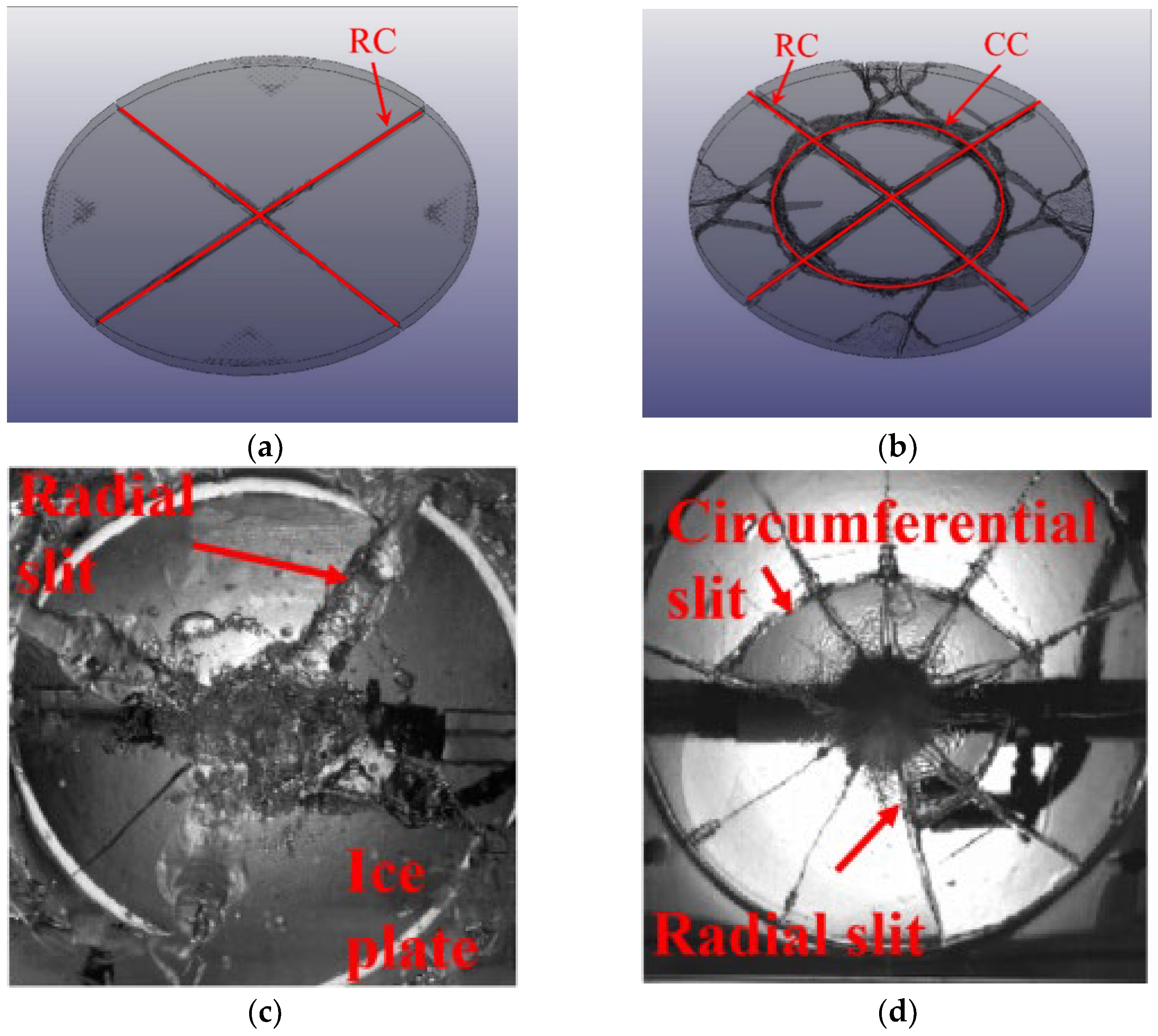
| UEXB | Underwater Explosion Bubble |
| CGB | Compressed Gas Bubble |
| RC | Radical Crack |
| CC | Circumferential Crack |
| CC-1 | First Circumferential Crack |
| CC-2 | Second Circumferential Crack |
References
- Sazonov, K.; Dobrodeev, A. Ice Resistance Assessment for a Large Size Vessel Running in a Narrow Ice Channel Behind an Icebreaker. J. Mar. Sci. Appl. 2021, 20, 446–455. [Google Scholar] [CrossRef]
- Ni, B.Y.; Chen, Z.W.; Zhong, K.; Li, X.A.; Xue, Y.Z. Numerical simulation of a polar ship moving in level ice based on a oneway coupling method. J. Mar. Sci. Eng. 2020, 8, 692. [Google Scholar] [CrossRef]
- Du, Y.; Sun, L.P.; Pang, F.Z.; Li, H.C.; Gao, C. Experimental research of hull vibration of a full-scale river icebreaker. J. Mar. Sci. Appl. 2020, 19, 182–194. [Google Scholar] [CrossRef]
- Ni, B.Y.; Wang, Q.; Xue, Y.Z.; Wang, Y.; Wu, Q.G. Numerical simulation on the damage of ice floe by high-pressure bubble jet loads. In Proceedings of the Workshop and Symposium on Safety and Integrity Management of Operations in Harsh Environments, St. John’s, NL, Canada, 15–17 July 2019. [Google Scholar]
- Ni, B.Y.; Pan, Y.T.; Yuan, G.Y.; Xue, Y.Z. An experimental study on the interaction between a bubble and an ice floe with a hole. Cold Reg. Sci. Technol. 2021, 187, 103281. [Google Scholar] [CrossRef]
- Cui, P.; Zhang, A.M.; Wang, S.; Khoo, B.C. Ice breaking by a collapsing bubble. J. Fluid Mech. 2018, 841, 287–309. [Google Scholar] [CrossRef]
- Kan, X.Y.; Zhang, A.M.; Yan, J.L.; Wu, W.B.; Liu, Y.L. Numerical investigation of ice breaking by a high-pressure bubble based on a coupled BEM-PD model. J. Fluids Struct. 2020, 96, 103016. [Google Scholar] [CrossRef]
- Yuan, G.Y.; Ni, B.Y.; Wu, Q.G.; Xue, Y.Z.; Zhang, A.M. An experimental study on the dynamics and damage capabilities of a bubble collapsing in the neighborhood of a floating ice cake. J. Fluids Struct. 2020, 92, 102833. [Google Scholar] [CrossRef]
- Jorgensen, J.K.; Gyselman, E.C. Hydroacoustic measurements of the behavioral response of arctic riverine fishes to seismic airguns. J. Acoust. Soc. Am. 2009, 126, 1598–1606. [Google Scholar] [CrossRef]
- Nikolaev, S.E. Cutting Sea Ice by Directed Blasting (Opyt Razrusheniya Morskogo lda Napravlennym Vzryovom); Cold regions research and engineering laboratory: Hanover, NH, USA, 1973. [Google Scholar]
- Mellor, M. Breaking Ice with Explosives; Cold Regions Research & Engineering Laboratory, US Army Corps of Engineers: Hanover, NH, USA, 1982; p. 3. [Google Scholar]
- Mellor, M. Derivation of guidelines for blasting floating ice. Cold Reg. Sci. Technol. 1987, 13, 193–206. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, Y.Z.; Yao, X.L. A combined experimental and numerical investigation on damage characteristics of ice sheet subjected to underwater explosion load. Appl. Ocean. Res. 2020, 103, 102347. [Google Scholar] [CrossRef]
- Mellor, M. Breakage of Floating Ice by Compressed Gas Blasting; Industrial Laboratory (USSR): Moscow, Russia, 1972. [Google Scholar]
- Zhang, A.M.; Yao, X.L.; Li, J. The interaction of an underwater explosion bubble and an elastic–plastic structure. Appl. Ocean. Res. 2008, 30, 159–171. [Google Scholar] [CrossRef]
- Zhang, A.M.; Wang, S.P.; Huang, C.; Wang, B. Influences of initial and boundary conditions on underwater explosion bubble dynamics. Eur. J. Mech. B/Fluids 2013, 42, 69–91. [Google Scholar] [CrossRef]
- Li, S.; Zhang, A.M.; Han, R.; Liu, Y.Q. Experimental and numerical study on bubble-sphere interaction near a rigid wall. Phys. Fluids 2017, 29, 092102. [Google Scholar] [CrossRef]
- Zhang, A.; Li, S.M.; Cui, P.; Li, S.; Liu, Y.L. A unified theory for bubble dynamics. Phys. Fluids 2023, 35, 033323. [Google Scholar] [CrossRef]
- Cui, P.; Zhang, A.M.; Wang, S.P.; Liu, Y.L. Experimental study on interaction shock wave emission and ice breaking of two collapsing bubbles. J. Fluid Mech. 2020, 897, A25. [Google Scholar] [CrossRef]
- Wu, Q.G.; Wang, Z.C.; Ni, B.Y.; Yuan, G.Y.; Semenov, Y.A.; Li, Z.Y.; Xue, Y.Z. Ice-Water-Gas Interaction during Icebreaking by an Airgun Bubble. J. Mar. Sci. Eng. 2022, 10, 1302. [Google Scholar] [CrossRef]
- Zhou, P.; Zhu, S. Mechanism analysis of ice damage under underwater near-field explosion. Inter-Noise Noise-Con Congr. Conf. Proc. 2019, 259, 647–658. [Google Scholar]
- Zhang, W.; Shi, D.; Feng, B.; Liu, T. Analysis of meso-mechanism of ice damage under two loads of underwater explosion. In Proceedings of the International Conference on Mechanical Design and Simulation (MDS 2022), Wuhan, China, 18–20 March 2022. [Google Scholar]
- Wang, Y.; Qin, Y.Z.; Wang, Z.K.; Yao, X.L. Numerical study on ice damage characteristics under single explosive and combination explosives. Ocean. Eng. 2021, 223, 108688. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, X.L.; Qin, Y.Z. Investigation on influence factors about damage characteristics of ice sheet subjected to explosion loads: Underwater explosion and air contact explosion. Ocean. Eng. 2022, 260, 111828. [Google Scholar] [CrossRef]
- Liu, J.H.; Wu, Y.; Zhao, B.L. Dynamic Response of FRP Structure under Underwater Explosion Shock Wave. Ship Mech. 2000, 3, 51–58. [Google Scholar]
- An, F.J.; Shi, H.J.; Liu, Q. Near-field pressure characteristics of underwater explosion and its fluid-structure interaction with structure. J. Ordnance Ind. 2015, 36, 13–24. (In Chinese) [Google Scholar]
- L.S. Technology. LS-DYNA Keyword User’s Manual; L.S. Technology: Driffield, UK, 2020. [Google Scholar]
- Zhang, T.T. Study on Protection Characteristics of Ship Side Structure and Equipment under Underwater Contact Explosion. Master’s Thesis, Harbin Engineering University, Harbin, China, 2017. (In Chinese). [Google Scholar]
- Green, L.; Lee, E.; Mitchell, A.; Tipton, R.; van Thiel, M.; Finger, M. UCRL-89664 CA; Lawrence Livemore National Laboratory: Livermore, CA, USA, 1993. [Google Scholar]
- Ralph, M. LA-UR-15-29536; Los Alamos National Laboratory: Los Alamos, NM, USA, 2015. [Google Scholar]
- Khalifa, Y.A.; Lotfy, M.N.; Fathallah, E. Effectiveness of Sacrificial Shielding for Blast Mitigation of Steel Floating Pontoons. J. Mar. Sci. Eng. 2023, 11, 96. [Google Scholar] [CrossRef]
- Alia, A.; Souli, M. High explosive simulation using multi-material formulations. Appl. Therm. Eng. 2006, 26, 1032–1042. [Google Scholar] [CrossRef]
- Hallquist, J.O. LS-DYNA Keyword User’s Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2007; Volume 970, pp. 299–800. [Google Scholar]
- Liu, W.T.; Ming, F.R.; Zhang, A.M.; Miao, X.H.; Liu, Y.L. Continuous simulation of the whole process of underwater explosion based on Eulerian finite element approach. Appl. Ocean. Res. 2018, 80, 125–135. [Google Scholar] [CrossRef]
- Anghileri, M.; Castelletti, L.M.; Invernizzi, F.; Mascheroni, M. A survey of numerical models for hail impact analysis using explicit finite element codes. Int. J. Impact Eng. 2005, 31, 929–944. [Google Scholar] [CrossRef]
- Kim, H.; Welch, D.A.; Kedward, K.T. Experimental investigation of high velocity ice impacts on woven carbon/epoxy composite panels. Compos. Part A Appl. Sci. Manuf. 2003, 34, 25–41. [Google Scholar] [CrossRef]
- Kim, J.H.; Shin, H.C. Application of the ALE technique for underwater explosion analysis of a submarine liquefied oxygen tank. Ocean. Eng. 2008, 35, 812–822. [Google Scholar] [CrossRef]
- Klaseboer, E.; Hung, K.C.; Wang, C.; Wang, C.W.; Khoo, B.C.; Boyce, P.; Debono, S.; Charlier, H. Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure. J. Fluid Mech. 2005, 537, 387–413. [Google Scholar] [CrossRef]
- Cole, R.H. Underwater Explosion; Princeton University Pass: Princeton, NJ, USA, 1948. [Google Scholar]
- Li, X.Y.; Ding, H.J.; Chen, W.Q. Axisymmetric elasticity solutions for a uniformly loaded annular plate of transversely isotropic functionally graded materials. Acta Mech. 2008, 196, 139–159. [Google Scholar] [CrossRef]
- Rabczuk, T. Computational methods for fracture in brittle and quasi-brittle solids: State-of-the-art review and future perspectives. Int. Sch. Res. Not. 2013, 2013, 849231. [Google Scholar] [CrossRef]
- Seagraves, A.N.; Radovitzky, R.A. An analytical theory for radial crack propagation: Application to spherical indentation. J. Appl. Mech. 2013, 80, 041018. [Google Scholar] [CrossRef]
- Yuan, G.Y.; Ni, B.Y.; Wu, Q.G.; Xue, Y.Z.; Han, D.F. Ice breaking by a high-speed water jet impact. J. Fluid Mech. 2022, 934, A1. [Google Scholar] [CrossRef]
- Zhang, A.M. Study on Three-Dimensional Dynamic Characteristics of Underwater Explosion Bubbles. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2006. (In Chinese). [Google Scholar]
- Zong, Z.; Zhao, Y.J.; Zou, L. Numerical Calculation of Damage to Underwater Explosive Structures; Science Press: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Li, J.; Rong, J.L.; Xiang, D.L. Numerical study of bubble motion by underwater explosion near free surface. Eng. Mech. 2011, 27, 200–205. [Google Scholar]
- An, F.J.; Wu, C.; Wang, N.F. A Research on the Energy Dissipation of Underwater Explosion. Trans. Beijing Inst. Technol. 2011, 4, 379–382. [Google Scholar]
- Gong, S.W.; Ohl, S.W.; Klaseboer, E.; Khoo, B.C. Scaling law for bubbles induced by different external sources: Theoretical and experimental study. Phys. Rev. E 2010, 81, 056317. [Google Scholar] [CrossRef] [PubMed]
- Cooper, P.W. Explosives Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Lauterborn, W.; Bolle, H. Experimental investigations of cavitation-bubble collapse in the neighborhood of a solid boundary. J. Fluid Mech. 1975, 72, 391–399. [Google Scholar] [CrossRef]
- Lauterborn, W. Cavitation bubble dynamics-New tools for an intricate problem. Appl. Sci. Res. 1982, 38, 165–178. [Google Scholar] [CrossRef]
- Li, S.; Zhang, A.M.; Han, R. Study on the formation mechanism and loading characteristics of water jet of high-pressure pulsating bubbles in water. Chin. J. Theor. Appl. Mech. 2019, 51, 1666–1681. (In Chinese) [Google Scholar]
- Petrenko, V.F.; Whitworth, R.W. Physics of Ice; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Nguyen, H.; Pathirage, M.; Rezaei, M.; Issa, M.; Cusatis, G.; Bažant, Z.P. New perspective of fracture mechanics inspired by gap test with crack-parallel compression. Proc. Natl. Acad. Sci. USA 2020, 117, 14015–14020. [Google Scholar] [CrossRef]









| 1630 | 3.71 × 1011 | 3.21 × 109 | 4.15 | 0.95 | 0.3 | 7 × 109 |
| 1.225 | 0 | 0 | 0 | 0 | 0.4 | 0.4 | 0 | 2.5 × 105 | 1 |
| 1025 | 2.56 | −1.986 | 0.2268 | 0.4934 | 0.0 |
| Young’ Modulus (GPa) | Poisson’s Ratio | Failure Strain | Tension Strength (MPa) | |
|---|---|---|---|---|
| 900 | 6.25 | 0.33 | 0.35 | −2 |
| Media | Model Size | Mesh Size | Mesh Type | Boundary Condition |
|---|---|---|---|---|
| Air | 10 m × 10 m × 0.5 m | 0.0125 m | Hexahedral mesh | Non-reflective boundary |
| Water | 10 m × 10 m × 10 m | 0.0125 m | Hexahedral mesh | Non-reflective boundary |
| Media | Model Size | Mesh Size | Mesh Type | Boundary Condition |
|---|---|---|---|---|
| Air | 0.4 m × 0.4 m × 0.2 m | 0.00125 m | Hexahedral mesh | Non-reflective boundary |
| Water | 0.4 m × 0.4 m × 0.2 m | 0.00125 m | Hexahedral mesh | Non-reflective boundary |
| Rigid circular board | Radius 0.19 m Thickness 0.15 m | 0.00125 m | Hexahedral mesh | Rigid fixing |
| Media | Model Size | Mesh Size | Mesh Type | Boundary Condition |
|---|---|---|---|---|
| Air | 0.4 m × 0.4 m × 0.2 m | 0.00125 m | Hexahedral mesh | Non-reflective boundary |
| Water | 0.4 m × 0.4 m × 0.2 m | 0.00125 m | Hexahedral mesh | Non-reflective boundary |
| Rigid ice plate | Radius 0.19 Thickness 0.15 m | 0.00125 m | Hexahedral mesh | Free-floating |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.; Ni, B.-Y.; Wu, Q.; Wang, Z.; Liu, P.; Xue, Y. Numerical Simulation of Icebreaking by Underwater-Explosion Bubbles and Compressed-Gas Bubbles Based on the ALE Method. J. Mar. Sci. Eng. 2024, 12, 58. https://doi.org/10.3390/jmse12010058
Yu Z, Ni B-Y, Wu Q, Wang Z, Liu P, Xue Y. Numerical Simulation of Icebreaking by Underwater-Explosion Bubbles and Compressed-Gas Bubbles Based on the ALE Method. Journal of Marine Science and Engineering. 2024; 12(1):58. https://doi.org/10.3390/jmse12010058
Chicago/Turabian StyleYu, Zerui, Bao-Yu Ni, Qigang Wu, Zuocheng Wang, Peng Liu, and Yanzhuo Xue. 2024. "Numerical Simulation of Icebreaking by Underwater-Explosion Bubbles and Compressed-Gas Bubbles Based on the ALE Method" Journal of Marine Science and Engineering 12, no. 1: 58. https://doi.org/10.3390/jmse12010058
APA StyleYu, Z., Ni, B.-Y., Wu, Q., Wang, Z., Liu, P., & Xue, Y. (2024). Numerical Simulation of Icebreaking by Underwater-Explosion Bubbles and Compressed-Gas Bubbles Based on the ALE Method. Journal of Marine Science and Engineering, 12(1), 58. https://doi.org/10.3390/jmse12010058







