Numerical Investigation into the Dynamic Responses of Floating Photovoltaic Platform and Mooring Line Structures under Freak Waves
Abstract
:1. Introduction
2. Modeling Methods
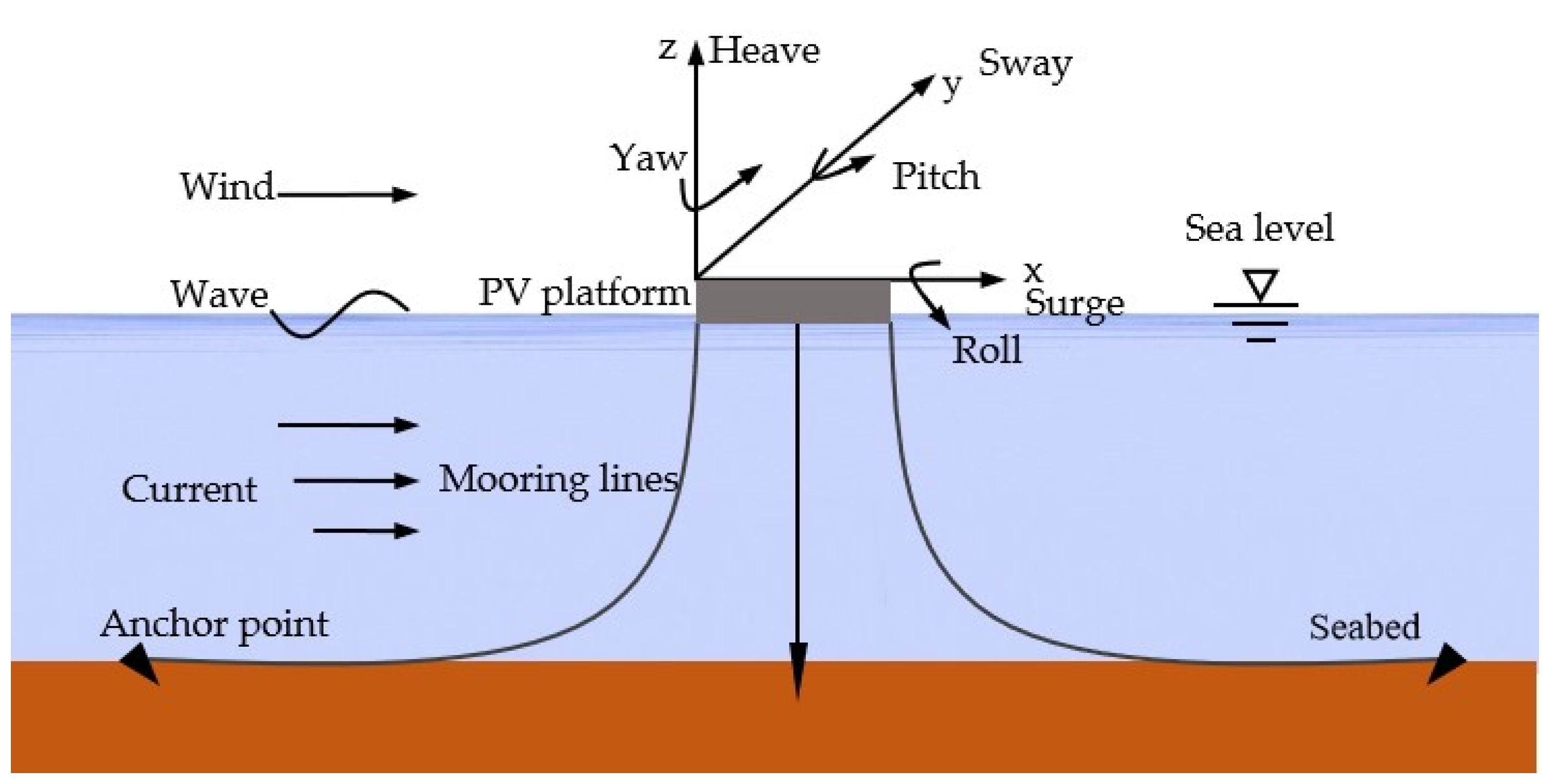
2.1. PV Platform Motion Equations
2.2. Mooring Line Model
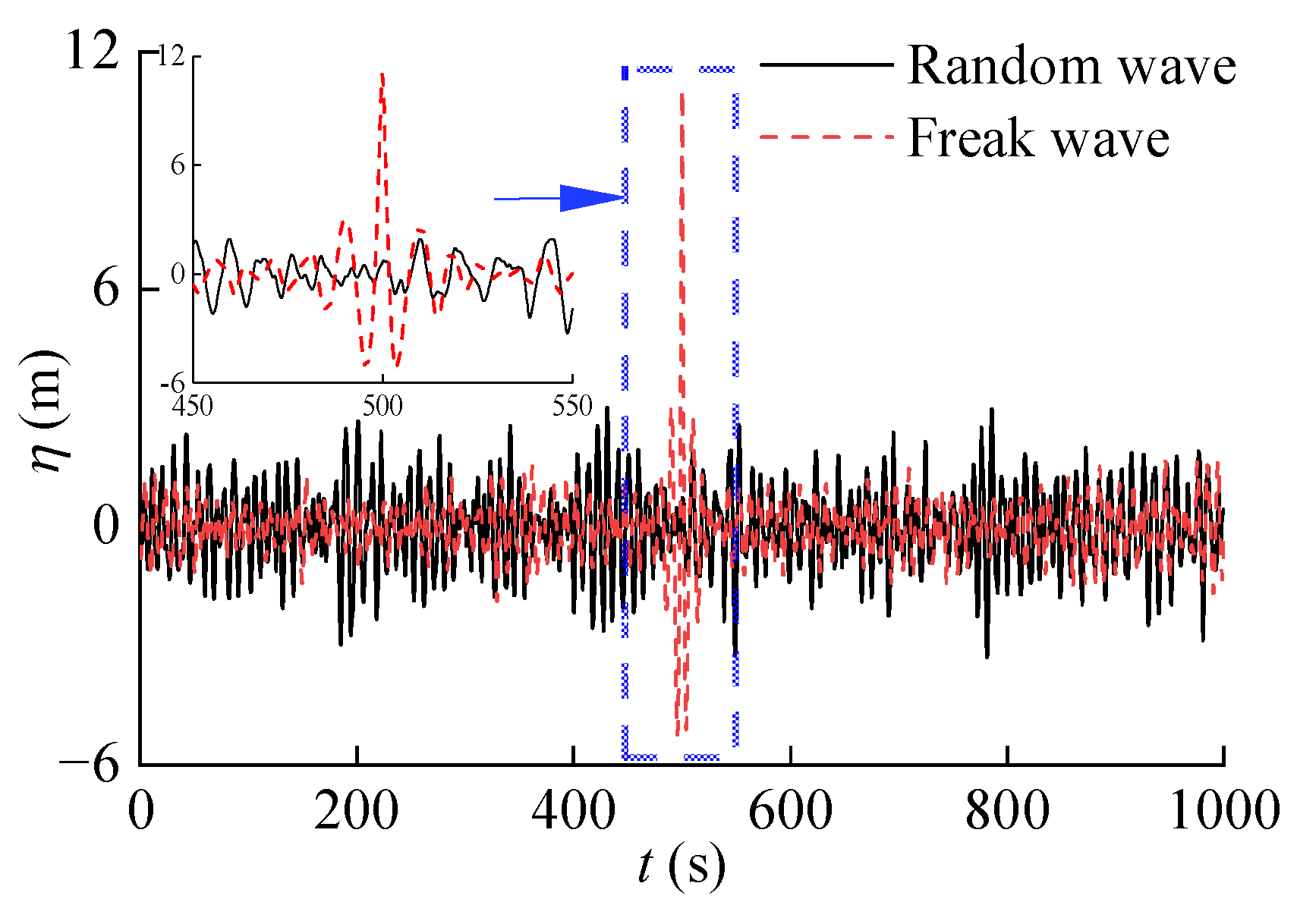
2.3. Generation Model of Random and Freak Waves
3. Numerical Implementation
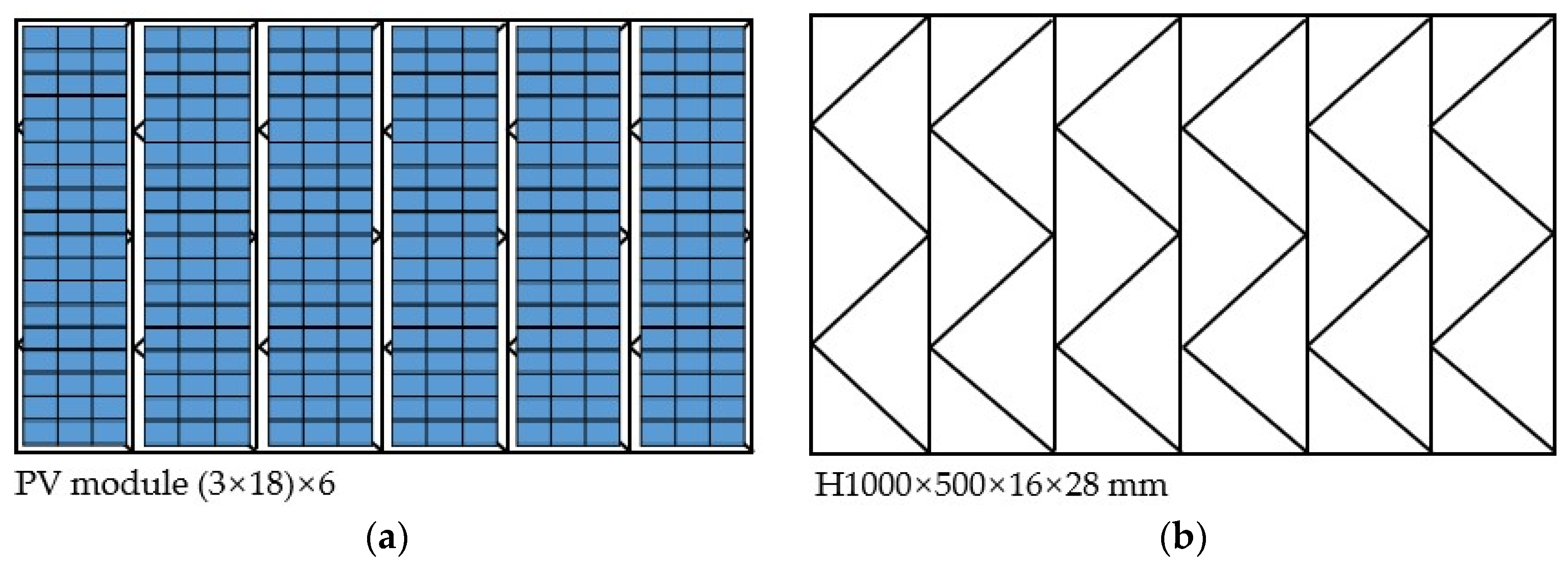
3.1. Basic Parameters of PV Platform and Mooring Structure
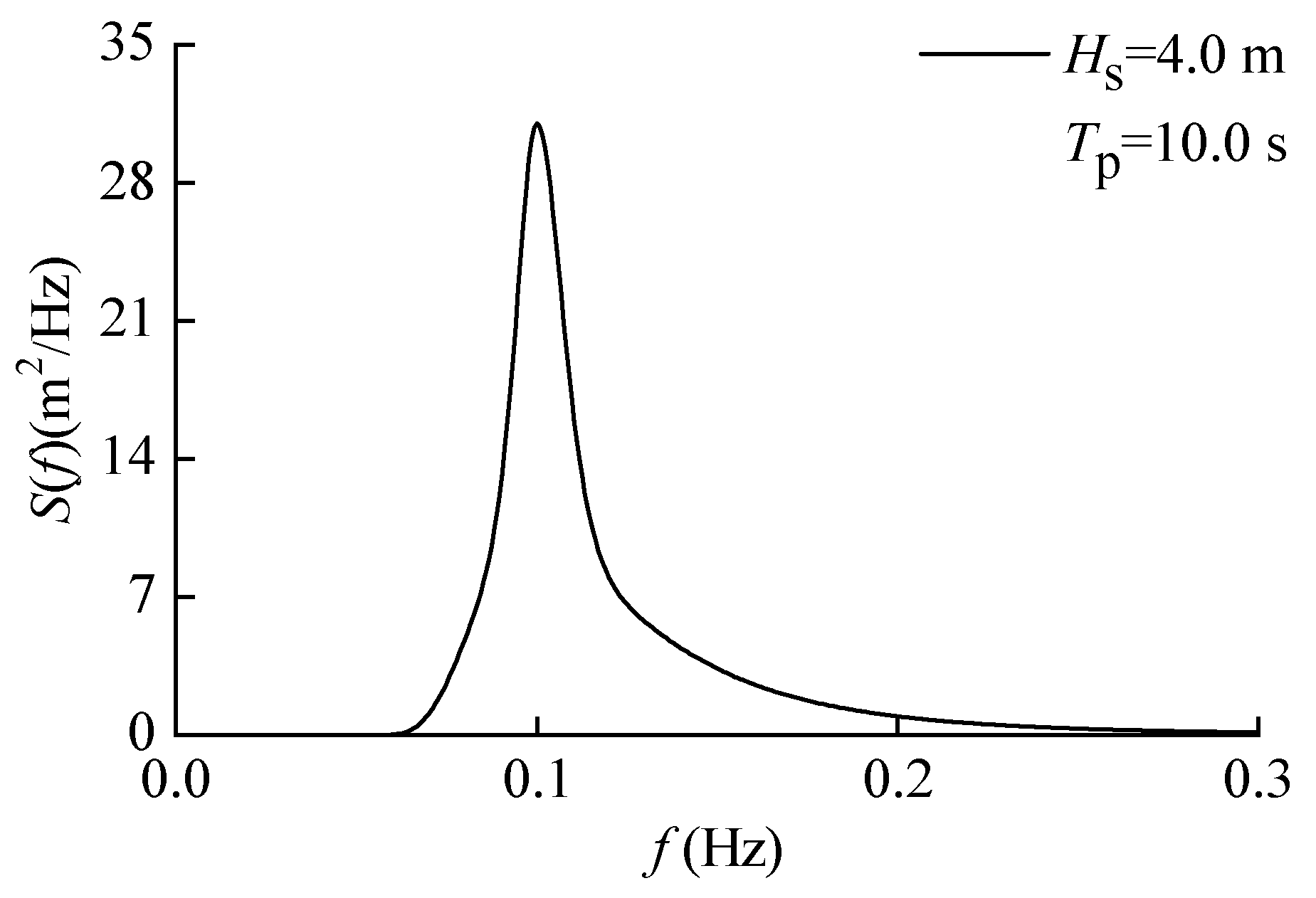
3.2. Ocean Environmental Conditions
3.3. Implementation Process
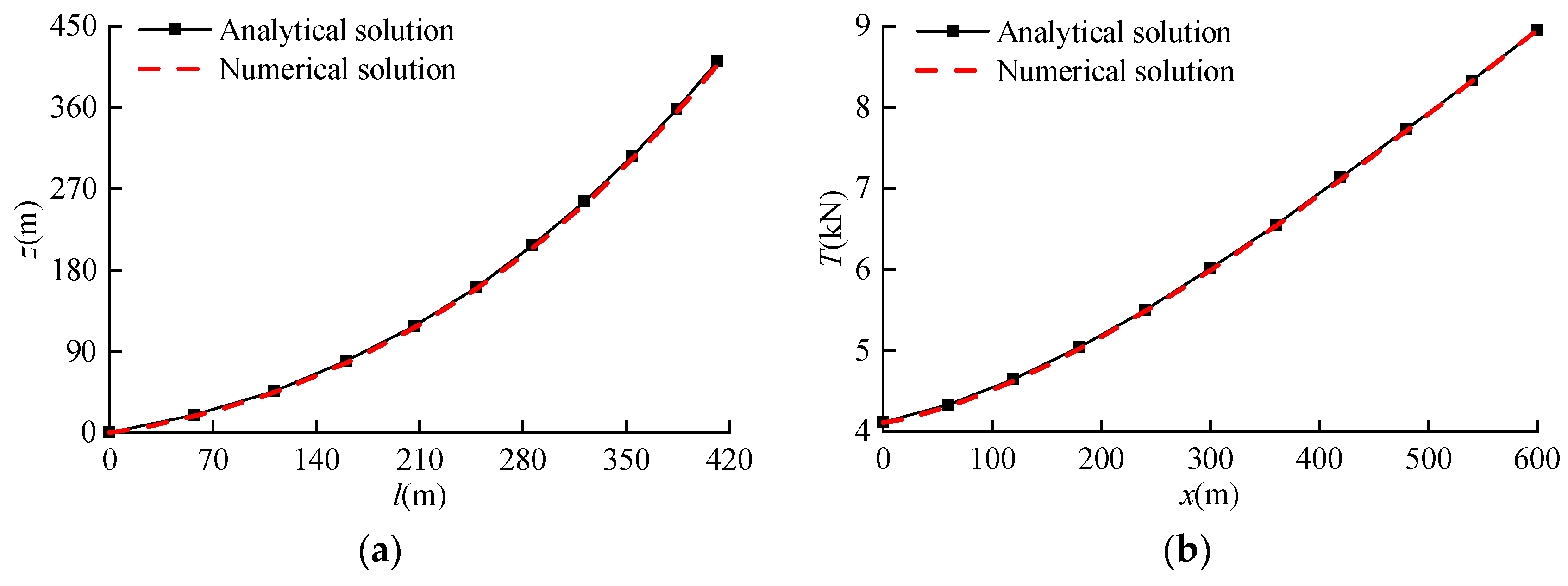
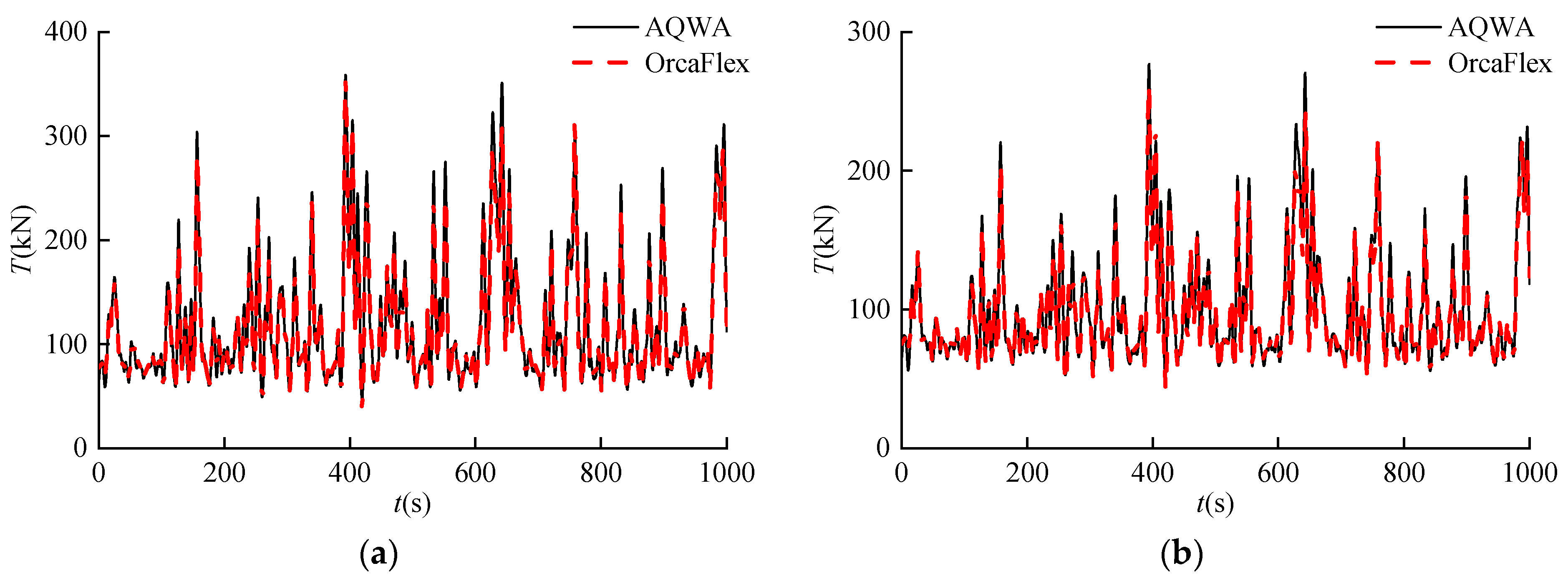
3.4. Comparison and Verification
4. Results and Discussion
4.1. PV Platform Motion Responses
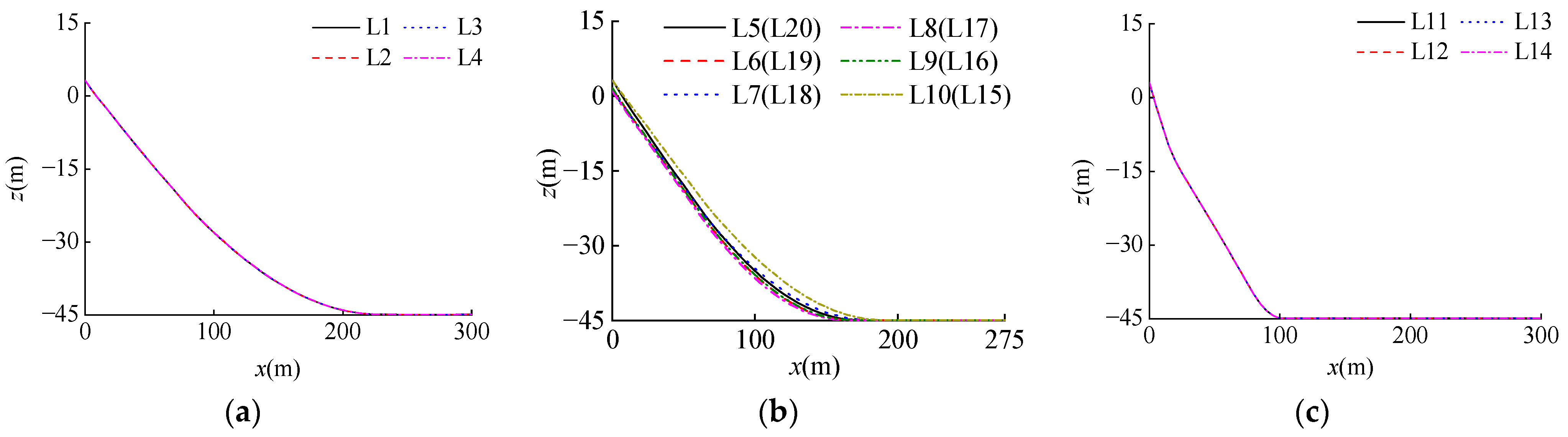
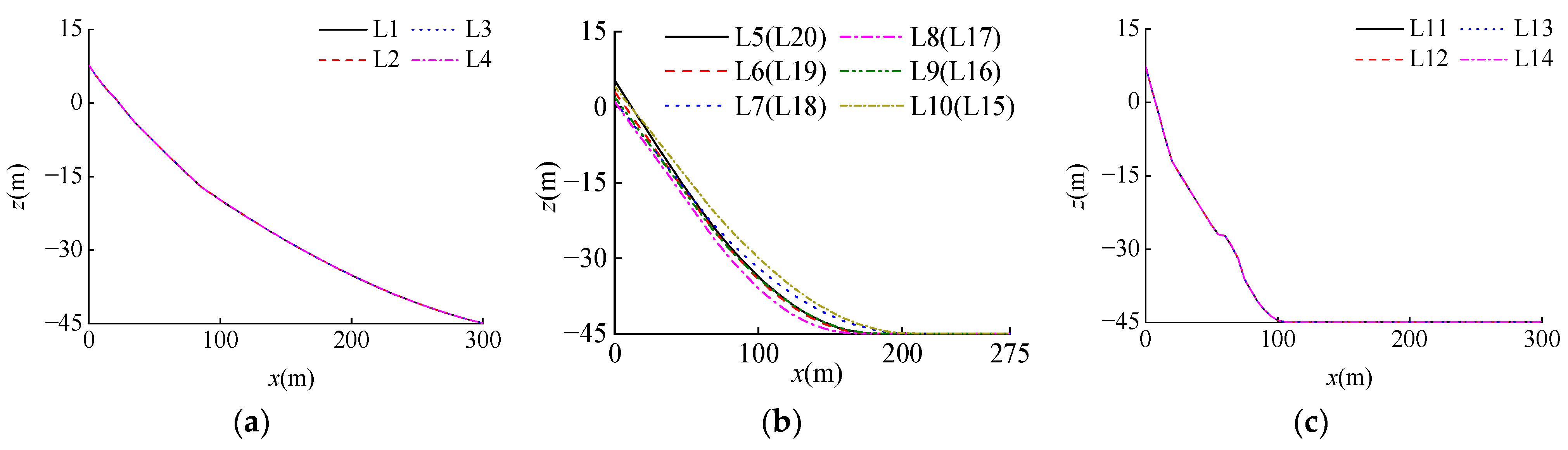
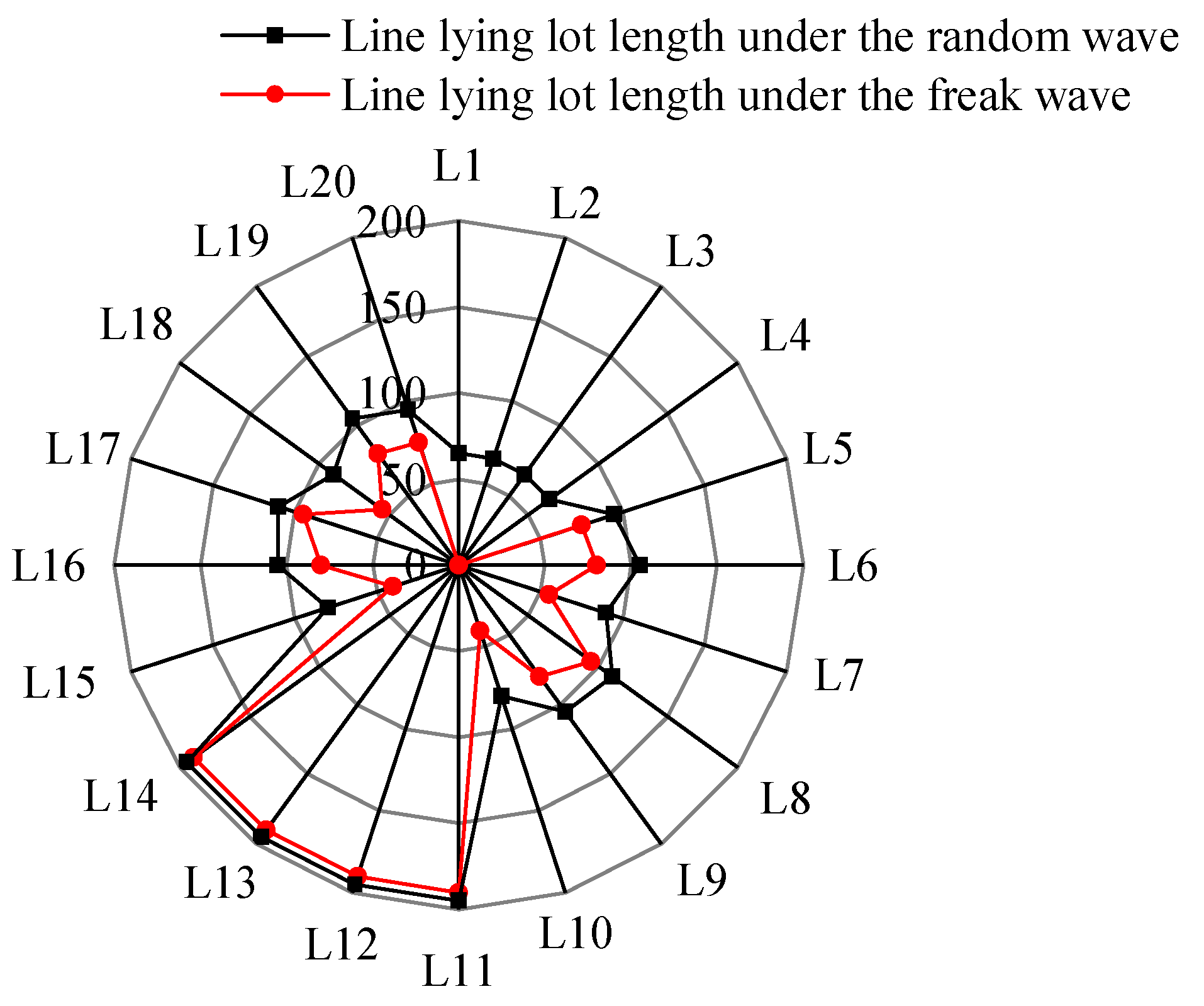
4.2. Mooring Line Configuration Responses
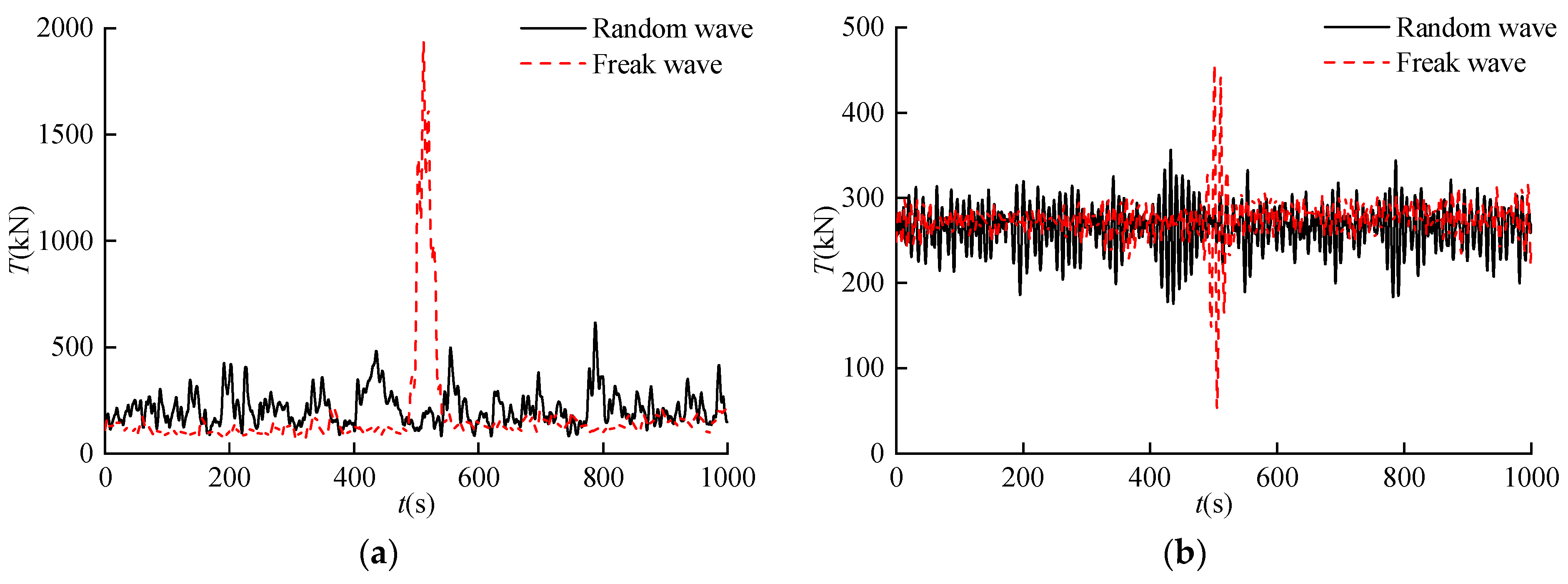
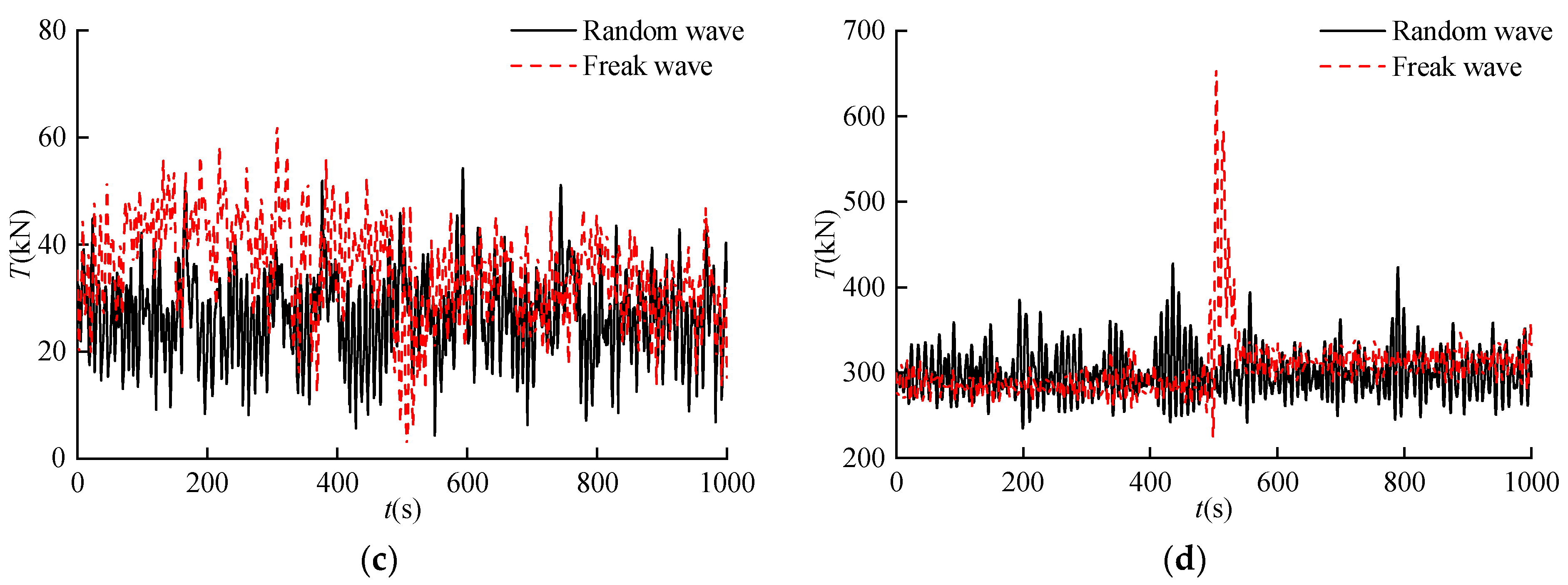
4.3. Mooring Line Tension Responses
5. Conclusions
- (1)
- The developed numerical model could reasonably simulate and calculate the response characteristics of the designed floating PV platform and mooring line structures. The accuracy and applicability of this model are reasonably verified by two groups of comparisons, including the static mooring line tension and the time history responses of the PV platform’s surge motion and mooring tension. The generated freak wave series could be effectively inserted into the created model to explore its effect on the floating PV platform’s motions, mooring line configuration, and tension responses.
- (2)
- The motion responses of the PV platform are noticeably remarkable under freak waves with a direction of 0°. Particularly nearby, the wave focusing time for all three motion responses of the PV platform attained the peak values, and the response amplitudes of the PV platform caused by the freak waves were evidently greater than those induced by the random waves. Among the three motions, the surge motion response is the most significant, which becomes the dominant motion of the PV platform and should be regarded with importance in the design stage.
- (3)
- The freak waves have a great influence on the configuration of the mooring line structures. Induced by the surface waves, the configurations of the mooring lines L1~L4 on the wave-facing direction are the tightest, and the corresponding lying lengths on the seabed are the smallest among the twenty mooring lines. The configurations of the mooring lines L1~L4 under the freak wave are tighter than those under the random wave, and the configurations of other mooring lines L5~L20 are similar under the two waves. The lying lengths of the mooring lines vary analogously for the comparison of both waves.
- (4)
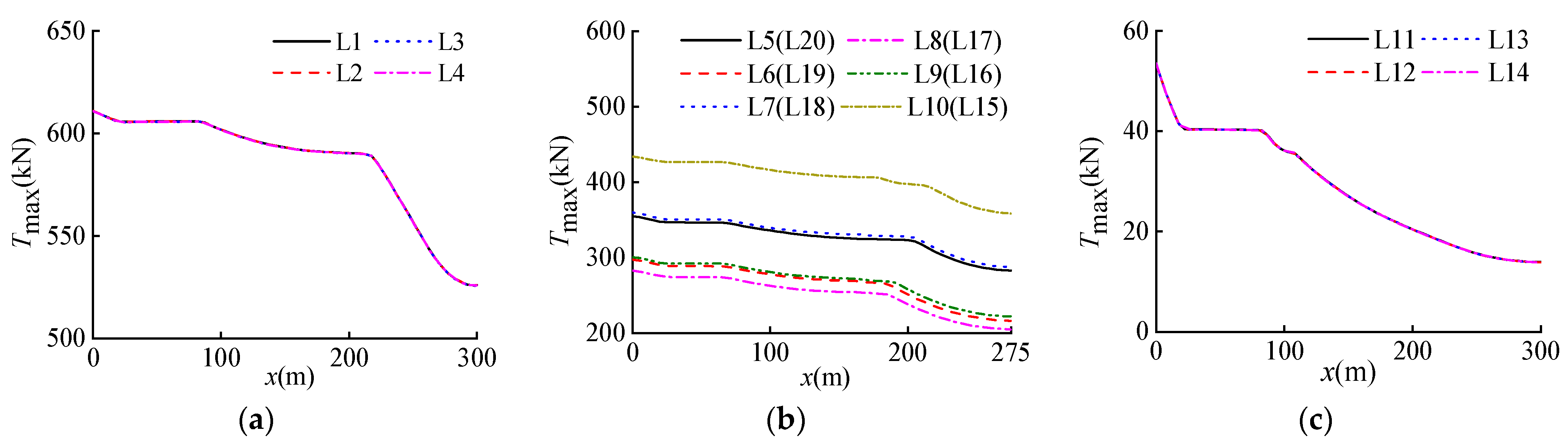
- The axial tension of the mooring lines has a clear variation due to the influence of freak waves. The maximum or minimum value of the tension based on the facing direction of the mooring lines is reached near the wave focusing time. Among the twenty mooring lines, the axial tensions are the largest for the mooring lines L1~L4 and the smallest for the mooring lines L11~L14. The maximum tensions of the mooring lines L1~L4 under the freak wave increase by 220.42% compared to the corresponding value under the random wave. The difference in the maximum top tensions of the mooring lines L11~L14 is only 12.90% for the two waves.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Trapani, K.; Santafé, R.M. A review of floating photovoltaic installations: 2007–2013. Prog. Photovolt. Res. Appl. 2015, 23, 524–532. [Google Scholar] [CrossRef]
- Ranjbaran, P.; Yousefi, H.; Gharehpetian, G.B.; Astaraei, F.R. A review on floating photovoltaic (FPV) power generation units. Renew. Sustain. Energy Rev. 2019, 110, 332–347. [Google Scholar] [CrossRef]
- Tina, G.M.; Scavo, F.B. Energy performance analysis of tracking floating photovoltaic systems. Heliyon 2022, 8, e10088. [Google Scholar] [CrossRef] [PubMed]
- Kjeldsen, S.P. Measurements of freak waves in Norway and related ship accidents. In Royal Institution of Naval Architects International Conference-Design and Operation for Abnormal Conditions III; Royal Institution of Naval Architects: London, UK, 2005. [Google Scholar]
- Nikolkina, I.; Didenkulova, I. Rogue waves in 2006–2010. Nat. Hazards Earth Syst. Sci. 2011, 11, 2913–2924. [Google Scholar] [CrossRef]
- Fochesato, C.; Grilli, S.; Dias, F. Numerical modeling of extreme rogue waves generated by directional energy focusing. Wave Motion 2007, 44, 395–416. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Zhang, N.C.; Yu, Y.X. An efficient focusing model for generation of freak waves. Acta Oceanol. Sin. 2011, 30, 19–26. [Google Scholar] [CrossRef]
- Cui, C.; Pan, W.B. Experimental study on the wavelengths of two-dimensional and three-dimensional freak waves. China Ocean Eng. 2023, 37, 154–164. [Google Scholar] [CrossRef]
- Zhao, X.Z.; Sun, Z.C.; Liang, S.X. Efficient focusing models for generation of freak waves. China Ocean Eng. 2009, 23, 429–440. [Google Scholar]
- Zhao, X.Z.; Ye, Z.T.; Fu, Y.N.; Cao, F.F. A CIP-based numerical simulation of freak wave impact on a floating body. Ocean Eng. 2014, 87, 50–63. [Google Scholar] [CrossRef]
- Hu, Z.Q.; Tang, W.Y.; Xue, H.X. A probability-based superposition model of freak wave simulation. Appl. Ocean Res. 2014, 47, 284–290. [Google Scholar] [CrossRef]
- Tang, Y.G.; Li, Y.; Wang, B.; Liu, S.X.; Zhu, L.H. Dynamic analysis of turret-moored FPSO system in freak wave. China Ocean Eng. 2016, 30, 521–534. [Google Scholar] [CrossRef]
- Qin, H.; Tang, W.; Xue, H.; Hu, Z. Numerical study of nonlinear freak wave impact underneath a fixed horizontal deck in 2-D space. Appl. Ocean Res. 2017, 64, 155–168. [Google Scholar] [CrossRef]
- Li, X.; Deng, Y.F.; Li, L.; Tian, X.L.; Li, J. Motion and dynamic responses of a semisubmersible in freak waves. China Ocean Eng. 2017, 31, 754–763. [Google Scholar] [CrossRef]
- Xu, P.; Du, Z.X.; Gong, S.F. Numerical investigation into freak wave effects on deepwater pipeline installation. J. Mar. Sci. Eng. 2020, 8, 119. [Google Scholar] [CrossRef]
- Xu, P.; Gong, S.F. Numerical investigation of deepwater S-lay pipeline under freak waves. J. Offshore Mech. Arct. Eng. 2020, 142, 041803. [Google Scholar] [CrossRef]
- Pan, W.; Liang, C.; Zhang, N.; Huang, G. Experimental study on hydrodynamic characteristics of a moored square cylinder under freak wave (II: Frequency-domain study). Ocean Eng. 2021, 219, 108452. [Google Scholar] [CrossRef]
- Chang, S.; Huang, W.; Liu, F.; Song, H. Influence of second-order wave force and focusing position on dynamic responses of tension leg platform under a freak wave. Ocean Eng. 2021, 242, 110126. [Google Scholar] [CrossRef]
- Zeng, F.; Zhang, N.; Huang, G.; Gu, Q.; He, M. Experimental study on dynamic response of a floating offshore wind turbine under various freak wave profiles. Mar. Struct. 2023, 88, 103362. [Google Scholar] [CrossRef]
- Huo, F.; Zhao, Y.; Zhang, J.; Zhang, M.; Yuan, Z.M. Study on wave slamming characteristics of a typical floating wind turbine under freak waves. Ocean Eng. 2023, 269, 113464. [Google Scholar] [CrossRef]
- Cazzaniga, R.; Cicu, M.; Rosa-Clot, M.; Rosa-Clot, P.; Tina, G.M.; Ventura, C. Compressed air energy storage integrated with floating photovoltaic plant. J. Energy Storage 2017, 13, 48–57. [Google Scholar] [CrossRef]
- Luo, W.; Isukapalli, S.N.; Vinayagam, L.; Ting, S.A.; Kumar, A. Performance loss rates of floating photovoltaic installations in the tropics. Sol. Energy 2021, 219, 58–64. [Google Scholar] [CrossRef]
- Choi, S.M.; Lee, G.R.; Park, C.D.; Cho, S.H.; Lim, B.J. Wind load on the solar panel array of a floating photovoltaic system under extreme hurricane conditions. Sustain. Energy Technol. Assess. 2021, 48, 101616. [Google Scholar] [CrossRef]
- Kaymak, M.K.; Şahin, A.D. Problems encountered with floating photovoltaic systems under real conditions: A new FPV concept and novel solutions. Sustain. Energy Technol. Assess. 2021, 47, 101504. [Google Scholar] [CrossRef]
- Xu, P.; Wellens, P.R. Fully nonlinear hydroelastic modeling and analytic solution of large-scale floating photovoltaics in waves. J. Fluids Struct. 2022, 109, 103446. [Google Scholar] [CrossRef]
- Jin, Z.; Liu, Y.; Zhu, M.; Fang, H.; Li, A. A novel analytical model coupling hydrodynamic-structural-material scales for very large floating photovoltaic support structures. Ocean Eng. 2023, 275, 114113. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, W.; Karimirad, M.; Michailides, C.; Jiang, Z. Second-order hydrodynamic effects on the response of three semisubmersible floating offshore wind turbines. Ocean Eng. 2020, 207, 107371. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of Wind-Wave Growth and Swell Decay During the Joint North Sea Wave Project (JONSWAP); Deutches Hydrographisches Institute: Hamburg, Germany, 1973. [Google Scholar]
- ANSYS. AQWA User Manual, Version 2021 R1; ANSYS: Canonsburg, PA, USA, 2021. [Google Scholar]
- Orcina. OrcaFlex User Manual, Version 10.2; Orcina: Cumbria, UK, 2017. [Google Scholar]
- Tcheou, G. Non-Linear Dynamics of Mooring Lines. Ph.D. Thesis, Massachusetts Institute of Technology: Cambridge, MA, USA, 1997. [Google Scholar]



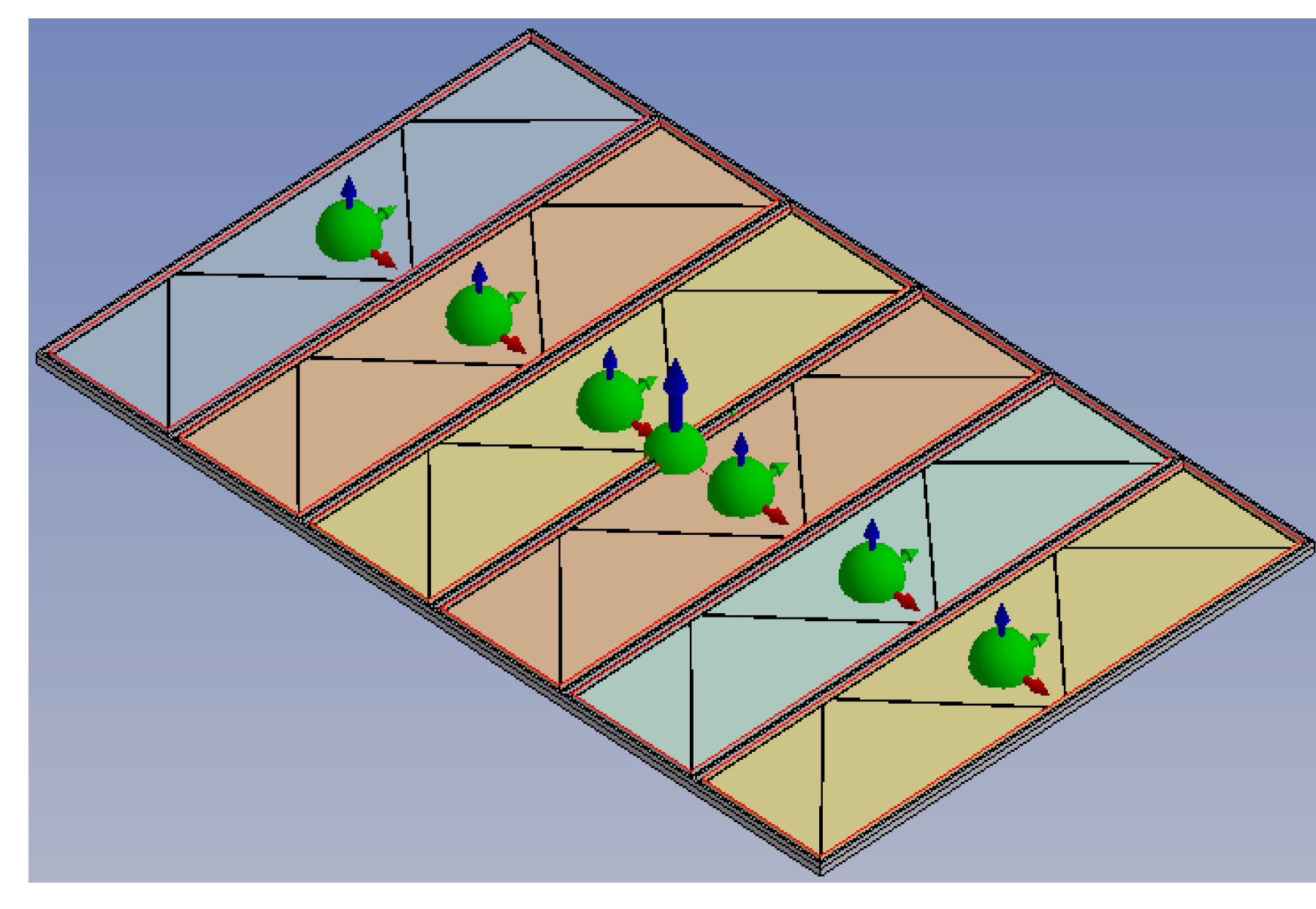






| Mooring Line | Mooring Radius/m | Design Length of Each Section | Mooring Line Length/m |
|---|---|---|---|
| L1/L2/L3/L4/L11/L12/L13/L14 | 290 | chain 20 m (top)-nylon 65 m-chain 215 m (bottom) | 300 |
| L5/L7/L8/L10/L15/L17/L18/L20 | 270 | chain 20 m (top)-nylon 45 m-chain 210 m (bottom) | 275 |
| L6/L9/L16/L19 | 269 | chain 20 m (top)-nylon 45 m-chain 210 m (bottom) | 275 |
| Mooring Line Type | Nominal Diameter/mm | Weight in Water/kg·m−1 | Axial Stiffness/MN | Breaking Strength/MN |
|---|---|---|---|---|
| R3 | 80 | 110.67 | 511 | 5.37 |
| Nylon | 200 | 2.64 | 4.72 | 6.56(Dry) 5.57(Wet) |
| Hs (m) | Tp (s) | Tz (s) | fm (Hz) | γ | α | σ1 | σ2 |
|---|---|---|---|---|---|---|---|
| 4.0 | 10.0 | 7.77 | 0.1 | 3.3 | 0.005 | 0.07 | 0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, P.; Zhang, Z.; Li, S.; Song, Q.; Liu, W. Numerical Investigation into the Dynamic Responses of Floating Photovoltaic Platform and Mooring Line Structures under Freak Waves. J. Mar. Sci. Eng. 2024, 12, 96. https://doi.org/10.3390/jmse12010096
Xu P, Zhang Z, Li S, Song Q, Liu W. Numerical Investigation into the Dynamic Responses of Floating Photovoltaic Platform and Mooring Line Structures under Freak Waves. Journal of Marine Science and Engineering. 2024; 12(1):96. https://doi.org/10.3390/jmse12010096
Chicago/Turabian StyleXu, Pu, Zirui Zhang, Siliang Li, Qiming Song, and Wei Liu. 2024. "Numerical Investigation into the Dynamic Responses of Floating Photovoltaic Platform and Mooring Line Structures under Freak Waves" Journal of Marine Science and Engineering 12, no. 1: 96. https://doi.org/10.3390/jmse12010096
APA StyleXu, P., Zhang, Z., Li, S., Song, Q., & Liu, W. (2024). Numerical Investigation into the Dynamic Responses of Floating Photovoltaic Platform and Mooring Line Structures under Freak Waves. Journal of Marine Science and Engineering, 12(1), 96. https://doi.org/10.3390/jmse12010096





