Adaptive Pitch-Tracking Control with Dynamic and Static Gains for Remotely Operated Towed Vehicles
Abstract
:1. Introduction
- A nonlinear adaptive output feedback tracking control algorithm is proposed, aimed at studying the attitude compensation during the motion of an ROTV, with the objective of controlling the pitch angle trajectory tracking problem of ROTVs;
- By employing a novel dynamic and static gain observer, the controller design issue is transformed into a problem of parameter computation and selection, thereby addressing the system’s nonlinearity and the handling of unmeasurable states;
- Global practical output tracking with globally bounded states is demonstrated for the ROTV system through appropriate design parameter selection.
2. Preliminaries
2.1. Description of the Towed Vehicle
2.2. Pitch-Control Model
- It is assumed that the control of pitch attitude commences once the towing system has reached a steady state, during which the parameters of the ROTV in the horizontal plane remain constant;
- Our attention is mostly focused on the pitch motion of the ROTV within the vertical plane;
- The model is based on the lumped mass approach, considering the tension forces transmitted from the cable to the center of gravity of the ROTV.
2.3. Presupposition
3. Tracking Control Algorithms
3.1. Dynamic and Static Gain Observers and Controller Design
3.2. Stability Analysis
4. Results
4.1. Simulation Setups
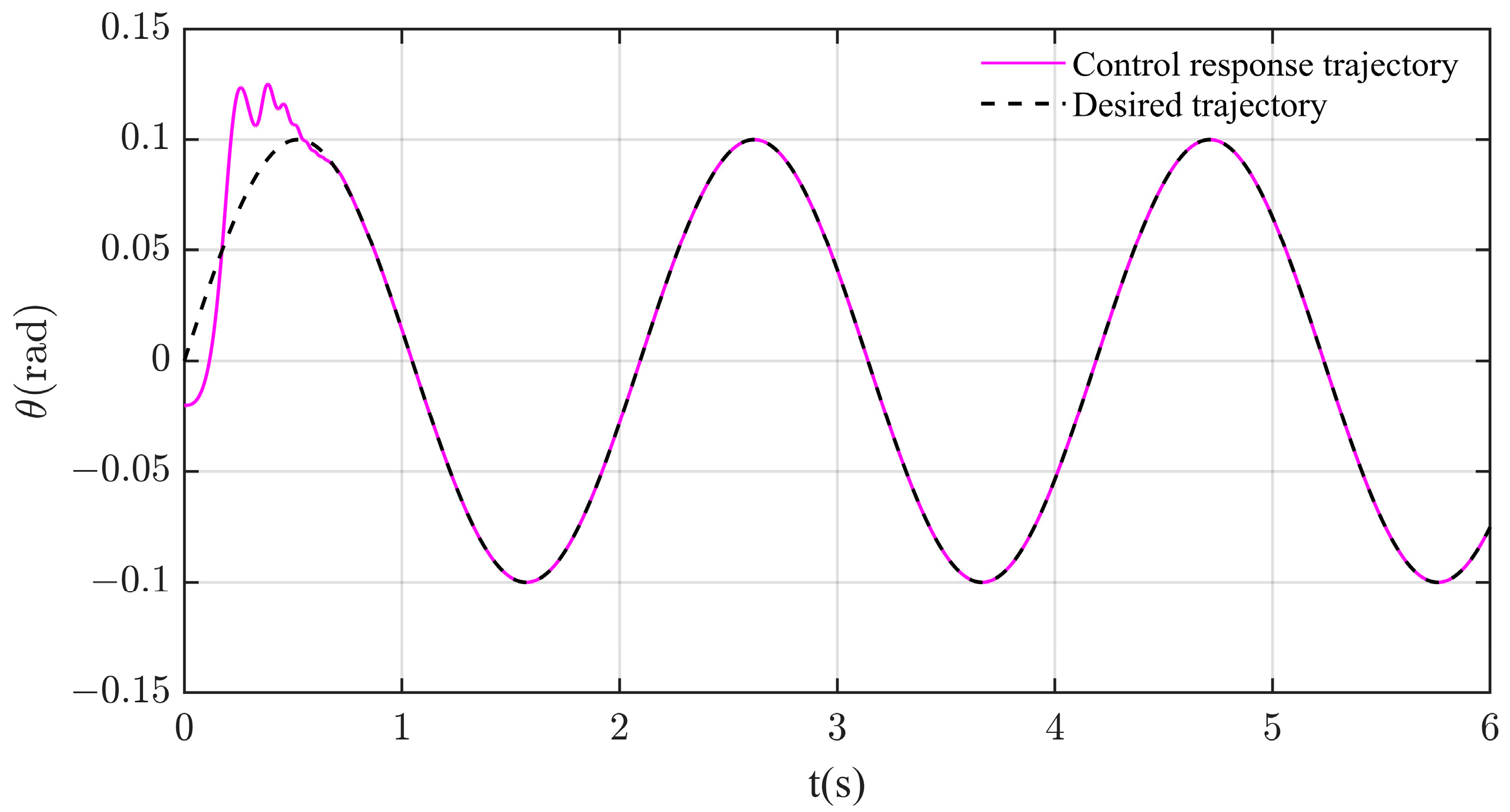
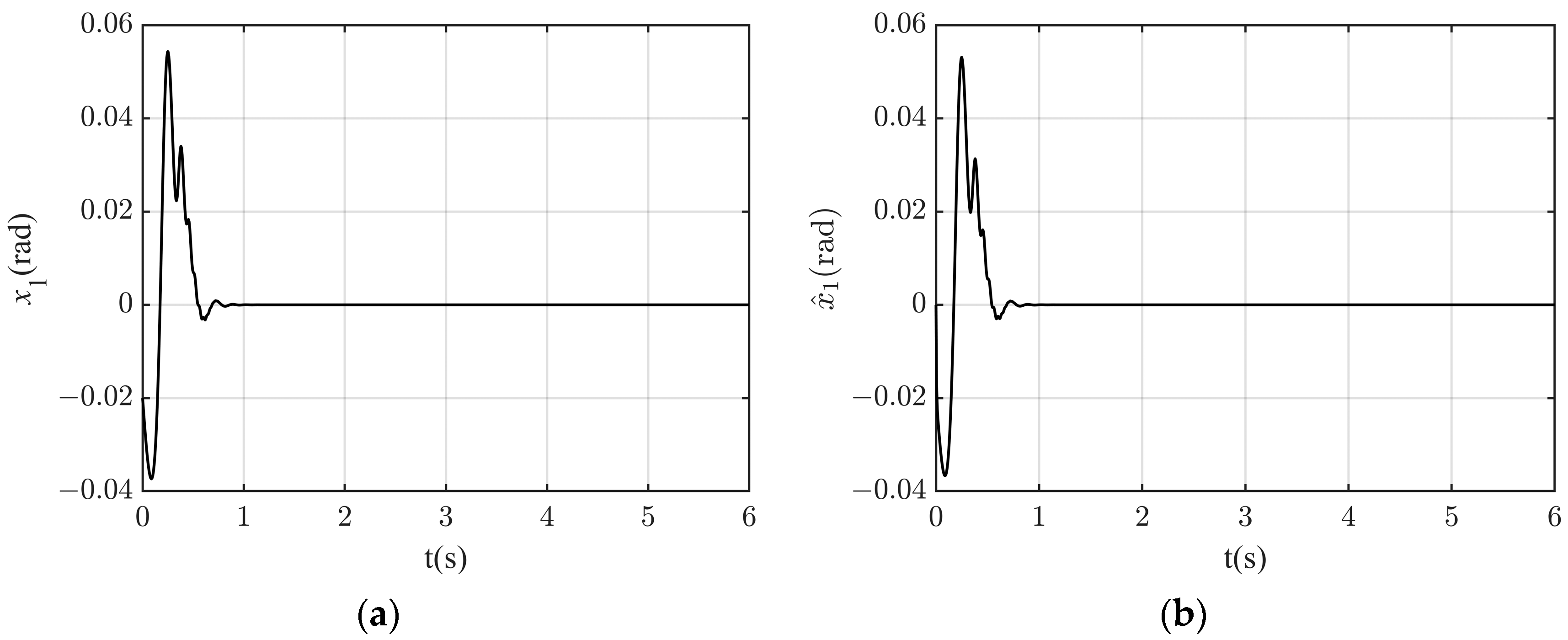
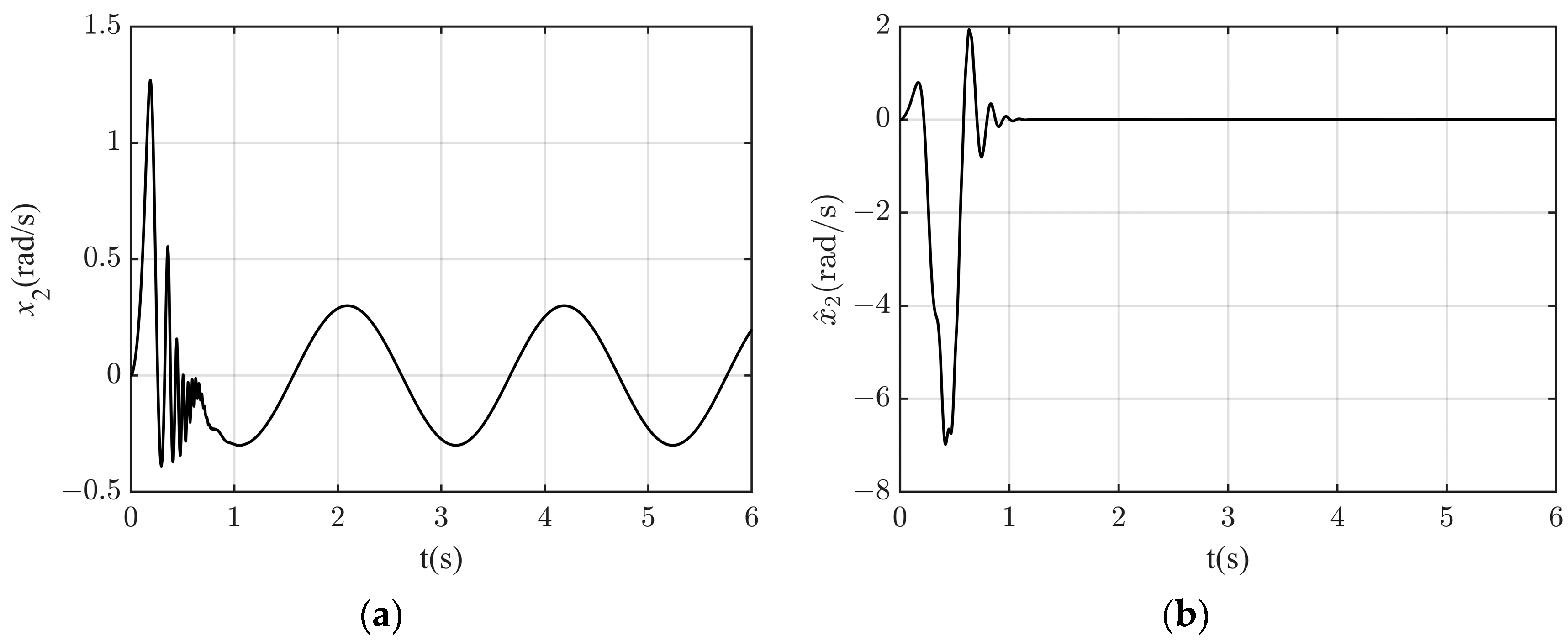
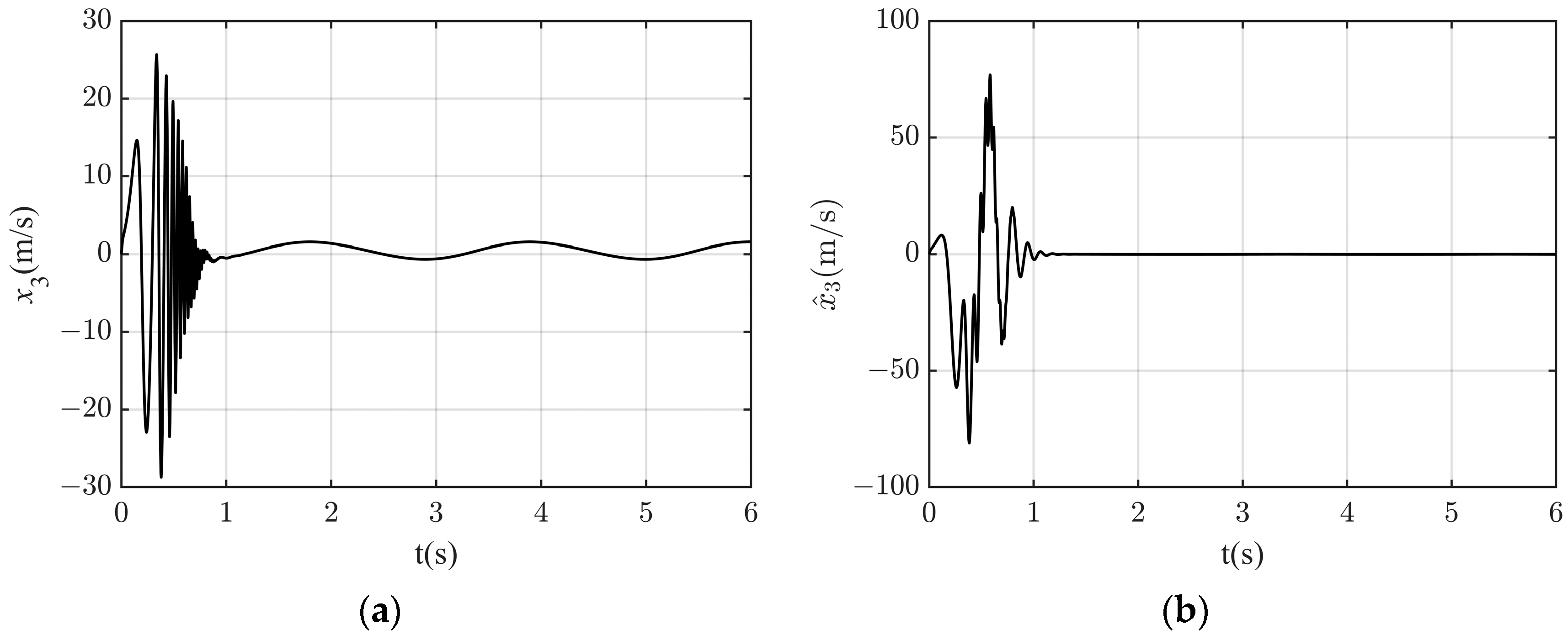
4.2. Simulation Result
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Mathematical Characterization of Immeasurable States
Appendix A.1. System Representation
Appendix A.2. Observability
Appendix A.3. Luenberger Observer for State Estimation
Appendix A.4. Unobservable Subspace
Appendix A.5. Controllability and Detectability
Appendix A.6. Controllability and Detectability
References
- Karimi, H.R.; Lu, Y. Guidance and control methodologies for marine vehicles: A survey. Control Eng. Pract. 2021, 111, 104785. [Google Scholar] [CrossRef]
- Wang, N.; Xu, H.; Li, C.; Yin, J. Hierarchical Path Planning of Unmanned Surface Vehicles: A Fuzzy Artificial Potential Field Approach. Int. J. Fuzzy Syst. 2021, 23, 1797–1808. [Google Scholar] [CrossRef]
- Paley, D.A.; Zhang, F.; Leonard, N.E. Cooperative Control for Ocean Sampling: The Glider Coordinated Control System. IEEE Trans. Contr. Syst. Technol. 2008, 16, 735–744. [Google Scholar] [CrossRef]
- Xiang, G.; Xiang, X. 3D trajectory optimization of the slender body freely falling through water using cuckoo search algorithm. Ocean Eng. 2021, 235, 109354. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, J.; Wang, D.; Han, Q.-L. An Overview of Recent Advances in Coordinated Control of Multiple Autonomous Surface Vehicles. IEEE Trans. Ind. Inf. 2021, 17, 732–745. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, J.; Chemori, A.; Xiang, X. Virtual Submerged Floating Operational System for Robotic Manipulation. Complexity 2018, 2018, 9528313. [Google Scholar] [CrossRef]
- Hashimoto, K.; Watanabe, M.; Tashiro, S.; Momma, H. Missing of the ROV kaiko vehicle -problem on the secondary cable. In Proceedings of the Oceans ’04 MTS/IEEE Techno-Ocean ’04 (IEEE Cat. No.04CH37600), Kobe, Japan, 9–12 November 2004; IEEE: Kobe, Japan, 2004; Volume 2, pp. 807–811. [Google Scholar]
- Gatto, A.; Sadik-Zada, E.R.; Özbek, S.; Kieu, H.; Nguyen Huynh, N.T. Deep-sea fisheries as resilient bioeconomic systems for food and nutrition security and sustainable development. Resour. Conserv. Recycl. 2023, 197, 106907. [Google Scholar] [CrossRef]
- Lembke, C.; Grasty, S.; Silverman, A.; Broadbent, H.; Butcher, S.; Murawski, S. The Camera-Based Assessment Survey System (C-BASS): A towed camera platform for reef fish abundance surveys and benthic habitat characterization in the Gulf of Mexico. Cont. Shelf Res. 2017, 151, 62–71. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Z.; Shan, R.; He, K.; Zhao, S. Research into the integrated navigation of a deep-sea towed vehicle with USBL/DVL and pressure gauge. Appl. Acoust. 2020, 159, 107052. [Google Scholar] [CrossRef]
- Lock, A.; Spiers, G.; Hostetler, B.; Ray, J.; Wallschläger, D. Multi-dimensional water quality assessment of an urban drinking water source elucidated by high resolution underwater towed vehicle mapping. Water Res. 2016, 93, 289–295. [Google Scholar] [CrossRef]
- Wang, M.; Deng, M.; Wu, Z.; Luo, X.; Jing, J.; Chen, K. The deep-tow marine controlled-source electromagnetic transmitter system for gas hydrate exploration. J. Appl. Geophys. 2017, 137, 138–144. [Google Scholar] [CrossRef]
- Park, J.; Rhee, S.H.; Im, J.-B.; Ji, B.H.; Lee, S.J. Experimental study on the towing stability of a towed underwater object. Int. J. Nav. Archit. Ocean Eng. 2023, 15, 100539. [Google Scholar] [CrossRef]
- Kim, H.-G.; Yun, S.-J.; Park, J.-W.; Lee, H.-J.; Hwang, J.-H.; Kim, J.-C.; Choi, Y.-H.; Ryu, J.-K.; Suh, J.-H. Estimation and Control of a Towed Underwater Vehicle with Active Stationary and Low-Speed Maneuvering Capabilities. JMSE 2023, 11, 1176. [Google Scholar] [CrossRef]
- Zhang, B.; Ji, D.; Liu, S.; Zhu, X.; Xu, W. Autonomous Underwater Vehicle navigation: A review. Ocean Eng. 2023, 273, 113861. [Google Scholar] [CrossRef]
- He, Y.; Wang, D.B.; Ali, Z.A. A review of different designs and control models of remotely operated underwater vehicle. Meas. Control 2020, 53, 1561–1570. [Google Scholar] [CrossRef]
- Hutapea, F.L.; Tsuji, T.; Katou, M.; Asakawa, E. Data processing and interpretation schemes for a deep-towed high-frequency seismic system for gas and hydrate exploration. J. Nat. Gas Sci. Eng. 2020, 83, 103573. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, S.; Setiawan, L.; Zhang, L.; Wang, R. Integral hollow fiber membrane with chemical cross-linking for pressure retarded osmosis operated in the orientation of active layer facing feed solution. J. Membr. Sci. 2018, 550, 163–172. [Google Scholar] [CrossRef]
- Li, B.; Huang, W.; Liang, H. An efficient method to assess effect of fin on the course stability of towing system. Ocean Eng. 2020, 217, 108005. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.; Chen, H.; Sun, Z.; Ye, X.; Xue, G. Hydrodynamic performance optimization and adjustment prediction of a novel deep-sea towed body with adjustable hydrofoils. Ocean Eng. 2024, 296, 116937. [Google Scholar] [CrossRef]
- Wang, M.; Pang, S.; Jin, K.; Liang, X.; Wang, H.; Yi, H. Construction and experimental verification research of a magnetic detection system for submarine pipelines based on a two-part towed platform. J. Ocean Eng. Sci. 2023, 8, 169–180. [Google Scholar] [CrossRef]
- Guo, L.; Yuan, Y.; Tang, W.; Xue, H. A numerical investigation on quasi-static configuration and nonlinear dynamic response characteristics of marine towing cable. Ocean Eng. 2021, 240, 110007. [Google Scholar] [CrossRef]
- Yang, X.; Wu, J.; Li, Q.; Lv, H. Numerical Simulation of Depth Tracking Control of an Underwater Towed System Coupled with Wave–Ship Interference. JMSE 2021, 9, 874. [Google Scholar] [CrossRef]
- Xin, X. Linear strong structural controllability and observability of an n -link underactuated revolute planar robot with active intermediate joint or joints. Automatica 2018, 94, 436–442. [Google Scholar] [CrossRef]
- Jia, J.; Trentelman, H.L.; Baar, W.; Camlibel, M.K. A Sufficient Condition for Colored Strong Structural Controllability of Networks. IFAC-Pap. 2018, 51, 16–21. [Google Scholar] [CrossRef]
- Pequito, S.; Popli, N.; Kar, S.; Ilic, M.D.; Aguiar, A.P. A framework for actuator placement in large scale power systems: Minimal strong structural controllability. In Proceedings of the 2013 5th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), St. Martin, France, 15–18 December 2013; IEEE: St. Martin, France, 2013; pp. 416–419. [Google Scholar]
- Weber, A.; Reissig, G.; Svaricek, F. A linear time algorithm to verify strong structural controllability. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; IEEE: Los Angeles, CA, USA, 2014; pp. 5574–5580. [Google Scholar]
- Jarczyk, J.C.; Svaricek, F.; Alt, B. Strong structural controllability of linear systems revisited. In Proceedings of the IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; IEEE: Orlando, FL, USA, 2011; pp. 1213–1218. [Google Scholar]
- Liu, C.; Li, J.; Yang, S.; Xiang, X. Simultaneously Tracking and Pitch Control of Underwater Towed Vehicle with Multiple Elevators: A Finite-Time Fuzzy Approach. Int. J. Fuzzy Syst. 2023, 25, 264–274. [Google Scholar] [CrossRef]
- Minowa, A.; Toda, M. A High-Gain Observer-Based Approach to Robust Motion Control of Towed Underwater Vehicles. IEEE J. Ocean. Eng. 2019, 44, 997–1010. [Google Scholar] [CrossRef]
- Su, Z.; Li, C.; Zhen, Z. Anti-disturbance constrained control of the air recovery carrier via an integral barrier Lyapunov function. Aerosp. Sci. Technol. 2020, 106, 106157. [Google Scholar] [CrossRef]
- Krishnamurthy, P.; Khorrami, F. Feedforward Systems With ISS Appended Dynamics: Adaptive Output-Feedback Stabilization and Disturbance Attenuation. IEEE Trans. Automat. Contr. 2008, 53, 405–412. [Google Scholar] [CrossRef]
- Curado Teixeira, F.; Pedro Aguiar, A.; Pascoal, A. Nonlinear adaptive control of an underwater towed vehicle. Ocean Eng. 2010, 37, 1193–1220. [Google Scholar] [CrossRef]
- Benazouz, R.; Chemori, A.; Creuze, V. A novel intelligent RISE feedback control of autonomous tethered underwater vehicles: Design & real-time experiments. Ocean Eng. 2024, 300, 117470. [Google Scholar]
- Tabataba’i-Nasab, F.S.; Keymasi Khalaji, A.; Moosavian, S.A.A. Adaptive nonlinear control of an autonomous underwater vehicle. Trans. Inst. Meas. Control 2019, 41, 3121–3131. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, S.; Yan, Y. Fixed-time extended state observer-based trajectory tracking and point stabilization control for marine surface vessels with uncertainties and disturbances. Ocean Eng. 2019, 186, 106109. [Google Scholar] [CrossRef]
- Sun, H.; Zong, G.; Cui, J.; Shi, K. Fixed-time sliding mode output feedback tracking control for autonomous underwater vehicle with prescribed performance constraint. Ocean Eng. 2022, 247, 110673. [Google Scholar] [CrossRef]
- Shi, Y.; Xie, W.; Chen, W.; Xing, L.; Zhang, W. Neural Adaptive Intermittent Output Feedback Control for Autonomous Underwater Vehicles With Full-State Quantitative Designs. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 12836–12848. [Google Scholar] [CrossRef]
- Shang, F.; Liu, Y.; Zhang, C. Adaptive practical tracking control by output feedback for a class of nonlinear systems. J. Syst. Sci. Complex. 2010, 23, 1210–1220. [Google Scholar] [CrossRef]
- Wu, G.; Li, L.-S.; Miao, X.-F.; Cong, X.-R. Luenberger-Type Observer Design for Stochastic Time-Delay Systems. Int. J. Theor. Phys. 2013, 52, 2065–2074. [Google Scholar] [CrossRef]
- Praly, L.; Jiang, Z.P. Linear output feedback with dynamic high gain for nonlinear systems. Syst. Control. Lett. 2004, 53, 107–116. [Google Scholar] [CrossRef]


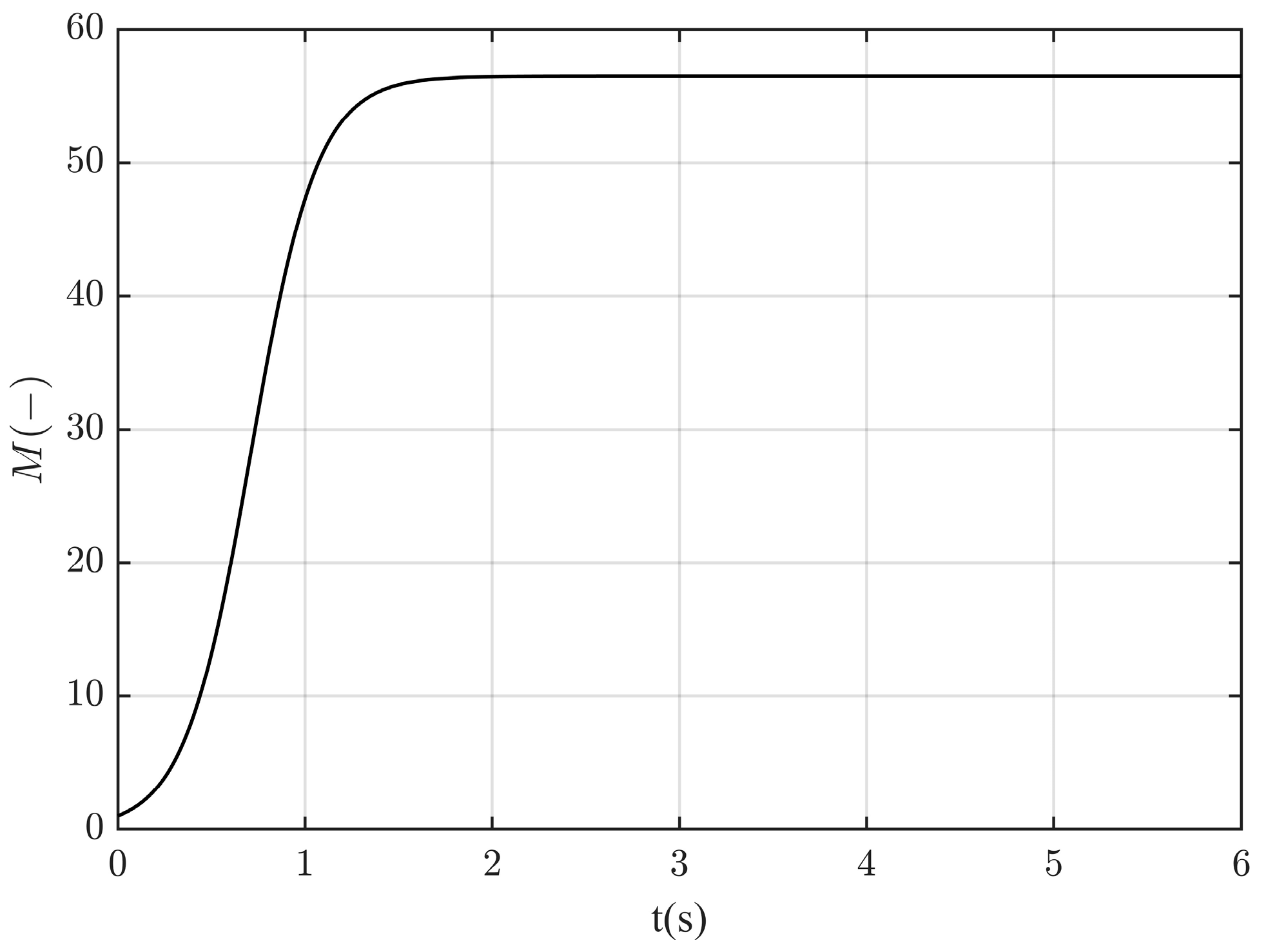
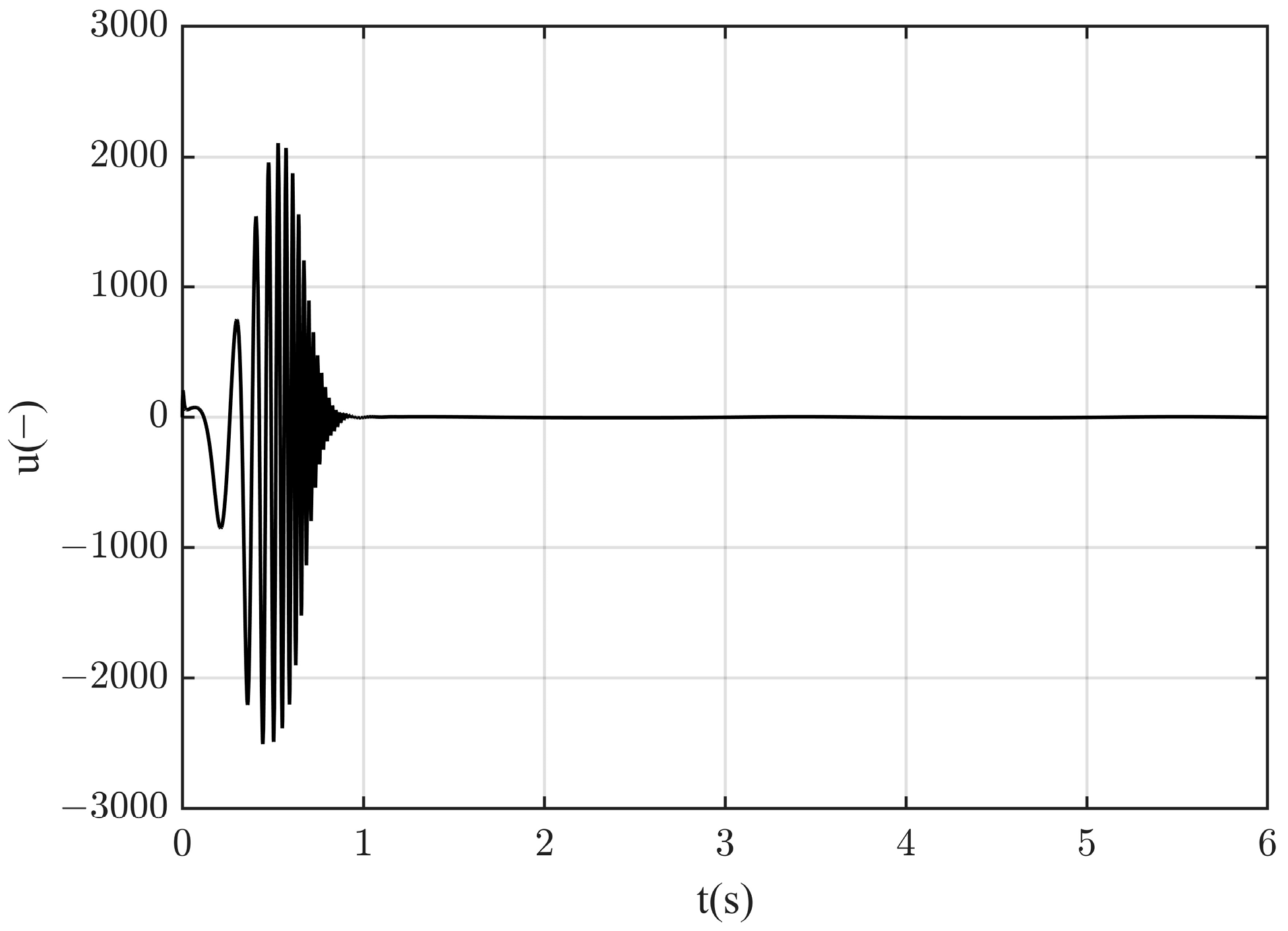


| Design Parameters | Symbol | Value |
|---|---|---|
| Static gain | ||
| Dynamic gain parameters | 60 | |
| 0.1 | ||
| 5.65 | ||
| State observer parameters | 40 | |
| 3 | ||
| 1 | ||
| Controller parameters | 80 | |
| 10 | ||
| 80 |
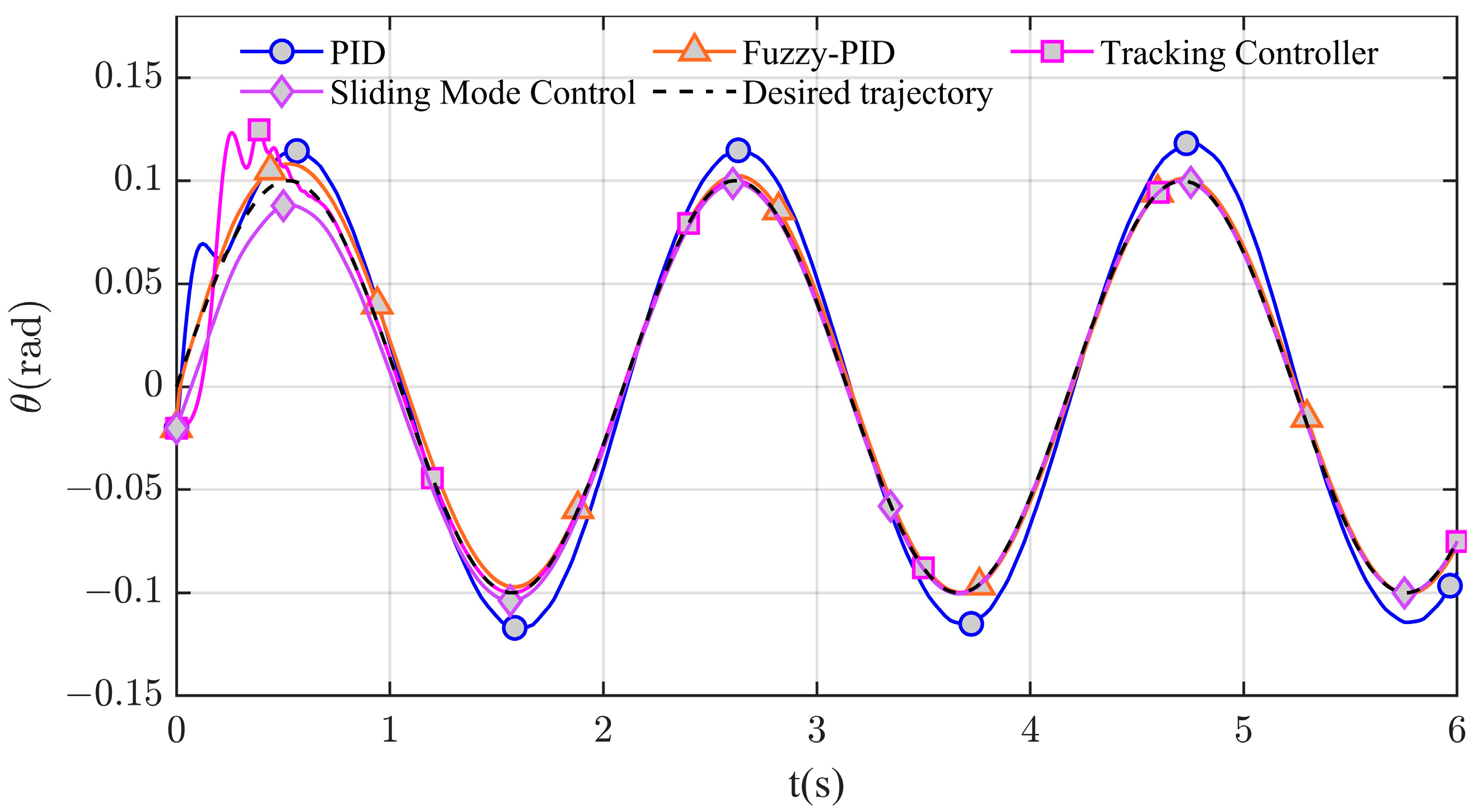
| Control Method | Settling Time | Peak Value | Steady-State Error |
|---|---|---|---|
| PID | - | 0.037 rad | 0.016 rad |
| Fuzzy PID | - | 0.010 rad | 0.002 rad |
| Sliding Mode Control | 3.5 s | 0.021 rad | rad |
| Tracking Controller | 0.9 s | 0.054 rad | rad |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, C.; Xu, H.; Ren, S.; Guo, L.; Tian, X.; Wang, J. Adaptive Pitch-Tracking Control with Dynamic and Static Gains for Remotely Operated Towed Vehicles. J. Mar. Sci. Eng. 2024, 12, 1953. https://doi.org/10.3390/jmse12111953
Tian C, Xu H, Ren S, Guo L, Tian X, Wang J. Adaptive Pitch-Tracking Control with Dynamic and Static Gains for Remotely Operated Towed Vehicles. Journal of Marine Science and Engineering. 2024; 12(11):1953. https://doi.org/10.3390/jmse12111953
Chicago/Turabian StyleTian, Cong, Hang Xu, Songkai Ren, Longchuan Guo, Xiaoqing Tian, and Jiyong Wang. 2024. "Adaptive Pitch-Tracking Control with Dynamic and Static Gains for Remotely Operated Towed Vehicles" Journal of Marine Science and Engineering 12, no. 11: 1953. https://doi.org/10.3390/jmse12111953
APA StyleTian, C., Xu, H., Ren, S., Guo, L., Tian, X., & Wang, J. (2024). Adaptive Pitch-Tracking Control with Dynamic and Static Gains for Remotely Operated Towed Vehicles. Journal of Marine Science and Engineering, 12(11), 1953. https://doi.org/10.3390/jmse12111953







