Study of Hydrofoil Boundary Layer Prediction with Two Correlation-Based Transition Models
Abstract
:1. Introduction
2. Transition Models
2.1. SST k-ω Model
2.2. γ-Reθt Transition Model
2.3. γ Transition Model
3. NACA0009 Blunt Trailing Edge Hydrofoil—Natural Transition
3.1. Modeling and Meshing
3.2. Verification of Grid Independence
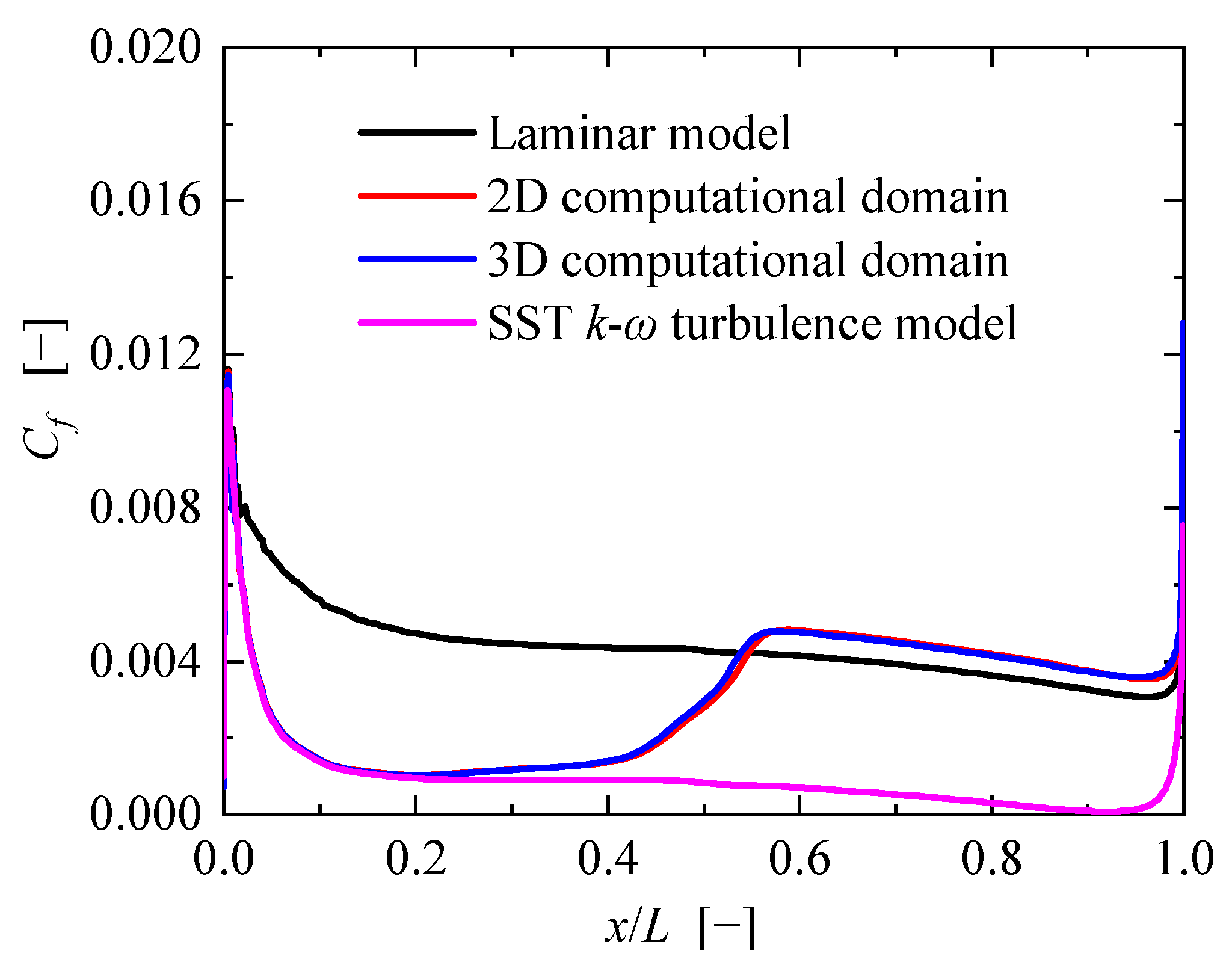
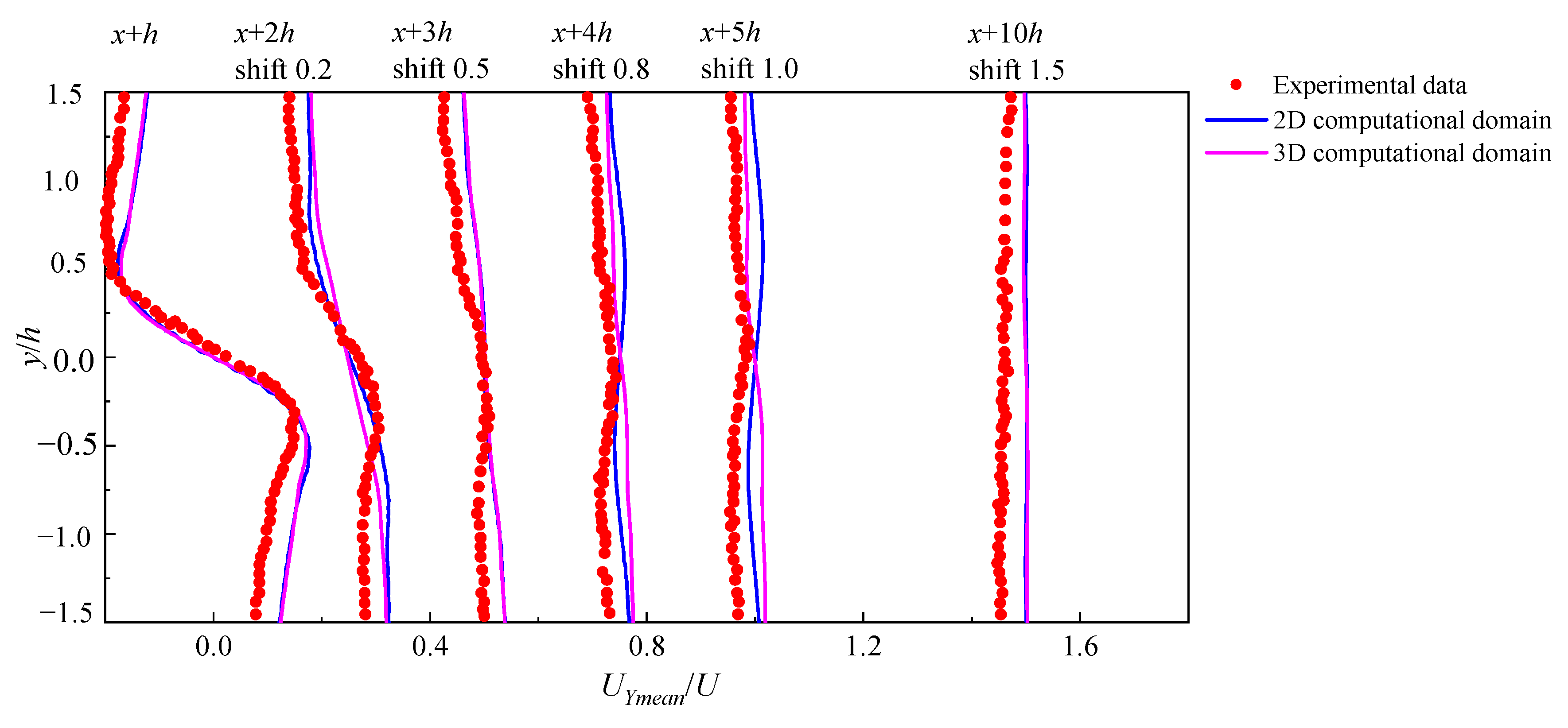
3.3. Comparative Analysis of 2D and 3D Calculation Results
3.4. Analysis of Numerical Results
3.5. Prediction Performance Analysis at Different Reynolds Numbers
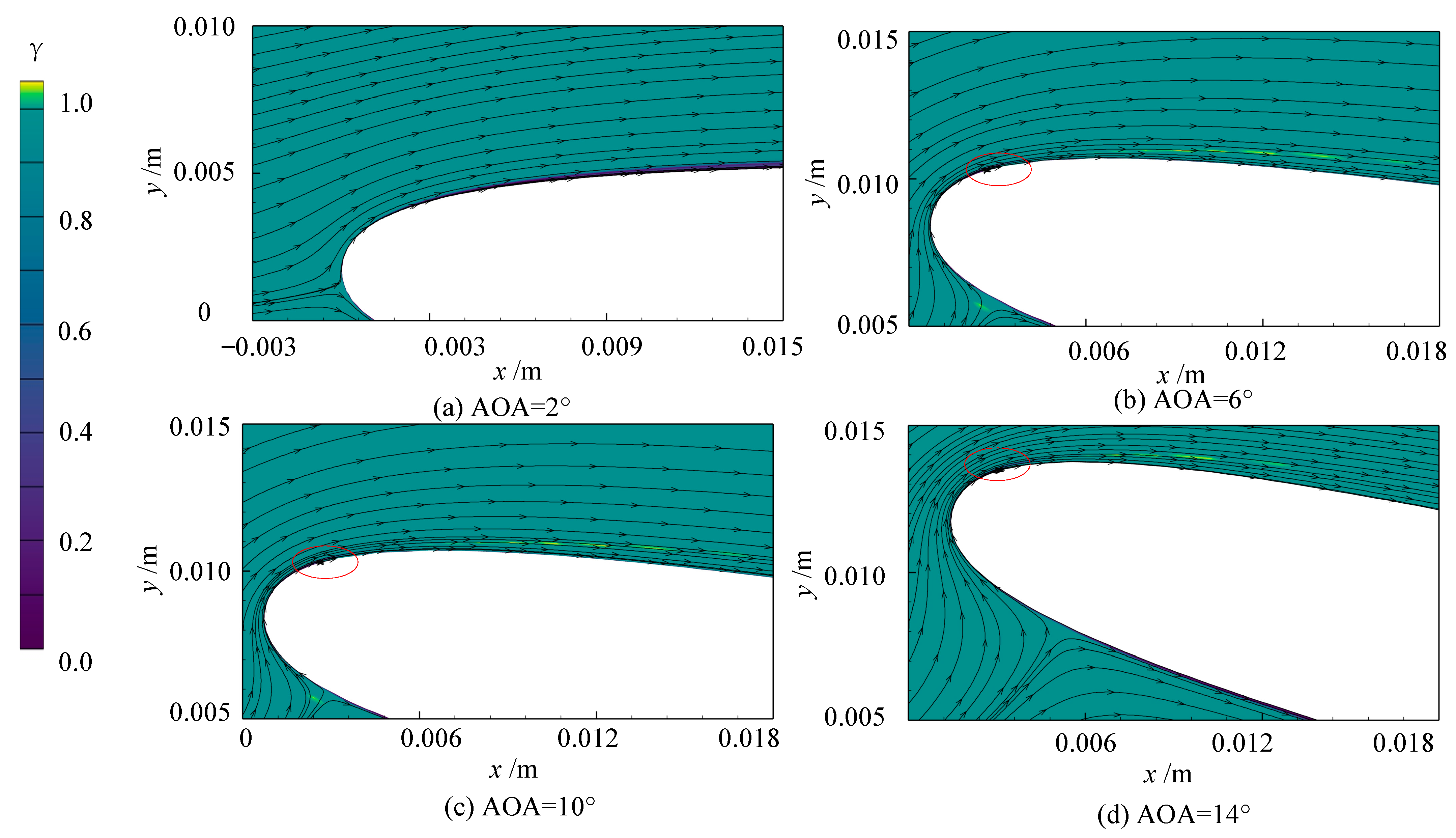
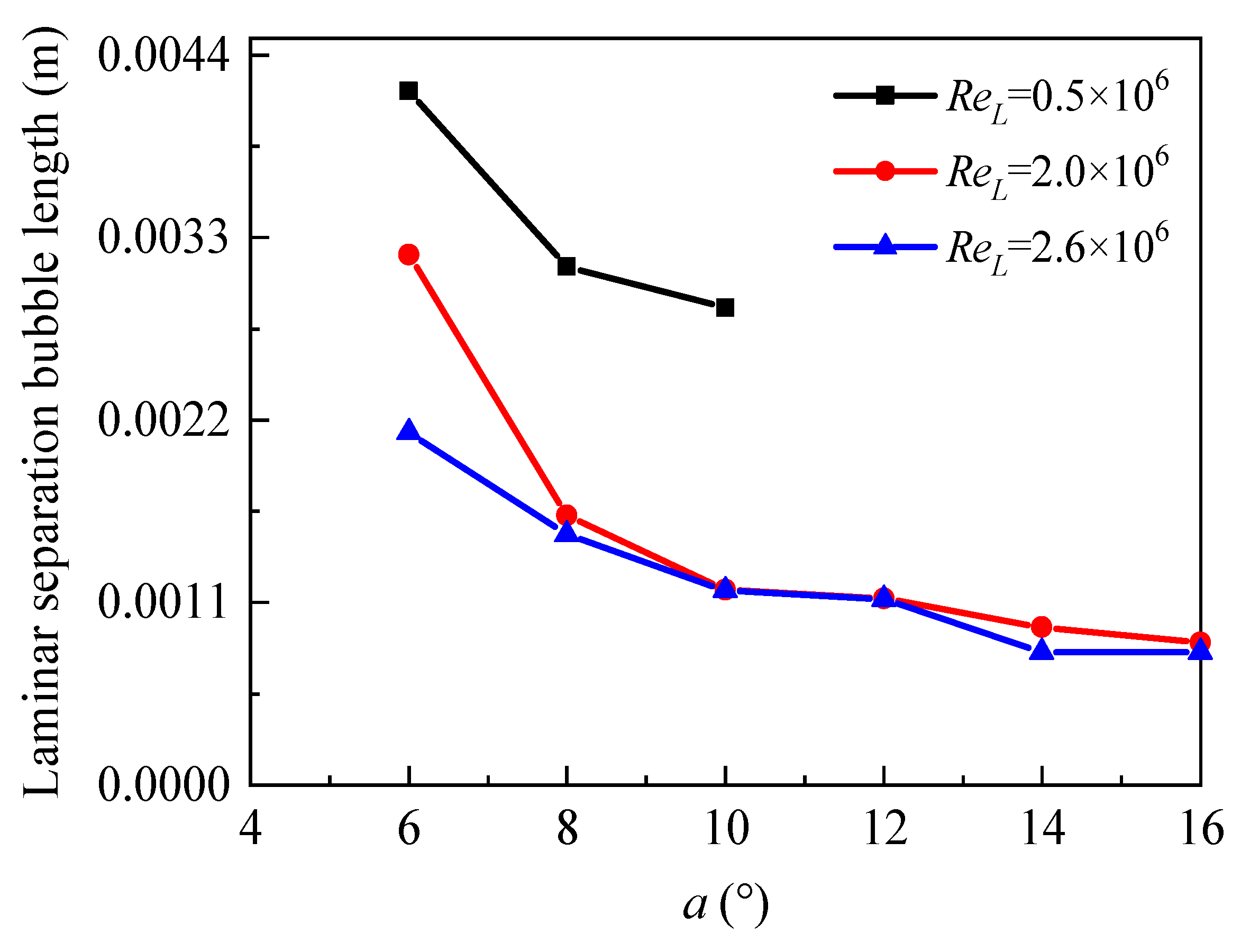
4. Analysis of Calculation Results at Different Angles of Attack
5. Conclusions and Future Prospects
5.1. Conclusions
- (1)
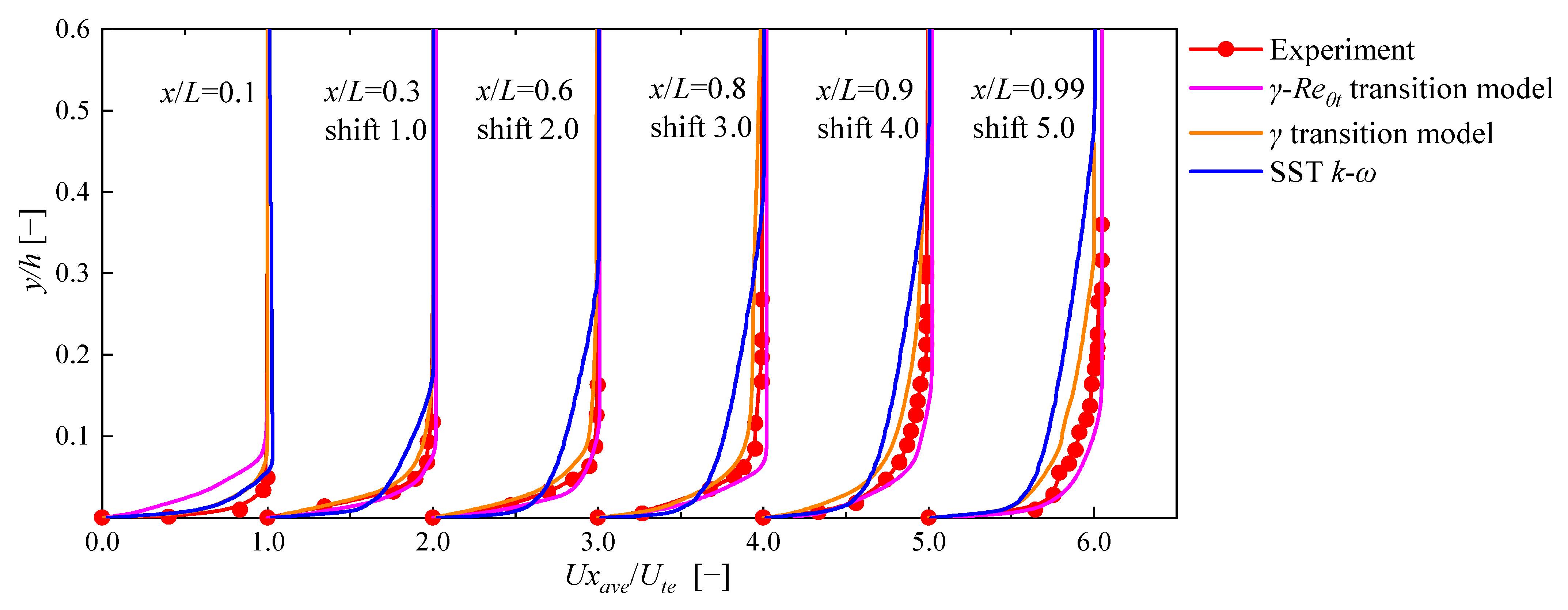
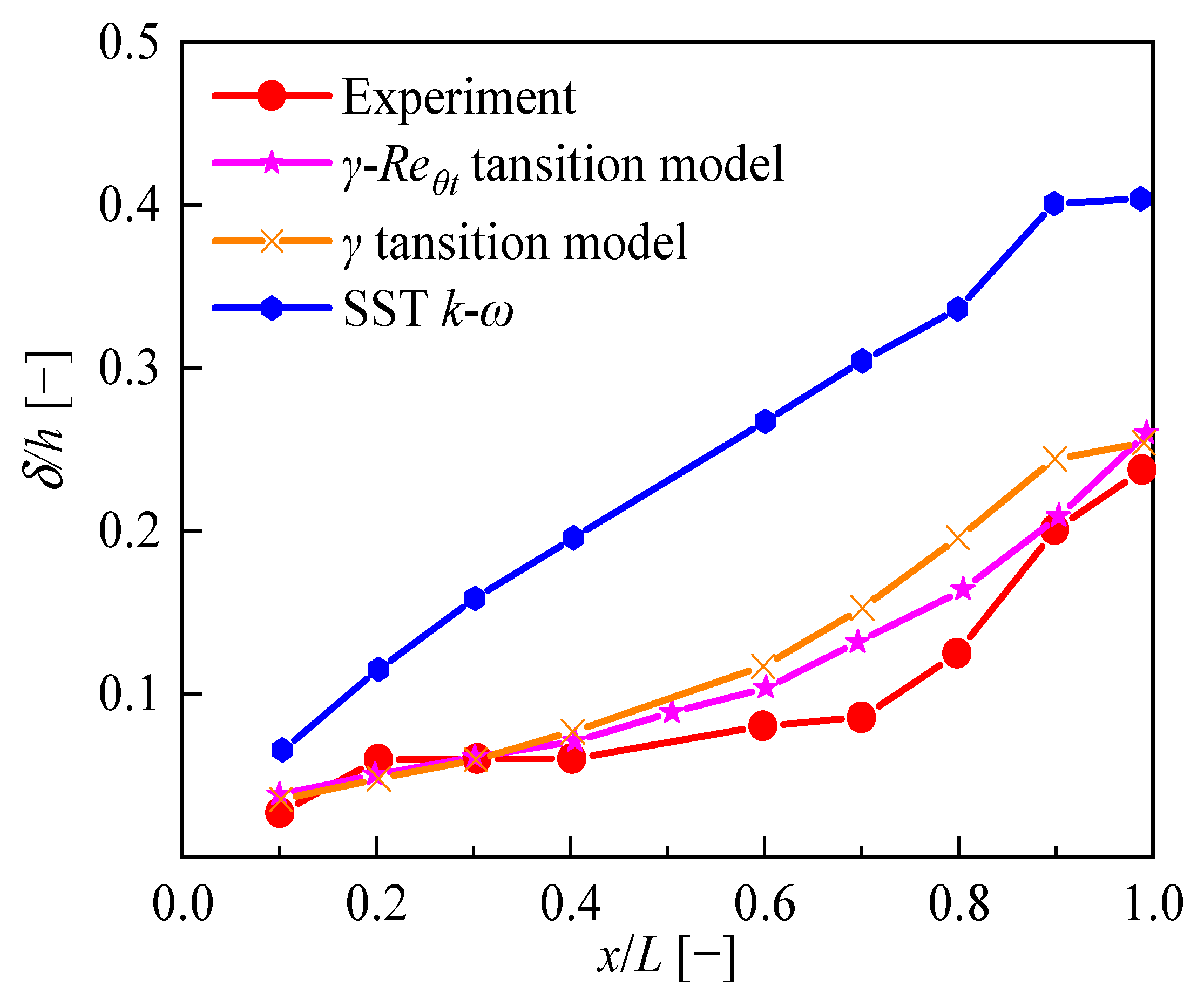
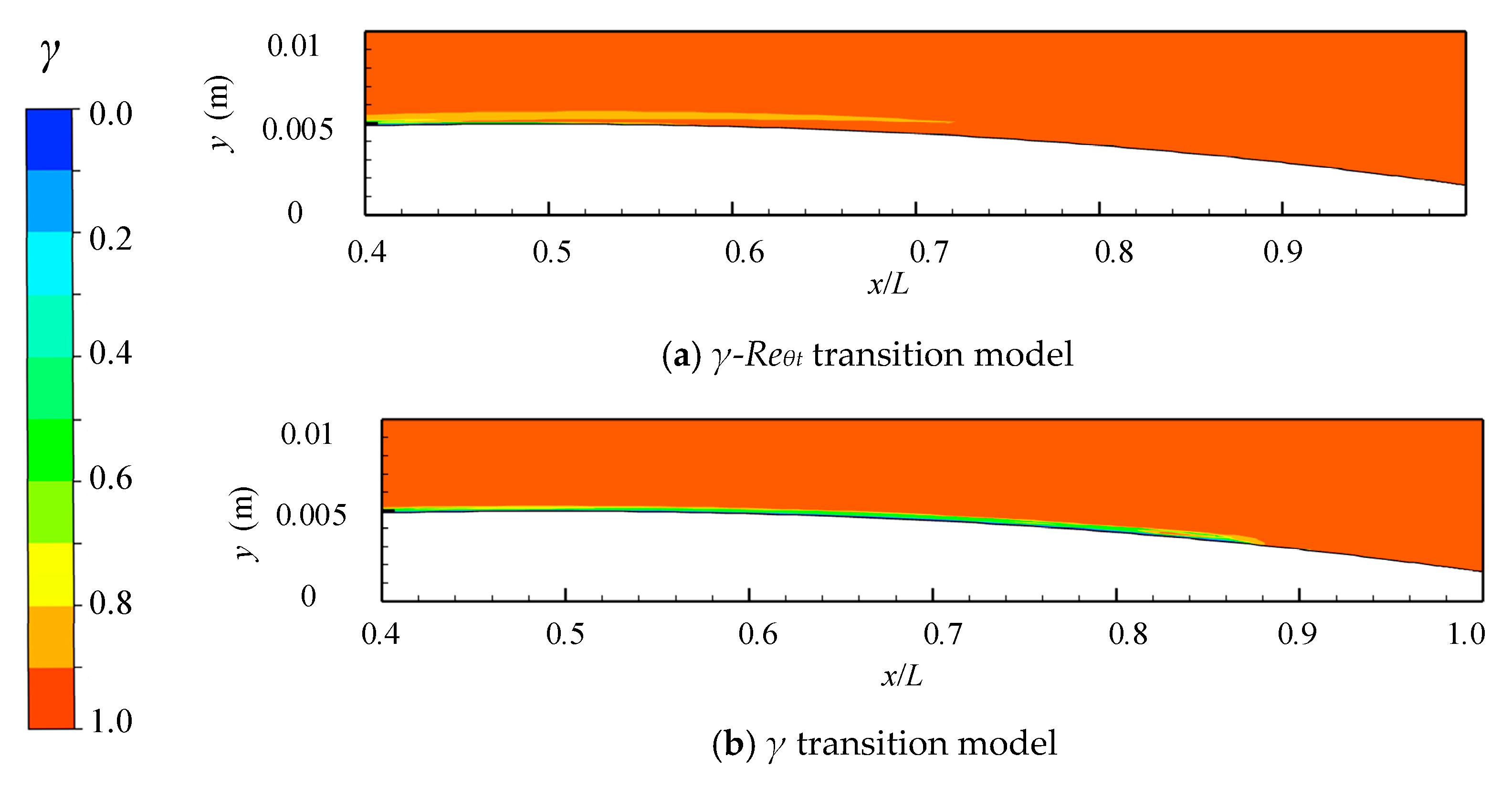
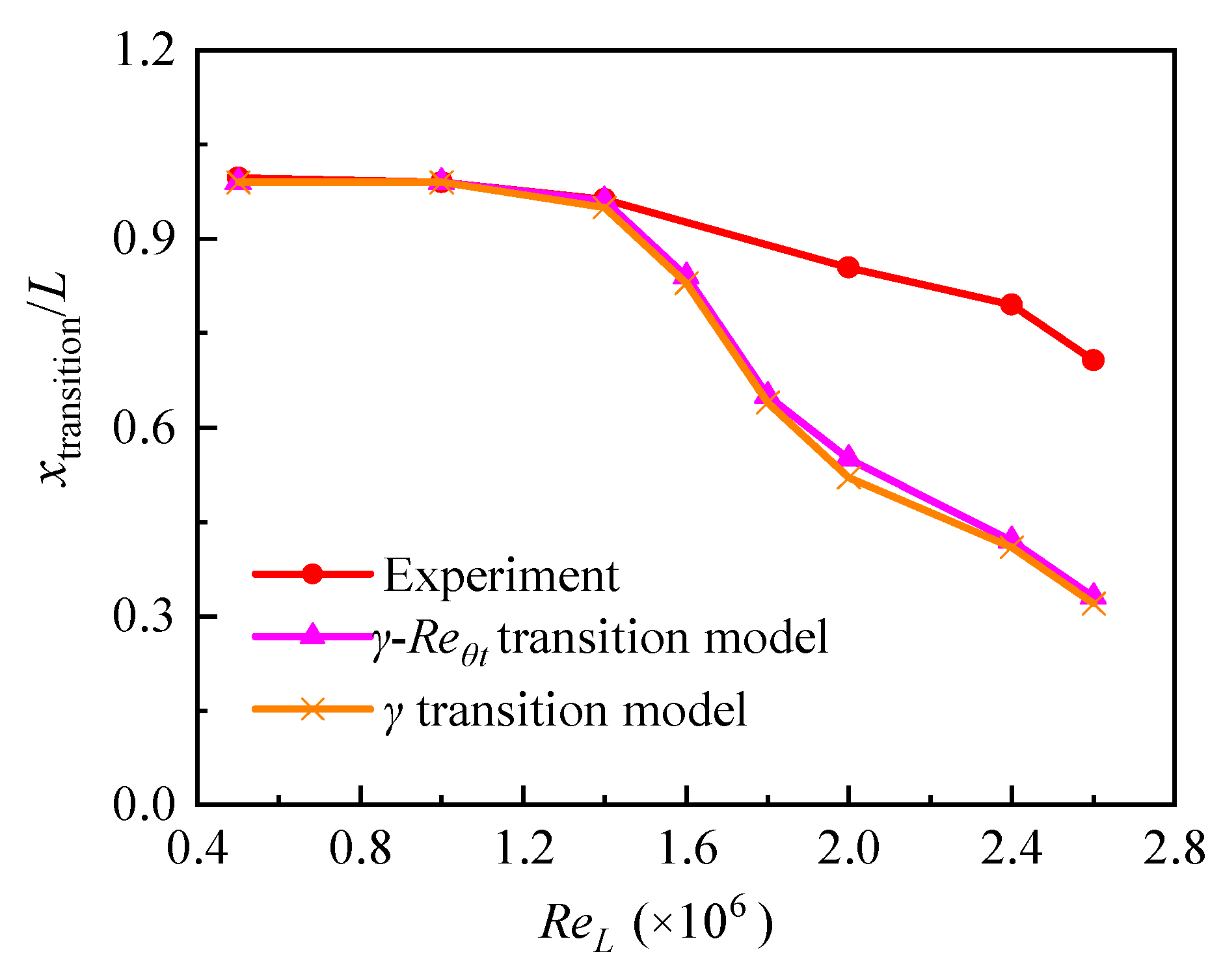
- For natural transition scenarios, the application of the γ-Reθt and γ transition models significantly improved the predictive capabilities of boundary layer flow distributions in comparison to the SST k-ω turbulence model. At ReL = 2 × 106, the experimentally determined position for transition completion is 0.85L. In contrast, the SST k-ω turbulence model predicts an earlier transition completion at 0.2L. The γ-Reθt and γ transition models estimate the transition completion positions at 0.53L and 0.55L, respectively, suggesting a delayed transition relative to the SST k-ω model, but earlier than observed in the experiment.
- (2)
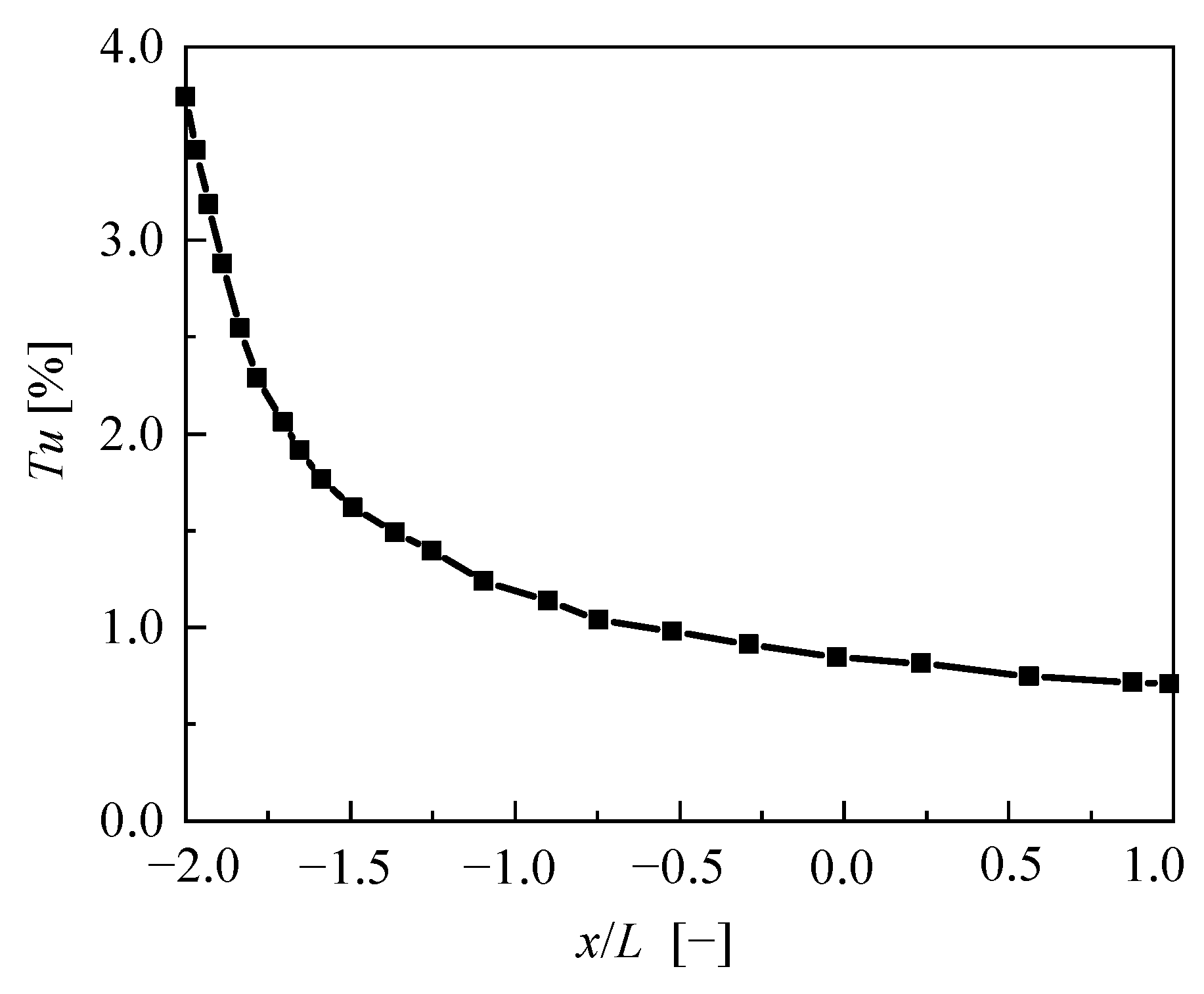
- For natural transitions, when the ReL is below 1.6 × 106, the predictive accuracy of both transition models exhibits a notable proximity to the values obtained through experimental analysis. As the ReL increases, the transition position gradually deviates from the measured value, indicating that the two transition models have poor prediction performance for high-Reynolds-number hydrofoil boundary layer transitions. By analyzing the development of turbulence along the flow direction, it is found that the primary cause of erroneous prediction of transition positions is the significant decrease in turbulence intensity in the free-flow field at high Reynolds numbers.
- (3)
- Using the γ transition model to study the effects of different angles of attack and Reynolds numbers on the hydrofoil’s leading edge boundary layer, it was found that the occurrence of the LSB is significantly correlated with the AOA, and its size decreases with an increase in the AOA. As the Reynolds number increases, the size of the LSB reduces and remains relatively stable until the onset of the trailing edge stall. Furthermore, an increase in the AOA leads to earlier separation of the boundary layer, which in turn affects the characteristics at the initiation and reattachment points of the LSB.
5.2. Future Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Variable | Definition |
| Reθt | Momentum Reynolds number based on the momentum thickness at the transition onset |
| γ | Intermittency factor, representing the local probability of turbulent flow in the boundary layer |
| u | Velocity component in the streamwise direction |
| x | Streamwise coordinate |
| y | Wall-normal coordinate |
| z | Spanwise coordinate (perpendicular to both streamwise and wall-normal directions) |
| t | Time |
| ρ | Fluid density |
| μ | Dynamic viscosity of the fluid |
| σ | Turbulent Prandtl number for temperature |
| k | Turbulent kinetic energy |
| ω | Specific dissipation rate of turbulent kinetic energy |
| Pk | Production term of turbulent kinetic energy in the SST k-ω turbulence model |
| Dk | Destruction term of turbulent kinetic energy in the SST k-ω turbulence model |
| P | Production term of the intermittency factor γ |
| E | Destruction term of the intermittency factor γ |
| fj | Damping function for the transition model |
| R | Correlation function used in the γ-Reθt transition model |
| θ | Momentum thickness |
| δ | Boundary layer thickness |
| δ1 | Displacement thickness |
| δ2 | Momentum thickness |
| H12 | Shape factor, the ratio of displacement thickness to momentum thickness |
| Tu | Turbulence intensity |
| AOA | Angle of attack |
| LSB | Laminar separation bubble, a region of separated flow in the boundary layer |
| xsep | The streamwise location where the laminar separation bubble separates from the hydrofoil |
| xre | The streamwise location where the flow reattaches after the laminar separation bubble |
| h | The thickness of the hydrofoil’s blunt trailing edge |
| Uxave | Time-averaged velocity at the outer boundary of the boundary layer |
| Ute | Time-averaged velocity at the outer edge of the boundary layer |
| UYmean | Average velocity in the y-direction over time near the trailing edge |
References
- Zhao, D.; Zhang, Y.; He, Q.; Sun, C.; Bi, M. Hydrodynamic and flow field characteristics of water jet propulsion under mooring conditions. J. Mar. Sci. Eng. 2022, 10, 953. [Google Scholar] [CrossRef]
- Shi, Z.; Tan, X.; Wang, Y.; Lv, P.; Zou, Y.; Wan, X.; Lv, K.; Li, B.; Duan, H.; Li, H. Experimental Investigation of High Speed Cross-Domain Vehicles with Hydrofoil. J. Mar. Sci. Eng. 2023, 11, 152. [Google Scholar] [CrossRef]
- Sheha, A.A.A.; Engineer, P.P.C.R.E.; Nasr, M.; Hosien, M.A.; Wahba, E. Computational and experimental study on the water-jet pump performance. J. Appl. Fluid Mech. 2018, 11, 1013–1020. [Google Scholar] [CrossRef]
- Gupta, S.; Sharma, A.; Agrawal, A.; Thompson, M.C.; Hourigan, K. Role of Shape and Kinematics in the Hydrodynamics of a Fish-like Oscillating Hydrofoil. J. Mar. Sci. Eng. 2023, 11, 1923. [Google Scholar] [CrossRef]
- Ye, C.; Zheng, Y.; Kan, K.; Tao, R.; Chen, H. Advances in Hydrodynamics of Water Pump Station System. Water 2024, 16, 1430. [Google Scholar] [CrossRef]
- Kan, K.; Chen, H.; Zheng, Y.; Zhou, D.; Binama, M.; Dai, J. Transient characteristics during power-off process in a shaft extension tubular pump by using a suitable numerical model. Renew. Energy 2021, 164, 109–121. [Google Scholar] [CrossRef]
- Ye, C.; An, D.; Huang, W.; Heng, Y.; Zheng, Y. Investigation on stall characteristics of centrifugal pump with guide vanes. Water 2023, 15, 21. [Google Scholar] [CrossRef]
- Arabnejad, M.H.; Svennberg, U.; Bensow, R.E. Numerical Assessment of Cavitation Erosion Risk in a Commercial Water-Jet Pump. J. Fluids Eng. 2022, 144, 051201. [Google Scholar] [CrossRef]
- Qian, Z.; Wang, F.; Guo, Z.; Lu, J. Performance evaluation of an axial-flow pump with adjustable guide vanes in turbine mode. Renew. Energy 2016, 99, 1146–1152. [Google Scholar] [CrossRef]
- Baltazar, J.; Rijpkema, D.; de Campos, J.F. On the use of the γ-Reθt transition model for the prediction of the propeller performance at model-scale. Ocean. Eng. 2018, 170, 6–19. [Google Scholar] [CrossRef]
- Ye, C.; Huang, W.; Yan, H.; Zheng, Y.; Kan, K.; van Esch, B.P.M. Study on rotating stall characteristics of centrifugal pumps based on gamma transition model. Phys. Fluids 2024, 36, 055101. [Google Scholar] [CrossRef]
- Guo, Q.; Huang, X.; Qiu, B. Numerical investigation of the blade tip leakage vortex cavitation in a waterjet pump. Ocean. Eng. 2019, 187, 106170. [Google Scholar] [CrossRef]
- Guo, Q.; Zhou, L.; Wang, Z. Numerical evaluation of the clearance geometries effect on the flow field and performance of a hydrofoil. Renew. Energy 2016, 99, 390–397. [Google Scholar] [CrossRef]
- Wang, C.; Wang, F.; Li, C.; Chen, W.; Wang, H.; Lu, L. Investigation on energy conversion instability of pump mode in hydro-pneumatic energy storage system. J. Energy Storage 2022, 53, 105079. [Google Scholar] [CrossRef]
- Wang, C.; Wang, F.; Xie, L.; Wang, B.; Yao, Z.; Xiao, R. On the vortical characteristics of horn-like vortices in stator corner separation flow in an axial flow pump. J. Fluids Eng. 2021, 143, 061201. [Google Scholar] [CrossRef]
- Ducoin, A.; Astolfi, J.A.; Deniset, F.; Sigrist, J.-F. Computational and experimental investigation of flow over a transient pitching hydrofoil. Eur. J. Mech. B/Fluids 2009, 28, 728–743. [Google Scholar] [CrossRef]
- Ducoin, A.; Astolfi, J.A.; Gobert, M.-L. An experimental study of boundary-layer transition induced vibrations on a hydrofoil. J. Fluids Struct. 2012, 32, 37–51. [Google Scholar] [CrossRef]
- Posa, A.; Broglia, R.; Balaras, E. Flow over a hydrofoil in the wake of a propeller. Comput. Fluids 2020, 213, 104714. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Zhu, Z.; Lin, P.; Li, L. Boundary vorticity analysis and shedding dynamics of transient cavitation flow around a twisted hydrofoil. J. Fluids Eng. 2021, 143, 071501. [Google Scholar] [CrossRef]
- Carabineanu, A. The study of the potential flow past a submerged hydrofoil by the complex boundary element method. Eng. Anal. Bound. Elements 2014, 39, 23–35. [Google Scholar] [CrossRef]
- Kant, R.; Bhattacharyya, A. A bio-inspired twin-protuberance hydrofoil design. Ocean Eng. 2020, 218, 108209. [Google Scholar] [CrossRef]
- Churkin, S.A.; Pervunin, K.S.; Kravtsova, A.Y.; Markovich, D.M.; Hanjalić, K. Cavitation on NACA0015 hydrofoils with different wall roughness: High-speed visualization of the surface texture effects. J. Vis. 2016, 19, 587–590. [Google Scholar] [CrossRef]
- Sedlář, M.; Komárek, M.; Šoukal, J.; Volkov, A.V.; Ryzhenkov, A.V.; Druzhinin, A.A.; Grigoriev, S.V.; Kachalin, G.V.; Kalakutskaya, O.V. Experimental and Numerical Studies into the Cavitation Impact of the Hydrofoil Surface with Different Treatments. Therm. Eng. 2022, 69, 418–428. [Google Scholar] [CrossRef]
- Rastan, M.R.; Foshat, S.; Sekhavat, S. High-reynolds number flow around coated symmetrical hydrofoil: Effect of streamwise slip on drag force and vortex structures. J. Mar. Sci. Technol. 2019, 24, 500–511. [Google Scholar] [CrossRef]
- Shahsavari, A.; Nejat, A.; Climent, E.; Chini, S.F. Unexpected trends of lift for hydrofoils with superhydrophobic coating. Eur. J. Mech. B/Fluids 2023, 101, 219–226. [Google Scholar] [CrossRef]
- Ye, C.; Xia, K.; Yan, H.; Cao, S.; Wang, Z.; Tian, Q.; van Esch, B.P.; Zheng, Y.; Yang, C. Study on the influence of volute structure on the performance of seawater-pumped storage hydropower plant unit. J. Energy Storage 2024, 90, 111848. [Google Scholar] [CrossRef]
- Kundu, P. Numerical simulation of the effects of passive flow control techniques on hydrodynamic performance improvement of the hydrofoil. Ocean Eng. 2020, 202, 107108. [Google Scholar] [CrossRef]
- Ge, M.; Svennberg, U.; Bensow, R.E. Improved prediction of sheet cavitation inception using bridged transition sensitive turbulence model and cavitation model. J. Mar. Sci. Eng. 2021, 9, 1343. [Google Scholar] [CrossRef]
- Kan, K.; Yang, Z.; Lyu, P.; Zheng, Y.; Shen, L. Numerical study of turbulent flow past a rotating axial-flow pump based on a level-set immersed boundary method. Renew. Energy 2021, 168, 960–971. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Krasilnikov, V.; Steen, S. Scale effects on open water characteristics of a controllable pitch propeller working within different duct designs. Ocean Eng. 2016, 112, 226–242. [Google Scholar] [CrossRef]
- Pawar, S.; Brizzolara, S. Relevance of transition turbulent model for hydrodynamic characteristics of low Reynolds number propeller. Appl. Ocean Res. 2019, 87, 165–178. [Google Scholar] [CrossRef]
- Menter, F.R.; Langtry, R.; Völker, S. Transition modelling for general purpose CFD codes. Flow Turbul. Combust. 2006, 77, 277–303. [Google Scholar] [CrossRef]
- Menter, F.R.; Smirnov, P.E.; Liu, T.; Avancha, R. A one-equation local correlation-based transition model. Flow Turbul. Combust. 2015, 95, 583–619. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Montazeri, H.; Blocken, B. CFD analysis of dynamic stall on vertical axis wind turbines using Scale-Adaptive Simulation (SAS): Comparison against URANS and hybrid RANS/LES. Energy Convers. Manag. 2019, 196, 1282–1298. [Google Scholar] [CrossRef]
- Fahland, G.; Stroh, A.; Frohnapfel, B.; Atzori, M.; Vinuesa, R.; Schlatter, P.; Gatti, D. Investigation of blowing and suction for turbulent flow control on airfoils. AIAA J. 2021, 59, 4422–4436. [Google Scholar] [CrossRef]
- D’amato, E.; Notaro, I.; Piscopo, V.; Scamardella, A. Hydrodynamic design of fixed hydrofoils for planing craft. J. Mar. Sci. Eng. 2023, 11, 246. [Google Scholar] [CrossRef]
- Rahman, M.M.; Hasan, K.; Pan, H. Capturing transition around low-Reynolds number hydrofoil with zero-equation transition model. Phys. Fluids 2022, 34, 074115. [Google Scholar] [CrossRef]
- Cui, B.; Wang, X.; Wang, R.; Xiao, Z. Numerical investigation of transonic axial compressor rotor flows using an improved transition-sensitized turbulence model. Phys. Fluids 2021, 33, 035149. [Google Scholar] [CrossRef]
- Li, H.; Huang, Q.; Pan, G.; Dong, X.; Li, F. An investigation on the flow and vortical structure of a pre-swirl stator pump-jet propulsor in drift. Ocean Eng. 2022, 250, 111061. [Google Scholar] [CrossRef]
- Rozhdestvensky, K. A simplified mathematical model of pumped hydrofoils. J. Mar. Sci. Eng. 2023, 11, 913. [Google Scholar] [CrossRef]
- Durbin, P.A. Some recent developments in turbulence closure modeling. Annu. Rev. Fluid Mech. 2018, 50, 77–103. [Google Scholar] [CrossRef]
- Rubino, G.; Visonneau, M. Improved crossflow transition predictions for the one-equation γ transition model. Comput. Fluids 2022, 245, 105580. [Google Scholar] [CrossRef]
- Venkatachari, B.S.; Gosin, S.A.; Choudhari, M.M. Implementation and Assessment of Menter’s Galilean-Invariant γ Transition Model in Overflow. In Proceedings of the AIAA Aviation 2023 Forum, San Diego, CA, USA, 12–16 June 2023. [Google Scholar]
- Choi, J.H.; Kwon, O.J. Recent improvement of a correlation-based transition model for simulating three-dimensional boundary layers. AIAA J. 2017, 55, 2103–2108. [Google Scholar] [CrossRef]
- Ye, C.; Tang, Y.; An, D.; Wang, F.; Zheng, Y.; van Esch, B. Investigation on stall characteristics of marine centrifugal pump considering transition effect. Ocean Eng. 2023, 280, 114823. [Google Scholar] [CrossRef]
- Ye, C.-L.; Wang, C.-Y.; Zi, D.; Tang, Y.; van Esch, B.P.M.; Wang, F.-J. Improvement of the SST γ-Reθt transition model for flows along a curved hydrofoil. J. Hydrodyn. 2021, 33, 520–533. [Google Scholar] [CrossRef]
- Mykhailyshyn, R.; Duchoň, F.; Virgala, I.; Sinčák, P.J.; Fey, A.M. Optimization of outer diameter bernoulli gripper with cylindrical nozzle. Machines 2023, 11, 667. [Google Scholar] [CrossRef]
- Santos, D.; Rogers, J.; De Rezende, A.; Maldonado, V. Exploring the Performance Boundaries of a Small Reconfigurable Multi-Mission UAV through Multidisciplinary Analysis. Aerospace 2023, 10, 684. [Google Scholar] [CrossRef]
- Carreño Ruiz, M.; D’ambrosio, D. Validation of the γ-Reθ transition model for airfoils operating in the very low Reynolds number regime. Flow Turbul. Combust. 2022, 109, 279–308. [Google Scholar] [CrossRef]
- Mishra, R.K.; Dua, H. Phase transition of cosmological model with statistical techniques. Astrophys. Space Sci. 2020, 365, 1–13. [Google Scholar] [CrossRef]
- Kontou, M.G.; Trompoukis, X.S.; Asouti, V.G.; Giannakoglou, K.C. The continuous adjoint method to the γ− Reθt transition model coupled with the Spalart–Allmaras model for compressible flows. Int. J. Numer. Methods Fluids 2024, 96, 1715–1740. [Google Scholar] [CrossRef]
- Pascal, L.; Delattre, G.; Deniau, H.; Cliquet, J. Stability-based transition model using transport equations. AIAA J. 2020, 58, 2933–2942. [Google Scholar] [CrossRef]
- Ji, B.; Zhong, K.; Xiong, Q.; Qiu, P.; Zhang, X.; Wang, L. CFD simulations of aerodynamic characteristics for the three-blade NREL Phase VI wind turbine model. Energy 2022, 249, 123670. [Google Scholar] [CrossRef]
- Anzalotta, C.; Joshi, K.; Fernandez, E.; Bhattacharya, S. Effect of forcing the tip-gap of a NACA0065 airfoil using plasma actuators: A proof-of-concept study. Aerosp. Sci. Technol. 2020, 107, 106268. [Google Scholar] [CrossRef]
- Dewan, A.; Tomar, S.S.; Bishnoi, A.K.; Singh, T.P. Computational fluid dynamics and turbulence modelling in various blades of Savonius turbines for wind and hydro energy: Progress and perspectives. Ocean Eng. 2023, 283, 115168. [Google Scholar] [CrossRef]
- Chegini, S.; Asadbeigi, M.; Ghafoorian, F.; Mehrpooya, M. An investigation into the self-starting of Darrieus-Savonius hybrid wind turbine and performance enhancement through innovative deflectors: A CFD approach. Ocean Eng. 2023, 287, 115910. [Google Scholar] [CrossRef]
- Celik, Y.; Ma, L.; Ingham, D.; Pourkashanian, M. Aerodynamic investigation of the start-up process of H-type vertical axis wind turbines using CFD. J. Wind. Eng. Ind. Aerodyn. 2020, 204, 104252. [Google Scholar] [CrossRef]
- Akhter, Z.; Ali, A.R.; Jawahar, H.K.; Omar, F.K.; Elnajjar, E. Performance enhancement of small-scale wind turbine featuring morphing blades. Energy 2023, 278, 127772. [Google Scholar] [CrossRef]
- Sridhar, S.; Joseph, J.; Radhakrishnan, J. Implementation of tubercles on vertical axis wind turbines (VAWTs): An aerodynamic perspective. Sustain. Energy Technol. Assessments 2022, 52, 102109. [Google Scholar] [CrossRef]
- Ausoni, P. Turbulent Vortex Shedding from a Blunt Trailing Edge Hydrofoil (No. THESIS). Ph.D. Thesis, EPFL, Lausanne, Switzerland, 2009. [Google Scholar] [CrossRef]
- Odetti, A.; Altosole, M.; Bruzzone, G.; Caccia, M.; Viviani, M. Design and construction of a modular pump-jet thruster for autonomous surface vehicle operations in extremely shallow water. J. Mar. Sci. Eng. 2019, 7, 222. [Google Scholar] [CrossRef]
- Yan, H.; Heng, Y.; Zheng, Y.; Tao, R.; Ye, C. Investigation on pressure fluctuation of the impellers of a double-entry two-stage double suction centrifugal pump. Water 2022, 14, 4065. [Google Scholar] [CrossRef]
- Zhao, H.-R.; Wang, F.-J.; Wang, C.-Y.; Ye, C.-L.; Yao, Z.-F.; Zhong, Q. A modified VLES model for simulation of rotating separation flow in axial flow rotating machinery. J. Hydrodyn. 2022, 34, 570–584. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, M.Q.; Liu, H.T. Numerical Simulation of the Gas Phase of Cyclone-separator Sand Trap Based on ICEM CFD and Fluent. Adv. Mater. Res. 2013, 774–776, 321–325. [Google Scholar] [CrossRef]
- Sharma, R.; Mishra, D.; Brar, L.S. Performance enhancement of a fin and tube heat exchanger with the novel arrangement of curved winglets using a multi-objective optimization approach. Int. Commun. Heat Mass Transf. 2024, 157, 107804. [Google Scholar] [CrossRef]
- Bulat, P.; Chernyshov, P.; Prodan, N.; Volkov, K. Control of Aerodynamic Characteristics of Thick Airfoils at Low Reynolds Numbers Using Methods of Boundary Layer Control. Fluids 2024, 9, 26. [Google Scholar] [CrossRef]
- Wang, R.; Xiao, Z. Transition effects on flow characteristics around a static two-dimensional airfoil. Phys. Fluids 2020, 32, 035113. [Google Scholar] [CrossRef]

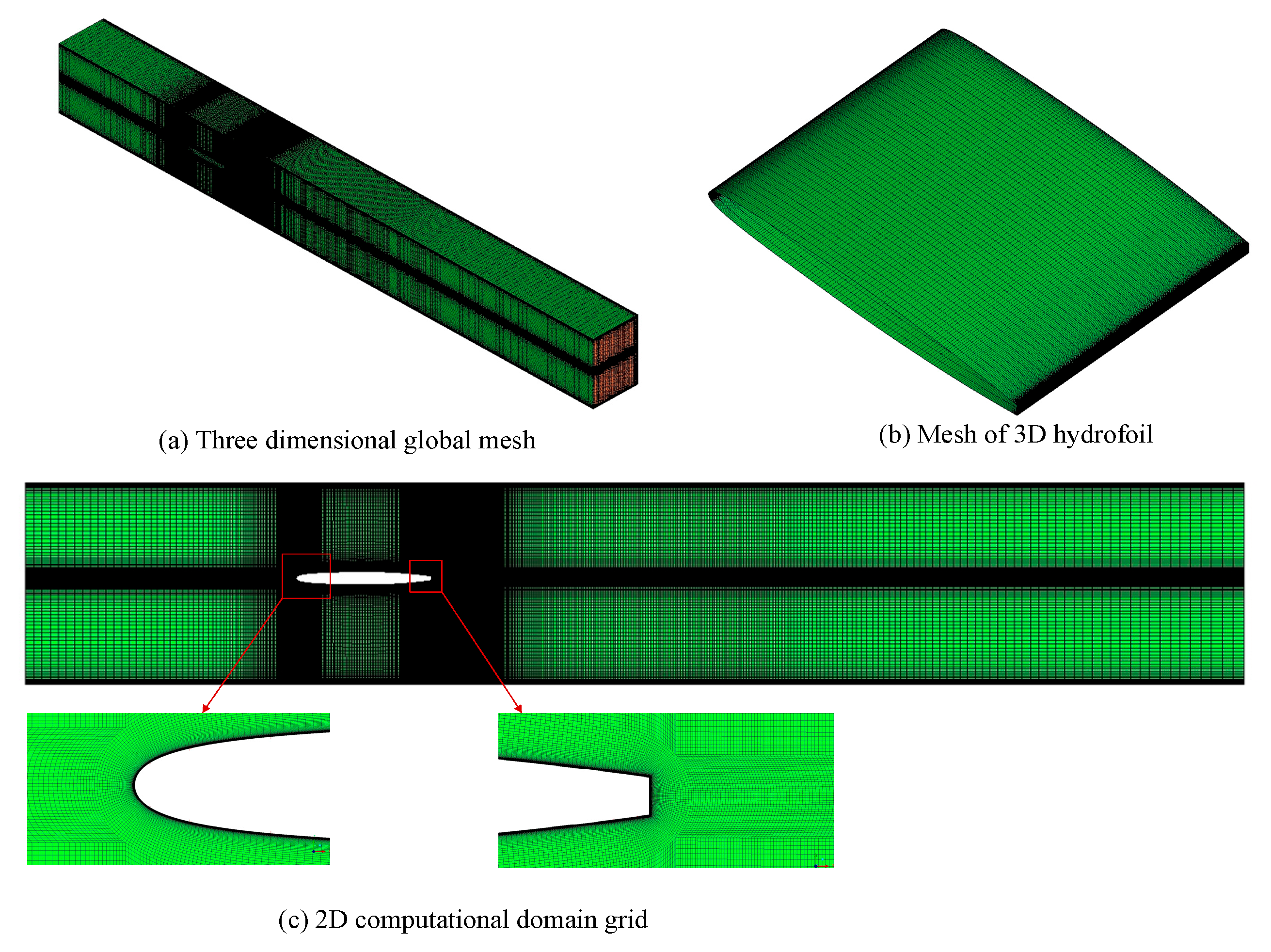



| Grid | Number of Nodes | Maximum y+ | Simulated Value | Tested Value |
|---|---|---|---|---|
| M1 | 6,521,238 | 0.62 | 1431 Hz | 1428 Hz |
| M2 | 5,538,952 | 0.79 | 1420 Hz | |
| M3 | 3,885,230 | 0.93 | 1336 Hz | |
| M4 | 2,750,156 | 1.12 | 1307 Hz |
| Onset Point (x/L) | Reattachment Point (x/L) | |||||
|---|---|---|---|---|---|---|
| ReL | 0.5 × 106 | 2.0 × 106 | 2.6 × 106 | 0.5 × 106 | 2.0 × 106 | 2.6 × 106 |
| AOA | ||||||
| 6° | 0.00164 | 0.00164 | 0.00164 | 0.00578 | 0.00479 | 0.00471 |
| 8° | 0.00147 | 0.00147 | 0.00147 | 0.00456 | 0.00305 | 0.00334 |
| 10° | 0.00102 | 0.00132 | 0.00132 | 0.00385 | 0.00225 | 0.00225 |
| 12° | / | 0.0012 | 0.0012 | / | 0.0021 | 0.00214 |
| 14° | / | 0.00115 | 0.00114 | / | 0.00219 | 0.00217 |
| 16° | / | 0.00114 | 0.00114 | / | 0.00199 | 0.00224 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, C.; Wang, Y.; An, D.; Chen, J.; Yan, H.; Zheng, Y.; Kan, K.; van Esch, B.P.M. Study of Hydrofoil Boundary Layer Prediction with Two Correlation-Based Transition Models. J. Mar. Sci. Eng. 2024, 12, 1965. https://doi.org/10.3390/jmse12111965
Ye C, Wang Y, An D, Chen J, Yan H, Zheng Y, Kan K, van Esch BPM. Study of Hydrofoil Boundary Layer Prediction with Two Correlation-Based Transition Models. Journal of Marine Science and Engineering. 2024; 12(11):1965. https://doi.org/10.3390/jmse12111965
Chicago/Turabian StyleYe, Changliang, Yang Wang, Dongsen An, Jun Chen, Hongyeyu Yan, Yuan Zheng, Kan Kan, and Bart P. M. van Esch. 2024. "Study of Hydrofoil Boundary Layer Prediction with Two Correlation-Based Transition Models" Journal of Marine Science and Engineering 12, no. 11: 1965. https://doi.org/10.3390/jmse12111965
APA StyleYe, C., Wang, Y., An, D., Chen, J., Yan, H., Zheng, Y., Kan, K., & van Esch, B. P. M. (2024). Study of Hydrofoil Boundary Layer Prediction with Two Correlation-Based Transition Models. Journal of Marine Science and Engineering, 12(11), 1965. https://doi.org/10.3390/jmse12111965








