Numerical Simulation of Ice and Structure Interaction Using Common-Node DEM in LS DYNA
Abstract
:1. Introduction
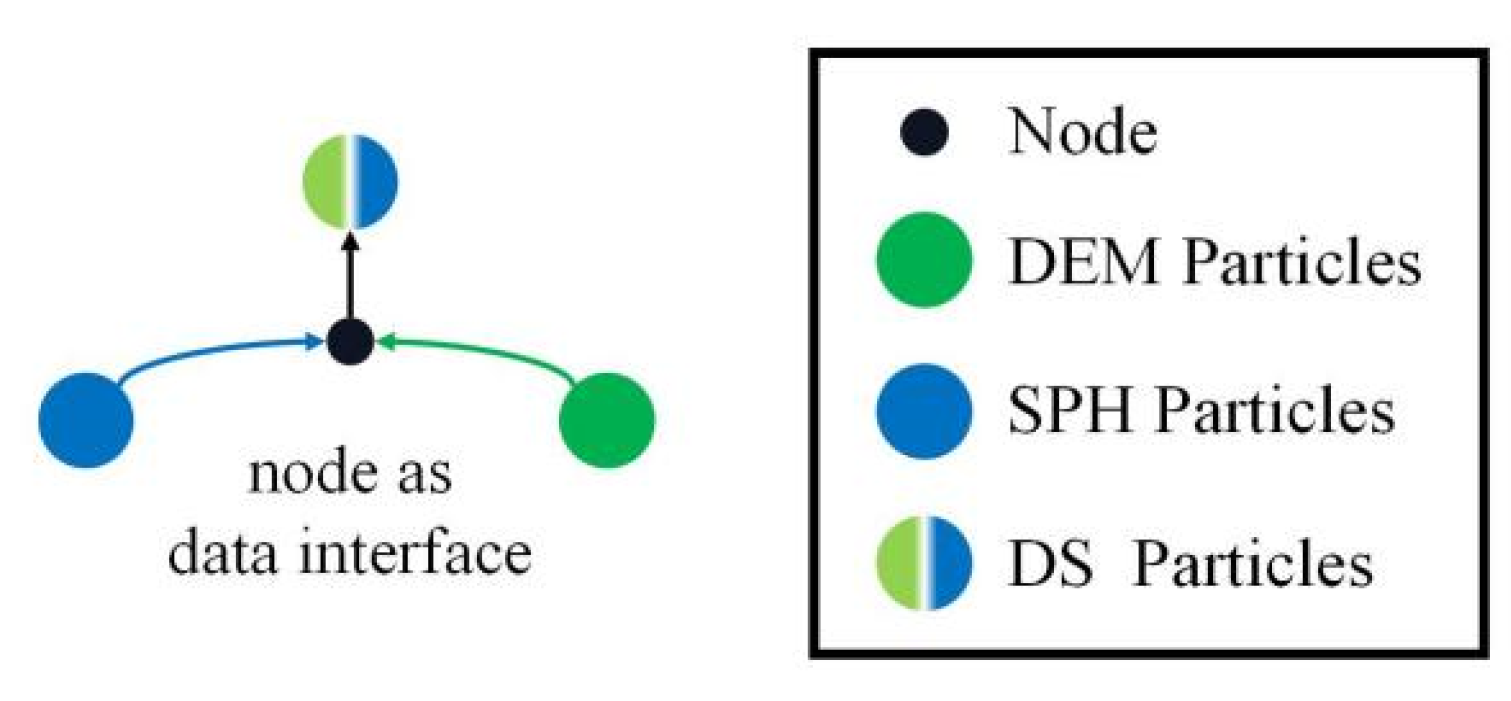
2. The Framework of Common-Node Discrete Element Method
2.1. Basic Principle
2.2. Equations of Motion
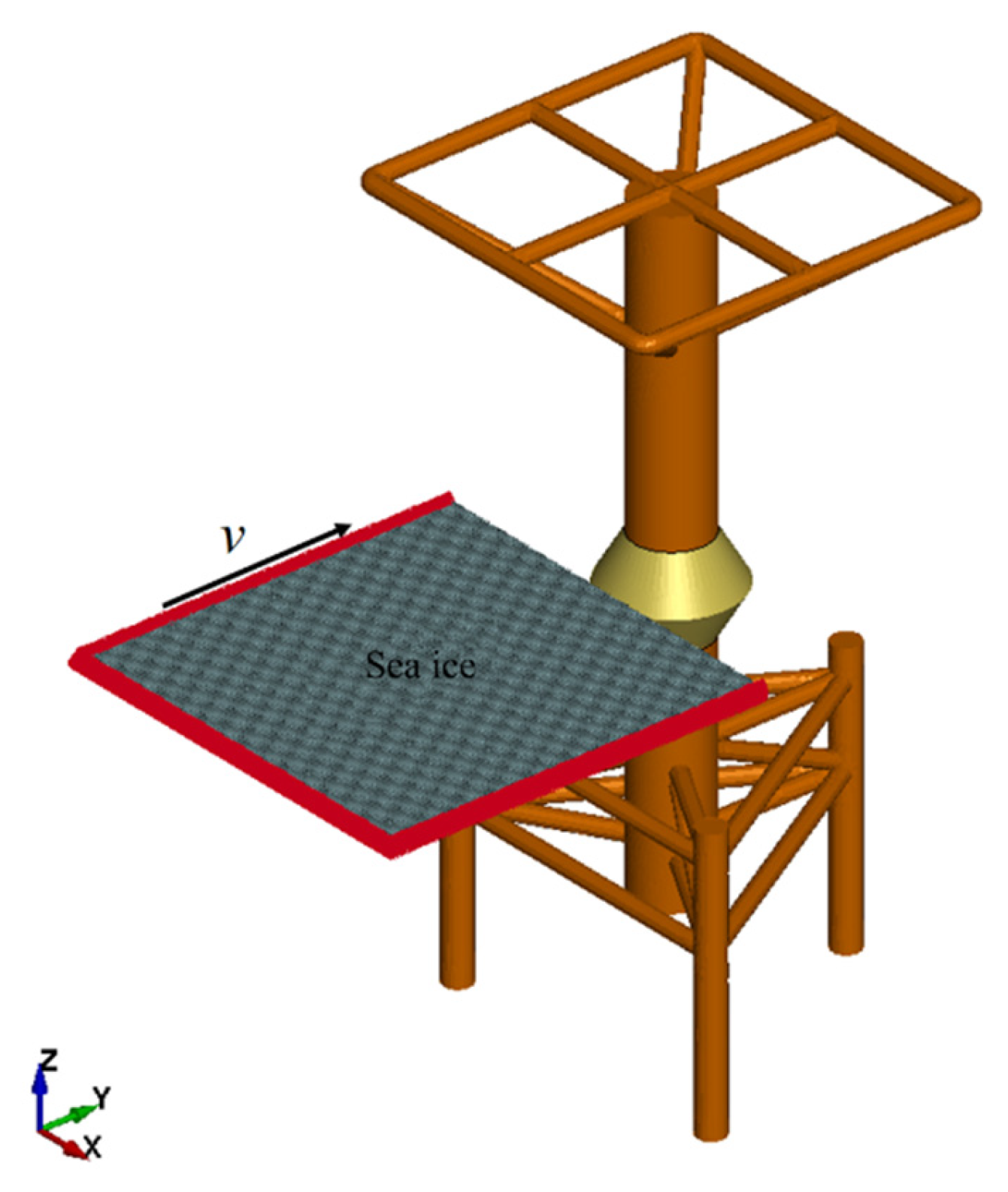
3. Setup of Ice and Structure Simulation
4. Modal Analysis of the Finite Element Model of the JZ20-2NW
5. Analysis of Simulation Results
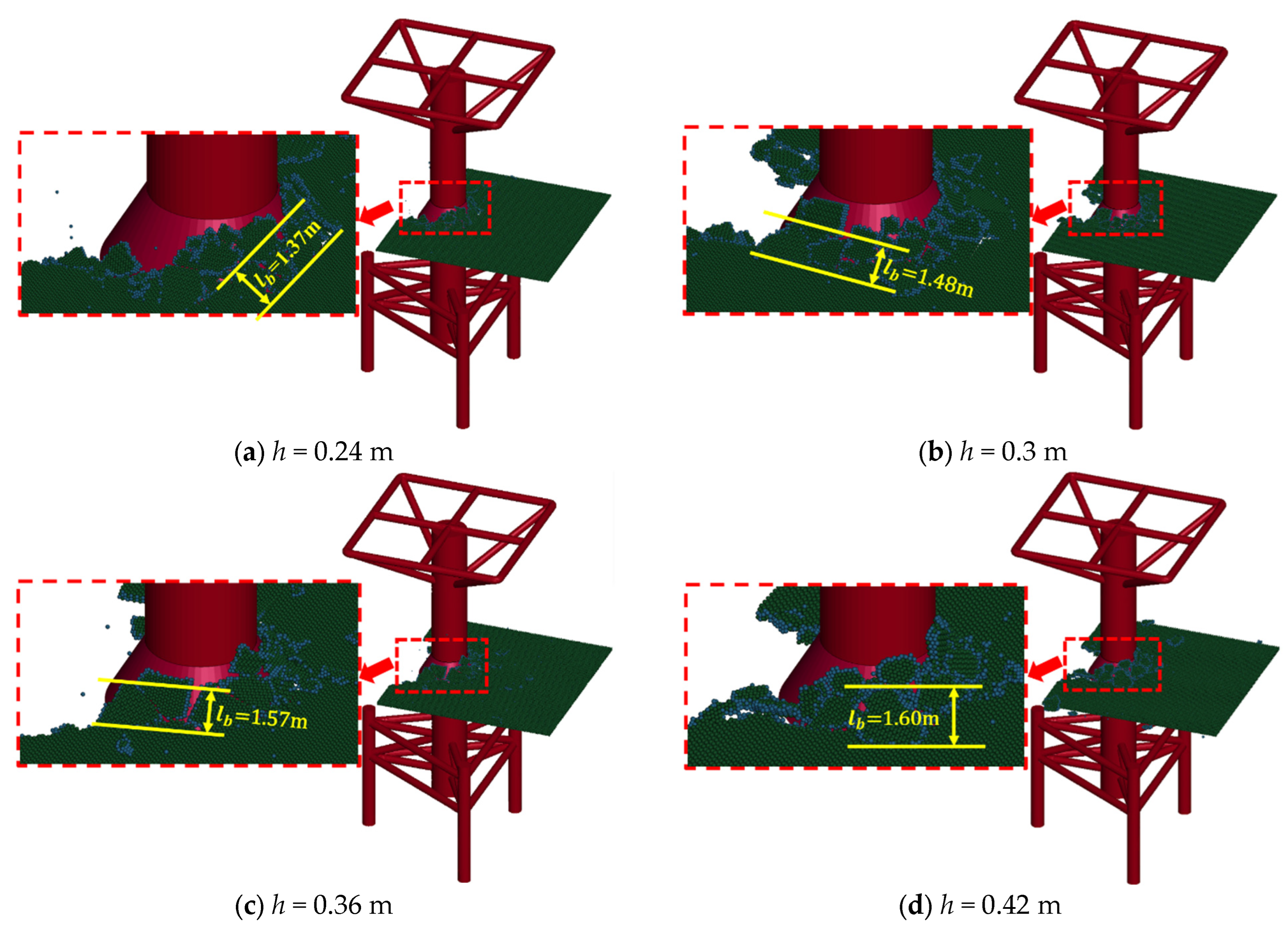
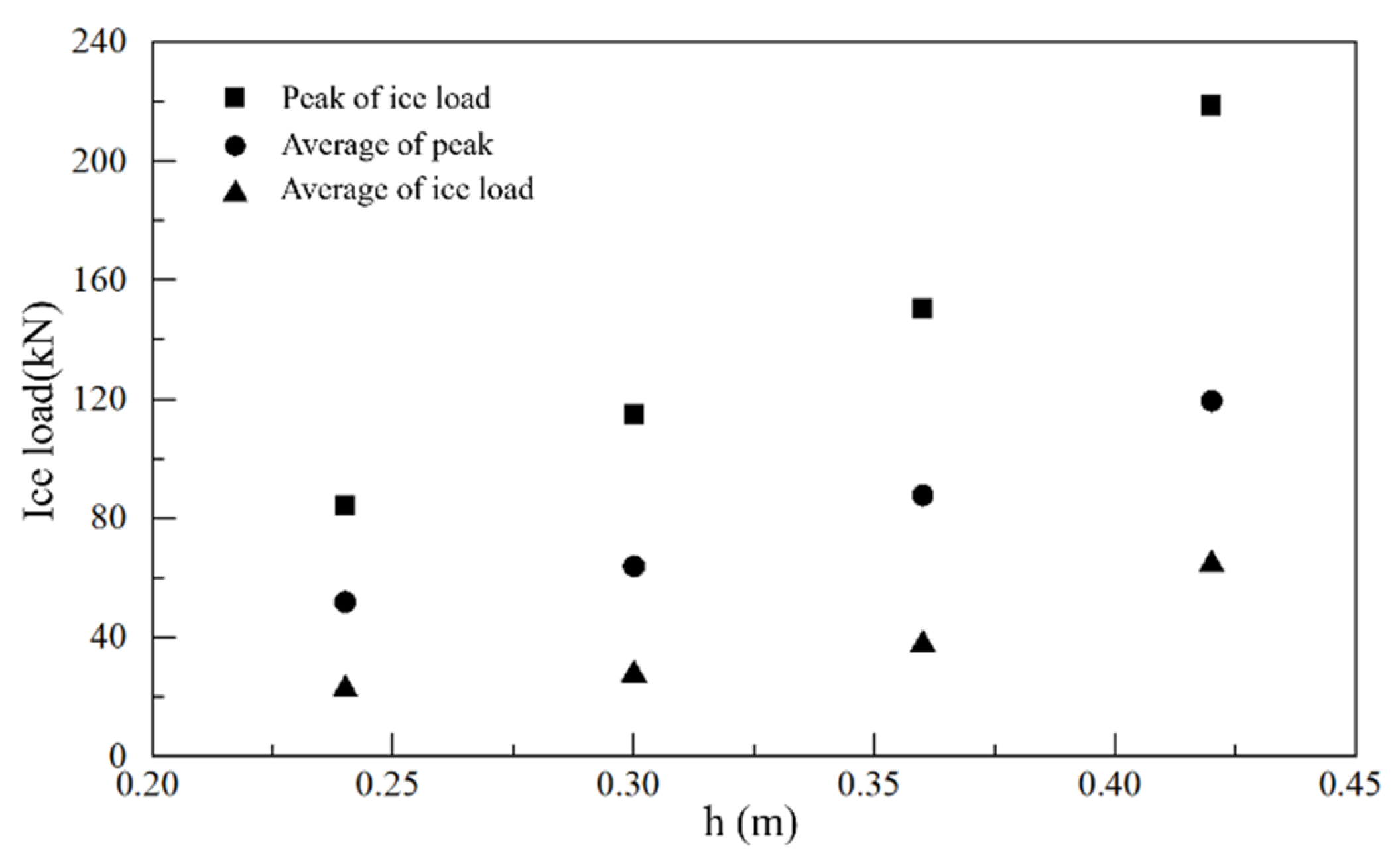
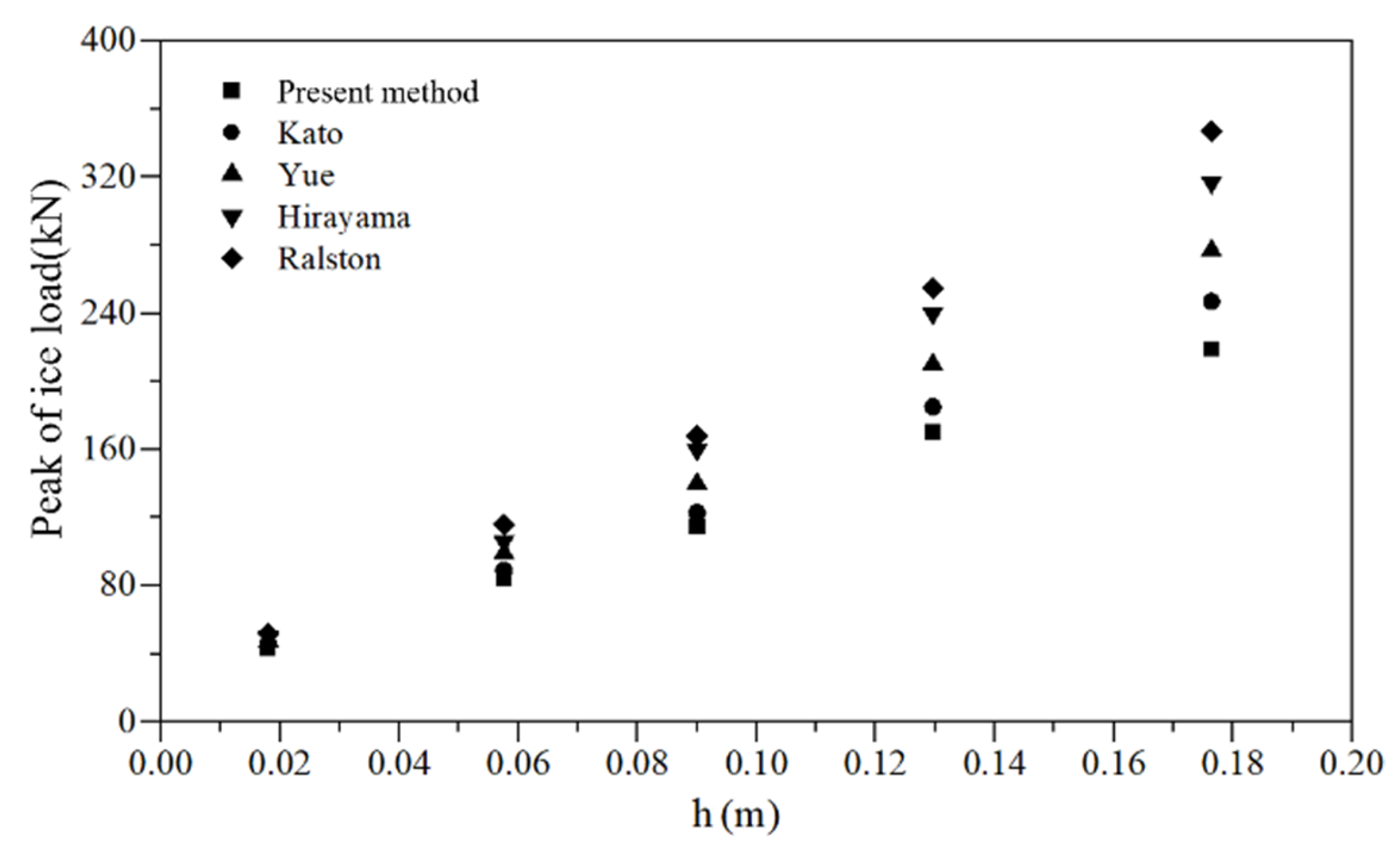
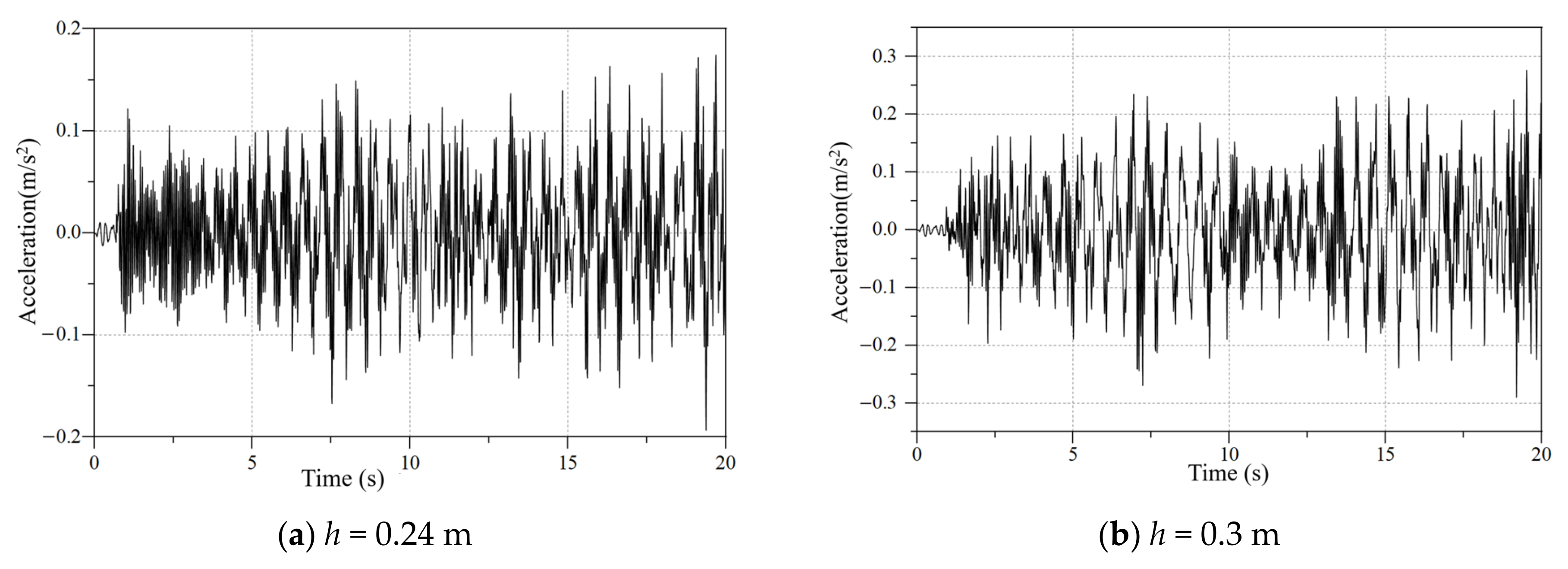
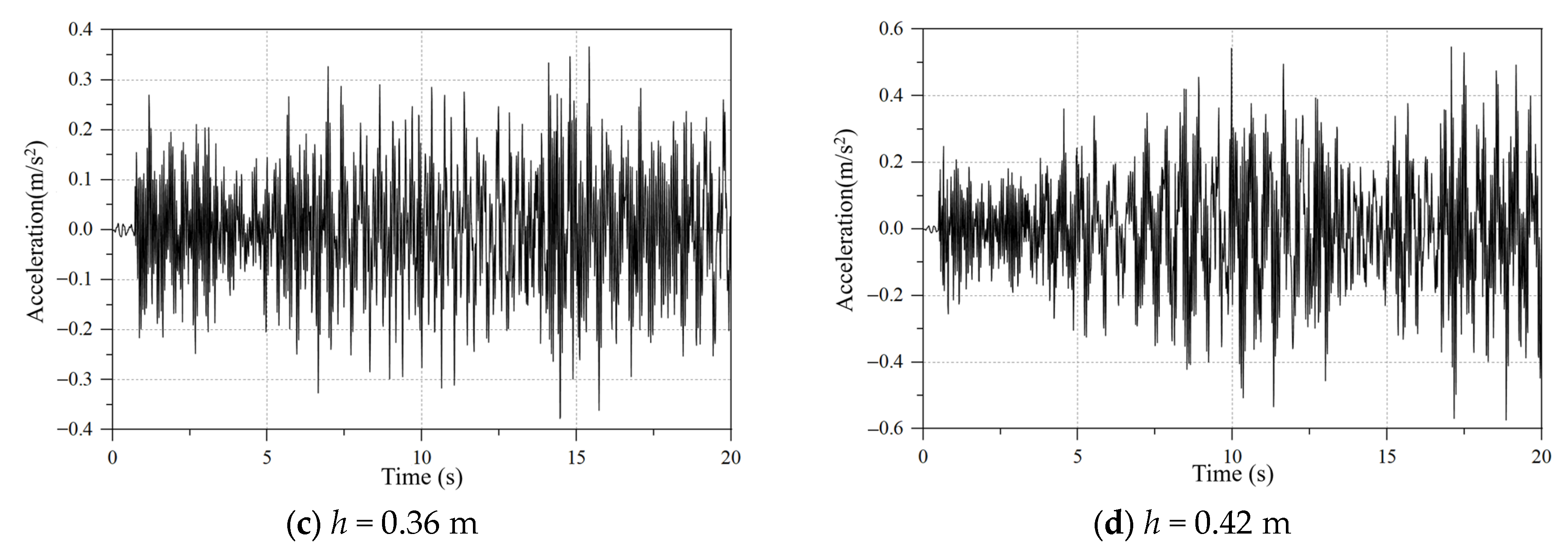
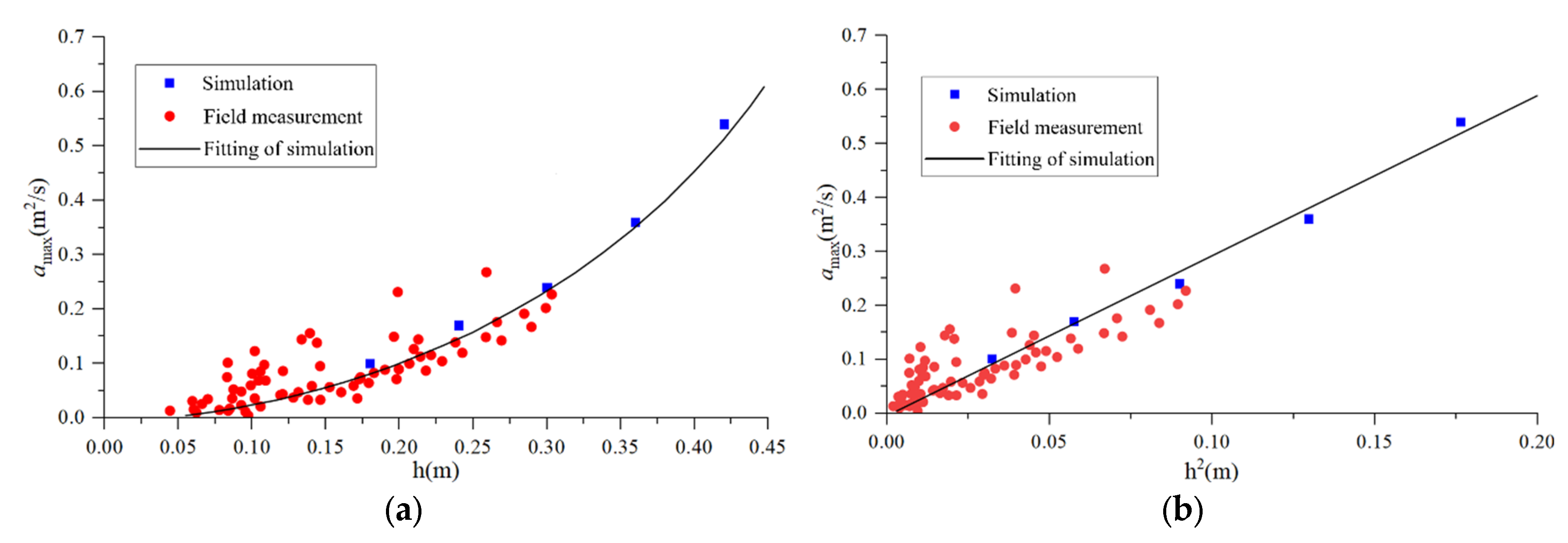
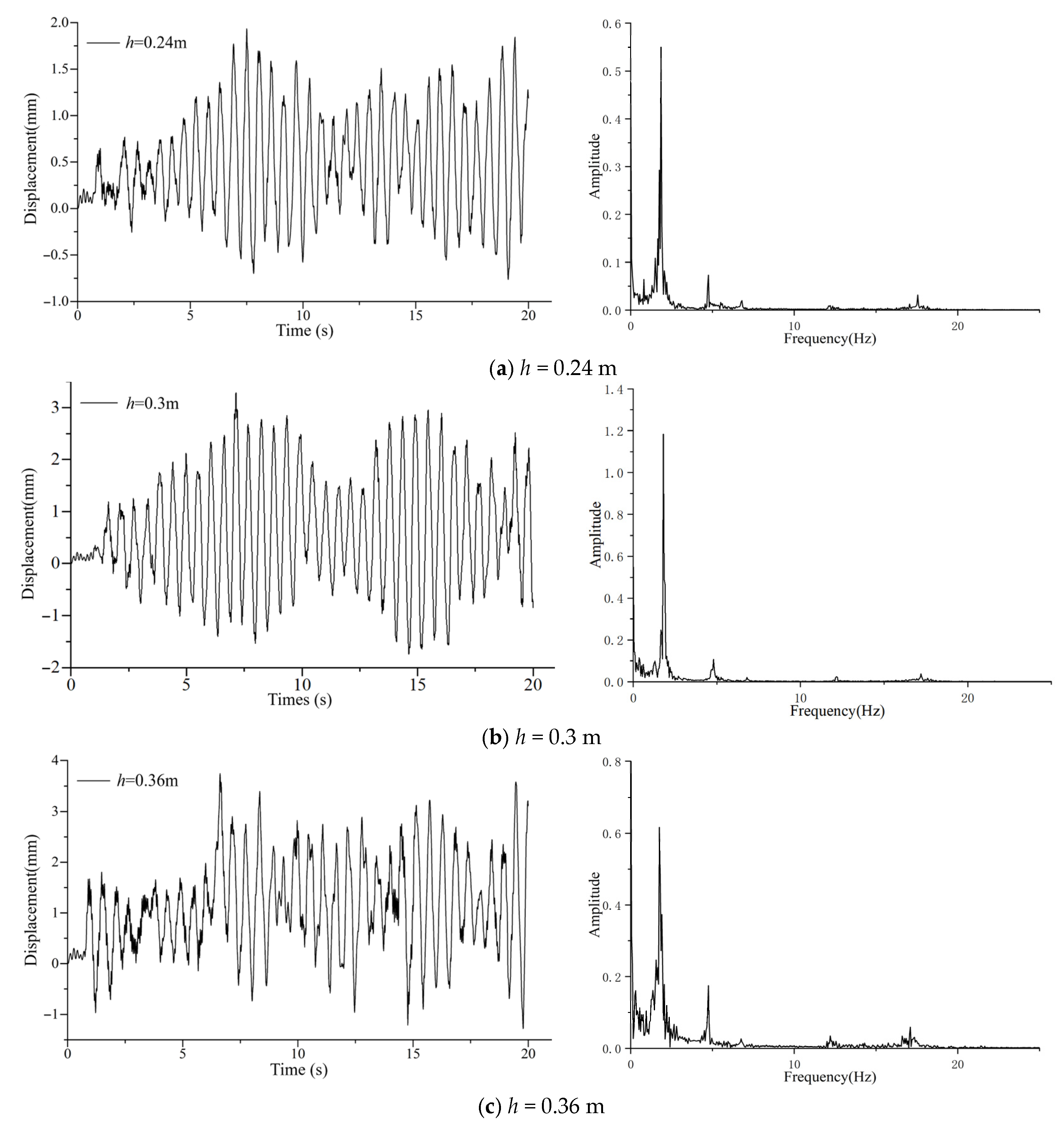
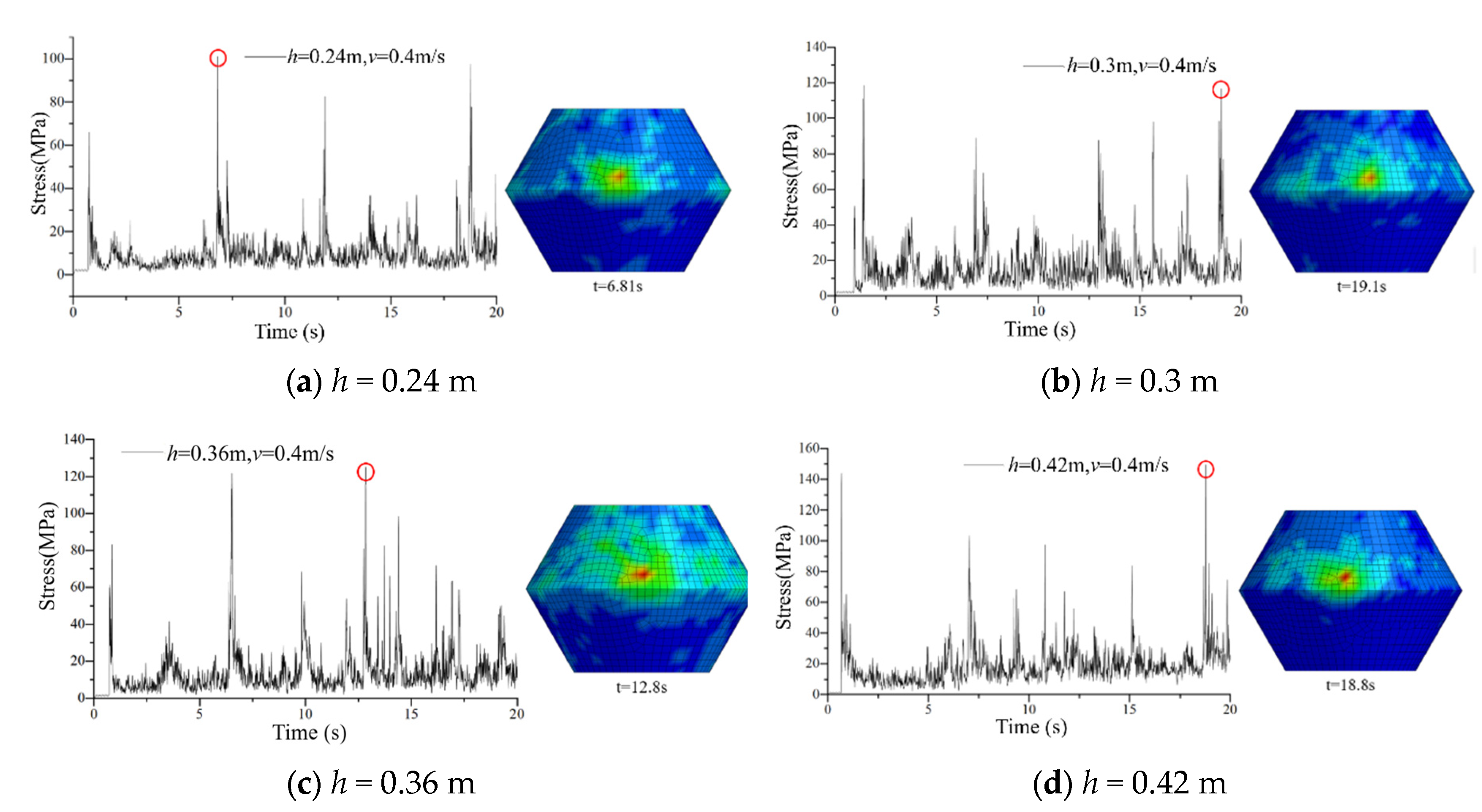
5.1. The Influence of Ice Thickness
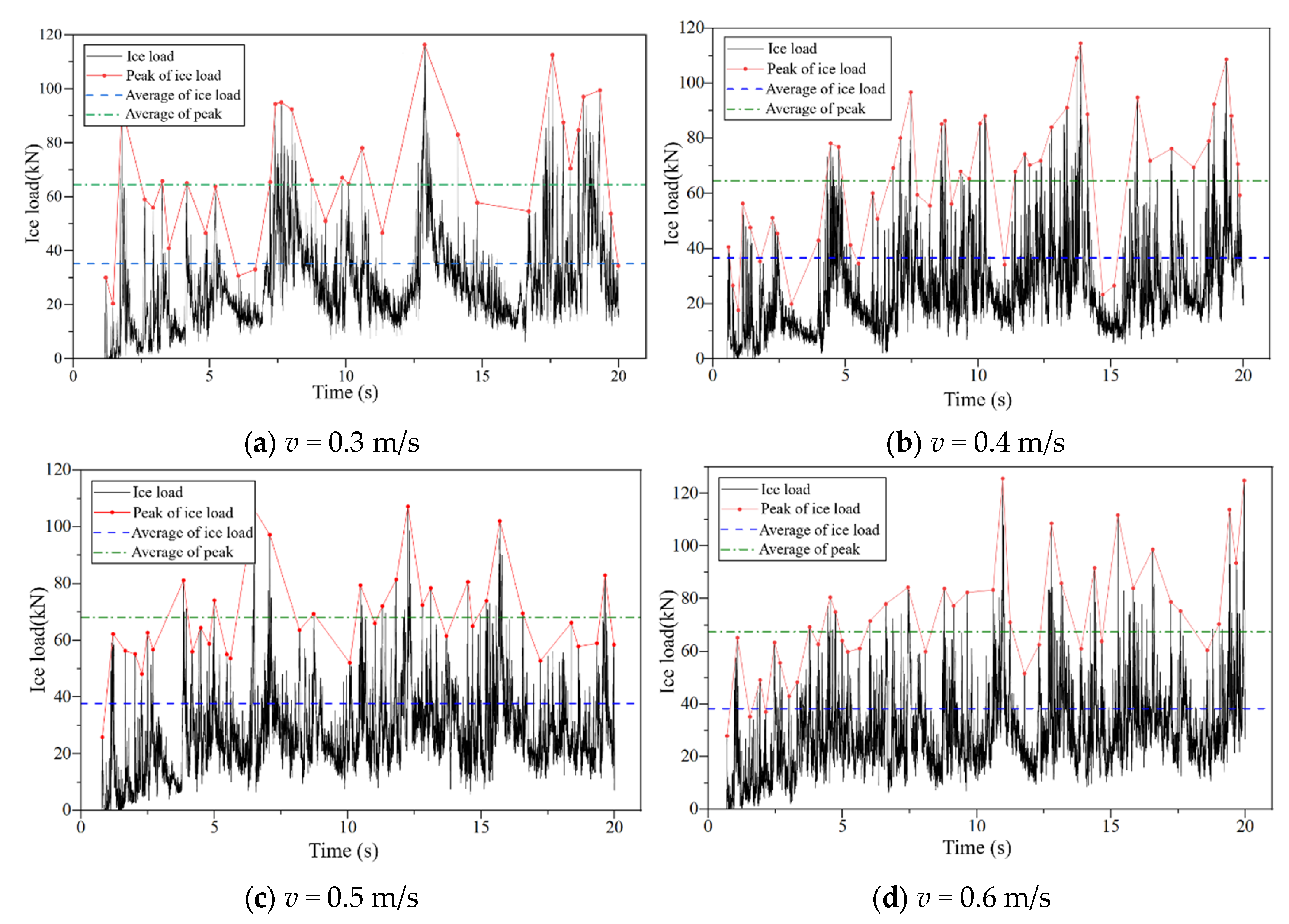
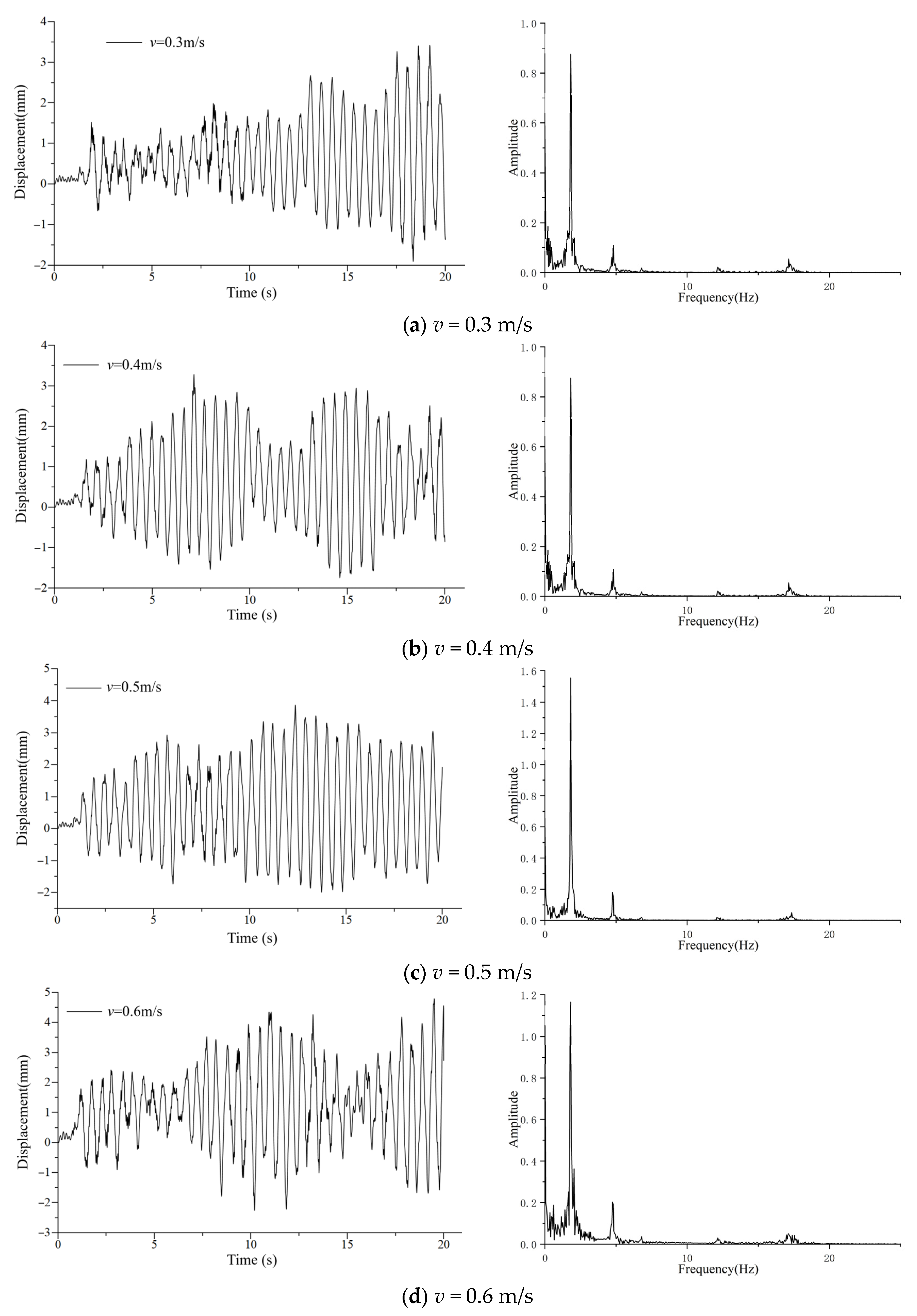
5.2. The Influence of Ice Velocity
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Brown, T.G.; Määttänen, M. Comparison of Kemi-I and Confederation Bridge cone ice load measurement results. Cold Reg. Sci. Technol. 2009, 55, 3–13. [Google Scholar] [CrossRef]
- Wu, Q.-G.; Wang, Z.-C.; Ni, B.-Y.; Yuan, G.-Y.; Semenov, Y.A.; Li, Z.-Y.; Xue, Y.-Z. Ice-water-gas interaction during icebreaking by an airgun bubble. J. Mar. Sci. Eng. 2022, 10, 1302. [Google Scholar] [CrossRef]
- Yuan, G.; Ni, B.; Wu, Q.; Lu, W.; Xue, Y. Experimental study on ice breaking by a cavitating water jet in a Venturi structure. Appl. Therm. Eng. 2024, 239, 122095. [Google Scholar] [CrossRef]
- Yuan, G.-Y.; Ni, B.-Y.; Wu, Q.-G.; Xue, Y.-Z.; Han, D.-F. Ice breaking by a high-speed water jet impact. J. Fluid Mech. 2022, 934, A1. [Google Scholar] [CrossRef]
- Ranta, J.; Polojärvi, A.; Tuhkuri, J. Ice loads on inclined marine structures—Virtual experiments on ice failure process evolution. Mar. Struct. 2018, 57, 72–86. [Google Scholar] [CrossRef]
- Sinsabvarodom, C.; Leira, B.J.; Høyland, K.V.; Næss, A.; Samardžija, I.; Chai, W.; Komonjinda, S.; Chaichana, C.; Xu, S. On Statistical Features of Ice Loads on Fixed and Floating Offshore Structures. J. Mar. Sci. Eng. 2024, 12, 1458. [Google Scholar] [CrossRef]
- Wang, B.; Yin, H.; Gao, S.; Qu, Y.; Chuang, Z. Ice-Induced Vibration Analysis of Fixed-Bottom Wind Turbine Towers. J. Mar. Sci. Eng. 2024, 12, 1159. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, D.; Wu, K.; Peng, X.; Jia, X.; Wang, G. Study on the Factors Influencing the Amplitude of Local Ice Pressure on Vertical Structures Based on Model Tests. J. Mar. Sci. Eng. 2024, 12, 1634. [Google Scholar] [CrossRef]
- Moslet, P.O. Field testing of uniaxial compression strength of columnar sea ice. Cold Reg. Sci. Technol. 2007, 48, 1–14. [Google Scholar] [CrossRef]
- Timco, G.W.; Frederking, R. Probabilistic analysis of seasonal ice loads on the Molikpaq. In Proceedings of the 17th International Association of Hydraulic Engineering and Research (IAHR), Saint Petersburg, Russia, 21–25 June 2004; Volume 2, pp. 68–76. [Google Scholar]
- Ji, S.; Di, S.; Liu, S. Analysis of ice load on conical structure with discrete element method. Eng. Comput. 2015, 32, 1121–1134. [Google Scholar] [CrossRef]
- Yue, Q.; Bi, X. Ice-Induced Jacket Structure Vibrations in Bohai Sea. J. Cold Reg. Eng. 2000, 14, 81–92. [Google Scholar] [CrossRef]
- Barker, A.; Timco, G. Beaufort sea rubble fields: Characteristics and implications for nearshore petroleum operations. Cold Reg. Sci. Technol. 2016, 121, 66–83. [Google Scholar] [CrossRef]
- Barker, A.; Timco, G.; Gravesen, H.; Vølund, P. Ice loading on Danish wind turbines: Part 1: Dynamic model tests. Cold Reg. Sci. Technol. 2005, 41, 1–23. [Google Scholar] [CrossRef]
- Hirayama, K.; Obara, I. Ice forces on inclined structure. In Proceedings of the 5th International Offshore Mechanics and Arctic Engineering, Tokyo, Japan, 13–18 April 1986; pp. 515–520. [Google Scholar]
- Yue, Q.; Qu, Y.; Bi, X.; Tuomo, K. Ice force spectrum on narrow conical structures. Cold Reg. Sci. Technol. 2007, 49, 161–169. [Google Scholar] [CrossRef]
- Yan, Q.; Yue, Q.; Bi, X.; Tuomo, K. A random ice force model for narrow conical structures. Cold Reg. Sci. Technol. 2006, 45, 148–157. [Google Scholar] [CrossRef]
- Xu, N.; Yue, Q.; Bi, X.; Tuomo, K.; Zhang, D. Experimental study of dynamic conical ice force. Cold Reg. Sci. Technol. 2015, 120, 21–29. [Google Scholar] [CrossRef]
- Tian, Y.; Huang, Y. The dynamic ice loads on conical structures. Ocean Eng. 2013, 59, 37–46. [Google Scholar] [CrossRef]
- Xu, N.; Yue, Q.; Yuan, S.; Liu, X.; Shi, W. Classification criterion of narrow/wide ice-resistant conical structures based on direct measurements. J. Mar. Sci. Appl. 2016, 15, 376–381. [Google Scholar] [CrossRef]
- Di, S.; Xue, Y.; Wang, Q.; Bai, X. Discrete element simulation of ice loads on narrow conical structures. Ocean Eng. 2017, 146, 282–297. [Google Scholar] [CrossRef]
- Long, X.; Liu, S.; Ji, S. Discrete element modelling of relationship between ice breaking length and ice load on conical structure. Ocean Eng. 2020, 201, 107152. [Google Scholar] [CrossRef]
- Ji, S.; Tian, Y. Numerical ice tank for ice loads based on multi-media and multi-scale discrete element method. Chin. J. Theor. Appl. Mech. 2021, 53, 2427–2453. [Google Scholar]
- Lu, W.; Lubbad, R.; Løset, S.; Kashafutdinov, M. Fracture of an ice floe: Local out-of-plane flexural failures versus global in-plane splitting failure. Cold Reg. Sci. Technol. 2016, 123, 1–13. [Google Scholar] [CrossRef]
- Su, B.; Riska, K.; Moan, T. A numerical method for the prediction of ship performance in level ice. Cold Reg. Sci. Technol. 2010, 60, 177–188. [Google Scholar] [CrossRef]
- Hopkins, M.A. Onshore ice pile-up: A comparison between experiments and simulations. Cold Reg. Sci. Technol. 1997, 26, 205–214. [Google Scholar] [CrossRef]
- Paavilainen, J.; Tuhkuri, J. Pressure distributions and force chains during simulated ice rubbling against sloped structures. Cold Reg. Sci. Technol. 2013, 85, 157–174. [Google Scholar] [CrossRef]
- Jia, B.; Ju, L.; Wang, Q. Numerical Simulation of Dynamic Interaction Between Ice and Wide Vertical Structure Based on Peridynamics. Comput. Model. Eng. Sci. 2019, 121, 501–522. [Google Scholar] [CrossRef]
- Liu, M.; Wang, Q.; Lu, W. Peridynamic simulation of brittle-ice crushed by a vertical structure. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 209–218. [Google Scholar] [CrossRef]
- Liu, R.; Xue, Y.; Han, D.; Ni, B. Studies on model-scale ice using micro-potential-based peridynamics. Ocean Eng. 2021, 221, 108504. [Google Scholar] [CrossRef]
- Liu, R.; Xue, Y.; Lu, X. Coupling of Finite Element Method and Peridynamics to Simulate Ship-Ice Interaction. J. Mar. Sci. Eng. 2023, 11, 481. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, P.; Xie, P.; Ji, S. Coupling of dilated polyhedral DEM and SPH for the simulation of rock dumping process in waters. Powder Technol. 2020, 374, 139–151. [Google Scholar] [CrossRef]
- Lu, W.; Lubbad, R.; Løset, S. Simulating Ice-Sloping Structure Interactions With the Cohesive Element Method. J. Offshore Mech. Arct. Eng. 2014, 136, 031501. [Google Scholar] [CrossRef]
- Shen, H.H.; Hibler, W.D.; Leppäranta, M. On applying granular flow theory to a deforming broken ice field. Acta Mech. 1986, 63, 143–160. [Google Scholar] [CrossRef]
- Tuhkuri, J.; Polojrvi, A. A review of discrete element simulation of ice-structure interaction. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20170335. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Liu, R.; Li, Z.; Han, D. A review for numerical simulation methods of ship–ice interaction. Ocean Eng. 2020, 215, 107853. [Google Scholar] [CrossRef]
- Ji, S.; Di, S.; Long, X. DEM Simulation of Uniaxial Compressive and Flexural Strength of Sea Ice: Parametric Study. J. Eng. Mech. 2017, 143, C4016010. [Google Scholar] [CrossRef]
- Huang, L.; Tuhkuri, J.; Igrec, B.; Li, M.; Stagonas, D.; Toffoli, A.; Cardiff, P.; Thomas, G. Ship resistance when operating in floating ice floes: A combined CFD&DEM approach. Mar. Struct. 2020, 74, 102817. [Google Scholar] [CrossRef]
- Zhong-Xiang, S.; Wen-Qing, W.; Cheng-Yue, X.U.; Hong-Bin, L.I.; Yin, J.; Ren-Wei, L. Numerical Simulation of Sea Ice and Structure Interaction Using Common Node DEM-SPH Model. China Ocean Eng. 2023, 37, 897–911. [Google Scholar]
- Wang, S.; Yue, Q.; Zhang, D. Ice-induced non-structure vibration reduction of jacket platforms with isolation cone system. Ocean Eng. 2013, 70, 118–123. [Google Scholar] [CrossRef]
- Wu, W.H.; Yu, B.J.; Xu, N.; Yue, Q.J. Numerical simulation of dynamic ice action on conical structure. Eng. Mech. 2008, 25, 192–196. (In Chinese) [Google Scholar]
- Ralston, T. Plastic limit analysis of sheet ice loads on conical structures. In Physics and Mechanics of Ice: Symposium Copenhagen, 6–10 August 1979, Copenhagen, Denmark; Technical University of Denmark: Lyngby, Denmark, 1979; pp. 289–308. [Google Scholar]
- Kato, K.; Izumiyama, K. Simulation of ice loads on a conical shaped structure: Comparison with experimental results. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Honolulu, HI, USA, 25–30 May 1997; p. ISOPE-I-97-207. [Google Scholar]
- Frederking, R.; Schwarz, J. Model tests of ice forces on fixed and oscillating cones. Cold Reg. Sci. Technol. 1982, 6, 61–72. [Google Scholar] [CrossRef]
- Wessels, E.; Kato, K. Ice forces on fixed and floating conical structures. In Proceedings of the 9th International IAHR Symposium on Ice, Sapporo, Japan, 23–27 August 1988; pp. 666–691. [Google Scholar]








| Parameter | Value |
|---|---|
| Sea ice thickness h/m | 0.24/0.3/0.36/0.42 |
| Particle diameter D/mm | 80/100/120/140 |
| Cementation modulus PBN/MPa | 759.1 |
| Ratio of cemented tangential to normal stiffness PBS | 0.574 |
| Cementation normal bond strength PBN_S/MPa | 0.519 |
| Cementation tangential bond strength PBS_S/MPa | 1.221 |
| Friction coefficient of ice and structure | 0.15 |
| Friction coefficient of particles | 0.1 |
| Viscosity coefficient Cn | 0.7 |
| Parameter | Value |
|---|---|
| Sea ice thickness h/m | 0.3 |
| Particle diameter D/mm | 100 |
| Cementation modulus PBN/MPa | 759.1 |
| Ratio of cemented tangential to normal stiffness PBS | 0.574 |
| Cementation normal bond strength PBN_S/MPa | 0.519 |
| Cementation tangential bond strength PBS_S/MPa | 1.221 |
| Friction coefficient of ice and structure | 0.15 |
| Friction coefficient of particles | 0.1 |
| Normal viscosity coefficient Cn | 0.7 |
| Tangential viscosity coefficient Cs | 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, X.; Jiang, Y.; Shen, Z.; Liu, R.; Liu, Z. Numerical Simulation of Ice and Structure Interaction Using Common-Node DEM in LS DYNA. J. Mar. Sci. Eng. 2024, 12, 1999. https://doi.org/10.3390/jmse12111999
Bai X, Jiang Y, Shen Z, Liu R, Liu Z. Numerical Simulation of Ice and Structure Interaction Using Common-Node DEM in LS DYNA. Journal of Marine Science and Engineering. 2024; 12(11):1999. https://doi.org/10.3390/jmse12111999
Chicago/Turabian StyleBai, Xiaolong, Yin Jiang, Zhongxiang Shen, Renwei Liu, and Zhen Liu. 2024. "Numerical Simulation of Ice and Structure Interaction Using Common-Node DEM in LS DYNA" Journal of Marine Science and Engineering 12, no. 11: 1999. https://doi.org/10.3390/jmse12111999
APA StyleBai, X., Jiang, Y., Shen, Z., Liu, R., & Liu, Z. (2024). Numerical Simulation of Ice and Structure Interaction Using Common-Node DEM in LS DYNA. Journal of Marine Science and Engineering, 12(11), 1999. https://doi.org/10.3390/jmse12111999




