Global Sensitivity Analysis of the Fundamental Frequency of Jacket-Supported Offshore Wind Turbines Using Artificial Neural Networks
Abstract
:1. Introduction
2. Methodology
2.1. Monte Carlo Sampling
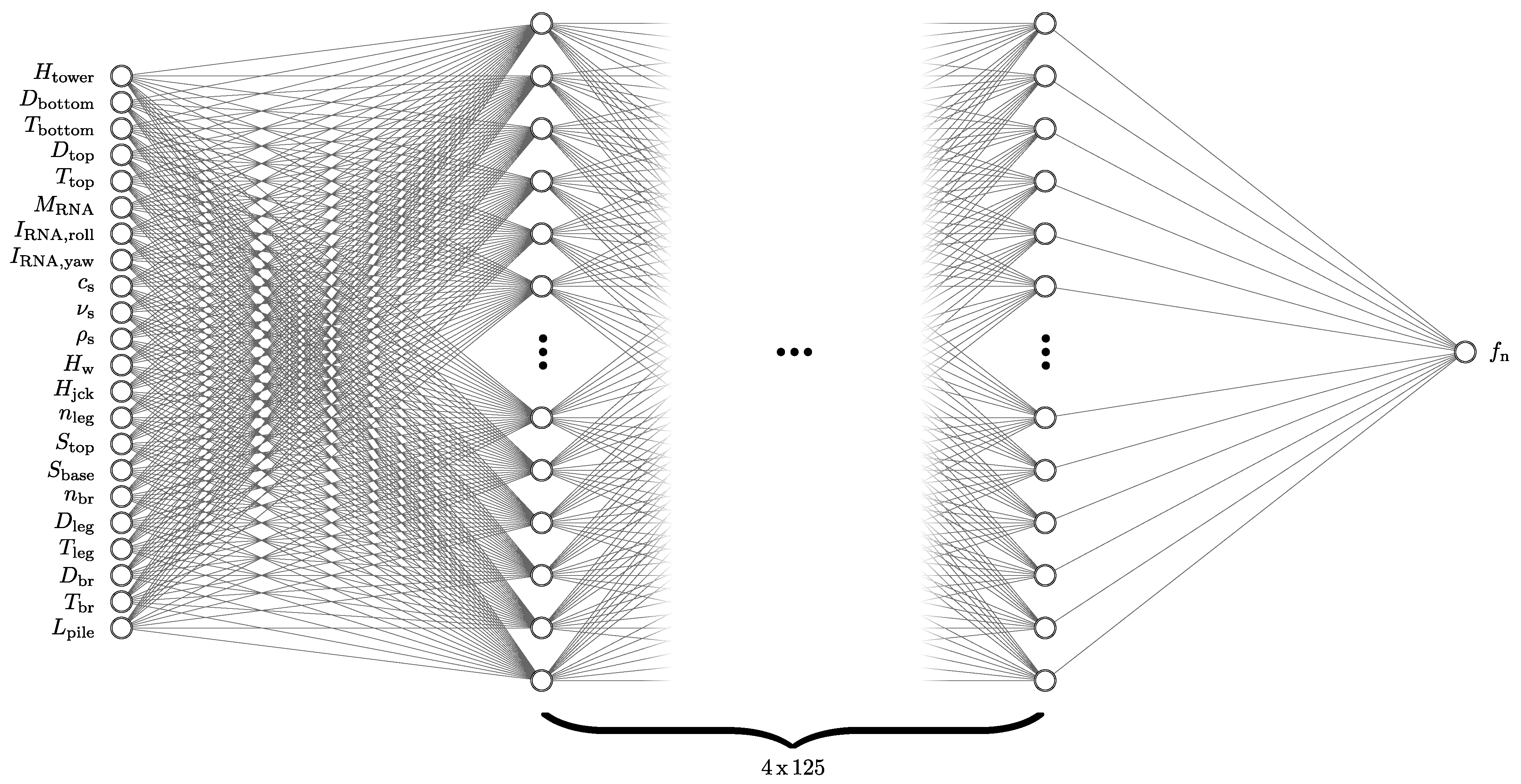
2.2. ANN-Based Surrogate Model
2.3. Sensitivity Analysis
3. Results
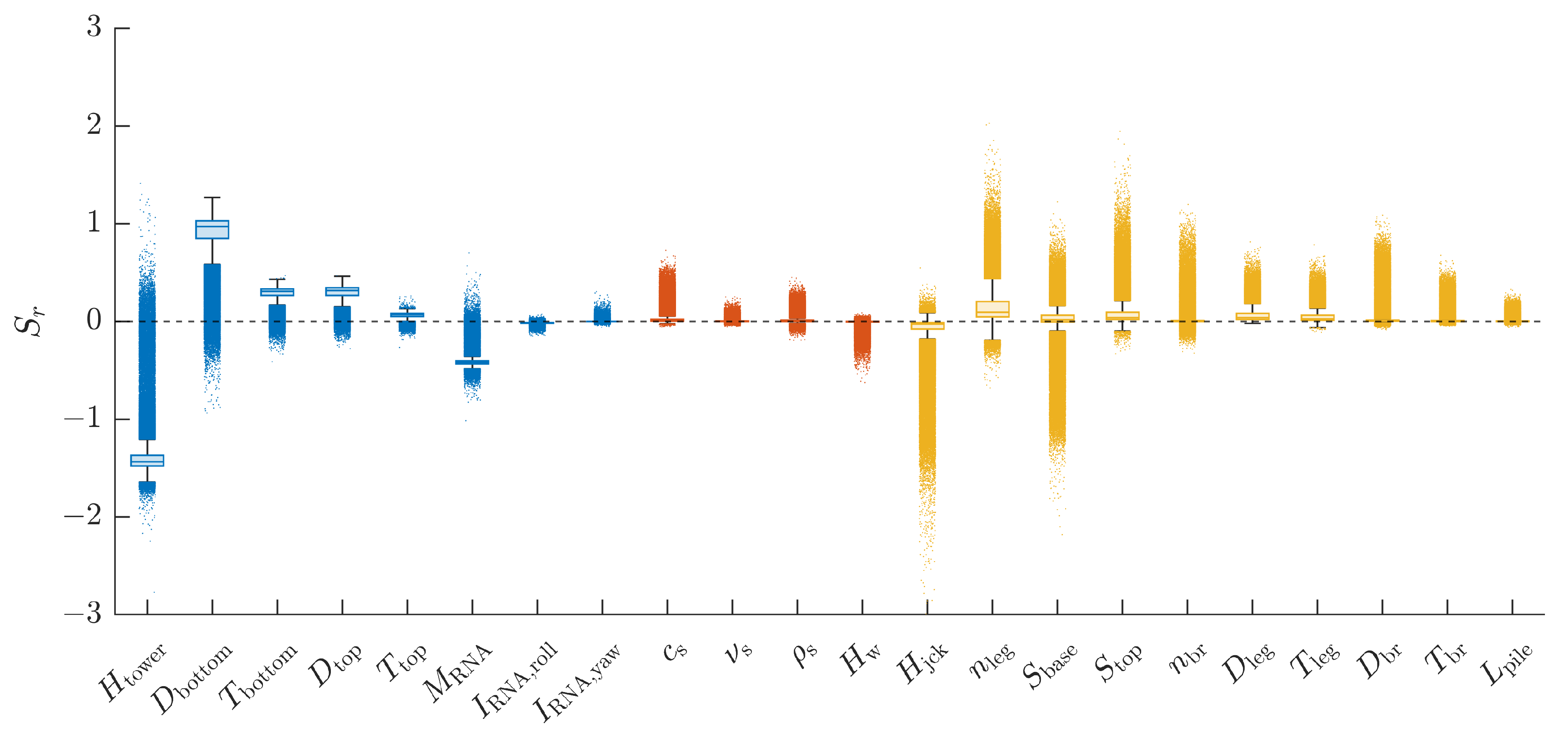
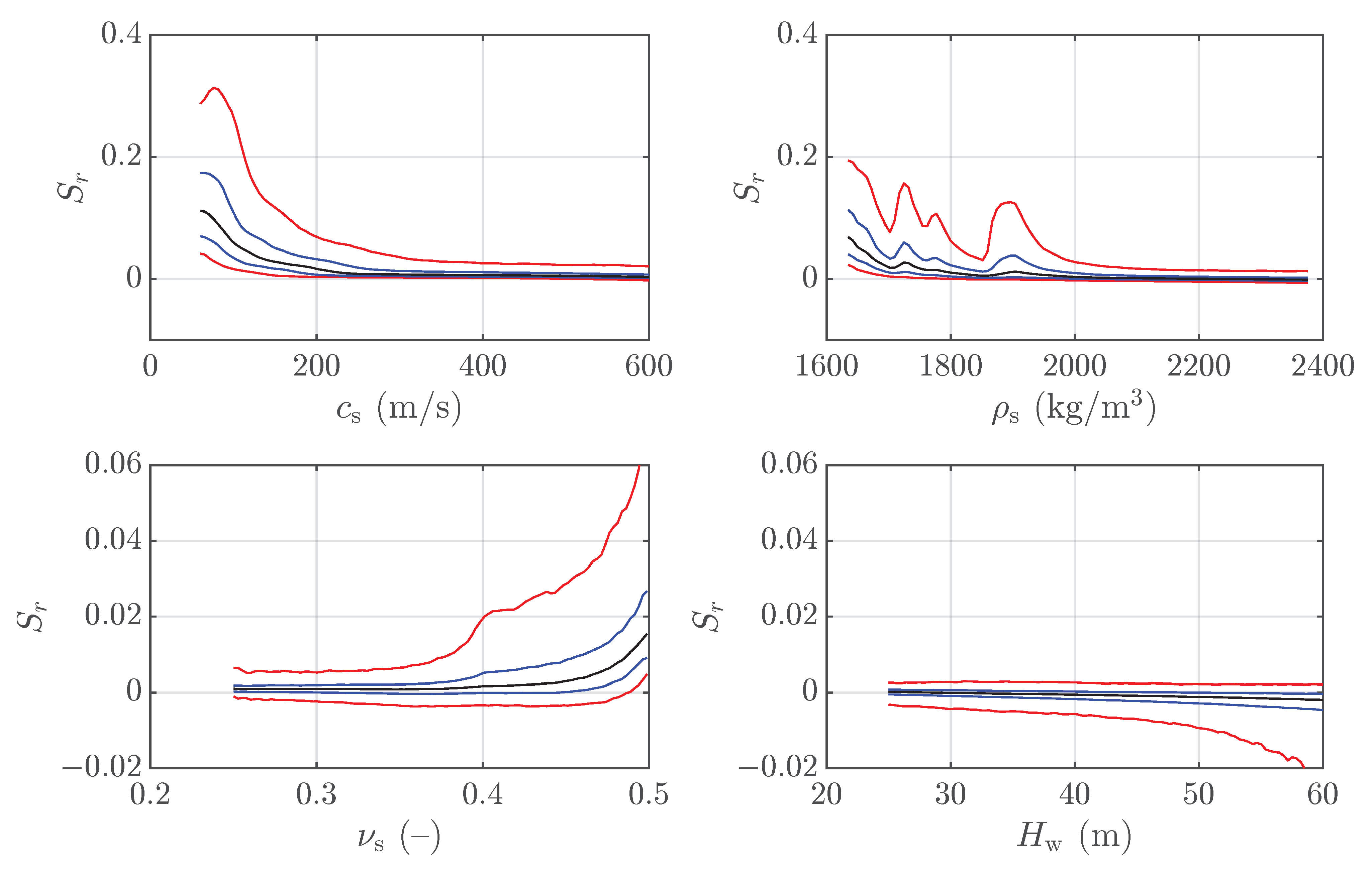
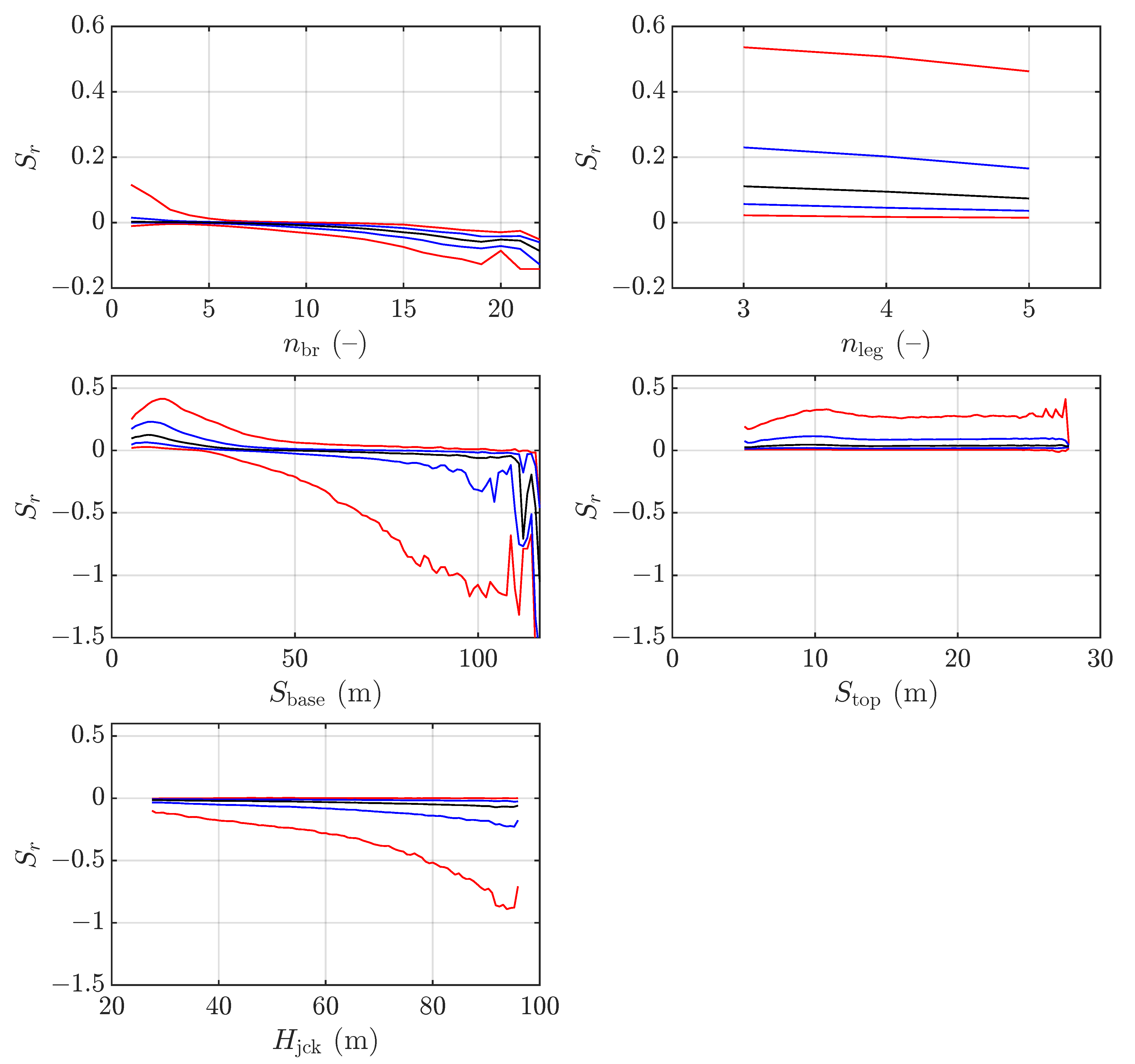
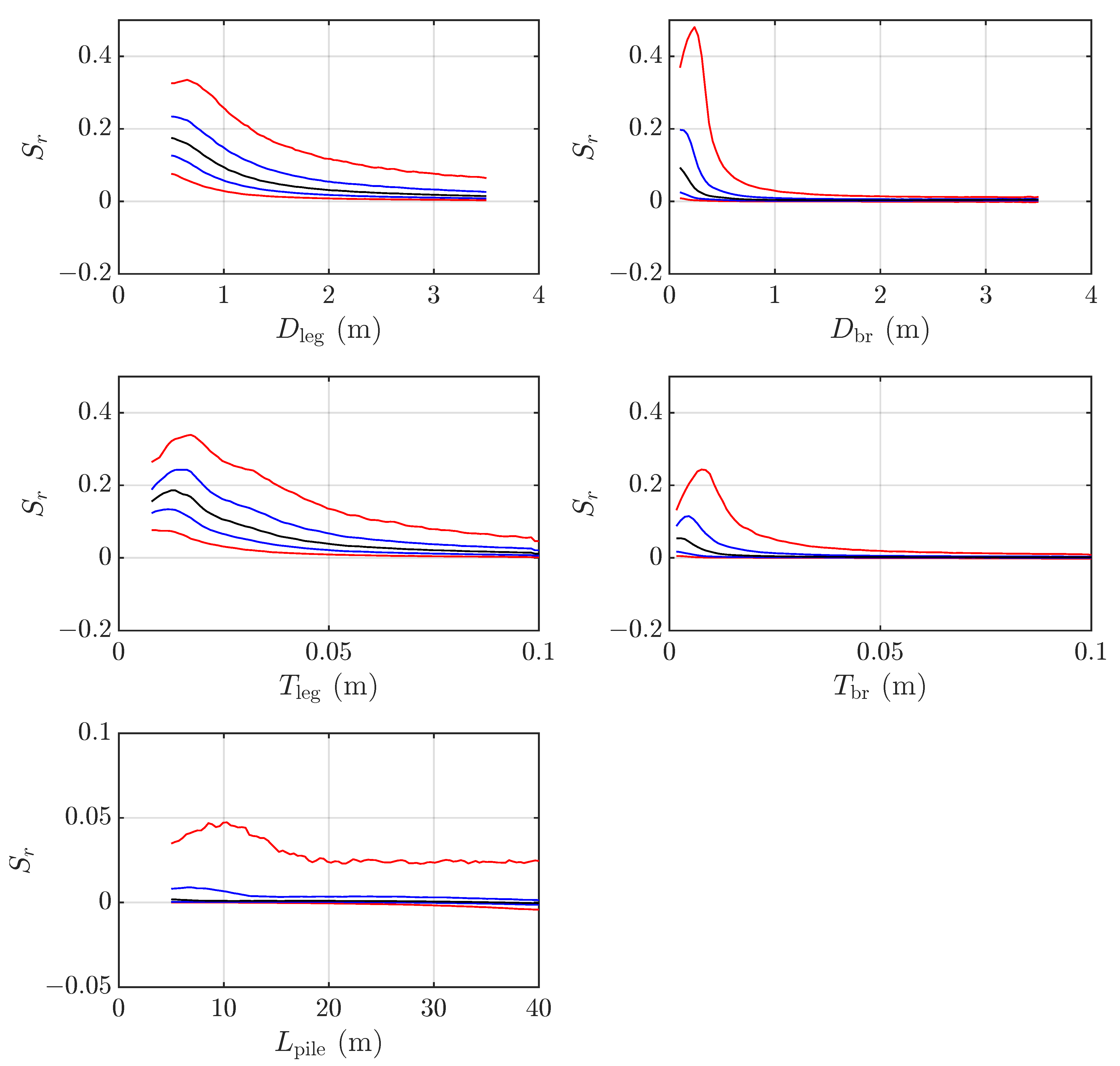
3.1. Global Sensitivity Analysis
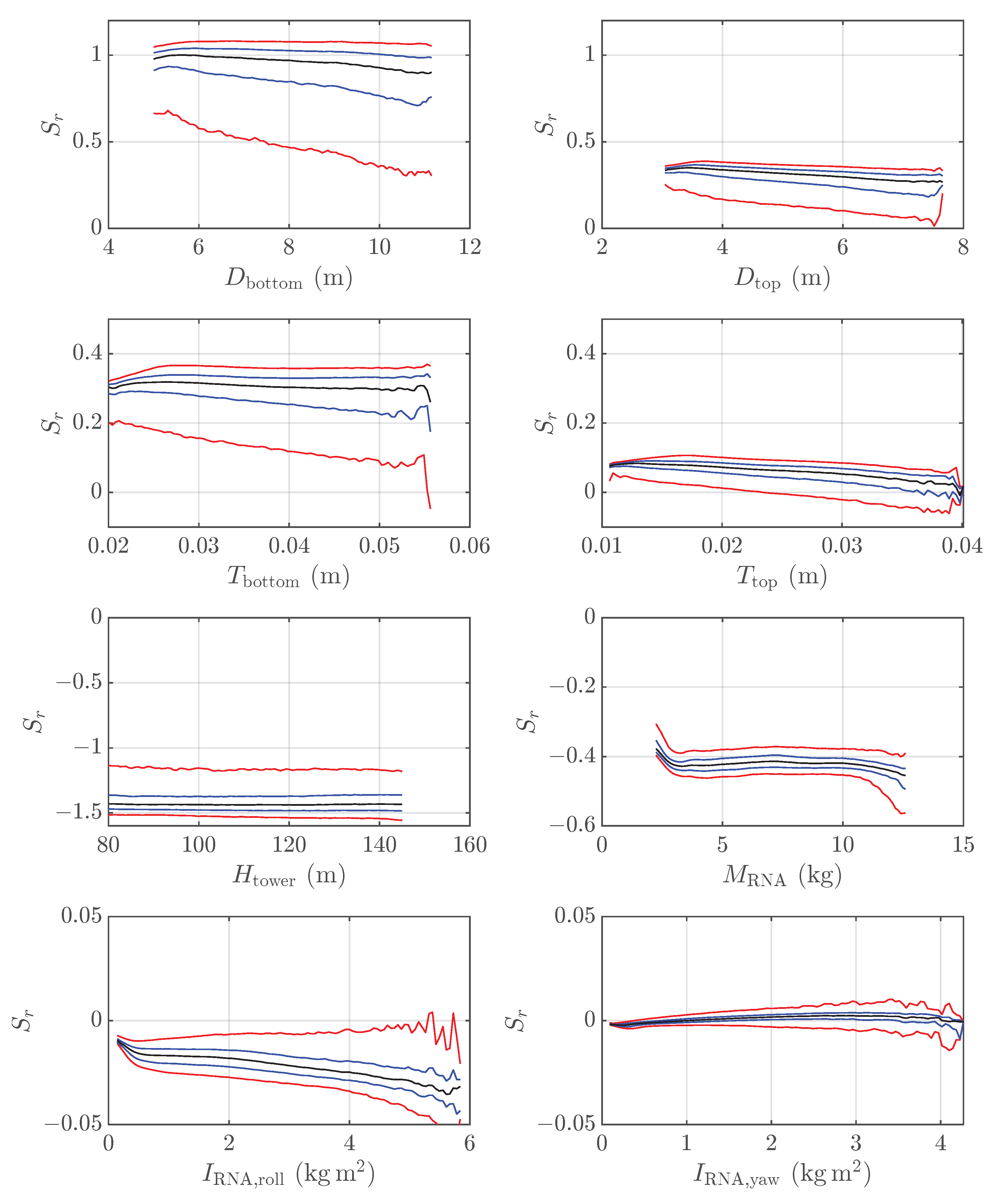
3.2. Relationship Between Relative Sensitivity and System Characteristics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, Z. Installation of offshore wind turbines: A technical review. Renew. Sustain. Energy Rev. 2021, 139, 110576. [Google Scholar] [CrossRef]
- Rodrigues, S.; Restrepo, C.; Kontos, E.; Teixeira Pinto, R.; Bauer, P. Trends of offshore wind projects. Renew. Sustain. Energy Rev. 2015, 49, 1114–1135. [Google Scholar] [CrossRef]
- McCoy, A.; Musial, W.; Hammond, R.; Hernando, D.M.; Duffy, P.; Beiter, P.; Pérez, P.; Baranowski, R.; Reber, G.; Spitsen, P. Offshore Wind Market Report: 2024 Edition; Office of Energy Efficiency & Renewable Energy: Washington, DC, USA, 2024.
- Musial, W.; Spitsen, P.; Duffy, P.; Beiter, P.; Shields, M.; Hernando, D.M.; Hammond, R.; Marquis, M.; King, J.; Sathish, S. Offshore Wind Market Report: 2023 Edition; Office of Energy Efficiency & Renewable Energy: Washington, DC, USA, 2023.
- DNVGL-ST-0126; Support Structures for Wind Turbines. Det Norske Veritas and Germanischer Lloyd: Høvik, Norway, 2016.
- Partovi-Mehr, N.; Branlard, E.; Song, M.; Moaveni, B.; Hines, E.M.; Robertson, A. Sensitivity Analysis of Modal Parameters of a Jacket Offshore Wind Turbine to Operational Conditions. J. Mar. Sci. Eng. 2023, 11, 1524. [Google Scholar] [CrossRef]
- Li, J.; Cui, C.; Xiao, Z.; Wang, B.; Xu, C. Reliability and sensitivity analyses of monopile supported offshore wind turbines based on probability density evolution method with pre-screening of controlling parameters. Ocean. Eng. 2024, 310, 118746. [Google Scholar] [CrossRef]
- Velarde, J.; Kramhøft, C.; Sørensen, J.D. Global sensitivity analysis of offshore wind turbine foundation fatigue loads. Renew. Energy 2019, 140, 177–189. [Google Scholar] [CrossRef]
- Shittu, A.A.; Mehmanparast, A.; Amirafshari, P.; Hart, P.; Kolios, A. Sensitivity analysis of design parameters for reliability assessment of offshore wind turbine jacket support structures. Int. J. Nav. Archit. Ocean. Eng. 2022, 14, 100441. [Google Scholar] [CrossRef]
- Braithwaite, J.; Goenaga, I.G.; Tafazzolimoghaddam, B.; Mehmanparast, A. Sensitivity analysis of friction and creep deformation effects on preload relaxation in offshore wind turbine bolted connections. Appl. Ocean. Res. 2020, 101, 102225. [Google Scholar] [CrossRef]
- Hübler, C.; Gebhardt, C.G.; Rolfes, R. Hierarchical four-step global sensitivity analysis of offshore wind turbines based on aeroelastic time domain simulations. Renew. Energy 2017, 111, 878–891. [Google Scholar] [CrossRef]
- Kim, N.; Jin, J.W. Sensitivity analysis of offshore wind turbine tower caused by the external force. KSCE J. Civ. Eng. 2013, 17, 859–864. [Google Scholar] [CrossRef]
- Karimirad, M.; Bachynski, E.E. Sensitivity Analysis of Limited Actuation for Real-time Hybrid Model Testing of 5MW Bottom-fixed Offshore Wind Turbine. Energy Procedia 2017, 137, 14–25. [Google Scholar] [CrossRef]
- Teixeira, R.; O’Connor, A.; Nogal, M. Probabilistic sensitivity analysis of offshore wind turbines using a transformed Kullback-Leibler divergence. Struct. Saf. 2019, 81, 101860. [Google Scholar] [CrossRef]
- Quevedo-Reina, R.; Álamo, G.M.; Padrón, L.A.; Aznárez, J.J. Surrogate model based on ANN for the evaluation of the fundamental frequency of offshore wind turbines supported on jackets. Comput. Struct. 2023, 274, 106917. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009. [CrossRef]
- Desmond, C.; Murphy, J.; Blonk, L.; Haans, W. Description of an 8 MW reference wind turbine. J. Phys. Conf. Ser. 2016, 753, 092013. [Google Scholar] [CrossRef]
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.; Natarajan, A.; Hansen, M. Description of the DTU 10 MW Reference Wind Turbine; DTU Wind Energy: Roskilde, Denmark, 2013. [Google Scholar]
- Gaertner, E.; Rinker, J.; Sethuraman, L.; Zahle, F.; Anderson, B.; Barter, G.; Abbas, N.; Meng, F.; Bortolotti, P.; Skrzypinski, W.; et al. Definition of the IEA 15-Megawatt Offshore Reference Wind Turbine; IEA Wind TCP Task 37; National Renewable Energy Laboratory: Golden, CO, USA, 2020.
- Couceiro, I.; París, J.; Navarrina, F.; Guizán, R.; Colominas, I. Optimization of Offshore Steel Jackets: Review and Proposal of a New Formulation for Time-Dependent Constraints. Arch. Comput. Methods Eng. 2020, 27, 1049–1069. [Google Scholar] [CrossRef]
- Vorpahl, F.; Popko, W.; Kaufer, D. Description of a Basic Model of the “UpWind Reference Jacket” for Code Comparison in the OC4 Project Under IEA Wind Annex 30; Fraunhofer Institute for Wind Energy and Energy System Technology (IWES): Bremerhaven, Germany, 2011; Volume 450. [Google Scholar]
- Stolpe, M.; Wandji, W.; Natarajan, A.; Shirzadeh, R.; Kühn, M.; Kaufer, D. Innovative Design of a 10MW Steel-Type Jacket; Deliverable D4.34; INNWIND.EU, 2016. Available online: http://www.innwind.eu/ (accessed on 5 November 2024).
- DNVGL-RP-C203; Fatigue Design of Offshore Steel Structures; Recommended Practice. Det Norske Veritas and Germanischer Lloyd: Hamburg, Germany, 2016.
- Matlab. Deep Learning Toolbox, Version 9.9.0.1592791 (R2020b) Update 5; The MathWorks Inc.: Natick, MA, USA, 2020.
- Moschytz, G.S. Elements of Sensitivity Theory. In Analog Circuit Theory and Filter Design in the Digital World: With an Introduction to the Morphological Method for Creative Solutions and Design; Springer International Publishing: Cham, Switzerland, 2019; pp. 299–333. [Google Scholar] [CrossRef]

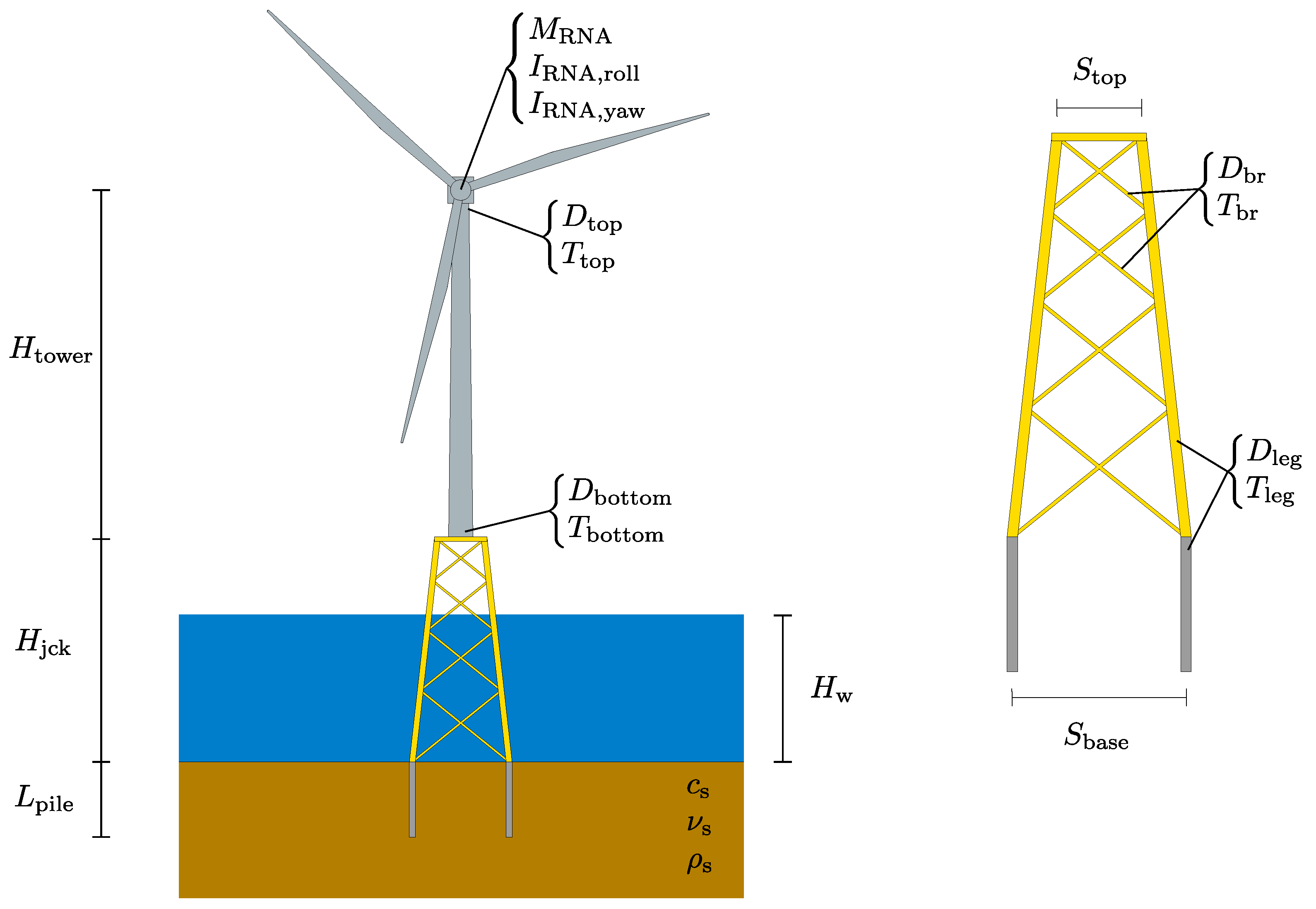

| Subsystem | Variable | Minimum Value | Maximum Value |
|---|---|---|---|
| Wind turbine | (m) | 80 | 145 |
| (m) | 5 | 11.15 | |
| (m) | 0.020 | 0.056 | |
| (m) | 3.05 | 7.65 | |
| (m) | 0.011 | 0.040 | |
| (kg) | |||
| (kg m2) | |||
| (kg m2) | |||
| Emplacement | (m/s) | 60 | 600 |
| (–) | 0.250 | 0.499 | |
| (kg/m3) | 1635 | 2376 | |
| (m) | 25 | 60 | |
| Jacket substructure | (m) | 27.55 | 95.94 |
| (–) | 3 | 5 | |
| (m) | 5.41 | 116.82 | |
| (m) | 5.06 | 27.79 | |
| (–) | 1 | 22 | |
| (m) | 0.5 | 3.5 | |
| (m) | 0.0078 | 0.1 | |
| (m) | 0.1 | 3.5 | |
| (m) | 0.0017 | 0.1 | |
| (m) | 5 | 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quevedo-Reina, R.; Álamo, G.M.; Aznárez, J.J. Global Sensitivity Analysis of the Fundamental Frequency of Jacket-Supported Offshore Wind Turbines Using Artificial Neural Networks. J. Mar. Sci. Eng. 2024, 12, 2011. https://doi.org/10.3390/jmse12112011
Quevedo-Reina R, Álamo GM, Aznárez JJ. Global Sensitivity Analysis of the Fundamental Frequency of Jacket-Supported Offshore Wind Turbines Using Artificial Neural Networks. Journal of Marine Science and Engineering. 2024; 12(11):2011. https://doi.org/10.3390/jmse12112011
Chicago/Turabian StyleQuevedo-Reina, Román, Guillermo M. Álamo, and Juan J. Aznárez. 2024. "Global Sensitivity Analysis of the Fundamental Frequency of Jacket-Supported Offshore Wind Turbines Using Artificial Neural Networks" Journal of Marine Science and Engineering 12, no. 11: 2011. https://doi.org/10.3390/jmse12112011
APA StyleQuevedo-Reina, R., Álamo, G. M., & Aznárez, J. J. (2024). Global Sensitivity Analysis of the Fundamental Frequency of Jacket-Supported Offshore Wind Turbines Using Artificial Neural Networks. Journal of Marine Science and Engineering, 12(11), 2011. https://doi.org/10.3390/jmse12112011






