CFD-DEM Simulation on the Main-Controlling Factors Affecting Proppant Transport in Three-Dimensional Rough Fractures of Offshore Unconventional Reservoirs
Abstract
:1. Introduction
2. Methodology
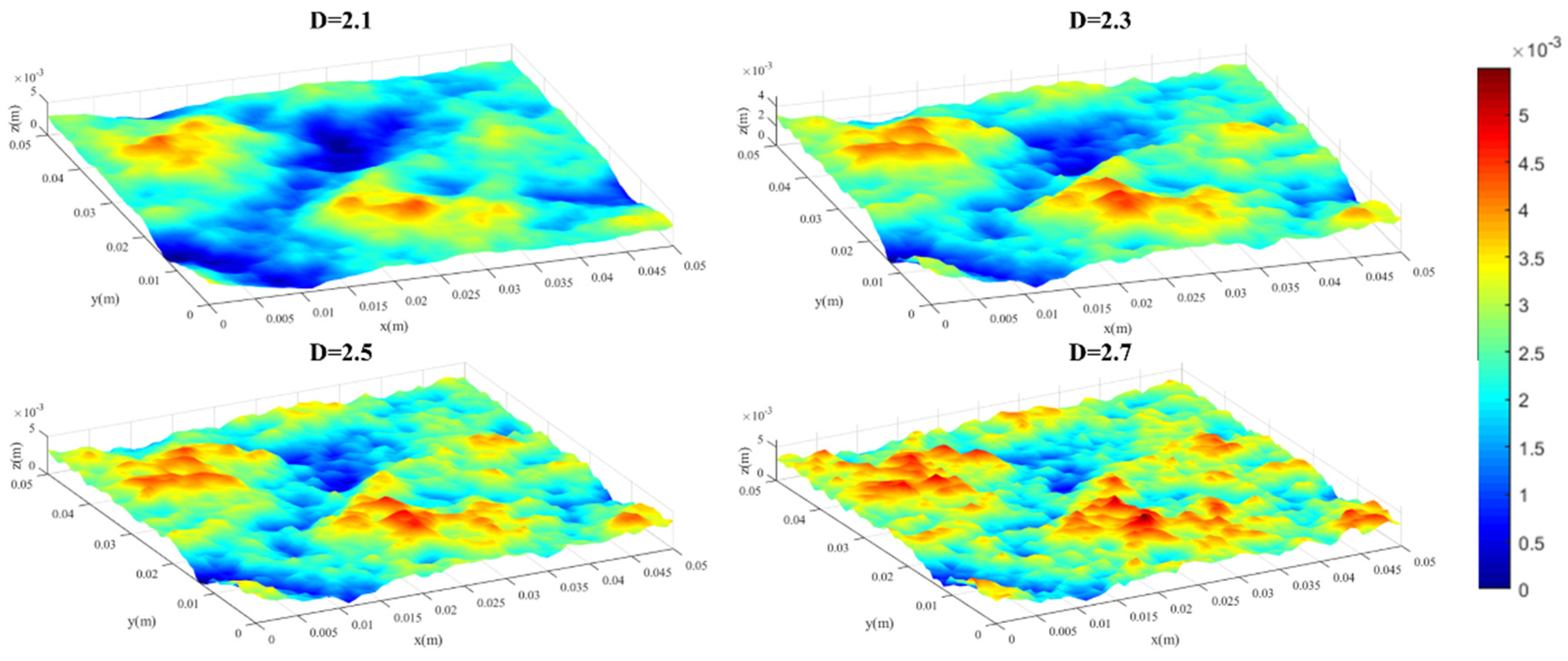
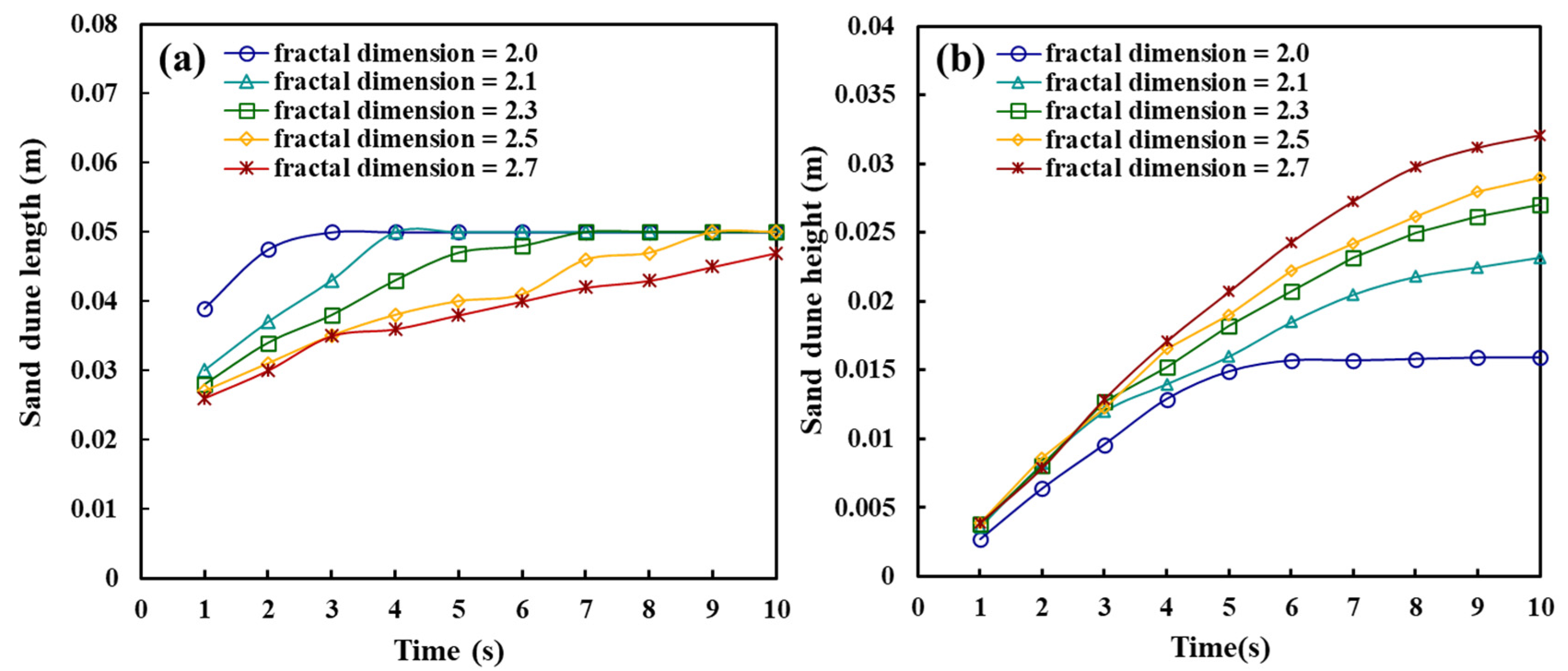
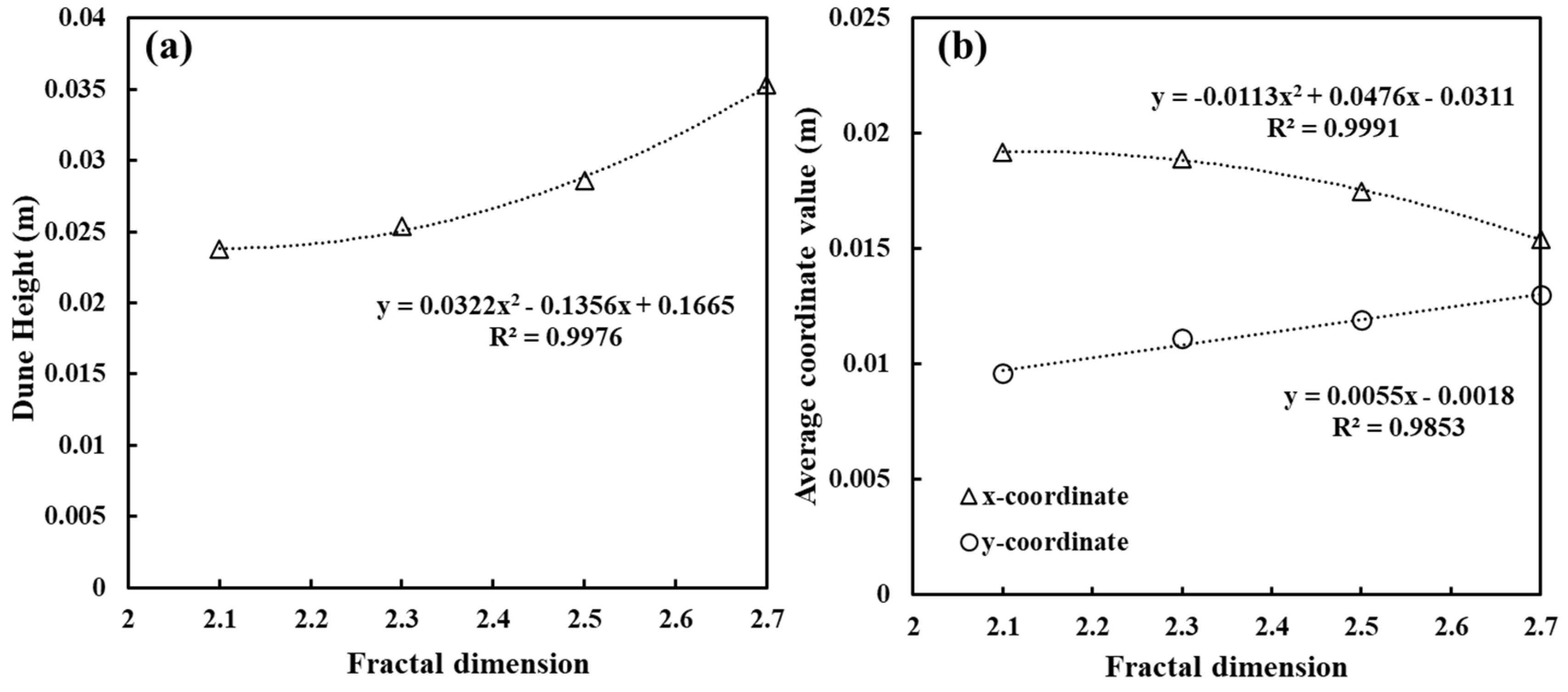
2.1. Construction of Rough Fractures Using Numerical Synthesis Method
2.2. CFD-DEM Coupling Approach
3. Numerical Model Verification and Simulation Setup
3.1. Numerical Model Verification
3.2. Simulation Setup
4. Results and Discussion
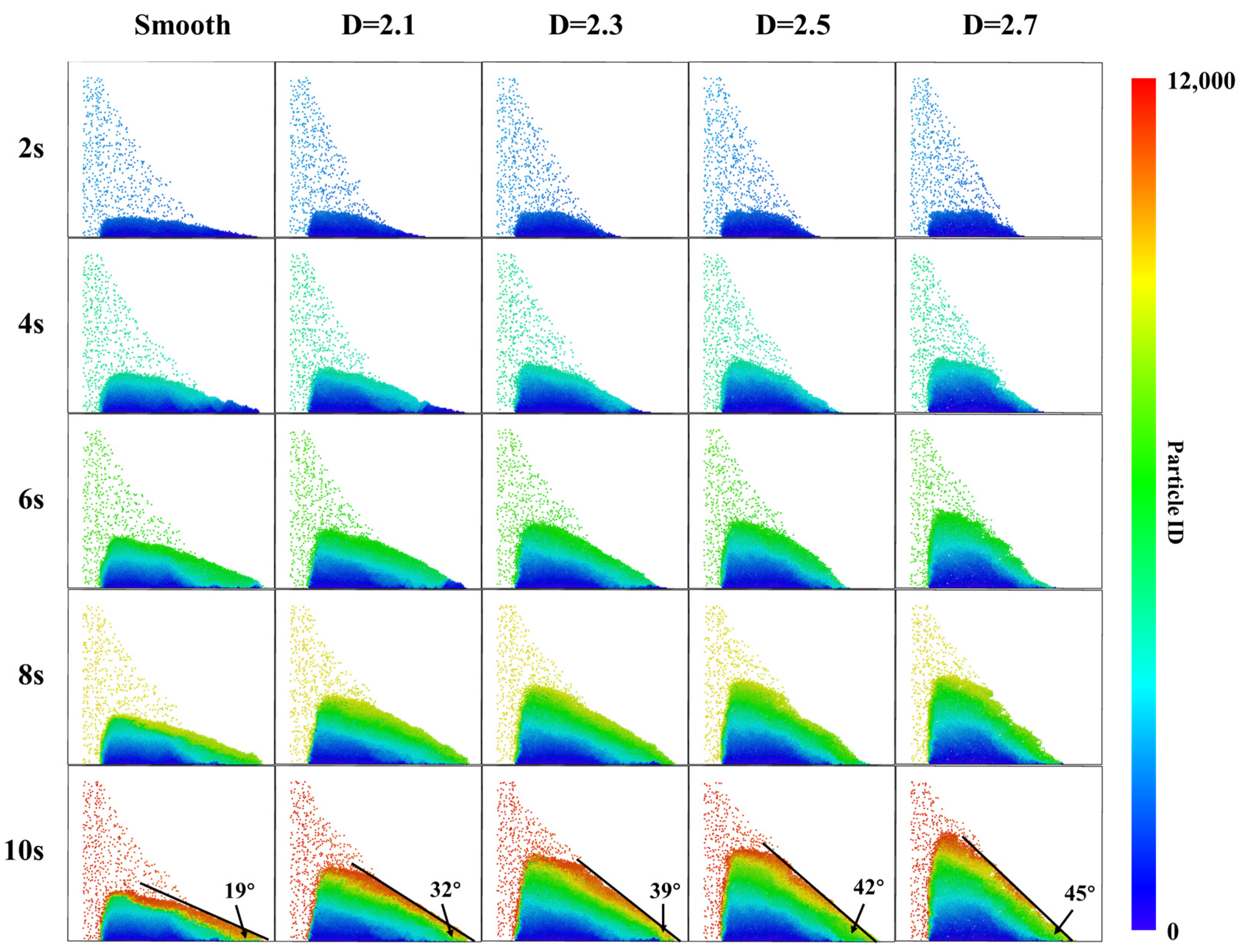
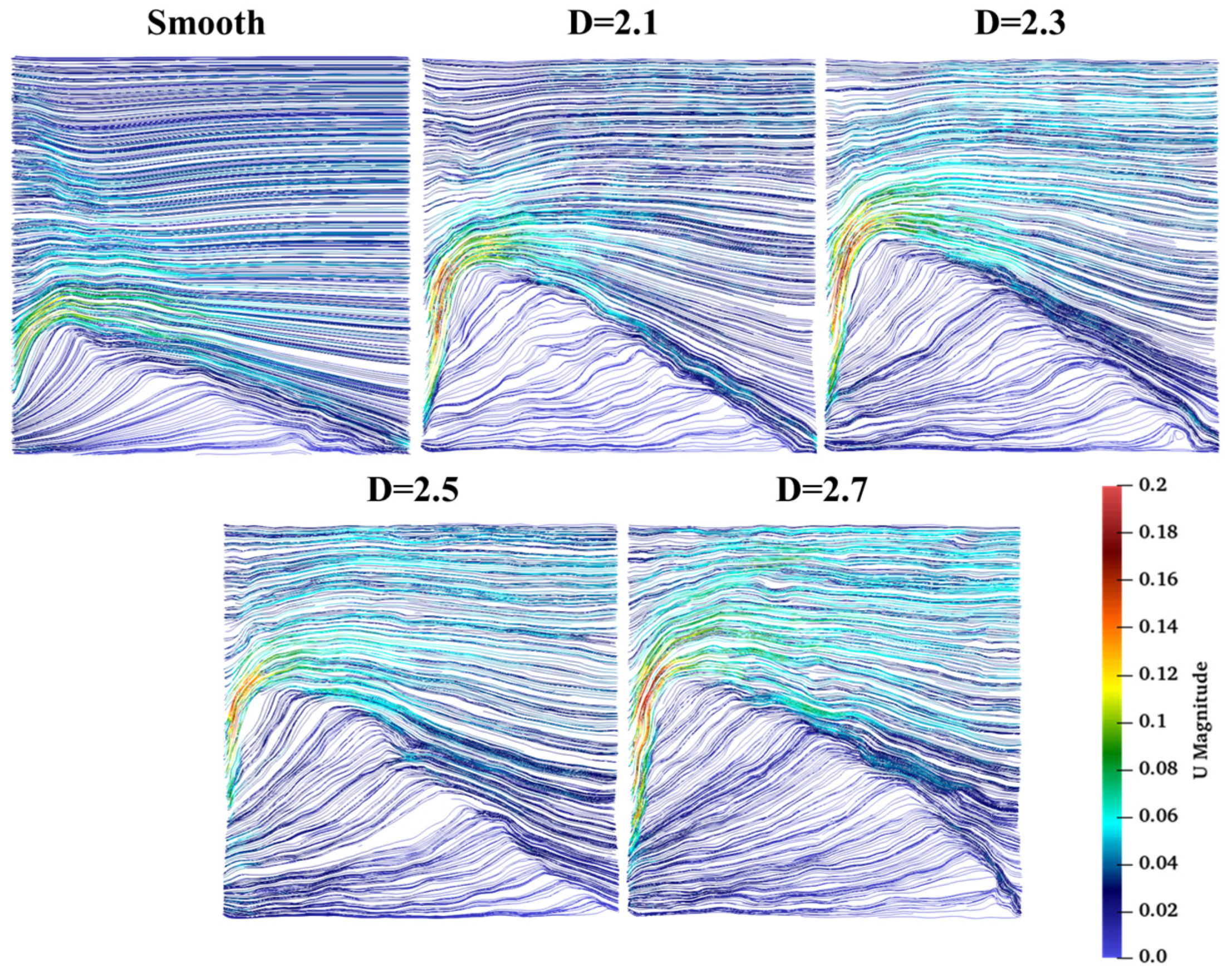
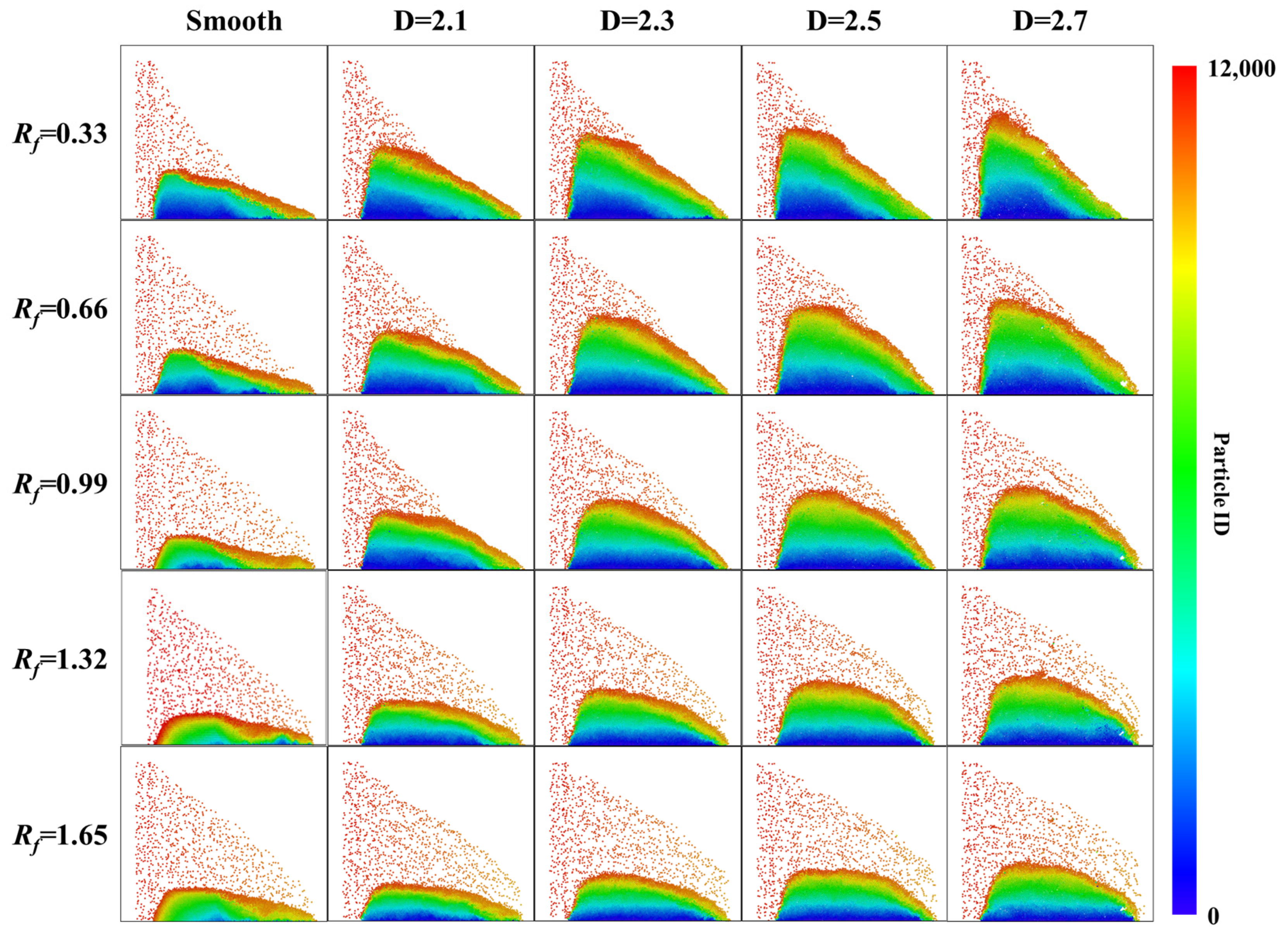
4.1. Proppant Transport in Vertical Fractures with Varying Roughness
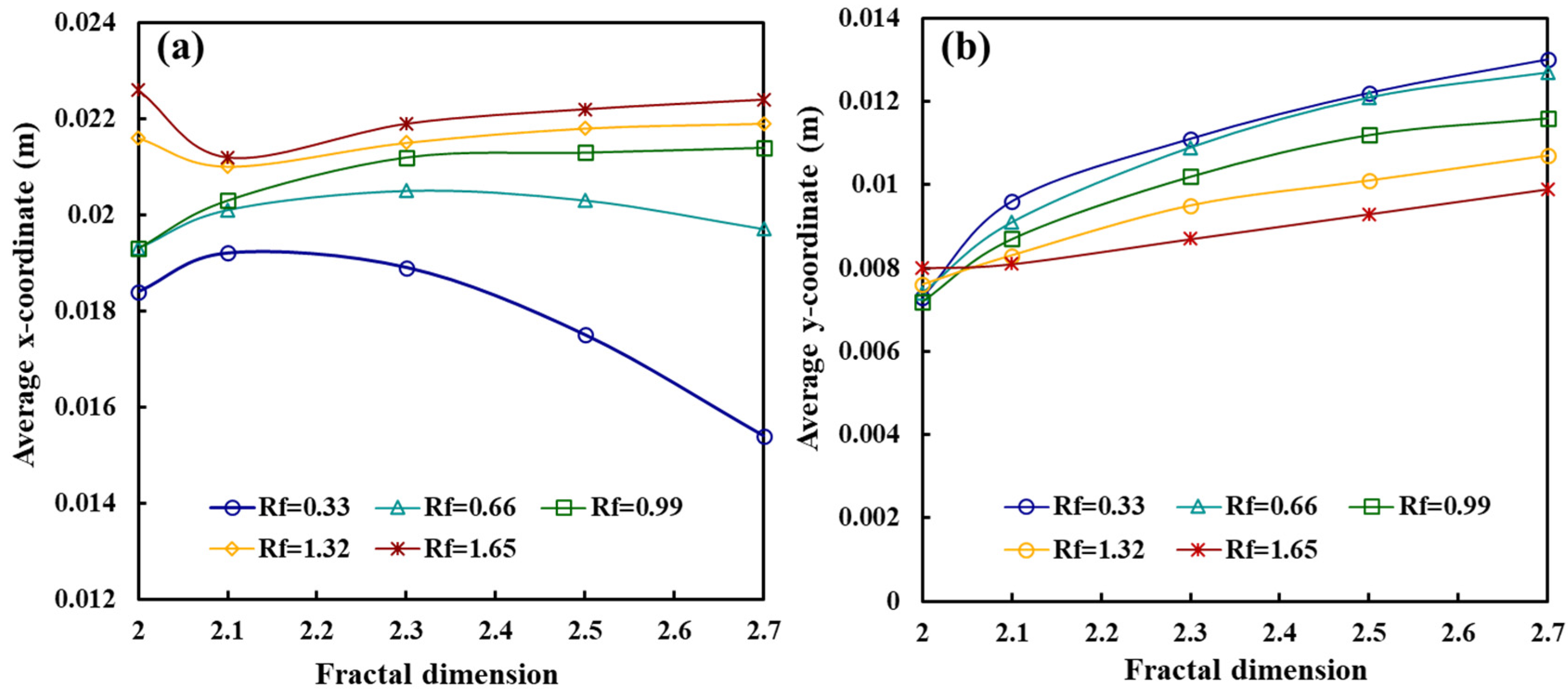
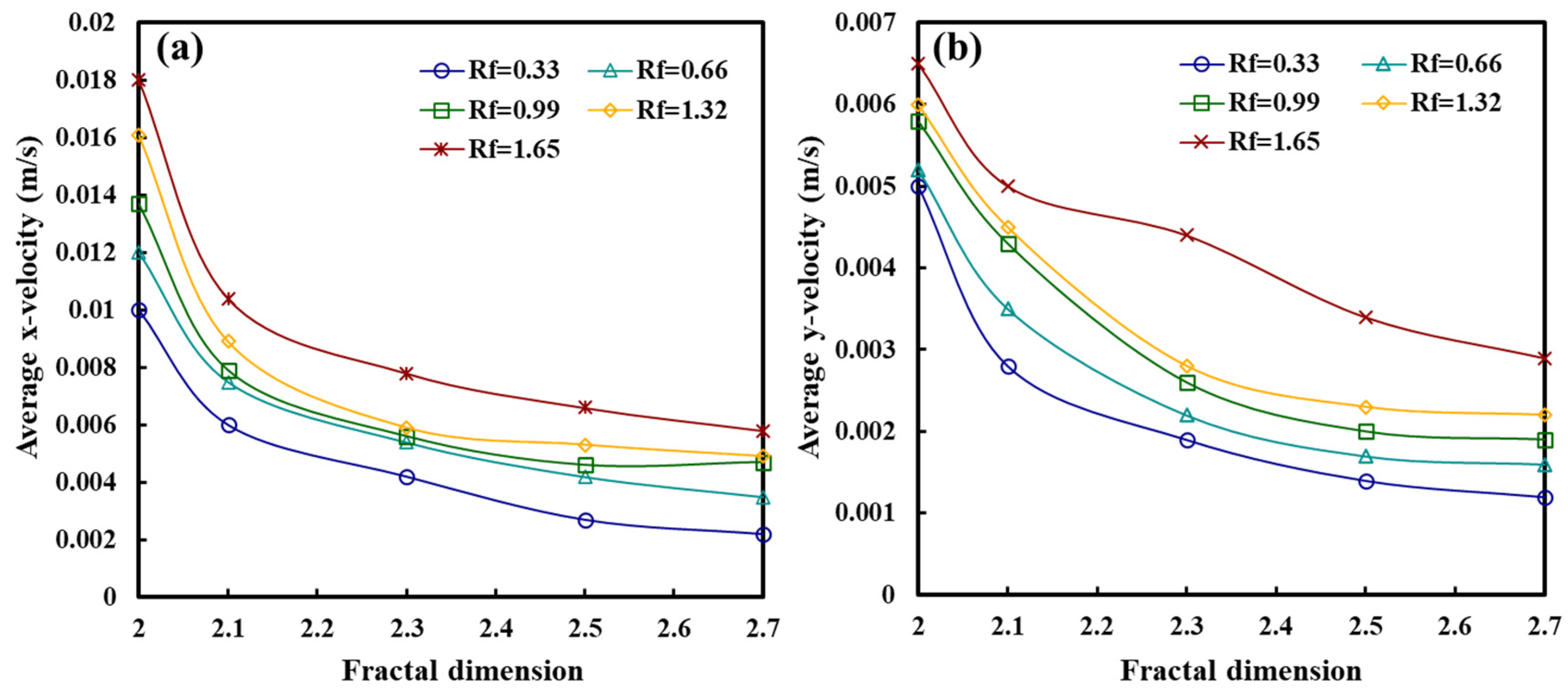
4.2. Effect of the Ratio of Lateral to Longitudinal Forces on the Proppant (Rf)
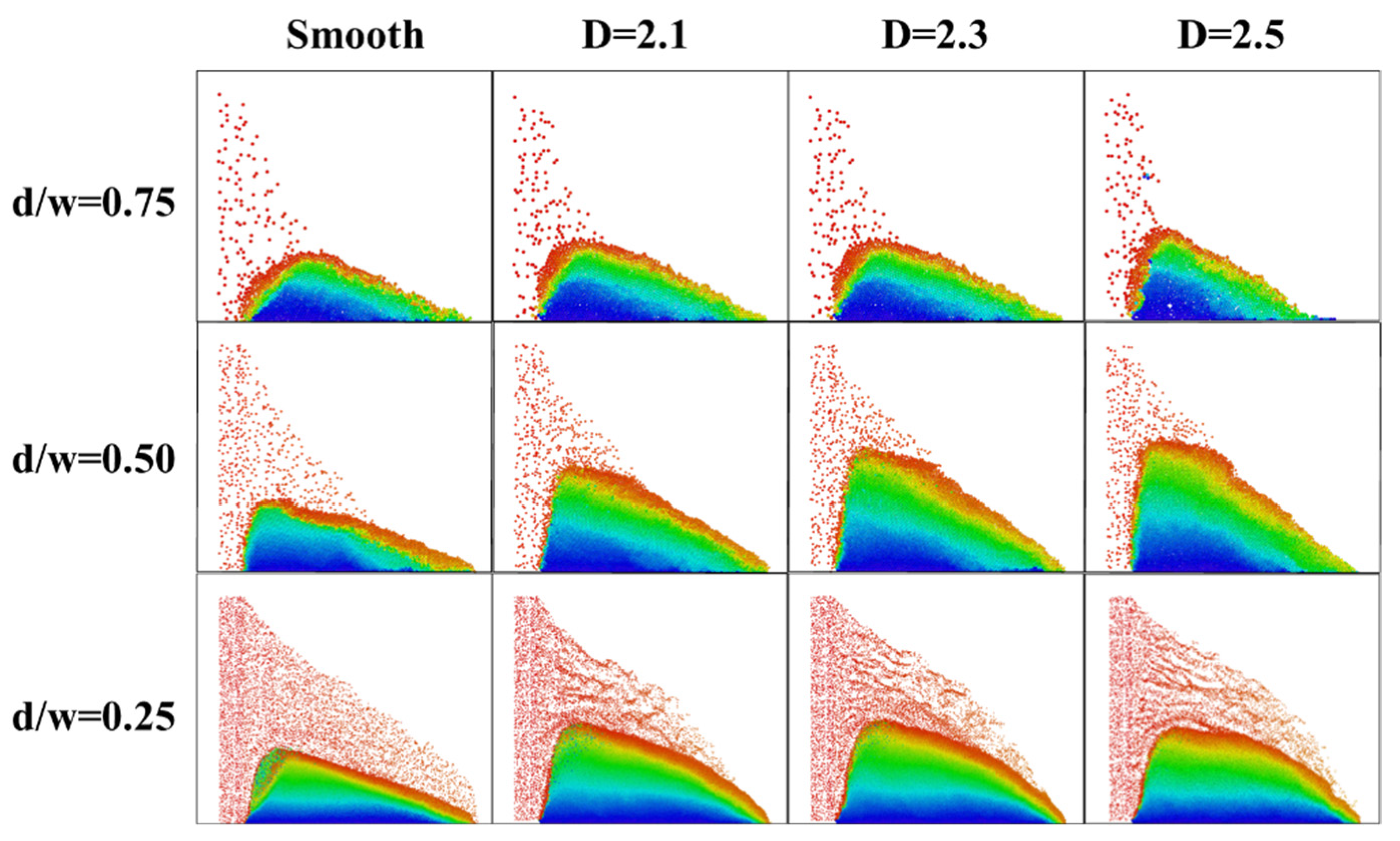
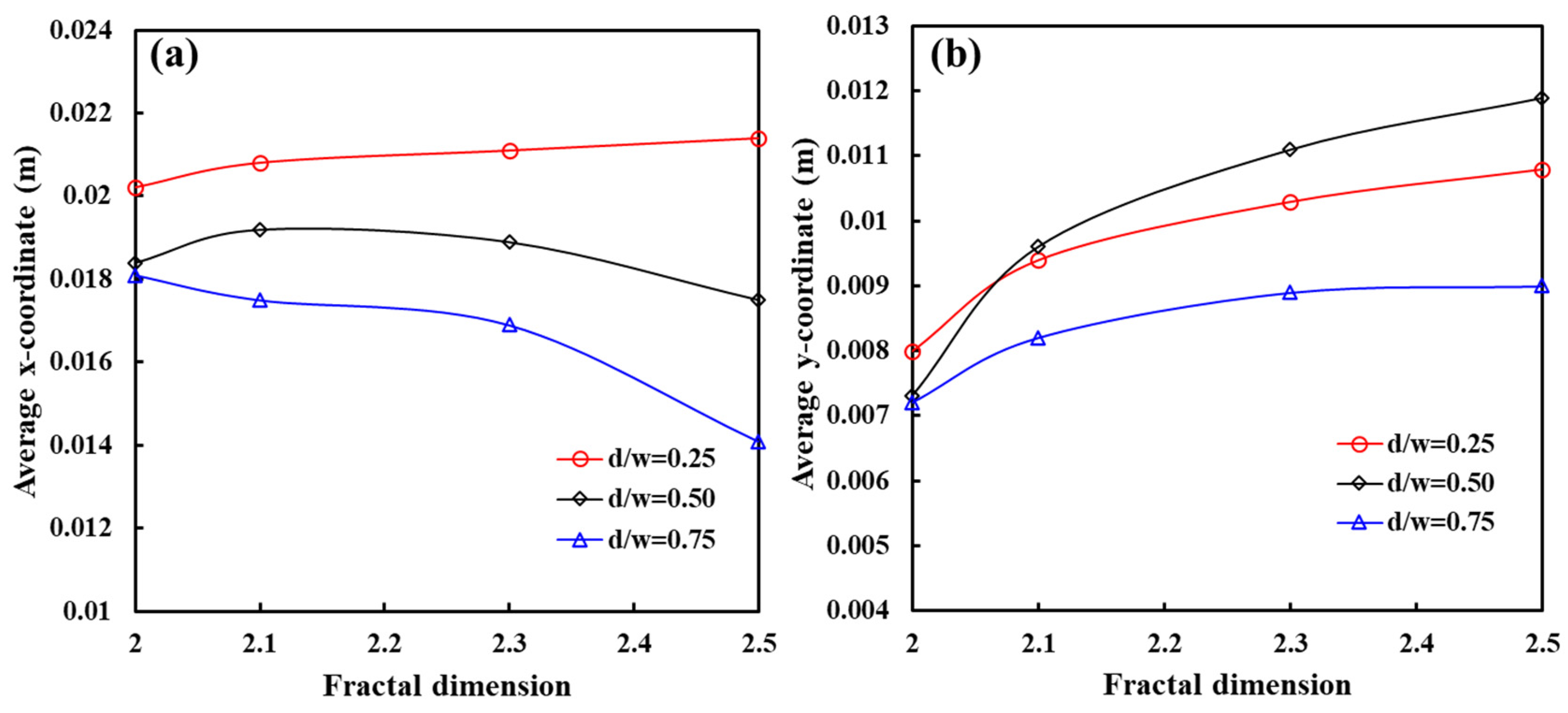
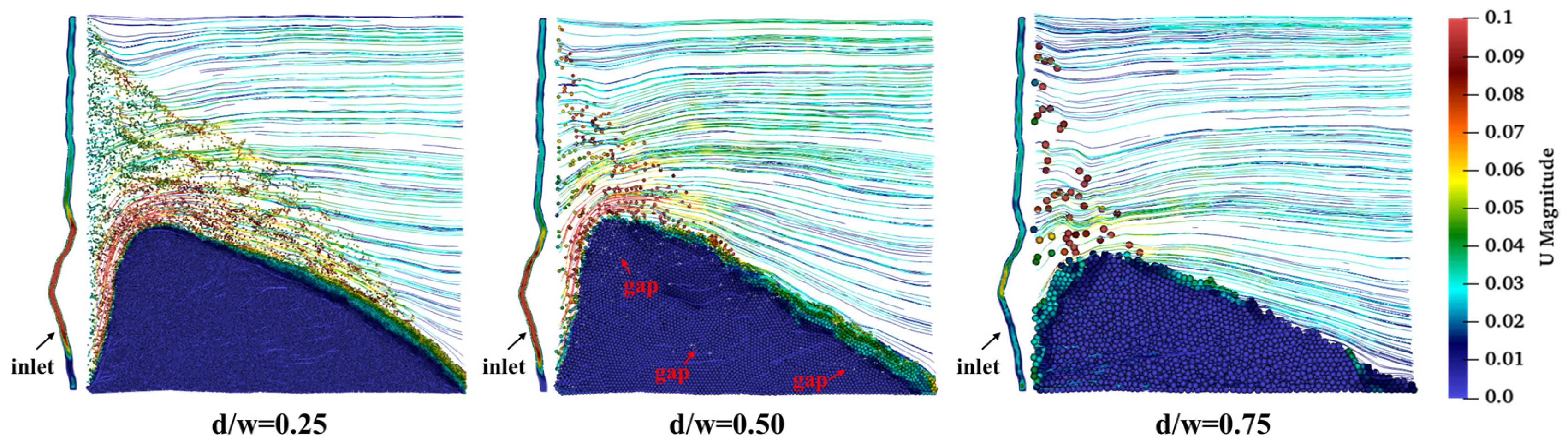
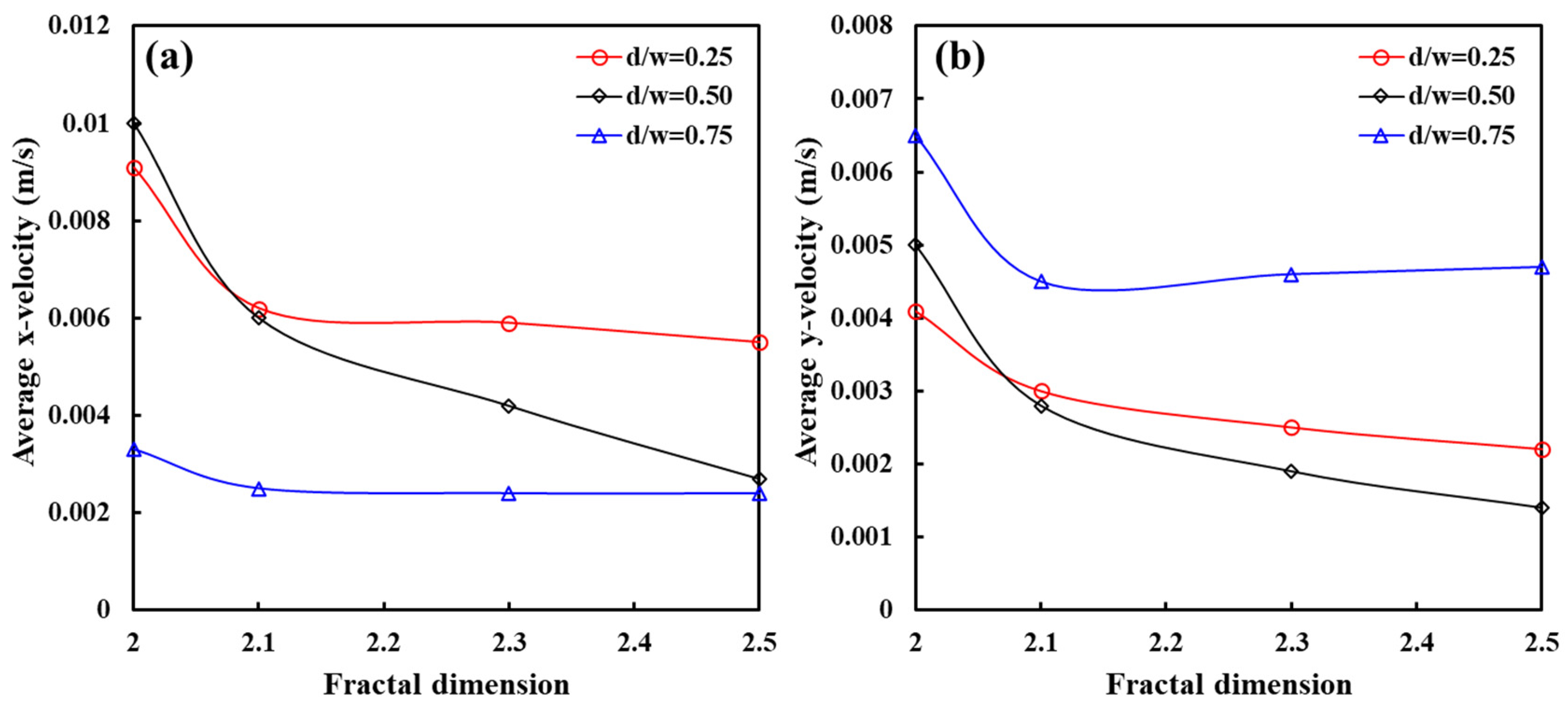
4.3. Effect of the Ratio of the Proppant Diameter to the Fracture Aperture (d/w)
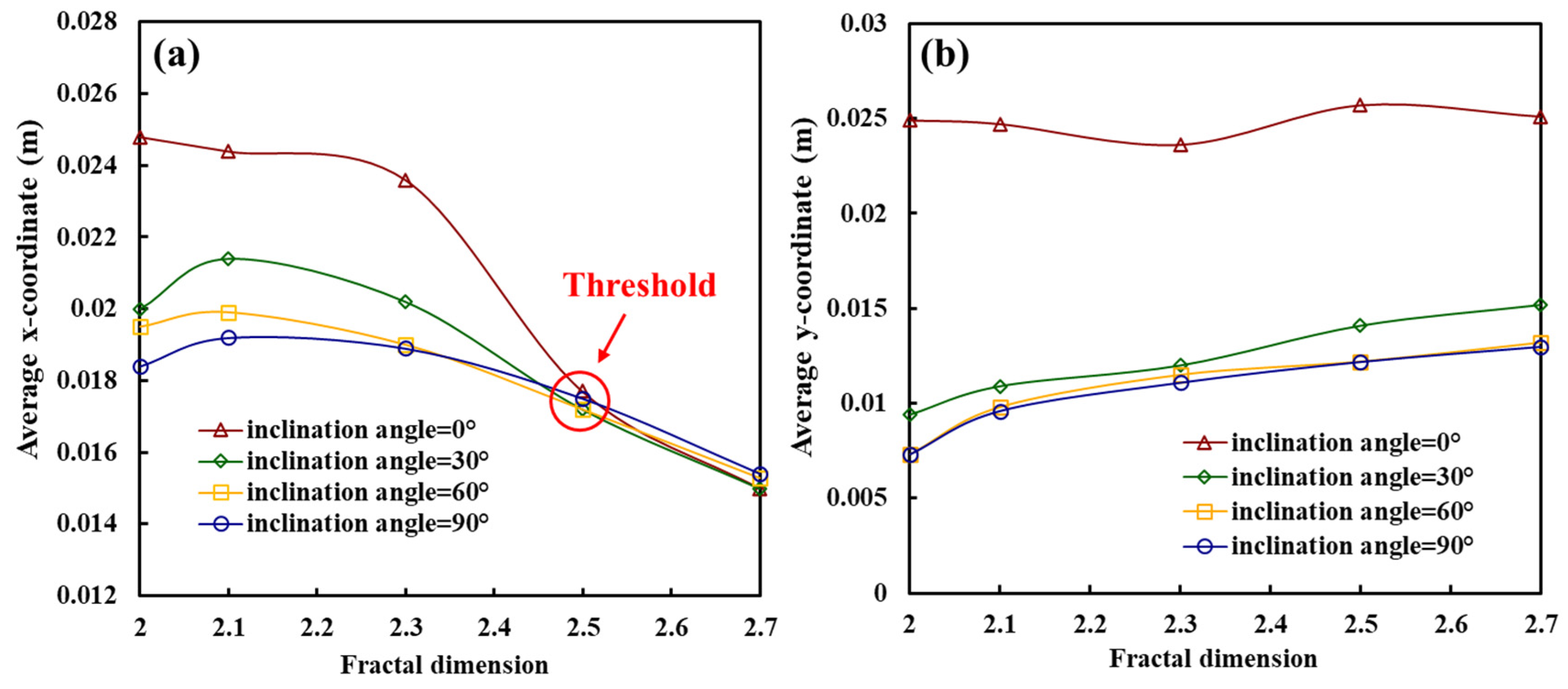
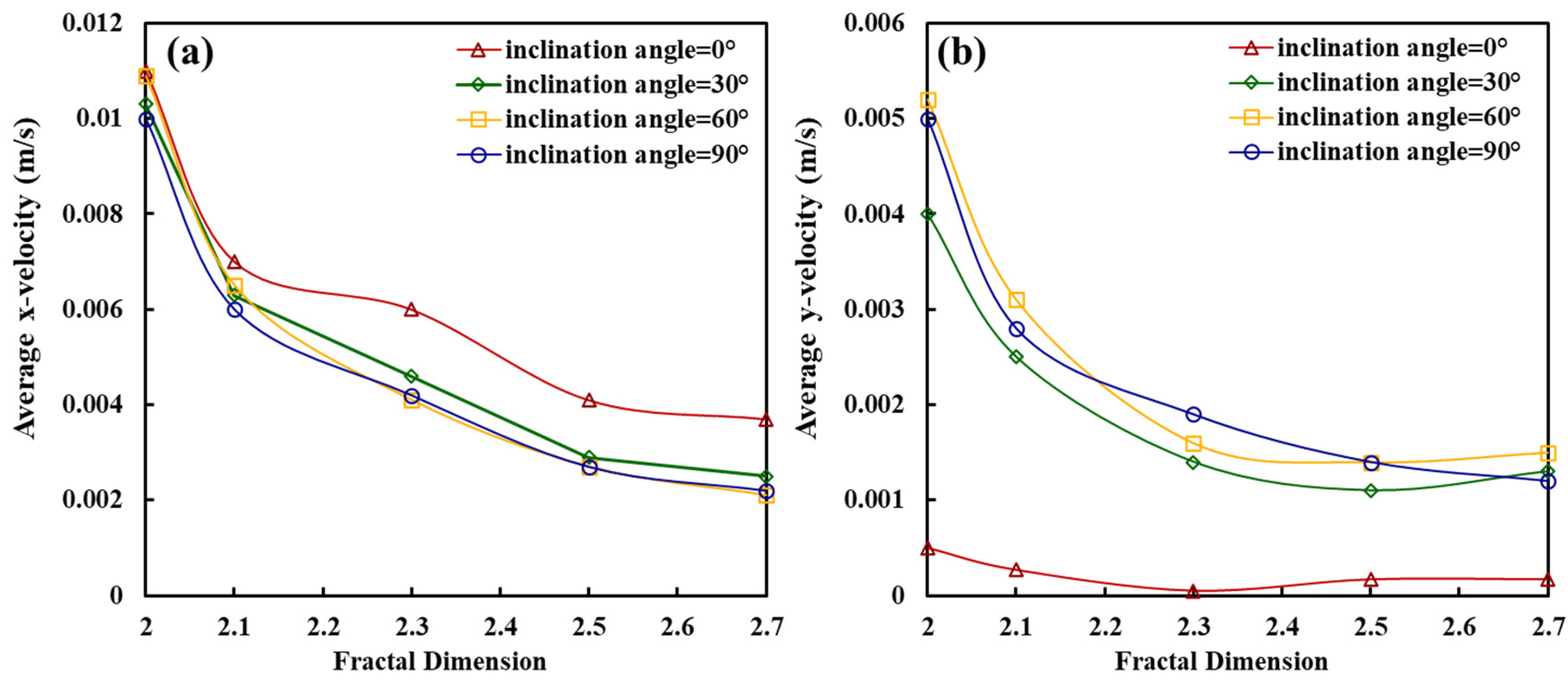
4.4. Effect of Inclination Angle at Different Fracture Dimensions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mayerhofer, M.; Lolon, E.; Warpinski, N. What is stimulated reservoir volume? SPE Prod. Oper. 2010, 25, 89–98. [Google Scholar] [CrossRef]
- Daneshy, A. Hydraulic fracturing to improve production. Way Ahead 2010, 6, 14–17. [Google Scholar] [CrossRef]
- Guo, X.; Hu, D.; Li, Y. Theoretical progress and key technologies of onshore ultra-deep oil/gas exploration. Engineering 2019, 5, 458–470. [Google Scholar] [CrossRef]
- Miller, C.; Waters, G.; Ryalander, E. Evaluation of production log data from horizontal wells drilled in organic shales. In Proceedings of the North American Unconventional Gas Conference and Exhibition, The Woodlands, TX, USA, 14–16 June 2011. Paper SPE-144326-MS. [Google Scholar]
- Zhao, J.; Ren, L.; Jiang, T. Ten years of gas shale fracturing in China: Review and prospect. Nat. Gas Ind. B 2022, 9, 158–175. [Google Scholar] [CrossRef]
- Ma, X.; Wang, H.; Zhang, Q. “Extreme utilization” development of deep shale gas in southern Sichuan Basin, SW China. Pet. Explor. Dev. 2022, 49, 1377–1385. [Google Scholar] [CrossRef]
- Aydin, A.; Schultz, R. Effect of mechanical interaction on the development of strike-slip faults with echelon patterns. J. Struct. Geol. 1990, 12, 123–129. [Google Scholar] [CrossRef]
- Babadagli, T.; Develi, K. Fractal characteristics of rocks fractured under tension. Theor. Appl. Fract. Mech. 2003, 39, 73–88. [Google Scholar] [CrossRef]
- Zhang, Y.; Chai, J. Effect of surface morphology on fluid flow in rough fractures: A review. J. Nat. Gas Sci. Eng. 2020, 79, 103343. [Google Scholar] [CrossRef]
- Zhu, G.; Zhao, Y.; Zhang, T. Micro-scale reconstruction and CFD-DEM simulation of proppant-laden flow in hydraulic fractures. Fuel 2023, 352, 129151. [Google Scholar] [CrossRef]
- Siddhamshetty, P.; Wu, K.; Kwon, J. Modeling and control of proppant distribution of multistage hydraulic fracturing in horizontal shale wells. Ind. Eng. Chem. Res. 2019, 58, 3159–3169. [Google Scholar] [CrossRef]
- Raimbay, A.; Babadagli, T.; Kuru, E. Quantitative and visual analysis of proppant transport in rough fractures. J. Nat. Gas Sci. Eng. 2016, 33, 1291–1307. [Google Scholar] [CrossRef]
- Huang, H.; Babadagli, T.; Li, H. A visual experimental study on proppants transport in rough vertical fractures. Int. J. Rock Mech. Min. Sci. 2020, 134, 104446. [Google Scholar] [CrossRef]
- Gong, F.; Huang, H.; Babadagli, T. A computational model to simulate proppant transport and placement in rough fractures. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 1–3 February 2022. p. D021S003R006.
- Huang, F.; Wang, F.; Chen, F. Transport and Retention of Coal Fines in Proppant Packs during Gas–Water Two–Phase Flow: Insights from Interface, Pore, to Laboratory Scales. Energy Fuels 2024, 38, 12672–12683. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Viete, D.R. Applicability of the ‘cubic law’ for non-Darcian fracture flow. J. Pet. Sci. Eng. 2011, 78, 321–327. [Google Scholar] [CrossRef]
- Chen, Y.; Liang, W.; Lian, H.; Yang, J.; Nguyen, V.P. Experimental study on the effect of fracture geometric characteristics on the permeability in deformable rough-walled fractures. Int. J. Rock Mech. Min. Sci. 2017, 98, 121–140. [Google Scholar] [CrossRef]
- Wang, L.; Cardenas, M.B.; Slottke, D.T.; Ketcham, R.A.; Sharp, J.M., Jr. Modification of the Local Cubic Law of fracture flow for weak inertia, tortuosity, and roughness. Water Resour. Res. 2015, 51, 2064–2080. [Google Scholar] [CrossRef]
- Yin, Q.; Ma, G.; Jing, H.; Wang, H.; Su, H.; Wang, Y.; Liu, R. Hydraulic properties of 3D rough-walled fractures during shearing: An experimental study. J. Hydrol. 2017, 555, 169–184. [Google Scholar] [CrossRef]
- Xie, J.; Hu, Y.; Kang, Y. Numerical study on proppant transport in supercritical carbon dioxide under different fracture shapes: Flat, wedge-shaped, and bifurcated. Energy Fuels 2022, 36, 10278–10290. [Google Scholar] [CrossRef]
- Zhou, M.; Yang, Z.; Xu, Z. CFD-DEM modeling and analysis study of proppant transport in rough fracture. Powder Technol. 2024, 436, 119461. [Google Scholar] [CrossRef]
- Cao, C.; Xu, Z.; Chai, J.; Qin, Y.; Tan, R. Mechanical and hydraulic behaviors in a single fracture with asperities crushed during shear. Int. J. Geomech. 2018, 18, 04018148. [Google Scholar] [CrossRef]
- Lee, J.; Kang, J.M.; Choe, J. Experimental analysis on the effects of variable apertures on tracer transport. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Huang, N.; Liu, R.; Jiang, Y. Numerical study of the geometrical and hydraulic characteristics of 3D self–affine rough fractures during shear. J. Nat. Gas Sci. Eng. 2017, 45, 127–142. [Google Scholar] [CrossRef]
- Xie, L.Z.; Gao, C.; Ren, L.; Li, C.B. Numerical investigation of geometrical and hydraulic properties in a single rock fracture during shear displacement with the Navier–Stokes equations. Environ. Earth Sci. 2015, 73, 7061–7074. [Google Scholar] [CrossRef]
- Suri, Y.; Islam, S.; Hossain, M. Effect of fracture roughness on the hydrodynamics of proppant transport in hydraulic fractures. J. Nat. Gas Sci. Eng. 2020, 80, 103401. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, C.; Sharma, M. Proppant placement in perforation clusters in deviated wellbores. In Proceedings of the Unconventional Resources Technology Conference, Denver, Colorado, 22–24 July 2019; p. D013S014R002, SPE/AAPG/SEG. [Google Scholar]
- Zhang, B.; Gamage, R.; Zhang, C. Hydrocarbon recovery: Optimized CFD-DEM modeling of proppant transport in rough rock fractures. Fuel 2022, 311, 122560. [Google Scholar] [CrossRef]
- Guo, T.; Luo, Z.; Zhou, J. Numerical simulation on proppant migration and placement within the rough and complex fractures. Pet. Sci. 2022, 19, 2268–2283. [Google Scholar] [CrossRef]
- Gong, Z.; Li, N.; Kang, W. Novel oleophilic tracer-slow-released proppant for monitoring the oil production contribution. Fuel 2024, 364, 130945. [Google Scholar] [CrossRef]
- Hu, X.; Wu, K.; Li, G. Effect of proppant addition schedule on the proppant distribution in a straight fracture for slickwater treatment. J. Pet. Sci. Eng. 2018, 167, 110–119. [Google Scholar] [CrossRef]
- Zhou, Z.; Shen, L.; Wang, J. Numerical investigating the effect of nonuniform proppant distribution and unpropped fractures on well performance in a tight reservoir. J. Pet. Sci. Eng. 2019, 177, 634–649. [Google Scholar] [CrossRef]
- Movassagh, A.; Haghighi, M.; Zhang, X. A fractal approach for surface roughness analysis of laboratory hydraulic fracture. J. Nat. Gas Sci. Eng. 2021, 85, 103703. [Google Scholar] [CrossRef]
- Xie, H.; Sun, H.; Ju, Y. Study on generation of rock fracture surfaces by using fractal interpolation. Int. J. Solids Struct. 2001, 38, 5765–5787. [Google Scholar] [CrossRef]
- Issa, M.; Islam, M. Fractal dimension––A measure of fracture roughness and toughness of concrete. Eng. Fract. Mech. 2003, 70, 125–137. [Google Scholar] [CrossRef]
- Charkaluk, E.; Bigerelle, M.; Iost, A. Fractals and fracture. Eng. Fract. Mech. 1998, 61, 119–139. [Google Scholar] [CrossRef]
- Babadagli, T.; Develi, K. On the application of methods used to calculate the fractal dimension of fracture surfaces. Fractals 2001, 9, 105–128. [Google Scholar] [CrossRef]
- Kloss, C.; Goniva, C.; Hager, A. Models, algorithms and validation for opensource DEM and CFD–DEM. Prog. Comput. Fluid Dyn. Int. J. 2012, 12, 140–152. [Google Scholar] [CrossRef]
- Weller, O.; Lange, D.; Tilmann, F. The structure of the Sumatran Fault revealed by local seismicity. Geophys. Res. Lett. 2012, 39, 1–7. [Google Scholar] [CrossRef]
- Hertz, H. Über die Berührung fester elastischer Körper. J. Reine Und Angew. Math. 1881, 92, 156. [Google Scholar]
- Mindlin, R.; Deresiewicz, H. Elastic spheres in contact under varying oblique forces. J. Appl. Mech. Sep. 1953, 20, 327–344. [Google Scholar] [CrossRef]
- Felice, R.D. The void age function for fluid-particle interaction systems. Int. J. Multiph. Flow 1994, 20, 153–159. [Google Scholar] [CrossRef]
- Tong, S.; Mohanty, K.K. Proppant transport study in fractures with intersections. Fuel 2016, 181, 463–477. [Google Scholar] [CrossRef]
- Isakov, E.; Ogilvie, S.; Taylor, C. Fluid flow through rough fractures in rocks I: High resolution aperture determinations. Earth Planet. Sci. Lett. 2001, 191, 267–282. [Google Scholar] [CrossRef]
- Ogilvie, G. On the dynamics of magneto rotational turbulent stresses. Mon. Not. R. Astron. Soc. 2003, 340, 969–982. [Google Scholar] [CrossRef]
- Xie, J.; Gao, M.; Zhang, R. Experimental investigation on the anisotropic fractal characteristics of the rock fracture surface and its application on the fluid flow description. J. Pet. Sci. Eng. 2020, 191, 107190. [Google Scholar] [CrossRef]
- Chun, T.; Li, Y.; Wu, K. Comprehensive experimental study of proppant transport in an inclined fracture. J. Pet. Sci. Eng. 2020, 184, 106523. [Google Scholar] [CrossRef]
- Daneshy, A. A study of inclined hydraulic fractures. Soc. Pet. Eng. J. 1973, 13, 61–68. [Google Scholar] [CrossRef]
- Agrawal, G.; Kumar, A.; Dutta, S. Productivity Optimization and Validation of Multistage Fracturing in a Rare et al. Geomechanical Setting with Production Logging. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 16–19 August 2021; p. D021S028R006. [Google Scholar]
- Kumar, A.; Sharma, M. Diagnosing hydraulic fracture geometry, complexity, and fracture wellbore connectivity using chemical tracer flowback. Energies 2020, 13, 5644. [Google Scholar] [CrossRef]

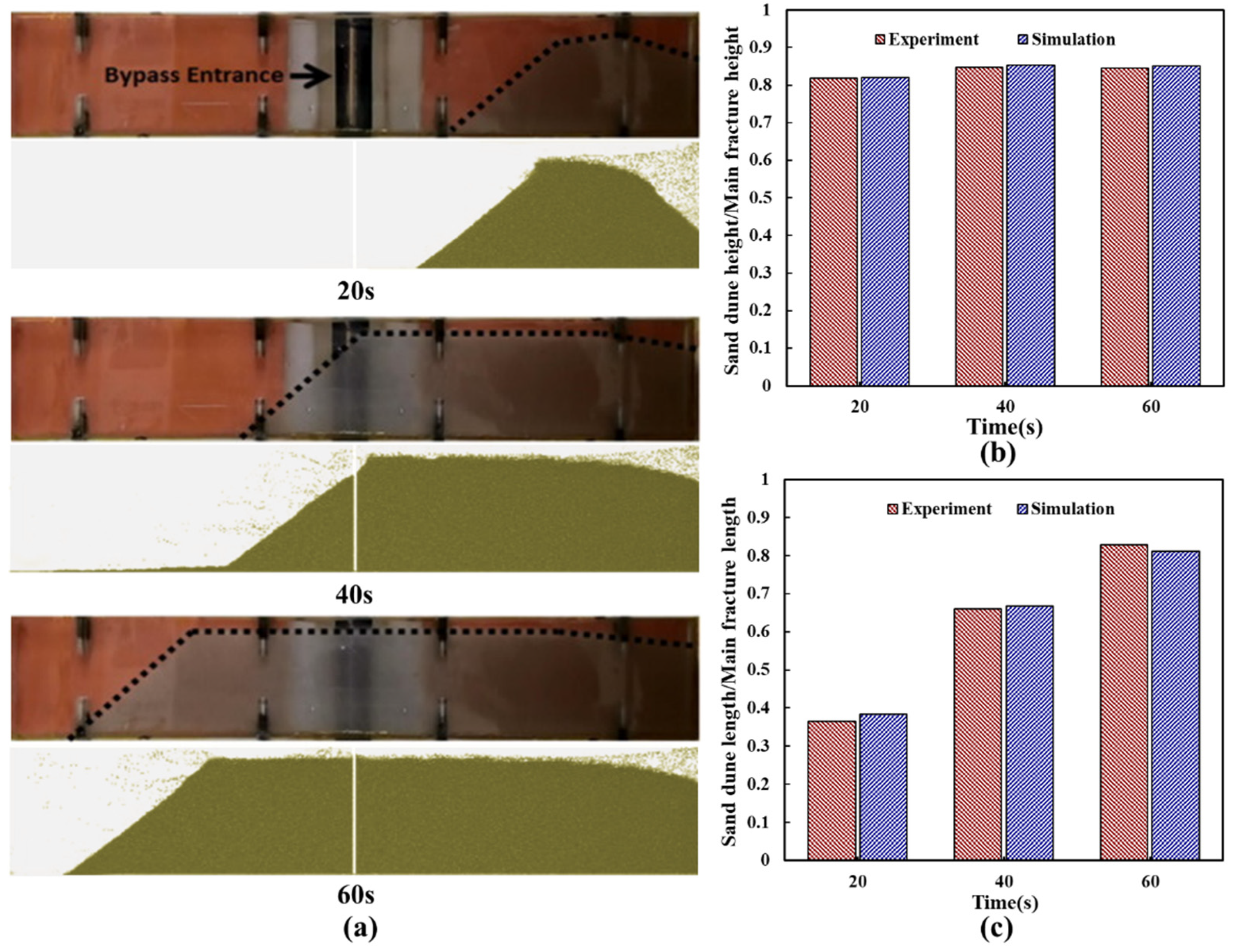
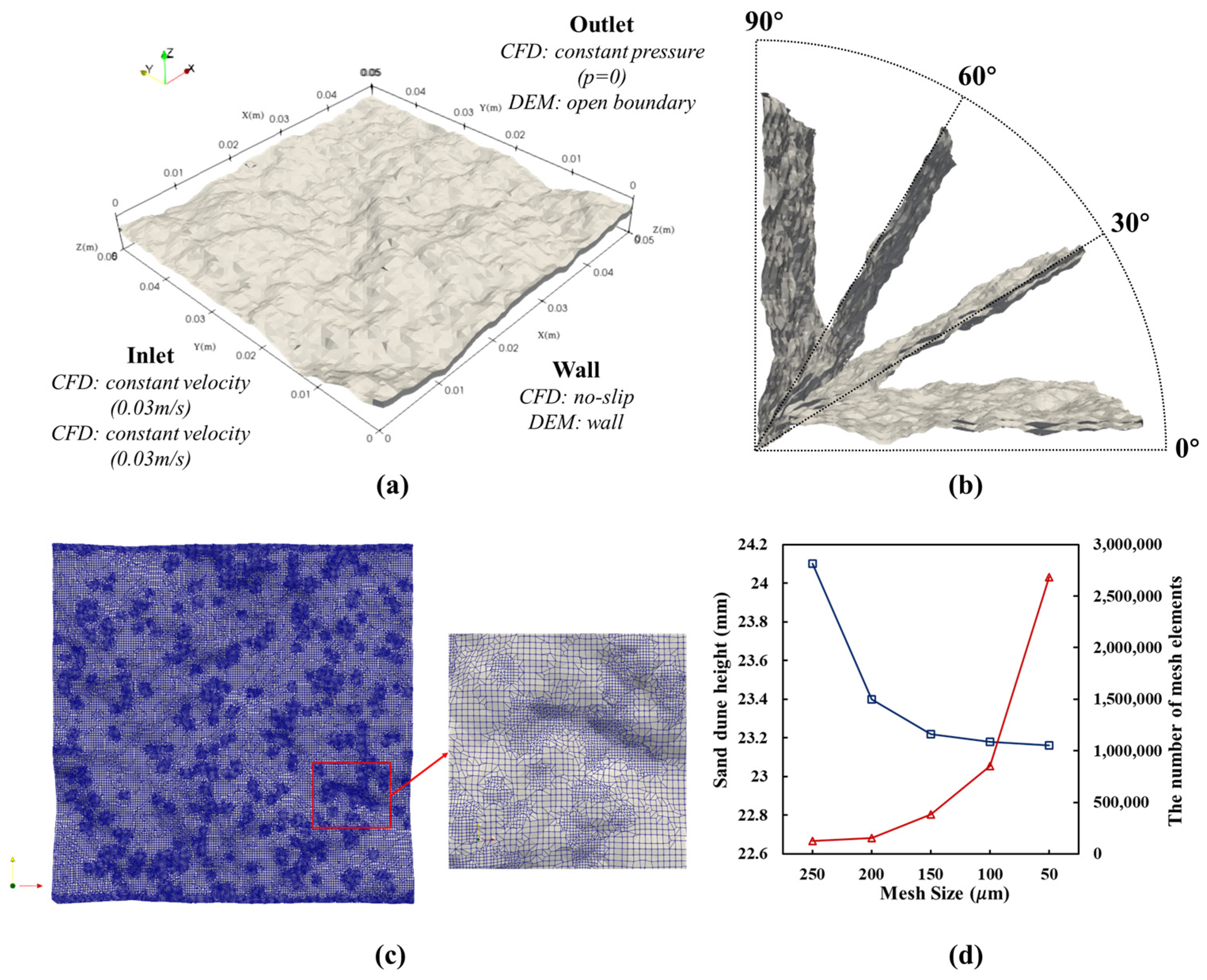


| Parameter | Range |
|---|---|
| Main Fracture Length (mm) | 381 |
| Fracture Height (mm) | 190.5 |
| Fracture Width (mm) | 2 |
| Cross Corner Angle (°) | 90 |
| Proppant Diameter (mm) | 0.6 |
| Proppant Density (kg/m3) | 2650 |
| Proppant Concentration (vol. fraction) | 0.038 |
| Injection Velocity (m/s) | 0.1 |
| Fluid Viscosity (mPa·s) | 1 |
| Parameter | Range |
|---|---|
| Fracture Length (mm) | 50 |
| Fracture Width/Height (mm) | 50 |
| Equivalent Hydraulic Aperture (mm) | 1 |
| Fracture Fractal Dimension | 2.1, 2.3, 2.5, 2.7 |
| Proppant Size (mm) | 0.25, 0.5, 0.75 |
| Proppant Density (kg/m3) | 2650 |
| Proppant Concentration (vol. fraction) | 0.05 |
| Injection Velocity (m/s) | 0.03 |
| Fluid Viscosity (mPa·s) | 1, 2, 3, 4, 5 |
| Inclination Angle (°) | 0, 30, 60, 90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Huang, J.; Xie, C.; Zhao, H. CFD-DEM Simulation on the Main-Controlling Factors Affecting Proppant Transport in Three-Dimensional Rough Fractures of Offshore Unconventional Reservoirs. J. Mar. Sci. Eng. 2024, 12, 2117. https://doi.org/10.3390/jmse12122117
Li Y, Huang J, Xie C, Zhao H. CFD-DEM Simulation on the Main-Controlling Factors Affecting Proppant Transport in Three-Dimensional Rough Fractures of Offshore Unconventional Reservoirs. Journal of Marine Science and Engineering. 2024; 12(12):2117. https://doi.org/10.3390/jmse12122117
Chicago/Turabian StyleLi, Yuanping, Jingwei Huang, Chenyue Xie, and Hui Zhao. 2024. "CFD-DEM Simulation on the Main-Controlling Factors Affecting Proppant Transport in Three-Dimensional Rough Fractures of Offshore Unconventional Reservoirs" Journal of Marine Science and Engineering 12, no. 12: 2117. https://doi.org/10.3390/jmse12122117
APA StyleLi, Y., Huang, J., Xie, C., & Zhao, H. (2024). CFD-DEM Simulation on the Main-Controlling Factors Affecting Proppant Transport in Three-Dimensional Rough Fractures of Offshore Unconventional Reservoirs. Journal of Marine Science and Engineering, 12(12), 2117. https://doi.org/10.3390/jmse12122117





