Experimental Investigation on Wave Dissipation of Perforated Pipe Breakwater Under Regular Wave Conditions
Abstract
:1. Introduction
2. Physical Model Tests
3. Results and Discussion
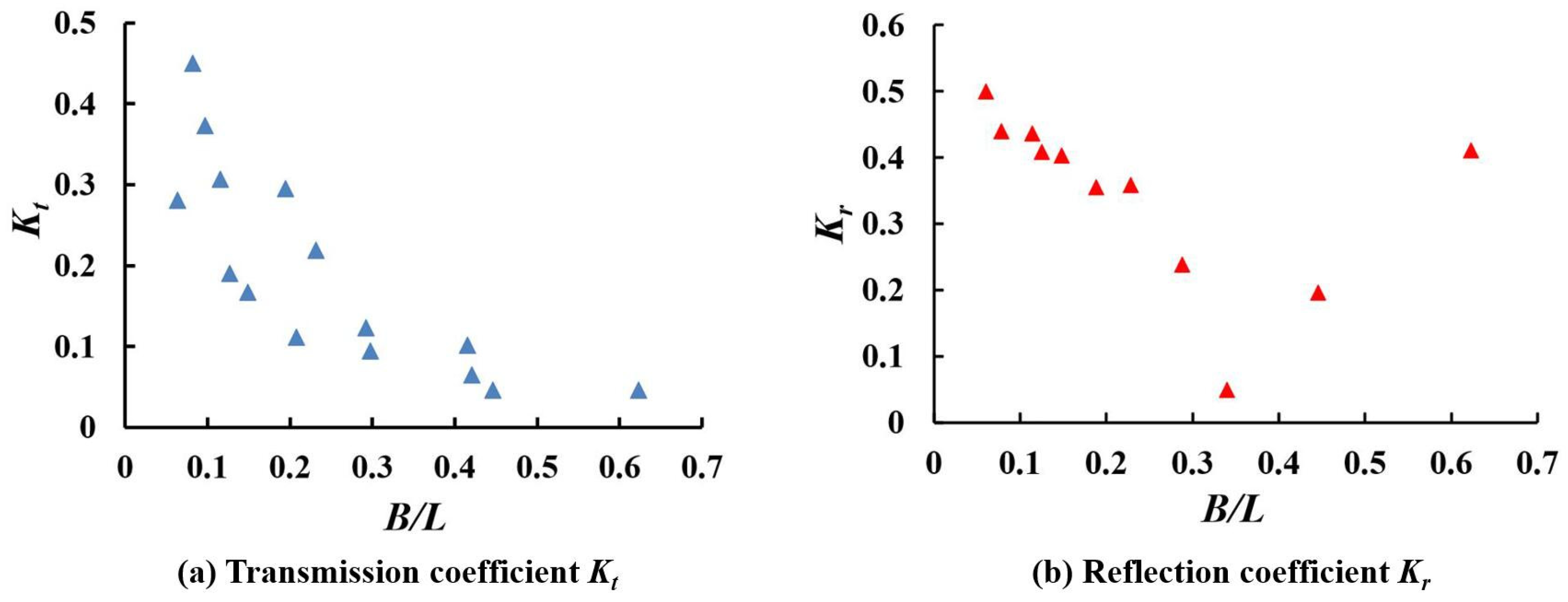
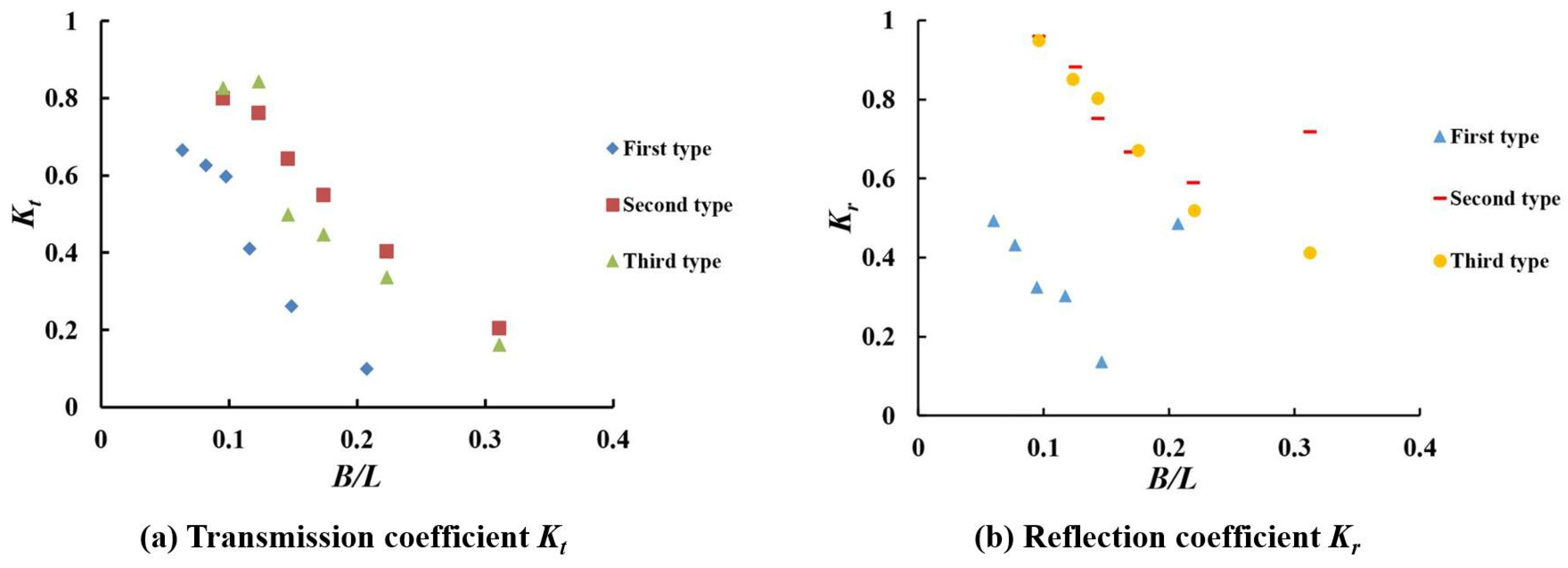
3.1. The Relative Top Width of the Breakwater (B/L)
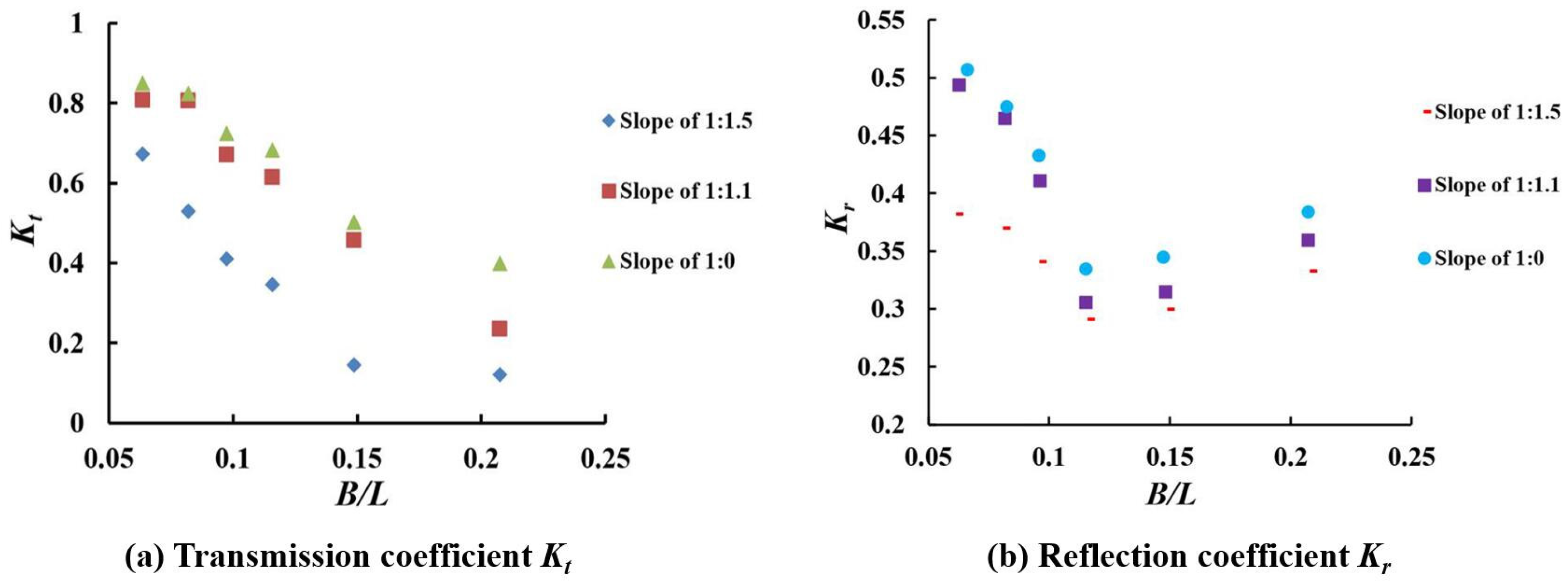
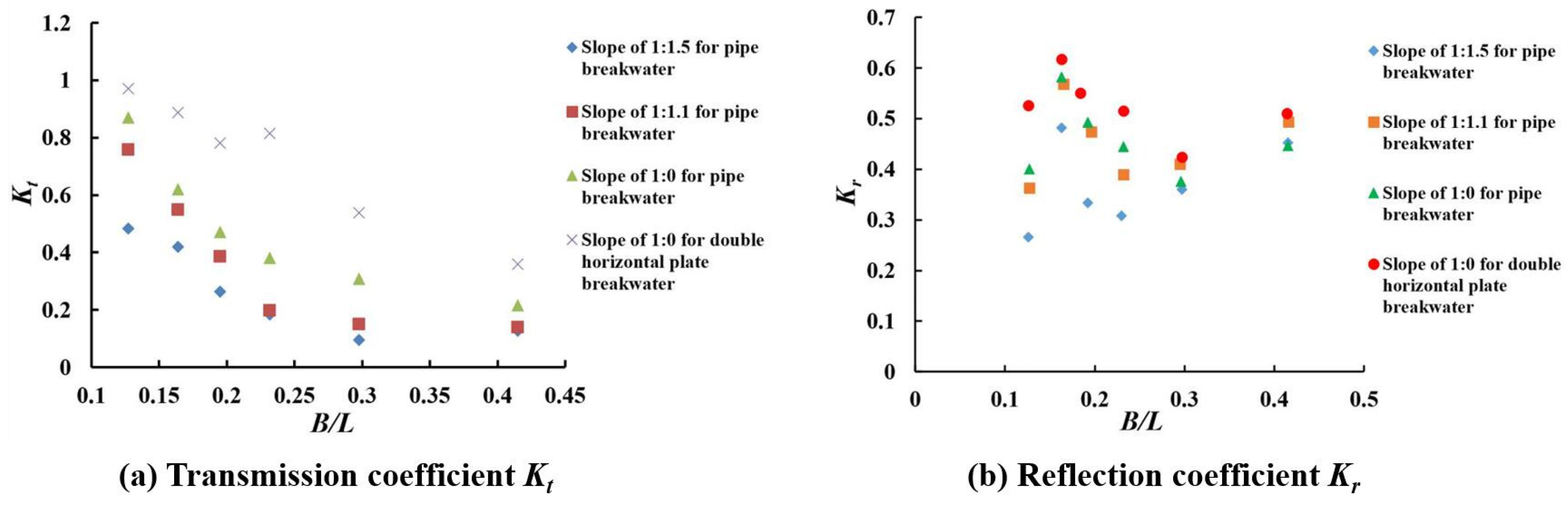
3.2. Effect of Breakwater Slope
3.2.1. Same Slope in Front and Behind of the Breakwater
3.2.2. Different Slopes in Front and Behind of the Breakwater
3.3. Different Structural Types
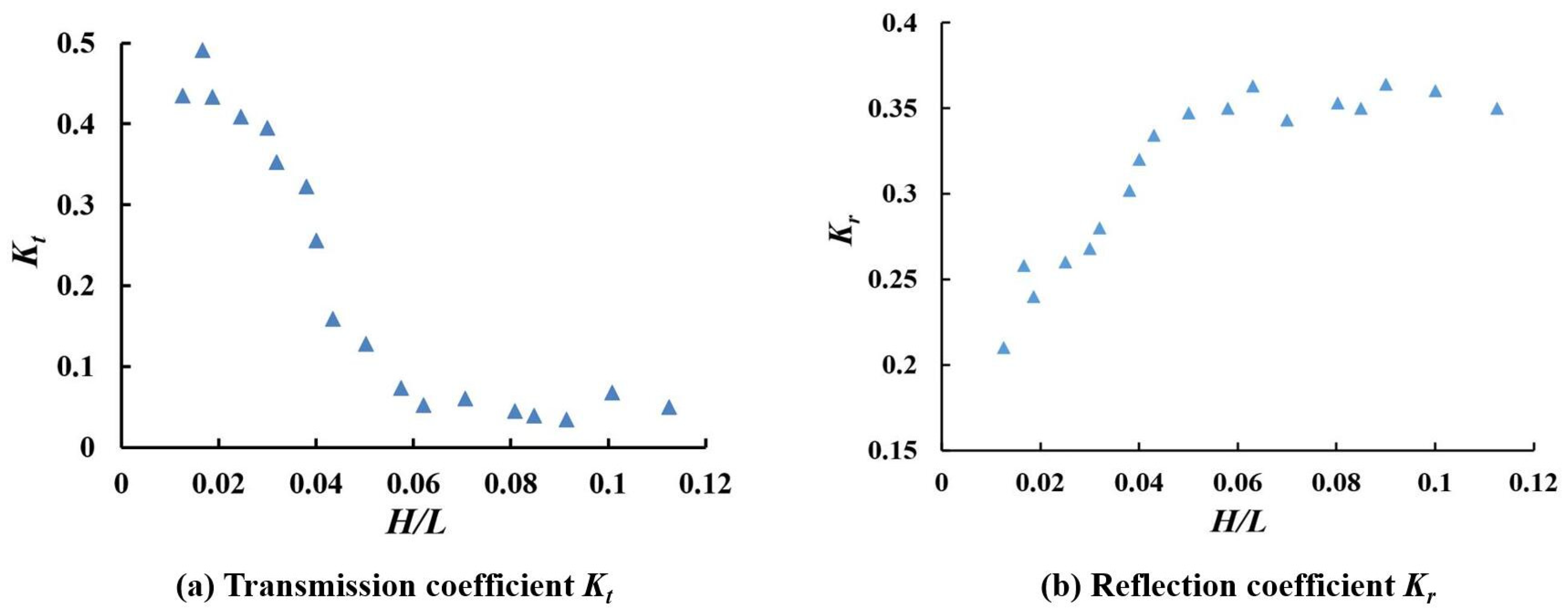
3.4. Wave Steepness (H/L)
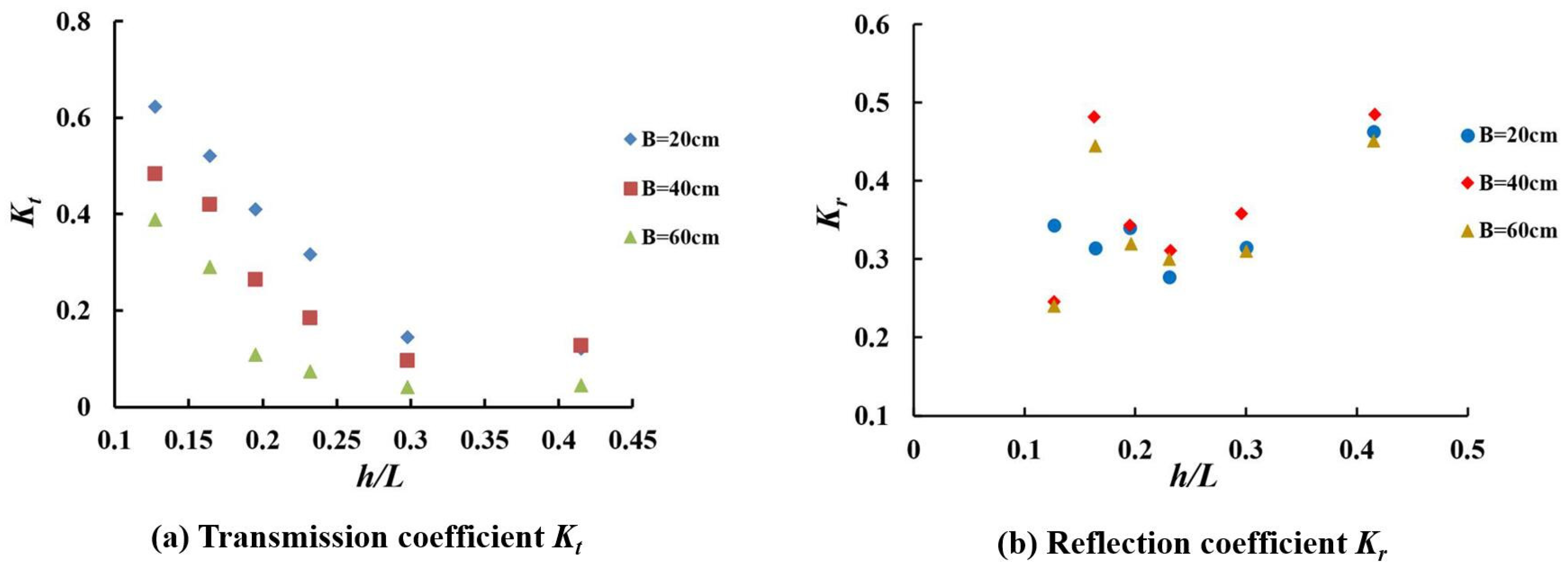
3.5. Relative Water Depths (h/L)
3.6. Comparison of Perforated Pipe and Double Horizontal Plate Breakwater
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, Z.; Li, Y.; Liu, Y. Hydraulic performance and wave loadings of perforated/slotted coastal structures: A review. Ocean Eng. 2011, 38, 1031–1053. [Google Scholar] [CrossRef]
- Reeve, D.; Chadwick, A.; Fleming, C. Coastal engineering: Processes Theory and Design Practice; Spon Press: New York, NY, USA, 2012. [Google Scholar]
- Isaacson, M.; Baldwin, J.; Allyn, N.; Cowdell, S. Wave interactions with perforated breakwater. J. Waterw. Port Coast. Ocean. Eng. 2000, 126, 229–235. [Google Scholar] [CrossRef]
- Weigel, R. Closely spaced piles as a breakwater. Dock Harbour Auth. 1961, 41, 150–165. [Google Scholar]
- Cмирнoв, Г.H. Port and Port Buildings; China Communications Press: Beijing, China, 1984. [Google Scholar]
- Hou, G.B. Experimental study on pipe permeable breakwater. Coastal Eng. 1982, 1, 1–8. (In Chinese) [Google Scholar]
- Li, C.Z.; Cai, Y.; Wei, S.L. Computation of reflection coefficient for hollow-pipe porous breakwater. Ocean Eng. 1991, 4, 69–79. (In Chinese) [Google Scholar]
- Wen, S.C. Wave Principle; Shandong People’s Publishing House Press: Jinan, China, 1962; pp. 382–393. [Google Scholar]
- Ministry of Transport of the People’s Republic of China. Code for Sea Port Hydrology; China Communication Press: Beijing, China, 1999; pp. 35–50. [Google Scholar]
- Qiu, D.H.; Wang, X.G. Theoretical analysis of deep water thin plate breakwater. Port Waterw. Eng. 1986, 4, 8–12. (In Chinese) [Google Scholar] [CrossRef]
- Ju, L.H.; Yang, Z.J. Experimental research on coefficient of wave transmission through single immersed vertical barrier of open-type breakwater. Port Waterw. Eng. 2008, 4, 19–22. (In Chinese) [Google Scholar]
- Zhu, D.T. Hydrodynamic characteristics of vertical monolayer baffle permeable dike. Marine Engineering. Branch of China Oceanic Society. In Proceedings of the 18th China Offshore Engineering Symposium (II), Beijing, China, 28–31 December 2017; pp. 894–900. [Google Scholar]
- Yin, F.A. Study on Wave Permeability Characteristics of Baffle-Type Permeable Breakwater. Master’s Thesis, Hohai University, Nanjing, China, 2005; pp. 18–35. [Google Scholar]
- Fan, J.; Wang, Y.A.; Yang, S.H.; Yan, S.C.; Wang, W.; Qian, X.S. Experimental research on reflection coefficient and transmitted coefficient of double barriers penetrated breakwater. Ocean Eng. 2011, 29, 60–67. (In Chinese) [Google Scholar]
- Shao, J.; Chen, G.P.; Yan, S.C.; Yang, Q. An experimental study of the wave-permeating coefficient of vertical baffle permeable breakwater under irregular waves. Ocean Eng. 2016, 34, 50–57. (In Chinese) [Google Scholar]
- Syamsuri, A.M.; Suriamihardja, D.A.; Thaha, M.A.; Rachman, T. Effect of pipe wall roughness on porous breakwater structure on wave deformation. J. Eng. Trends Technol. 2021, 69, 147–151. [Google Scholar]
- Wang, Y.K. Experimental Study on Wave Attenuation of Different Open-Hole Porous Breakwaters. Master’s Thesis, Ludong University, Yantai, China, 2019. [Google Scholar]
- Neelamni, S.; Gayathri, T. Wave interaction with twin plate wave barrier. Ocean Eng. 2006, 33, 495–516. [Google Scholar] [CrossRef]
- Neelamni, S.; Rajendran, R. Wave interaction with T-type breakwaters. Ocean Eng. 2002, 29, 151–175. [Google Scholar] [CrossRef]
- Neelamni, S.; Rajendran, R. Wave interaction with ‘┴’-type breakwaters. Coastal Eng. 2002, 29, 561–589. [Google Scholar]
- Tao, J.W.; Wu, J.P.; Zheng, X.W. Experimental study on wave attenuation performance of +-type breakwater. J. Wuhan Univer. Technol. (Transp. Sci. Eng.) 2018, 42, 349–352. [Google Scholar]
- Wang, G.Y. Investigation on the Structure Type and Performance of the Special Breakwater. Master’s Thesis, Dalian University of Technology, Dalian, China, 2005. [Google Scholar]
- Yan, Y.X.; Zheng, J.H.; Zeng, X.C.; Xie, H.D. Experimental research on wave dissipation characteristics of multi-layer baffle piled permeable breakwater. Ocean Eng. 1998, 16, 68–75. (In Chinese) [Google Scholar]
- Wang, Q.; Liu, R.; Liang, B.C. Experimental study on wave-dissipating performance of pile-supported breakwater with perforated inclined wave screen. Coastal Eng. 2022, 41, 95–104. (In Chinese) [Google Scholar]
- Teh, H.M.; Venugopal, V. Performance evaluation of a semicircular breakwater with truncated wave screens. Ocean Eng. 2013, 70, 160–176. [Google Scholar] [CrossRef]
- He, F.; Huang, Z. Hydrodynamic performance of pile-supported OWC-type structures as breakwaters: An experimental study. Ocean Eng. 2014, 88, 618–626. [Google Scholar] [CrossRef]
- He, F.; Zhang, H.S.; Zhao, J.J.; Zheng, S.M.; Iglesias, G. Hydrodynamic performance of a pile-supported OWC breakwater: An analytical study. Appl. Ocean. Res. 2019, 88, 326–340. [Google Scholar] [CrossRef]
- Yu, D.J.; Feng, W.B.; Li, Y.B.; Yang, B. Experimental study and calculation of horizontal wave pressure of piled baffle penetrated breakwater. Port Waterw. Eng. 2015, 1, 19–24. (In Chinese) [Google Scholar]
- Lv, X.; Cheng, Y.Z.; Hu, Y.C.; Hang, X.Y. Experimental study on wave force characteristics of the porous I-type plate composition breakwater. Ocean Eng. 2020, 38, 49–55. (In Chinese) [Google Scholar]
- He, F.; Chen, Y.; Pan, J.P. Experimental study on hydrodynamic performance of labyrinth-type permeable breakwater. Ocean Eng. 2024, 5, 1–12. (In Chinese) [Google Scholar]
- Yu, D.Y.; Gao, Z.Y.; Dou, Z.H.; Qu, M.; Ge, X.L. Experimental study on the wave dissipation performance of a permeable breakwater structure with reverse-arc inclined plate. Coastal Eng. 2023, 42, 111–120. (In Chinese) [Google Scholar]
- Pan, C.C. Experimental Investigation on the Hydrodynamic Characteristics of Arc-Plate Type Breakwater. Master’s Thesis, Dalian University of Technology, Dalian, China, 2014. [Google Scholar]
- Zhao, L.P.; Zhu, Y.Z.; Xie, A.Y.; Zhou, J.F. Experimental study on wave forces on curved breakwater. Ocean Eng. 2015, 33, 35–41. [Google Scholar]
- Wang, L.X. Study on Random Wave Action on Twin-Arc-Plate Permeable Breakwater. Master’s Thesis, Ludong University, Yantai, China, 2021. [Google Scholar]
- Yagci, O.; Kirca VS, O.; Kabdasli, M.S.; Celik, A.O.; Unal, N.E.; Aydingakko, A. An experimental model application of wave screen: Dynamic pressure, water particle velocity, and wave measurements. Ocean Eng. 2006, 33, 1299–1321. [Google Scholar] [CrossRef]
- Rao, S.; Shirlal, K.G.; Varghese, R.V.; Govindaraja, K.R. Physical model studies on wave transmission of a submerged inclined plate breakwater. Ocean Eng. 2009, 36, 1199–1207. [Google Scholar] [CrossRef]
- Wang, G.Y.; Zhao, W.J.; Xiang, Z.Q.; Zhu, G.C. Experimental study on wave damping performance of porous inclined plate. Adv. Sci. Technol. Water Resour. 2017, 37, 22–26. [Google Scholar]
- Fan, Y.P.; Li, J.X.; Liu, S.X.; Liu, Y.; Sui, J.K. Study on wave dissipation performance of permeable breakwater of double porous inclined baffle. Port Waterw. Eng. 2020, 7, 7–12. (In Chinese) [Google Scholar]
- Tang, W.; Hu, J.; Chen, Y.Z.; Hu, Y.C. Analysis of structure and wave dissipation characteristics of a new type of perforated composite plate breakwater. Hydro-Sci. Eng. 2017, 5, 37–44. [Google Scholar]
- Guo, Y.C.; Mohapatra, S.C.; Guedes, S.C. Experimental performance of multi-layered membrane breakwaters. Ocean Eng. 2023, 281, 114716. [Google Scholar] [CrossRef]
- Guo, Y.C.; Mohapatra, S.C.; Guedes, S.C. An experimental study on the performance of combined membrane breakwaters against incident waves. Ocean Eng. 2023, 280, 114793. [Google Scholar] [CrossRef]
- Zhu, Y.L.; Li, Y.; Chen, D.C.; Tao, A.F. Numerical study on wave attenuation properties of piled baffle penetrated breakwater. Ocean Eng. 2015, 33, 53–62. (In Chinese) [Google Scholar]
- Yu, T.S.; Tang, J.H.; Meng, X.Y. Analysis of the hydrodynamic characteristics of an anti-deposition permeable breakwater. J. Harbin Eng. Univ. 2023, 44, 1295–1303. [Google Scholar]
- Yu, T.S.; Zhao, X.W.; Tang, J.H.; Zhang, Z.Y.; Chen, X.Y. Experimental and prediction study on wave run-up of anti-deposited permeable breakwater. J. Tianjin Univ. (Sci. Technol.) 2023, 56, 831–839. [Google Scholar]
- Sundar, V.; Subbarao, B.V.V. Hydrodynamic performance characteristics of quadrant front-face pile-supported breakwater. J. Waterw. Port Coast. Ocean. Eng. 2003, 129, 22–33. [Google Scholar] [CrossRef]
- Du, P.L.; Sun, Z.C.; Liang, S.X. Numerical study on wave dissipation performance of new type vertical permeable breakwater. Ocean Eng. 2021, 39, 12–20. (In Chinese) [Google Scholar]
- Wu, Y.Y.; Li, X.Y.; Wang, Q.; Zhu, X.S.; Guo, W.J.; Dong, D.L.; Lu, D.W. Numerical study on the influence factors of the wave attenuation performance of an arc-plate type open breakwater. Ocean Eng. 2019, 37, 59–67. (In Chinese) [Google Scholar]
- Wang, X.L.; Chen, Y.K.; Liu, Y.; Wang, X.G. Numerical and experimental study on wave dissipation characteristics of a new-type floating breakwater with anti-arc surface. J. Waterw. Harb. 2021, 42, 567–581. [Google Scholar]
- Cho, I.H.; Kim, M.H. Wave absorbing system using inclined perforated plates. Fluid Mech. 2008, 608, 1–20. [Google Scholar] [CrossRef]
- Gayen, R.; Mondal, A. Water wave interaction with two symmetric inclined permeable plates. Ocean Eng. 2016, 124, 180–191. [Google Scholar] [CrossRef]
- Cheng, Y.Z.; Lin, Z.Y.; Hu, G.; Lv, X. Numerical Simulation of the Hydrodynamic Characteristics of the Porous I-type Composite Breakwater. J. Mar. Sci. Appl. 2022, 21, 140–150. [Google Scholar] [CrossRef]
- JTJ/T 234-2001; Wave Model Test Regulation. China Communication Press: Beijing, China, 2001.
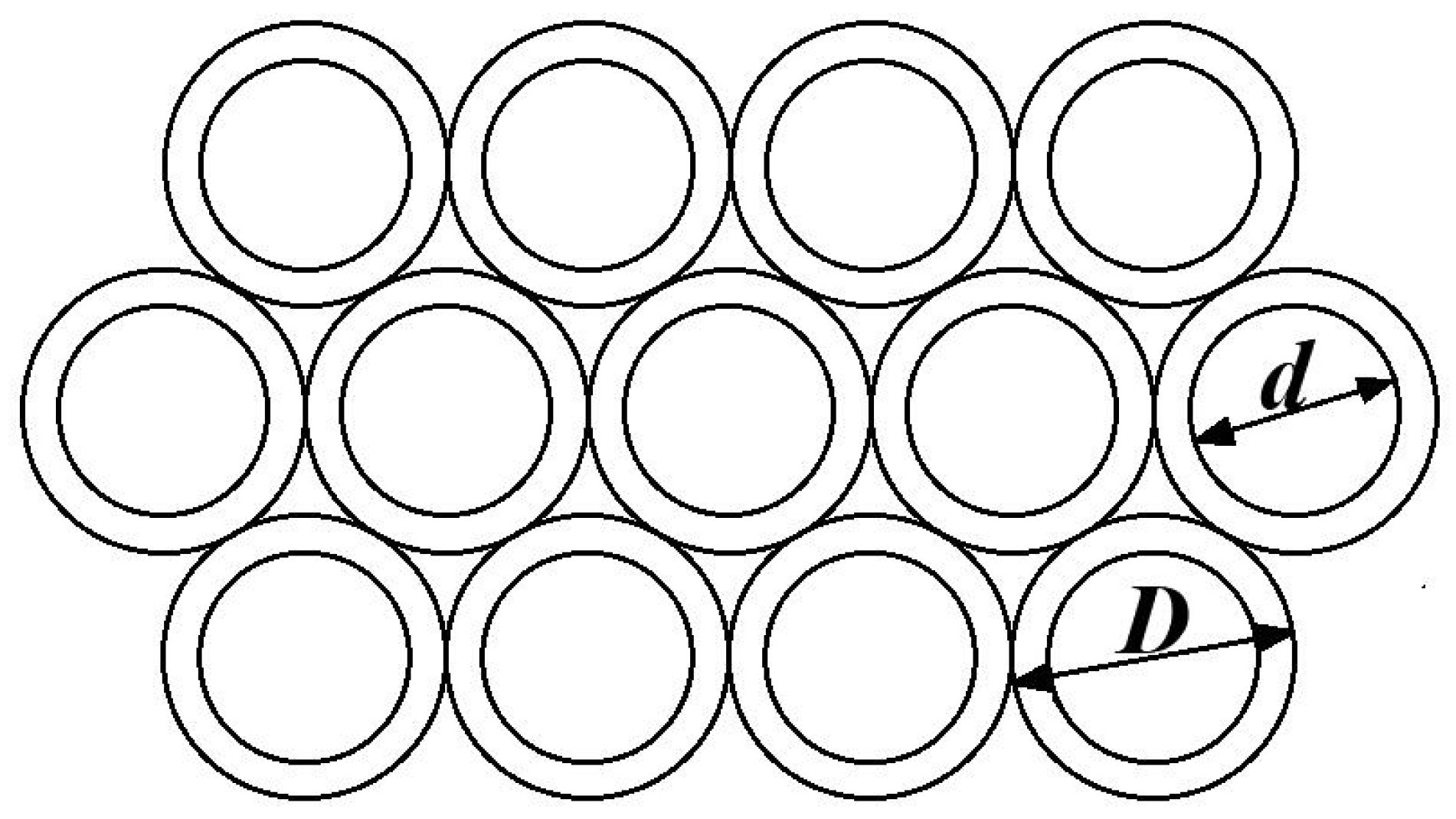
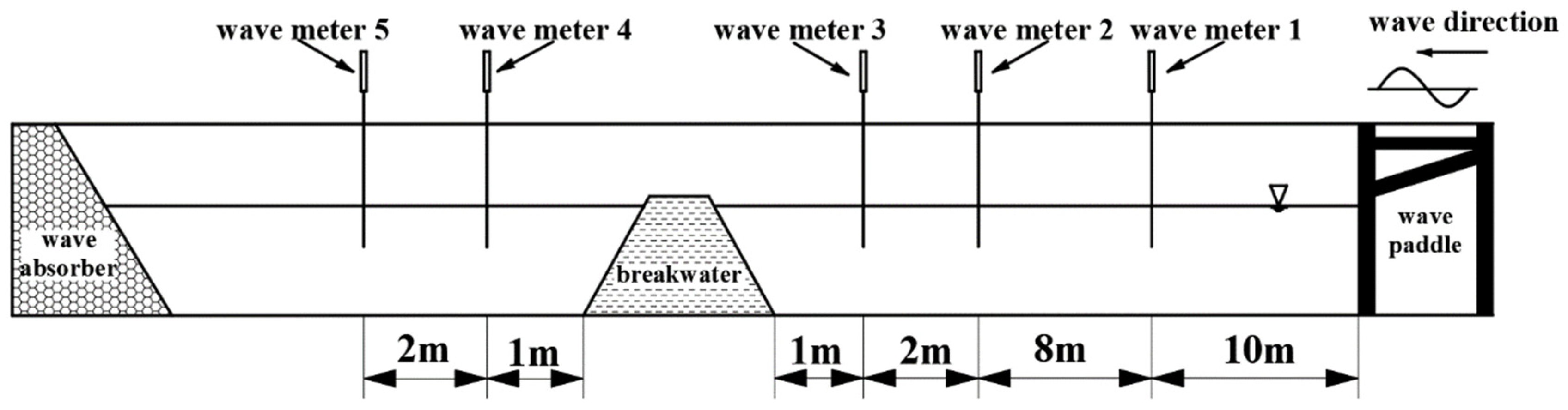

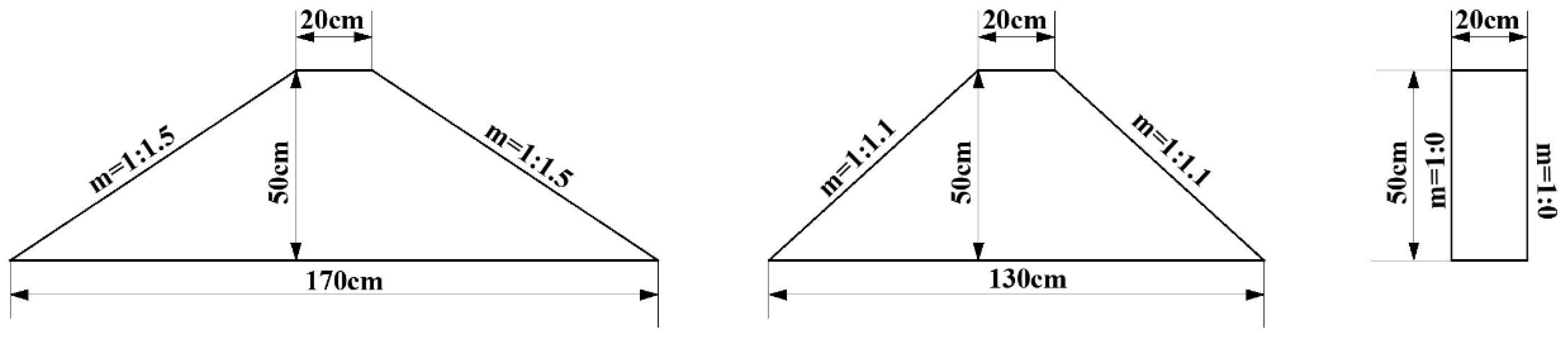


| Run | Breakwater Types | Slope in Front of the Breakwater | Slope Behind the Breakwater | Top Width of the Breakwater (cm) | Wave Height (cm) | Wave Period (s) |
|---|---|---|---|---|---|---|
| 1 | First type of breakwater | 1:1.5 | 1:1.5 | 20, 40, 60 | 4, 8 | 0.79, 0.95, 1.11, 1.25, 1.42, 1.74 |
| 2 | 1:1.5 | 1:1.5 | 60 | 6, 10, 12, 14 | ||
| 3 | 1:1.1 | 1:1.1 | 20, 40 | 8 | ||
| 4 | 1:0 | 1:0 | 20, 40 | 8 | ||
| 5 | 1:1.5 | 1:1.1 | 20 | 8 | ||
| 6 | 1:1.5 | 1:0 | 20 | 4, 8 | ||
| 7 | Second type of breakwater | 1:1.5 | 1:0 | 30 | 4 | |
| 8 | Third type of breakwater | 1:1.5 | 1:0 | 30 | 4 | |
| 9 | Double horizontal plate of breakwater | 1:0 | 1:0 | 40 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Yang, L.; Shi, B.; Na, J.; Guo, Y. Experimental Investigation on Wave Dissipation of Perforated Pipe Breakwater Under Regular Wave Conditions. J. Mar. Sci. Eng. 2024, 12, 2137. https://doi.org/10.3390/jmse12122137
Yang S, Yang L, Shi B, Na J, Guo Y. Experimental Investigation on Wave Dissipation of Perforated Pipe Breakwater Under Regular Wave Conditions. Journal of Marine Science and Engineering. 2024; 12(12):2137. https://doi.org/10.3390/jmse12122137
Chicago/Turabian StyleYang, Shaopeng, Lipeng Yang, Bing Shi, Jing Na, and Yakun Guo. 2024. "Experimental Investigation on Wave Dissipation of Perforated Pipe Breakwater Under Regular Wave Conditions" Journal of Marine Science and Engineering 12, no. 12: 2137. https://doi.org/10.3390/jmse12122137
APA StyleYang, S., Yang, L., Shi, B., Na, J., & Guo, Y. (2024). Experimental Investigation on Wave Dissipation of Perforated Pipe Breakwater Under Regular Wave Conditions. Journal of Marine Science and Engineering, 12(12), 2137. https://doi.org/10.3390/jmse12122137









