Vibration Characteristic Analysis of Sandwich Composite Plate Reinforced by Functionally Graded Carbon Nanotube-Reinforced Composite on Winkler/Pasternak Foundation
Abstract
1. Introduction
2. Theoretical Formulation
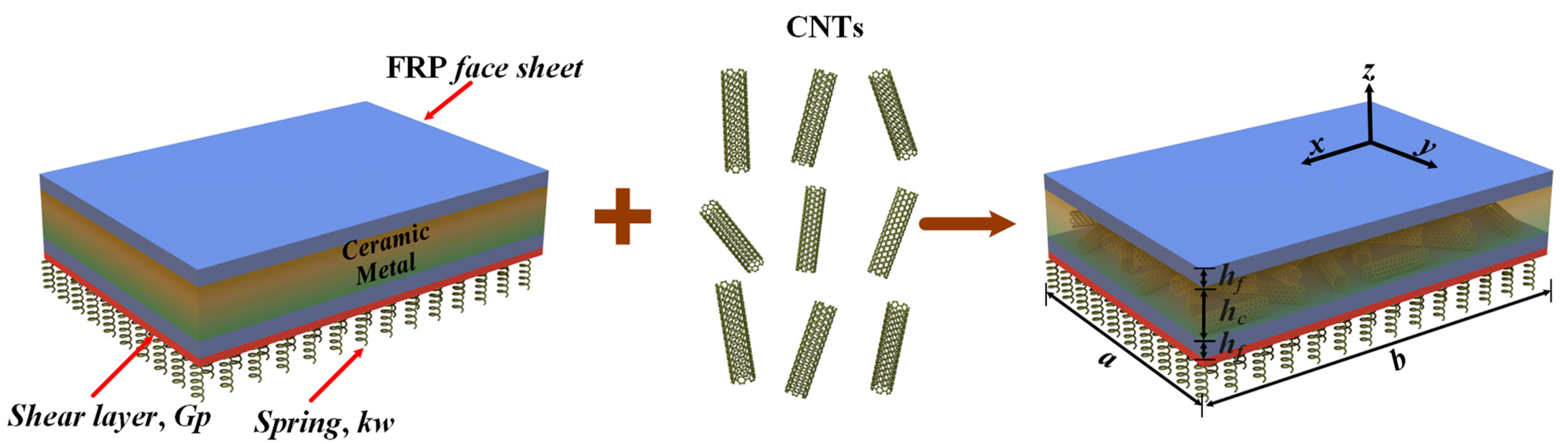
2.1. Description of the Model
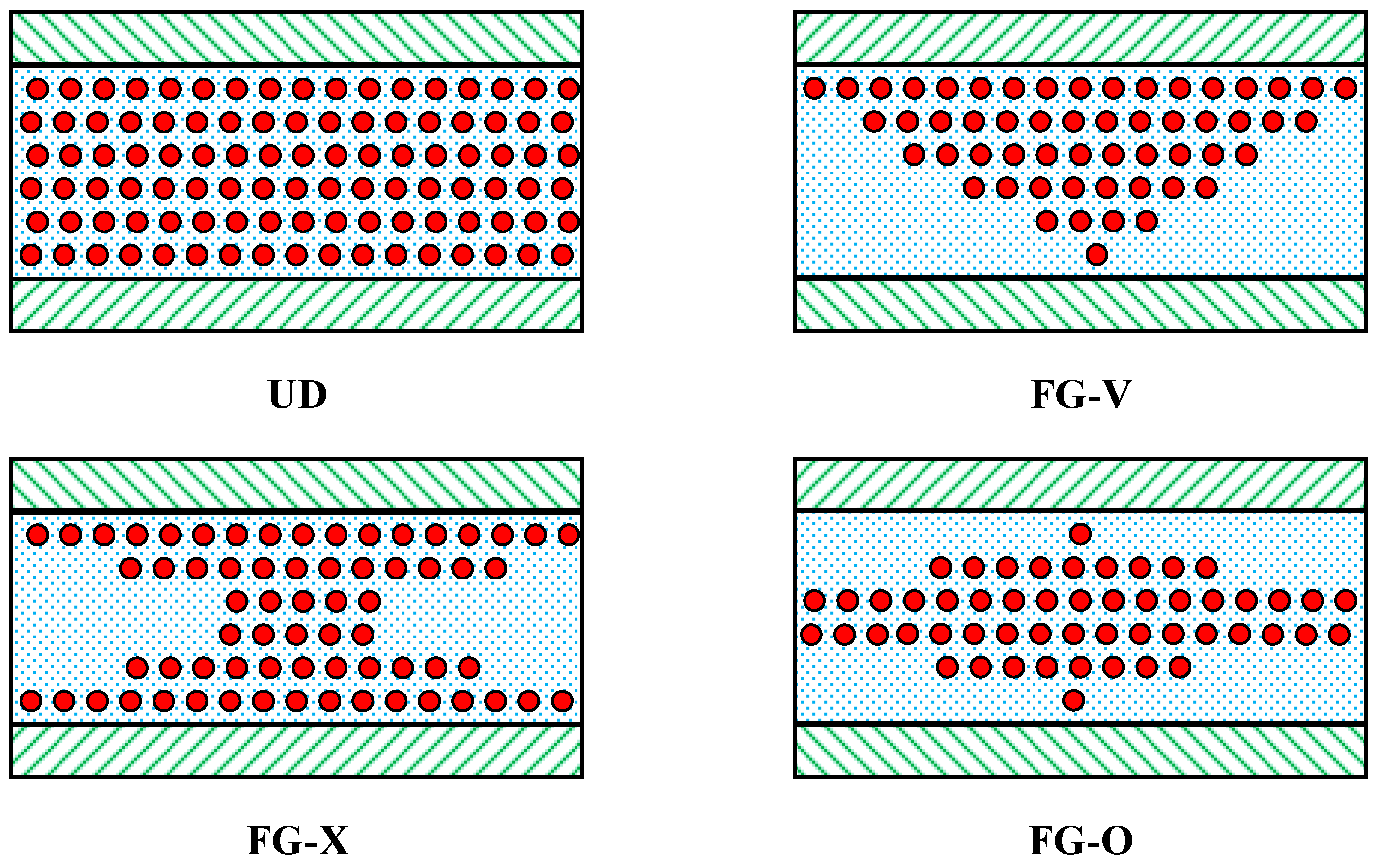
2.2. Material Properties of CNT-Reinforced Plates
2.3. HSDT-Based Models
2.4. Solutions for Simply Supported Sandwich Plates
3. Results and Discussion
3.1. Comparison and Validation
3.2. Parametric Studies
4. Conclusions
- (1)
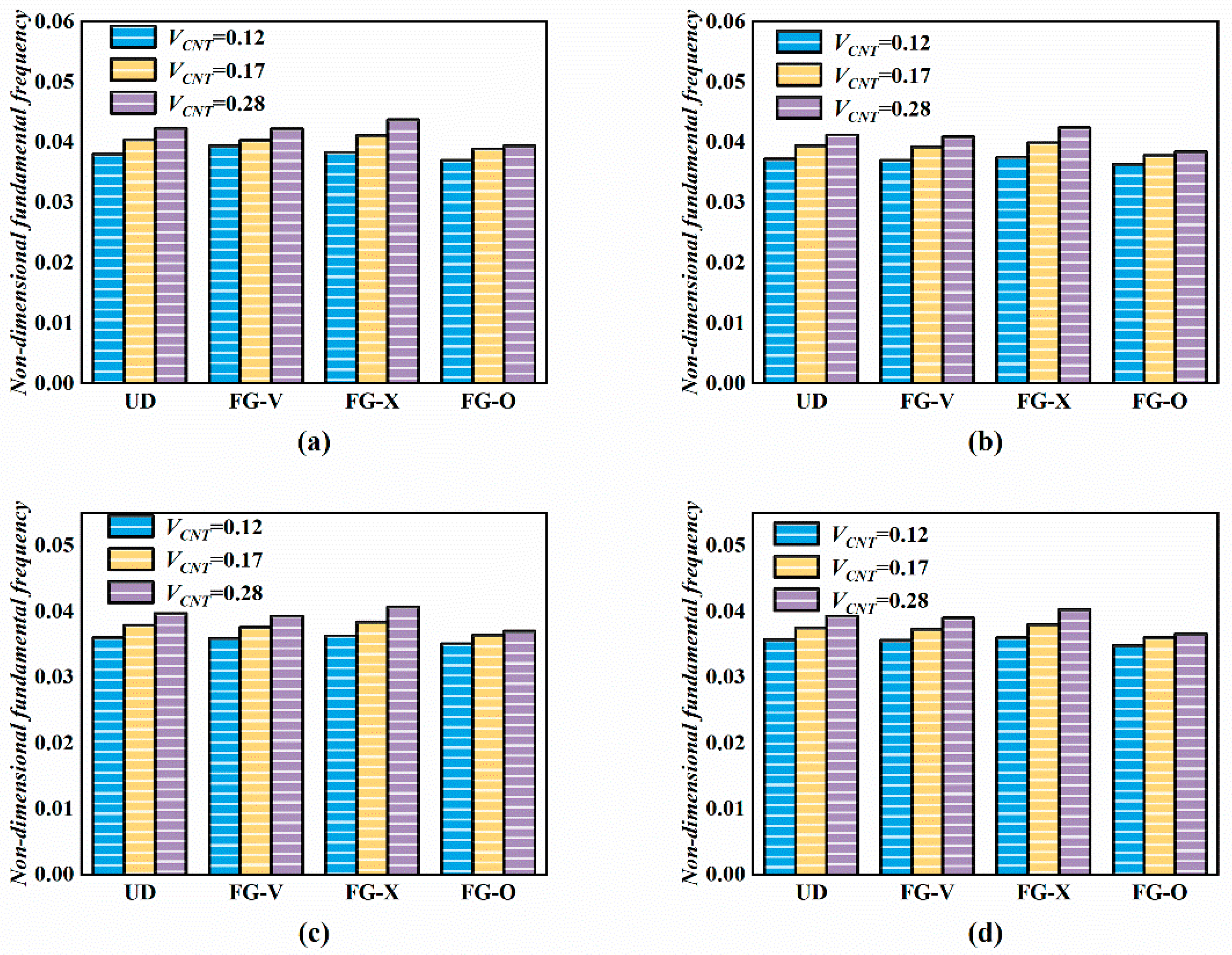
- As the volume fraction of ceramics and CNTs increases, it leads to an increase in the stiffness of the plate and produces larger dimensionless free vibration frequencies.
- (2)
- For different distributions of CNT (UD, FG-V, FG-X, FG-O), the FG-O distribution significantly reduces the dimensionless frequency, while the remaining three distributions have no significant effect on the dimensionless frequency.
- (3)
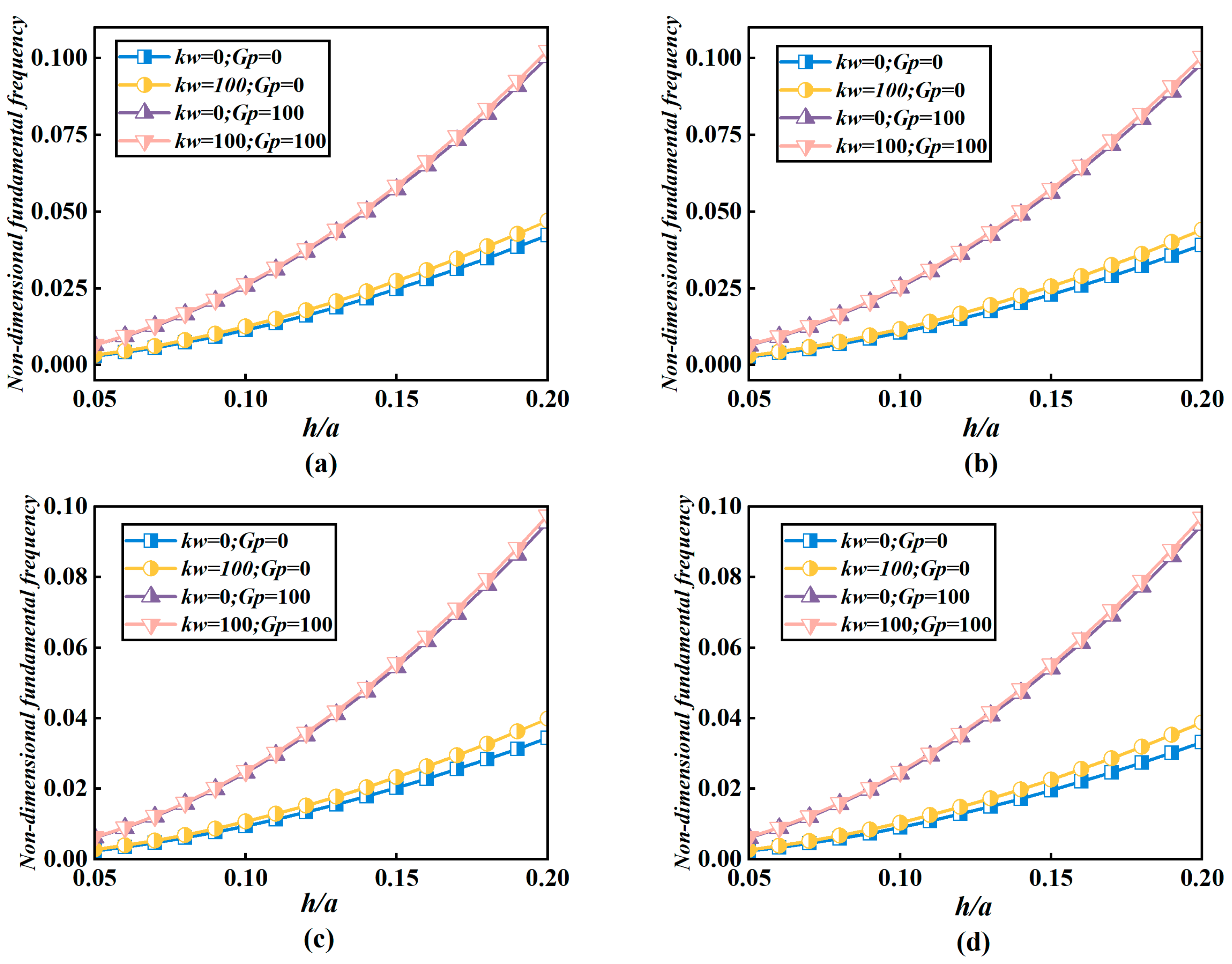
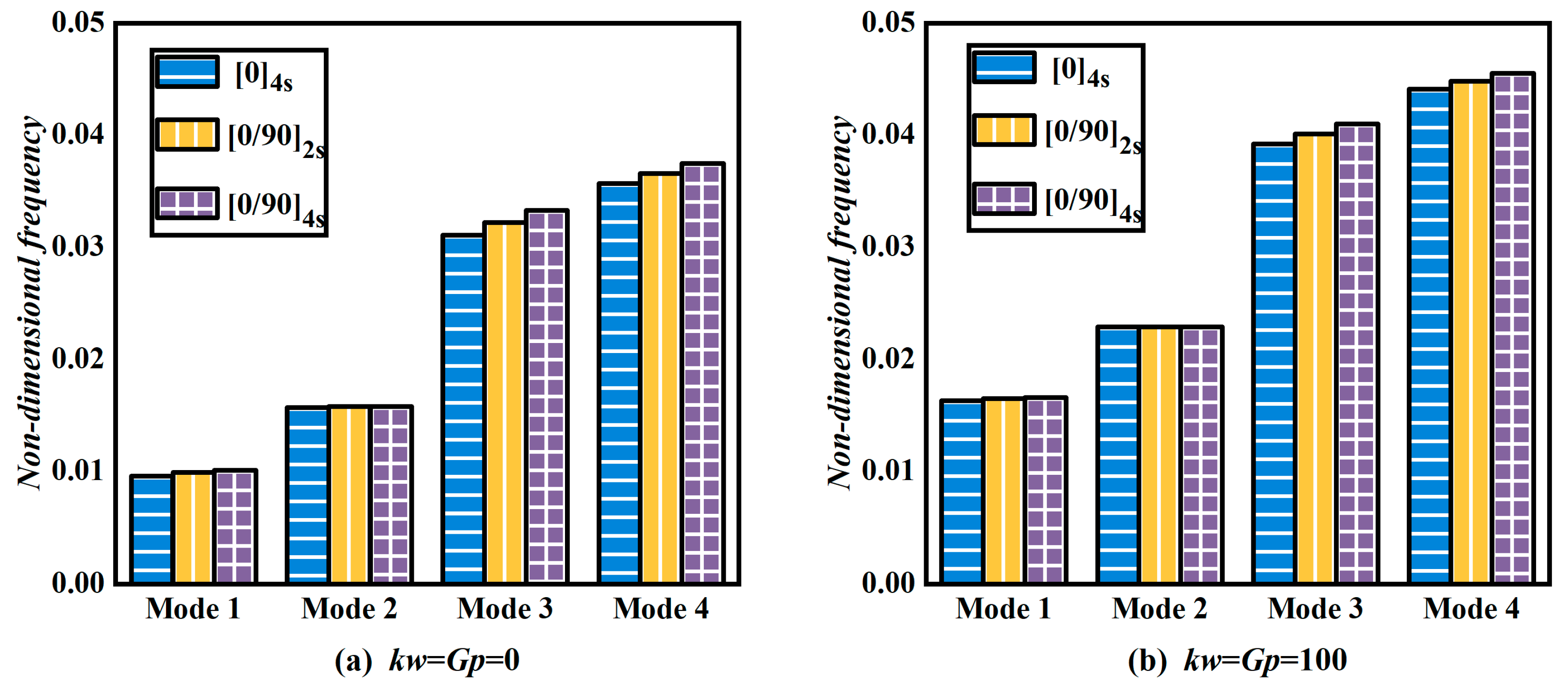
- Both the elastic foundation parameters kw and Gp have positively correlated effects on the free vibration behavior of the FRP_FG-CNTRC_FRP plate. However, Gp affects the dimensionless fundamental frequency to a much greater extent than kw.
- (4)
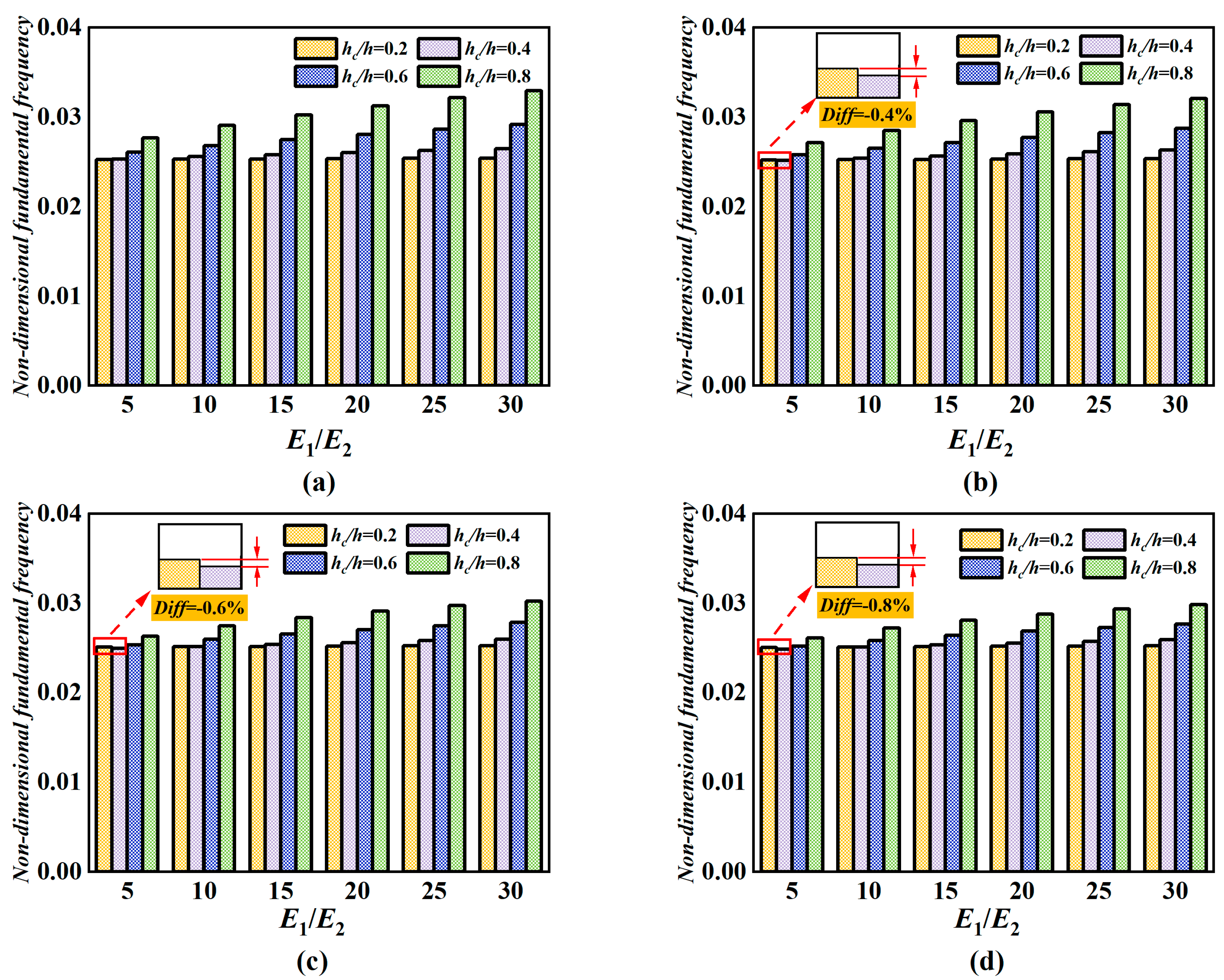
- It can be clearly observed that the dimensionless fundamental frequency of the sandwich composite plate increases significantly with the increase in hc/h, indicating that the FG-CNTRC core layer mentioned in this paper can enhance the stiffness of the plate well.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Li, M.; Yan, R.; Shen, W.; Qin, K.; Li, J.; Liu, K. Fatigue Characteristics of Sandwich Composite Joints in Ships. Ocean Eng. 2022, 254, 111254. [Google Scholar] [CrossRef]
- Li, M.; Liu, Z.; Yan, R.; Lu, J.; Guedes Soares, C. Experimental and Numerical Investigation on Composite Single-Lap Single-Bolt Sandwich Joints with Different Geometric Parameters. Mar. Struct. 2022, 85, 103259. [Google Scholar] [CrossRef]
- Wang, H.; Li, M.; Liu, X. A Non-Uniform Equivalent Model for Free Vibration Analysis of Sandwich Composite Panels with Trapezoidal Lattice Core. J. Vib. Eng. Technol. 2024, 12, 7009–7019. [Google Scholar] [CrossRef]
- Qiu, Y.; Shen, W.; Yan, R.; Li, X.; Ye, Z.; Li, M.; Liu, K.; Qin, K. An Improved Numerical Method for Calculating Mechanical Properties of Bi-Modulus Sandwich Composite Structures. Ocean Eng. 2022, 250, 110998. [Google Scholar] [CrossRef]
- Meng, S.; Zhong, R.; Wang, Q.; Shi, X.; Qin, B. Vibration Characteristic Analysis of Three-Dimensional Sandwich Cylindrical Shell Based on the Spectro-Geometric Method. Compos. Struct. 2024, 327, 117661. [Google Scholar] [CrossRef]
- Hu, S.; Wang, Q.; Zhong, R.; Qin, B. Random Thermal-Vibration Mechanisms of Sandwich Ventral Fin-Type Plate-Shell Systems with Porous Functionally Graded Core. Thin-Walled Struct. 2024, 204, 112333. [Google Scholar] [CrossRef]
- Chen, W.; Chen, C.; Zhang, Y.; Li, P.; Li, M.; Li, X. Study on the Deformation Mode and Energy Absorption Characteristics of Protective Honeycomb Sandwich Structures Based on the Combined Design of Lotus Root Nodes and Leaf Stem Veins. J. Mar. Sci. Eng. 2024, 12, 652. [Google Scholar] [CrossRef]
- Fan, Z.; Li, X.; Huang, T.; Chen, W. An Investigation of the Damage Mechanism of Multilayer Liquid-Containing Protective Structure under Combined Blast Wave and Fragment Loading. J. Mar. Sci. Eng. 2023, 11, 2327. [Google Scholar] [CrossRef]
- Corigliano, P.; Palomba, G.; Crupi, V.; Garbatov, Y. Stress-Strain Assessment of Honeycomb Sandwich Panel Subjected to Uniaxial Compressive Load. J. Mar. Sci. Eng. 2023, 11, 365. [Google Scholar] [CrossRef]
- Lin, H.; Han, C.; Yang, L.; Zhang, L.; Luan, H.; Han, P.; Xu, H.; Zhang, S. Numerical Investigation on Performance Optimization of Offshore Sandwich Blast Walls with Different Honeycomb Cores Subjected to Blast Loading. J. Mar. Sci. Eng. 2022, 10, 1743. [Google Scholar] [CrossRef]
- Chen, H.; Cai, Y.; Zhang, J.; Lv, X.; Li, X. Analytical Solutions for Out-of-Plane Response of Curved Beams Resting on an Elastic Foundation under a Random Moving Load. Eng. Struct. 2024, 318, 118753. [Google Scholar] [CrossRef]
- Rui, S.; Zhang, H.; Xu, H.; Zha, X.; Xu, M.; Shen, K. Seabed Structures and Foundations Related to Deep-Sea Resource Development: A Review Based on Design and Research. Deep Undergr. Sci. Eng. 2024, 3, 131–148. [Google Scholar] [CrossRef]
- Li, M.; Yan, R.; Guedes Soares, C. Free Vibration of Advanced Composite Plates Using a New Higher Order Shear Deformation Theory. Eur. J. Mech.-A/Solids 2021, 88, 104236. [Google Scholar] [CrossRef]
- Li, M.; Yan, R.; Xu, L.; Guedes Soares, C. A General Framework of Higher-Order Shear Deformation Theories with a Novel Unified Plate Model for Composite Laminated and FGM Plates. Compos. Struct. 2021, 261, 113560. [Google Scholar] [CrossRef]
- Li, M.; Guedes Soares, C.; Yan, R. Free Vibration Analysis of FGM Plates on Winkler/Pasternak/Kerr Foundation by Using a Simple Quasi-3D HSDT. Compos. Struct. 2021, 264, 113643. [Google Scholar] [CrossRef]
- Li, M.; Guedes Soares, C.; Yan, R. A Novel Shear Deformation Theory for Static Analysis of Functionally Graded Plates. Compos. Struct. 2020, 250, 112559. [Google Scholar] [CrossRef]
- Fotouhi, S.; Fotouhi, M.; Pavlovic, A.; Djordjevic, N. Investigating the Pre-Damaged PZT Sensors under Impact Traction. J. Mar. Sci. Eng. 2018, 6, 142. [Google Scholar] [CrossRef]
- Strozzi, M.; Giacomobono, R.; Rubini, R.; Cocconcelli, M. Preliminary Orthotropic Elastic Model for the Study of Natural Frequencies and Mode Shapes of a 3D Printed Onyx Thin Circular Cylindrical Shell. Int. J. Mech. Control 2020, 21, 51–56. [Google Scholar]
- Arani, H.K.; Shariyat, M. Nonlinear 2D-DQ Volume-Preservative Global–Local Dynamic Analysis of Composite Sandwich Plates with Soft Hyperelastic Cores and Viscoelastic Winkler-Pasternak Foundations. Structures 2023, 55, 727–746. [Google Scholar] [CrossRef]
- Kumar, P.; Harsha, S.P. Static Analysis of Porous Core Functionally Graded Piezoelectric (PCFGP) Sandwich Plate Resting on the Winkler/Pasternak/Kerr Foundation under Thermo-Electric Effect. Mater. Today Commun. 2022, 32, 103929. [Google Scholar] [CrossRef]
- Hadji, L.; Avcar, M.; Zouatnia, N. Natural Frequency Analysis of Imperfect FG Sandwich Plates Resting on Winkler-Pasternak Foundation. Polym. Mediterr. Fiber Int. 2022, 53, 153–160. [Google Scholar] [CrossRef]
- Li, Q.; Wu, D.; Chen, X.; Liu, L.; Yu, Y.; Gao, W. Nonlinear Vibration and Dynamic Buckling Analyses of Sandwich Functionally Graded Porous Plate with Graphene Platelet Reinforcement Resting on Winkler–Pasternak Elastic Foundation. Int. J. Mech. Sci. 2018, 148, 596–610. [Google Scholar] [CrossRef]
- El-Shahrany, H.D.; Zenkour, A.M. Control of Dynamic Response of the Functionally Graded Smart Sandwich Beam Coupled Variable Kelvin–Voigt–Pasternak’s Model. Ain Shams Eng. J. 2024, 15, 102476. [Google Scholar] [CrossRef]
- Selim, B.A.; Liu, Z. Impact Analysis of Functionally-Graded Graphene Nanoplatelets-Reinforced Composite Plates Laying on Winkler-Pasternak Elastic Foundations Applying a Meshless Approach. Eng. Struct. 2021, 241, 112453. [Google Scholar] [CrossRef]
- Zaitoun, M.W.; Chikh, A.; Tounsi, A.; Al-Osta, M.A.; Sharif, A.; Al-Dulaijan, S.U.; Al-Zahrani, M.M. Influence of the Visco-Pasternak Foundation Parameters on the Buckling Behavior of a Sandwich Functional Graded Ceramic–Metal Plate in a Hygrothermal Environment. Thin-Walled Struct. 2022, 170, 108549. [Google Scholar] [CrossRef]
- Zenkour, A.M.; El-Shahrany, H.D. Hygrothermal Effect on Vibration of Magnetostrictive Viscoelastic Sandwich Plates Supported by Pasternak’s Foundations. Thin-Walled Struct. 2020, 157, 107007. [Google Scholar] [CrossRef]
- Singh, S.J.; Harsha, S.P. Nonlinear Dynamic Analysis of Sandwich S-FGM Plate Resting on Pasternak Foundation under Thermal Environment. Eur. J. Mech.-A/Solids 2019, 76, 155–179. [Google Scholar] [CrossRef]
- Shahsavari, D.; Shahsavari, M.; Li, L.; Karami, B. A Novel Quasi-3D Hyperbolic Theory for Free Vibration of FG Plates with Porosities Resting on Winkler/Pasternak/Kerr Foundation. Aerosp. Sci. Technol. 2018, 72, 134–149. [Google Scholar] [CrossRef]
- Paik, J.K.; Seo, J.K. Nonlinear Finite Element Method Models for Ultimate Strength Analysis of Steel Stiffened-Plate Structures under Combined Biaxial Compression and Lateral Pressure Actions—Part II: Stiffened Panels. Thin-Walled Struct. 2009, 47, 998–1007. [Google Scholar] [CrossRef]
- Putranto, T.; Kõrgesaar, M.; Jelovica, J.; Tabri, K.; Naar, H. Ultimate Strength Assessment of Stiffened Panel under Uni-Axial Compression with Non-Linear Equivalent Single Layer Approach. Mar. Struct. 2021, 78, 103004. [Google Scholar] [CrossRef]
- Gavali, V.C.; Kubade, P.R.; Kulkarni, H.B. Mechanical and Thermo-Mechanical Properties of Carbon Fiber Reinforced Thermoplastic Composite Fabricated Using Fused Deposition Modeling Method. Meter. Proc. 2020, 22, 1786–1795. [Google Scholar] [CrossRef]
- He, D.; Wang, Q.; Zhong, R.; Qin, B. A Unified Spectral-Geometric Model of FGM Double Conical/Cylindrical/Spherical Shell Coupled with Annular Plates. Comput. Math. Appl. 2023, 143, 348–371. [Google Scholar] [CrossRef]
- He, D.; Wang, Q.; Zhong, R.; Qin, B. Vibration Analysis of Functionally Graded Material (FGM) Double Layered Floating Raft Structure by the Spectro-Geometric Method. Structures 2023, 48, 533–550. [Google Scholar] [CrossRef]
- Zhang, S.; Bu, R.; Zhang, Z.; Gao, L.; Li, Z. A Systematic Model for the Mechanical Behavior of Thin-Walled Composite FGM Pipelines Subjected to Strike-Slip Faults in Geohazard Area. Thin-Walled Struct. 2024, 202, 112135. [Google Scholar] [CrossRef]
- Penna, R.; Lovisi, G.; Feo, L. Dynamic Response of Multilayered Polymer Functionally Graded Carbon Nanotube Reinforced Composite (FG-CNTRC) Nano-Beams in Hygro-Thermal Environment. Polymers 2021, 13, 2340. [Google Scholar] [CrossRef]
- Daikh, A.A.; Houari, M.S.A.; Karami, B.; Eltaher, M.A.; Dimitri, R.; Tornabene, F. Buckling Analysis of CNTRC Curved Sandwich Nanobeams in Thermal Environment. Appl. Sci. 2021, 11, 3250. [Google Scholar] [CrossRef]
- Lovisi, G. Application of the Surface Stress-Driven Nonlocal Theory of Elasticity for the Study of the Bending Response of FG Cracked Nanobeams. Compos. Struct. 2023, 324, 117549. [Google Scholar] [CrossRef]
- Miao, X.; Li, C.; Jiang, Y. Free Vibration Analysis of Metal-Ceramic Matrix Composite Laminated Cylindrical Shell Reinforced by CNTs. Compos. Struct. 2021, 260, 113262. [Google Scholar] [CrossRef]
- Feng, Z.; Yang, X.; Keshavarzpour, H.; Ghasemi, A. Free Vibration Analysis of Hybrid CNT/GPL-Reinforced Porous Composite Plates under Fluid-Loading. Aerosp. Sci. Technol. 2024, 148, 109116. [Google Scholar] [CrossRef]
- Wang, J.F.; Cao, S.H.; Zhang, W. Thermal Vibration and Buckling Analysis of Functionally Graded Carbon Nanotube Reinforced Composite Quadrilateral Plate. Eur. J. Mech.-A/Solids 2021, 85, 104105. [Google Scholar] [CrossRef]
- Qin, B.; Zhong, R.; Wang, T.; Wang, Q.; Xu, Y.; Hu, Z. A Unified Fourier Series Solution for Vibration Analysis of FG-CNTRC Cylindrical, Conical Shells and Annular Plates with Arbitrary Boundary Conditions. Compos. Struct. 2020, 232, 111549. [Google Scholar] [CrossRef]
- Zhong, R.; Wang, Q.; Tang, J.; Shuai, C.; Qin, B. Vibration Analysis of Functionally Graded Carbon Nanotube Reinforced Composites (FG-CNTRC) Circular, Annular and Sector Plates. Compos. Struct. 2018, 194, 49–67. [Google Scholar] [CrossRef]
- Maoudj, S.; Tiberkak, R.; Lazar, M.E.; Ezzraimi, M.; Bachene, M.; Rechak, S. Free Vibration Analysis of Cracked Composite Plates Reinforced with CNTs Using Extended Finite Element Method (XFEM). Mech. Adv. Mater. Struct. 2023. [Google Scholar] [CrossRef]
- Ghadirian, H.; Mohebpour, S.; Malekzadeh, P.; Daneshmand, F. Nonlinear Free Vibrations and Stability Analysis of FG-CNTRC Pipes Conveying Fluid Based on Timoshenko Model. Compos. Struct. 2022, 292, 115637. [Google Scholar] [CrossRef]
- TAYEB, T.S.; Amir, M.; Kim, S.-W.; Choi, D. An Analytical Modelling of Free Vibration in Porous FG-CNTRC Plate Resting on Elastic Foundations. Mater. Today Commun. 2024, 40, 109925. [Google Scholar] [CrossRef]
- Cho, J.R. Nonlinear Bending Analysis of FG-CNTRC Plate Resting on Elastic Foundation by Natural Element Method. Eng. Anal. Bound. Elem. 2022, 141, 65–74. [Google Scholar] [CrossRef]
- Duong, V.Q.; Tran, N.D.; Luat, D.T.; Thom, D.V. Static Analysis and Boundary Effect of FG-CNTRC Cylindrical Shells with Various Boundary Conditions Using Quasi-3D Shear and Normal Deformations Theory. Structures 2022, 44, 828–850. [Google Scholar] [CrossRef]
- Duc, N.D.; Minh, P.P. Free Vibration Analysis of Cracked FG CNTRC Plates Using Phase Field Theory. Aerosp. Sci. Technol. 2021, 112, 106654. [Google Scholar] [CrossRef]
- Taheri, M.H.; Memarzadeh, P. Effect of Crack on Shear Buckling of CNTRC Plates. Int. J. Mech. Sci. 2022, 229, 107519. [Google Scholar] [CrossRef]
- Zeighami, V.; Jafari, M. Thermal Stress Analysis of Perforated Unsymmetric FG-CNTRC Plate Using a General Analytical Solution. Thin-Walled Struct. 2022, 173, 108956. [Google Scholar] [CrossRef]
- Cong, P.H.; Trung, V.D.; Khoa, N.D.; Duc, N.D. Vibration and Nonlinear Dynamic Response of Temperature-Dependent FG-CNTRC Laminated Double Curved Shallow Shell with Positive and Negative Poisson’s Ratio. Thin-Walled Struct. 2022, 171, 108713. [Google Scholar] [CrossRef]
- Watts, G.; Kumar, R.; Singh, S.; Sengar, V.; Reddy, G.R.; Patel, S.N. Postbuckling and Postbuckled Vibration Behaviour of Imperfect Trapezoidal Sandwich Plates with FG-CNTRC Face Sheets under Nonuniform Loadings. Aerosp. Sci. Technol. 2022, 127, 107716. [Google Scholar] [CrossRef]
- Lin, B.; Zhu, B.; Chen, B.; Han, J.; Li, Y. Nonlinear Primary Resonance Behaviors of Rotating FG-CNTRC Beams with Geometric Imperfections. Aerosp. Sci. Technol. 2022, 121, 107333. [Google Scholar] [CrossRef]
- Liu, J.; Ke, L.-L.; Wang, Y.-S.; Yang, J.; Alam, F. Thermoelastic Frictional Contact of Functionally Graded Materials with Arbitrarily Varying Properties. Int. J. Mech. Sci. 2012, 63, 86–98. [Google Scholar] [CrossRef]
- Wang, Z.-X.; Shen, H.-S. Nonlinear Vibration of Nanotube-Reinforced Composite Plates in Thermal Environments. Comput. Mater. Sci. 2011, 50, 2319–2330. [Google Scholar] [CrossRef]
- Wang, Y.; Tham, L.; Cheung, Y. Beams and Plates on Elastic Foundations: A Review. Prog. Struct. Eng. Mater. 2005, 7, 174–182. [Google Scholar] [CrossRef]
- Avramidis, I.E.; Morfidis, K. Bending of Beams on Three-Parameter Elastic Foundation. Int. J. Solids Struct. 2006, 43, 357–375. [Google Scholar] [CrossRef]
- Karamanli, A.; Vo, T.P.; Eltaher, M.A. Comprehensive Analysis of Bio-Inspired Laminated Composites Plates Using a Quasi-3D Theory and Higher Order FE Models. Thin-Walled Struct. 2024, 198, 111735. [Google Scholar] [CrossRef]
- Hasani Baferani, A.; Saidi, A.R.; Ehteshami, H. Accurate Solution for Free Vibration Analysis of Functionally Graded Thick Rectangular Plates Resting on Elastic Foundation. Compos. Struct. 2011, 93, 1842–1853. [Google Scholar] [CrossRef]
- Selim, B.A.; Zhang, L.W.; Liew, K.M. Vibration Analysis of CNT Reinforced Functionally Graded Composite Plates in a Thermal Environment Based on Reddy’s Higher-Order Shear Deformation Theory. Compos. Struct. 2016, 156, 276–290. [Google Scholar] [CrossRef]
- Pasha Zanussi, V.; Shahverdi, H.; Khalafi, V.; Navardi, M.M. Nonlinear Flutter Analysis of Quadrilateral Plates Consisting of Functionally Graded Carbon Nanotubes Reinforced Composites Using Isogeometric Analysis. Thin-Walled Struct. 2024, 198, 111701. [Google Scholar] [CrossRef]
- Lee, S.; Reddy, J. Vibration Suppression of Laminated Shell Structures Investigated Using Higher Order Shear Deformation Theory. SMART Mater. Struct. 2004, 13, 1176–1194. [Google Scholar] [CrossRef]





| VCNT | η1 | η2 | η3 |
|---|---|---|---|
| 0.12 | 0.137 | 1.022 | 0.715 |
| 0.17 | 0.142 | 1.626 | 1.138 |
| 0.28 | 0.141 | 1.585 | 1.109 |
| Material | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | |
|---|---|---|---|---|---|---|---|
| FRP | 40 | 1 | 0.25 | 0.6 | 0.6 | 0.6 | 0.5 |
| Material | Eb (GPa) | ρb (kg/m3) | Et (GPa) | ρt (kg/m3) | ||
|---|---|---|---|---|---|---|
| FGM | 70 | 2702 | 210 | 2400 | 0.3 | 0.3 |
| Material | (GPa) | (GPa) | (GPa) | (kg/m3) | VCNT | |
|---|---|---|---|---|---|---|
| CNT | 5.6466 | 70.8 | 1.9445 | 0.175 | 1150 | 0.12 |
| kw | Gp | h/a | Model | p | ||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 1 | 2 | 5 | ||||
| 0 | 0 | 0.1 | TSDT [59] | 0.1134 | 0.0975 | 0.0891 | 0.0819 | 0.0767 |
| Quasi-3D [28] | 0.1135 | 0.0970 | 0.0882 | 0.0806 | 0.0755 | |||
| Li et al. [15] | 0.1135 | 0.0970 | 0.0882 | 0.0806 | 0.0756 | |||
| Present | 0.1134 | 0.0963 | 0.0868 | 0.0788 | 0.0740 | |||
| 0.2 | TSDT [59] | 0.4154 | 0.3606 | 0.3299 | 0.30160 | 0.2765 | ||
| Quasi-3D [28] | 0.4168 | 0.3586 | 0.3260 | 0.29610 | 0.2722 | |||
| Li et al. [15] | 0.4168 | 0.3586 | 0.3260 | 0.29610 | 0.2723 | |||
| Present | 0.4150 | 0.3551 | 0.3205 | 0.28920 | 0.2667 | |||
| 100 | 0 | 0.1 | TSDT [59] | 0.1162 | 0.1012 | 0.0933 | 0.0867 | 0.0821 |
| Quasi-3D [28] | 0.1163 | 0.1006 | 0.0923 | 0.0853 | 0.0809 | |||
| Li et al. [15] | 0.1163 | 0.1006 | 0.0923 | 0.0853 | 0.0809 | |||
| Present | 0.1161 | 0.0999 | 0.0910 | 0.0836 | 0.0795 | |||
| 0.2 | TSDT [59] | 0.4273 | 0.3758 | 0.3476 | 0.3219 | 0.2999 | ||
| Quasi-3D [28] | 0.4284 | 0.3734 | 0.3431 | 0.3159 | 0.2950 | |||
| Li et al. [15] | 0.4281 | 0.373 | 0.3427 | 0.3154 | 0.2946 | |||
| Present | 0.4269 | 0.3702 | 0.3381 | 0.3097 | 0.2901 | |||
| 100 | 100 | 0.1 | TSDT [59] | 0.1619 | 0.1563 | 0.1542 | 0.1535 | 0.1543 |
| Quasi-3D [28] | 0.1616 | 0.1551 | 0.1525 | 0.1512 | 0.1521 | |||
| Li et al. [15] | 0.1613 | 0.1548 | 0.1521 | 0.1509 | 0.1517 | |||
| Present | 0.1617 | 0.1549 | 0.1519 | 0.1505 | 0.1515 | |||
| 0.2 | TSDT [59] | 0.6162 | 0.6026 | 0.5978 | 0.5970 | 0.5993 | ||
| Quasi-3D [28] | 0.6137 | 0.5940 | 0.5856 | 0.5815 | 0.5843 | |||
| Li et al. [15] | 0.6085 | 0.5878 | 0.5792 | 0.5750 | 0.5720 | |||
| Present | 0.6156 | 0.5950 | 0.5852 | 0.5810 | 0.5834 | |||
| Type | a/ℎ | Mode | Method | ||
|---|---|---|---|---|---|
| TSDT [60] | RPT [61] | Present | |||
| FG-V | 10 | (1,1) | 12.461 | 12.755 | 12.4138 |
| (1,2) | 17.077 | 17.128 | 16.9426 | ||
| (2,1) | 27.401 | 27.158 | 31.2429 | ||
| (2,2) | 31.943 | 33.227 | 33.558 | ||
| 20 | (1,1) | 15.09 | 15.127 | 15.040 | |
| (1,2) | 19.883 | 19.606 | 19.715 | ||
| (2,1) | 38.936 | 38.855 | 47.316 | ||
| (2,2) | 47.858 | 48.298 | 49.655 | ||
| 50 | (1,1) | 16.230 | 16.093 | 16.1644 | |
| (1,2) | 21.114 | 20.683 | 20.9135 | ||
| (2,1) | 60.094 | 59.872 | 59.4529 | ||
| (2,2) | 62.682 | 62.118 | 61.9633 | ||
| FG-O | 10 | (1,1) | 11.319 | 11.773 | 9.568 |
| (1,2) | 16.137 | 16.469 | 14.906 | ||
| (2,1) | 26.555 | 26.827 | 26.553 | ||
| (2,2) | 29.408 | 31.858 | 29.507 | ||
| 20 | (1,1) | 13.405 | 13.50 | 10.567 | |
| (1,2) | 18.398 | 18.371 | 16.309 | ||
| (2,1) | 38.938 | 38.855 | 34.945 | ||
| (2,2) | 42.997 | 44.759 | 38.272 | ||
| 50 | (1,1) | 14.265 | 14.153 | 10.914 | |
| (1,2) | 19.338 | 19.154 | 16.803 | ||
| (2,1) | 52.653 | 52.616 | 39.268 | ||
| (2,2) | 55.451 | 55.123 | 42.846 | ||
| FG-X | 10 | (1,1) | 14.683 | 15.254 | 14.586 |
| (1,2) | 18.687 | 18.825 | 18.551 | ||
| (2,1) | 28.524 | 28.004 | 33.447 | ||
| (2,2) | 34.442 | 35.980 | 35.488 | ||
| 20 | (1,1) | 19.94 | 20.241 | 19.866 | |
| (1,2) | 23.771 | 23.573 | 23.611 | ||
| (2,1) | 38.938 | 38.855 | 56.591 | ||
| (2,2) | 52.336 | 49.581 | 58.344 | ||
| 50 | (1,1) | 22.954 | 22.880 | 22.873 | |
| (1,2) | 26.741 | 26.183 | 26.547 | ||
| (2,1) | 83.153 | 83.604 | 82.218 | ||
| (2,2) | 84.956 | 83.703 | 83.992 | ||
| VCNT | Method | Mode | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Diff. (%) | ||
| 0.12 | ABAQUS | 668.7 | 1552.9 | 1698.1 | 2387.5 | 2890.9 | 3188.7 | 3552.7 | 3725.4 | – |
| Present—Reddy [62] | 669.0 | 1554.0 | 1700.0 | 2391.9 | 2895.3 | 3195.9 | 3560.4 | 3734.8 | 0.16 | |
| Present | 668.7 | 1555.0 | 1701.6 | 2391.8 | 2899.6 | 3201.1 | 3561.8 | 3737.1 | 0.22 | |
| 0.17 | ABAQUS | 835.5 | 2012.6 | 2020.8 | 3004.6 | 3765.2 | 3781.6 | 4577.8 | 4589.9 | – |
| Present—Reddy [62] | 834.8 | 2012.6 | 2018.8 | 3006.1 | 3767.9 | 3777.6 | 4582.5 | 4590.2 | 0.06 | |
| Present | 832.8 | 2011.6 | 2017.6 | 3001.4 | 3771.0 | 3780.6 | 4580.0 | 4587.5 | 0.11 | |
| 0.28 | ABAQUS | 922.9 | 2193.7 | 2269.2 | 3308.1 | 4095.9 | 4254.8 | 5001.3 | 5089.4 | – |
| Present—Reddy [62] | 916.3 | 2178.6 | 2256.7 | 3291.4 | 4067.0 | 4235.7 | 4973.2 | 5067.9 | 0.57 | |
| Present | 914.7 | 2181.3 | 2260.6 | 3290.8 | 4081.4 | 4252.5 | 4979.5 | 5076.5 | 0.43 | |
| (kw,Gp) | VCNT | a/b | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.2 | 1.4 | 1.6 | 1.8 | 2 | 3 | 4 | |||
| (0,0) | 0.12 | UD | 0.0158 | 0.0133 | 0.0118 | 0.0109 | 0.0103 | 0.0099 | 0.0089 | 0.0086 |
| FG-V | 0.0155 | 0.0131 | 0.0117 | 0.0108 | 0.0103 | 0.0099 | 0.0089 | 0.0086 | ||
| FG-X | 0.0164 | 0.0138 | 0.0122 | 0.0112 | 0.0106 | 0.0101 | 0.0092 | 0.0088 | ||
| FG-O | 0.0145 | 0.0124 | 0.0111 | 0.0103 | 0.0097 | 0.0094 | 0.0085 | 0.0082 | ||
| 0.17 | UD | 0.0196 | 0.0168 | 0.0151 | 0.0140 | 0.0133 | 0.0128 | 0.0116 | 0.0112 | |
| FG-V | 0.0193 | 0.0166 | 0.0150 | 0.0140 | 0.0133 | 0.0129 | 0.0117 | 0.0113 | ||
| FG-X | 0.0207 | 0.0176 | 0.0149 | 0.0147 | 0.0139 | 0.0134 | 0.0121 | 0.0117 | ||
| FG-O | 0.0177 | 0.0153 | 0.0139 | 0.0130 | 0.0124 | 0.0119 | 0.0109 | 0.0105 | ||
| 0.28 | UD | 0.0216 | 0.0183 | 0.0164 | 0.0152 | 0.0144 | 0.0138 | 0.0125 | 0.0121 | |
| FG-V | 0.0212 | 0.0182 | 0.0164 | 0.0153 | 0.0146 | 0.014 | 0.0128 | 0.0123 | ||
| FG-X | 0.0237 | 0.0201 | 0.018 | 0.0167 | 0.0158 | 0.0152 | 0.0138 | 0.0133 | ||
| FG-O | 0.0182 | 0.0157 | 0.0142 | 0.0132 | 0.0125 | 0.0121 | 0.0110 | 0.0107 | ||
| (100,100) | 0.12 | UD | 0.0372 | 0.029 | 0.0239 | 0.0206 | 0.0182 | 0.0165 | 0.0122 | 0.0105 |
| FG-V | 0.0370 | 0.0289 | 0.0239 | 0.0205 | 0.0182 | 0.0164 | 0.0122 | 0.0105 | ||
| FG-X | 0.0375 | 0.0292 | 0.0241 | 0.0208 | 0.0184 | 0.0166 | 0.0123 | 0.0107 | ||
| FG-O | 0.0363 | 0.0283 | 0.0233 | 0.0200 | 0.0177 | 0.0160 | 0.0118 | 0.0101 | ||
| 0.17 | UD | 0.0394 | 0.0310 | 0.0259 | 0.0226 | 0.0202 | 0.0185 | 0.0143 | 0.0128 | |
| FG-V | 0.0392 | 0.0309 | 0.0259 | 0.0225 | 0.0202 | 0.0185 | 0.0144 | 0.0129 | ||
| FG-X | 0.0399 | 0.0315 | 0.0264 | 0.0230 | 0.0206 | 0.0189 | 0.0147 | 0.0132 | ||
| FG-O | 0.0378 | 0.0298 | 0.0249 | 0.0216 | 0.0193 | 0.0177 | 0.0136 | 0.0121 | ||
| 0.28 | UD | 0.0412 | 0.0325 | 0.0272 | 0.0237 | 0.0213 | 0.0195 | 0.0152 | 0.0136 | |
| FG-V | 0.0409 | 0.0324 | 0.0272 | 0.0237 | 0.0213 | 0.0196 | 0.0154 | 0.0139 | ||
| FG-X | 0.0424 | 0.0336 | 0.0282 | 0.0247 | 0.0223 | 0.0205 | 0.0163 | 0.0147 | ||
| FG-O | 0.0384 | 0.0303 | 0.0253 | 0.0219 | 0.0196 | 0.0179 | 0.0138 | 0.0123 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Liu, X.; Yazdi, M.; Chen, W. Vibration Characteristic Analysis of Sandwich Composite Plate Reinforced by Functionally Graded Carbon Nanotube-Reinforced Composite on Winkler/Pasternak Foundation. J. Mar. Sci. Eng. 2024, 12, 2157. https://doi.org/10.3390/jmse12122157
Li M, Liu X, Yazdi M, Chen W. Vibration Characteristic Analysis of Sandwich Composite Plate Reinforced by Functionally Graded Carbon Nanotube-Reinforced Composite on Winkler/Pasternak Foundation. Journal of Marine Science and Engineering. 2024; 12(12):2157. https://doi.org/10.3390/jmse12122157
Chicago/Turabian StyleLi, Mengzhen, Xiaolong Liu, Mohammad Yazdi, and Wei Chen. 2024. "Vibration Characteristic Analysis of Sandwich Composite Plate Reinforced by Functionally Graded Carbon Nanotube-Reinforced Composite on Winkler/Pasternak Foundation" Journal of Marine Science and Engineering 12, no. 12: 2157. https://doi.org/10.3390/jmse12122157
APA StyleLi, M., Liu, X., Yazdi, M., & Chen, W. (2024). Vibration Characteristic Analysis of Sandwich Composite Plate Reinforced by Functionally Graded Carbon Nanotube-Reinforced Composite on Winkler/Pasternak Foundation. Journal of Marine Science and Engineering, 12(12), 2157. https://doi.org/10.3390/jmse12122157








