Drag Reduction Through Air-Trapping Discrete Grooves in Underwater Applications
Abstract
1. Introduction
2. Materials and Methods
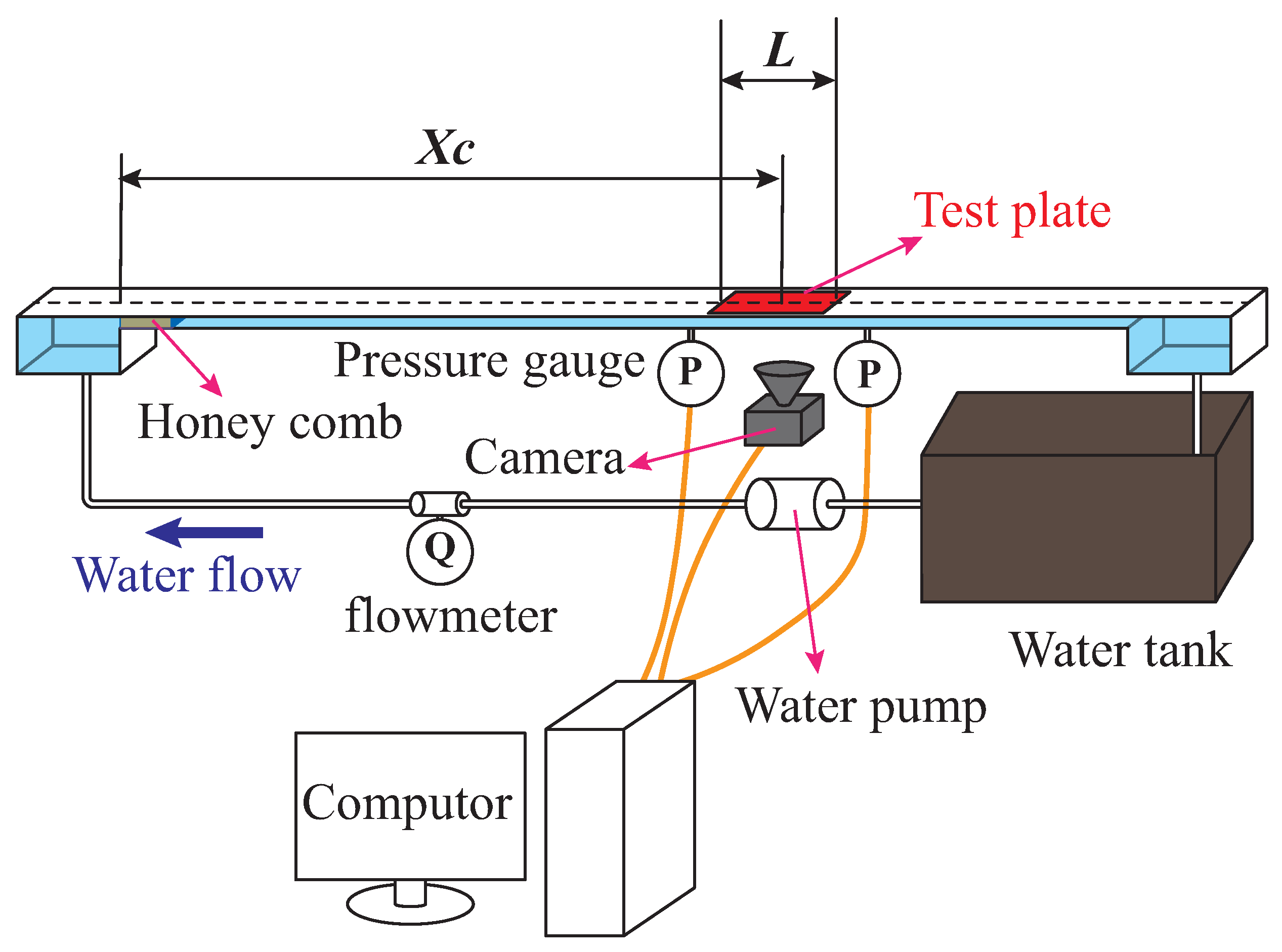
2.1. Experimental Details
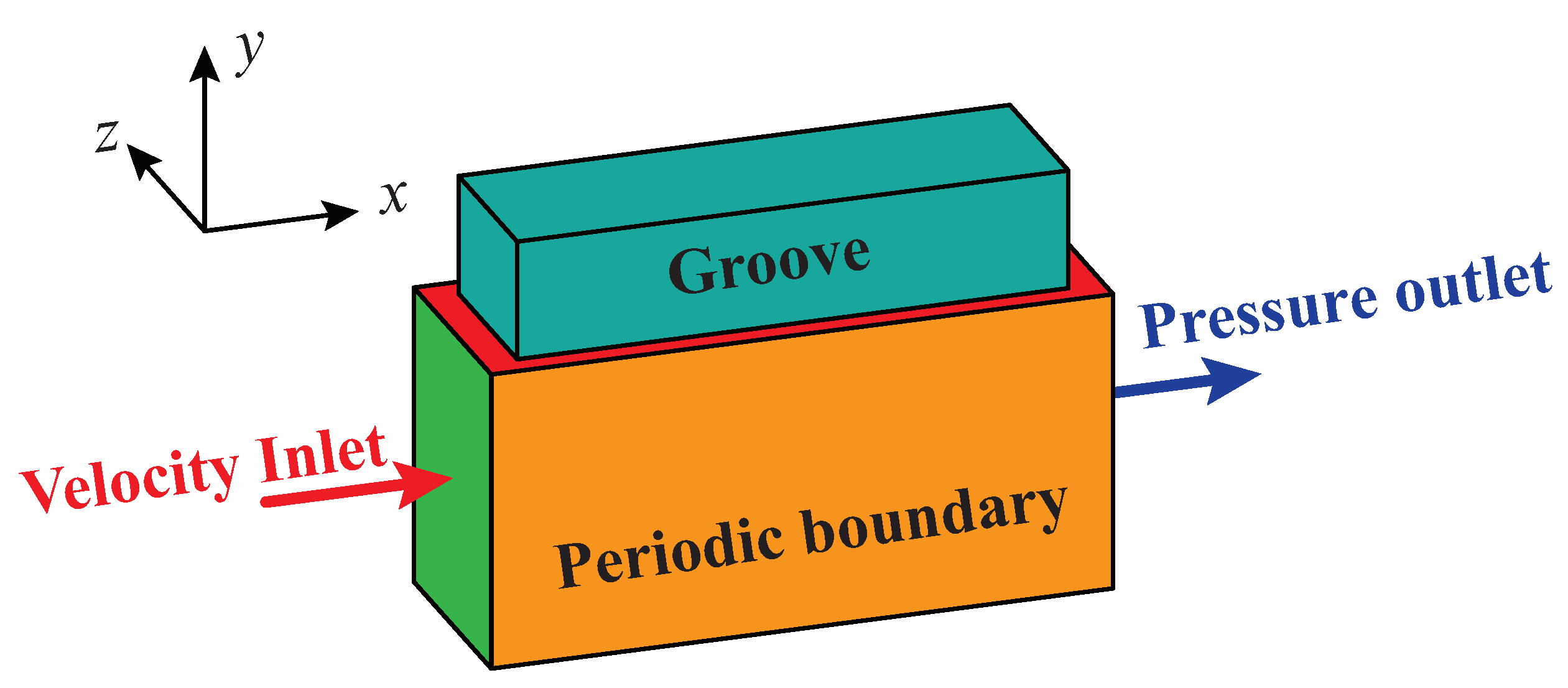
2.2. Numerical Details
3. Results and Discussion
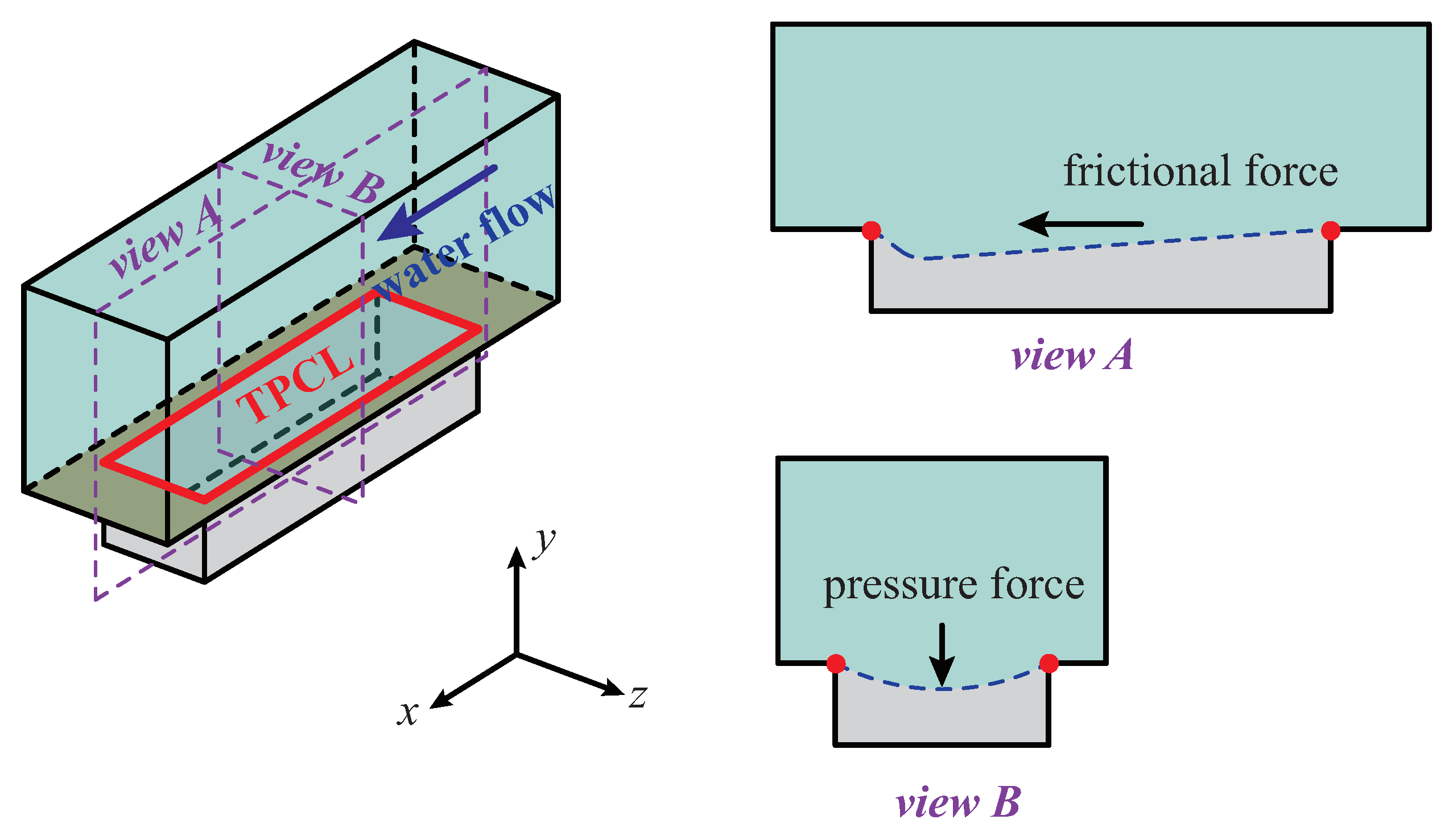
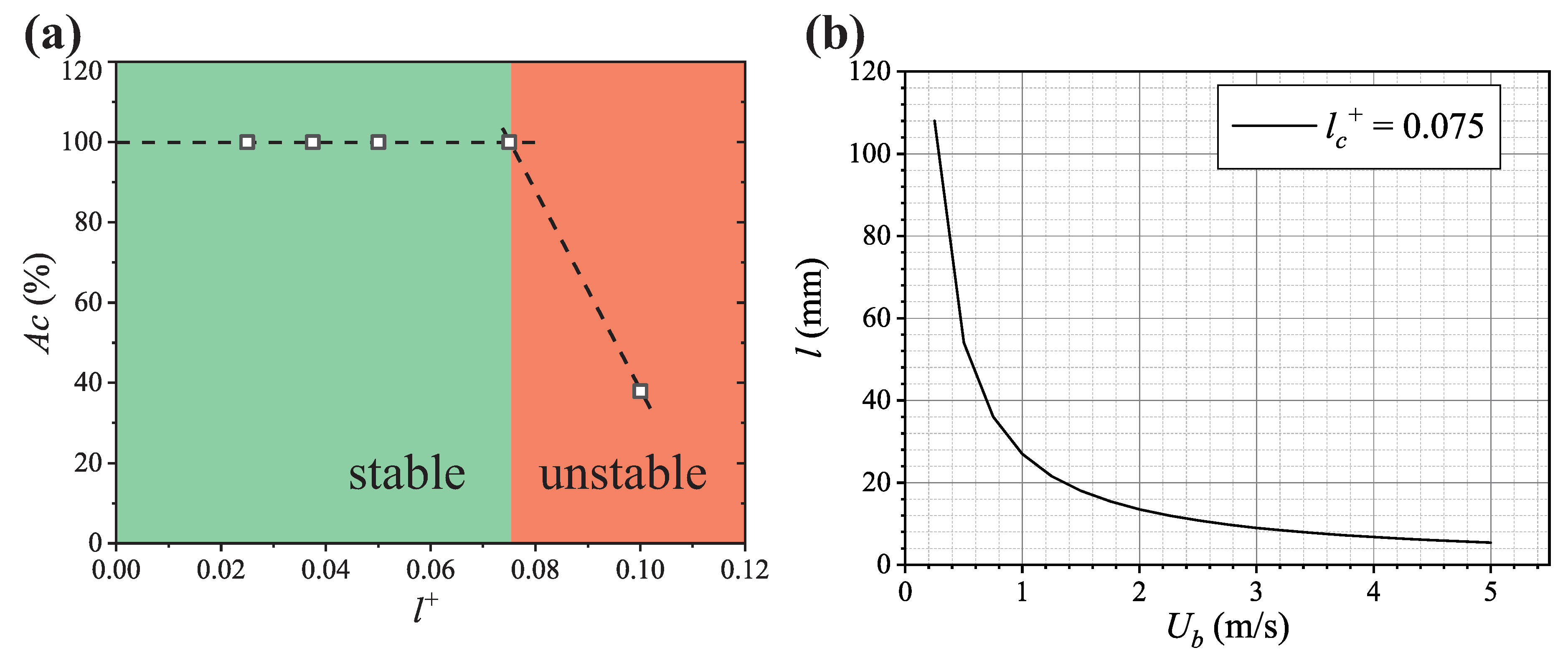
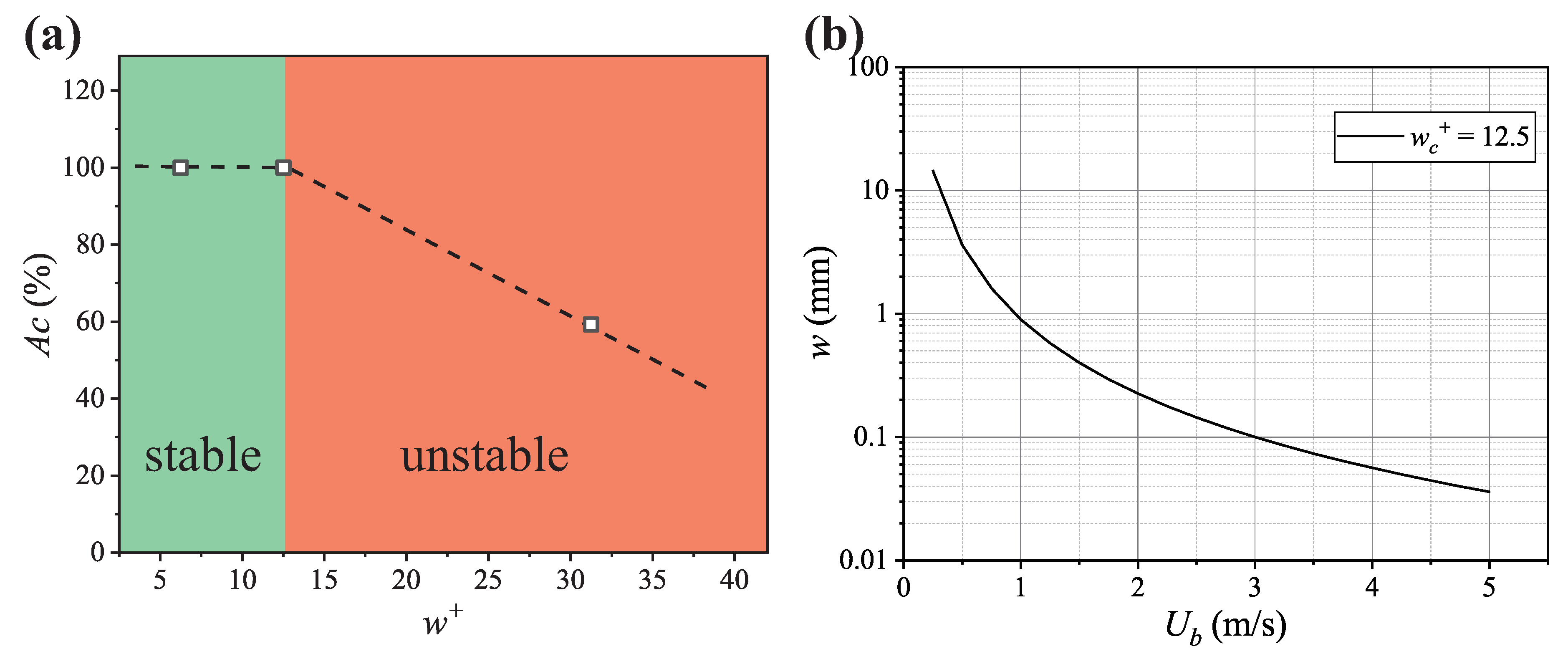
3.1. The Trapped Air Stability
3.2. The Numerical Result
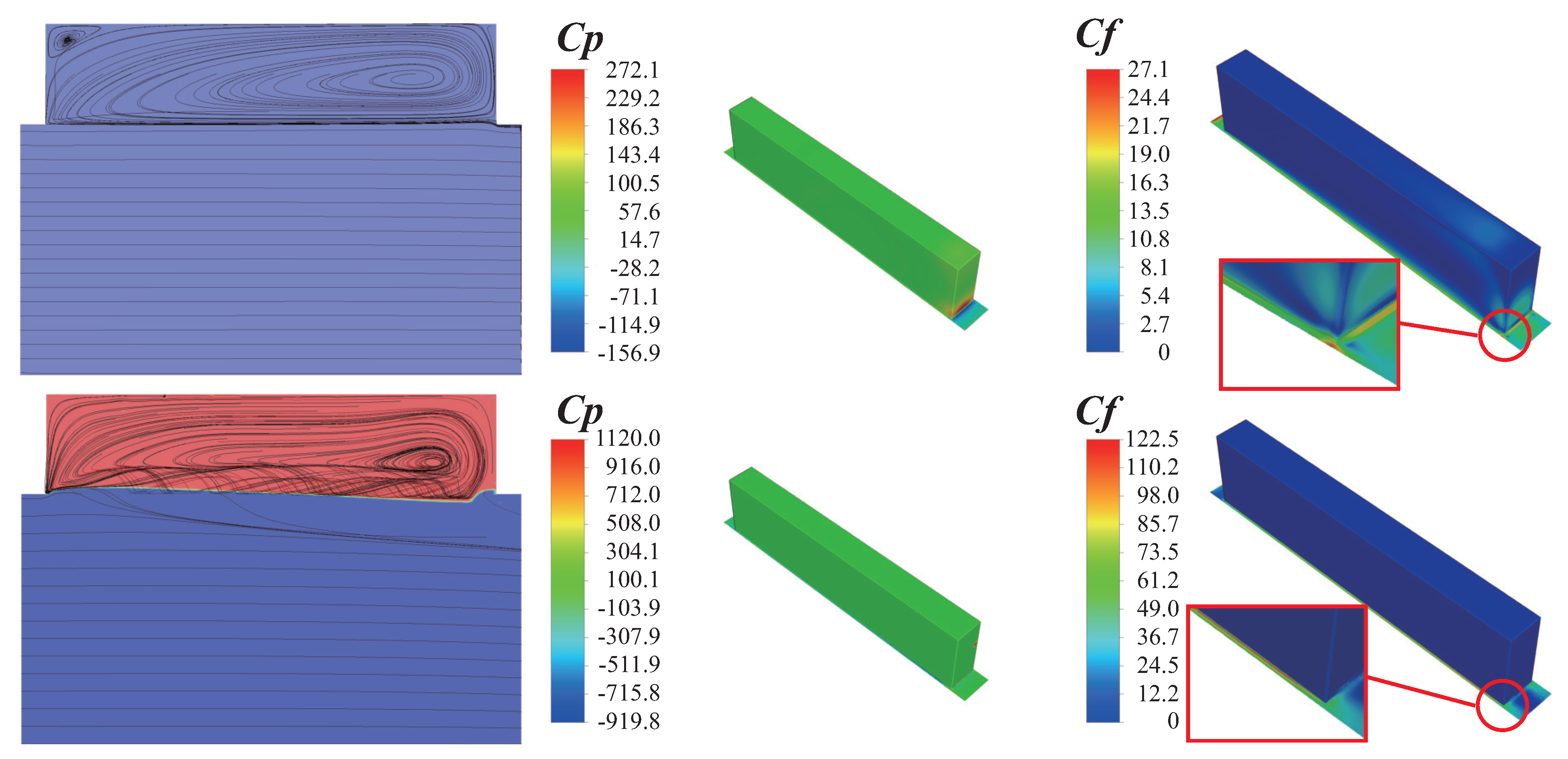
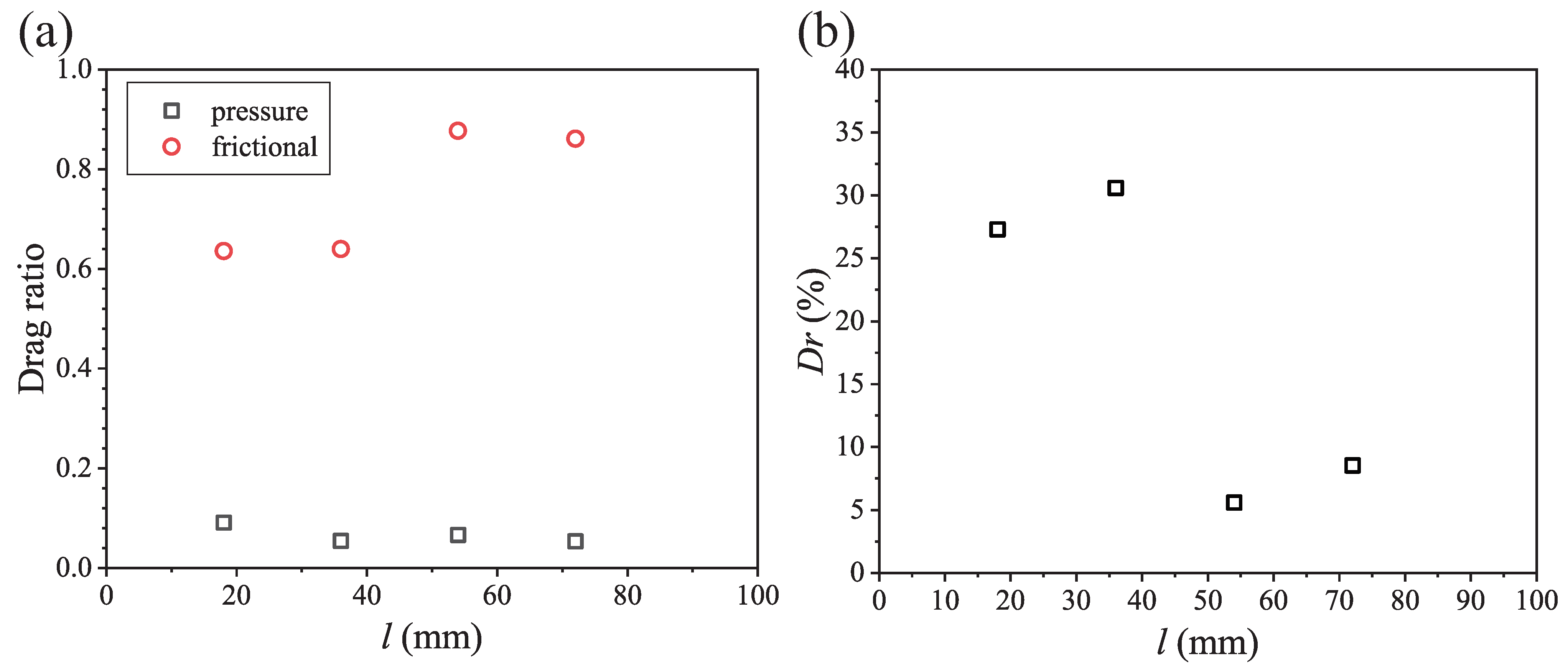
3.2.1. The Drag Reduction Mechanism
3.2.2. Optimizing the Groove Length for Better Drag Reduction
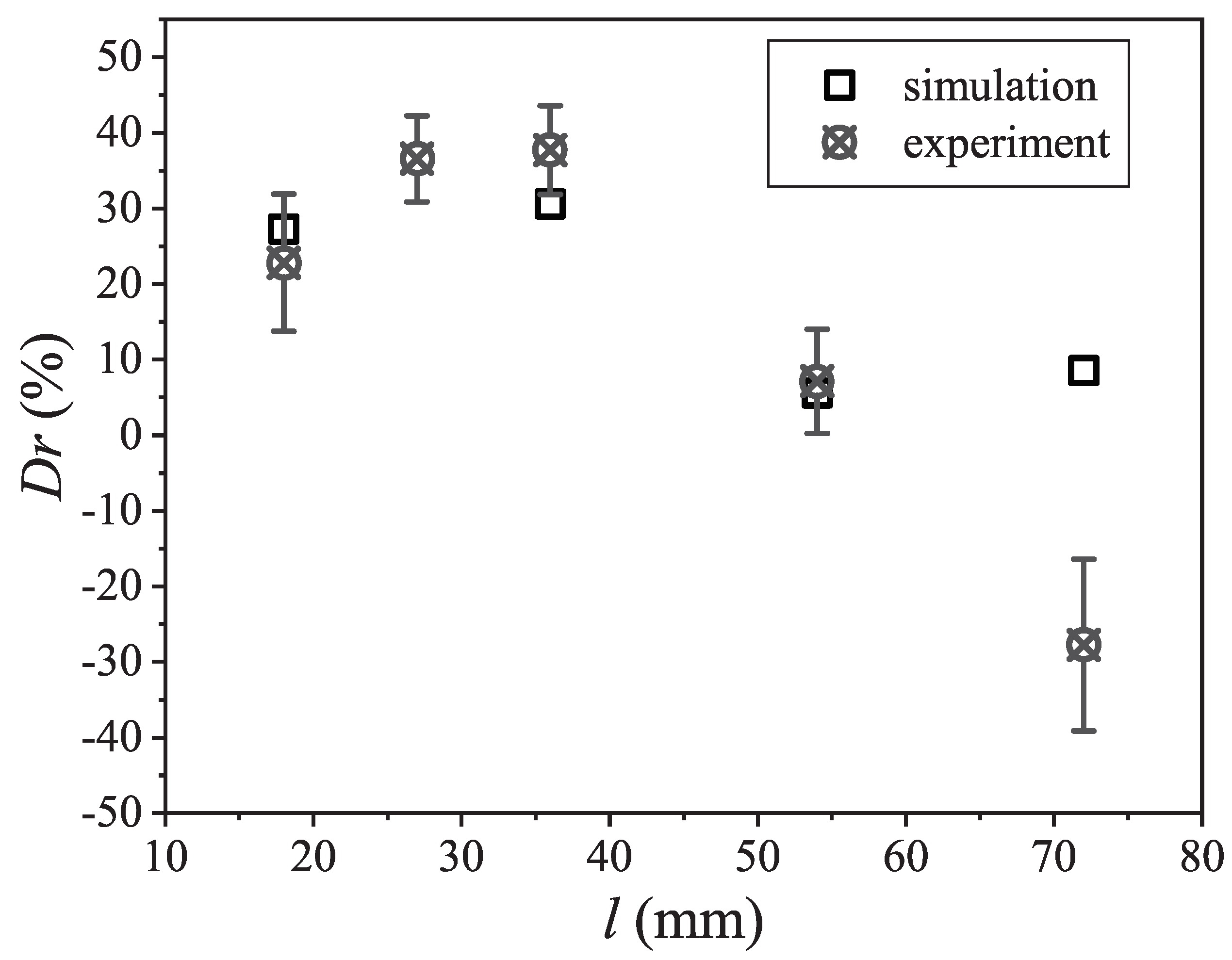
3.3. The Experimental Result
3.3.1. The Repeatability of the Pressure Drop Measurements
3.3.2. The Influence of the Groove Length on the Trapped Air Stability and Drag Reduction
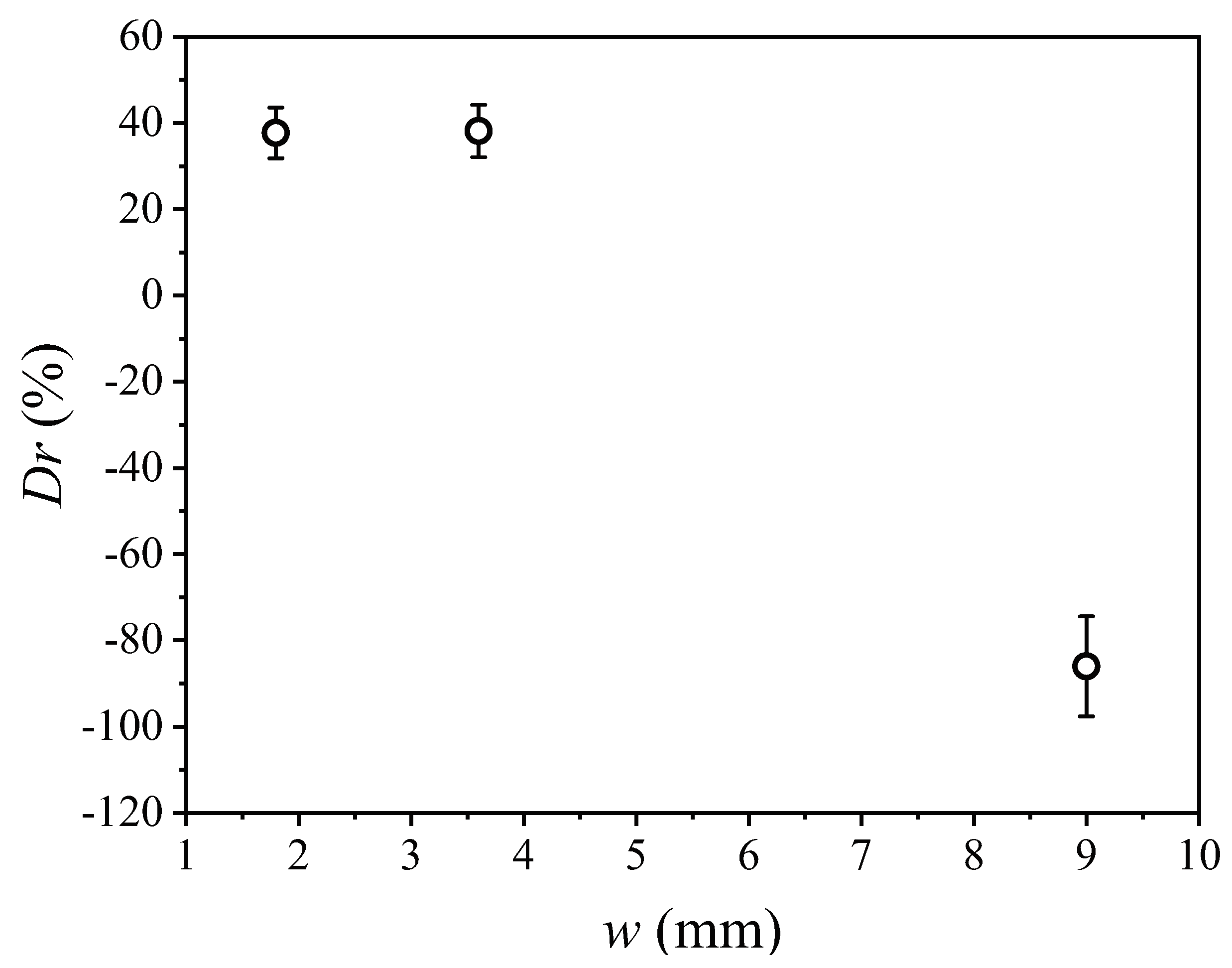
3.3.3. The Influence of the Groove Width on the Trapped Air Stability and Drag Reduction
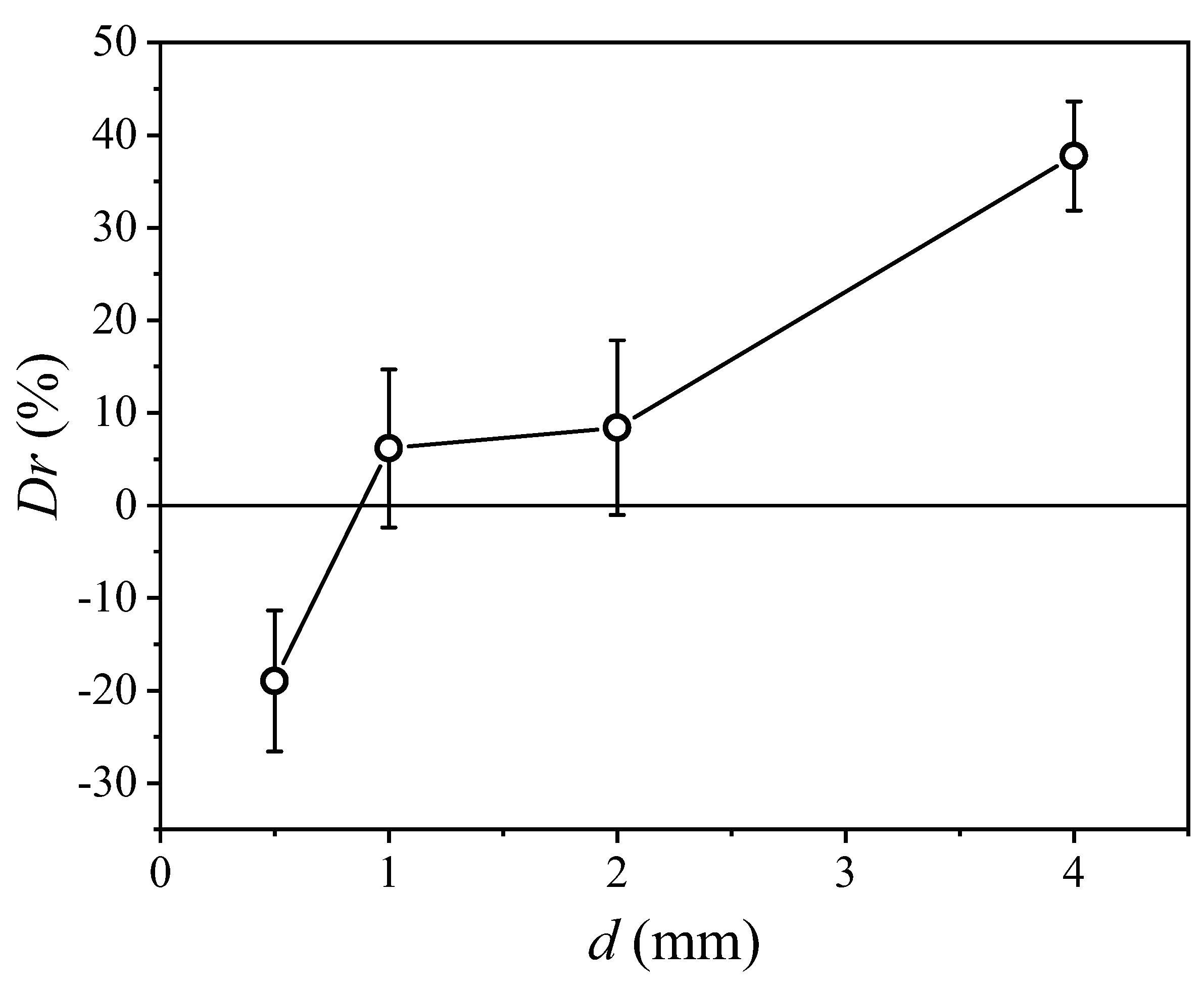
3.3.4. The Influence of the Groove Depth on the Trapped Air Stability and Drag Reduction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Drag reduction rate | |
| trapped air coverage rate | |
| Bulk velocity | |
| TPCL | Three phase contact line |
References
- Zhang, X.; Zhang, D.Y.; Pan, J.F.; Li, X.; Chen, H.W. Controllable Adjustment of Bio-Replicated Shark Skin Drag Reduction Riblets. Appl. Mech. Mater. 2013, 461, 677–680. [Google Scholar] [CrossRef]
- Walsh, M.J.; Weinstein, L.M. Drag and Heat-Transfer Characteristics of Small Longitudinally Ribbed Surfaces. AIAA J. 1979, 17, 770–771. [Google Scholar] [CrossRef]
- Choi, K.S.; Clayton, B.R. The mechanism of turbulent drag reduction with wall oscillation. Int. J. Heat Fluid Flow 2001, 22, 1–9. [Google Scholar] [CrossRef]
- Gatti, D.; Guttler, A.; Frohnapfel, B.; Tropea, C. Experimental assessment of spanwise-oscillating dielectric electroactive surfaces for turbulent drag reduction in an air channel flow. Exp. Fluids 2015, 56, 110. [Google Scholar] [CrossRef]
- Rajappan, A.; McKinley, G.H. Cooperative drag reduction in turbulent flows using polymer additives and superhydrophobic walls. Phys. Rev. Fluids 2020, 5, 114601. [Google Scholar] [CrossRef]
- Fichman, M.; Hetsroni, G. Electrokinetic aspects of turbulent drag reduction in surfactant solutions. Phys. Fluids 2004, 16, 4346–4352. [Google Scholar] [CrossRef]
- Bidkar, R.A.; Leblanc, L.; Kulkarni, A.J.; Bahadur, V.; Ceccio, S.L.; Perlin, M. Skin-friction drag reduction in the turbulent regime using random-textured hydrophobic surfaces. Phys. Fluids 2014, 26, 18. [Google Scholar] [CrossRef]
- Xu, M.; Yu, N.; Kim, J.; Kim, C.J.C. Superhydrophobic drag reduction in high-speed towing tank. J. Fluid Mech. 2020, 908, A6. [Google Scholar] [CrossRef]
- Kim, H.N.; Kim, S.J.; Choi, W.; Sung, H.J.; Lee, S.J. Depletion of lubricant impregnated in a cavity of lubricant-infused surface. Phys. Fluids 2021, 33, 022005. [Google Scholar] [CrossRef]
- Yao, W.H.; Wu, L.; Sun, L.D.; Jiang, B.; Pan, F.S. Recent developments in slippery liquid-infused porous surface. Prog. Org. Coatings 2022, 166, 106806. [Google Scholar] [CrossRef]
- Park, H.; Sun, G.; Kim, C.J.C. Superhydrophobic turbulent drag reduction as a function of surface grating parameters. J. Fluid Mech. 2014, 747, 722–734. [Google Scholar] [CrossRef]
- Reholon, D.; Ghaemi, S. Plastron morphology and drag of a superhydrophobic surface in turbulent regime. Phys. Rev. Fluids 2018, 3, 104003. [Google Scholar] [CrossRef]
- Lay, K.A.; Yakushiji, R.; Mäkiharju, S.; Perlin, M.; Ceccio, S.L. Partial Cavity Drag Reduction at High Reynolds Numbers. J. Ship Res. 2010, 54, 109–119. [Google Scholar] [CrossRef]
- Mäkiharju, S.A.; Elbing, B.R.; Wiggins, A.; Schinasi, S.; Vanden-Broeck, J.M.; Perlin, M.; Dowling, D.R.; Ceccio, S.L. On the scaling of air entrainment from a ventilated partial cavity. J. Fluid Mech. 2013, 732, 47–76. [Google Scholar] [CrossRef]
- Hao, W.U.; Ou, Y.; Qing, Y.E. Experimental study of air layer drag reduction on a flat plate and bottom hull of a ship with cavity. Ocean Eng. 2019, 183, 236–248. [Google Scholar] [CrossRef]
- Qin, S.J.; Sun, S.; Fang, H.Z.; Wang, L.Y.; Chen, Y.; Wu, D.Z. Experimental and numerical investigation on the cavity regime and drag reduction of ventilated partial cavity. Ocean Eng. 2021, 234, 109257. [Google Scholar] [CrossRef]
- Liu, T.; Huang, B.; Wang, G.; Zhang, M.; Gao, D. Experimental investigation of the flow pattern for ventilated partial cavitating flows with effect of Froude number and gas entrainment. Ocean Eng. 2017, 129, 343–351. [Google Scholar] [CrossRef]
- Qu, Z.Y.; Yang, N.N.; Ma, G.H.; Yao, X.L.; Zhang, W.K.; Zhang, H.T.; Cheng, S.H.; Quan, X.B.; Chen, Y.Y. Experimental study on ventilated cavity flow at the tail of underwater vehicle under low surface tension. Ocean Eng. 2023, 267, 113230. [Google Scholar] [CrossRef]
- Aljallis, E.; Sarshar, M.A.; Datla, R.; Sikka, V.; Jones, A.; Choi, C.H. Experimental study of skin friction drag reduction on superhydrophobic flat plates in high Reynolds number boundary layer flow. Phys. Fluids 2013, 25, 14. [Google Scholar] [CrossRef]
- Kim, T.J.; Hidrovo, C. Pressure and partial wetting effects on superhydrophobic friction reduction in microchannel flow. Phys. Fluids 2012, 24, 112003. [Google Scholar] [CrossRef]
- Lv, P.Y.; Xue, Y.H.; Shi, Y.P.; Lin, H.; Duan, H.L. Metastable States and Wetting Transition of Submerged Superhydrophobic Structures. Phys. Rev. Lett. 2014, 112, 196101. [Google Scholar] [CrossRef] [PubMed]
- Ling, H.; Katz, J.; Fu, M.; Hultmark, M. Effect of Reynolds number and saturation level on gas diffusion in and out of a superhydrophobic surface. Phys. Rev. Fluids 2017, 2, 124005. [Google Scholar] [CrossRef]
- Hokmabad, B.V.; Ghaemi, S. Effect of Flow and Particle-Plastron Collision on the Longevity of Superhydrophobicity. Sci. Rep. 2017, 7, 41448. [Google Scholar] [CrossRef] [PubMed]
- Vullers, F.; Peppou-Chapman, S.; Kavalenka, M.N.; Holscher, H.; Neto, C. Effect of repeated immersions and contamination on plastron stability in superhydrophobic surfaces. Phys. Fluids 2019, 31, 012102. [Google Scholar] [CrossRef]
- Kim, H.; Park, H. Diffusion characteristics of air pockets on hydrophobic surfaces in channel flow: Three-dimensional measurement of air-water interface. Phys. Rev. Fluids 2019, 4, 074001. [Google Scholar] [CrossRef]









| No. | Length | Width | Depth | Research Contents | |
|---|---|---|---|---|---|
| Smooth | - | - | - | 2500 | control sample |
| #1 | 20 | 2 | 4 | 2500 | length |
| #2 | 30 | 2 | 4 | 2500 | length |
| #3 | 40 | 2 | 4 | 2500 | length, width, depth |
| #4 | 60 | 2 | 4 | 2500 | length |
| #5 | 80 | 2 | 4 | 2500 | length |
| #6 | 40 | 4 | 4 | 2500 | width |
| #7 | 40 | 10 | 4 | 2500 | width |
| #8 | 40 | 2 | 2 | 2500 | depth |
| #9 | 40 | 2 | 1 | 2500 | depth |
| #10 | 40 | 2 | 0.5 | 2500 | depth |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, Y.; Weng, D.; Wang, J. Drag Reduction Through Air-Trapping Discrete Grooves in Underwater Applications. J. Mar. Sci. Eng. 2024, 12, 2224. https://doi.org/10.3390/jmse12122224
Nie Y, Weng D, Wang J. Drag Reduction Through Air-Trapping Discrete Grooves in Underwater Applications. Journal of Marine Science and Engineering. 2024; 12(12):2224. https://doi.org/10.3390/jmse12122224
Chicago/Turabian StyleNie, You, Ding Weng, and Jiadao Wang. 2024. "Drag Reduction Through Air-Trapping Discrete Grooves in Underwater Applications" Journal of Marine Science and Engineering 12, no. 12: 2224. https://doi.org/10.3390/jmse12122224
APA StyleNie, Y., Weng, D., & Wang, J. (2024). Drag Reduction Through Air-Trapping Discrete Grooves in Underwater Applications. Journal of Marine Science and Engineering, 12(12), 2224. https://doi.org/10.3390/jmse12122224




