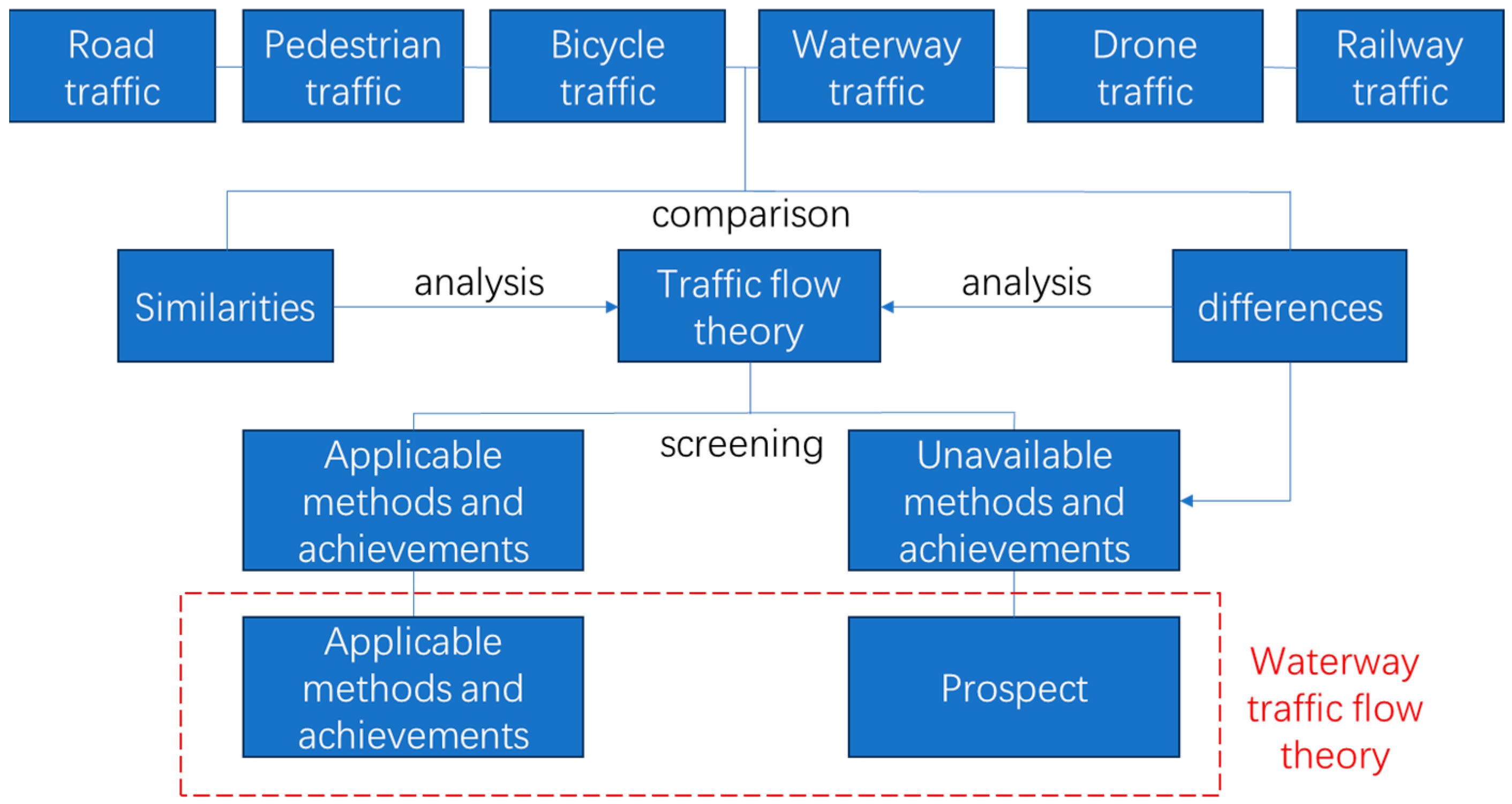
Traffic Flow Theory for Waterway Traffic: Current Challenges and Countermeasures

Abstract

Researchers are increasingly turning to roadway traffic flow theory to propose effective solutions for challenges such as traffic congestion and low efficiency in waterway transportation. However, since roadway traffic flow theory was originally developed for highway transportation, its direct application to waterways raises questions due to the inherent differences between the two modes of transportation. Meanwhile, research results and methodologies from other transportation modes can provide valuable insights for studying waterway traffic flow theory. Addressing these questions is essential for advancing research in this field. This research conducts a comparative analysis to explore the similarities and differences between typical transportation modes and waterway transportation, examining how these distinctions affect the application of existing traffic flow theories. It also categorizes recent research outcomes related to traffic flow theories from various transportation modes based on their relevance to waterway traffic flow theory. The discussion includes the applicability of these models and methods in the context of waterway transportation, considering the unique characteristics of waterway traffic. Finally, this study highlights current challenges in applying traffic flow theories to waterways and offers suggestions for future research.

1. Introduction

Roadway traffic flow theory studies the properties, mechanisms, and dynamics of traffic flow from various perspectives, addressing transportation challenges such as deciphering traffic phenomena and promoting safe, efficient, and intelligent transportation [1]. The macroscopic approach conceptualizes vehicles in road traffic as fluids with continuous flow characteristics, applying principles from fluid mechanics to study traffic behavior [2,3,4,5,6,7,8,9,10]. In contrast, the microscopic approach treats vehicles as active particles whose motion and interaction collectively reflect traffic behavior.

Throughout the evolution of road traffic, this theory has been widely applied across various fields, providing effective solutions to traffic problems for managers [11]. It serves as a crucial tool for guiding the development of road traffic systems [12,13,14]. Recently, researchers have extended the research findings and methodologies of roadway traffic flow theory to pedestrian, bicycle, rail, and drone traffic [15,16,17,18], yielding valuable insights that have become integral to traffic flow theory.

The increasing disparity between the demand and supply of waterway transportation has intensified challenges related to traffic congestion and low efficiency. Researchers are now turning to roadway traffic flow theory as a valuable resource for developing effective mitigation strategies for waterway transportation issues [19,20,21]. Furthermore, as one of the significant tools for promoting the development of driving assistance, autonomous collision avoidance, and autonomous driving-related technologies, the study of waterway traffic flow theory has garnered increasing attention from scholars [22,23,24,25].

While fundamental differences between waterway and roadway traffic are becoming increasingly evident, there are also notable similarities with other transportation modes. These commonalities suggest that research findings and methods from these modes can provide valuable insights for waterway traffic studies. Therefore, it is essential to explore how to integrate these insights into waterway traffic flow research.

As shown in Figure 1, this research aims to summarize the characteristics of waterway traffic by comparing the similarities and differences among several typical traffic modes. Based on these characteristics, it analyzes and discusses the theoretical research findings and methodologies related to traffic flow. The main achievements and key limitations of these approaches are outlined, and their applicability to waterway traffic is evaluated.

The remainder of this paper is organized as follows: Section 2 briefly analyzes the similarities and differences among several typical types of traffic. Section 3 provides a detailed description of the research methods and findings related to various traffic types, focusing on their definitions of traffic flow characteristics, traffic flow fundamental diagrams, and simulation models. In Section 4, we discuss the advantages and challenges of applying the aforementioned research methods and findings to the study of waterway transportation. Section 5 outlines future directions for development, and Section 6 concludes with final remarks and an outlook.

2. Comparison of Similarities and Differences Among Various Modes of Transportation

This section provides an in-depth analysis of the similarities and differences among various modes of transportation. As a system of engineering, transportation is fundamentally classified into four elements: humans, machines, the environment, and management. A full analysis of the distinctions across transportation modalities can be undertaken by comparing these four elements to elucidate the characteristics of waterway transportation. Hence, these similarities and differences are analyzed in several aspects involving humans, machines, and the environment of these modes of transportation.

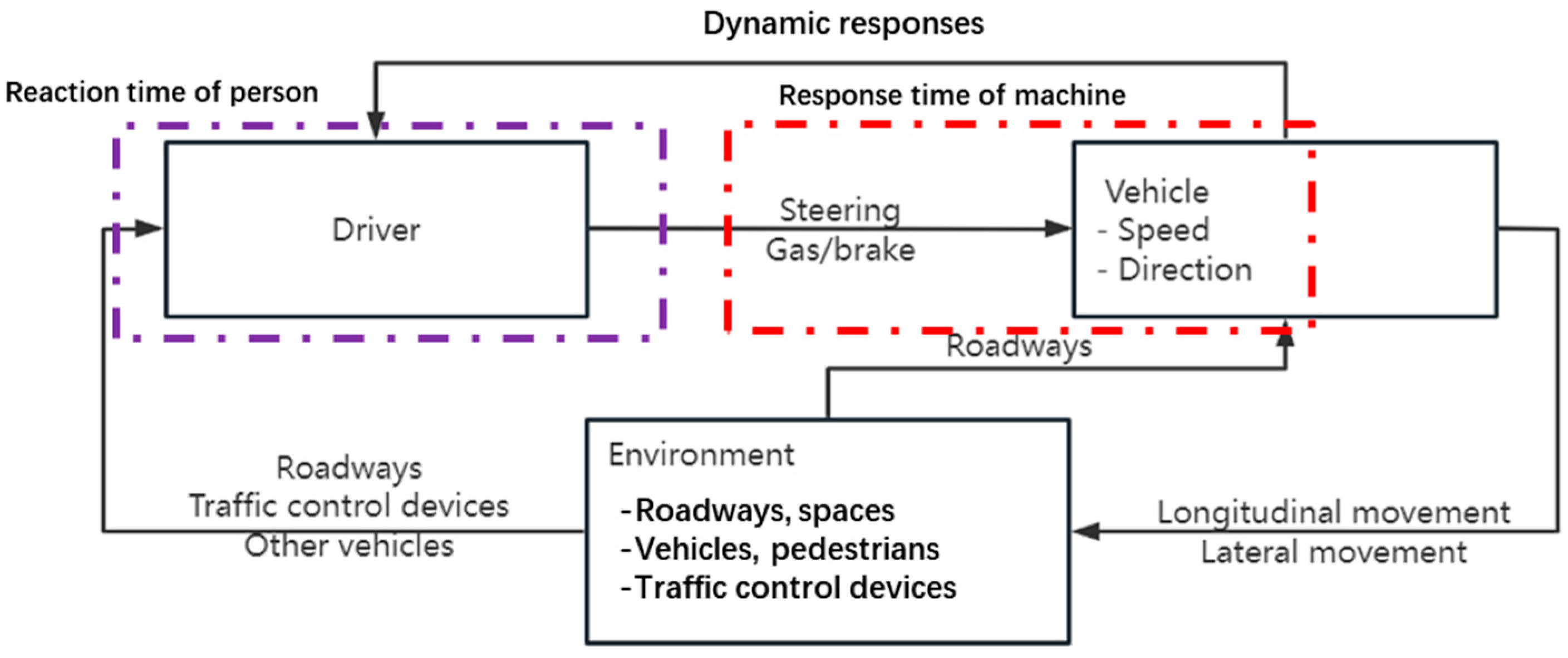
2.1. Human–Machine–Environment

The vessel’s dimensions, the mode of transportation, the average free-flow speed, the pilot’s reaction time, the navigational environment, and the organizational and management strategies of waterway traffic are representative key aspects among these four elements. Hence, comparisons mainly focus on these aspects.

2.1.1. The Size of the Carrier

As shown in

Table 1. Differences and similarities of several typical transportation modes on human–machine–environment.

Traffic Classification	Cars	Bicycles	Pedestrians	Vessels	Trains	Aircraft	Small Unmanned Aircraft
Dimensions (length)	0–24 m [26]	1.7–1.9 m [27]	0.43 m [28]	0–399.9 m [29]	209 m (CR300AF Renaissance EMU Train)	38.9 m (C919) 68.28 m (787-10)	0.35 m (DJI Mavic 3) 0.6 m (INSPIRE 2)
Average speed in free flow	100 km/h [30]	14–22 km/h [27]	2.5–4.3 km/h [31]	6–30 km/h [32]	200 km/h~250 km/h CR300AF Renaissance EMU Train	903 km/h	Max 76k m/h (DJI Mavic 3) Max 94 km/h (INSPIRE 2)
Order of magnitude of reaction time	Second level	Second level	Second level	Minute level	Second level	Second level	Second level
Transportation medium	Roads and air	Roads and air	Roads and air	Air and water	Air and orbits	Air	Air
Lane discipline	Yes	No	No	No	Yes	No	No
Dimension of motion	1.5D	2D	2D	2D/3D	1D	3D	3D

, in terms of carrier length, road traffic typically accommodates vehicles with maximum lengths in the order of tens of meters, such as cars, while bicycles usually measure a few meters and pedestrians are generally a few tens of centimeters. In contrast, waterway traffic includes vessels that can reach lengths of up to 399.9 m. As a result, the scale variations in waterway traffic far exceed those observed in cars, bicycles, and pedestrians. For instance, the traffic dynamics of ten 100 m vessels in a channel differ significantly from those of ten 300 m vessels in the same channel. Consequently, accurately describing waterway traffic solely by counting the number of vessels is inadequate due to these substantial differences in size.

2.1.2. Reaction Time

In terms of reaction time, the perception–response times in road, pedestrian, bicycle, railroad, drone, and air traffic are generally measured in seconds, while in waterway traffic, this time is typically measured in minutes. As shown in Figure 2, this difference arises from collision-avoidance decision-making processes; in road, pedestrian, bicycle, railroad, drone, and airplane traffic, these processes usually involve a single operator (such as a driver or a pilot). The reaction time in these modes mainly consists of the operator’s perception–response time.

In contrast, as shown in Figure 3, the collision-avoidance decision-making process in waterway traffic often involves multiple operators (pilot, captain, helmsman, etc.) and several stages. As a result, the overall reaction time comprises the operators’ perception–response times, the machine’s response time, and the information transfer time. Additionally, the mechanical systems of cars, bicycles, trains, drones, and airplanes are highly responsive, making their mechanical response times almost negligible compared to their operator’s perception–reaction time. Conversely, the mechanical systems of vessels are larger and more complex, resulting in longer response times that cannot be ignored.

Consequently, the perception–response time in waterway transportation differs significantly from that of other transportation types. This extended response time increases the heterogeneity of waterway traffic, making it much greater than that of other traffic types. As a result, accurately describing the characteristics of waterway traffic flow becomes more challenging.

2.1.3. The Environment

In terms of the navigational environment, roadway traffic, including automobiles, bicycles, and pedestrians, operates on pavements, while trains travel on rail tracks, and drones and airplanes fly through the air. In contrast, vessels navigate on or in moving bodies of water. The significantly greater complexity of water resistance—compared to the relatively minor air resistance and the resistance from stationary roads—along with the intricate computational models required for vessel hydrodynamics poses substantial challenges in constructing accurate models for vessel maneuvering and motion.

2.1.4. Traffic Movement

In terms of movement, roadways are typically delineated by pavement markings, requiring roadway traffic to maintain their lanes as they move in a one-dimensional space. This is particularly true for railway traffic. When considering lane changes, roadway traffic can be described as at most 1.5-dimensional. In contrast, vessels navigate on water surfaces, which can be considered two-dimensional. Bicycles and pedestrians exhibit similar two-dimensional characteristics. Airway traffic, such as drones and airplanes, operates in a three-dimensional space, allowing for greater freedom of movement.

Regarding conflict resolution, roadway traffic primarily relies on reducing speed and stopping to avoid collisions, with changing direction or swerving as secondary options. In contrast, vessel operators tend to prioritize steering to avoid collisions rather than decelerating. This preference arises from the large size and mass of vessels, which results in low acceleration and deceleration capabilities, leading to excessively long stopping distances on water.

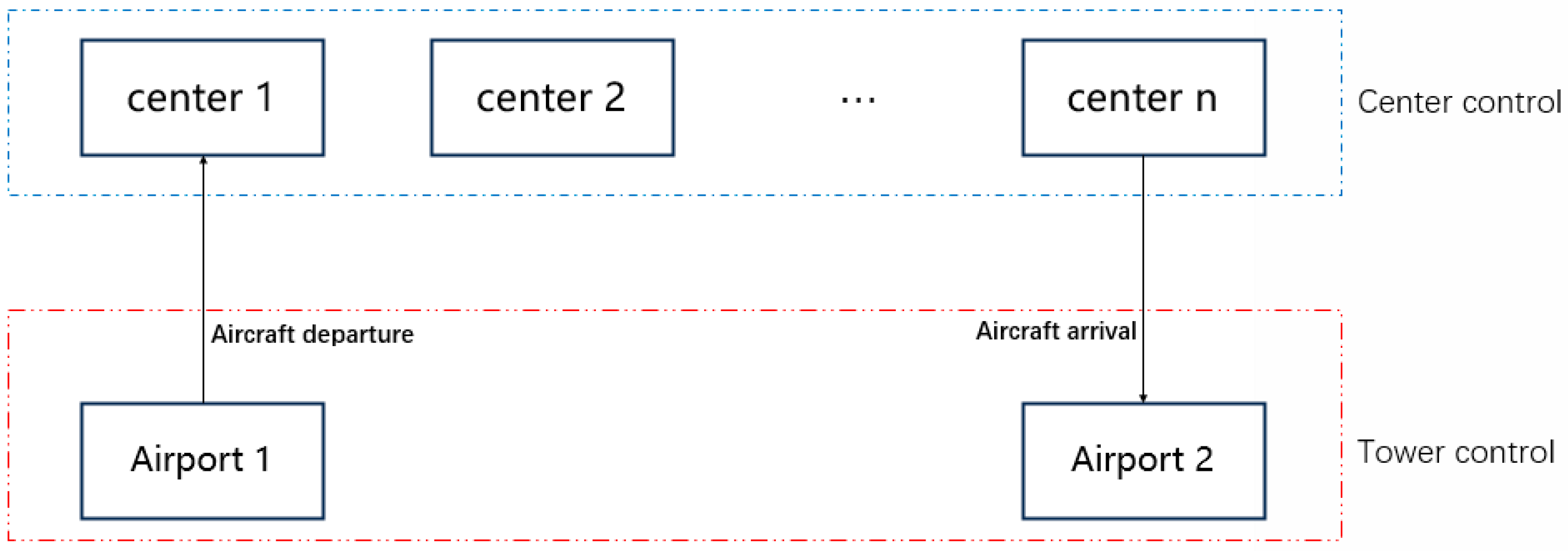
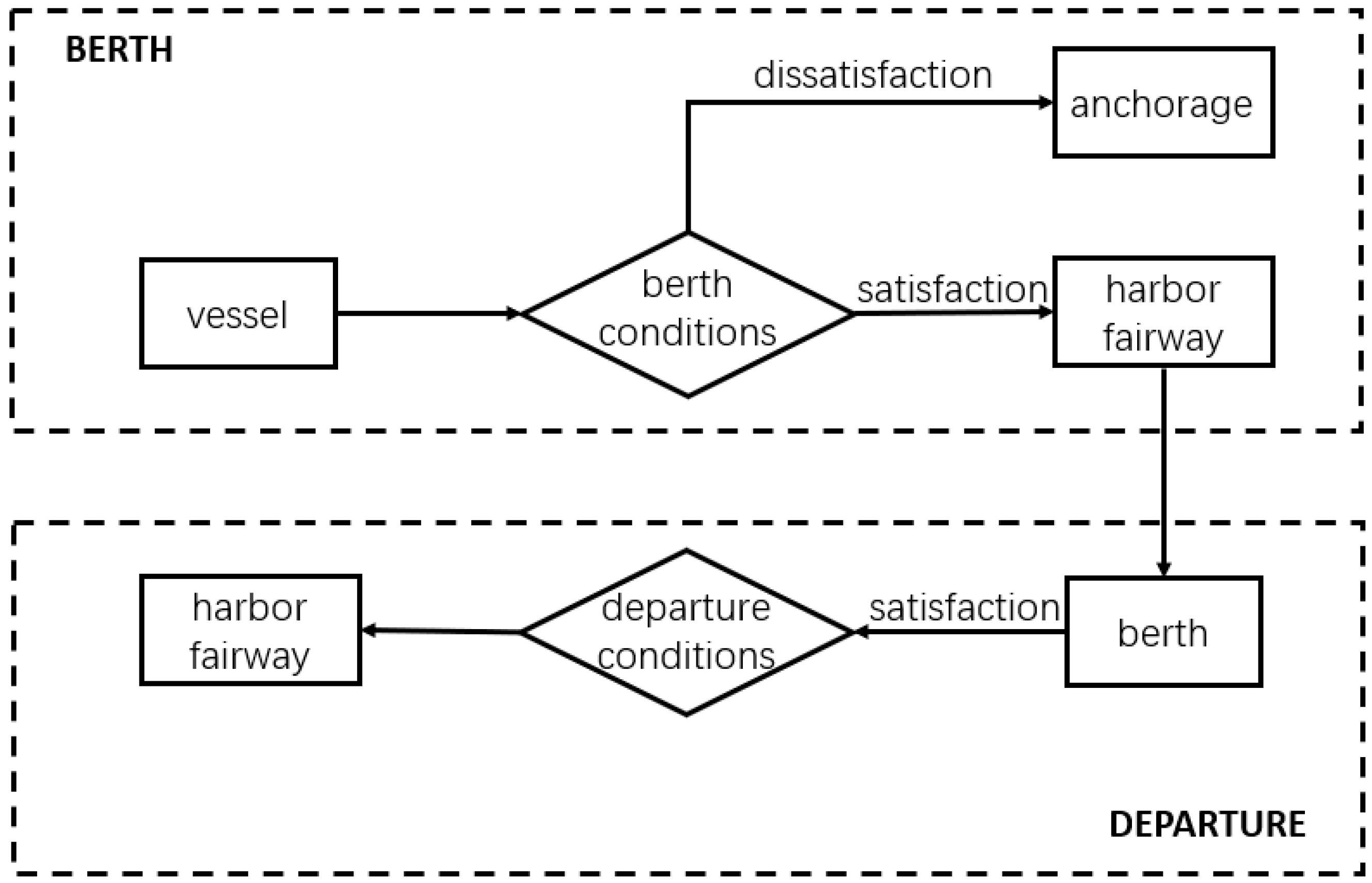
2.2. Organization of Traffic Flow

As shown in

Table 2. Differences and similarities between several typical transportation modes and traffic organization modes.

Traffic Classification	Traffic Organization Mode
Cars	Self-organizing	Free competition	Driver takes control	Traffic rules
Bicycles	Self-organizing	Free competition	Driver takes control	Traffic rules
Pedestrians	Self-organizing	Free competition	Driver takes control	Traffic rules
Trains	Schedule/Management	No free competition	Center control	-
Aircraft	Schedule/Management	No free competition	Center control	-
Small Unmanned Aircraft	Self-organizing	Free competition	Driver takes control	-
Vessels	Hybrid	Hybrid	Hybrid	Traffic rules

and Figure 4 and Figure 5, in roadway traffic, vehicles, bicycles, and pedestrians are operated in a way that is self-organizing, has free competition, and is driver-controlled, and all participants are subject to traffic rules. In railroad and air traffic, the operation of carriers has to be carried out in strict accordance with pre-determined plans; there is no free competition, and the carriers have to obey the management of the tower or the control center at almost any time. In waterway transportation, the arrangement of vessels in and out of ports is affected by the progress and plans of port terminal operations, the water depth conditions of the channel, and other natural conditions. When vessels travel in and out of the port channel, the traffic control personnel only provides navigation and collision avoidance suggestions for these vessels, and the final collision-avoidance decision-making power still belongs to the navigators of the vessel, and the organization of the traffic has certain self-organizing characteristics. In addition, the speed of the vessels is decided by the navigators and pilots of the vessels according to the navigation environment, tidal conditions, etc., and the speed of the vessels has the characteristics of free competition in uncontrolled approach areas. Taken together, the organization of waterway traffic in some regions is the same as that of road traffic, but there are also regions where the organization of waterway traffic is the same as that of railroad or air traffic.

After a comparative analysis of the characteristics of different traffic types from the viewpoints of carrier size, reaction time, operation environments, and traffic movement, the characteristics of waterway traffic can be summarized as follows:

• Waterway traffic comprises vessels that are significantly larger and heavier than those in roadway traffic. Additionally, the perception–response times of vessel operators are considerably longer than those of road vehicle drivers. As a result, waterway traffic exhibits greater heterogeneity compared to roadway traffic.
• Unlike roadway traffic, which is regulated by lane discipline and moves in a one- or one-and-a-half-dimensional space, in uncontrolled approach channel lanes, waterway traffic operates freely on the water surface and is considered moving in a two-dimensional space.
• Compared to other modes of transportation, the environment associated with waterway transportation is relatively complex, and the influence of environmental factors on waterway transport is significantly greater.

Consequently, the distinctive characteristics of waterway traffic pose significant challenges for modeling. Established models and theories for roadway traffic cannot be directly applied to waterway traffic without accounting for these fundamental differences. Therefore, it is essential to compile the research findings and methodologies of existing traffic flow theories and analyze the challenges and potential solutions that may arise when applying them to the field of waterway traffic, considering these key differences.

3. The Latest Research Progress in Traffic Flow Theory

The objectives of waterway traffic flow theory are similar to those of road traffic flow theory, concentrating on traffic characteristics, underlying mechanisms, and dynamic changes. By exploring the distinctions between waterway traffic and other transportation modes, we can glean valuable insights from existing road traffic research to enhance our understanding of waterway traffic flow. Given that traffic flow characteristics, traffic flow fundamental diagrams, equilibrium traffic flow models, and traffic flow simulations are the core components of traffic flow theory, this section organizes and analyzes the research findings and methodologies from various transportation modes to meet the specific needs of waterway traffic theory.

3.1. The Properties of Traffic Flow

Traffic flow characteristics such as density, flow, and speed are fundamental variables that describe the properties of road traffic. Accurate information about these variables is essential for studying intrinsic traffic patterns and their dynamic responses [33]. As shown in

Table 3. Comparison of several methods for defining traffic flow characteristics.

No.	Way		Flow	Density	Speed	Application Scenario
1	one-dimensional	-	${\displaystyle \frac{N}{T}}$	${\displaystyle \frac{M}{L}}$	${\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}{\dot{x}}_i$	homogeneous traffic flow	lane discipline
2	one-dimensional	-	${\displaystyle \frac{N}{T}}$	${\displaystyle \frac{M}{L}}$	${\displaystyle \frac{1}{M}}{\displaystyle \sum _{i=1}^M}{\dot{x}}_i$	homogeneous traffic flow	lane discipline
3	two-dimensional	X-T	${\displaystyle \frac{d\left(A\right)}{\left|A\right|}}$	${\displaystyle \frac{t\left(A\right)}{\left|A\right|}}$	${\displaystyle \frac{d\left(A\right)}{t\left(A\right)}}$	homogeneous traffic flow	lane discipline
4	three-dimensional	N-X-T	${\displaystyle \frac{\partial N(x, t)}{\partial t}}$	$-{\displaystyle \frac{\partial N(x, t)}{\partial x}}$	${\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}{\dot{x}}_i$	homogeneous traffic flow	lane discipline
5	three-dimensional	X-Y-T	${\displaystyle \frac{d\left(V\right)}{\left|V\right|}}$	${\displaystyle \frac{t\left(V\right)}{\left|V\right|}}$	${\displaystyle \frac{d\left(V\right)}{t\left(V\right)}}$	homogeneous traffic flow	no lane discipline
6	three-dimensional (adjusted by area)	X-Y-T	${\displaystyle \frac{d\left(V\right)\ast S_i\left(V\right)}{\left|V\right|}}$	${\displaystyle \frac{t\left(V\right)\ast S_i\left(V\right)}{\left|V\right|}}$	${\displaystyle \frac{d\left(V\right)}{t\left(V\right)}}$	heterogeneous traffic flow	no lane discipline

Notations: N and M represent the total number of vessels; T represents the time interval; L represents the length of the channel; ${\dot{x}}_i$ represents the displacement derivative for the ith vessel; d(A) and d(V) represent the cumulative displacement covered by all vessels during the time interval; t(A) and t(V) represent the total time traveled by all vessels; |A| denotes the area enclosed by the channel length within the time interval; |V| denotes the area enclosed by the channel length and width within the time interval; and S_i(V) represents the area of the ith vessel.

, definitions of traffic flow characteristics are as follows. Table 3 analyzes and evaluates the definitions of traffic flow characteristics from three perspectives. These three perspectives are ways, methods, and applicable scenarios.

A widely accepted definition of traffic flow characteristics is the one presented in the Highway Capacity Manual (HCM 2022) [34]. This definition describes flow as the number of vehicles passing a fixed location per unit of time, density as the number of vehicles occupying a specific length of lane or roadway at a given moment, and speed as the rate of motion expressed as distance per unit of time. However, this definition can yield misleading results for the following reasons. It defines flow in the time domain and density in the space domain and utilizes two types of speed: the time-mean speed in the time domain and space-mean speed in the space domain. As a result, the definition relies on domain distinctions, whereas traffic flow characteristics should ideally be independent of these domains. Furthermore, due to this domain issue, the assumption that flow equals the product of speed and density may not hold, as it may lack a common basis in the time–space plane [35,36].

A more effective definition was proposed by Edie [37] which is based on a region in the time–space domain. Three quantities are computed: the total distance traveled by all vehicles in a region, the total time spent by all vehicles in the region, and the area of the region. Consequently, flow is defined as the total distance divided by the area, density as the total time divided by the area, and the space-mean speed as the total distance divided by the total time. This set of definitions effectively addresses the issues arising from domain distinctions.

Makigami et al. [38] extended the two-dimensional (2D) time–space domain to a three-dimensional (3D) domain by introducing the third dimension: the cumulative number of vehicles. In this model, each vehicle’s trajectory in the 2D domain can be elevated to a height corresponding to its ID number. As such, a 3D surface is created by smoothing the “stairs“ formed by the elevated trajectories. They defined flow as the partial derivative of the 3D surface with respect to time while holding the space constant and density as the negative partial derivative of the 3D surface with respect to space while holding the time constant and speed as the partial derivative of space with respect to time while keeping the cumulative number (vehicle ID) constant.

Unfortunately, these definitions are applicable only to homogeneous traffic flows with lane discipline, making it challenging to apply them to waterway traffic, which is often heterogeneous and lacks lane discipline.

Y. liu et al. [39] expanded Edie’s definition by incorporating the lateral motion of vehicles, making it applicable for describing traffic flows without lane discipline. However, this definition still has the limitation of not accounting for differences in vehicle sizes. CH. Mallikarjuna and K. R. Rao [40] redefined the density of traffic flow by using the carrier area occupancy method. P. V. Suvin et al. [41] also defined the flow rate and speed in addition to continuing the definition of density by using the carrier area occupancy to form a definition that is suitable for describing heterogeneous traffic flow with no lane discipline.

In road traffic flow, the passenger car-equivalent (PCE) is used to convert vehicles of different lengths into an equivalent number of passenger cars [34], aiding in capacity analysis and the level of service determination. Similarly, the motorcycle-equivalent unit (MEU) and bicycle-equivalent unit (BEU) have been introduced to account for these vehicle types, as shown in Table 3, with corresponding documentation available in the HCM. However, in waterway transportation, the concept of a vessel-equivalent unit (VEU) has yet to be developed to address vessels of varying sizes.

For bicycle and motorcycle traffic, quantities such as headway, vehicle delay time, traffic speed, traffic volume, vehicle-occupied area, vehicle moving area, etc. are used as the basis for the calculating the PCE, MEU, and BEU. According to the formula and principle of calculation, these approaches in

Table 4. Differences and similarities between several methods to determine PCE, MEU, and BEU.

No.	Method	Basis for Determining Conversion Factors	Calculation Formula or Principle	Application Scenario		Remark
1	Overtaking	Number of vehicles overtaking	The ratio of the number of cars that surpass non-standard cars relative to the number of non-standard cars and the number of standard cars with lower performance relative to the number of standard cars with lower performance.	Lane discipline	Mixed traffic flow with two types of vehicles	Measurable
2	Headway	Headway	The ratio of the average lagged headway of non-standard vehicles to the average lagged headway of PCUs.	Lane discipline	Mixed traffic flow with two types of vehicles	Measurable
3	Delay	Vehicle delay time	The ratio of delays experienced by PCUs due to non-standard cars to delays experienced by PCUs due to other PCUs.	Lane discipline	Mixed traffic flow with two or more types of vehicles	Unmeasurable
4	Equal Speed	Flow speed	Remove a certain number of PCUs and add a certain number of non-standard vehicles to heterogeneous traffic flow so that the flow speeds of the two traffic flows are the same.	Lane discipline	Mixed traffic flow with two or more types of vehicles	Measurable
5	Macroscopic Relationships	LOS	Under the same performance indicators, a traffic flow that only includes PCUs and another mixed flow that includes both PCUs and non-standard vehicles with the same LOS are considered equivalent.	Lane discipline	Mixed traffic flow with two or three types of vehicles	Unmeasurable
6	Regression	Vehicle speed, headway	Estimate the PCE value of heavy vehicles driving on a dual-lane, two-way highway based on the relative deceleration caused by an equal amount of each vehicle type.	No lane discipline	Mixed traffic flow with two or more types of vehicles	Measurable
7	Capacity	Road capacity	According to the principle of equal capacity, when the traffic flow of standard and non-standard vehicles reaches saturation, the conversion coefficient is calculated based on the saturation flow under the same road width.	Lane discipline	Mixed traffic flow with two or more types of vehicles	Measurable
8			Calculated based on the fact that the traffic flow remains almost unchanged after reaching the road capacity.	No lane discipline	Mixed traffic flow with two or more types of vehicles	Measurable
9	Vehicle Moving Space	Vehicle moving space	The space occupied by non-standard cars relative to standard cars.	No lane discipline	Mixed traffic flow with two or more types of vehicles	Unmeasurable
10	Speed Area	Vehicle speed and area	The ratio between the speed ratio of the standard cars and non-standard cars to that of the space ratio of the cars.	No lane discipline	Mixed traffic flow with two or more types of vehicles	Measurable
11	Modified Density	Traffic density and width	The ratio of the area occupancy rate of non-standard cars to the area occupancy rate of standard cars.	No lane discipline	Mixed traffic flow with two or more types of vehicles	Measurable
12	Area Occupancy	Flow	Calculate the flow corresponding to standard vehicle traffic flow and mixed traffic flow under the same area occupancy rate.	No lane discipline	Mixed traffic flow with two or more types of vehicles	Measurable

are named the overtaking method, headway method, etc. [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57].

Methods 1–5 and 7 are applicable only to traffic flows that adhere to lane discipline, while Methods 1, 2, and 5 are restricted to scenarios involving two or three vehicle types. In contrast, Methods 6, 8, 9, and 10 are suited for environments without lane discipline and those exhibiting high rates of heterogeneity. However, the metrics and calculations for the vehicle delay time and movement space in Methods 3 and 9 present challenges, particularly regarding the subjective determination of the vehicle movement space, which complicates practical application.

3.2. The Mechanisms of Traffic Flow

The fundamental diagram of traffic flow depicting the pairwise relationships between flow, density, and speed reveals the inherent mechanism of traffic flow operation. This concept has been used to study roadway traffic, pedestrian traffic, and bicycle traffic. In roadway traffic, Greenshields et al. [58] initiated research on the fundamental diagram which inspired the development of traffic flow theory. Cassidy et al. [59,60] utilized the area occupancy method to characterize traffic density while studying the continuous flow of vehicles on multilane roads and bicycles. Wang et al. [61,62,63] also applied this method to study both bi-directional and uni-directional pedestrian traffic. The analysis of these studies revealed that, as shown in

Table 5. Comparison of fundamental diagrams of traffic flow.

Ref.	Domain	Author	Characteristics of Traffic Flow	Number of Lanes	Definition Method of Traffic Flow Characteristic	Completeness of Fundamental Diagram
[59]	Road	M. J. Cassidy	Continuous flow with lane discipline	Multiple lanes	Using area occupancy to indicate density	Complete
[60]	Bicycle	N. Guo et al.	Continuous flow	Multiple lanes	Using occupancy to indicate density	Complete
[61]	Pedestrian	P. Wang et al.	Continuous flow	Multiple lanes with bidirectional pedestrian flow	Using area occupancy to indicate density	Complete
[62]	Pedestrian	C.-J. Jin et al.	Continuous flow	Multiple lanes with bidirectional pedestrian flow	Using area occupancy to indicate density	Complete
[63]	Pedestrian	J. Zhang et al.	Continuous flow	Multiple lanes with bidirectional pedestrian flow	Using area occupancy to indicate density	Complete
[64]	Road	M. Treiber et al.	Continuous flow with lane discipline	Single lane	Using Edie’s definition to indicate density	Complete
[58]	Road	B. D. Greenshields et al.	Continuous flow with lane discipline	Single lane	Using Edie’s definition to indicate density	Complete
[65]	Road	Greenberg et al.	Continuous flow with lane discipline	Single lane	Using Edie’s definition to indicate density	Complete
[66]	Road	L. A. Pipes	Continuous flow with lane discipline	Single lane	Using Edie’s definition to indicate density	Complete
[67]	Road	D. Ni	Continuous flow with lane discipline	Single lane	Using Edie’s definition to indicate density	Complete

, regardless of whether the traffic involved single or multi-lane scenarios, with or without lane discipline, and irrespective of how traffic density was measured, the flow–density subplots of the fundamental diagrams showed an initial rise followed by a decline. All scenarios included both light and heavy traffic, providing a comprehensive view of the fundamental diagrams of traffic flow and indicating a discernible pattern.

Recent research using waterway traffic data has revealed a different pattern in the fundamental diagram than that using roadway traffic data [20,31,68]. Fundamental diagrams of waterway traffic flow usually also contain three sub-diagrams, which are used to describe the relationship between speed, density, and flow, respectively. The speed, density, and flow data are calculated based on the collected traffic flow data. For instance, the fundamental diagram of waterway traffic shown in Figure 6 shows data points clustered primarily in the free-flow region, with few, if any, points in the congested area. This raises the question of whether a fundamental diagram exists for waterway traffic. If it does, is this difference due to the way fundamental diagrams are presented, or is the traffic pattern genuinely different across types? Answering this question is crucial before formulating a theory for waterway traffic flow. Additionally, observing Figure 6 reveals that the speed–density and speed–flow relationships exhibit a triangular shape. This contrasts sharply with the results shown in the fundamental diagram of roadway traffic flow. The reasons behind this discrepancy warrant further exploration.

Based on the spatial and temporal movement trajectories of vessels, traffic flow characteristics can be calculated using Equations (1)–(3) to evaluate the aforementioned conjecture, assuming the total length of the channel is l nautical mile and the total width is 1 nautical mile, with a time interval of 1 min. Figure 7 illustrates the vessel spatial and temporal movement trajectory points. By observing the positions of the vessels (labeled 1–5) at two different times (T₁ and T₂) in the left channel, right channel, and pre-subdivided channel, the traffic flow characteristics can be determined both with and without channel subdivision. The results of these calculations are presented in

Table 6. Calculation results of traffic flow characteristics.

	Flow	Speed	Density
Without channel subdivision	5	96	480
Left channel	4	130	260
Right channel	6	73.3	440

.

$$V={\displaystyle \frac{Total displacement}{Total time}}$$

(1)

$$K={\displaystyle \frac{Total number of vessels}{L\ast W}}={\displaystyle \frac{Total time}{L\ast W\ast dt}}$$

(2)

$$Q=V\ast K={\displaystyle \frac{Total displacement}{L\ast W\ast dt}}$$

(3)

$V$ represents speed; $K$ represents density; $Q$ represents flow; $L \mathrm{a}\mathrm{n}\mathrm{d} W$ represent the length and width of the channel, respectively; and $dt$ represents the time interval.

As shown in Figure 8, The right channel exhibits the highest density, while the left channel has the lowest. The pre-subdivided channel shows the highest flow, followed by the right channel, with the left channel exhibiting the lowest flow. The computed traffic flow characteristics before and after channel subdivision reveal notable discrepancies: the density in the right channel exceeds that of the pre-subdivided channel, while its flow is lower. This trend indicates a decrease in flow alongside an increase in density, which aligns with the characteristics of congested flow. Therefore, differences in the current fundamental diagrams of road traffic and waterway traffic flows may be influenced by the way their fundamental diagrams are presented. This method shows promise for identifying ship traffic flow data in congested areas.

3.3. The Dynamics of Traffic Flow

The primary application of traffic flow theory is to model the dynamic changes in traffic flow conditions over time and space. For roadway traffic, as shown in

Table 7. Classification of traffic flow simulation models.

Geographical Scope	Level of Detail for Road Traffic	Level of Detail for Waterway Traffic
Macroscopic	Nation-wide, state-wide, regional	Nation-wide, regional
Mesoscopic	Regional, metropolitan, city-wide transportation network	Port-wide, canal-wide, strait-wide, regional
Microscopic	Highways, streets, sections	Small-scale waters, sections of the channel
Picoscopic	Sections, blocks, junctions, intersections	Confined water area, crossing water area, small-scale waters

and Table 8, traffic flow models vary in detail, encompassing a spectrum that includes macroscopic, mesoscopic, microscopic, and picoscopic levels. Due to the fact that some current waterway traffic flow models draw inspiration from those used in road traffic flow, it is possible to categorize these models into four levels based on their specific details. The Lighthill–Whitham–Richards (LWR) model [6] is macroscopic and describes traffic dynamics using variables such as flow, speed, and density. TRANSIMS [69,70], a mesoscopic model, employs cellular automata to depict vehicle motion and interaction. The cellular automata approach has been widely applied in research on waterway, pedestrian, and bicycle traffic [71,72,73]. At the microscopic level, the focus shifts to individual driver decisions and vehicle motions, including route choice, lane changes, gap acceptance, and car-following behavior [69,70,71]. In particular, car-following and lane-changing behaviors are closely linked to driving safety and collision avoidance, forming the foundation of these models.

With the advancement of big data and artificial intelligence, Peng et al. [74] utilized deep learning to develop an integrated model that addresses the limitations of separate models for driver behavior. However, this model is based on statistical methods and struggles to explain certain traffic flow phenomena. Liang et al. [75] constructed a physical–psychological model specifically for bicycle traffic; however, some parameters in this model are challenging to calibrate, making it difficult to be applied in waterway transportation.

Ni [76,77,78] proposed a field theory of traffic flow and formulated a picoscopic model that represents heterogeneous components in driving environments—such as roadways, vehicles, and traffic control devices—as homogeneous potential fields. Within this framework, drivers’ control strategies can be viewed as navigating through the overall field along the route with the lowest potential. Additionally, field theory can serve as a unifying framework for models at the macroscopic, mesoscopic, microscopic, and picoscopic levels, effectively bridging the gap between roadway and waterway traffic modeling.

Table 8. Comparison of traffic flow simulation models.

Geographical Scope	Road Traffic	Waterway Traffic	Bicycle and Pedestrian Traffic	Remark
Macroscopic	LWR [6]	-	-
Mesoscopic	TRANSIMS, cellular automata [69,70]	Cellular automata, multi-agent model [71,72]	Cellular automata [73]
Microscopic	GM, OVM, Newell [79,80,81]	GM, IDM, LCM, vessel-following model based on deep reinforcement learning [25,82]	IDM [83]	Following
	Lane-changing model [84]	-	-	Lane-changing
	Integrated model [74]	Artificial potential field models, optimal control models [85,86]	Psychological–physical force model [75]	Integrated
Picoscopic	Picoscopic model [76,77,78]	-	-	-

Table 8. Comparison of traffic flow simulation models.

Geographical Scope	Road Traffic	Waterway Traffic	Bicycle and Pedestrian Traffic	Remark
Macroscopic	LWR [6]	-	-
Mesoscopic	TRANSIMS, cellular automata [69,70]	Cellular automata, multi-agent model [71,72]	Cellular automata [73]
Microscopic	GM, OVM, Newell [79,80,81]	GM, IDM, LCM, vessel-following model based on deep reinforcement learning [25,82]	IDM [83]	Following
	Lane-changing model [84]	-	-	Lane-changing
	Integrated model [74]	Artificial potential field models, optimal control models [85,86]	Psychological–physical force model [75]	Integrated
Picoscopic	Picoscopic model [76,77,78]	-	-	-

4. The Challenge of Applying Roadway Traffic Flow Theory to Waterways

By synthesizing the research findings from various transportation modes discussed in the previous section, it becomes clear that, in terms of traffic flow properties, the definition of waterway traffic flow characteristics often adopts or references the methods used for road traffic flow. Similarly, when it comes to the mechanisms of traffic flow, the approach to plotting the fundamental diagram of waterway transportation is generally consistent with that used in road transportation. Moreover, several waterway traffic flow models have been developed based on existing road traffic flow models, highlighting the influence of road traffic flow theory on the development of waterway traffic flow theory.

However, it appears that the distinctions between waterway and road traffic modes may not have been fully acknowledged or adequately addressed. As a result, the implications of these differences for theoretical studies on waterway traffic flow might be overlooked. Despite significant efforts to extend road traffic flow theory to waterway transportation, applying road traffic flow models to waterway traffic continues to face challenges, largely due to these unresolved differences.

4.1. The Properties of Traffic Flow

• A precise and scientifically sound depiction of waterway traffic flow is essential for the comprehensive study of this field. Flow, density, and speed have long been important concepts for characterizing road traffic flow, and researchers in waterway traffic have similarly adopted these concepts. However, the significant variation in vessel sizes renders the traditional traffic flow characteristics used for roadways unsuitable and clearly unscientific for capturing the unique features of waterway traffic.
• In the field of road traffic, the concept of the PCE is used to convert vehicles of varying sizes into an equivalent number of passenger cars, allowing for a more objective and accurate reflection of road traffic conditions and composition. The question of how many passenger cars each vehicle should be converted to has led to the development of a relatively mature procedure in road traffic [29]. In contrast, waterway traffic is inherently heterogeneous and exhibits a notably high degree of variability. Unlike road traffic, which benefits from established and precise traffic-equivalent conversion standards, waterway traffic lacks a similarly scientific and comprehensive framework. This gap complicates the accurate description of waterway traffic characteristics and poses challenges in quantifying the level of service for waterways. Moreover, the absence of standardized metrics makes it even more difficult to compare the level of service across different temporal and spatial contexts.
• In contrast to road traffic, waterway traffic typically exhibits prominent two-dimensional characteristics, as vessels can move freely on a planar surface. Additionally, unlike the stationary pavement for roadway traffic, waterway traffic operates on water, which is itself in motion. Addressing these two significant discrepancies presents considerable challenges in formulating a comprehensive waterway traffic flow theory.

4.2. The Mechanisms of Traffic Flow

The fundamental diagram of traffic flow depicts the relationships between flow, speed, and density. This diagram can be utilized to address transportation problems such as minimizing travel delays, reducing traffic accidents, and enhancing the overall efficiency of transportation facilities, forming a significant part of traffic flow theory. In road transportation, research on the fundamental diagram has greatly contributed to effective traffic management solutions for authorities. In essence, the fundamental diagram serves as a core of roadway traffic flow theory.

In recent years, attempts to apply the fundamental diagram to waterway traffic have uncovered a significant lack of data regarding congested flow. This absence has led researchers to question whether a fundamental diagram for waterway traffic flow exists. If it does, it raises further inquiries about whether the missing data relate to how the fundamental diagram is presented or whether the shape of the waterway fundamental diagram differs from those of other transportation modes. Addressing these questions presents substantial challenges that must be overcome in the study of waterway traffic flow.

4.3. The Dynamics of Traffic Flow

• In waterway traffic, there are no physical boundaries, and vessel movement typically occurs in two dimensions. In contrast, road traffic flow is often represented through models that focus on car-following and lane-changing behaviors. Applying this research approach to waterway traffic requires addressing two key aspects. First, the control of vessels in both longitudinal and lateral directions are closely interconnected aspects of a single operational process. Therefore, effective models must account for both directions simultaneously. Second, vessel control involves complex maneuvering and reaction characteristics, making it significantly more intricate than vehicle control. Consequently, accurately simulating waterway traffic flow by directly applying road traffic flow theory presents considerable challenges.
• In road traffic flow, some researchers have developed integrated models using deep learning and other artificial intelligence methods to simulate traffic flow. This approach eliminates the need to construct mathematical models for activities such as car following and lane changing. However, these models inherently lack transparency, making it difficult to understand the underlying processes and analytically explain the resulting phenomena. When applying this methodology to waterway traffic, these inherent disadvantages remain and are not easily overcome.

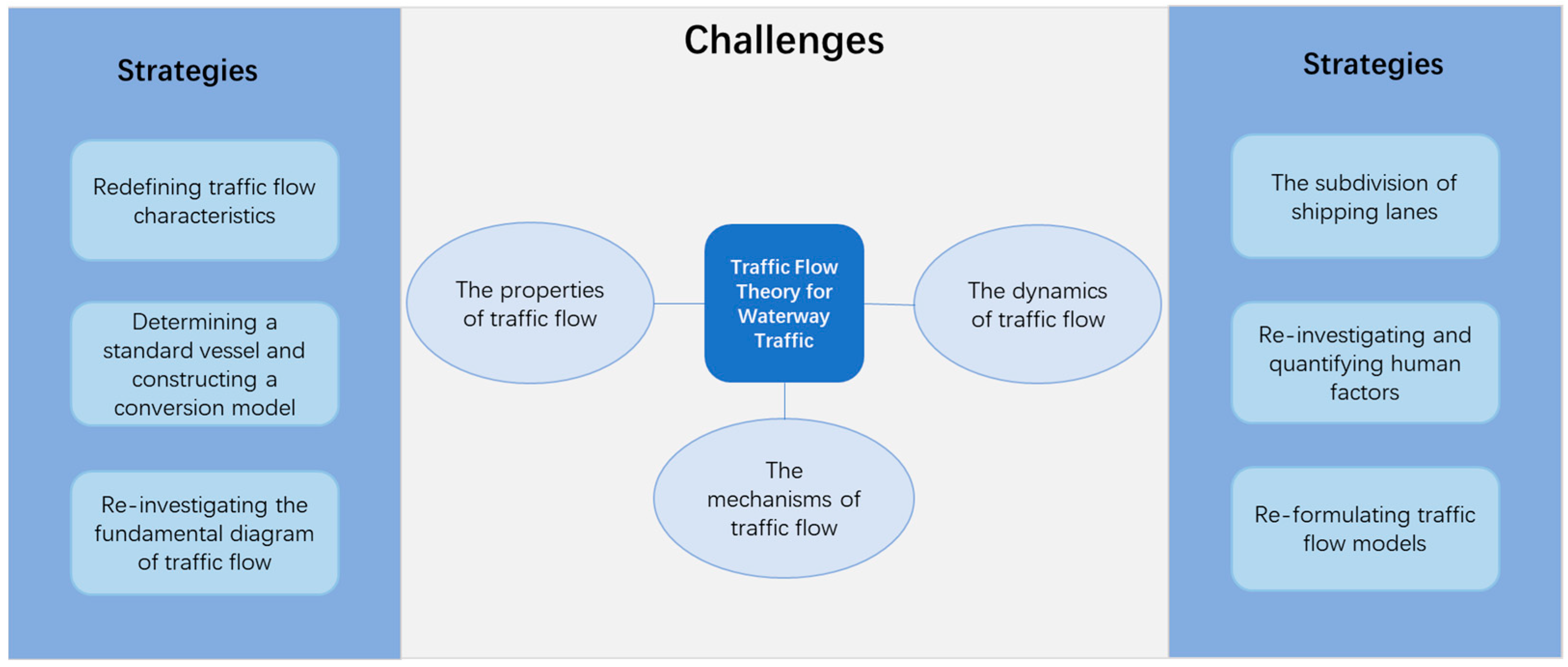
5. Recommendations for Future Research

Building on the challenges outlined in Section 4 and the existing literature, this section presents a list of critical issues that require further research and urgent attention in waterway traffic flow theory, along with brief details for the academic community. As shown in Figure 9, by addressing these challenges, advancements in waterway traffic flow theory can yield more effective and scientifically sound tools to tackle the issues faced by waterway transportation.

(a)

Re-investigating and quantifying human factors in waterway transportation: Reaction times and ship maneuvering characteristics are essential input parameters in traffic flow models. Vessel collision-avoidance behavior encompasses several key aspects, including the avoidance timing, magnitude, mode, and effect, which are critical for assessing the simulation accuracy of traffic flow models. Despite the importance of these parameters, few researchers have systematically organized data on reaction time and ship maneuvering characteristics. In the future, obtaining information about these parameters could involve extensive field data collection. Alternatively, inspired by advancements in the road traffic field, establishing an ergonomics laboratory for waterway traffic could be a viable option. Such a laboratory would facilitate the measurement and statistical analysis of crucial parameters related to waterway traffic, providing valuable insights for research and development.

(b)

Redefining traffic flow characteristics: In waterway traffic, it is not reasonable to rely on traditional methods of counting vessels to describe traffic flow characteristics. However, several studies have made progress in defining these characteristics [39,40,41]. Some definitions effectively address the challenges of characterizing traffic flow in lane-free environments and can indicate the size of carriers within the traffic flow. While these definitions have been successfully applied in road traffic, they have yet to be utilized in the context of waterway traffic. Additionally, waterway traffic flow characteristics may need to account for a vessel’s cross-sectional area, three-dimensional size, and even its displacement of water.

(c)

Determining a standard vessel and constructing a conversion model: Given the lack of a robust procedure for converting heterogeneous vessels into equivalent units, similar to the methods employed in road traffic, it is challenging to accurately describe waterway traffic flow characteristics. Therefore, the following measures are recommended for future research. (1) Determine standard ships and construct a conversion model: given the diversity of ship types, a standard vessel should be defined for each category. (2) Formulate a traffic conversion model: for waterway traffic, characterized by lane-free environments and high heterogeneity, the methods proposed in the literature [51,53,55] could provide valuable insights for studying waterway traffic flow. (3) Utilize effective water area: in addition to these three methods, the size of the effective water area occupied by both standard and non-standard ships during navigation could serve as a basis for developing ship-equivalent traffic conversion models. (4) Incorporate environmental factors: future models could also integrate environmental factors related to waterways to enhance their accuracy.

(d)

Re-investigating the fundamental diagram of traffic flow: To address the question of whether a fundamental diagram for waterway traffic flow exists, future research can determine traffic flow characteristics based on redefined parameters and the traffic conversion model. Given the absence of physical lane markings in waterways and the lack of data for congested flow, the fundamental diagram for waterway traffic can be obtained by using extensive AIS data. This approach may reveal the full picture of the fundamental diagram including conditions of light and heavy traffic.

(e)

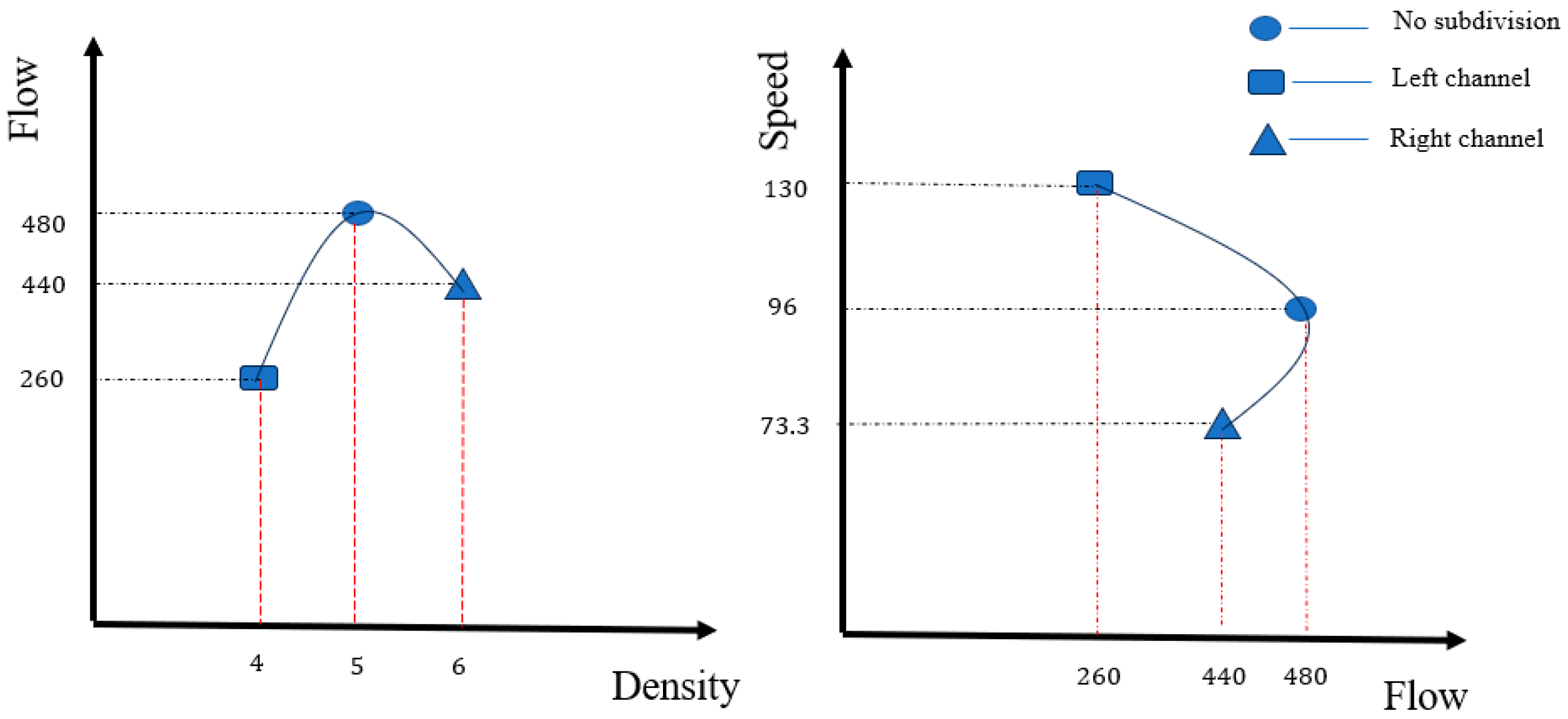
The subdivision of shipping lanes: Based on the simple experiment presented in Section 3.2 and illustrated in Figure 8, it appears that congestion flow has been discovered. The subdivision of shipping lanes seems to facilitate the verification of the existence of the fundamental diagram for waterway traffic flow and reveal the panorama of the fundamental diagram, thereby providing a more comprehensive understanding of this fundamental diagram. Given the close relationship between ship-following behavior and the fundamental diagram of waterway traffic, future research could explore methods for subdividing shipping lanes through ship-following analysis and techniques for plotting the fundamental diagram based on the subdivision of shipping lanes.

(f)

Re-formulating traffic flow models: Currently, waterway traffic flow simulations primarily rely on methodologies developed for road traffic, despite significant differences between the two. This reliance results in two main issues: insufficient detail in the traffic flow information and a substantial gap between a model’s accuracy and actual conditions. Future research should aim to address both these aspects. The literature [76,77,78] shows that the picoscopic traffic flow model not only unifies macroscopic, mesoscopic, and microscopic models but also contains detailed traffic flow information. Furthermore, this model is expected to facilitate the two-dimensional simulation of waterway traffic flow, greatly enhancing the accuracy of simulations. Therefore, establishing a picoscopic model for waterway traffic flow that considers the impact of multiple factors such as environment and dynamic water conditions will be a key focus for future development.

6. Conclusions

As the gap between demand and supply for water transport continues to widen, congestion and inefficiencies in waterways are escalating. Researchers have recognized the need for solutions and attempted to apply the findings from roadway traffic flow theory to waterway transportation to develop effective strategies for alleviating these challenges. However, due to the unique characteristics of waterway transportation, the direct applicability of this theory remains questionable.

To enhance the application of road traffic flow theory in the context of waterway traffic flow, this study primarily examines the differences among various modes of transportation and analyzes their effects on waterway traffic flow. The analysis is conducted from multiple perspectives, such as the carrier scale, the response time, the navigation environment, and traffic organization and management. It analyzes the existing definitions of traffic flow characteristics, the fundamental diagram of traffic flow, and traffic flow simulation models in light of these differences identified in this paper. Finally, this paper highlights the main challenges and issues encountered in the direct application of road traffic flow theory in waterway transportation and offers suggestions for future research directions.

Through the study of re-investigating and quantifying human factors in waterway transportation, redefining traffic flow characteristics, determining a standard vessel and constructing a conversion model, re-investigating the fundamental diagram of traffic flow, subdividing shipping lanes, and re-formulating traffic flow models, a method for studying waterway traffic flow can hopefully be developed in the future. We advocate for an approach to waterway traffic flow research that not only emphasizes its unique characteristics but also examines the differences and similarities with other modes of transportation. This perspective will facilitate the more reasonable and scientific application of traffic flow theory methods and findings to waterway traffic.