Aeroelastic Simulation of Full-Machine Wind Turbines Using a Two-Way Fluid-Structure Interaction Approach
Abstract
:1. Introduction
2. Methodology
2.1. Fluid Dynamics Model
2.1.1. Governing Equations
2.1.2. Turbulence Model
2.1.3. Numerical Methods
2.2. Structural Model
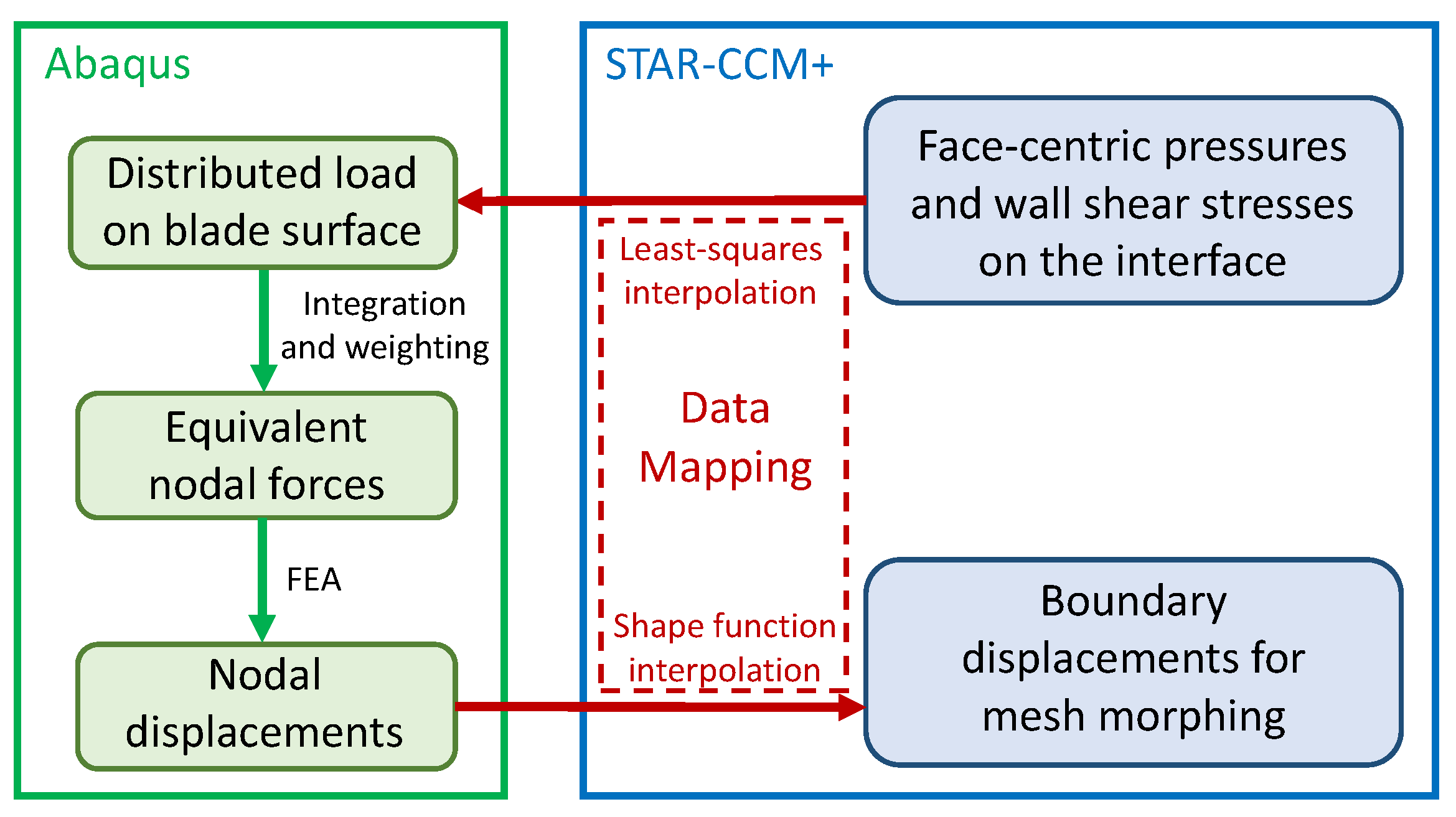
2.3. FSI Coupling Method
2.4. Model Setup
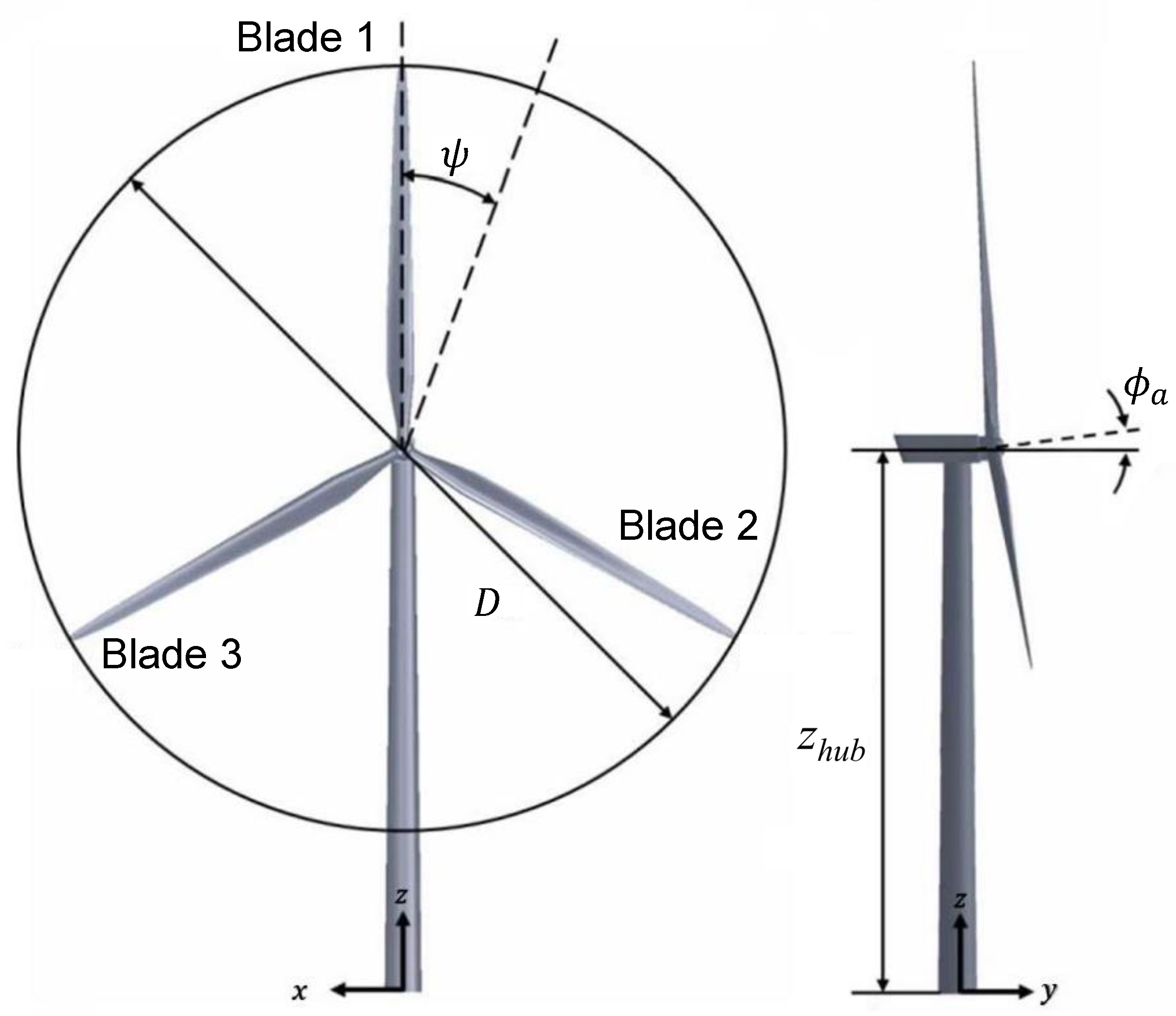
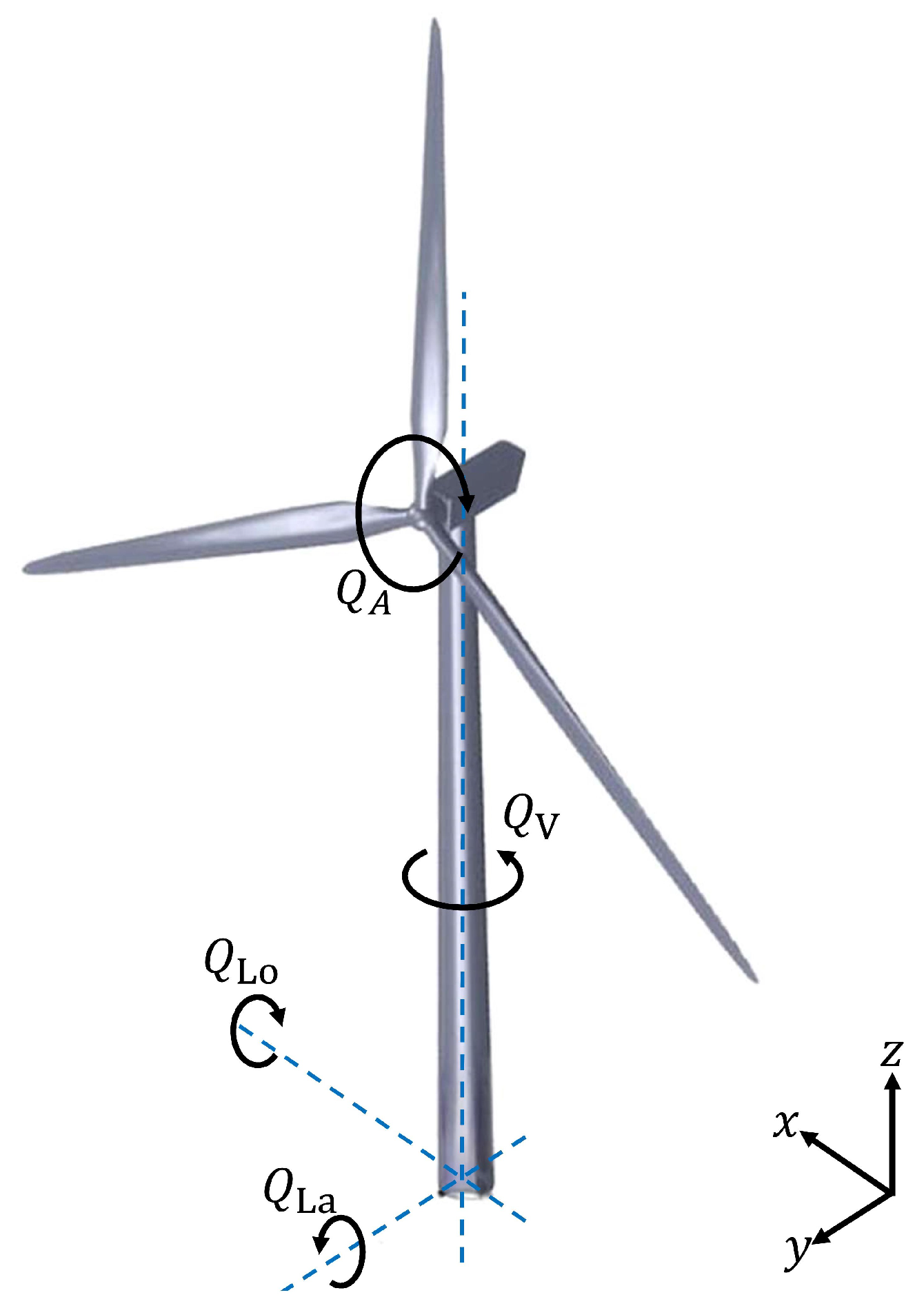
2.4.1. Wind Turbine Model
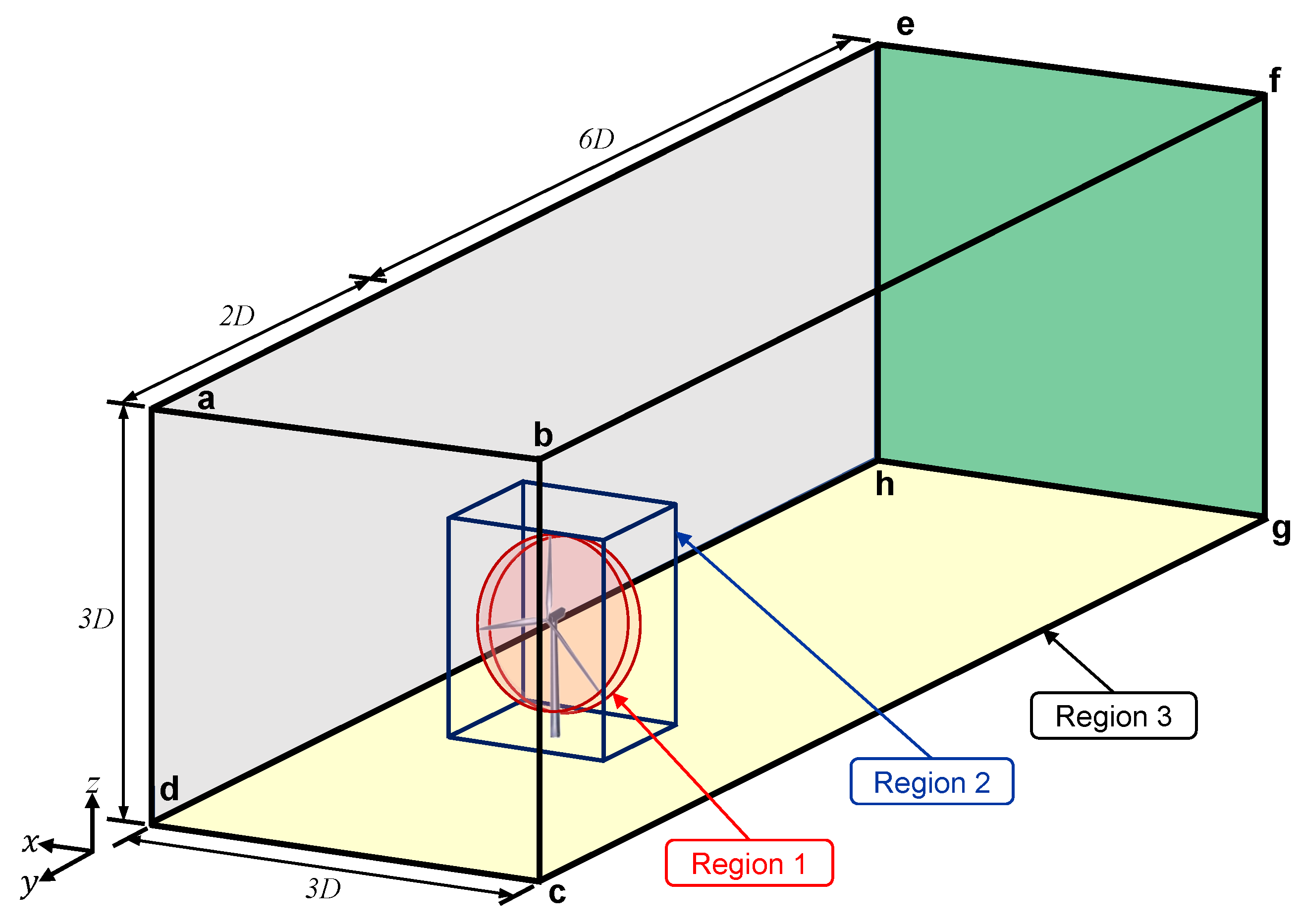
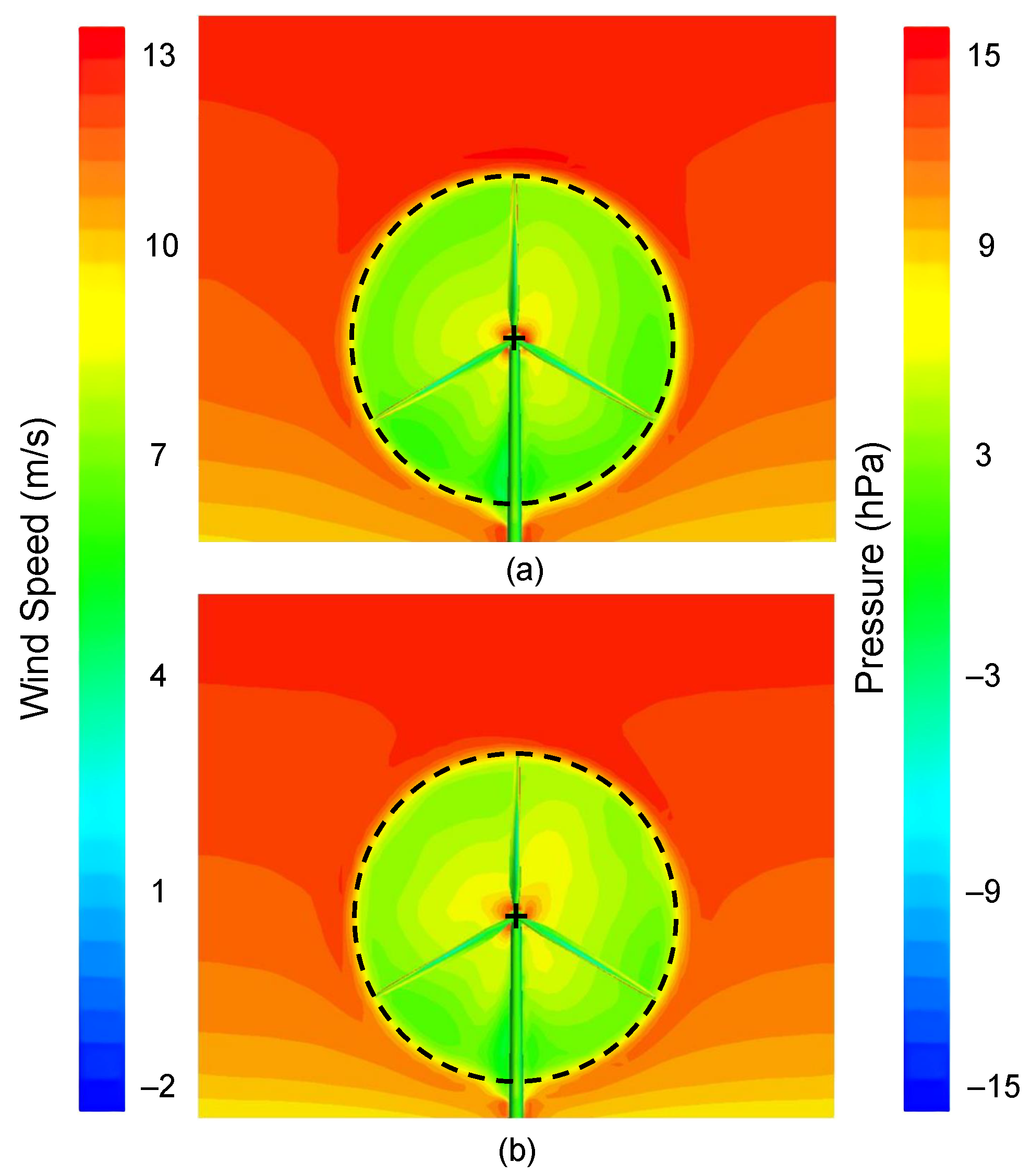
2.4.2. CFD Modeling
2.4.3. Finite Element Model
2.4.4. Coupling Settings
2.5. Numerical Verification
2.6. OpenFAST Simulation
3. Results and Discussions
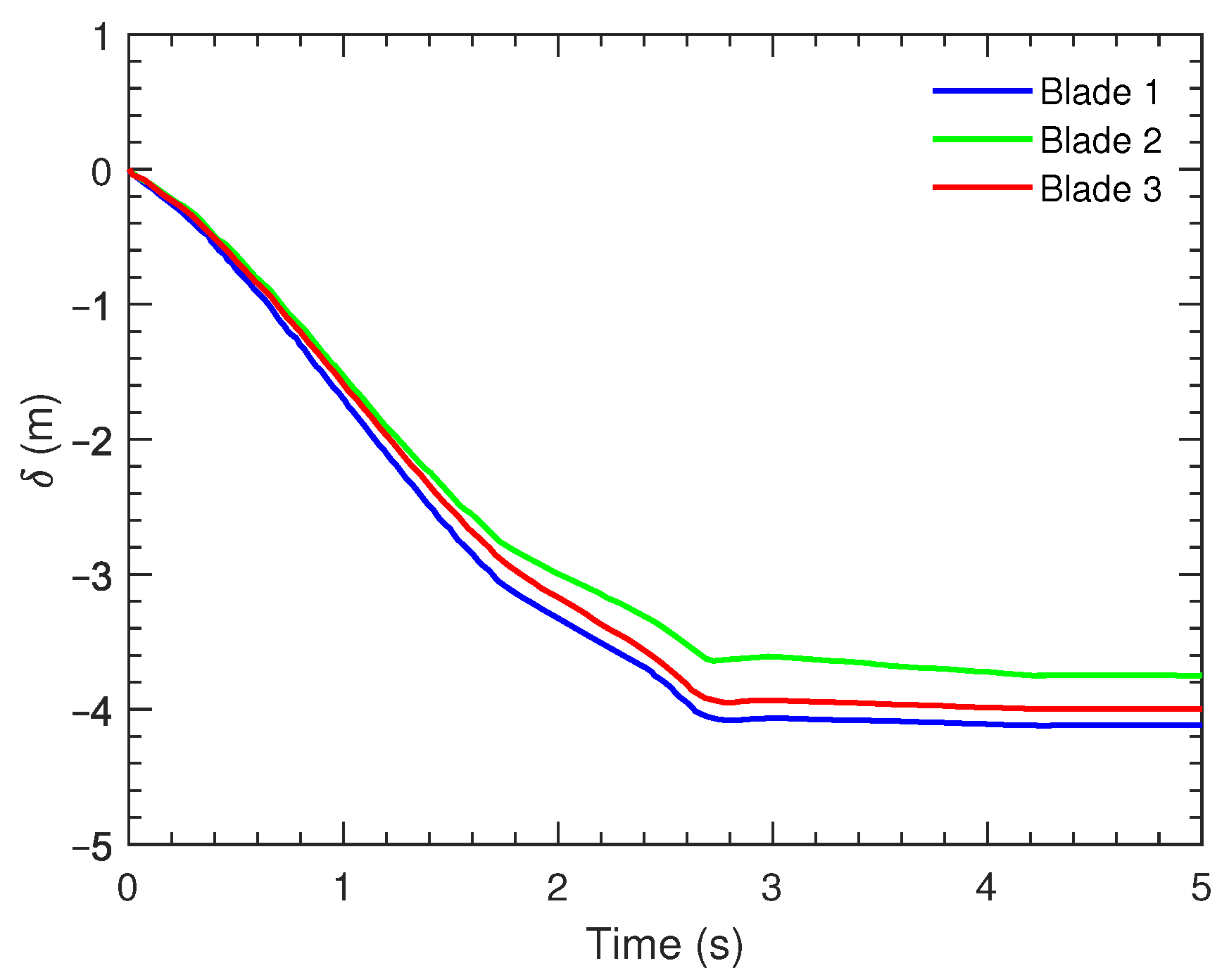
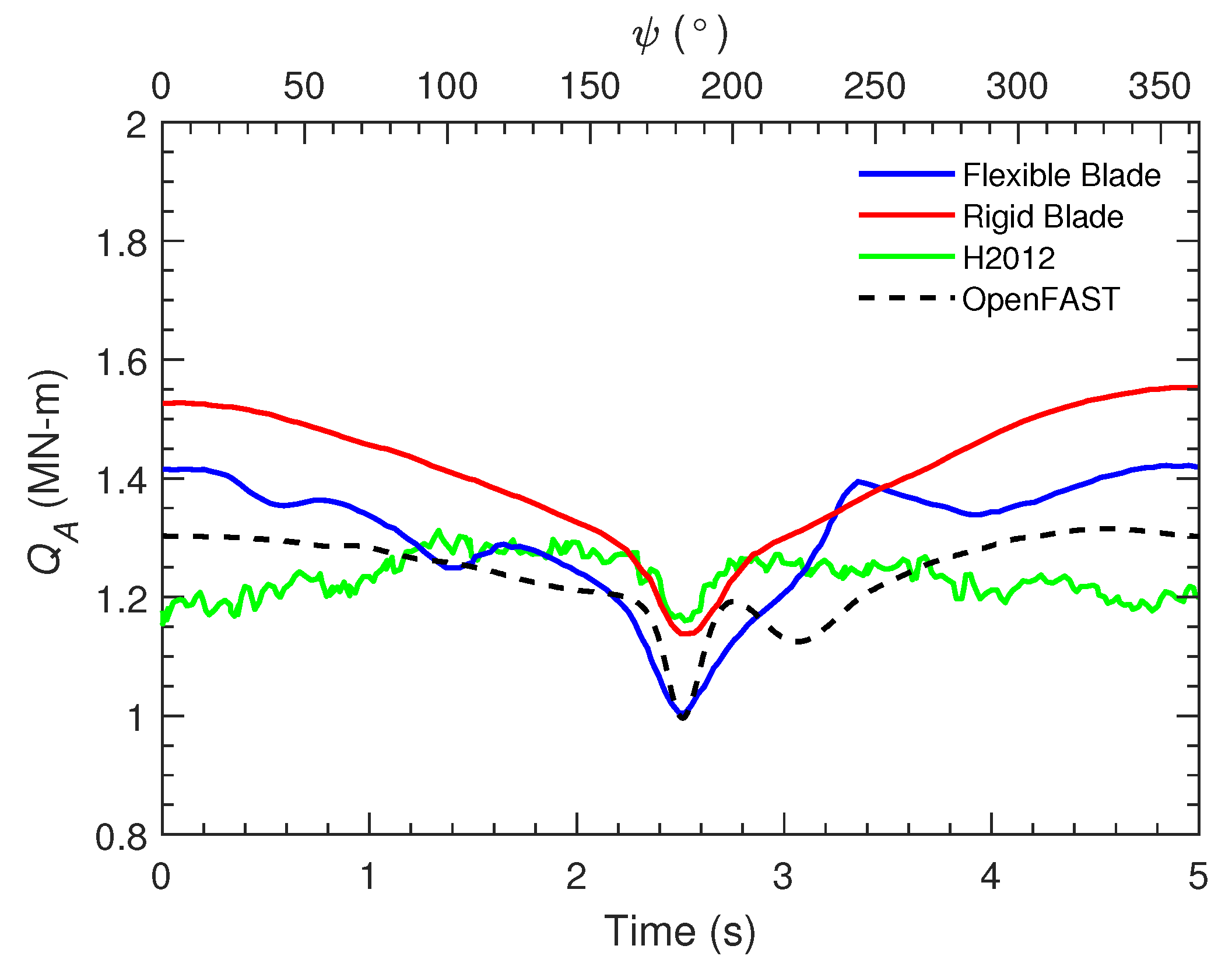
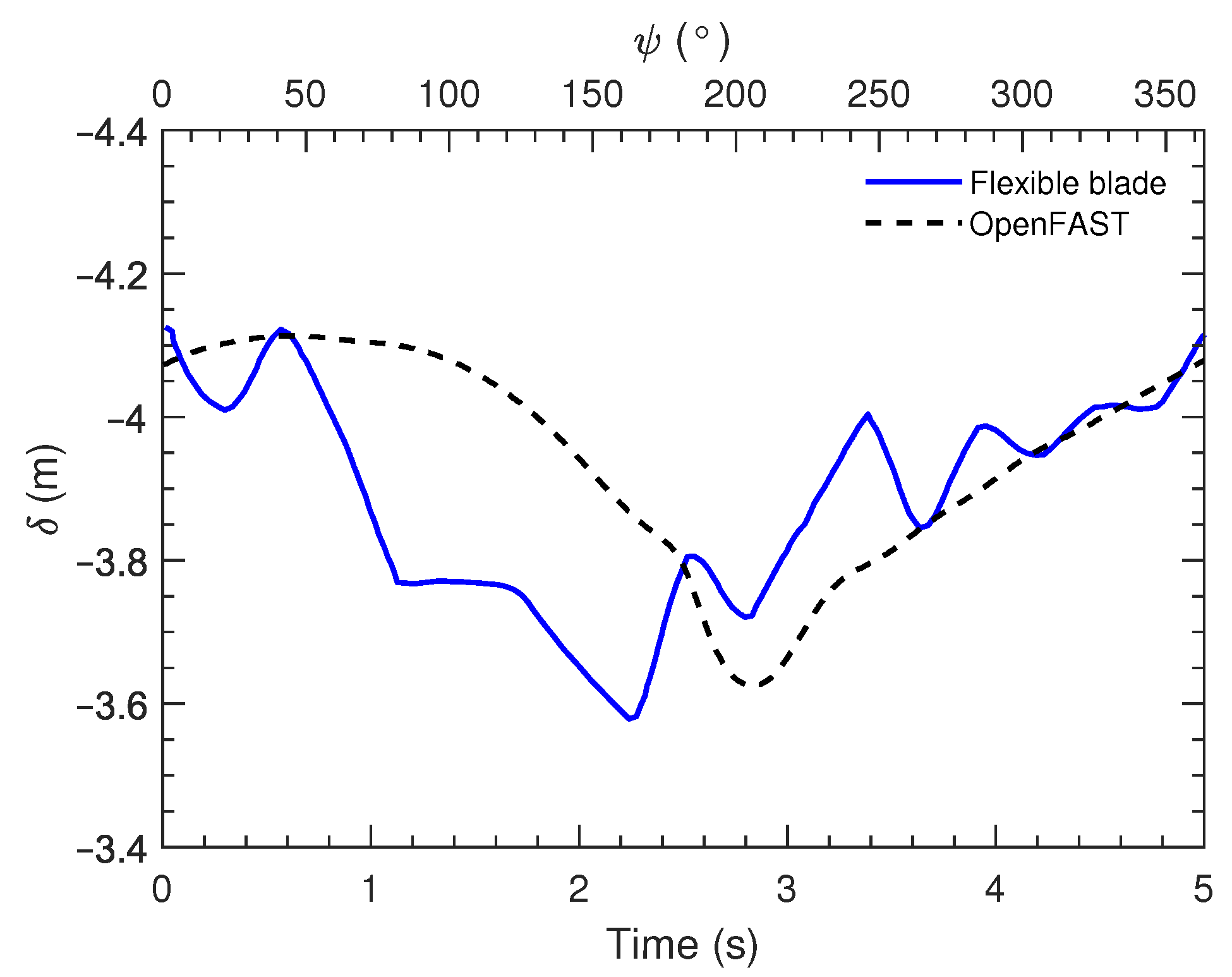
3.1. Blade Load and Deformation
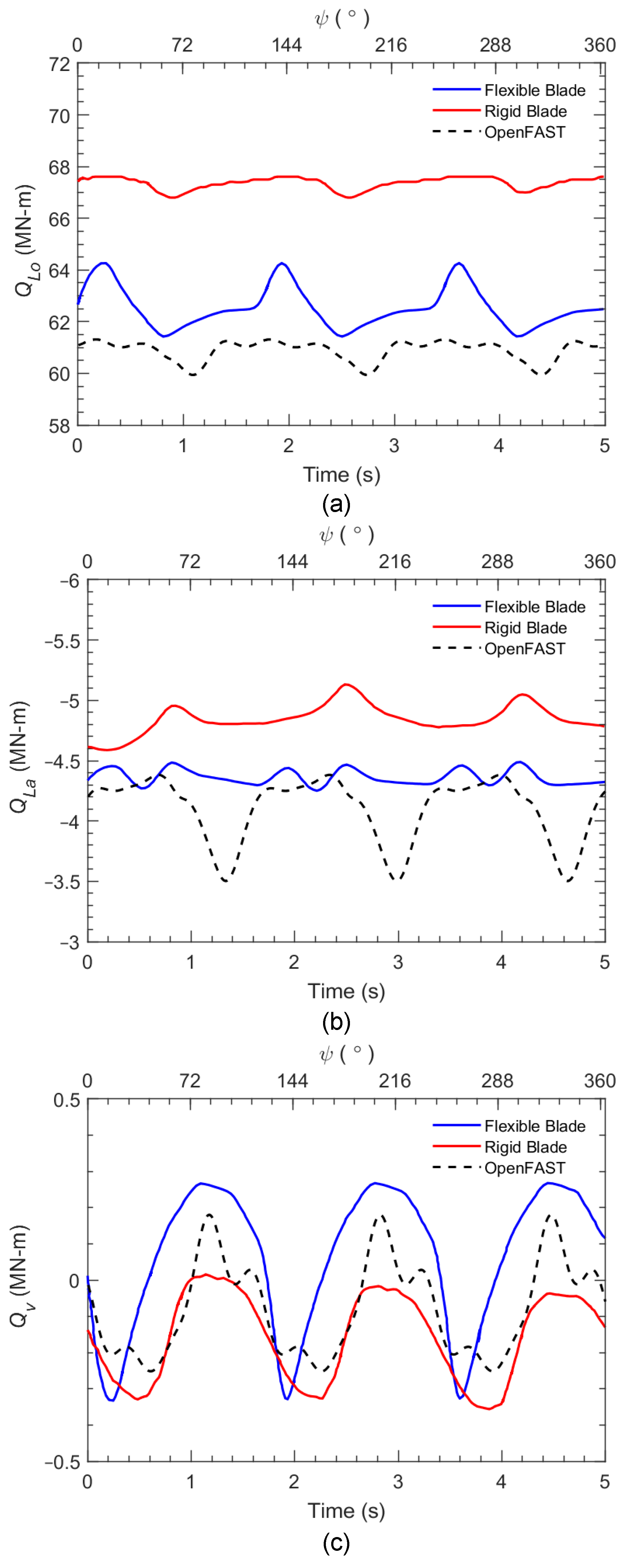
3.2. Tower Base Loads
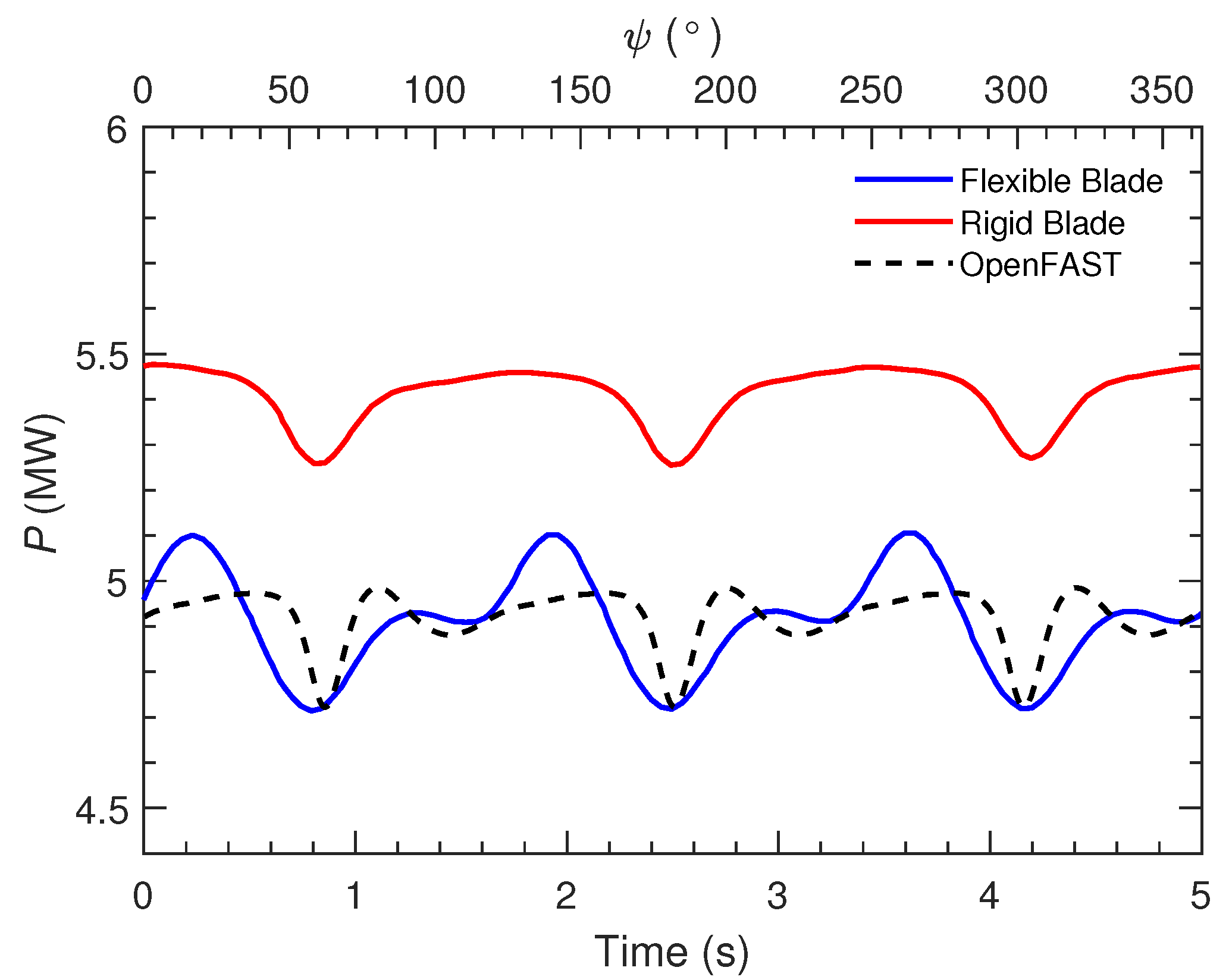
3.3. Turbine Power
3.4. Computational Time
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALM | Actuator Line Model |
| ADM | Actuator Disk Model |
| BEMT | Blade Element Momentum Theory |
| CFD | Computational Fluid Dynamics |
| CPU | Central Processing Unit |
| FEA | Finite Element Analysis |
| FSI | Fluid–Structure Interaction |
| H2012 | Hsu and Bazilevs [30] |
| IEC | International Electrotechnical Commission |
| NREL | National Renewable Energy Lab |
| NWTC | National Wind Technology Center |
| RNA | Rotor-Nacelle Assembly |
| RANS | Reynolds-averaged Navier–Stokes |
| SCADA | Supervisory Control and Data Acquisition |
| SIMPLE | Semi-implicit Method for Pressure-linked Equations |
| SST | Shear Stress Transport |
Symbols
| D | Rotor diameter |
| Turbulent cross-diffusion term in transport equations | |
| Discretization error of turbine power | |
| , , | Blade Young’s modulus in the edgewise, flapwise, and spanwise directions |
| Nodal external force vector of wind loads | |
| G | Blade shear modulus |
| , | Production terms in transport equations |
| Gravitational acceleration vector | |
| Turbulence intensity | |
| Identity matrix | |
| k | Turbulent kinetic energy |
| Inlet turbulent kinetic energy | |
| Turbulence characteristic length scale | |
| , , | Nodal matrices of mass, damping, and stiffness |
| P | Turbine power |
| p | Averaged dynamic pressure |
| Aerodynamic torque about the rotor axis | |
| , , | Lateral, longitudinal, and vertical moments about the tower base |
| , , | Acceleration, velocity, and displacement vectors at the structural mesh nodes |
| t | Time |
| Time step for blade deflection | |
| Time step for rotor rotation | |
| Mean wind speed at the inlet | |
| Mean wind speed at hub height | |
| Averaged wind velocity vector | |
| Distances along the longitudinal, lateral, and vertical directions | |
| , | Dissipation terms in transport equations |
| Dimensionless wall distance | |
| Hub height | |
| Power law exponent | |
| Blade tip displacement | |
| Turbulent viscosity | |
| Constant density of dry air | |
| , | Turbulent Prandtl numbers in transport equations |
| Viscous shear stress | |
| Rotor tilt angle | |
| Azimuthal angle | |
| Specific dissipation rate | |
| Inlet specific dissipation rate |
References
- NREL. OpenFAST Documentation. 2019. Available online: https://openfast.readthedocs.io (accessed on 14 November 2024).
- DNV GL. Bladed Theory Manual, version 4.8; DNV GL-Energy: Oslo, Norway, 2016. [Google Scholar]
- Larsen, T.J.; Hansen, A.M. How 2 HAWC2, The User’s Manual; Risø National Laboratory: Roskilde, Denmark, 2007. [Google Scholar]
- Mortensen, N.G.; Landberg, L.; Rathmann, O.; Frank, H.; Troen, I.; Petersen, E. Wind atlas analysis and application program (WAsP). In Wind Energy Department: Scientific and Technical Progress 1999–2000; Forskningscenter Risoe: Roskilde, Denmark, 2001. [Google Scholar]
- Larsen, T.J.; Hansen, A.M.; Buhl, T. Aeroelastic effects of large blade deflections for wind turbines. In Special Topic Conference: The Science of Making Torque from Wind; Delft University of Technology: Delft, The Netherlands, 2004; pp. 238–246. [Google Scholar]
- Lu, H.; Porté-Agel, F. Large-eddy simulation of a very large wind farm in a stable atmospheric boundary layer. Phys. Fluids 2011, 23, 065101. [Google Scholar] [CrossRef]
- Churchfield, M.J.; Lee, S.; Michalakes, J.; Moriarty, P.J. A numerical study of the effects of atmospheric and wake turbulence on wind turbine dynamics. J. Turbul. 2012, 13, N14. [Google Scholar] [CrossRef]
- Sørensen, J.N.; Shen, W.Z. Numerical modeling of wind turbine wakes. J. Fluids Eng. 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Ravensbergen, M.; Mohamed, A.B.; Korobenko, A. The actuator line method for wind turbine modelling applied in a variational multiscale framework. Comput. Fluids 2020, 201, 104465. [Google Scholar] [CrossRef]
- Calaf, M.; Meneveau, C.; Meyers, J. Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 2010, 22, 015110. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Wu, Y.T.; Lu, H.; Conzemius, R.J. Large-eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms. J. Wind Eng. and Ind. Aerodyn. 2011, 99, 154–168. [Google Scholar] [CrossRef]
- Behrouzifar, A.; Darbandi, M. An improved actuator disc model for the numerical prediction of the far-wake region of a horizontal axis wind turbine and its performance. Energy Conv. Manag. 2019, 185, 482–495. [Google Scholar] [CrossRef]
- Simisiroglou, N.; Breton, S.P.; Ivanell, S. Validation of the actuator disc approach using small-scale model wind turbines. Wind Energy Sci. 2017, 2, 587–601. [Google Scholar] [CrossRef]
- Sørensen, J.N.; Nilsson, K.; Ivanell, S.; Asmuth, H.; Mikkelsen, R.F. Analytical body forces in numerical actuator disc model of wind turbines. Renew. Energy 2020, 147, 2259–2271. [Google Scholar] [CrossRef]
- Hansen, M.H. Vibrations of a three-bladed wind turbine rotor due to classical flutter. In Proceedings of the ASME 2002 Wind Energy Symposium, Reno, NV, USA, 14–17 January 2002; Volume 7476, pp. 256–266. [Google Scholar]
- Kiendl, J.; Bazilevs, Y.; Hsu, M.C.; Wüchner, R.; Bletzinger, K.U. The bending strip method for isogeometric analysis of Kirchhoff–Love shell structures comprised of multiple patches. Comput. Methods Appl. Mech. Eng. 2010, 199, 2403–2416. [Google Scholar] [CrossRef]
- Şener, Ö.; Farsadi, T.; Ozan Gözcü, M.; Kayran, A. Evaluation of the effect of spar cap fiber angle of bending–torsion coupled blades on the aero-structural performance of wind turbines. J. Sol. Energy Eng. 2018, 140, 041004. [Google Scholar] [CrossRef]
- Ju, D.; Sun, Q. Modeling of a wind turbine rotor blade system. J. Vib. Acoust. 2017, 139, 051013. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Hsu, M.C.; Kiendl, J.; Benson, D. A computational procedure for prebending of wind turbine blades. Int. J. Numer. Methods Eng. 2012, 89, 323–336. [Google Scholar] [CrossRef]
- Roul, R.; Kumar, A. Fluid–structure interaction of wind turbine blade using four different materials: Numerical investigation. Symmetry 2020, 12, 1467. [Google Scholar] [CrossRef]
- Wang, L.; Quant, R.; Kolios, A. Fluid structure interaction modelling of horizontal-axis wind turbine blades based on CFD and FEA. J. Wind Eng. Ind. Aerodyn. 2016, 158, 11–25. [Google Scholar] [CrossRef]
- Zhu, R.; Chen, D.d.; Wu, S.w. Unsteady flow and vibration analysis of the horizontal-axis wind turbine blade under the fluid–structure interaction. Shock Vib. 2019, 2019, 3050694. [Google Scholar] [CrossRef]
- Ageze, M.B.; Hu, Y.; Wu, H. Comparative study on uni-and bi-directional fluid structure coupling of wind turbine blades. Energies 2017, 10, 1499. [Google Scholar] [CrossRef]
- Benra, F.K.; Dohmen, H.J.; Pei, J.; Schuster, S.; Wan, B. A comparison of one-way and two-way coupling methods for numerical analysis of fluid–structure interactions. J. Appl. Math. 2011, 2011, 853560. [Google Scholar] [CrossRef]
- Della Posta, G.; Leonardi, S.; Bernardini, M. A two-way coupling method for the study of aeroelastic effects in large wind turbines. Renew. Energy 2022, 190, 971–992. [Google Scholar] [CrossRef]
- Dose, B.; Rahimi, H.; Herráez, I.; Stoevesandt, B.; Peinke, J. Fluid–structure coupled computations of the NREL 5 MW wind turbine by means of CFD. Renew. Energy 2018, 129, 591–605. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Hsu, M.C.; Kiendl, J.; Wüchner, R.; Bletzinger, K.U. 3D simulation of wind turbine rotors at full scale. Part II: Fluid–structure interaction modeling with composite blades. Int. J. Numer. Methods Fluids 2011, 65, 236–253. [Google Scholar] [CrossRef]
- Grinderslev, C.; González Horcas, S.; Sørensen, N.N. Fluid–structure interaction simulations of a wind turbine rotor in complex flows, validated through field experiments. Wind. Energy 2021, 24, 1426–1442. [Google Scholar] [CrossRef]
- Santo, G.; Peeters, M.; Van Paepegem, W.; Degroote, J. Dynamic load and stress analysis of a large horizontal axis wind turbine using full scale fluid–structure interaction simulation. Renew. Energy 2019, 140, 212–226. [Google Scholar] [CrossRef]
- Hsu, M.C.; Bazilevs, Y. Fluid–structure interaction modeling of wind turbines: Simulating the full machine. Comput. Mech. 2012, 50, 821–833. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Korobenko, A.; Deng, X.; Yan, J. Novel structural modeling and mesh moving techniques for advanced fluid–structure interaction simulation of wind turbines. Int. J. Numer. Methods Eng. 2015, 102, 766–783. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, Z.; Li, W.; Hu, G. LES simulation study of wind turbine aerodynamic characteristics with fluid–structure interaction analysis considering blade and tower flexibility. Energy 2023, 282, 128840. [Google Scholar] [CrossRef]
- Felippa, C.A.; Park, K.C.; Farhat, C. Partitioned analysis of coupled mechanical systems. Comput. Methods Appl. Mech. Eng. 2001, 190, 3247–3270. [Google Scholar] [CrossRef]
- Förster, C.; Wall, W.A.; Ramm, E. Artificial added mass instabilities in sequential staggered coupling of nonlinear structures and incompressible viscous flows. Comput. Methods Appl. Mech. Eng. 2007, 196, 1278–1293. [Google Scholar] [CrossRef]
- Lin, Y. Aerodynamic prediction of horizontal-axis offshore wind turbine via a two-way fluid–structure interaction approach. Master’s Thesis, Department of Mechanical Engineering, College of Engineering, National Taiwan University of Science and Technology, Taipei, Taiwan, 2014. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference wind Turbine for Offshore System Development; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009. [Google Scholar]
- CD-Adapco. User Guide, Star-CCM+ (9.02.007-R8); CD-adapco: Melville, NY, USA, 2014. [Google Scholar]
- Menter, F. Zonal two equation kw turbulence models for aerodynamic flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993; p. 2906. [Google Scholar]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Elsevier: Amsterdam, The Netherlands, 1983; pp. 54–73. [Google Scholar]
- Simulia. Abaqus/CAE User’s Manual, version 6.13; Simulia/Dassault: Johnston, RI, USA, 2014. [Google Scholar]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Lakshmynarayanana, P.A. Application of 3D-CFD Modelling for Dynamic Behaviour of Ship in Waves. Ph.D. Thesis, University of Southampton, Southampton, UK, 2017. [Google Scholar]
- Buhl, M. The NWTC design-codes suite: An overview. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; p. 592. [Google Scholar]
- IEC. Wind Turbines-Part 1: Design Requirements; Technical Report; International Electrotechnical Commission and others: Geneva, Switzerland, 2007. [Google Scholar]
- Lindenburg. Modelling of the LMH64-5 Blade; Technical Report; Energy Research Center of the Netherlands: Petten, The Netherlands, 2002; DOWEC Dutch Offshore Wind Energy Converter 1997–2003 Public Reports [CD-ROM], DOWEC 10083_001, DOWEC-02-KL-083/0. [Google Scholar]
- Kooijman, H.J.T.; Lindenburg, C.; Winkelaar, D.; van der Hooft, E. Pre-Design: Aero-Elastic Modeling of the DOWEC 6 MW Pre-Design in PHATAS; Technical Report; Energy Research Center of the Netherlands: Petten, The Netherlands, 2003; DOWEC Dutch Offshore Wind Energy Converter 1997–2003 Public Reports [CD-ROM], DOWEC 10046_009, ECN-CX–01-135. [Google Scholar]
- Richardson, L.F., IX. The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam. Philos. Trans. Royal Soc. London. Ser. A Contain. Papers Math. Phys. Character 1911, 210, 307–357. [Google Scholar]
- Jonkman, J.; Buhl, M. FAST User’s Guide; Technical Report; National Renewable Energy Laboratory: Golden, CO, USA, 2005. [Google Scholar]
- Jonkman, J.M.; Hayman, G.; Jonkman, B.; Damiani, R.; Murray, R. AeroDyn v15 User’s Guide and Theory Manual; NREL Draft Report 46; National Renewable Energy Lab.: Golden, CO, USA, 2015. [Google Scholar]
- Jonkman, B. Turbsim User’s Guide v2.00.00; Technical Report; National Renewable Energy Lab.: Golden, CO, USA, 2014. [Google Scholar]
- Bak, C.; Madsen, H.A.; Johansen, J. Influence from blade-tower interaction on fatigue loads and dynamics (poster). In Proceedings of the 2001 European Wind Energy Conference and Exhibition (EWEC’01), WIP-Renewable Energies, Copenhagen, Denmark, 2–6 July 2001; pp. 394–397. [Google Scholar]







| Properties | Values |
|---|---|
| Power rating | 5 MW |
| Rotor type | Upwind/ 3-bladed |
| Rotor diameter (D) | 126 m |
| Hub height () | 90 m |
| Cut-in, rated, cut-out speed | 3, 11.4, 25 m s−1 |
| Rated rotor speed | 12.1 rpm |
| Faces | Conditions |
|---|---|
| abcd, aehd, abfe, and bfgc | Inlet |
| efgh | Outlet |
| dcgh | No-slip wall |
| Metrics | Results |
|---|---|
| Maximum skewness angle | (<) |
| Minimum cell quality | 0.06 (<) |
| Maximum volume change | 0.06 (>0.01) |
| Spanwise | Eflap | Eedge | Espan | G |
|---|---|---|---|---|
| Locations (m) | (GPa) | (GPa) | (GPa) | (GPa) |
| 2.7 | 24.7479 | 24.6171 | 3.4351 | 3.4508 |
| 10.7 | 4.5577 | 1.8842 | 0.8516 | 0.2086 |
| 21.7 | 3.2320 | 1.4109 | 0.6336 | 0.0640 |
| 31.7 | 4.6679 | 2.0857 | 0.5386 | 0.0557 |
| 41.7 | 5.1216 | 2.2581 | 0.4276 | 0.0442 |
| 51.7 | 6.1338 | 2.1226 | 0.3199 | 0.0357 |
| 63.0 | 28.3333 | 7.6372 | 0.1262 | 0.2870 |
| Refinement | Total Grid Number | P (MW) | Relative Error |
|---|---|---|---|
| 1 | 3.88 | −28.4% | |
| 2 | 5.15 | −5.0% | |
| 3 | 5.30 | −2.2% | |
| 4 | 5.41 | −0.2% | |
| 5 | 5.42 | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, N.-Y.; Lam, J.K.; Lin, Y.; Chau, S.-W. Aeroelastic Simulation of Full-Machine Wind Turbines Using a Two-Way Fluid-Structure Interaction Approach. J. Mar. Sci. Eng. 2024, 12, 2271. https://doi.org/10.3390/jmse12122271
Lu N-Y, Lam JK, Lin Y, Chau S-W. Aeroelastic Simulation of Full-Machine Wind Turbines Using a Two-Way Fluid-Structure Interaction Approach. Journal of Marine Science and Engineering. 2024; 12(12):2271. https://doi.org/10.3390/jmse12122271
Chicago/Turabian StyleLu, Nan-You, Jia Kai Lam, Yu Lin, and Shiu-Wu Chau. 2024. "Aeroelastic Simulation of Full-Machine Wind Turbines Using a Two-Way Fluid-Structure Interaction Approach" Journal of Marine Science and Engineering 12, no. 12: 2271. https://doi.org/10.3390/jmse12122271
APA StyleLu, N.-Y., Lam, J. K., Lin, Y., & Chau, S.-W. (2024). Aeroelastic Simulation of Full-Machine Wind Turbines Using a Two-Way Fluid-Structure Interaction Approach. Journal of Marine Science and Engineering, 12(12), 2271. https://doi.org/10.3390/jmse12122271






