Numerical Simulation of Hydrodynamic Performance of an Offshore Oscillating Water Column Wave Energy Converter Device
Abstract
:1. Introduction
2. Numerical Method
2.1. Governing Equations
2.2. Numerical Model Setup
3. Model Validation
3.1. Convergence Test for Numerical Computational Grids
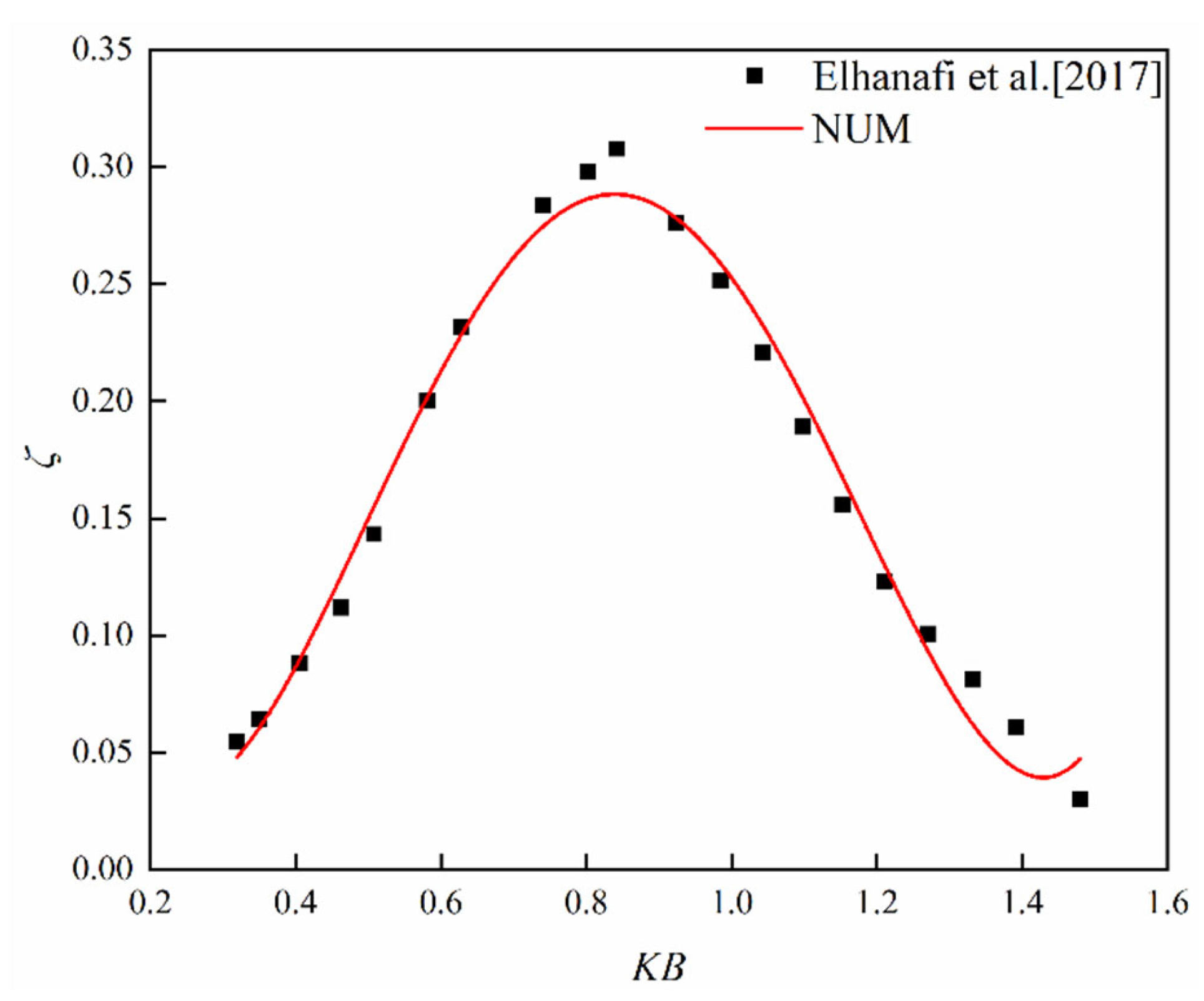
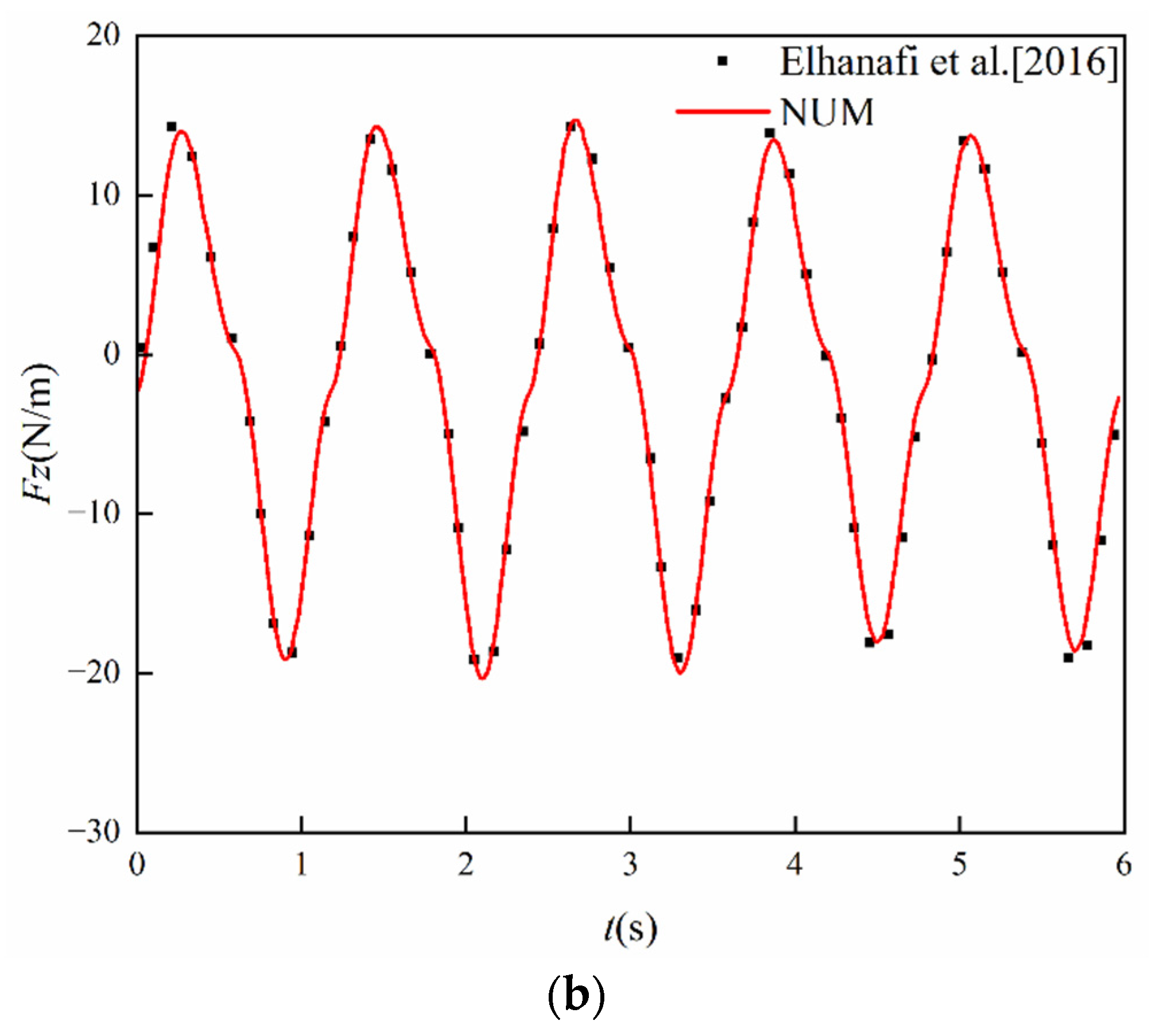
3.2. Verification with Single OWC Results
4. Results and Discussion
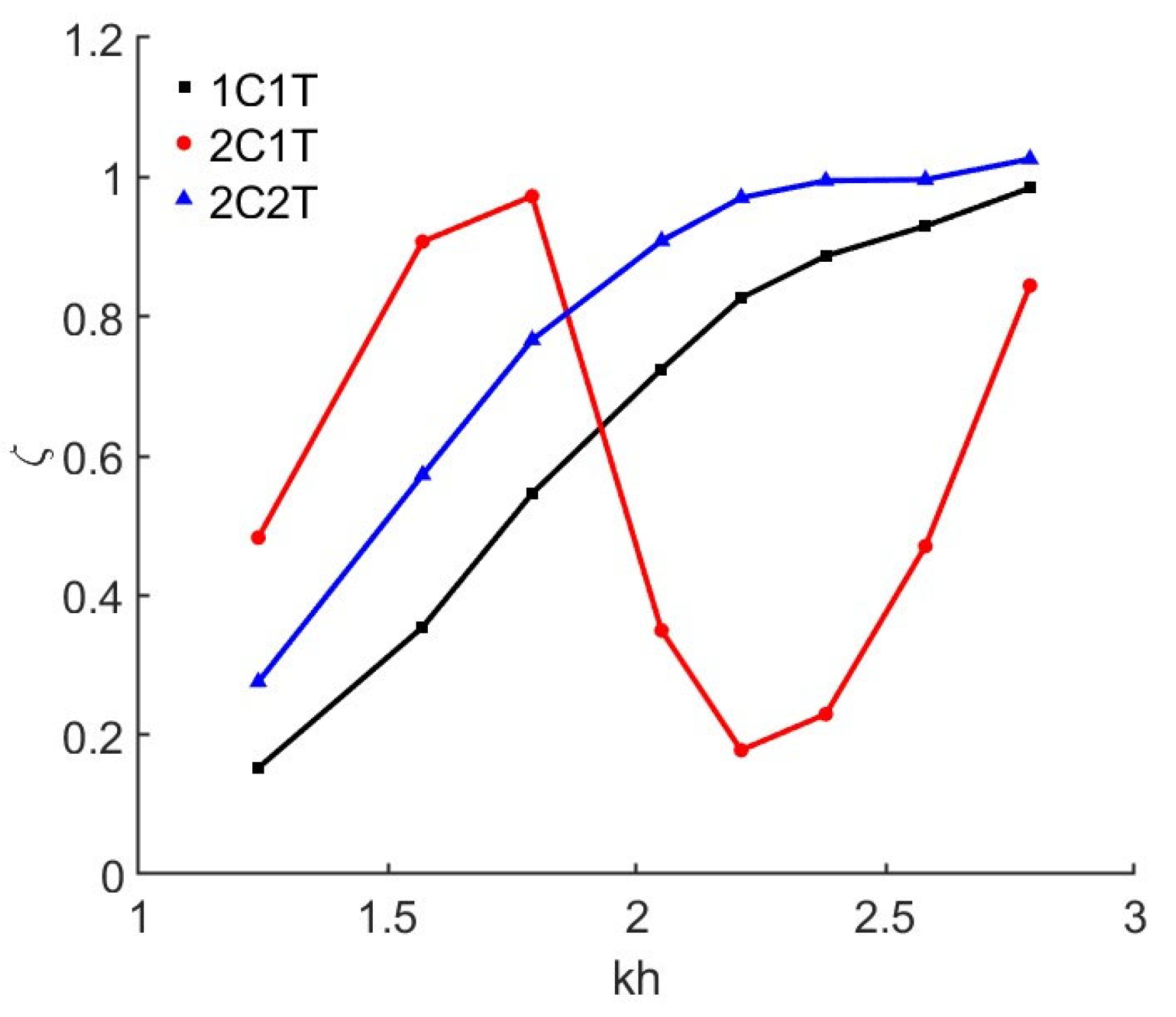
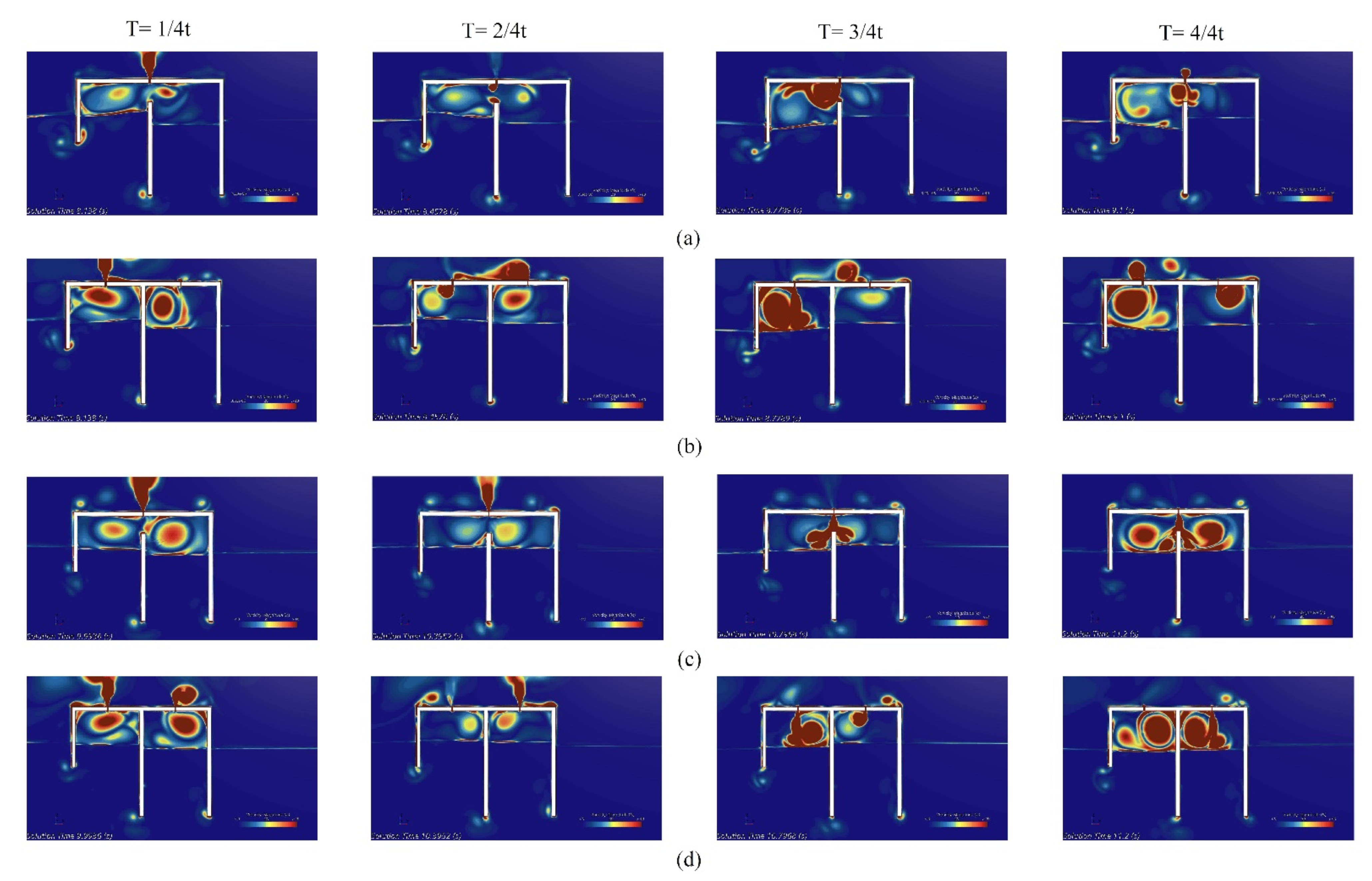
4.1. Effects of Types of Chamber Structure
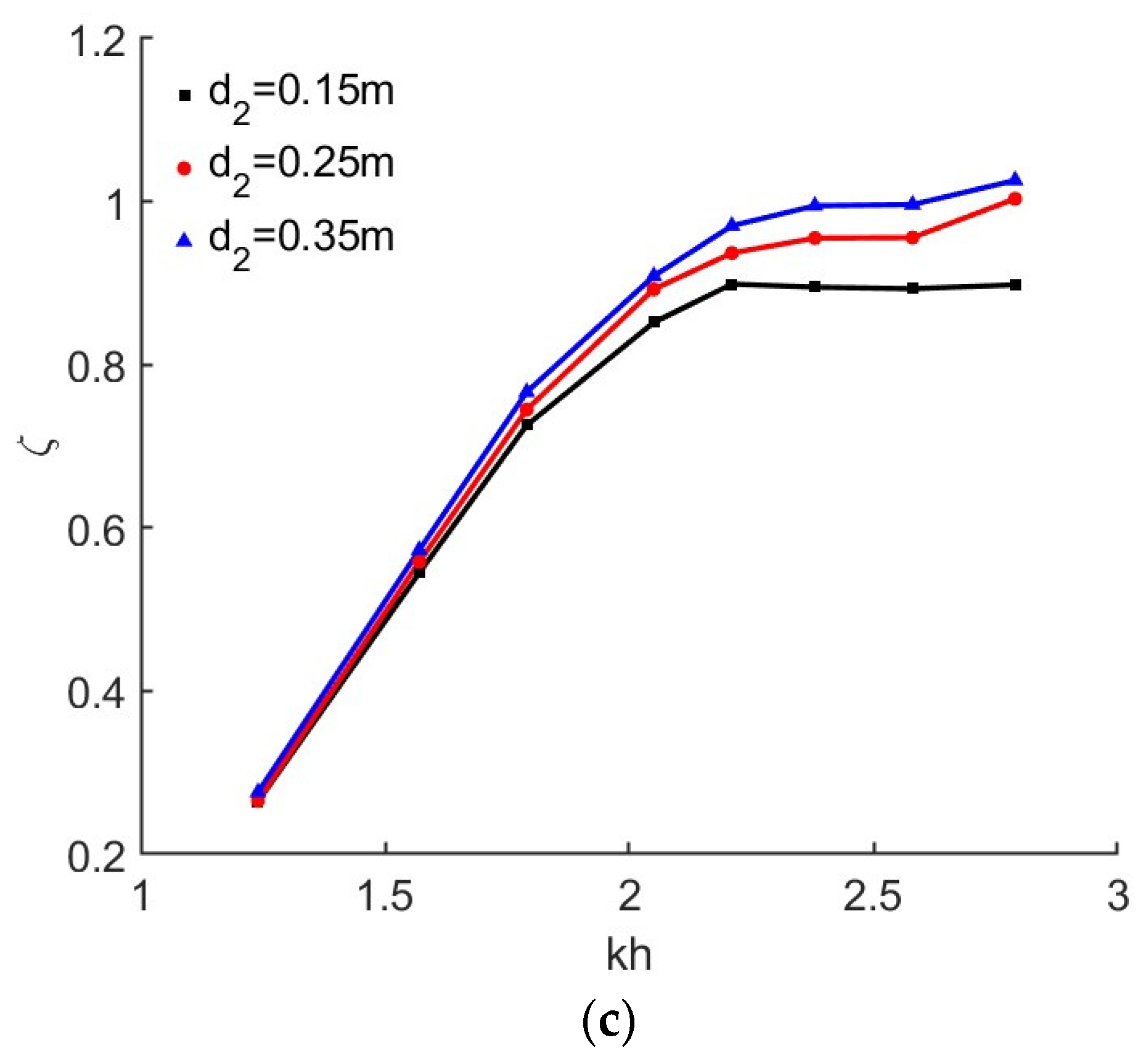
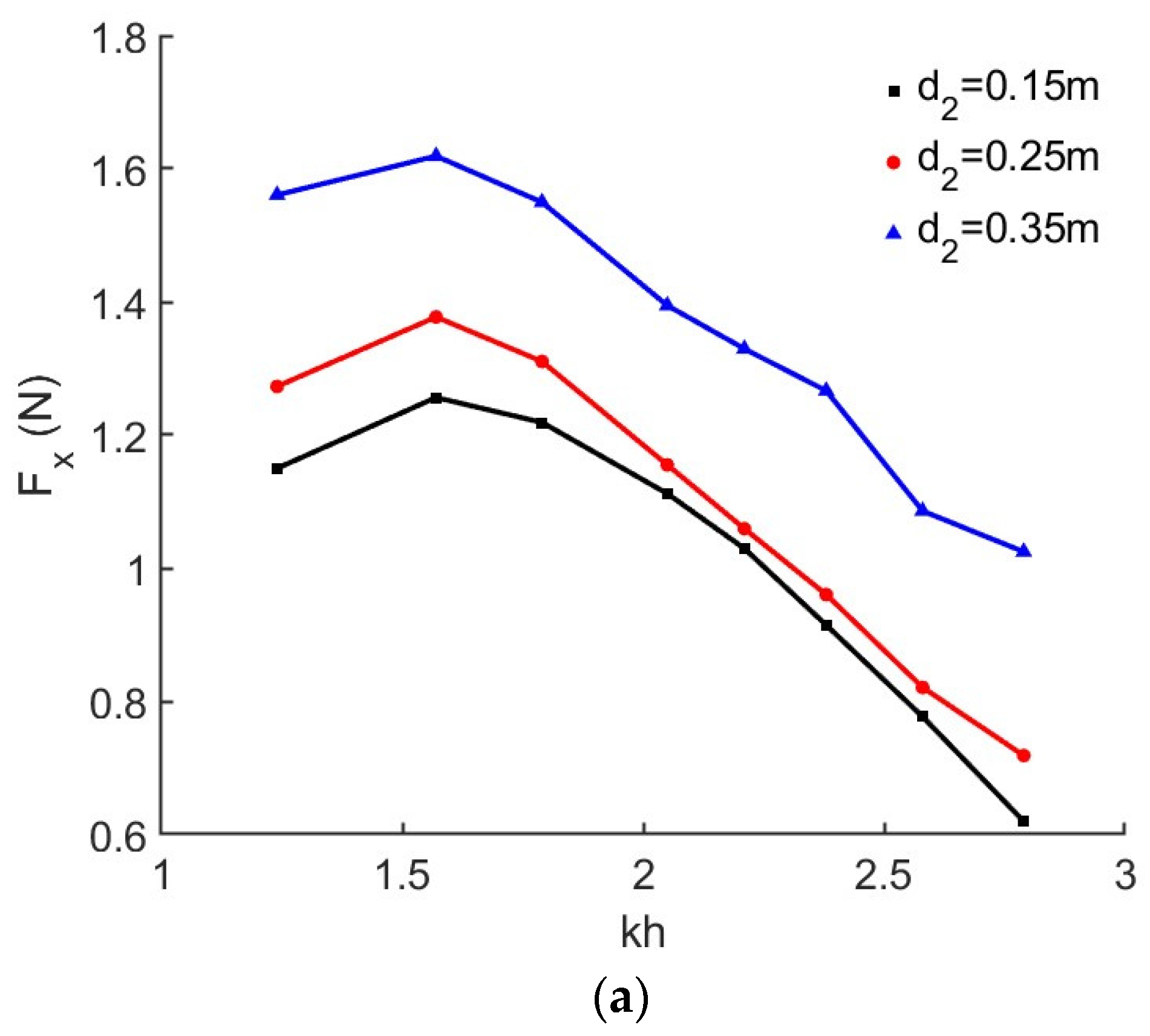
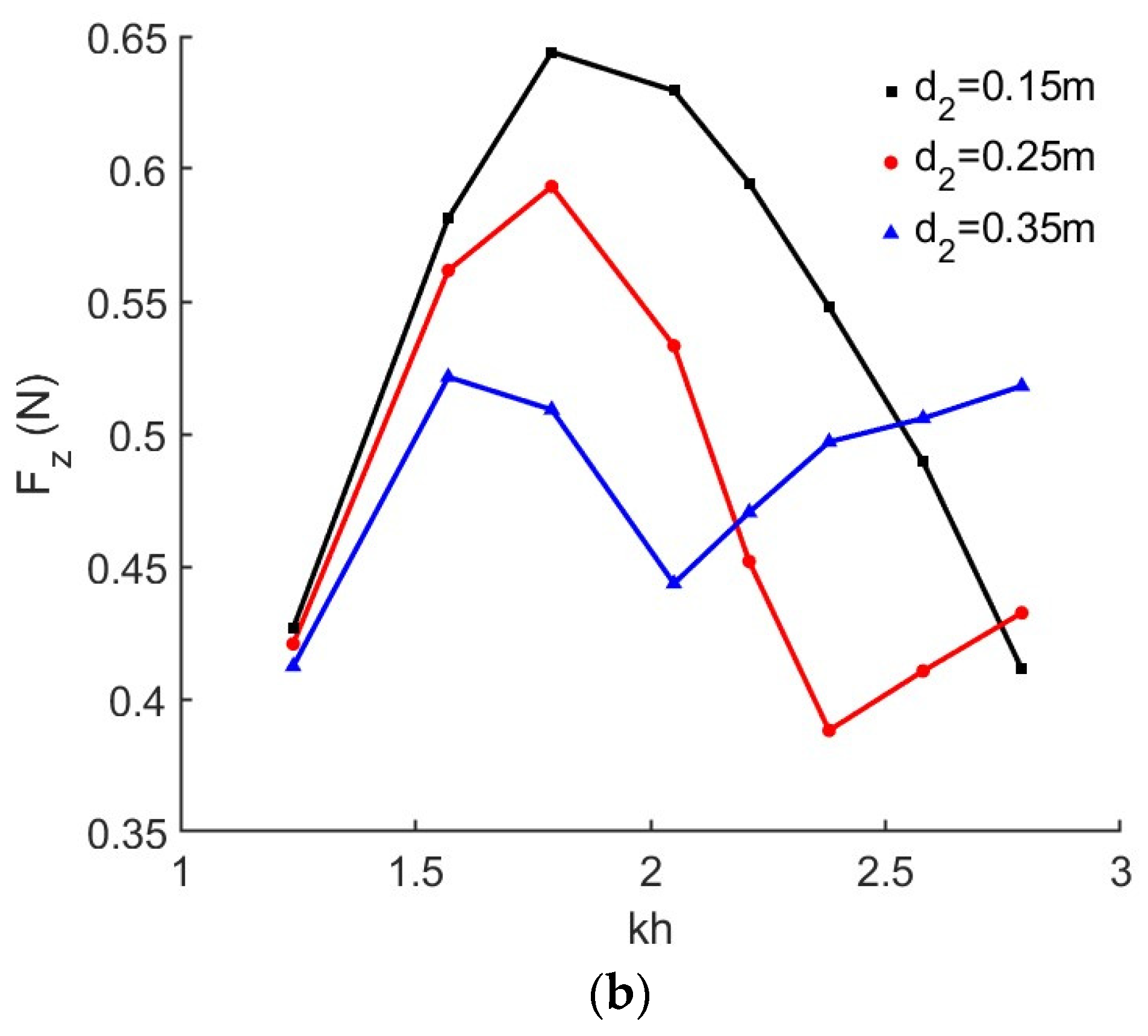
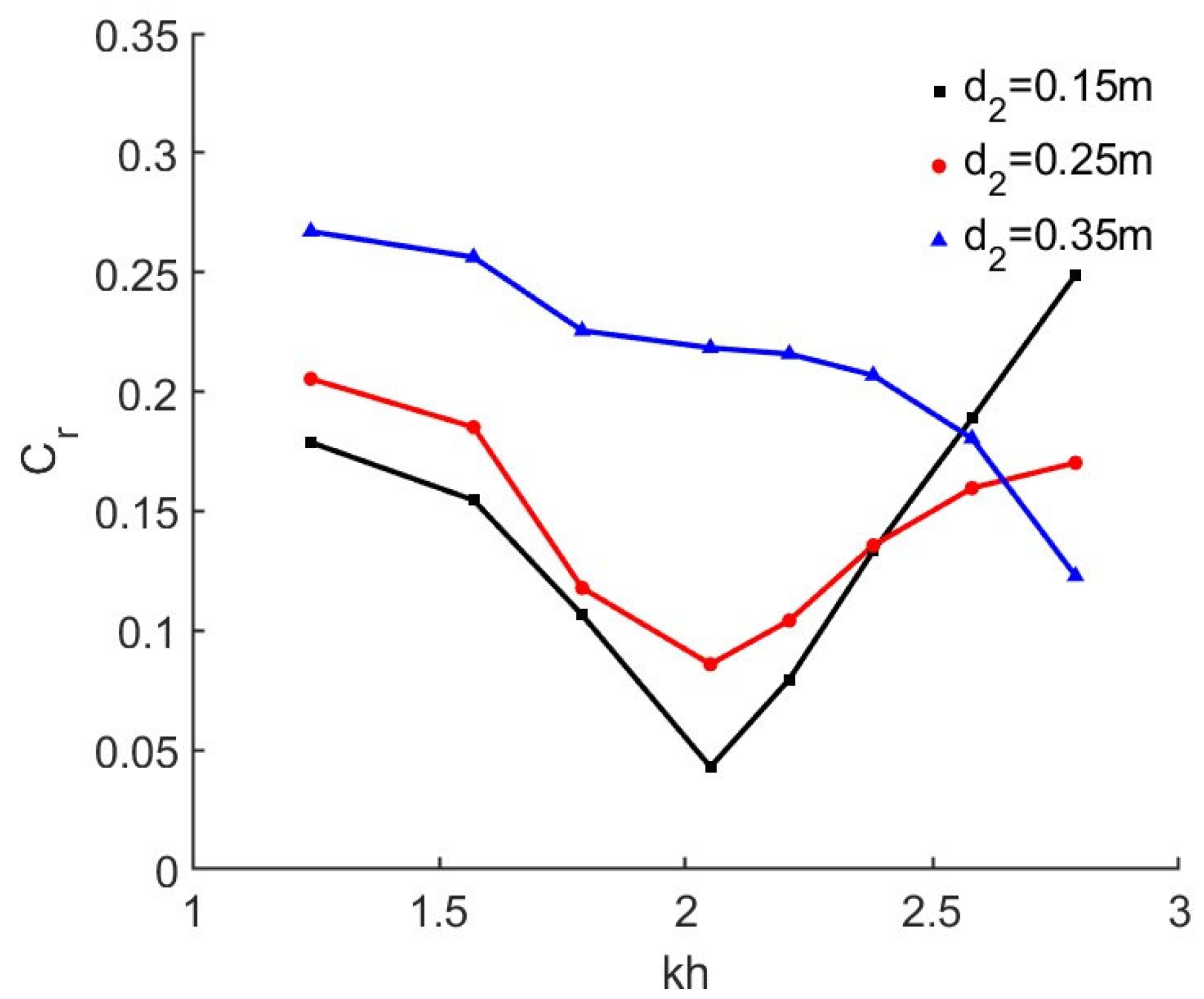
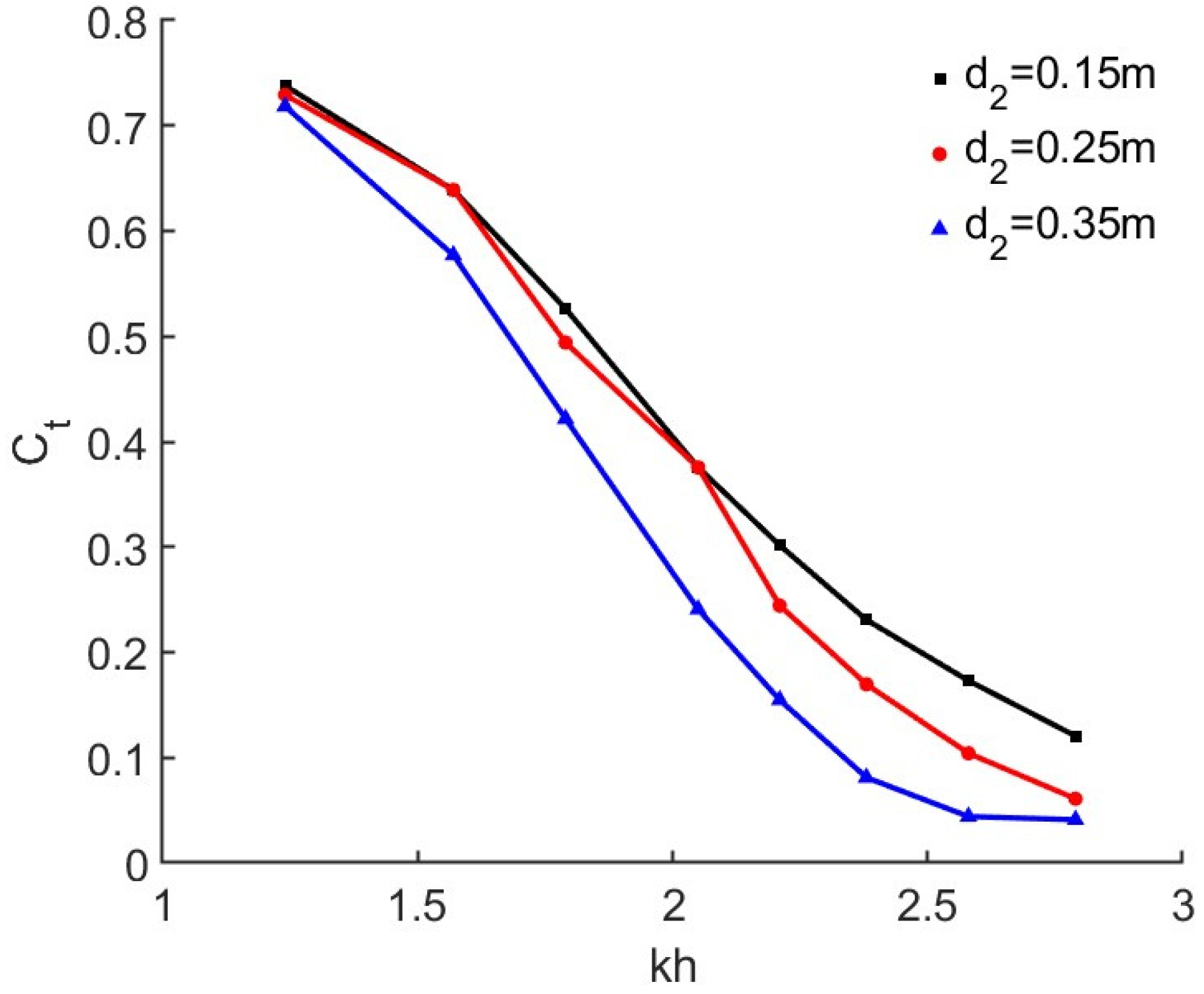
4.2. Effects of Intermediate Wall Draught
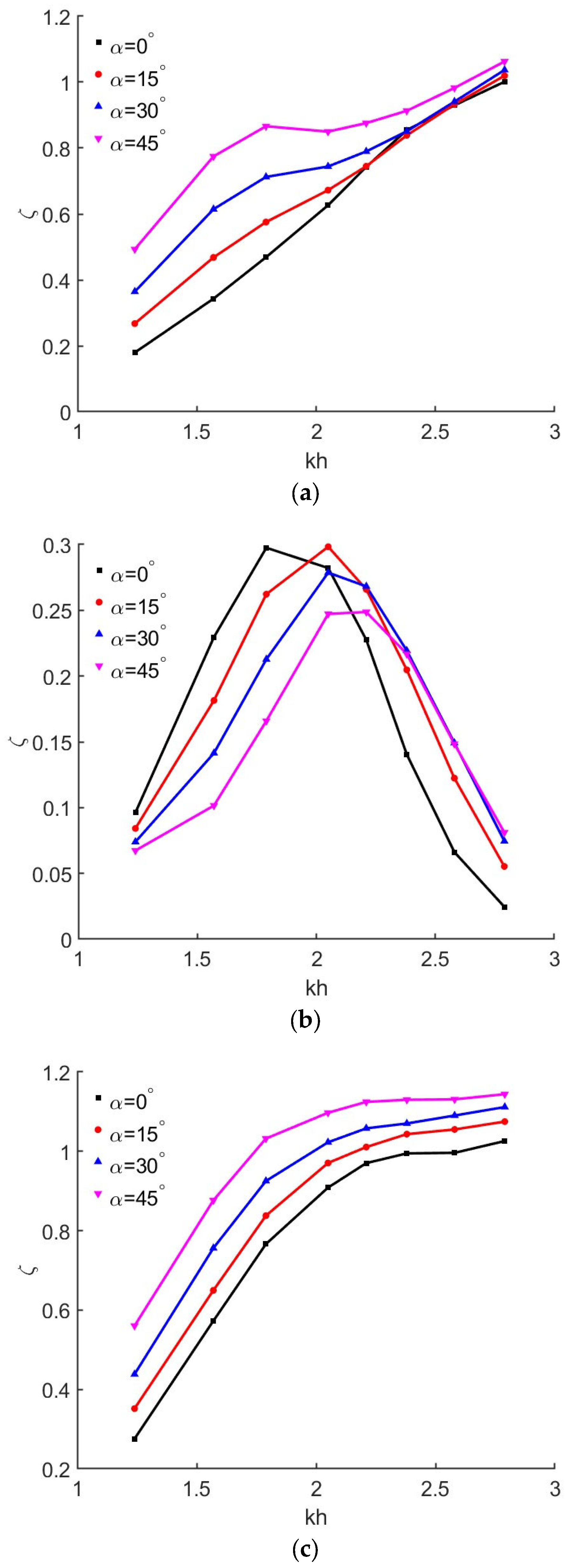
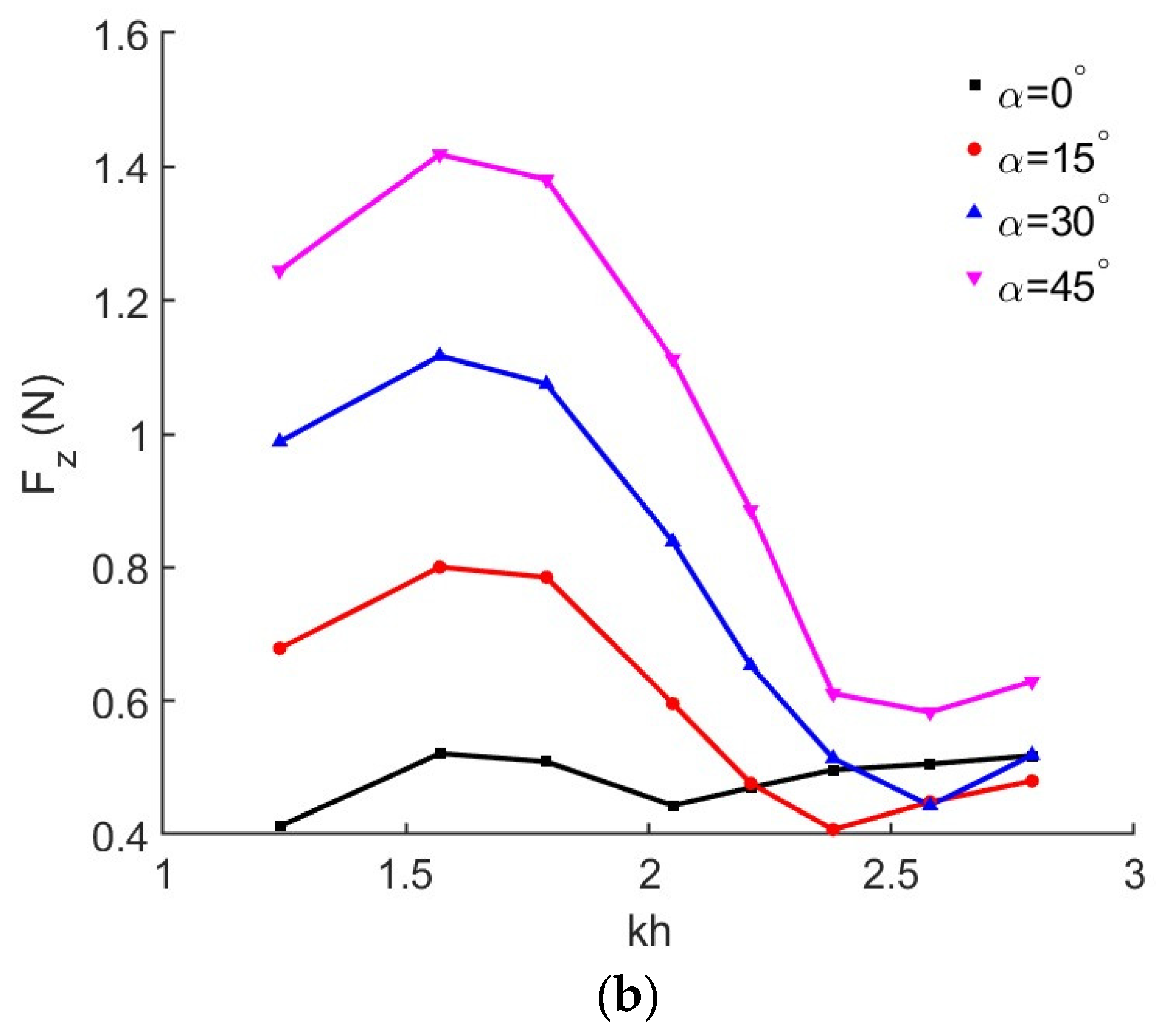
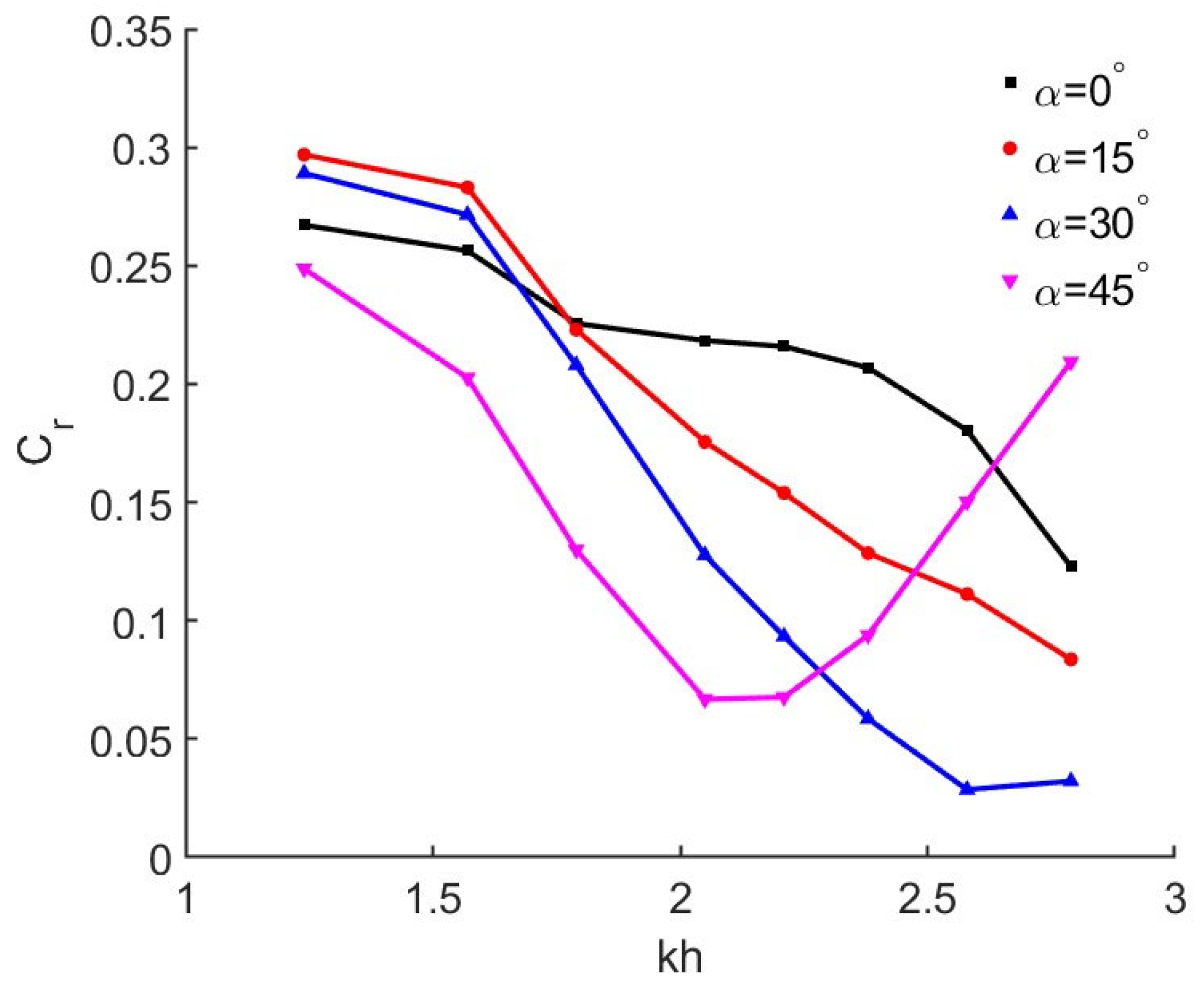
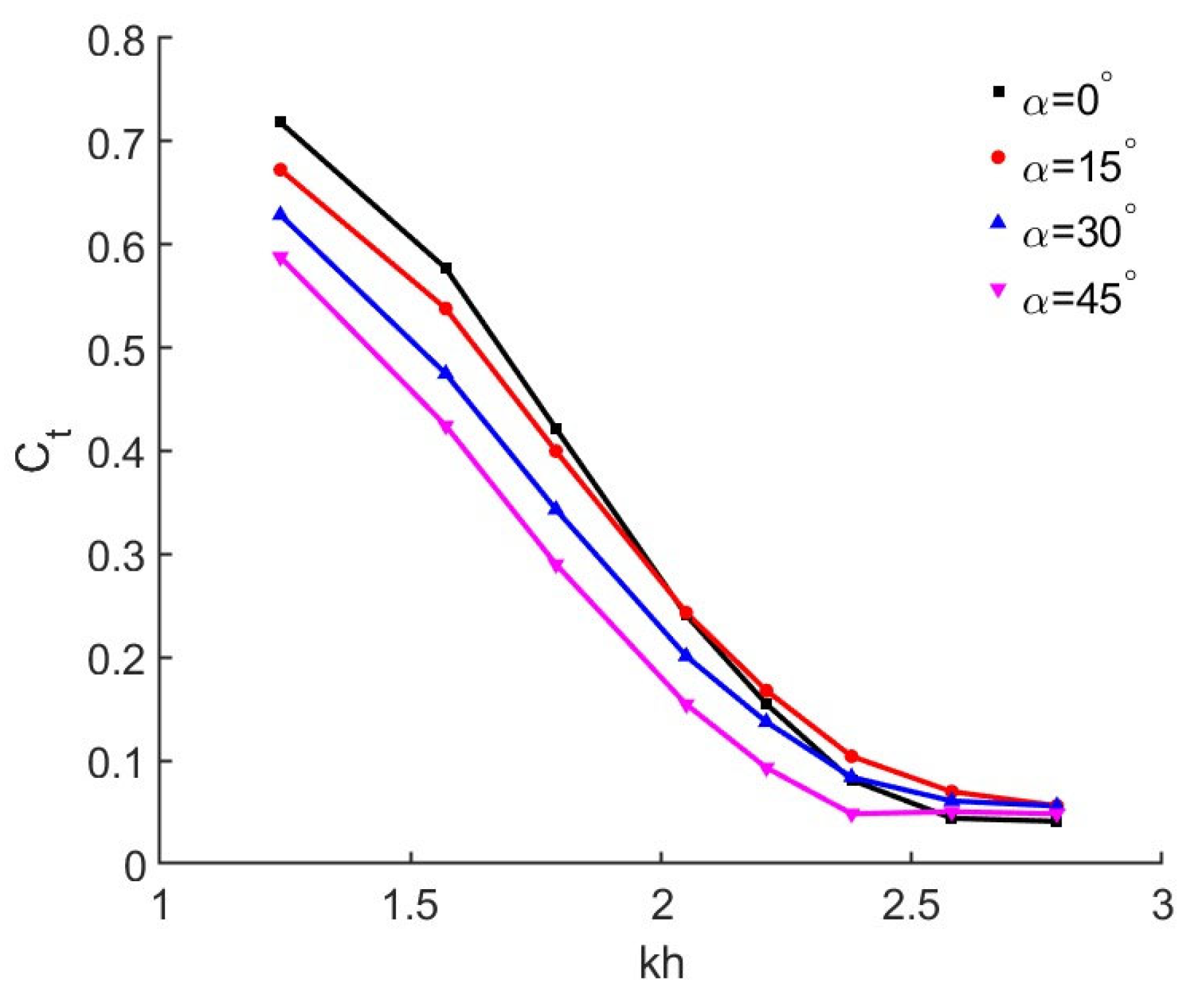
4.3. Effects of Wall Angles
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Example Appendix Section
| Greek | Latin | ||
| ρ | Fluid density | L | Incident wavelength |
| σ | Surface tension coefficient | Hi | Incident wave height |
| η | Wave height | Hr | Transmitted wave height |
| Angular frequency | Cr | Reflection coefficient | |
| ζ | Energy conversion efficiency | Ct | Transmission coefficient |
| α | wall angle | h | Water depth |
| Latin | hc | Internal heights of the OWC chamber | |
| Cg | Group velocity of the wave | C | Wall thickness of OWC |
| P | Pressure of the chamber | e | Diameter of the upper orifice |
| Q | Air volume flow rate | B | Chamber width |
| Ai | Amplitude of the incoming wave | d | Draft depth |
| k | Wave number of the waves | H | Wave height |
| PT | Extracted pneumatic power | T | Wave period |
| PW | Wave power per unit width | Fx | Horizontal wave load |
| a | Width of tank | Fz | Vertical wave load |
Appendix B. Energy Conversion Efficiency of Different Tests
| Test | Parameter | Energy Conversion Efficiency | |||||||||
| Type | d2(m) | α(°) | kh = 2.79 | kh = 2.58 | kh = 2.38 | kh = 2.21 | kh = 2.05 | kh = 1.79 | kh = 1.57 | kh = 1.24 | |
| 1 | 2C2T | 0.25 | 0 | 1.003 | 0.956 | 0.955 | 0.937 | 0.892 | 0.745 | 0.558 | 0.265 |
| 2 | 2C2T | 0.35 | 0 | 1.026 | 0.996 | 0.995 | 0.970 | 0.909 | 0.766 | 0.573 | 0.276 |
| 3 | 2C2T | 0.15 | 0 | 0.898 | 0.893 | 0.895 | 0.899 | 0.852 | 0.726 | 0.545 | 0.264 |
| 4 | 2C1T | 0.35 | 0 | 0.844 | 0.470 | 0.230 | 0.178 | 0.350 | 0.973 | 0.907 | 0.483 |
| 5 | 2C2T | 0.35 | 15 | 1.075 | 1.055 | 1.043 | 1.011 | 0.971 | 0.838 | 0.650 | 0.352 |
| 6 | 2C2T | 0.35 | 30 | 1.112 | 1.090 | 1.070 | 1.058 | 1.023 | 0.925 | 0.756 | 0.438 |
| 7 | 2C2T | 0.35 | 45 | 1.144 | 1.131 | 1.130 | 1.124 | 1.097 | 1.032 | 0.876 | 0.560 |
References
- Bhuiyan, M.A.; Zhang, Q.; Khare, V.; Mikhaylov, A.; Pinter, G.; Huang, X. Renewable energy consumption and economic growth nexus—A systematic literature review. Front. Environ. Sci. 2022, 10, 878394. [Google Scholar] [CrossRef]
- Veigas, M.; López, M.; Iglesias, G. Assessing the optimal location for a shoreline wave energy converter. Appl. Energy 2014, 132, 404–411. [Google Scholar] [CrossRef]
- Falcão, A.D.; Gato, L.M.; Nunes, E.P. A novel radial self-rectifying air turbine for use in wave energy converters. Renew. Energy 2013, 50, 289–298. [Google Scholar] [CrossRef]
- Falcão, A.F. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Mia, M.R.; Zhao, M.; Wu, H.; Palmer, H. Numerical simulation of a stationary offshore multi-chamber OWC wave energy converter. Ocean Eng. 2022, 265, 112546. [Google Scholar] [CrossRef]
- Heath, T.V. A review of oscillating water columns. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 235–245. [Google Scholar] [CrossRef]
- Gouaud, F.; Rey, V.; Piazzola, J.; Van Hooff, R. Experimental study of the hydrodynamic performance of an onshore wave power device in the presence of an underwater mound. Coast. Eng. 2010, 57, 996–1005. [Google Scholar] [CrossRef]
- He, F.; Huang, Z.; Law, A.W. Hydrodynamic performance of a rectangular floating breakwater with and without pneumatic chambers: An experimental study. Ocean Eng. 2012, 51, 16–27. [Google Scholar] [CrossRef]
- He, F.; Huang, Z.; Law, A.W. An experimental study of a floating breakwater with asymmetric pneumatic chambers for wave energy extraction. Appl. Energy 2013, 106, 222–231. [Google Scholar] [CrossRef]
- Ning, D.Z.; Wang, R.Q.; Zou, Q.P.; Teng, B. An experimental investigation of hydrodynamics of a fixed OWC Wave Energy Converter. Appl. Energy 2016, 168, 636–648. [Google Scholar] [CrossRef]
- Vyzikas, T.; Deshoulières, S.; Barton, M.; Giroux, O.; Greaves, D.; Simmonds, D. Experimental investigation of different geometries of fixed oscillating water column devices. Renew. Energy 2017, 104, 248–258. [Google Scholar] [CrossRef]
- Evans, D.V. The oscillating water column wave-energy device. IMA J. Appl. Math. 1978, 22, 423–433. [Google Scholar] [CrossRef]
- Malara, G.; Arena, F. Analytical modelling of an U-Oscillating Water Column and performance in random waves. Renew. Energy 2013, 60, 116–126. [Google Scholar] [CrossRef]
- Cong, P.; Teng, B.; Liu, Y.; Ning, D. A numerical approach for hydrodynamic performance evaluation of multi-degree-of-freedom floating oscillating water column (OWC) devices. J. Fluids Struct. 2022, 114, 103730. [Google Scholar] [CrossRef]
- Cheng, Y.; Du, W.; Dai, S.; Ji, C.; Collu, M.; Cocard, M.; Cui, L.; Yuan, Z.; Incecik, A. Hydrodynamic characteristics of a hybrid oscillating water column-oscillating buoy wave energy converter integrated into a π-type floating breakwater. Renew. Sustain. Energy Rev. 2022, 161, 112299. [Google Scholar] [CrossRef]
- Opoku, F.; Uddin, M.N.; Atkinson, M. A review of computational methods for studying oscillating water columns–the Navier-Stokes based equation approach. Renew. Sustain. Energy Rev. 2023, 174, 113124. [Google Scholar] [CrossRef]
- Wang, R.; Ning, D.; Zhang, C. Numerical investigation of the hydrodynamic performance of the dual-chamber oscillating water columns. In Proceedings of the 27th International Ocean and Polar Engineering Conference, International Society of Offshore and Polar Engineers (ISOPE), San Francisco, CA, USA, 25–30 June 2017; pp. 1–20. [Google Scholar]
- Ning, D.; Wang, R.; Zhang, C. Numerical simulation of a dual-chamber oscillating water column wave energy converter. Sustainability 2017, 9, 1599. [Google Scholar] [CrossRef]
- Ning, D.; Zhou, Y.; Zhang, C. Hydrodynamic modeling of a novel dual-chamber OWC wave energy converter. Appl. Ocean Res. 2018, 78, 180–191. [Google Scholar] [CrossRef]
- Ahmed, E.; Gregor, M.; Dezhi, N. Hydrodynamic performance of single–chamber and dual–chamber offshore–stationary oscillating water column devices using CFD. Appl. Energy 2018, 228, 82–96. [Google Scholar]
- Yu, T.S.; Guo, Q.Y.; Shi, H.D.; Li, T.Y.; Meng, X.Y.; He, S.K.; Li, P.X. Experimental investigation of a novel OWC wave energy converter. Ocean Eng. 2022, 257, 111567. [Google Scholar] [CrossRef]
- Zheng, S.; Antonini, A.; Zhang, Y.; Miles, J.; Greaves, D.; Zhu, G.; Iglesias, G. Hydrodynamic performance of a multi-Oscillating Water Column (OWC) platform. Appl. Ocean Res. 2020, 99, 1–20. [Google Scholar] [CrossRef]
- Doyle, S.; Aggidis, G.A. Experimental investigation and performance comparison of a single OWC, array and M-OWC. Renew. Energy 2021, 168, 365–374. [Google Scholar] [CrossRef]
- Hsieh, M.F.; Lin, I.H.; Dorrell, D.G.; Hsieh, M.J.; Lin, C.C. Development of a wave energy converter using a two chamber oscillating water column. IEEE Trans. Sustain. Energy 2012, 3, 482–497. [Google Scholar] [CrossRef]
- Fenu, B.; Bonfanti, M.; Bardazzi, A.; Pilloton, C.; Lucarelli, A.; Mattiazzo, G. Experimental investigation of a Multi-OWC wind turbine floating platform. Ocean Eng. 2023, 281, 114619. [Google Scholar] [CrossRef]
- Chao, Z.; Fowmes, G.; Mousa, A.; Zhou, J.; Zhao, Z.; Zheng, J.; Shi, D. A new large-scale shear apparatus for testing geosynthetics-soil interfaces incorporating thermal condition. Geotext. Geomembr. 2024, 52, 999–1010. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, L.; Li, M.; Johanning, L. Experimental investigation on the hydrodynamic performance of a multi-chamber OWC-breakwater. Renew. Sustain. Energy Rev. 2021, 150, 111512. [Google Scholar] [CrossRef]
- Howe, D.; Nader, J.R.; Macfarlane, G. Experimental investigation of multiple Oscillating Water Column Wave Energy Converters integrated in a floating breakwater: Energy extraction performance. Appl. Ocean Res. 2020, 97, 102086. [Google Scholar] [CrossRef]
- Henriques, J.; Portillo, J.; Sheng, W.; Gato, L.; Falcão, A. Dynamics and control of air turbines in oscillating-water-column wave energy converters: Analyses and case study. Renew. Sustain. Energy Rev. 2019, 112, 571–589. [Google Scholar] [CrossRef]
- Ciappi, L.; Simonetti, I.; Bianchini, A.; Cappietti, L.; Manfrida, G. Application of integrated wave-to-wire modelling for the preliminary design of oscillating water column systems for installations in moderate wave climates. Renew. Energy 2022, 192, 232–248. [Google Scholar] [CrossRef]
- Fenu, B.; Henriques, J.C.; Glorioso, M.; Gato, L.M.; Bonfanti, M. Real-time Wells turbine simulation on an oscillating-water-column wave energy converter physical model. Appl. Energy 2024, 376, 124121. [Google Scholar] [CrossRef]
- Naik, N.; Gayathri, R.; Behera, H.; Tsai, C.C. Wave power extraction by a dual OWC chambers over an undulated bottom. Renew. Energy 2023, 216, 119026. [Google Scholar] [CrossRef]
- Elhanafi, A.; Macfarlane, G.; Fleming, A.; Leong, Z. Scaling and air compressibility effects on a three-dimensional offshore stationary OWC wave energy converter. Appl. Energy 2017, 189, 1–20. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Babarit, A. A database of capture width ratio of wave energy converters. Renew. Energy 2015, 80, 610–628. [Google Scholar] [CrossRef]
- Goda, Y.; Suzuki, Y. Estimation of Incident and Reflected Waves in Random Wave Experiments. Coast. Eng. 1976, 1976, 828–845. [Google Scholar] [CrossRef]
- Elhanafi, A.; Fleming, A.; Macfarlane, G.; Leong, Z. Investigations on 3D effects and correlation between wave height and lip submergence of an offshore stationary OWC wave energy converter. Appl. Ocean Res. 2017, 64, 203–216. [Google Scholar] [CrossRef]
- Elhanafi, A. Prediction of regular wave loads on a fixed offshore oscillating water column-wave energy converter using CFD. J. Ocean Eng. Sci. 2016, 1, 268–283. [Google Scholar] [CrossRef]
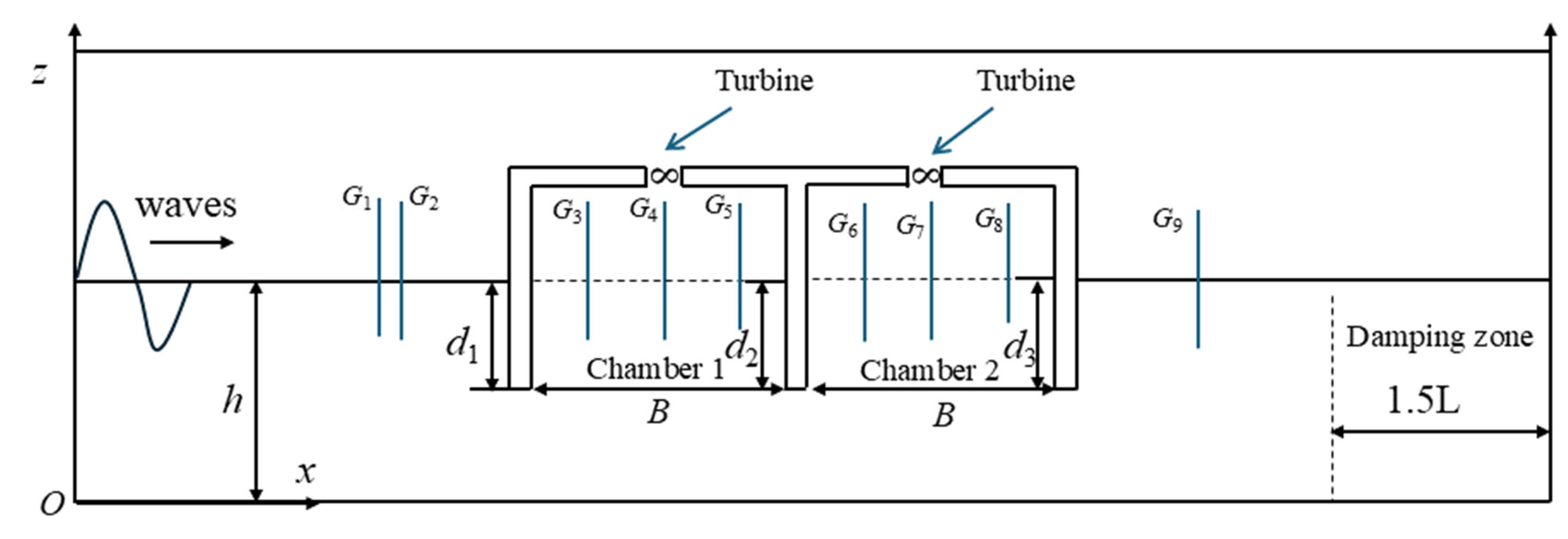
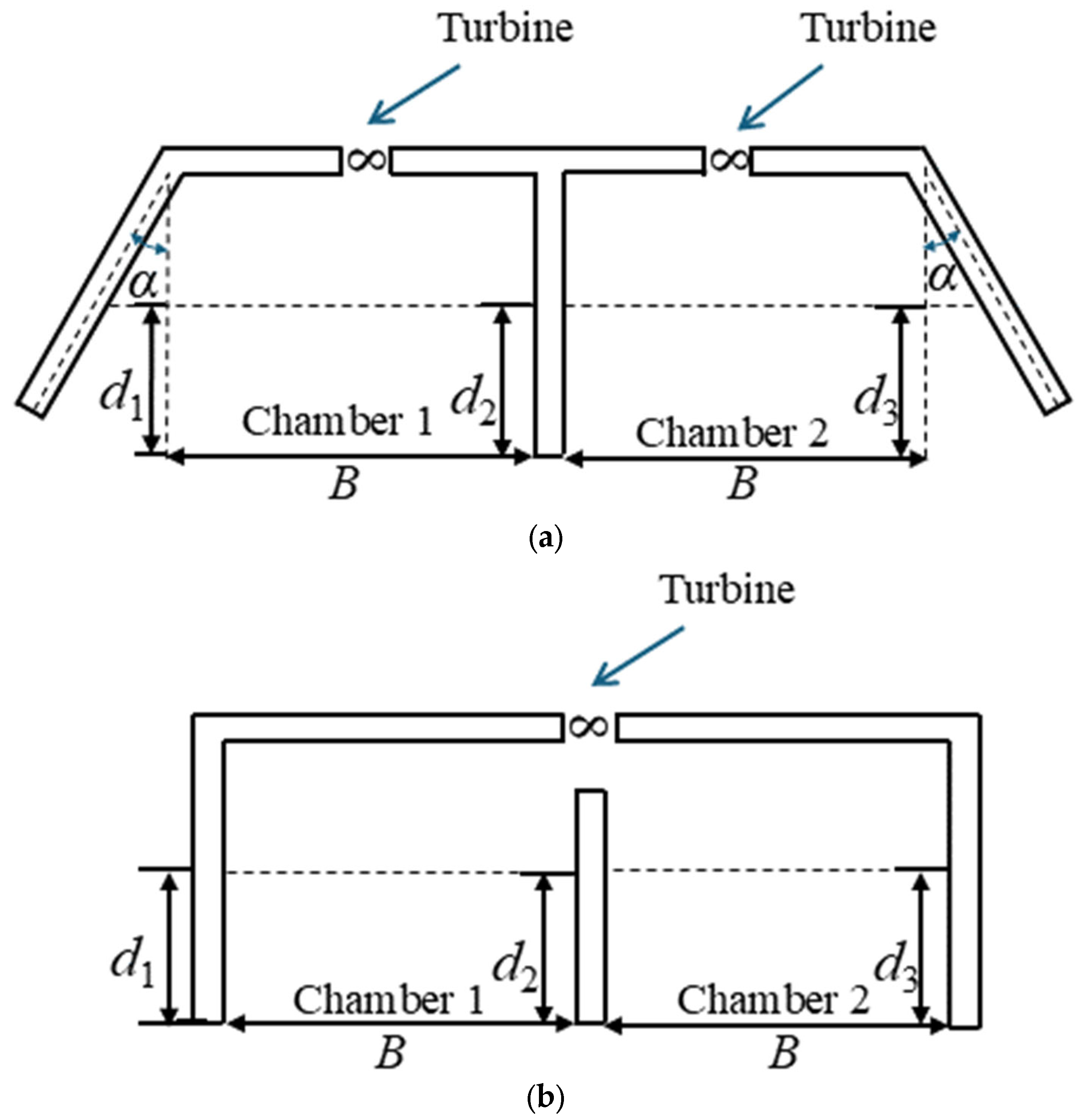
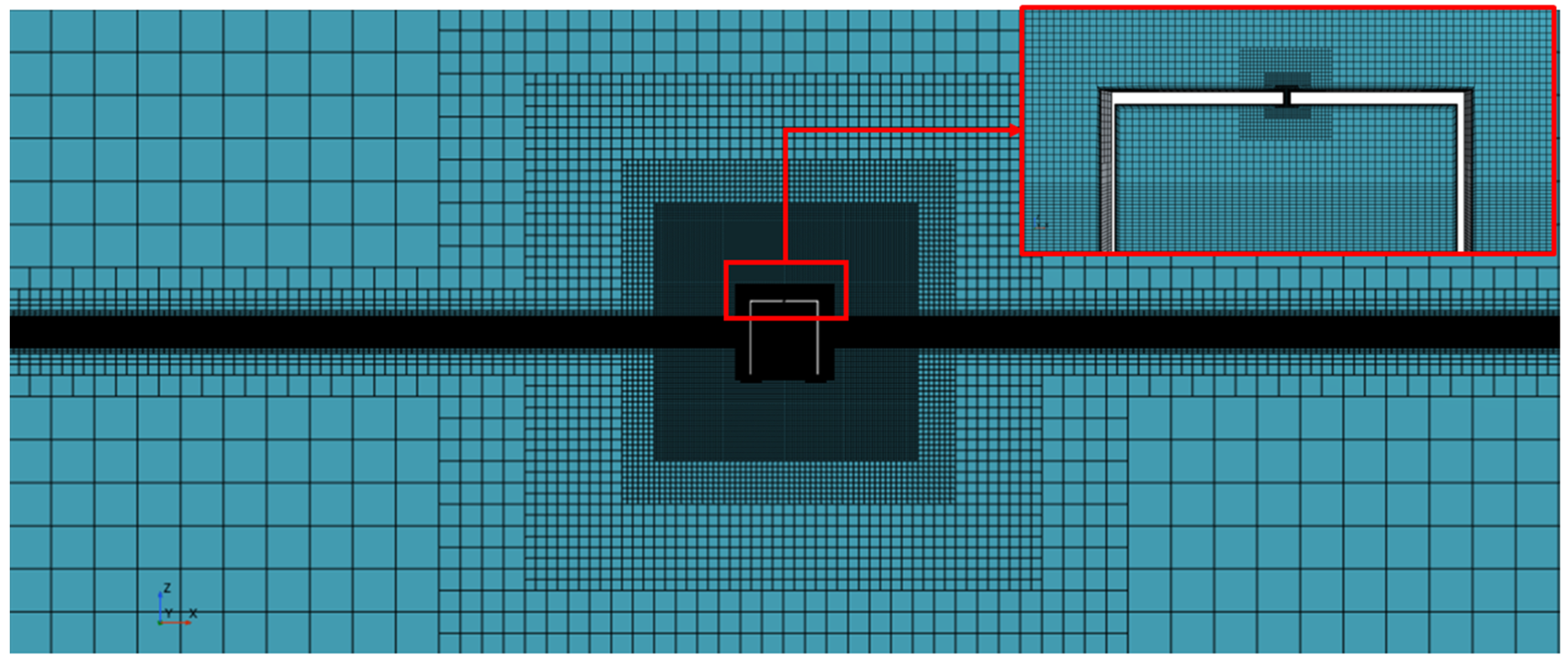
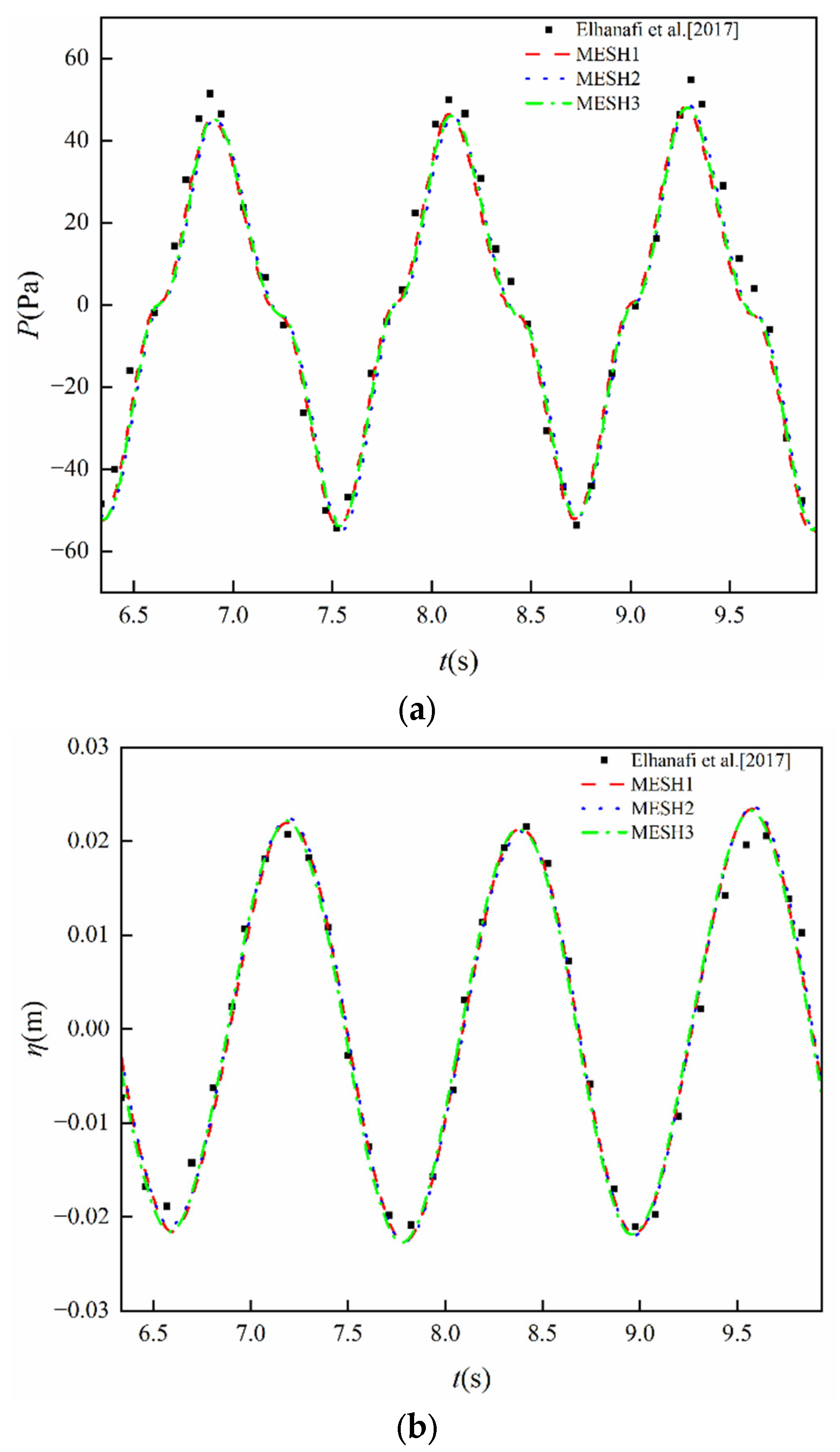



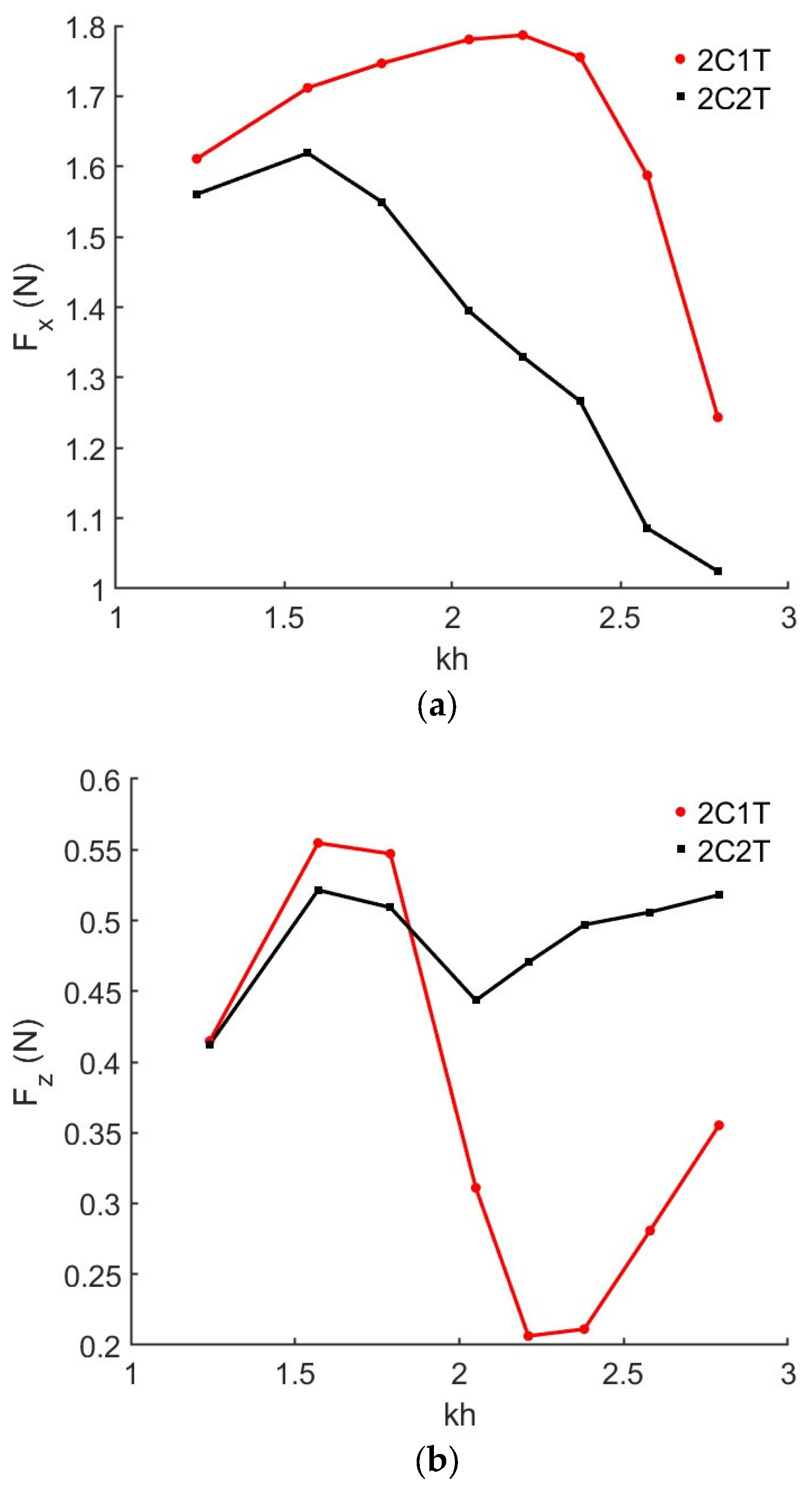
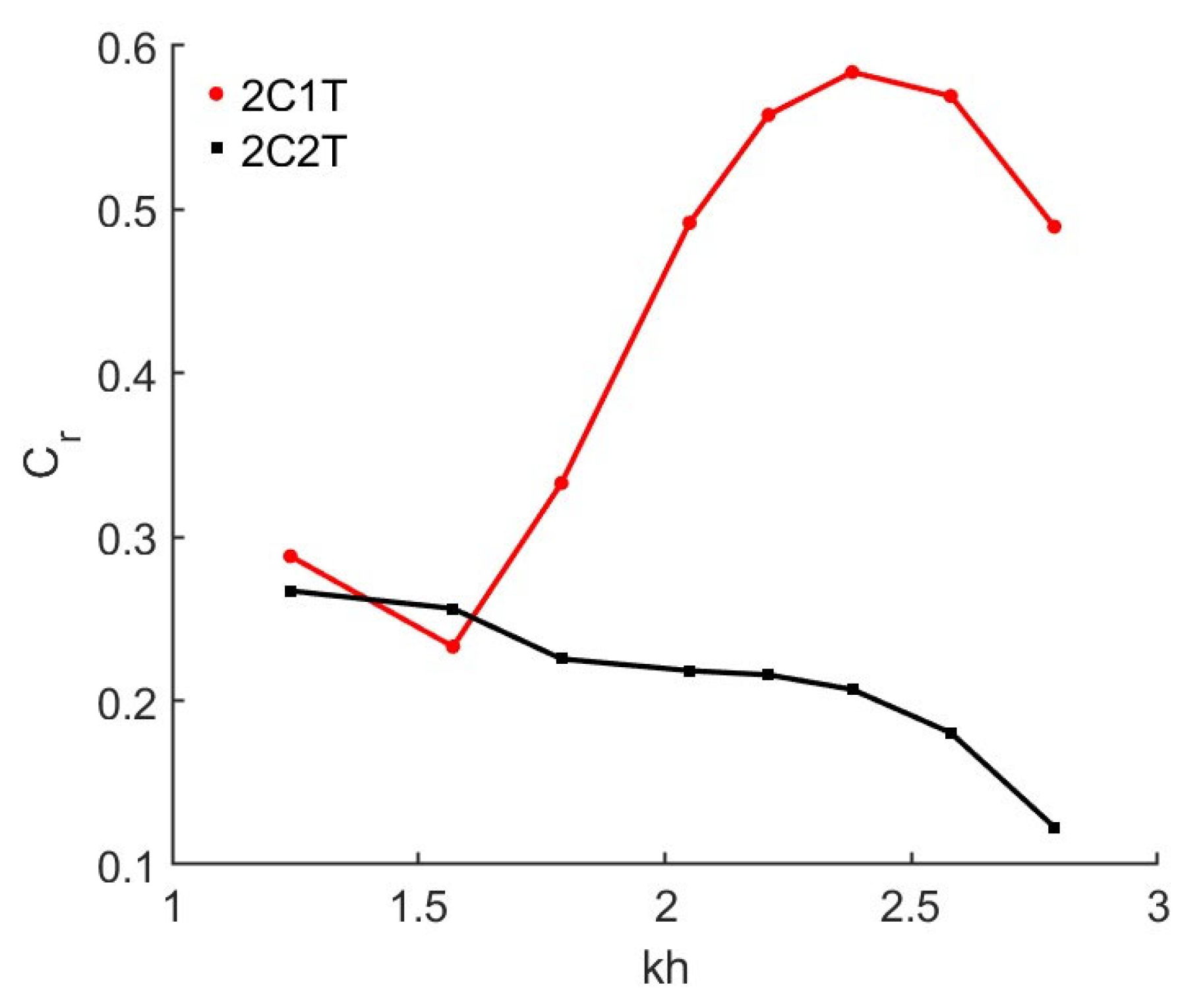
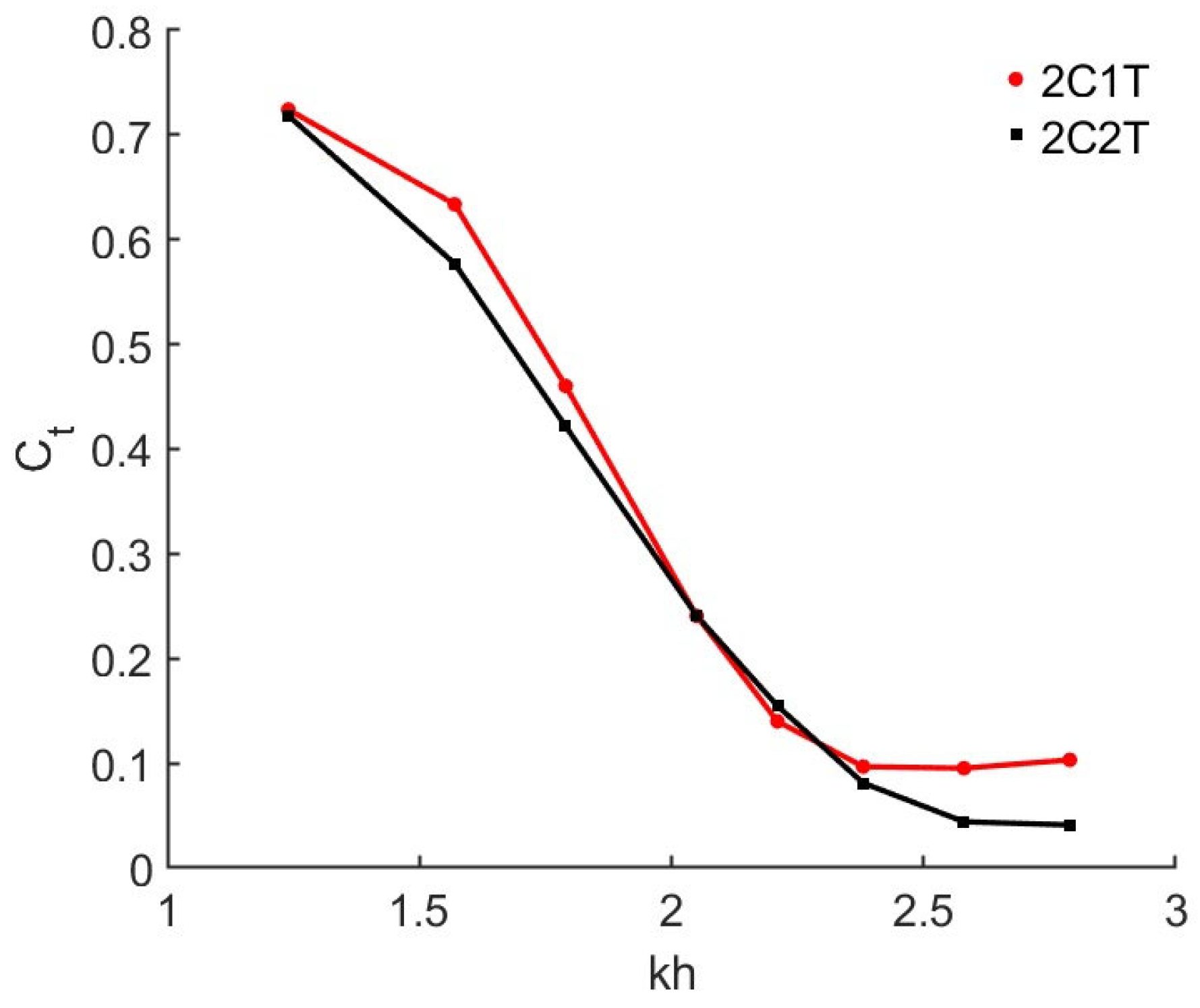
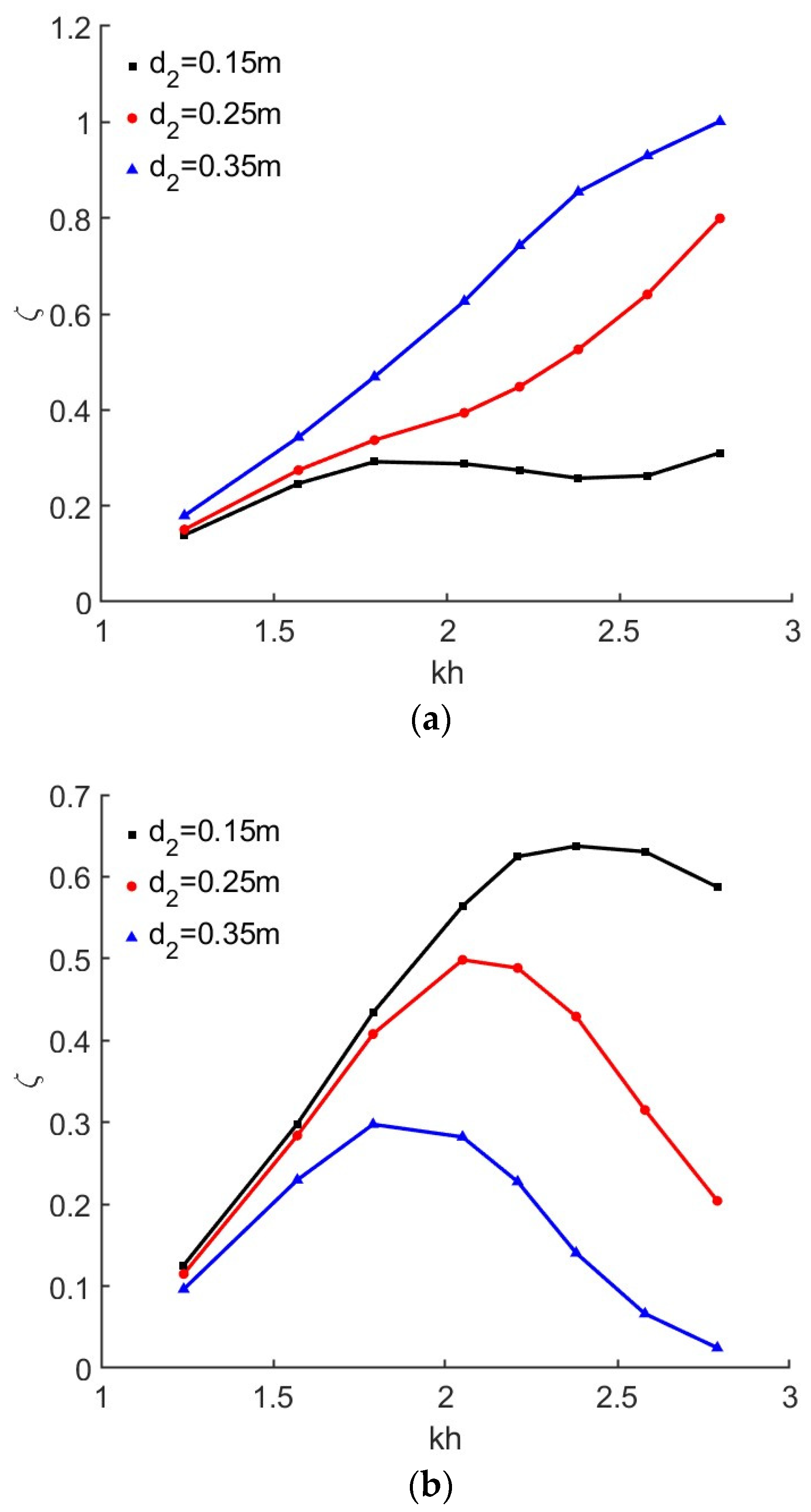

| Test | Type of Chamber | Barrier Wall Draught d2 (m) | Wall Angle α (°) | T (s) | H (m) | B/L |
|---|---|---|---|---|---|---|
| 1 | 2C2T | 0.25 | 0 | 1.2~1.8 | 0.04 | 0.04~0.14 |
| 2 | 2C2T | 0.35 | 0 | |||
| 3 | 2C2T | 0.15 | 0 | |||
| 4 | 2C1T | 0.35 | 0 | |||
| 5 | 2C2T | 0.35 | 15 | |||
| 6 | 2C2T | 0.35 | 30 | |||
| 7 | 2C2T | 0.35 | 45 |
| Index | mesh1 | mesh2 | mesh3 | |||
|---|---|---|---|---|---|---|
| Wave Refinement (m) | X | Z | X | Z | X | Z |
| 0.028 | 0.005 | 0.02 | 0.0025 | 0.013 | 0.0017 | |
| Total Number of Grids | 149,188 | 386,108 | 671,168 | |||
| Index | mesh1 | mesh2 | mesh3 |
|---|---|---|---|
| NRMSE of ηOWC | 4.43% | 4.39% | 4.36% |
| NRMSE of P | 4.76% | 4.56% | 4.56% |
| Computing Time | 4 h 36 min | 5 h 02 min | 9 h 58 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, P.; Lin, X.; Wang, W.; Zhang, H. Numerical Simulation of Hydrodynamic Performance of an Offshore Oscillating Water Column Wave Energy Converter Device. J. Mar. Sci. Eng. 2024, 12, 2289. https://doi.org/10.3390/jmse12122289
Tang P, Lin X, Wang W, Zhang H. Numerical Simulation of Hydrodynamic Performance of an Offshore Oscillating Water Column Wave Energy Converter Device. Journal of Marine Science and Engineering. 2024; 12(12):2289. https://doi.org/10.3390/jmse12122289
Chicago/Turabian StyleTang, Peng, Xinyi Lin, Wei Wang, and Hongsheng Zhang. 2024. "Numerical Simulation of Hydrodynamic Performance of an Offshore Oscillating Water Column Wave Energy Converter Device" Journal of Marine Science and Engineering 12, no. 12: 2289. https://doi.org/10.3390/jmse12122289
APA StyleTang, P., Lin, X., Wang, W., & Zhang, H. (2024). Numerical Simulation of Hydrodynamic Performance of an Offshore Oscillating Water Column Wave Energy Converter Device. Journal of Marine Science and Engineering, 12(12), 2289. https://doi.org/10.3390/jmse12122289







