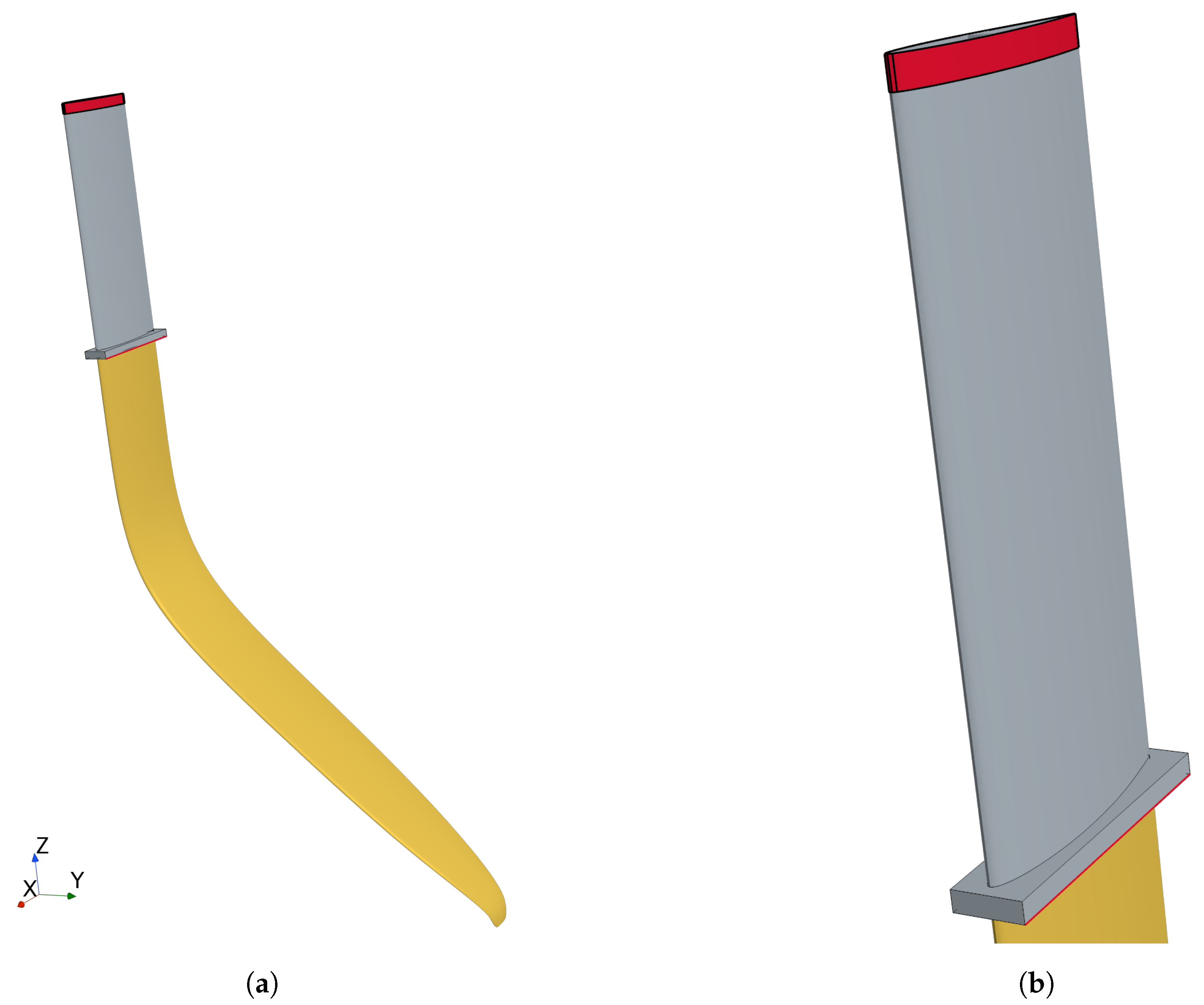
Figure 1.
NACRA 17 foil geometry for solid model. The interface to the fluid model is highlighted in yellow, and the constraints of the solid model are highlighted in red: (a) overview; (b) zoom.
Figure 1.
NACRA 17 foil geometry for solid model. The interface to the fluid model is highlighted in yellow, and the constraints of the solid model are highlighted in red: (a) overview; (b) zoom.
Figure 2.
Solid model mesh: (a) cross section; (b) mesh of tip section.
Figure 2.
Solid model mesh: (a) cross section; (b) mesh of tip section.
Figure 3.
Cavitation tunnel domain.
Figure 3.
Cavitation tunnel domain.
Figure 4.
Domain for foil performance simulations.
Figure 4.
Domain for foil performance simulations.
Figure 5.
Rudder and elevator: (a) CAD model; (b) zoom of elevator mesh from scanning and reconstruction curves.
Figure 5.
Rudder and elevator: (a) CAD model; (b) zoom of elevator mesh from scanning and reconstruction curves.
Figure 6.
Boat geometry including rudders and foils.
Figure 6.
Boat geometry including rudders and foils.
Figure 7.
FVM mesh on foil and a section showing the prismatic layers.
Figure 7.
FVM mesh on foil and a section showing the prismatic layers.
Figure 8.
FVM mesh for foil performance simulations: (a) cross section; (b) cross section zoom.
Figure 8.
FVM mesh for foil performance simulations: (a) cross section; (b) cross section zoom.
Figure 9.
FVM mesh of case with both rudders and foil horizontal cut plane.
Figure 9.
FVM mesh of case with both rudders and foil horizontal cut plane.
Figure 10.
Cavitation tunnel test section with foil as presented in [
8].
Figure 10.
Cavitation tunnel test section with foil as presented in [
8].
Figure 11.
Rig used to test the structural twist and deformation of a NACRA 17 foil.
Figure 11.
Rig used to test the structural twist and deformation of a NACRA 17 foil.
Figure 12.
Mesh convergence. Displacement over chord c as a function of relative cell size including power curve fitting for uncertainty estimation. (a) span-wise resolution; (b) chord-wise resolution.
Figure 12.
Mesh convergence. Displacement over chord c as a function of relative cell size including power curve fitting for uncertainty estimation. (a) span-wise resolution; (b) chord-wise resolution.
Figure 13.
Mesh convergence. Forces and displacement as a function of base size (BS) over chord (c) including power curve fitting for uncertainty estimation. (a) displacement over chord c; (b) drag force coefficient ; (c) side force coefficient ; (d) lift force coefficient .
Figure 13.
Mesh convergence. Forces and displacement as a function of base size (BS) over chord (c) including power curve fitting for uncertainty estimation. (a) displacement over chord c; (b) drag force coefficient ; (c) side force coefficient ; (d) lift force coefficient .
Figure 14.
Numerical and experimental values as a function of rake angle with a constant leeway of 0°. Error bars indicate uncertainties. (a) displacement over chord c; (b) drag force coefficient ; (c) side force coefficient ; (d) lift force coefficient .
Figure 14.
Numerical and experimental values as a function of rake angle with a constant leeway of 0°. Error bars indicate uncertainties. (a) displacement over chord c; (b) drag force coefficient ; (c) side force coefficient ; (d) lift force coefficient .
Figure 15.
Foil performance simulation results for 0.6 m flying height. (a) displacement ; (b) drag force coefficient ; (c) side force coefficient ; (d) lift force coefficient .
Figure 15.
Foil performance simulation results for 0.6 m flying height. (a) displacement ; (b) drag force coefficient ; (c) side force coefficient ; (d) lift force coefficient .
Figure 16.
Side view of the volume fraction of water on the surface of the foils for case with Flying height 0.6 m, Leeway 2° and rake 2°. The free surface is included as a transparent surface. Flow from right to left.
Figure 16.
Side view of the volume fraction of water on the surface of the foils for case with Flying height 0.6 m, Leeway 2° and rake 2°. The free surface is included as a transparent surface. Flow from right to left.
Figure 17.
The convective Courant number on the free surface for the case with flying height 0.6 m, leeway 2°, rake 2°, and a time step of 5 ms.
Figure 17.
The convective Courant number on the free surface for the case with flying height 0.6 m, leeway 2°, rake 2°, and a time step of 5 ms.
Figure 18.
Effect of speed change on foil performance for leeway 2°: (a) displacement ; (b) drag force coefficient ; (c) side force coefficient ; (d) lift force coefficient .
Figure 18.
Effect of speed change on foil performance for leeway 2°: (a) displacement ; (b) drag force coefficient ; (c) side force coefficient ; (d) lift force coefficient .
Figure 19.
Effect of transition on foil forces for leeway 2°: (a) displacement ; (b) drag force coefficient ; (c) side force coefficient .
Figure 19.
Effect of transition on foil forces for leeway 2°: (a) displacement ; (b) drag force coefficient ; (c) side force coefficient .
Figure 20.
The wall shear stress on the foil (seen from above) with transition modeling illustrates the point of transition. Leeway 2° and rake 2°. Flow from right to left.
Figure 20.
The wall shear stress on the foil (seen from above) with transition modeling illustrates the point of transition. Leeway 2° and rake 2°. Flow from right to left.
Figure 21.
Foil performance in heave motion; (a) displacement ; (b) drag force coefficient ; (c) side force coefficient ; (d) lift force coefficient .
Figure 21.
Foil performance in heave motion; (a) displacement ; (b) drag force coefficient ; (c) side force coefficient ; (d) lift force coefficient .
Figure 22.
Free surface deformation in the area between the foils and rudders.
Figure 22.
Free surface deformation in the area between the foils and rudders.
Figure 23.
Rudder force with changing toe out angle of rudders: (a) drag force ; (b) side force ; (c) lift/drag .
Figure 23.
Rudder force with changing toe out angle of rudders: (a) drag force ; (b) side force ; (c) lift/drag .
Figure 24.
Foil lift forces in waves.
Figure 24.
Foil lift forces in waves.
Figure 25.
Foil displacement in waves.
Figure 25.
Foil displacement in waves.
Figure 26.
Foil and rudder in waves with free heave motion.
Figure 26.
Foil and rudder in waves with free heave motion.
Figure 27.
Heave motion in waves with and without free pitch.
Figure 27.
Heave motion in waves with and without free pitch.
Figure 28.
Pitch motion in waves with free heave and pitch.
Figure 28.
Pitch motion in waves with free heave and pitch.
Table 1.
Material properties used for the solid model. denotes density, E is Youngs modulus and is Poisson’s ratio.
Table 1.
Material properties used for the solid model. denotes density, E is Youngs modulus and is Poisson’s ratio.
| [] | E [GPa] | [-] |
|---|
| 1600 | 61.0 | 0.33 |
Table 2.
Simulation models, settings and cells.
Table 2.
Simulation models, settings and cells.
| Model | Domain | Parts Included | Time | Flow Models | FSI Stabilisation | # FVM Cells | # FEM Cells |
|---|
| Validation | Cavitation tunnel | 1 foil | Steady | Single phase | Under-relaxation | 3,733,065 | 48,453 |
| Foil open water | Box domain | 1 foil | Unsteady | VOF | Added mass | 3,985,861 | 49,296 |
| Full hydro | Box domain | 2 foils, 2 rudders | Unsteady | VOF | Added mass | 19,775,282 | 96,592 |
Table 3.
Mesh sizes for the fluid mesh.
Table 3.
Mesh sizes for the fluid mesh.
| | Relative Size to BS [%] | Absolute Size [mm] |
|---|
| Base size (BS) | - | 200 |
| Maximum size | 100 | 200 |
| Target surface size | 100 | 200 |
| Foil target surface size | 3 | 6 |
| LE minimum isotropic size | 0.15 | 0.3 |
| TE minimum isotropic size | 0.15 | 0.3 |
| Prism layer near wall thickness | - | 0.0022 |
| Prism layer total wall thickness | - | 8 |
| Free surface z-refinement | 3.125 | 6.225 |
| Free surface wake z-refinement | 6.25 | 12.25 |
| Free surface wake xy-refinement | 12.5 | 25 |
Table 4.
Mass moment of inertia of the boat.
Table 4.
Mass moment of inertia of the boat.
| | |
|---|
| [] | [] | [] |
|---|
| 1364.6 | 1913.0 | 1863.5 |
Table 5.
Test matrix used for performance evaluation.
Table 5.
Test matrix used for performance evaluation.
| | Values | Units |
|---|
| Flying height | 0.4, 0.6, 0.8 | [m] |
| Leeway | −2, 0, 2 | [°] |
| Rake | −2, 0, 2, 4 | [°] |
Table 6.
Fluid properties used in simulations.
Table 6.
Fluid properties used in simulations.
| | T | | |
|---|
| | [°C] | [] | [] |
|---|
| Sea water | 22.0 | 1024.3 | |
| Air | 22.0 | 1.196 | |
| Fresh water (cavitation tunnel) | 19.0 | 998.4 | |
Table 7.
Weather data used in simulations. TWS is True Wind Speed, TWD is True Wind Direction, T is wave period and H is wave height.
Table 7.
Weather data used in simulations. TWS is True Wind Speed, TWD is True Wind Direction, T is wave period and H is wave height.
| | TWS | TWD | T | H |
|---|
| | [] | [°] | [] | [] |
|---|
| Mistral condition | 8.5 | 320 | 4.0 | 0.5 |
Table 8.
Boat parameters for simulation of boat sailing upwind in Mistral condition.
Table 8.
Boat parameters for simulation of boat sailing upwind in Mistral condition.
| | Values | Units |
|---|
| Leeward foil rake | 5.0 |
°
|
| Windward foil rake | 3.0 |
°
|
| Leeward rudder rake | 3.0 |
°
|
| Windward rudder rake | −1.0 |
°
|
| Boat speed | 13.7 | knots |
| TWA | 45 |
°
|
| Flying height | 0.5 | m |
| Leeway | 2.5 |
°
|
Table 9.
Discretisation uncertainties for solid model for span-wise resolution (), chord-wise resolution (), and total ().
Table 9.
Discretisation uncertainties for solid model for span-wise resolution (), chord-wise resolution (), and total ().
| | [%] | [%] | [%] |
|---|
| 0.30 | 0.02 | 0.32 |
Table 10.
Meshes used for the verification of the fluid model. BS denotes the mesh base size and c the chord length.
Table 10.
Meshes used for the verification of the fluid model. BS denotes the mesh base size and c the chord length.
| Mesh Number | [-] | Cell Count [millions] |
|---|
| 1 | 0.315 | 29.5 |
| 2 | 0.397 | 19.0 |
| 2 | 0.500 | 12.4 |
| 3 | 0.630 | 8.3 |
| 4 | 0.794 | 5.6 |
| 5 | 1.000 | 3.9 |
| 6 | 1.260 | 2.7 |
| 7 | 1.587 | 2.0 |
| 8 | 2.000 | 1.5 |
| 9 | 2.520 | 1.1 |
Table 11.
Discretisation uncertainties. is the difference between the value at the applied mesh size and the asymptotic value, is standard deviation of the fit and S is the safety factor.
Table 11.
Discretisation uncertainties. is the difference between the value at the applied mesh size and the asymptotic value, is standard deviation of the fit and S is the safety factor.
| Parameter | [-] | [-] | S [-] | Uncertainty [%] |
|---|
| 0.0297 | 0.0032 | 1.25 | 3.8 |
| 0.0014 | 0.0001 | 1.50 | 16.5 |
| 0.0060 | 0.0001 | 1.25 | 2.7 |
| 0.0085 | 0.0007 | 1.25 | 3.9 |
Table 12.
Validation summary for displacement . U is uncertainty, subscripts and denote experimental and numerical, respectively.
Table 12.
Validation summary for displacement . U is uncertainty, subscripts and denote experimental and numerical, respectively.
| Rake | [°] | −2.0 | −1.0 | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 4.6 |
|---|
| [-] | 0.235 | 0.275 | 0.395 | 0.545 | 0.710 | 0.890 | 1.085 | 1.200 |
| [-] | 0.165 | 0.335 | 0.514 | 0.699 | 0.894 | 1.095 | 1.301 | 1.427 |
| [-] | 0.079 | 0.109 | 0.130 | 0.147 | 0.160 | 0.169 | 0.155 | 0.154 |
| [-] | 0.046 | 0.047 | 0.054 | 0.064 | 0.076 | 0.090 | 0.106 | 0.115 |
| [-] | 0.091 | 0.119 | 0.141 | 0.160 | 0.177 | 0.191 | 0.187 | 0.193 |
| [-] | 0.070 | 0.060 | 0.119 | 0.154 | 0.184 | 0.205 | 0.216 | 0.227 |
| Validated? | [-] | Yes | Yes | Yes | Yes | No | No | No | No |
| [%] | 38.7 | 43.2 | 35.6 | 29.4 | 24.9 | 21.5 | 17.3 | 16.1 |
Table 13.
Validation summary for drag force . U is uncertainty, subscripts and denote experimental and numerical, respectively.
Table 13.
Validation summary for drag force . U is uncertainty, subscripts and denote experimental and numerical, respectively.
| Rake | [°] | −2.0 | −1.0 | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 4.6 |
|---|
| [-] | 0.0080 | 0.0083 | 0.0092 | 0.0104 | 0.0118 | 0.0132 | 0.0157 | 0.0175 |
| [-] | 0.0120 | 0.0121 | 0.0126 | 0.0133 | 0.0144 | 0.0158 | 0.0174 | 0.0187 |
| [-] | 0.0010 | 0.0016 | 0.0020 | 0.0024 | 0.0029 | 0.0041 | 0.0043 | 0.0043 |
| [-] | 0.0023 | 0.0023 | 0.0023 | 0.0023 | 0.0023 | 0.0023 | 0.0023 | 0.0023 |
| [-] | 0.0025 | 0.0028 | 0.0030 | 0.0033 | 0.0037 | 0.0046 | 0.0049 | 0.0049 |
| [-] | 0.0040 | 0.0038 | 0.0034 | 0.0029 | 0.0026 | 0.0025 | 0.0017 | 0.0012 |
| Validated? | [-] | No | No | No | Yes | Yes | Yes | Yes | Yes |
| [%] | 30.9 | 33.2 | 33.0 | 31.4 | 31.0 | 35.1 | 30.9 | 27.9 |
Table 14.
Validation summary for side force . U is uncertainty, subscripts and denote experimental and numerical, respectively.
Table 14.
Validation summary for side force . U is uncertainty, subscripts and denote experimental and numerical, respectively.
| Rake | [°] | −2.0 | −1.0 | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 4.6 |
|---|
| [-] | 0.061 | 0.101 | 0.140 | 0.177 | 0.214 | 0.252 | 0.276 | 0.294 |
| [-] | 0.080 | 0.123 | 0.166 | 0.207 | 0.246 | 0.284 | 0.318 | 0.336 |
| [-] | 0.034 | 0.031 | 0.031 | 0.031 | 0.033 | 0.028 | 0.024 | 0.025 |
| [-] | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 |
| [-] | 0.035 | 0.032 | 0.032 | 0.032 | 0.034 | 0.029 | 0.026 | 0.026 |
| [-] | 0.019 | 0.023 | 0.026 | 0.030 | 0.031 | 0.032 | 0.041 | 0.042 |
| Validated? | [-] | Yes | Yes | Yes | Yes | Yes | No | No | No |
| [%] | 57.5 | 31.5 | 22.9 | 18.2 | 16.0 | 11.4 | 9.2 | 8.7 |
Table 15.
Validation summary for lift force . U is uncertainty, subscripts and denote experimental and numerical, respectively.
Table 15.
Validation summary for lift force . U is uncertainty, subscripts and denote experimental and numerical, respectively.
| Rake | [°] | −2.0 | −1.0 | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 4.6 |
|---|
| [-] | 0.038 | 0.077 | 0.118 | 0.158 | 0.201 | 0.246 | 0.288 | 0.313 |
| [-] | 0.041 | 0.084 | 0.131 | 0.181 | 0.237 | 0.297 | 0.361 | 0.401 |
| [-] | 0.030 | 0.029 | 0.030 | 0.032 | 0.034 | 0.031 | 0.030 | 0.030 |
| [-] | 0.011 | 0.011 | 0.011 | 0.011 | 0.011 | 0.011 | 0.011 | 0.011 |
| [-] | 0.032 | 0.031 | 0.033 | 0.034 | 0.036 | 0.033 | 0.032 | 0.032 |
| [-] | 0.003 | 0.007 | 0.013 | 0.023 | 0.036 | 0.052 | 0.073 | 0.088 |
| Validated? | [-] | Yes | Yes | Yes | Yes | Yes | No | No | No |
| [%] | 85.3 | 40.3 | 27.6 | 21.7 | 18.0 | 13.4 | 11.2 | 10.3 |
Table 16.
Flow parameters of speed change study.
Table 16.
Flow parameters of speed change study.
| | Flow Speed | Re | Fn | | g |
|---|
| | [knots] | [-] | [-] | [] | |
|---|
| Baseline | 18.0 | | | | 9.81 |
| Reduce speed | 14.0 | | | | 9.81 |
| Reduce Re | 18.0 | | | | 9.81 |
| Reduce Fn | 18.0 | | | | 9.00 |