A Review of Methods for Modelling Flooding, Its Progression and Outcome in Damaged Ships

Abstract

The timely and precise prediction of flooding progression and its eventual outcome in ships with breached hulls can lead to dramatic improvements in maritime safety through improved guidance for both emergency response and ship design. The traditional approach to assessing damage-induced flooding in both these stages, which also fully complies with statutory rules, is through static calculations. On the other hand, the application of models that simulate the flooding progression and the behaviour of flooded ships from, or close to, first principles allows for increased accuracy of the modelling of the phenomenon. This increase in accuracy can then be used to support advanced design for safety procedures. Furthermore, it can considerably enhance a ship’s capability for damage identification and inference-based logic for emergency decision support systems and marine accident response in general. This paper conducts a review of selected state-of-the-art methods, procedures, and case studies in recent years which aimed to model progressive flooding and damage ship behaviour and provide some explanations of fundamentals. Applications related to damage identification, the prediction of outcome/situation awareness, and flooding emergency response are also briefly discussed. The paper concludes with a brief reflection on salient gaps in the context of accelerating the development of these methods and their applicability.

1. Introduction

Flooding events in ships with breached hulls pose significant risks to maritime safety, making the timely and precise prediction of their progression and ultimate outcomes of paramount importance. The ability to accurately assess and respond to such incidents not only contributes directly to cargo safety, environmental protection, and the well-being of crew members and passengers, but it also plays a crucial role in enhancing emergency response strategies and ship design practices.

Traditionally, the evaluation of damage-induced flooding in ships has relied on static calculations to comply with statutory safety rules. However, recent advances in modelling techniques allow for a more accurate analysis.

In the present paper, state-of-the-art methods, procedures, and case studies regarding progressive flooding simulation are reviewed. Furthermore, a brief depiction of recent efforts targeting damage identification, the prediction of outcomes and situation awareness, and enhanced emergency response strategies is carried out. The paper concludes by briefly reflecting on significant research gaps in the context of rapidly advancing these methods and their applicability. It is the intention of the author that the current review will offer insights into the potential for safer and more effective maritime and naval operations, thereby reinforcing the vital role of accurate flooding prediction and response strategies in the maritime and naval industries.

1.1. Other Reviews

Several reviews related to the subject of ship intact and damage stability have been published throughout the years. While most are focused on very specific topics within the subject, others aim to provide state-of-the-art techniques in a more encompassing way. An arguable chronological selection of these efforts is analysed in this section. To the best judgement of the author, these works should be complementary to each other and provide a good overview of the historical reviewing of damaged ship stability and direct methods for simulating progressive flooding in ships.

Papanikolaou [1] presented a review of the developments and trends in the damage stability of ships in 2007. Developments in numerical simulation methods for the prediction of damaged ship motion in waves were considered, compared with three ITTC benchmark studies whose results are summarised by Papanikolaou, Spanos and van Walree [2,3,4]. Model experiments were deemed essential for assessing damaged ship survivability in waves, even though theoretical–numerical methods could aid in pre-assessing intact and damaged ship survivability despite some of their limitations. Those limitations were mainly related to considerable uncertainties related to the viscosity effects and roll responses of ships. The accuracy of the floodwater dynamics methods considering horizontal floodwater free surface at all times was considered inaccurate for predictions in waves and the prediction of flooding rates and transient phenomena. A review of regulatory issues was also conducted, highlighting the probabilistic concept of a ship’s damage stability.

Santos and Guedes Soares [5] reviewed the development of the traditional method for ship subdivision and of the deterministic damage stability method and its limitations. The theoretical foundations for the probabilistic method were introduced, while the authors described and stressed the sound theoretical principles on which it was based, allowing it to take into account the numerous uncertainties that arise regarding ship survivability in damage condition.

In 2016, Bačkalov et al. [6] provided an extensive review of the findings presented at the International Conferences on the Stability of Ships and Ocean Vehicles (STAB) and International Ship Stability Workshops (ISSW) in the 2009–2014 period, while Manderbacka et al. [7] carried out a review in 2019 of a selection of papers from ISSW2014 [8] and ISSW2016/17 [9,10]. The review covered intact and damage stability, regulatory issues (including probabilistic approaches), advanced numerical methods for ship motion, and stability failure prediction, including roll damping, operational issues related to ship stability, and environmental modelling. When it came to methods for simulating transient flooding and floodwater dynamics on a vehicle deck, the review mentioned the lack of attention and efforts towards in-depth refinement at that time. On the other hand, it highlighted the then-recent research towards the development of new probabilistic approaches for naval vessels, although the papers listed seemed to be focused only on intact stability.

Although not pertaining to methods addressing the behaviour of damaged ships, the statistical review reports from the European Maritime Safety Agency (EMSA) [11] are worth referencing as they are key references concerning the continuing relevance of such methods and the significance of what they address. Specifically, the reviews focus on the safety level of ships, concluding with important observations from performing a statistical analysis of accidents. Basic risk contributors, namely the frequency of main accidents’ occurrence and related consequences, are therein quantified and assessed covering the 2000–2021 period. The reports show a significant reduction in the number of accidents in the last decade, but a growth in the frequency of ship total losses and fatalities (although this mostly relates to vessels not complying with safety regulations). An important observation is that grounding and contact accidents dominate the statistics of passenger ships accidents of all subtypes, whereas collision accidents account for a minority of the events and can potentially lead to flooding.

1.2. The Present Review

This review offers an updated overview of the state of the art concerning the simulation of progressive flooding in ships, while providing a deliberately broader, albeit less detailed, perspective compared to the ones in Section 1.1. In addition to simulation, it also discusses, although briefly, the application of these methods towards: identification (focusing on situation awareness and damage identification), prediction (addressing outcome prediction), and response (discussing flooding emergency response).

Furthermore, the review presented in this paper and its discussion aims to provide a practical reference source concerning development and applications of progressive simulation in ships, which, to the best of the author’s knowledge, is currently unavailable in the published literature in terms of its broadness and condensed presentation.

The paper is structured as follows. The motivation for developing methods for modelling flooding, its progression, and its outcomes in damaged ships and challenges are given in Section 2. In Section 3, the fundamentals of ship flooding are explained, in particular some critical considerations relevant to modelling the progressive flooding of ships, together with the main approaches used to simulate it. A succinct historical review concerning scientific developments in the field in the last decades is presented in Section 4. A summary of state-of-the-art numerical tools and the latest experimental datasets and validations is given in Section 5, followed by some examples of recent studies towards application of those methods in identifying/characterizing damages, predicting its outcomes, and guiding response actions in the context of onboard emergency response in Section 6. The paper concludes in Section 7, with a reflection on any salient gaps that are not yet addressed, focusing on accelerating the development of these methods and their applicability in the maritime and naval industries.

2. Importance and Challenges Related to Simulating Flooding in Damaged Ships

The enduring challenge of ensuring the safety and performance of vessels continues to evolve. Central to this challenge is the very essence of ships and floating devices: an equilibrium rooted in an intricate dance of density imbalances, meticulously upheld by the structural framework known as the hull. Ship’s hulls weather an unending array of forces and actions, each vying to disrupt this delicate equilibrium. From the early days when a hollowed log served as the rudimentary hull, the structural integrity of these vessels assumed paramount significance. It needed to withstand not only the external pressures exerted by the surrounding water but also the complex interplay of forces stemming from its cargo. Any substantial breach would most surely lead to catastrophic consequences.

In modern times, the humble log has evolved into a sophisticated ship structure intricately tied to resistance against a myriad of complex loads. The advent of compartmentalisation, epitomised by the introduction of bulkheads, has raised the bar in terms of maintaining this equilibrium. Compartmentalisation, while crucial for enhancing the ship’s survivability, imposes additional complexities, particularly in passenger and navy ships. This partitioning of spaces avoids the mixing of cargo and, in the unfortunate event of an accident, the progression of flooding. However, this same compartmentalisation, while essential for damage containment, may also complicate evacuation procedures, potentially impeding the swift and safe evacuation of passengers and crew in emergency situations.

The ingress of seawater into previously empty compartments, coupled with the potential shifting and flow of cargo, fundamentally disrupts the force system for which the vessel would otherwise be meticulously designed were these ignored. This destabilisation can lead to a cascade of consequences, ranging from direct capsizing and foundering to a catastrophic increase in structural loads, rendering the original framework incapable of withstanding them. Furthermore, structural damage can compromise critical elements that, due to their properties and strategic location, are vital for the ship’s resistance, even under intact conditions. A domino effect may ensue as structural components begin to fail, triggering a spiralling sequence of events characterised by increasing flooding and further structural collapse.

2.1. Flooding Risk in Ship Safety

While shipping losses have witnessed a notable overall steady reduction since 2005, owing in part to stringent regulatory measures, these incidents are still far from being rare occurrences. As per data from EMSA [11], the cumulative count of recorded casualty event categories related to fatalities in ship-related incidents spanning from 2014 to 2021 reached a tally of 535, as shown in

Table 1. Fatalities in occurrences with ships, organised by casualty event type [11].

Event Type	2014	2015	2016	2017	2018	2019	2020	2021
Collision	48	4	74	16	2	16	16	6
Flooding/Foundering	30	50	29	6	6	4	0	0
Capsizing/Listing	25	16	23	5	6	14	9	3
Fire/Explosion	14	6	1	1	7	7	4	4
Damage/loss of equipment	18	1	1	2	3	2	0	1
Loss of control—Loss of propulsion power	11	0	0	1	0	11	0	0
Loss of control—Loss of electrical power	11	0	0	0	0	0	0	0
Grounding/stranding—Power	8	0	0	0	1	2	0	0
Loss of control—Loss of containment	0	0	0	0	1	1	3	0
Grounding/stranding—Other	0	3	0	0	1	0	0	0
Loss of control—Loss of directional control	0	0	0	1	0	0	0	0
Contact	0	0	0	0	0	0	0	0
Hull failure	0	0	0	0	0	0	0	0
Loss of control—Other	0	0	0	0	0	0	0	0

. Among these fatalities, collisions and flooding/foundering emerged as the primary causes, constituting 34.0% and 23.4% of the total fatalities, respectively. Together, these two event types accounted for a substantial 57.4% of the total fatalities. Following closely, capsizing/listing accounted for 18.9% of the recorded fatalities.

Conversely, injuries predominantly occurred in scenarios categorised as collisions, contact, damage or loss of equipment, and fire/explosion, yielding totals of 347 (24.5%), 316 (22.3%), 210 (14.8%), and 165 (11.6%) injuries, respectively, as shown in

Table 2. Injuries in occurrences with ships, organised by casualty event type [11].

Event Type	2014	2015	2016	2017	2018	2019	2020	2021
Capsizing/Listing	38	3	1	8	10	9	0	5
Collision	64	36	16	61	36	82	32	20
Contact	72	35	16	84	48	35	14	12
Damage/loss of equipment	51	20	38	17	21	29	16	18
Fire/Explosion	74	9	23	12	23	10	8	6
Flooding/Foundering	15	6	9	12	23	12	1	3
Grounding/stranding—Other	4	1	0	1	4	0	0	0
Grounding/stranding—Power	5	7	5	3	5	4	3	2
Hull failure	0	0	2	0	0	0	0	0
Loss of control—Loss of containment	7	2	4	0	1	4	3	2
Loss of control—Loss of directional control	1	9	13	1	10	5	7	0
Loss of control—Loss of electrical power	31	0	2	0	0	0	0	0
Loss of control—Loss of propulsion power	32	3	2	3	0	35	0	1
Loss of control—Other	0	0	0	1	0	0	0	0

. Remarkably, flooding and foundering, which also featured prominently among fatality causes, accounted for 81 (5.7%) of the total injuries. The comprehensive count of reported casualty event types pertaining to injuries in ship-related incidents during the period from 2014 to 2021 amounted to 1418.

The statistics provided underscore a sobering reality: despite notable overall reductions in shipping losses over the years, the risk posed by flooding to human lives remains a significant concern in the maritime industry. The cumulative count of recorded casualty event categories related to fatalities during the period from 2014 to 2021, as reported by EMSA [11], paints a compelling picture. Collisions and flooding/foundering continue to stand out as the primary culprits, together constituting a substantial 57.4% of total fatalities. Capsizing/listing follows closely, adding to the gravity of the situation. As we strive to enhance safety in modern shipping, it is evident that addressing the complex dynamics of flooding and its consequences remains an imperative task, one that demands ongoing vigilance and the development of advanced strategies to mitigate the enduring risk to human lives at sea and to the environment.

Still focusing on accidents that lead to flooding and, possibly, to foundering, Eliopoulou et al. [12] highlight the fact that grounding and contact accidents dominate the statistics of passenger ships of all subtypes, whereas collision accidents only account for about 30% of the events potentially leading to flooding. This observation, although restricted to passenger ships in their work, corroborates the certainty that detailed physical characterisation of the accidents is as important as the knowledge of their outcomes. A challenge being in what way are these characterisations, with all relevant details, accounted for statistically in a structured way, at the same time that underlying uncertainties are significant due to the scarcity of available empirical comprehensive data.

2.2. Addressing Complexity in Damage Stability with Advanced Methods

The predominant approach in ship damage stability assessment has traditionally been deterministic and grounded in empiricism. While this method has found suitability for smaller vessels and cargo ships, it has proven notably inadequate for larger passenger ships, especially contemporary ones designed to accommodate thousands of passengers. To achieve a dependable estimation of the risk of flooding in serious maritime incidents, there is a growing imperative to treat damage stability as a scientific discipline [13]. This involves a shift away from empirical methodologies and a move towards approaches firmly rooted in first principles.

This shift is motivated by an understanding that relying solely on generalised formulations for damage stability assessments can lead to shortcomings. A comprehensive grasp of the underlying mechanisms that can result in vessel capsizing or sinking post-flooding incidents, potentially causing loss of human life, is essential. It is crucial to identify the key design and operational parameters that can effectively reduce these risks in a cost-efficient manner. Achieving this ambition calls for the development of advanced methods, tools, and techniques capable of meaningfully addressing the intricate physical phenomena at play. In the contemporary landscape, the availability of numerical flooding simulation tools within the scientific community, coupled with enhanced computational capabilities in the industry, opens the door to a potential transition in damage stability assessment towards direct numerical simulations (direct methods) for modelling the physics of progressive flooding and its effects on the behaviour of a ship [14].

2.3. Challenges

Challenges present in modelling the behaviour of damaged ships during flooding and its application within the four aspects listed in Section 1.2 (simulation, identification, prediction, and response) include combinations of the following:

• Complex flow dynamics. Progressive flooding in a ship involves complex flow dynamics, including turbulent flows, sloshing, and interactions with ship motions and structures. Accurately capturing these dynamics is challenging [15].
• Nonlinear interactions. As the water floods progressively, it interacts with ship structures in nonlinear ways [16]. It can, and typically does, lead to changes in the ship’s stability and motion response characteristics, which needs to be addressed in a robust, yet efficient, manner.
• Compartmentalisation. Modelling how water moves from one compartment to another, especially when multiple breaches are involved, can be very complex and difficult to perform with fast algorithms [17].
• Impact of damaged structures. The damaged state of the ship’s structure, including buckled plates, destroyed bulkheads, or distorted frames, can significantly affect water flow. Modelling this accurately and efficiently is difficult [18].
• Large number of variables. The initial conditions such as ship’s speed, list, trim, wave conditions, breach location, and size can vary greatly, leading to a vast parameter space to consider in modelling [19].
• Time dependency. The nature of progressive flooding means predictions are time-dependent. Over time, as water continues to ingress, different compartments may become affected and structural integrity may degrade. In a process which can take hours, the environment loads can also change. This leads to a challenge to accurately model and predict the final outcomes of an accident [20].
• Direct methods’ assumptions and limitations. While direct methods aim to provide a more detailed and realistic assessment of the ship’s state after damage, compared to the typical empirically rule-based simplified assumptions, they often come with inherent assumptions that might not hold true in all scenarios [21].
• Computational intensity. Accurate simulations require high-resolution models and might be computationally intensive, leading to long simulation times which are typically a constraint in real-time decision making [22].
• Validation challenges. Validating the models against real-world scenarios is difficult due to limited data on actual ship-flooding incidents. Experimental setups, like tank tests, may also not capture all complexities and can only be used for a limited set of configurations [16].
• Human factors. While models can predict the physical behaviour of a flooding ship, predicting how people onboard will react, and incorporating those reactions into safety measures, is an added layer of complexity [23].
• Interplay with other systems. A ship comprises multiple systems (electrical, mechanical, etc.). Flooding might impact these systems, and vice versa. Considering this interplay increases modelling complexity [22].
• Safety protocols and mitigations. Even with accurate models, deriving actionable safety protocols or mitigations from the insights can be challenging, especially when considering the practical constraints onboard [24].

In the context of increasing the safety of people on board, it is crucial to address these challenges. Aiming for simulation-based models to not only predict the physical progression of flooding but also guide effective emergency responses is vital. The overarching goal is to translate these complex models into actionable insights that can be deployed in real-world scenarios to safeguard lives at either design or operational stages.

3. Fundamentals of Ship Flooding and Simulation Approaches

3.1. Flooding Phases

Consider a ship floating which has a sudden damage opening in its hull. If the damage is totally, or partially, below the waterline, there is a sudden ingress of water into the interior of the ship—unless the affected compartments are already occupied, naturally. It is common to divide the subsequent flooding process in three phases: transient, progressive, steady [25]—see Figure 1.

The transient phase corresponds to the initial water ingress on the ship. If the damage is at the side of the ship and has a substantial extent, it may cause a significant heeling moment, leading to a permanent list, or even, due to its suddenness, to the immediate capsizing of the ship. The initial layout of flooded compartments does not need to be asymmetric for the phenomenon to occur. In fact, due to the ship’s oscillations in the seaway as the damage occurs, the presence of obstacles in the way of the otherwise free water discharge jet, the momentum inherent to the discharge, or just the presence of crests and troughs, water may rush into a symmetric space enforcing an asymmetric load. Such a phenomenon is more relevant in Ro-Ro ships, with their poorly subdivided vehicle decks.

After the transient phase, if the ship has not capsized or sank, a process is reached with a nature closer to steady: the progressive flooding phase. In this phase, the ship has achieved a quasi-equilibrium position (average position if in presence of waves), which steadily changes as the flooding progresses gradually through the permanent or damaged induced openings. Damaged ships of considerable size can remain on this phase for several hours, and fast estimations of the outcome of the flooding process may be carried out. However, one must not forget that in this phase, like in any other, the vessel suffers the effects of the seaway and its wave loads.

If the ship survives the previous phases, an invariant mean equilibrium position is finally reached. The average ingress of water is zero and the process may be said to be in its steady state. However, floodwater may still be passing between compartments and through the existing hull breaches as a result of the ship motions in the seaway.

Structural failure is possible in all three phases, while the effects of the wave-induced loads become, statistically speaking, of higher significance as the time span extends, i.e., in the steady phase. Regulations’ criteria, numerical simulations, and model tests of damaged ships in waves mostly focus on this phase.

All three stages of flooding may be simulated using different approaches, depending on the accuracy of the results that is required and, most importantly, on the actual quantities one aims to assess. Given the scale of the problem, both in space and time, one is typically not interested in the details of the flow inside compartments and the local distributions of loads in structural elements of the ship which result from the event. On the other hand, knowledge of details of the flow at breaches and openings between compartments and loads on, say, non-watertight doors, subjected to the action of flooding-induced pressures, can be crucial for a proper prediction of the progression of the flooding and its outcome.

3.2. Field Methods

The application of field computational fluid dynamics (CFD) methods, which consider the full physics of the problem with relatively minor simplifications (e.g., URANS: unsteady Reynolds averaged Navier–Stokes) to the entire (physical) domain of the problem, is typically not appropriate, nor is their inclusion as part of practical tools such as decision support systems and risk assessment-related studies. For these applications, such codes may pollute the system with unnecessary detail and greatly increase the complexity of code development, in addition to requiring a prohibitive amount of processing power, especially for delivering data for the application of Monte Carlo methods.

On the other hand, they can be used as benchmark references for the development of lower-fidelity solutions or to explore flow details of particular interest, such as at openings, or simply to have a better understanding of the phenomenon for research purposes, e.g., [17,26,27]. URANS also allows us to investigate complex flooding phenomena and capture the complex hydrodynamic behavior in the flooding process, including splash, jet, water column, and bubble [28,29].

In many cases, the transient flooding phase is only accurately predicted by using field methods as they are able (in principle) to model the phenomenon to an arbitrary precision. For example, Ruth et al. [30] used STAR-CCM+ 9.04.011 to perform full-scale simulations of the fully coupled behaviour of a damaged vessel. External and internal flows and all stages of the flooding process were included. They concluded field methods to be satisfactory tools for simulating flooding events; however, they pointed out the computational burden/simulation time, particularly for progressive flooding and statistical evaluations where multiple runs need to be considered.

3.3. Hybrid Methods

A simplified step relative to obtaining a full RANS implementation is to perform a domain decomposition in RANS (interior) and potential flow theory (exterior) regions, e.g., [31]. RANS is used to simulate the flow inside and around the ship’s hull, being suitable for capturing the complex flow patterns near the ship’s hull and other detailed fluid–structure interactions.

One important aspect is that of the dynamic free-surface effects inside the affected compartments, occurring due to the ocean wave excitation. Sloshing may occur in partially flooded compartments. Typically, a standing internal free-surface wave arises in nearly fully flooded spaces, whereas a progressive wave arises in nearly empty spaces. Both the full and partial field method approaches mentioned above inherently capture these phenomena, e.g., [32,33,34]. On the other hand, one can apply shallow water equations (SWE), as in [35], or analytical or semi-analytical methods such as in [36], depending on the water level.

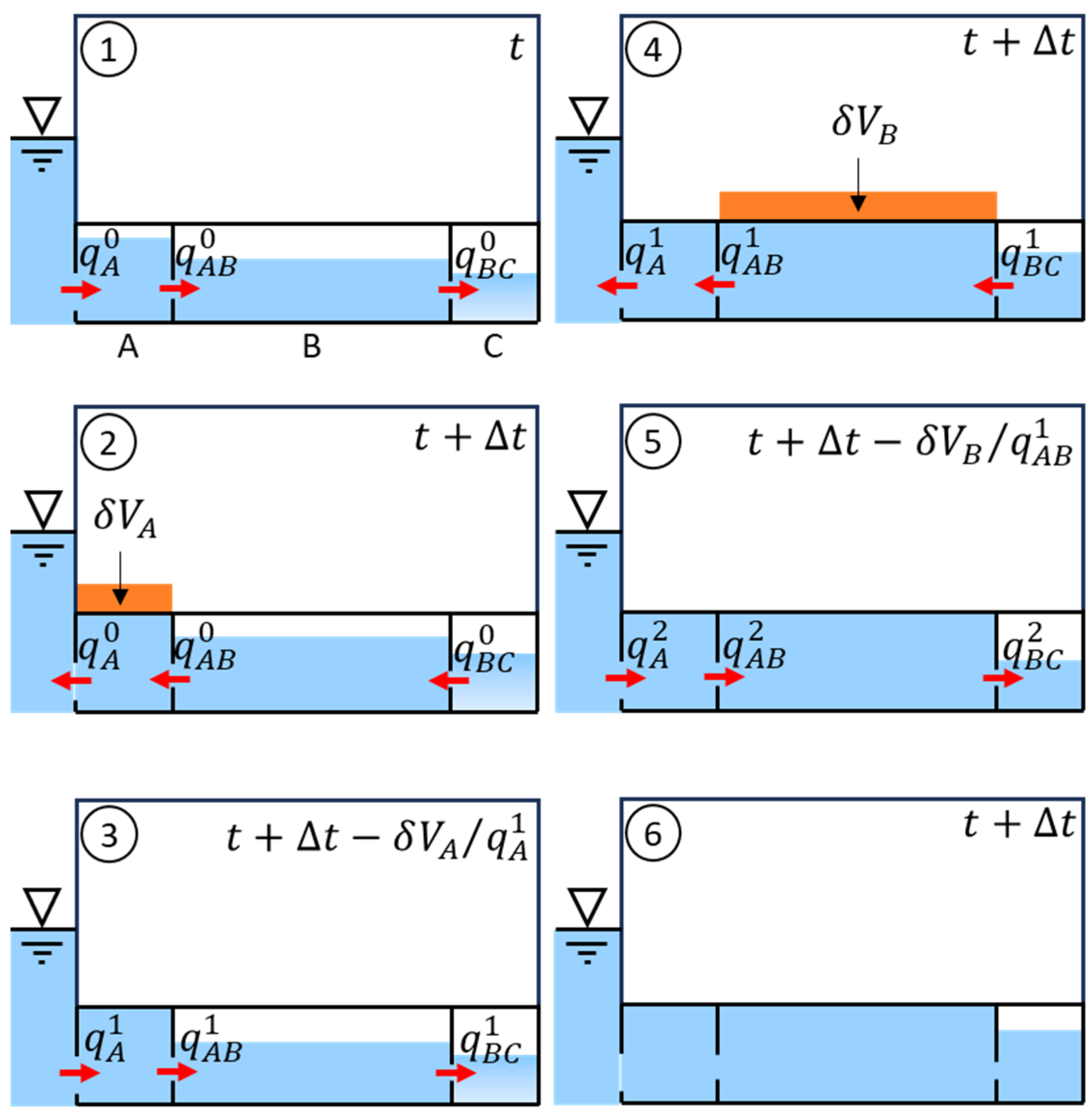
3.4. Fast Methods

Continuing down the ladder of simplification are the methods implemented in time domain, typically using impulse response functions derived from linear diffraction codes in the frequency domain for the motion of the ship while the progressive flooding is modelled using hydraulic methods such as resorting to the Bernoulli equation.

These are the most common methods in progressive flooding numerical simulation and a selection of these is listed in Section 5.1. The degree to which the progressive flooding, flow at the openings, free surface effects, and ship dynamics are accurately modelled, and the extent to which all these are coupled, varies between codes. The same is also true in terms of introducing aspects such as air entrapment, tank venting, and waves. Furthermore, there are also quasi-static or fully dynamic approaches, depending on the method.

There are three fundamental components of modelling in these methods: the flooding rate, which governs the transfer of fluids between compartments and at the hull breach; the free surface of the fluids inside the flooded compartments; and the seakeeping model and the way it is coupled with the previous two components.

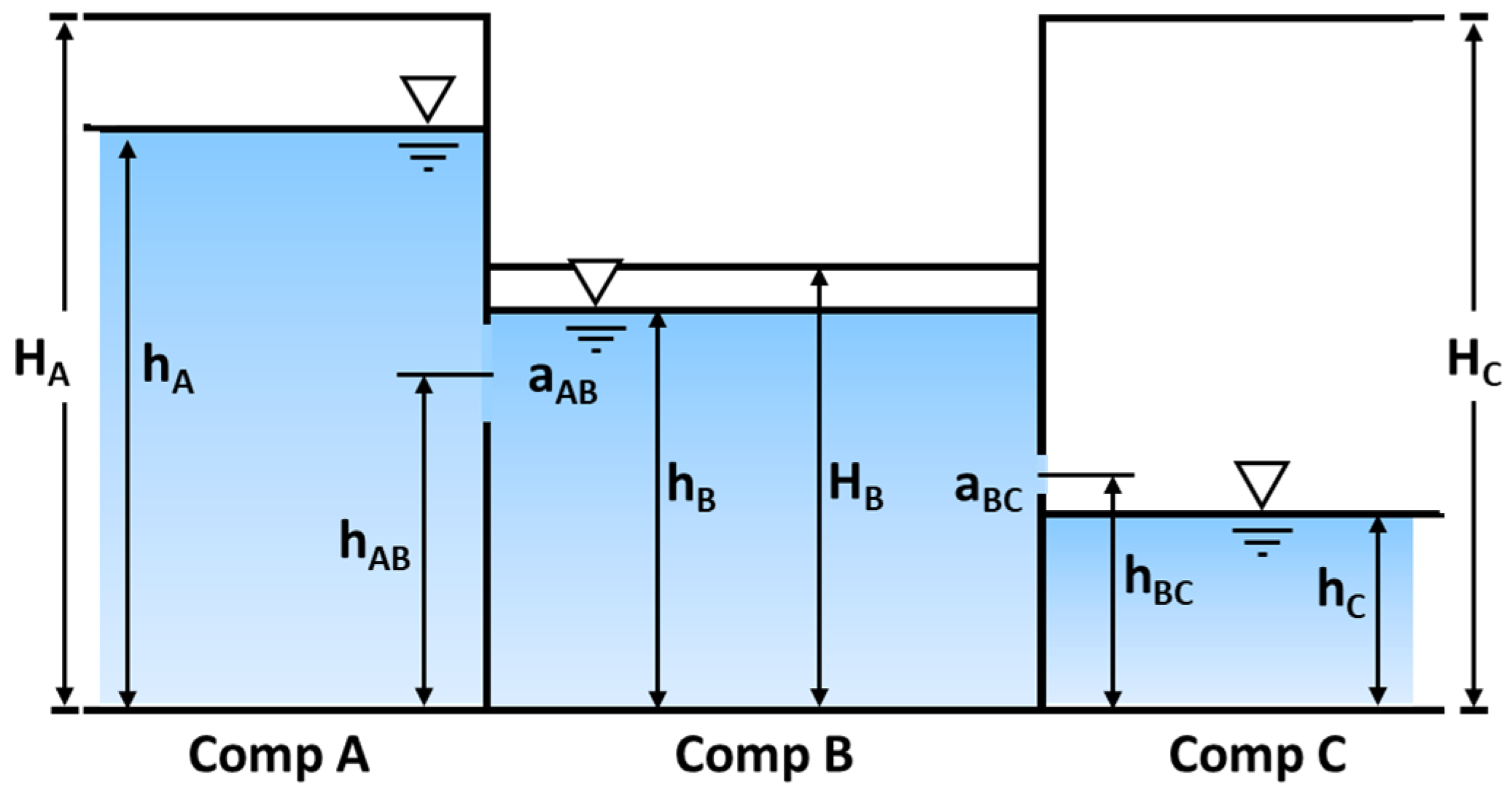
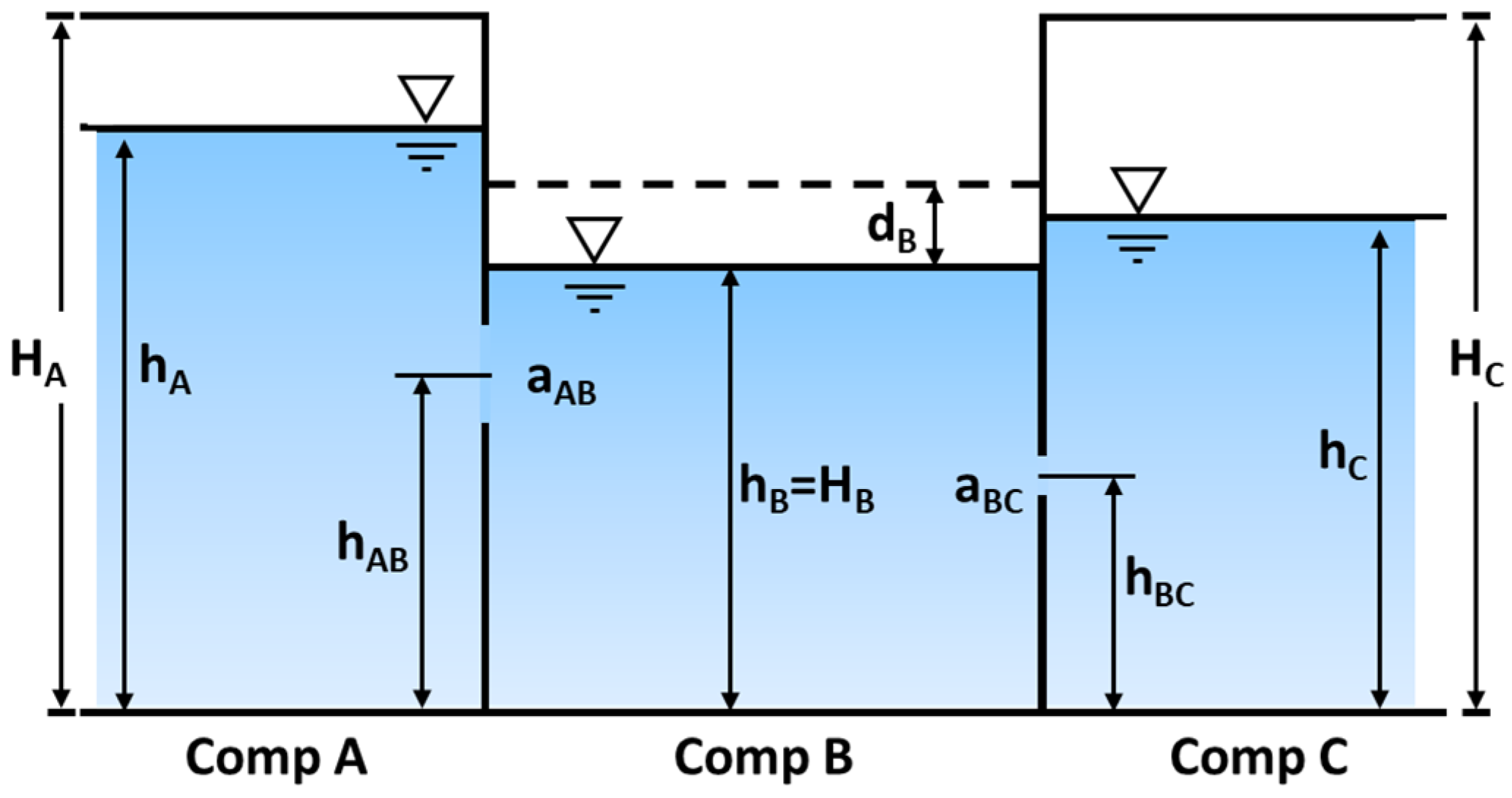
3.4.1. Flooding Rate

In its simplest implementation, e.g., under a quasi-static approach, the Bernoulli equation allows for calculating the flow at an opening from the water levels in the compartments to which the opening is connected. Taking the example in Figure 2, the fluid progression from compartments A to B ($q_{AB}$) and from B to C ($q_{BC}$) can be calculated as [25]:

$$q_{AB}=a_{AB}{k}_{AB}\sqrt{2g\left(h_A-h_B\right)},$$

(1)

$$q_{BC}=a_{BC}{k}_{BC}\sqrt{2g\left(h_C-h_B\right)},$$

(2)

where $k_{AB}$ and $k_{BC}$ are discharge coefficients. These are typically obtained from empirical data and usually considered to lie in the range of 0.6–0.7. These values typically hold for relatively small openings with steady flows and with water on both sides of the opening.

Connecting a compartment that is at capacity to adjacent spaces with water levels exceeding its own maximum height (as depicted in Figure 3) can lead to the erroneous calculation of flows if Equations (1) and (2) are applied without modification. One way to solve this problem is to enforce a zero net flow in full compartments. The added pressures applied at each side of the openings can be calculated iteratively at each time step using a nonlinear system of equations [25,37]. For the case in Figure 3, the added pressure in compartment B ($p_B$) corresponds to an additional virtual added column of water $d_B,$ the system of equations reduces to a single equation, and the added pressure is calculated as follows:

$$k_{AB}·a_{AB}·\sqrt{{\rho }_{W}g\left(h_B-h_A\right)+p_B}+k_{BC}·a_{BC}·\sqrt{{\rho }_{W}g\left(h_B-h_C\right)}=0,$$

(3)

In terms of the implementation of the time domain procedure, different time-marching schemes can be used, e.g., implicit Euler [38] or the more common Runge–Kutta 4th-order explicit scheme [39]. An adaptive time step can also be used [40]. When using explicit time-marching schemes, the instant a compartment becomes full requires special attention. It is very unlikely that it happens precisely at the end of a time step. As such, to avoid spurious overfilling of a tank, a possible procedure is to monitor the filling status of each compartment and, when overfilling is detected, perform a series of regress–progress steps, as depicted in Figure 4. Here, an algorithm tracks cases where the fluid volumes become higher than the corresponding compartments’ volumes, or when the net flow of a compartment that was full in the previous step results in it no longer being full in the current step.

It is important to stress that no air entrapment effects or resistance effect to flooding due to the compartments’ internal atmosphere are introduced until this point. Several methods have been proposed to account for air entrapment and partial venting of the internal spaces, although its practical relevance is not widely accepted. For instance, two equations of continuity for each compartment—one for water and the other for air—can be considered and used in a pressure-correction method to govern a two-phase problem, as in [38].

Another aspect worth noticing is that the Bernoulli equation describes a steady flow in an inertial frame of reference, which is not the case when the vessel is moving and when in the presence of waves. Furthermore, the Bernoulli equation assumes the flow into an opening to be solely dependent on the pressure difference across it and that the flow reacts instantly to changes in that difference. This is not realistic and may result in slightly shorter times to capsize being predicted [21]. A dynamic orifice equation is a way to approach this issue [41].

3.4.2. Internal Free Surface

Free surface effects are fundamental and well-known phenomena in ship stability. When introduced statically or quasi-statically, the effect of a translation of the centre of gravity of the fluid inside a tank due to heeling results in a shortening of the metacentric height and a corresponding detrimental effect on transverse stability [42]. The fundamental assumption being made is that the free surface of fluids inside the vessel always remains horizontal, including that of floodwater in damaged ships (Figure 5, left). On the other hand, dynamic effects may be relevant and even include phenomena like sloshing, especially when modelling the seakeeping behaviour of the vessel in response to waves.

In that case, modelling the internal free surface and the centre of gravity of floodwater as a mass–damper–spring system is a common approach (Figure 5, middle). However, in other approaches, the force resulting from integrating the pressure over the compartment’s surface encompasses all aspects of floodwater inertia and flow characteristics, provided that the body force accounts for the real acceleration [43] (Figure 5, right).

Figure 5. Floodwater and ship motion interaction—adapted from [44]. (left) static or quasi-static, (middle) point mass–damper–spring, (right) direct pressure integration.

Figure 5. Floodwater and ship motion interaction—adapted from [44]. (left) static or quasi-static, (middle) point mass–damper–spring, (right) direct pressure integration.

Naturally, the free surface in a compartment that has been breached to the sea will experience a transient flooding process which is usually too violent and complex to be properly handled by fast methods and much more well captured by field and hybrid methods. A common approach to work around this issue with expedite methods based on the Bernoulli equation is to subdivide the breached compartment into numerical partitions and treat each partition as compartments themselves. This, in effect has a conceptual parallel to solving the flow between contiguous cells in a field method. This approach allows for hindering the flooding process add mimic to some extent the transient flow in the breached compartment. A more advanced approach is the one described by Valanto [21], where a modified boundary condition for damage openings is formulated. It defines the speed at the damage opening as a combination of the speed given by the application of shallow water equations and that given by the Bernoulli equation or dynamic orifice equation.

3.4.3. Seakeeping

Some methods do not account for the presence of waves or aim to simulate the behaviour of the ship as a result of the wave–structure interaction. Quasi-static approaches, which disregard all dynamic effects, focus solely on the hydraulics of progressive flooding and the consequent sinkage and attitude of the vessel, which responds hydrostatically [38,45]. Others apply dynamic approaches even if considering an external, still-water free surface, e.g., [46].

Given the variation in mass, sinkage, and attitude of the vessel during progressive flooding, linear implementations of the equations of motion may not provide the best results in many cases in the presence of waves. Although other methodologies can be considered, a common approach is for the dynamics of a rigid body to be formulated in the body (vessel) frame and for the angular motions to be expressed in terms of Euler angles. Relations between the rate of change of Euler angles and the body angular velocities ($\overrightarrow{\omega }$) are expressed as tensors and are well known. The Euler angles can also be used to convert body frame translational velocities ($\overrightarrow{U}$) into the earth frame. There is no assumption of linearity or very small displacements of the body for these relations to hold, meaning that this approach allows for a fully nonlinear formulation of the problem. Then, the translation and rotation equations of motion in a body frame (b) are, respectively:

$$\overrightarrow{F}=\frac{d\overrightarrow{p}}{dt}={\left.\frac{d\left(m\overrightarrow{U}\right)}{dt}\right|}_b+\overrightarrow{\omega }\times m\overrightarrow{U}$$

(4)

$$\overrightarrow{M}=\frac{d\overrightarrow{L}}{dt}={\left.\frac{d\left(\left[I\right]\overrightarrow{\omega }\right)}{dt}\right|}_b+\overrightarrow{\omega }\times \left(\left[I\right]\overrightarrow{\omega }\right)$$

(5)

In Equations (4) and (5), the second terms in the RHS of each introduce the Coriolis contributions to the force (i.e., the effect of the accelerations of the body frame itself), and the following quantities are expressed in (or are relative to) the body frame:

• $\overrightarrow{F}$: force acting on the body;
• $\overrightarrow{M}$: moment acting on the body;
• $\overrightarrow{p}$: linear momentum;
• $\overrightarrow{L}$: angular momentums;
• $m$: mass of the vessel (and its contents);
• $\left[I\right]$: inertia matrix;
• $\overrightarrow{U}$: linear velocity vector;
• $\overrightarrow{\omega }$: angular velocity vector.

The LHS terms in Equations (4) and (5) include all hydrodynamic and external forces/moments applied to the body frame, such as hydrodynamic ones, but also consider contributions from the floodwater (see Section 3.4.2). A common tactic used to introduce the hydrodynamic forces is to apply a weakly nonlinear approach that calculates the Froude–Krylov forces by integrating the pressures on the varying hull wet surface—in this case, the hydrostatic forces should also be updated. The Cummins equation can then be used to smoothly introduce the effects of the varying vessel mass and mean position/attitude in waves due to the progressive flooding. On the other hand, the impulse response functions in the Cummins equation assume constant hydrodynamic coefficients, which is not the case for significant changes in the mean position and attitude of the ship. An extension of the weakly nonlinear approach to include nonlinear radiation forces is reported by Suresh et al. [47].

It is worth noticing the difficulty of accurately accounting for transient effects in the coupled seakeeping–flooding problem, especially for the case of a large compartment being breached on the side of the ship, in the typical fast methods. These methods typically fail to properly predict the significant transient roll that results from this. Manderbacka et al. [48] address this problem by accounting for the momentum flux of the flood water.

3.5. Methods Focused on the Steady Phase

Finally, there are methods that aim to simulate the steady phase. There have been many studies performed using field methods to simulate the behaviour of damaged ships in waves in this phase. These can be aimed simply at obtaining a higher-fidelity simulation of the phenomenon, addressing particular nonlinear aspects that may be relevant. An example is that of Huang et al. [49], who applied a RANS-based CFD model to simulate the motion of a damaged frigate DTMB-5415 with the objective of studying the effects of wave steepness and rolling parameters on the roll dynamics of damaged ships. Other studies may address other relevant problems, such as the resistance performance of damaged ships in waves, e.g., the work by Zhang et al. [50], who simulated the motion responses of the same DTMB-5415 damaged ship and the total resistance in calm water and regular head waves using field CFD.

On the other hand, it is very common to investigate the behaviour of damaged ships using linear diffraction codes, e.g., modelling the affected compartments as an additional part of the domain, as in [51], or by solving the problem without consideration of breaches or openings. The most basic and least accurate approach is to then solve the dynamics of the flooded ship, either by removing the breached compartments entirely from the domain boundary or adding the mass of the flooded water and solving for an intact ship under these modified load conditions (as all the participants did in the benchmark study in [52]).

4. Historical Development of Progressive Flooding Simulation and Selected Associated Studies

A brief description of the historical evolution of the development of progressive flooding methods and selected application studies is provided in this section.

4.1. Early Developments: 1986–1999

The capsizing of the ro-pax ferry Herald of Free Enterprise in 1987 and the sinking of the Estonia in 1994 served as strong catalysts for the development of simulation methods aimed at modelling the progressive flooding of ships, with a particular focus on ro-ro vessels characterised by their expansive continuous vehicle decks. Prior to these significant incidents, earlier efforts in this domain were already underway. For instance, Spouge contributed to the field by presenting capsizing simulations for the ro-ro passenger vessel European gateway in 1986 [53], while Sen and Konstantinidis published a study in 1987 that adopted a quasi-stationary approach to address the still-water problem, introducing a semi-empirical variation in the centre of gravity of the floodwater [54].

Subsequent advancements in this area saw the introduction of hydraulic flow models, e.g., by Vredeveldt and Journée in 1991 [55], which considered the inclusion of roll-added inertia resulting from water flow, while maintaining other degrees of freedom in a quasi-stationary state. Xia et al. [56] followed a similar approach but introduced an artificial damping effect within the hydraulic model to enhance numerical stability.

Incorporating the influence of waves, the pioneering work of de Kat and Paulling in 1989 [57] presented a 6-degree-of-freedom (DOF) coupled system, representing a significant advancement considering the computational constraints of that era. Turan and Vassalos [58] expanded upon this foundation in 1994 by incorporating coupled sway, heave, and roll motions, while continuously updating trim in simulations conducted under irregular sea states. Initially, flooding rates were treated as time-invariant, but Vassalos and Turan [58] introduced Bernoulli’s equation for flow calculation at openings.

Vermeer et al. [59] introduced a method in 1994 which considered the inertial effects of roll, sway, and yaw from the floodwater, introducing convolution integrals for added mass and damping coefficients related to radiation forces. However, this method did not account for incoming or diffracted wave excitation. In contrast, Journée et al. [60] further expanded their approach in 1997 to encompass the full 6-DOF methods, supported by experimental tests validating its applicability in cases where sloshing effects were negligible.

A nonlinear coupled 6-DOF methodology was published by Vassalos in 2000 [61], incorporating memory effects of radiation forces. Similarly, Zaraphonitis et al. [62] also incorporated radiation forces, albeit considering the floodwater mass as concentrated at its centre of gravity. They used the lump mass concept to determine motion through coupled ship-floodwater equations, with the floodwater free surface assumed to remain flat.

4.2. Consolidation of Models: 2000–2017

In the early 21st century, significant advancements in time-domain methods for evaluating the behaviour of damaged ships emerged. Santos et al. [63], in 2002, included a 6-degree-of-freedom (DOF) time-domain simulation approach to model the transient flooding of ro-ro ferries. Their methodology accommodated the consideration of obstacles within compartments by introducing artificial sub-compartments to control the flow of flooding. Notably, this method did not account for wave effects.

Building on the foundation laid by Zaraphonitis et al. [62], Papanikolaou and Spanos made progressive improvements to the methodology. Of particular significance, they provided experimental validation for the lump mass approximation used to represent floodwater and applied this methodology in the analysis of the loss of the Express Samina, as detailed by Papanikolaou et al. in 2004 [64].

In 2006, Valanto [65] presented a detailed description of a method that relied on response amplitude operators (RAOs), calculated using a strip theory code to predict heave, pitch, sway, and yaw motions. Non-linear equations were employed for roll and surge motions, founded on a cascade of simplifying assumptions regarding the terms in these equations. In modelling the floodwater, the method adopted either shallow water equations or the lump mass approach based on the water level, but it did not account for a transient phase in flooding.

Worth mentioning are studies conducted by van’t Veer et al. between 2000 and 2003 on time to sink simulations [66] for damaged large passenger vessels, building upon the method initially introduced by de Kat and Paulling [57]. The method was validated using damaged frigates and passenger vessels under still-water and wave conditions, with enhancements made to account for non-watertight door collapse due to water pressure in 2002 by de Kat and Peters [67]. The results and conclusions of these studies were later reported in 2005 [68].

Efforts continued to be carried out, focusing on refining and consolidating the solutions to the various aspects of the problem, extending code capabilities following others, performing validations, or introducing other implementations at the numerical level. Lee et al. [69] performed 6-DOF time-domain numerical simulations in 2007 and model tests for damaged passenger ferries in waves, uncovering challenges in accurately predicting roll motion. Ruponen [70] presented a still-water flooding model in 2007 that linearised water levels within each tank. Santos and Guedes Soares [71] in 2009 extended their previous still-water method to incorporate wave effects, including analysis under irregular sea states. Gao et al. [72] employed VOF in 2013 for flooding alongside a seakeeping code originally developed by Jasionowski and Vassalos in 2001 [73] for ship motion calculations. In terms of experimental validation, the studies of Begovic et al. [74] in 2013 and Manderbacka et al. [75] in 2015 are noteworthy, covering damaged ships in waves and transient response to flooding in still water, respectively.

Another tool, applying a generalised adaptive mesh pressure integration technique (GAMPIT), was presented and validated by Rodrigues and Guedes Soares in 2015 [25]. The exact pressure integration expressions for Froude–Krylov forces and moments applied on arbitrary polygons had been derived in 2014 [76]. Application to cases of progressive flooding of ships in calm waters [77,78,79,80], including waves in intact [81,82] and damaged [46] ships, were presented throughout 2015–2017.

4.3. Recent Development: 2018–2023

The application of GAMPIT in a hybrid experimental–numerical analysis of a reduced-scale model of a barge, focusing on studying the variation in the empirically obtained discharge coefficients at damage and inter-compartment openings and the uncertainties arising from relying on flooding sensors, was published in 2018 [17].

A new calculation technique for onboard progressive flooding simulation, implementing a linearised assessment of floodwater levels, was presented in 2019 by Braidotti and Mauro [83], with different linearisation formulations being investigated in 2021 [84]. A sensitivity analysis of the method was performed on a box-shaped barge undergoing progressive flooding [85], concluding that many of the input parameters significantly affect the flooding simulation.

Another rapid simulation tool, utilising the lumped mass approach, was introduced in by Acanfora et al. in 2019 [86]. The tool incorporates viscous effects in floodwater dynamics, drawing from a model that addresses energy dissipation in standing waves within rectangular spaces.

Targeting higher-fidelity methods, the URANS approach, integrated with the overset mesh technique and a 6 degree-of-freedom (DOF) solver, was utilised to study the impact of side and bottom damage on both the flooding process and motion responses by Zhang et al. in 2020 [28]. A methodology (SHARC) combining advanced nonlinear finite element simulations that simulate the collision scenario, a dynamic damage stability simulation tool (SIMCAP; see Section 5.1)and a modified Smith method for the ULS analysis of a collision-damaged ship structure was published by Kuznecovs in 2021 [87].

Arguably, the most important latest developments in the field of damaged ship stability are the recent Horizon 2020 EU project FLARE (2019–2022) [88] and the joint industry project eSAFE [89]. To the best of the author’s knowledge, no significant developments have been observed in the numerical modelling of damaged ships in the implementation of these projects in terms of new practical methods in addition to the ones already mentioned. Both projects appear to have had a strong commitment to enhancing risk-related frameworks and methodologies. Indeed, substantial efforts were made to refine methodologies for probabilistic assessments of damaged stability in grounding, collision, and contact accidents in eSAFE [90], while emergency response and flooding mitigation were also an important target of FLARE [23]. In addition, three benchmark studies on progressive flooding and damaged ship behaviour with model test reference data were carried out under FLARE [91,92,93].

5. Summary of State of the Art

This study is a non-exhaustive review of the state of the art of progressive flooding simulation. It is important to stress that, apart from the GAMPIT tool [25], which was developed by the same author that wrote the present paper, the full capabilities and drawbacks of the tools and their status in terms of current usage and maintenance are only known to the author rather superficially and in line with what could arguably be expected in a non-exhaustive literature review.

5.1. Numerical Methods and Tools

A brief description of known software tools that have been referenced in the literature for implementing fast methods to simulate progressive flooding is herein presented. A selected literature reference for each tool is listed in Table 3. The methods and tools highlighted in Table 3 are suitable for simulations related to progressive flooding. The majority of these methods employ hydraulics rooted in the Bernoulli equation for such flooding scenarios. They are then integrated with time-domain strategies that utilize either linear or mildly nonlinear hydrodynamic techniques when dealing with waves, or use hydrostatic techniques when assuming still-water conditions.

CAPSIM. Developed at the Ship Design Laboratory (SDL) of the National Technical University of Athens (NTUA) in Greece, this is a non-linear seakeeping code that considers flooding-induced flow effects. It employs a lumped mass approach to simulate the dynamic motions of the vessel. Additionally, objects within the compartments, such as main engines and generators, are represented as 3D geometric spaces. This method’s detailed description can be found in [62].

E4 Flooding. Initially developed at the Technical University of Hamburg, although recent publications show the affiliation of University of Applied Science Kiel (UAK), the tool employs Bernoulli’s equation to calculate flooding. It models both the horizontal surface and flooding path as directed graphs and can perform analysis of 6-degrees-of-freedom (6-DOF) dynamic ship motions, assuming linear roll damping [37,92].

FloodW. This tool, developed at University of Naples Federico II (UNINA), is implemented using Matlab-Simulink. It calculates flooding rates by applying Bernoulli’s equation with empirical discharge coefficients. In this analysis, floodwater is considered as a non-horizontal flat surface in accordance with the pendulum model. The model also accounts for regular and irregular wave effects, incorporating all relevant nonlinearities. Comprehensive information can be found in [86].

FREDYN. Developed at the Maritime Research Institute Netherlands (MARIN), it is a tool for simulating non-linear ship motions for maneuvering studies conducted in wave-filled environments. Its foundation can be traced back to the pioneering work of de Kat (1988). The time-domain method employed relies on a non-linear strip theory approach to compute hydrodynamic forces, while the modelling of floodwater effects draws inspiration from the research conducted by van’t Veer and de Kat [94] and Palazzi and de Kat [95].

GAMPIT. Standing for the generalised adaptive mesh pressure integration technique, the input process in GAMPIT regarding geometric, mass and inter-compartment openings characteristics gives way to straightforward pre-processing procedures and flexible simulations [25]. The code is based on the pressure integration technique, evaluated at unstructured meshes composed of quadrilaterals. Polyhedral and polygonal intersection algorithms work together with a quad-tree mesh subdivision and cutting adaptive process to become the kernel of the domain setup and intra-simulation dynamic modification, on which analytic formulations of pressure calculations are evaluated [76]. A weakly nonlinear approach is implemented for seakeeping, while the progressive flooding uses the Bernoulli equation.

HSVA-Rolls. This is an in-house version of the time domain Rolls code developed by HSVA (The Hamburg Ship Model Basin). It is reported in [91] that the ship roll motion and surge are solved with ordinary differential equations using nonlinear hydrostatics in waves (based on the NAPA software). Strip theory is used to calculate the RAOS for the other modes. Flooding rates are computed according to the Bernoulli equation with empirical discharge coefficients. Either the pendulum model or shallow-water equations (SWE) are used to model the dynamic effects of floodwater.

LARAMP. Developed at the Centre for Marine Technology and Engineering (CENTEC) of the Technical University of Lisbon, Portugal, this is a time domain code, with hydrostatic forces acting on the wet hull being computed via direct pressure integration. The motion of water within flooded compartments is modelled using the shallow water equations. A comprehensive description of this method can be found in [96].

LDAE. The in-house code LDAE developed in UNITS (University of Trieste) models the flooding process using a differential-algebraic equation (DAE) system derived from the Bernoulli equation, which is subsequently linearised and analytically solved. In this model, a flat horizontal free surface is presumed for both the sea and the waterplanes inside flooded compartments. An adaptive integration time step, reliant on the derivatives of the floodwater level, is implemented to enhance the model’s accuracy. However, it is important to note that the model does not account for dynamic ship motions and focuses solely on the quasi-steady changes in heel, trim, and sinkage. Further details and insights into the model can be found in [83,84,97]

NAPA. A well-known software suite for ship design and operation, the flow rates are calculated from Bernoulli’s equation, with user-defined discharge coefficients for each opening. A horizontal flat free surface is assumed in all flooded rooms. A pressure-correction algorithm [38] is applied to solve the governing equations (continuity and Bernoulli).

PROTEUS. The PROTEUS in-house code, owned by Safety at Sea Ltd., was originally developed at the University of Strathclyde (MSRC) [98]. It determines flooding rates by utilising Bernoulli’s equation and employs a fixed discharge coefficient of 0.6. Hydrodynamic forces such as Froude–Krylov and restoring forces are accounted for by the instantaneous wave elevation, applicable to both regular and irregular waves. The code derives radiation and diffraction effects using 2D strip theory. As the ship undergoes flooding, its changing attitude (heave, heel, and trim) affects the hydrodynamic coefficients. The code interpolates hydrodynamic forces based on the ship’s current attitude using precomputed data from 2D strip theory calculations.

SIMA. The SIMA workbench developed by SINTEF Ocean is a simulation and analysis tool for marine operations and floating systems—from modelling to results—built on software for non-linear time domain analysis. Tanks can be filled with fluid to mimic flooded compartments, accounting for free surface effects. A damaged tank model is also available [99].

SIMCAP. The tool was developed at the department of Shipping and Technology at Chalmers University of Technology. This model utilizes linear strip theory for the computation of the radiation and diffraction forces, while Froude–Krylov forces are addressed non-linearly through the integration of incident wave pressure over the hull’s current wetted surface. Water inflow and floodwater forces in the model are based on quasi-static principles, employing a gridded domain with elements of constant pressure. Further details and methodological descriptions are available in [100].

SMTP. An in-house code developed by KRISO (Korea Research Institute of Ships and Ocean Engineering), SMTP determines flooding rates via Bernoulli’s equation combined with empirical discharge coefficients [91]. Within compartments, floodwater can be represented in two ways: a straightforward horizontal free surface or a dynamic model. The latter calculates the equation of motion for the mass centre, using the tank’s resonance mode aligned with the current water depth. This yields an inclined free surface, which then aids in pressure calculation at openings. Ship motions are derived from 6-DOF non-linear time-domain equations. Both Froude–Krylov and restoring forces are computed using the varying wetted surface, while hydrodynamic forces draw from a strip method. The effect of floodwater is in the mass and its gravitational centre, thereby influencing inertial and gravitational forces. Comprehensive insights into this method are available in [41,101]. Tank ventilation can be assessed across all compartments.

wDamstab. The wDamstab in-house code developed by CSSRC (China Ship Scientific Research Center) utilizes Bernoulli’s equation to compute flooding rates via openings, adopting a horizontal flat plane assumption for the floodwater surfaces [32,91,102]. The model encompasses four degrees of freedom, specifically sway, heave, roll, and pitch. Ship motions are evaluated using the potential flow theory, specifically drawing from the Salvesen–Tuck–Faltinsen (STF) strip theory framework. Calculations for Froude–Krylov and hydrostatic forces are performed by integrating pressure over the current wetted surface.

XMF. The extensible modelling framework (XMF) developed by MARIN uses the principles of Newtonian dynamics. Well-known derivatives of this are FREDYN and ANySim [103]. XMF has recently been augmented with a flooding module library (XHL), which applies Bernoulli’s equation combined with empirical discharge coefficients, making use of universally described 3D objects susceptible to flooding. Trapped air in spaces and adjustments in hydrostatic pressures of fully water-filled compartments are approached via a graph solver. It features an added inertia-centric flow solver, termed the unified internal flow (UIF) module. A comprehensive breakdown of this solver’s mechanics and its early results is available in [104].

Table 3. Numerical tools for simulation of progressive flooding.

Name	Origin/Proprietary/Developed in	Reference
CAPSIM	National Technical University of Athens (NTUA)	[62]
E4 Flooding	University of Applied Science Kiel (UAK)	[37]
FloodW	University of Naples Federico II	[86]
FREDYN	Maritime Research Institute Netherlands (MARIN)	[105]
GAMPIT	University of Lisbon (CENTEC)	[25]
HSVA-Rolls	Hamburgische Schiffbau- Versuchsanstalt GmbH (HSVA)	[106]
LARAMP	University of Lisbon (CENTEC)	[96]
LDAE	University of Trieste (UNITS)	[97]
NAPA	NAPA Group	[40]
PROTEUS	Safety at Sea	[98]
SIMA	SINTEF Ocean	[99]
SIMCAP	Chalmers University of Technology (CHALMERS)	[107]
SMTP	Korea Research Institute of Ships and Ocean Engineering (KRISO)	[41]
wDamstab	China Ship Scientific Research Center (CSSRC)	[102]
XMF	Maritime Research Institute Netherlands (MARIN)	[108]

Table 3. Numerical tools for simulation of progressive flooding.

Name	Origin/Proprietary/Developed in	Reference
CAPSIM	National Technical University of Athens (NTUA)	[62]
E4 Flooding	University of Applied Science Kiel (UAK)	[37]
FloodW	University of Naples Federico II	[86]
FREDYN	Maritime Research Institute Netherlands (MARIN)	[105]
GAMPIT	University of Lisbon (CENTEC)	[25]
HSVA-Rolls	Hamburgische Schiffbau- Versuchsanstalt GmbH (HSVA)	[106]
LARAMP	University of Lisbon (CENTEC)	[96]
LDAE	University of Trieste (UNITS)	[97]
NAPA	NAPA Group	[40]
PROTEUS	Safety at Sea	[98]
SIMA	SINTEF Ocean	[99]
SIMCAP	Chalmers University of Technology (CHALMERS)	[107]
SMTP	Korea Research Institute of Ships and Ocean Engineering (KRISO)	[41]
wDamstab	China Ship Scientific Research Center (CSSRC)	[102]
XMF	Maritime Research Institute Netherlands (MARIN)	[108]

Although the codes listed in Table 3 that consider the effects of waves may, and usually do, handle the steady phase as well, they are probably not computationally efficient if the problem is indeed steady. In that case, traditional radiation and diffraction solvers can, with different degrees of accuracy, predict numerically important quantities such as distribution of global loads and seakeeping behaviour in general in a much faster way. Three of the most widely known are briefly described next.

Hydrostar. Developed by Bureau Veritas and implementing a green function-based 3D boundary element method (BEM) for solving the potential flow, this frequency domain diffraction code includes the possibility to extend the problem domain to that of compartments carrying liquids. A pressure drop across openings can also be introduced in the more recent versions. Among other capabilities, the software considers multi-body interactions and the effects of forward speed. Examples of its use for the simulation of damaged ships in waves can be found in [51,52,109,110]. Hydrostar can be used to provide frequency domain solutions to the hydrodynamic radiation and diffraction problems to feed time domain codes such as SIMA and most of the ones listed in Table 3.

WAMIT. Originally developed at MIT in 1987, it comprises a set of tools for analysing wave–structure interactions for bodies without advance speed. The hydrodynamic diffraction and radiation problems are solved through the implementation of a green function-based BEM in the frequency domain. This can account for the effects of flooded tanks, pressure drops at permeable boundaries, and damaged compartments within the linear potential flow paradigm and confined to offshore structures or other vessels with no advance speed. An example of its application to model the behaviour of a damaged ship in waves can be found in [51,111]. Like Hydrostar, WAMIT can be used for providing hydrodynamic forces data for codes such as SIMA and most of the ones listed in Table 3.

WADAM. WADAM stands for wave analysis by diffraction and Morison theory. It is developed by DNVGL and based on the source code from WAMIT. Both Morison and potential theory can be applied.

Hydrostar, WAMIT, and WADAM all implemented procedures to account for the dynamics of fluids in compartments. However, a cruder approximation is for the liquid in damaged compartments to be assumed frozen. As an example, all participants of a benchmark study targeting the numerical prediction of global wave loads on damaged ships organised by the MARSTRUCT Virtual Institute chose that approach using a variety of different numerical tools [52].

5.2. Experimental Validation

Empirical data regarding progressive flooding are essential for calibrating and validating numerical tools. Model tests have been regularly carried out in the past decades, mostly with models exhibiting openings but in the steady phase regime, i.e., no progressive flooding [69,112,113,114]. Focusing on progressive flooding, the more recent relevant experimental datasets are the ones of the model tests campaigns carried out under the H2020 EU project FLARE [88]. The datasets and supporting documentation are freely available [115] and include data from three distinct experimental studies.

The first of these was a fundamental compartment flooding campaign with a model composed of a flooding box, a cross flooding box, and a composite box composed of up- and down-flooding boxes [116]. The model included adjustable openings for flooding and ventilation and was mounted in a hexapod to perform a variety of tests including waves and forced motions at a depressurised wave basin. The second of these tests, denoted fundamental deck flooding [117], consisted of flooding tests of a cruise vessel deck scaled model with three different configurations: simplified, intermediate, and detailed subdivision geometries. This model was also mounted to a hexapod to perform static and forced motion tests, as well as tests with incoming waves. The third campaign used a model of a cruise ship with floodable internal geometry to simulate different flooding scenarios [118]. Basin tests were carried out in calm and irregular waves for different metacentric heights.

Recent benchmarking studies, including comparison of numerical results from different codes with the abovementioned empirical datasets, can be found in [91,92,93,119].

6. Recent Applications of Progressive Flooding Numerical Models

One of the applications of the numerical methods and tools described in Section 5.1 relates to supporting risk assessment and its mitigation during design. In fact, the difficulty in acquiring statistical data in terms of quantity, number of configurations, detailing, and accuracy of reporting concerning events involving flooding leads to the obvious attractiveness of simulation-based datasets. A recent example is the simulation-based analysis method for the damage survivability of passenger ships presented by Ruponen et al. [120].

6.1. Identification

Another, more challenging, application is to the rapid identification of damage upon a damage, involving a breach and consequent flooding. These tools can be combined with flooding sensor arrangements to increase the reliability of the damage detection and characterisation, examples of which among recent studies are seen in [121,122].

6.2. Prediction

Damage identification and characterisation are essential inputs to decision support systems (DSS) to aid the response to emergency situations involving flooding on board. Typically, progressive flooding numerical models try to predict the outcome (or most probable outcomes) of the current situation with as much accuracy as possible. The time to flood or capsize and the ability of the ship to return safely to port are, among other quantities, important qualities that help the decision-making process and guide the actions of the crew and rescue responses. Progressive flooding numerical tools have been shown to provide considerably better estimates than traditional non-simulation-based procedures [14,123]. Other studies have introduced hybrid or multi-level real-time flooding risk evaluation [124]. Furthermore, recent studies have shown the potential for the application of data-driven techniques to the problem based on pre-calculated progressive flooding simulations [125,126,127,128,129].

6.3. Response

Following a damage identification and outcome prediction, an emergency response by the crew is put in place (e.g., damage control). Though passive and active containment systems for flooding incidents—e.g., high-expansion foam products—have been proposed [130], active measures by the crew like counter flooding can be potentially assessed to determine their outcome using the tools described in Section 5.1. These types of actions, targeting flooding mitigation for stability enhancement in a damaged RoPax ship, were studied recently by Valanto [23].

7. Discussion, Salient Gaps and Next Steps

The present review went through some of the latest developments in the simulation of damaged ships subject to flooding. Not meant to be exhaustive, this study should still provide the reader with a good grasp of the state of the art of the application of direct methods in order to accurately simulate damaged stability related phenomena. Here, a discussion on the present status is carried out, together with the identification of salient gaps and proposed next steps regarding the research and overall development of these methods and their application. It is worth noting that discussion on regulatory affairs per se is intentionally left out, as it is not the focus of the paper.

7.1. Fidelity of the Simulation Methodologies

The review shows there is a significant number of numerical codes addressing the prediction of progressive flooding in ships, which have been developed and applied throughout the years. The latest developments seem to focus on increasing the fidelity of the models; however, most of the codes do not seem to have undergone any considerable upgrade in the last few years, while some knowledge gaps remain open. For instance, it is not clear from the reports and publications how exactly methods other than field methods are able to accurately simulate or account for the effects of violent transverse rushes of floodwater in the transient phase on large compartments without a priori knowledge of the results to which they can be calibrated.

The experimental datasets published within the FLARE project may provide some grounds for continuous development in this front. In order to foster the development of novel approaches, it may perhaps be necessary to consider surrogate models and/or hybrid physics-data-driven models.

7.2. Risk Assessment at Design Stage

When it comes to applications targeting safety risk assessment at the design stage, most of the recent developments are not centred on these tools, but on refining traditional approaches to safety assessment. Such is the case of the framework implemented in the joint industry project eSAFE—enhanced Stability After a Flooding Event for the probabilistic damage stability assessment of passenger ships [131] and the non-zonal approach used to determine damage probabilistic distribution [90]. Likewise, Bulian et al. in their probabilistic assessment of the damaged survivability of passenger ships in the case of grounding or contact also do not account for the use of direct methods, but rather their NEI approach, which they claim to be more efficient in practical regulatory calculations [132]. However, design in terms of damage stability assessment is to a large degree governed by regulatory issues.

One can argue that this regulatory lead design approach hinders the development of new designs and approaches to safety which are truly focused on the safety of the vessel’s occupants first and not on the ship itself. It can also be argued that these frameworks continue to perpetuate that situation. Notably, in the present when a massive surge in the generalised use of data-driven methods in industry and society in general is taking place, one should ask if these are perhaps not due.

7.3. Identification, Prediction and Response

When it comes to damage identification and/or characterisation, prediction of outcome, and emergency response actions’ guidance, the fact of the matter is that the use of direct methods is far from being common despite its obvious advantages. Not only is this not common in the offshore and maritime industry, but also, perhaps somewhat surprisingly, in the naval industry.

Despite this, recent research works such as Karolius et al.’s study on the risk-based, sensor-fused detection of flooding casualties for emergency response [133] introduce the necessity for the usage of direct methods to provide a simulation environment with which to train surrogate models to identify damage locations and characterize hull breaches.

Likewise, Braidotti et al. [128,129] have developed promising machine learning-based flooding progression methodologies.

When it comes to response guidance, to the best of the author’s knowledge there are still no published tools that in fact provide concrete actions to be taken by the crew under an arbitrary incident involving flooding. On the other hand, one may be right at the onset of the fast development of these functionalities with the fast growth of artificial intelligence developments in recent times.

7.4. Integration and Software Development

One important aspect of the progressive flooding simulation tools and their potential use in onboard increased functionalities or other real time tasks is their deployment in real world scenarios. This relates to aspects such as the simulation running stability and the adaptability, scalability, speed of execution, and safety of the code implementing them. These aspects are critical for the generalised use of these tools in both civil and military or other types of vessels.

This is an important salient gap in the literature, as no indication of the ability of the tools listed in Section 5.1 is reported or demonstrated to the best of the author’s knowledge. Naturally, since the tools are mostly developed and maintained by academia and also used in-house by research institutes, this is expected and not meant to be a criticism. On the other hand, a serious effort in addressing these issues is perhaps due.