Kinematic Calibration for the 3-UPS/S Shipborne Stabilized Platform Based on Transfer Learning
Abstract
1. Introduction
- When using the same small sample number, the transfer network will effectively solve the problems of inadequate prediction accuracy and weak generalization ability.
- When the same prediction accuracy is reached, the sample number required by the transfer network will be smaller, contributing to higher efficiency and lower costs.
- In ocean engineering, the obtained impact pattern is capable of providing reference recommendations on the optimal choice of calibration method (i.e., the type of predictive network), thereby maximizing calibration efficiency.
2. 3-UPS/S Shipborne Stabilized Platform
2.1. System Description
2.2. Establishment of the Coordinate System and Pose Description
2.3. Inverse Displacement Kinematics Analysis
3. Methods of Transfer Learning
3.1. Motivation
3.2. Transfer Scheme
3.3. Evaluation Index
3.4. Implementation of Transfer Learning
3.4.1. Simulation Process
- Step 1: Select source domain configurations. The rotational angle ranges of the moving platform around the x, y, and z axes are −20° to 20°, −20° to 20°, and −10° to 10°, respectively. Considering the typical scenario in transfer learning, where the source domain often has a much larger sample size than the target domain, 1331 desired end-effector poses within the workspace are uniformly selected as the source domain configurations (as shown in Figure 5a).
- Step 2: Select target domain configurations. According to the method described in reference [29], a full-parameter geometric error model for the 3-UPS/S mechanism is established. The error source parameters identified through the preliminary geometric identification method are assigned to each error source. The error model is then used to generate end-effector pose errors. Superimposing these end-effector pose errors onto 150 uniformly selected configurations (as shown in Figure 5b) and adding Gaussian noise with a standard deviation of 2 µm to simulate measurement noise according to the method mentioned in ISO-9283 [30] yields 150 actual end-effector poses for simulation.
- Step 3: Obtain the source domain and target domain datasets. For the selected two types of configurations, nominal actuated joint variables are calculated by substituting into Equation (2) and used as inputs for both the source and target networks. The desired poses and the actual poses obtained in steps 1 and 2 are taken as the outputs of the source and target networks, respectively.
- Step 4: A four-layer BP neural network is established and randomly initialized. Pre-training is performed using 1331 source domain samples.
- Step 5: The weights and biases, trained by the pre-training network, are all extracted and transferred as the initial value for the target network. Subsequently, the target network is further trained using target domain samples, randomly selecting 80% for training and the remaining 20% for testing.
- Step 6: The predictive accuracy is assessed by the testing set.
3.4.2. Simulation Results and Discussion
3.5. Relationship between Transfer Learning and the Sample Number of the Actual Pose
3.5.1. Simulation Process
- Step 1: Select source domain configurations. The selection of source domain configurations is the same as step 1 in Section 3.4.1, i.e., 1331 configurations as shown in Figure 5a.
- Step 2: Select target domain configurations. To account for variations in the sample number of the actual pose, the number of selected configurations in the target domain is appropriately increased here to establish a broader research range for the sample size. Consequently, 216 configurations are uniformly selected in the workspace (as shown in Figure 8). Following the methodology outlined in step 2 of Section 3.4.1, the corresponding 216 end-effector actual poses are obtained for simulation purposes.
- Step 3: Obtain the source domain and target domain datasets. For the selected two types of configurations, nominal actuated joint variables are calculated by substituting them into Equation (2) and used as inputs for both the source and target networks. The desired poses and the actual poses obtained in steps 1 and 2 are taken as the outputs of the source and target networks, respectively.
- Step 4: A four-layer BP neural network is established and randomly initialized. Pre-training is performed using 1331 source domain samples.
- Step 5: “n” samples are selected from a total of 216 samples to construct the training set and testing set, with 80% for training and 20% for testing.
- Step 6: The weights and biases, trained by the pre-training network, are all extracted and transferred as the initial value for the target network. Subsequently, the target network is further trained using target domain samples, and the completed training model is saved.
- Step 7: Steps 4~6 are repeated for each value of “n”.
- Step 8: The predictive accuracy of each group of models is assessed by the testing set.
- Note: .
3.5.2. Simulation Results and Discussion
- . In this sample range, the transfer networks exhibit a lower average prediction error compared to the BP networks, indicating a notable performance advantage. However, due to the extremely limited number of samples, the predicted accuracy of the networks is constrained. Even for the higher-precision transfer network, the average orientation volumetric error after calibration in this range can only be reduced to 1.158°, which is larger than that before calibration of 0.203°. This contradicts the purpose of error compensation. As a result, within this range, neither the transfer network nor the BP network can meet the practical application requirements in marine engineering. They are not acceptable in the field of shipborne stabilized platforms’ kinematic calibration.
- . In this range, considering each evaluation index, transfer networks continue to demonstrate certain performance advantages over the BP networks. The average for transfer networks is 0.364°, smaller than the BP networks’ 0.038°. Furthermore, as the sample size increases, the transfer network achieves improved absolute prediction accuracy, notably surpassing the accuracy before calibration. This indicates that not only can the transfer network meet the practical calibration application requirements, but it also exhibits stronger predictive capabilities than the conventional BP network. Thus, transfer learning is the most appropriate approach within this range.
- . In this range, it can be observed that the lines representing the transfer network and the BP network in the figure closely overlap, indicating no significant difference in their performance. The performance improvement effect of the transfer learning method becomes weak or even non-existent. Therefore, establishing and training a relatively simple BP network is a better choice.
4. Experiments
4.1. Experimental Scheme
4.2. Experimental Results and Discussion
5. Conclusions
- A kinematic calibration method for the 3-UPS/S shipborne stabilized platform based on transfer learning was proposed. The method takes “building a mapping model from nominal actuated joint variables to desired end-effector poses” as the source task and “building a mapping model from nominal actuated joint variables to actual end-effector poses” as the target task. Compared with the conventional BP neural network, the method can fully explore and utilize the kinematic information of ideal robot systems. It not only effectively solves the problem of low accuracy when approximating small-sample datasets, but also greatly reduces calibration costs and improves calibration efficiency.
- The impact of the sample number of the actual pose on the effectiveness of transfer learning was investigated. By constructing multiple sets of transfer network models and BP network models under varying sample numbers of the actual pose, the impact pattern was generalized to be that “as the number of the actual pose increases, the performance benefit of transfer learning gradually declines and eventually vanishes.” Furthermore, the research range of actual pose sample sizes was quantitatively categorized into three scenarios, and optimal kinematic calibration methods were recommended for each, providing valuable ocean engineering guidance.
- Stability compensation experiments were conducted in a simulated maritime environment. After kinematic calibration based on the transfer learning method, the average orientation volumetric error of the 3-UPS/S robot decreased from 0.257° to 0.017°, representing a 93.4% improvement in accuracy, which is significantly better than the calibration effect achieved by the BP network. The experimental results demonstrate that kinematic calibration based on transfer learning substantially enhances the end-effector accuracy of the shipborne stabilized platform.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Y.; Yuan, H.; Xiao, Z.; Xiao, C. An Offshore Self-Stabilized System Based on Motion Prediction and Compensation Control. J. Mar. Sci. Eng. 2023, 11, 745. [Google Scholar] [CrossRef]
- Qiang, H.; Jin, S.; Feng, X.; Xue, D.; Zhang, L. Model predictive control of a shipborne hydraulic parallel stabilized platform based on ship motion prediction. IEEE Access 2020, 8, 181880–181892. [Google Scholar] [CrossRef]
- Karan, B.; Vukobratović, M. Calibration and accuracy of manipulation robot models—An overview. Mech. Mach. Theory 1994, 29, 479–500. [Google Scholar] [CrossRef]
- Jiang, Y.; Yu, L.; Jia, H.; Zhao, H.; Xia, H. Absolute positioning accuracy improvement in an industrial robot. Sensors 2020, 20, 4354. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Bazzoli, P.; Sammons, P.M.; Landers, R.G.; Bristow, D.A. Modeling and calibration of high-order joint-dependent kinematic errors for industrial robots. Robot. Comput.-Integr. Manuf. 2018, 50, 153–167. [Google Scholar] [CrossRef]
- Messay, T.; Messay, R.; Marcil, E. Computationally efficient and robust kinematic calibration methodologies and their application to industrial robots. Robot. Comput.-Integr. Manuf. 2016, 37, 33–48. [Google Scholar] [CrossRef]
- Chen, G.; Kong, L.; Li, Q.; Wang, H.; Lin, Z. Complete, minimal and continuous error models for the kinematic calibration of parallel manipulators based on POE formula. Mech. Mach. Theory 2018, 121, 844–856. [Google Scholar] [CrossRef]
- Tian, W.; Mou, M.; Yang, J.; Yin, F. Kinematic calibration of a 5-DOF hybrid kinematic machine tool by considering the ill-posed identification problem using regularisation method. Robot. Comput.-Integr. Manuf. 2019, 60, 49–62. [Google Scholar] [CrossRef]
- Li, T.; Li, F.; Jiang, Y.; Wng, H. Kinematic calibration of a 3-P(Pa)S parallel-type spindle head considering the thermal error. Mechatronics 2017, 43, 86–98. [Google Scholar] [CrossRef]
- Slamani, M.; Nubiola, A.; Bonev, I.A. Modeling and assessment of the backlash error of an industrial robot. Robotica 2012, 30, 1167–1175. [Google Scholar] [CrossRef]
- Nubiola, A.; Bonev, I.A. Absolute calibration of an ABB IRB 1600 robot using a laser tracker. Robot. Comput.-Integr. Manuf. 2013, 29, 236–245. [Google Scholar] [CrossRef]
- Liu, H.; Yan, Z.; Xiao, J. Pose error prediction and real-time compensation of a 5-DOF hybrid robot. Mech. Mach. Theory 2022, 170, 104737. [Google Scholar] [CrossRef]
- Li, B.; Tian, W.; Zhang, C.; Hua, F.; Cui, G.; Li, Y. Positioning error compensation of an industrial robot using neural networks and experimental study. Chin. J. Aeronaut. 2022, 35, 346–360. [Google Scholar] [CrossRef]
- Gao, G.; Zhang, H.; San, H.; Wu, X.; Wang, W. Modeling and error compensation of robotic articulated arm coordinate measuring machines using BP neural network. Complexity 2017, 2017, 5156264. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Zhou, J.; Kang, H.J. A calibration method for enhancing robot accuracy through integration of an extended Kalman filter algorithm and an artificial neural network. Neurocomputing 2015, 151, 996–1005. [Google Scholar] [CrossRef]
- Yu, D. A new pose accuracy compensation method for parallel manipulators based on hybrid artificial neural network. Neural. Comput. Appl. 2021, 33, 909–923. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Zu, H.; Zhang, X.; Mao, C.; Wang, Z. Improvement of heavy load robot positioning accuracy by combining a model-based identification for geometric parameters and an optimized neural network for the compensation of nongeometric errors. Complexity 2020, 2020, 5896813. [Google Scholar] [CrossRef]
- Maghami, A.; Imbert, A.; Côté, G.; Monsarrat, B.; Birglen, L.; Khoshdarregi, M. Calibration of multi-Robot cooperative systems using deep neural networks. Int. J. Intell. Syst. 2023, 107, 55. [Google Scholar] [CrossRef]
- Zhao, G.; Zhang, P.; Ma, G.; Xiao, W. System identification of the nonlinear residual errors of an industrial robot using massive measurements. Robot. Comput.-Integr. Manuf. 2019, 59, 104–114. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE Inst. Electr. Electron. Eng. 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Venkateswara, H.; Chakraborty, S.; Panchanathan, S. Deep-learning systems for domain adaptation in computer vision: Learning transferable feature representations. IEEE Signal. Process. Mag. 2017, 34, 117–129. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.; Li, X.; Roberts, C. Deep targeted transfer learning along designable adaptation trajectory for fault diagnosis across different machines. IEEE Trans. Ind. Electron. 2022, 70, 9463–9473. [Google Scholar] [CrossRef]
- Mosin, V.; Samenko, I.; Kozlovskii, B.; Tikhonov, A.; Yamshchikov, I.P. Fine-tuning transformers: Vocabulary transfer. Artif. Intell. 2023, 317, 103860. [Google Scholar] [CrossRef]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks? Adv. Neural Inf. Process. Syst. 2014, 27, 3320–3328. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Frank, C.P.; Kevin, M.L. Modern Robotics: Mechanics, Planning, and Control; Cambridge University Press: New York, NY, USA, 2017; pp. 68–89. [Google Scholar]
- ISO 230-1; Test Code for Machine Tools—Part 1: Geometric Accuracy of Machines Operating Under No-Load or Quasi-Static Conditions. International Organization for Standardization: Geneva, Switzerland, 2012.
- Huang, T.; Zhao, D.; Yin, F.; Tian, W.; Chetwynd, D.G. Kinematic calibration of a 6-DOF hybrid robot by considering multicollinearity in the identification Jacobian. Mech. Mach. Theory 2019, 131, 371–384. [Google Scholar] [CrossRef]
- ISO 9283; Manipulating Industrial Robots—Performance Criteria and Related Test Methods. International Organization for Standardization: Geneva, Switzerland, 1998.
- Yang, F.; Zhang, W.; Tao, L.; Ma, J. Transfer learning strategies for deep learning-based PHM algorithms. Appl. Sci. 2020, 10, 2361. [Google Scholar] [CrossRef]




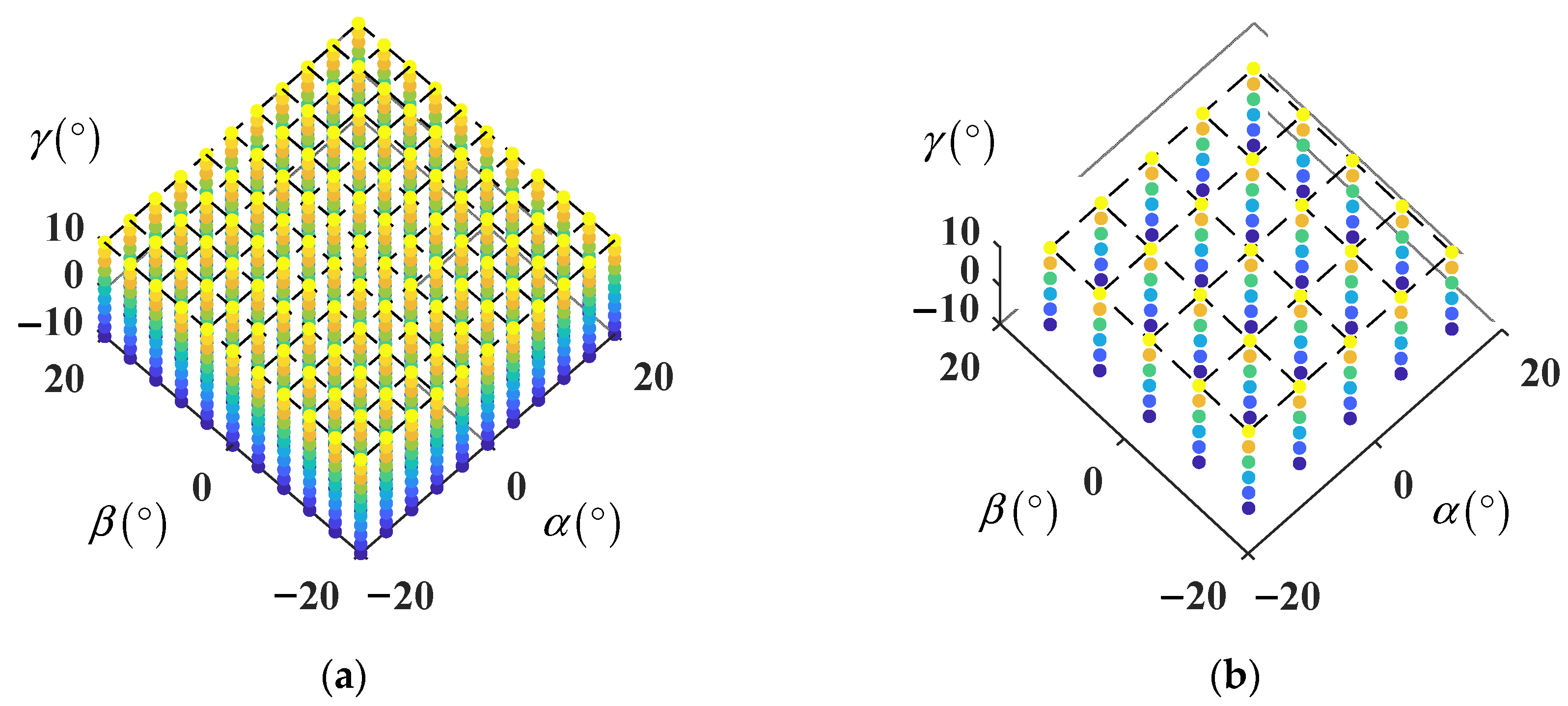












| Before Calibration | BP Network | Transfer Network | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean (°) | 0.177 | 0.047 | 0.051 | 0.021 | 0.018 | 0.024 | 0.005 | 0.007 | 0.010 |
| Maximum (°) | 0.421 | 0.144 | 0.196 | 0.112 | 0.067 | 0.089 | 0.024 | 0.042 | 0.049 |
| SD (°) | 0.093 | 0.038 | 0.043 | 0.024 | 0.016 | 0.021 | 0.005 | 0.009 | 0.011 |
| Before Calibration | BP Network | Transfer Network | |
|---|---|---|---|
| Mean (°) | 0.195 | 0.040 | 0.015 |
| Maximum (°) | 0.479 | 0.136 | 0.055 |
| SD (°) | 0.099 | 0.031 | 0.014 |
| Before Calibration | BP Network | Transfer Network | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean (°) | 0.245 | 0.051 | 0.043 | 0.015 | 0.025 | 0.032 | 0.009 | 0.006 | 0.008 |
| Maximum (°) | 0.495 | 0.150 | 0.151 | 0.138 | 0.125 | 0.159 | 0.055 | 0.026 | 0.056 |
| SD (°) | 0.093 | 0.038 | 0.033 | 0.025 | 0.032 | 0.037 | 0.011 | 0.006 | 0.010 |
| Before Calibration | BP Network | Transfer Network | |
|---|---|---|---|
| Mean (°) | 0.257 | 0.051 | 0.017 |
| Maximum (°) | 0.506 | 0.245 | 0.062 |
| SD (°) | 0.090 | 0.049 | 0.014 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Tian, W.; Zhang, X. Kinematic Calibration for the 3-UPS/S Shipborne Stabilized Platform Based on Transfer Learning. J. Mar. Sci. Eng. 2024, 12, 275. https://doi.org/10.3390/jmse12020275
Xu M, Tian W, Zhang X. Kinematic Calibration for the 3-UPS/S Shipborne Stabilized Platform Based on Transfer Learning. Journal of Marine Science and Engineering. 2024; 12(2):275. https://doi.org/10.3390/jmse12020275
Chicago/Turabian StyleXu, Min, Wenjie Tian, and Xiangpeng Zhang. 2024. "Kinematic Calibration for the 3-UPS/S Shipborne Stabilized Platform Based on Transfer Learning" Journal of Marine Science and Engineering 12, no. 2: 275. https://doi.org/10.3390/jmse12020275
APA StyleXu, M., Tian, W., & Zhang, X. (2024). Kinematic Calibration for the 3-UPS/S Shipborne Stabilized Platform Based on Transfer Learning. Journal of Marine Science and Engineering, 12(2), 275. https://doi.org/10.3390/jmse12020275






