Modelling the Dynamics of Outbreak Species: The Case of Ditrupa arietina (O.F. Müller), Gulf of Lions, NW Mediterranean Sea
Abstract
:1. Introduction
- interpreted as having a particular interest for carbon cycling [14] because they build an external tube made of CaCO3;
- treated as an example of a spatially distributed metapopulation [15] in which the pelagic larval stage and hydrodynamic transport ensure dispersion and mixing at regional scales [16,17]. This highlighted possible links between climate patterns on hydrodynamic conditions that could modify the distribution of the species and its preferred habitat to different extents.
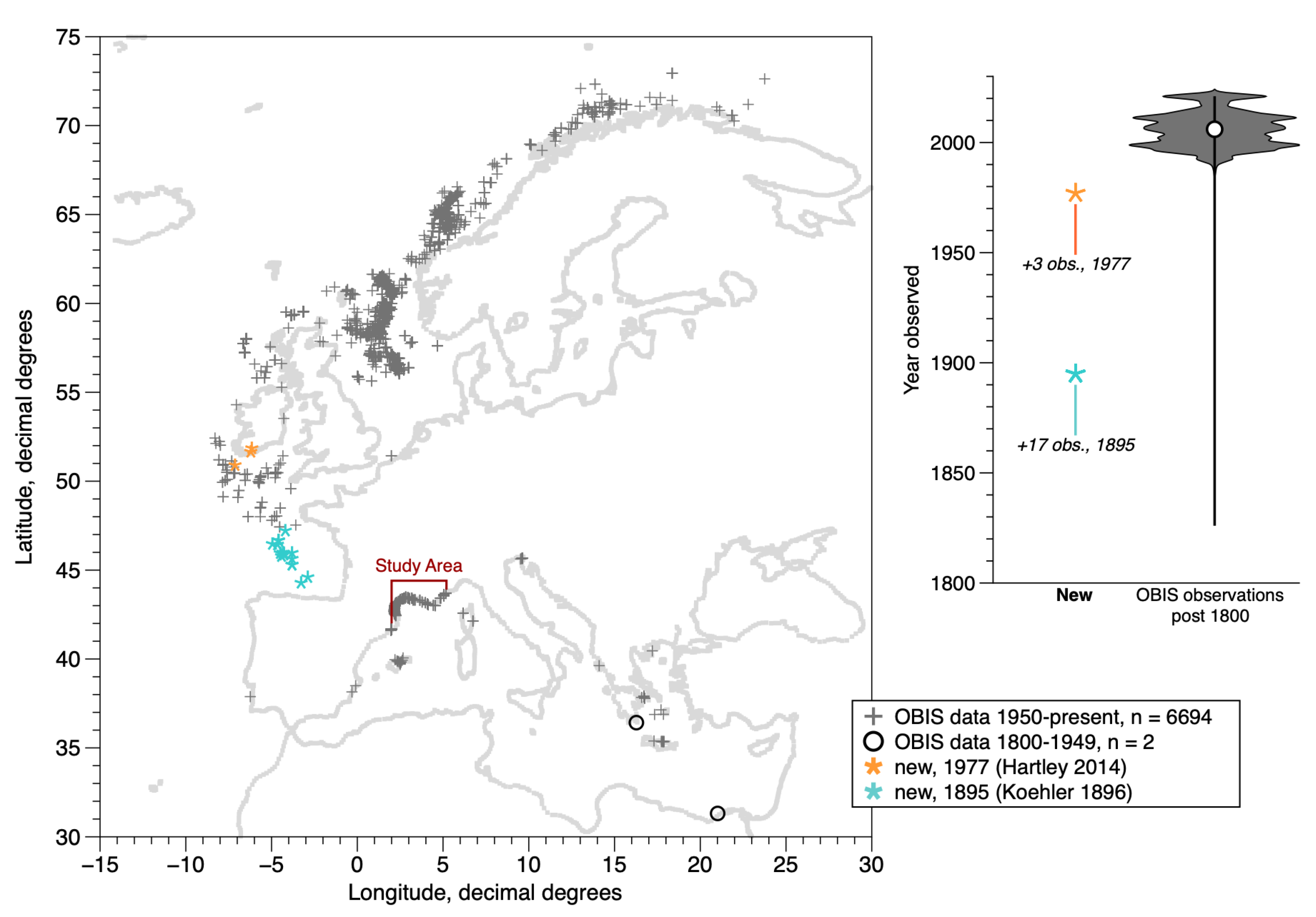
2. Materials and Methods
2.1. Brief Description of the Species Distribution and Field Studies
2.2. Modelling
2.2.1. Continuous Model
2.2.2. Hybrid Modelling
2.3. Extrapolations of the Hybrid Model
2.3.1. Long-Term Local Extrapolation for Hindcasting
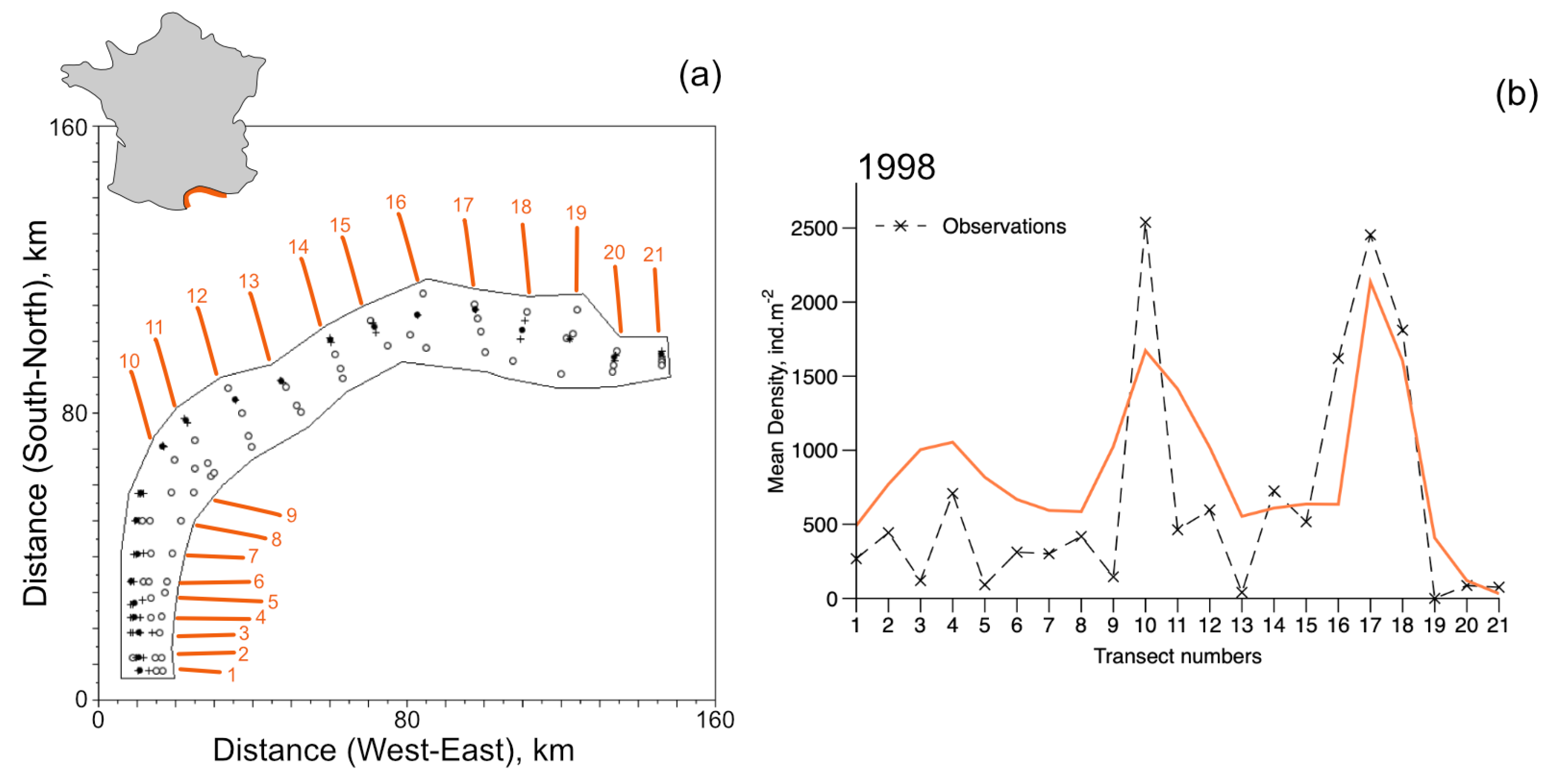
2.3.2. Spatial, Steady-State Extrapolation for Regional Scale Trends
3. Results
3.1. Spatial Structures of the Population Densities of D. arietina in Banyuls Bay
3.2. Demographic Parameters of the D. arietina Population
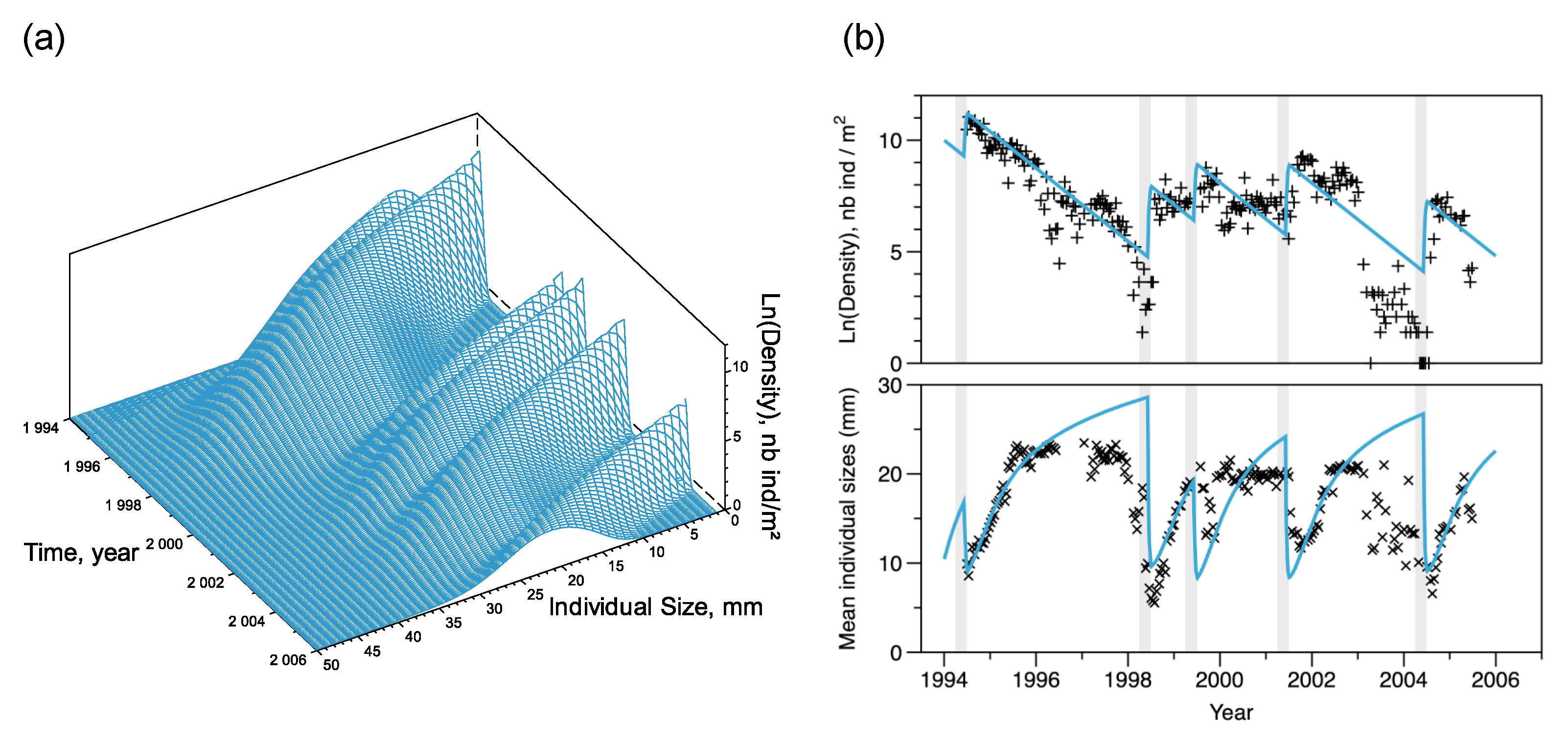
3.3. Simulating the Temporal Variations
3.4. Extrapolating the Population Dynamics in Time and Space
- For a yearly-averaged NAOi, the estimate for was recruits per reproducer. This produced a maximum density during 1930, of almost ; the minimum value occurred during 1881 (, or about 72 individuals in the entire bay).
- If the first 6 months of the NAOi are averaged, then the estimate was slightly lower ( recruits per reproducer); this simulation reached its maximum density value in 1928, with fewer individuals: . The minimum value was reached during 1874 ().
- Using a 3 month averaged NAOi (April, May, and June concerned by larval dispersal and recruitment), the highest estimate for was obtained: recruits per reproducer. In this case, the maximum value was reached earlier in 1914, with about ; the minimum value occurred later, in 1943, i.e., after the maximum peak. This minimum was only , and is lower than the other two cases.
4. Discussion
4.1. Mathematical Properties of the Population Outbreak Models
- The system is controlled by an external flux of individuals from outside of the study area (Equation (16)).
4.2. Characteristics of the Local Population Dynamics
4.3. Influence of the NAO on Recruitment
4.4. Is the Population of D. arietina a Metapopulation?
4.5. Implications of the Modelling
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gremare, A.; Sarda, R.; Medernach, L.; Pinedo, S.; Amouroux, J.M.; Martin, D.; Nozais, C.; Charles, F. On the dramatic increase of Ditrupa arietina O.F. Müller (Annelida: Polychaeta) along both the French and the Spanish Catalan coasts. Estuarine Coast. Shelf Sci. 1998, 47, 447–457. [Google Scholar] [CrossRef]
- Hanski, I. Density dependence, regulation and variability in animal populations. Philos. Trans. Biol. Sci. 1990, 330, 141–150. [Google Scholar] [CrossRef]
- Condon, R.H.; Duarte, C.M.; Pitt, K.A.; Robinson, K.L.; Lucas, C.H.; Sutherland, K.R.; Mianzan, H.W.; Bogeberg, M.; Purcell, J.E.; Decker, M.B.; et al. Recurrent jellyfish blooms are a consequence of global oscillations. Proc. Natl. Acad. Sci. USA 2013, 110, 1000–1005. [Google Scholar] [CrossRef]
- Uthicke, S.; Schaffelke, F.; Byrne, M. A boom-bust phylum? Ecological and evolutionary consequences of density variations in echinoderms. Ecol. Monogr. 2009, 79, 3–24. [Google Scholar] [CrossRef]
- Harris, L.G.; Gibson, J.L. Contrasting decadal recruitment patterns in the sea urchin Strongylocentrotus droebachiensis in the Gulf of Maine. J. Exp. Mar. Biol. Ecol. 2023, 558, 151832. [Google Scholar] [CrossRef]
- Pratchett, M.S.; Caballes, C.F.; Cvitanovic, C.; Raymundo, M.L.; Babcock, R.C.; Bonin, M.C.; Bozec, Y.M.; Burn, D.; Byrne, M.; Castro-Sanguino, C.; et al. Knowledge Gaps in the Biology, Ecology, and Management of the Pacific Crown-of-Thorns Sea Star Acanthaster sp. on Australia’s Great Barrier Reef. Biol. Bull. 2021, 241, 330–346. [Google Scholar] [CrossRef] [PubMed]
- Guarini, J.M.; Sari, N.; Moritz, C. Modelling the dynamics of the microalgal biomass in semi-enclosed shallow-water ecosystems. Ecol. Model. 2008, 211, 267–278. [Google Scholar] [CrossRef]
- Hartley, J.P. A review of the occurrence and ecology of dense populations of Ditrupa arietina (Polychaeta: Serpulidae). Mem. Mus. Vic. 2014, 71, 85–95. [Google Scholar] [CrossRef]
- Buhl-Mortensen, L.; Ellingsen, K.E.; Buhl-Mortensen, P.; Skaar, K.L.; Gonzalez-Mirelis, G. Trawling disturbance on megabenthos and sediment in the Barents Sea: Chronic effects on density, diversity, and composition. ICES J. Mar. Sci. 2016, 73, 98–114. [Google Scholar] [CrossRef]
- OBIS. Distribution Records of Ditrupa arietina (O. F. Müller, 1776); Ocean Biodiversity Information System; Intergovernmental Oceanographic Commission of UNESCO: Ostend, Belgium, 2023. [Google Scholar]
- Resgalla, C.J.; Petri, L.; da Silva, B.G.T.; Brilha, R.T.; Araujo, T.C.; Almeida, M. Outbreaks, coexistence, and life cycle of jellyfish species in relation to abiotic and biological factors along a South American coast. Hydrobiologia 2019, 839, 87–102. [Google Scholar] [CrossRef]
- Labrune, C.; Amouroux, J.M.; Sarda, R.; Dutrieux, E.; Thorin, S.; Rosenberg, R.; Gremare, A. Characterization of the ecological quality of the coastal Gulf of Lions (NW Mediterranean). A comparative approach based on three biotic indices. Mar. Pollut. Bull. 2006, 52, 34–47. [Google Scholar] [CrossRef]
- Muxika, I.; Borja, A.; Bonne, W. The suitability of the marine biotic index (AMBI) to new impact sources along European coasts. Ecol. Indic. 2005, 5, 19–31. [Google Scholar] [CrossRef]
- Medernach, L.; Jordana, E.; Gremare, A.; Nozais, C.; Charles, F.; Amouroux, J.M. Population dynamics, secondary production and calcification in a Mediterranean population of Ditrupa arietina (Annelida: Polychaeta). Mar. Ecol. Prog. Ser. 2000, 199, 171–184. [Google Scholar] [CrossRef]
- Kritzer, J.P.; Sale, P.F. Metapopulation ecology in the sea: From Levins’ model to marine ecology and fisheries science. Fish Fish. 2004, 5, 131–140. [Google Scholar] [CrossRef]
- Guizien, K.; Charles, F.; Hurther, D.; Michallet, H. Spatial redistribution of Ditrupa arietina (soft bottom Mediterranean epifauna) during a moderate swell event. Cont. Shelf Res. 2010, 30, 239–251. [Google Scholar] [CrossRef]
- Guizien, K.; Bramanti, L. Modelling ecological complexity for marine species conservation: The effect of variable connectivity on species spatial distribution and age-structure. Theor. Biol. Forum 2014, 107, 47–56. [Google Scholar]
- Labrune, C.; Gremare, A.; Amouroux, J.M.; Sarda, R.; Gil, J.; Taboada, S. Assessment of soft-bottom polychaete assemblages in the Gulf of Lions (NW Mediterranean) based on a mesoscale survey. Estuar. Coast. Shelf Sci. 2007, 71, 133–147. [Google Scholar] [CrossRef]
- Koehler, R. Résultats Scientifiques de la Campagne du “Caudan” Dans le Golfe de Gascogne, Août-Septembre 1895 (1896); Fascicule 26 in Annales de l’Université de Lyon, Masson et Cie: Paris, France, 1896; p. 740. [Google Scholar]
- Charles, F.; Jordana, E.; Amouroux, J.M.; Gremare, A.; Desmalades, M.; Zudaire, L. Reproduction, recruitment and larval metamorphosis in the serpulid polychaete Ditrupa arietina (O.F. Müller). Estuar. Coast. Shelf Sci. 2003, 57, 435–443. [Google Scholar] [CrossRef]
- Jordana, E.; Gremare, A.; Lantoine, F.; Courties, C.; Charles, F.; Amouroux, J.M.; Vétion, G. Seasonal changes in the grazing of coastal picoplankton by the suspension-feeding polychaete Ditrupa arietina O.F. Müller). J. Sea Res. 2001, 46, 245–259. [Google Scholar] [CrossRef]
- Guizien, K.; Brochier, T.; Duchêne, J.C.; Koth, B.S.; Marsaleix, P. Dispersal of Owenia fusiformis larvae by wind-driven currents: Turbulence, swimming behaviour and mortality in a three dimensional stochastic model. Mar. Ecol. Prog. Ser. 2006, 311, 47–66. [Google Scholar] [CrossRef]
- Gremare, A.; Amouroux, J.M.; Vetion, G. Long-term comparison of macrobenthos within the soft bottoms of the Bay of Banyuls-sur-mer (Northwestern Mediterranean Sea). J. Sea Res. 1998, 40, 281–302. [Google Scholar] [CrossRef]
- Labrune, C.; Grémare, A.; Guizien, K.; Amouroux, J.M. Long-term comparison of soft bottom macrobenthos in the Bay of Banyuls-sur-Mer (North-Western Mediterranean Sea): A reappraisal. J. Sea Res. 2007, 58, 125–143. [Google Scholar] [CrossRef]
- Bonifácio, P.; Grémare, A.; Gauthier, O.; Romero-Ramirez, A.; Bichon, S.; Amouroux, J.M.; Labrune, C. Long-term (1998 vs. 2010) large-scale comparison of soft-bottom benthic macrofauna composition in the Gulf of Lions, NW Mediterranean Sea. J. Sea Res. 2018, 131, 32–45. [Google Scholar] [CrossRef]
- Bonifacio, P.; Grémare, A.; Amouroux, J.M.; Labrune, C. Climate-driven changes in macrobenthic communities in the Mediterranean Sea: A 10-year study in the Bay of Banyuls-sur- Mer. Ecol. Evol. 2019, 9, 10483–10498. [Google Scholar] [CrossRef]
- Moritz, C.; Loeuille, N.; Guarini, J.M.; Guizien, K. Quantifying the dynamics of marine invertebrate metacommunities: What processes can maintain high diversity with low densities in the Mediterranean Sea? Ecol. Model. 2009, 220, 3021–3032. [Google Scholar] [CrossRef]
- Guille, A. Bionomie benthique du plateau continental de la côte catalane française IV. Densités, biomasses, et variations saisonnières de la macrofaune. Vie Milieu 1971, 22, 93–158. [Google Scholar]
- Gupta, A.K.; T, C. Goodness-of-fit tests for the skew-normal distribution. Commun.-Stat.–Simul. Comput. 2001, 30, 907–930. [Google Scholar] [CrossRef]
- Gros, P. Prévision à moyen terme des fluctuations des ressources halieutiques: Modèles tautologiques ou autoregenerants ? Ann. L’institut Océanogr. 1992, 68, 211–225. [Google Scholar]
- Hirsch, C. Numerical Computation of Internal and External Flows. Fundamentals of Numerical Discretization; Wiley Series in Numerical Methods in Engineering; John Wiley and Sons: Hoboken, NJ, USA, 1989; p. 515. [Google Scholar]
- Jones, P.D.; Jónsson, T.; Wheeler, D. Extension to the North Atlantic Oscillation using early instrumental pressure observations from Gibraltar and South-West Iceland. Int. J. Climatol. 1997, 17, 1433–1450. [Google Scholar] [CrossRef]
- Climate Research Unit. North Atlantic Oscillation (NAO); University of East Anglia: Norwich, UK, 2017. [Google Scholar]
- Kutzbach, J.E. Large-scale features of monthly mean northern hemisphere anomaly maps of sea-level pressure. Mon. Weather. Rev. 1970, 98, 708–716. [Google Scholar] [CrossRef]
- Hurrell, J.W. Decadal trends in the North Atlantic Oscillation and relationships to regional temperature and precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef]
- Chesson, P.; Lee, C.T. Families of discrete kernels for modeling dispersal. Theor. Popul. Biol. 2005, 67, 241–256. [Google Scholar] [CrossRef]
- McHugh, D.; Fong, P.P. Do life history traits account for diversity of polychaete annelids? Invertebr. Biol. 2002, 121, 325–338. [Google Scholar] [CrossRef]
- Marshall, D.J.; Keough, M.J. Effects of settler size and density on early post-settlement survival of Ciona intestinalis in the field. Mar. Ecol. Prog. Ser. 2003, 259, 139–144. [Google Scholar] [CrossRef]
- Botsford, L.W. Physical influences on recruitment to Californa current invertebrate populations on multiple scales. ICES J. Mar. Sci. 2001, 58, 1081–1091. [Google Scholar] [CrossRef]
- Ripley, B.J.; Caswell, H. Recruitment variability and stochastic population growth of the soft-shell clam, Mya arenaria. Ecol. Model. 2006, 193, 517–530. [Google Scholar] [CrossRef]
- Dekshenieks, M.M.; Hofmann, E.E.; Klinck, J.M.; Powell, E.N. A modelling study of the effects of size and depth-dependent predation on larval survival. J. Plankton Res. 1997, 19, 1583–1598. [Google Scholar] [CrossRef]
- Hiddink, J.G.; Hofstede, R.; Wolff, W.J. Predation of intertidal infauna on juveniles of the bivalve Macoma balthica. J. Sea Res. 2002, 47, 141–159. [Google Scholar] [CrossRef]
- Weissberger, E.J.; Grassle, J.P. Settlement, first year growth, and mortality of surf clams Spisula solidissima. Estuar. Coast. Shelf Sci. 2003, 56, 669–684. [Google Scholar] [CrossRef]
- Takasuka, A.; Oozeki, Y.; Kimura, R.; Kubota, H.; Aoki, I. Growth selective predation hypothesis revisited for larval anchovy in offshore waters: Cannibalism by juveniles versus predation by skipjack tunas. Mar. Ecol. Prog. Ser. 2004, 278, 297–302. [Google Scholar] [CrossRef]
- Ellien, C.; Thiebaut, E.; Barnay, S.; Dauvin, J.C.; Gentil, F.; Salomon, J.C. The influence of variability in larval dispersal on the dynamics of a metapopulation in the eastern Channel. Oceanol. Acta 2004, 23, 423–442. [Google Scholar] [CrossRef]
- Broitman, B.R.; Mieszkowska, N.; Helmuth, B.; Blanchette, C.A. Climate and recruitment of rocky shore intertidal invertebrates in the eastern North Atlantic. Ecology 2008, 89, S81–S90. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Kushnir, Y.; Ottersen, G.; Visbeck, M. An Overview of the North Atlantic Oscillation. In The North Atlantic Oscillation: Climatic Significance and Environmental Impact; Hurrell, J.W., Kushnir, Y., Ottersen, G., Visbeck, M., Eds.; Geophysical Monograph Series; American Geophysical Union: Washington, DC, USA, 2003; pp. 1–35. [Google Scholar] [CrossRef]
- Visbeck, M.; Chassignet, E.P.; Curry, R.G.; Delworth, T.L.; Dickson, R.R.; Krahmann, G. The Ocean’s Response to North Atlantic Oscillation Variability. In The North Atlantic Oscillation: Climatic Significance and Environmental Impact; Hurrell, J.W., Kushnir, Y., Ottersen, G., Visbeck, M., Eds.; Geophysical Monograph Series; American Geophysical Union: Washington, DC, USA, 2003; pp. 113–145. [Google Scholar] [CrossRef]
- Drinkwater, K.F.; Belgrano, A.; Borja, A.; Conversi, A.; Edwards, M.; Greene, C.H.; Ottersen, G.; Pershing, A.J.; Walker, H. The Response of Marine Ecosystems to Climate Variability Associated with the North Atlantic Oscillation. In The North Atlantic Oscillation: Climatic Significance and Environmental Impact; Hurrell, J.W., Kushnir, Y., Ottersen, G., Visbeck, M., Eds.; Geophysical Monograph Series; American Geophysical Union: Washington, DC, USA, 2003; pp. 211–234. [Google Scholar] [CrossRef]
- Criado-Aldeneuva, F.; Soto-Navarro, J. Climatic Indices over the Mediterranean Sea: A Review. Appl. Sci. 2020, 10, 5790. [Google Scholar] [CrossRef]
- Martin-Vide, J.; Lopez-Bustins, J.A. The Western Mediterranean Oscillation and rainfall in the Iberian Peninsula. Int. J. Climatol. 2006, 26, 1455–1475. [Google Scholar] [CrossRef]
- Lopez-Bustins, J.A.; Arbiol-Roca, L.; Martin-Vide, J.; Barrera-Escoda, A.; Prohom, M. Intra-annual variability of the Western Mediterranean Oscillation (WeMO) and occurrence of extreme torrential precipitation in Catalonia (NE Iberia). Nat. Hazards Earth Syst. Sci. 2020, 20, 2483–2501. [Google Scholar] [CrossRef]
- Perkins, P.J.; Daniel, K. Variation in larval growth can predict the recruitment of a temperate, seagrass-associated fish. Oecologia 2006, 147, 641–649. [Google Scholar] [CrossRef]
- Grassle, J.P.; Butman, C.; Mills, S. Active habitat selection by Capitella sp. I Larvae II. Multiple choice experiments in still water and flume flows. J. Mar. Res. 1992, 50, 717–743. [Google Scholar] [CrossRef]
- Snelgrove, P.V.R.; Butman, C.A.; Grassle, J.P. Hydrodynamic enhancement of larval settlement in the bivalve Mulinia lateralis (Say) and the polychaete Capitella sp. I. in microdepositional environments. J. Exp. Mar. Biol. Ecol. 1993, 168, 71–109. [Google Scholar] [CrossRef]
- Régnière, J.; Nealis, V.G. Ecological mechanisms of population change during outbreaks of the spruce budworm. Ecol. Entomol. 2007, 32, 461–477. [Google Scholar] [CrossRef]
- Clare, D.S.; Spencer, M.; Robinson, L.A.; Frid, C.L.J. Species densities, biological interactions and benthic ecosystem functioning: An in situ experiment. Mar. Ecol. Prog. Ser. 2016, 547, 149–161. [Google Scholar] [CrossRef]
- Savage, A.A. Density dependent and density independent relationships during a twenty-seven year study of the population dynamics of the benthic macroinvertebrate community of a chemically unstable lake. Hydrobiologia 1996, 335, 115–131. [Google Scholar] [CrossRef]
- Weerman, E.J.; van de Koppel, J.; Eppinga, M.B.; Montserrat, F.; Liu, Q.X.; Herman, P.M.J. Spatial self-organization on intertidal mudflats through biophysical stress divergence. Am. Nat. 2010, 176, E15–E32. [Google Scholar] [CrossRef] [PubMed]
- Serruys, M.W. The Societal Effects of the Eighteenth Century Shipworm Epidemic in the Austrian Netherlands (c. 1730–1760). J. Hist. Environ. Soc. 2022, 6, 95–127. [Google Scholar] [CrossRef]
- Charles, F.; Coston-Guarini, J.; Guarini, J.M.; Fanfard, S. Wood decay at sea. J. Sea Res. 2016, 114, 22–25. [Google Scholar] [CrossRef]
- Charles, F.; Garrigue, J.; Coston-Guarini, J.; Guarini, J.M. Estimating the integrated degradation rates of woody debris at the scale of a Mediterranean coastal catchment. Sci. Total Environ. 2022, 815, 152810. [Google Scholar] [CrossRef] [PubMed]
- Gibson, G.D.; Chia, F.S. Contrasting reproductive modes in two sympatric species of Haminaea (Opisthobranchia: Cephalaspidea). J. Molluscan Stud. 1991, 57, 49–60. [Google Scholar] [CrossRef]
- Swetnam, T.W.; Allen, C.D.; Betancourt, J.L. Applied historical ecology: Using the past to manage for the future. Ecol. Appl. 1999, 9, 1189–1206. [Google Scholar] [CrossRef]
- McKelvey, K.S.; Aubry, K.B.; Schwartz, M.K. Using anecdotal occurrence data for rare or elusive species: The illusion of reality and a call for evidentiary standards. BioScience 2008, 58, 549–555. [Google Scholar] [CrossRef]
- Ben Chehida, Y.; Stelwagen, T.; Hoekendijk, J.P.A.; Ferreira, M.; Eira, C.; Torres-Pereira, A.; Nicolau, L.; Thumloup, J.; Fontaine, M.C. Harbor porpoise losing its edge: Genetic time series suggests a rapid population decline in Iberian waters over the last 30 years. Ecol. Evol. 2023, 13, e10819. [Google Scholar] [CrossRef]
- Coston-Guarini, J. Epistemic Values of Historical Information in Marine Ecology and Conservation [2016BRES0124]. Ph.D. Thesis, Université de Bretagne Occidentale, Brest, France, 2017. [Google Scholar] [CrossRef]
- Johnston, A.S.A.; Boyd, R.J.; Watson, J.W.; Paul, A.; Evans, L.C.; Gardner, E.L.; Boult, V.L. Predicting population responses to environmental change from individual-level mechanisms: Towards a standardized mechanistic approach. Proc. R. Soc. B Biol. Sci. 2019, 286, 20191916. [Google Scholar] [CrossRef]
- Niu, S.; Luo, Y.; Dietze, M.C.; Keenan, T.F.; Shi, Z.; Li, J.; Chapin, F.S., III. The role of data assimilation in predictive ecology. Ecosphere 2014, 5, 65. [Google Scholar] [CrossRef]
- Bates, A.E.; Helmuth, B.; Burrows, M.T.; Duncan, M.I.; Garrabou, J.; Guy-Haim, T.; Lima, F.; Queiros, A.M.; Seabra, R.; Marsh, R.; et al. Biologists ignore ocean weather at their peril. Nature 2018, 560, 299–301. [Google Scholar] [CrossRef] [PubMed]
- Guarini, J.M.; Hinz, S.; Coston-Guarini, J. Designing the Next Generation of Condition Tracking and Early Warning Systems for Shellfish Aquaculture. J. Mar. Sci. Eng. 2021, 9, 1084. [Google Scholar] [CrossRef]


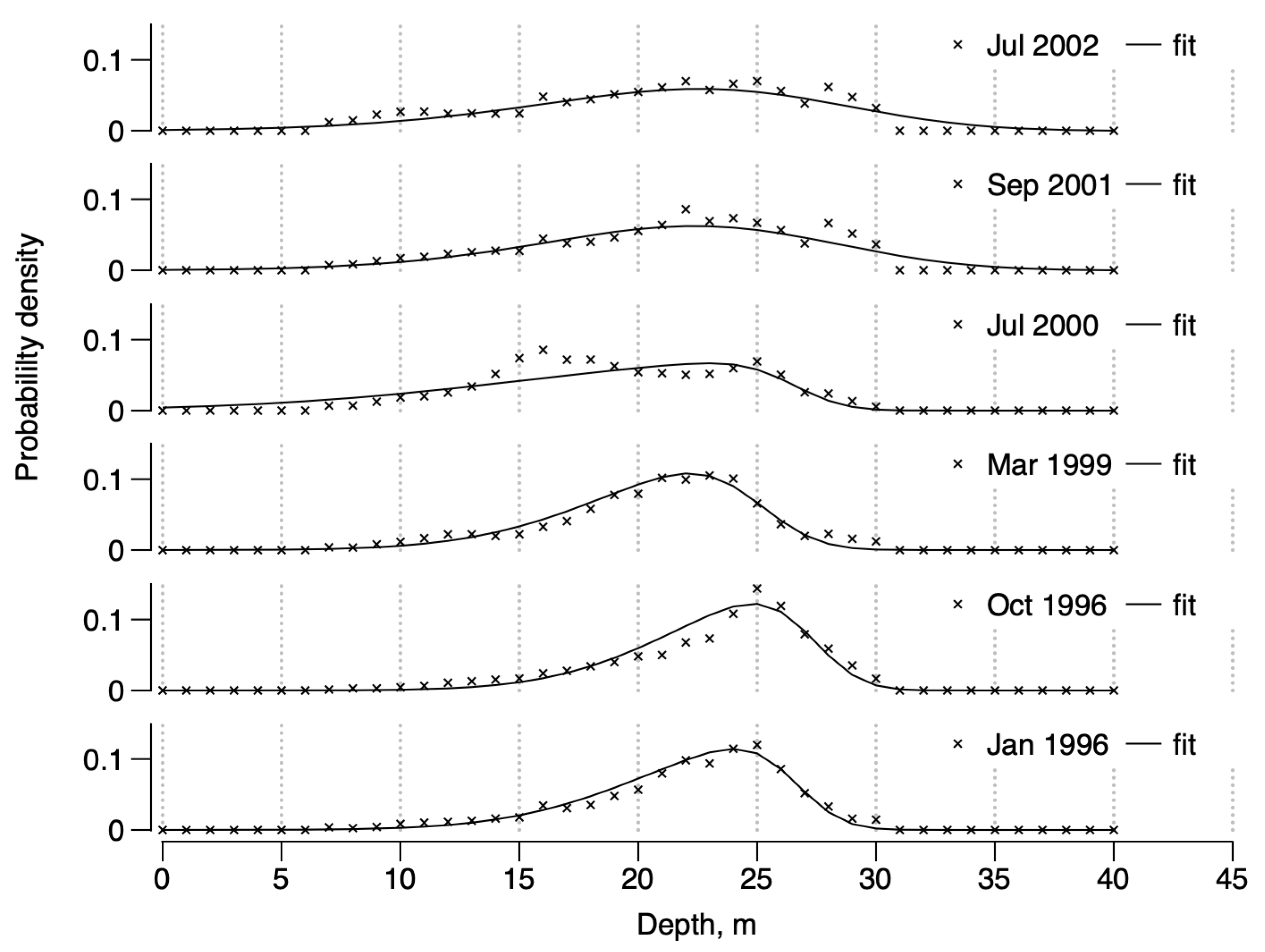


| z | Jan. 1996 | Oct. 1996 | Jan. 1998 | Mar. 1999 | Jul. 2000 | Sep. 2001 | Jul. 2002 | Sep. 2003 | |
|---|---|---|---|---|---|---|---|---|---|
| Unit | m | ||||||||
| Nb pts | 76 | 78 | 78 | 78 | 78 | 78 | 78 | 78 | 78 |
| Min | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Max | 32 | 3550 | 3000 | 25 | 2395 | 1895 | 5940 | 1685 | 280 |
| Mean | 21 | 491 | 325 | 2 | 174 | 381 | 597 | 245 | 12 |
| Variance | 61 | 504,245 | 316,133 | 17 | 154,064 | 271,005 | 1,200,771 | 157,037 | 1665 |
| Model | Gau | Sph | Sph | - | Sph | Sph | Exp | Exp | - |
| Mode | Ani | Iso | Iso | - | Iso | Iso | Iso | Iso | - |
| 0.1 | 104,000 | 100 | 15 | 100 | 1800 | 1000 | 100 | 1611 | |
| 121 | 524,000 | 314,400 | - | 135,100 | 267,900 | 1,330,000 | 159,700 | - | |
| Range (m) | >1600 | 524 | 275 | - | 308 | 368 | 543 | 549 | - |
| XV-SLP | - | 0.925 | 0.996 | - | 0.957 | 1.086 | 0.893 | 0.905 | - |
| XV-OAO | - | −12.76 | −44.48 | - | −36.65 | −94.52 | −43.95 | −18.07 | - |
| Mean | Variance | Skewness | Kurtosis | ||||
|---|---|---|---|---|---|---|---|
| January 1996 | 6.02 | 26.62 | −3.77 | 21.98 | 14.70 | −0.76 | 0.61 |
| October 1996 | 5.48 | 27.32 | −3.27 | 23.14 | 12.53 | −0.71 | 0.55 |
| January 1998 | - | - | - | - | - | - | - |
| March 1999 | 6.06 | 25.04 | −2.96 | 20.46 | 15.75 | −0.66 | 0.50 |
| July 2000 | 11.15 | 26.54 | −6.55 | 17.75 | 46.96 | −0.91 | 0.77 |
| September 2001 | 8.21 | 26.85 | −1.31 | 21.64 | 40.27 | −0.24 | 0.13 |
| July 2002 | 9.24 | 27.65 | −1.60 | 21.40 | 46.29 | −0.33 | 0.20 |
| September 2003 | - | - | - | - | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coston-Guarini, J.; Charles, F.; Guarini, J.-M. Modelling the Dynamics of Outbreak Species: The Case of Ditrupa arietina (O.F. Müller), Gulf of Lions, NW Mediterranean Sea. J. Mar. Sci. Eng. 2024, 12, 350. https://doi.org/10.3390/jmse12020350
Coston-Guarini J, Charles F, Guarini J-M. Modelling the Dynamics of Outbreak Species: The Case of Ditrupa arietina (O.F. Müller), Gulf of Lions, NW Mediterranean Sea. Journal of Marine Science and Engineering. 2024; 12(2):350. https://doi.org/10.3390/jmse12020350
Chicago/Turabian StyleCoston-Guarini, Jennifer, François Charles, and Jean-Marc Guarini. 2024. "Modelling the Dynamics of Outbreak Species: The Case of Ditrupa arietina (O.F. Müller), Gulf of Lions, NW Mediterranean Sea" Journal of Marine Science and Engineering 12, no. 2: 350. https://doi.org/10.3390/jmse12020350
APA StyleCoston-Guarini, J., Charles, F., & Guarini, J.-M. (2024). Modelling the Dynamics of Outbreak Species: The Case of Ditrupa arietina (O.F. Müller), Gulf of Lions, NW Mediterranean Sea. Journal of Marine Science and Engineering, 12(2), 350. https://doi.org/10.3390/jmse12020350






