Dynamic Positioning Control for Marine Crafts: A Survey and Recent Advances
Abstract
:1. Introduction
2. Thorny Issues in DP Control Design
2.1. Impact of Multiple Source Disturbance
2.2. Unavailable Velocity Measurement Information
2.3. Resource Conservation and Performance Optimization
2.4. Destabilizing Impact of Faults and Network Security
2.5. Compound Multi-Constraint Restrictions
3. DP Control Methodologies for Marine Crafts
3.1. Classical Nonlinear Control Design
3.2. Neural Network Adaptive Control Design Scheme
3.3. Fuzzy Adaptive Control Design Scheme
3.4. Anti-Disturbance Control Design
- Anti-disturbance control based on a Kalman filter [19,20,76]: A Kalman filter is a filter used to estimate the state of a linear system with Gaussian noise. By continuously measuring and predicting the system’s state, the Kalman filter can estimate the system’s state and provide an optimal estimation result for DP.
- Anti-disturbance control based on the disturbance observer (DO) [16,77,78,79,80,81,82,83,84]: As it is known that ocean disturbances can be considered slow and bounded disturbances [77], DO can use auxiliary states to estimate unknown disturbances, and has excellent capabilities in handling slow and variation rate bounded disturbances. Therefore, DP control based on DO has made rapid progress [16,77,78,80,81]. Experts and scholars have improved DP control based on finite-time DO [15,17,82] and fixed-time DO [83,84] compared to the general form of DO.
- Anti-disturbance control based on ESO: The core idea of the ESO is to introduce an extended state that represents the uncertain dynamics of the system, unknown disturbances and noises. By observing and feedback controlling the system’s extended state, the estimation and control of the system’s state can be achieved. In the design of the ESO for marine DP systems, the system position and velocity equations need to be combined with the extended state equation, and the parameters need to be known to ensure that the ESO can accurately estimate the uncertainties. Due to the outstanding estimation performance of the ESO, it was often used to design DP anti-disturbance output feedback control [18,23,85]. Furthermore, Liu et al. proposed an event-based finite-time ESO for DP to achieve a good observation performance [86].
- Anti-disturbance control based on the method: The basic idea is to maximize the system’s robustness while ensuring system stability. The input and output of the system are represented as complex matrix forms, and the norm is used as an indicator to evaluate the system’s robustness. By minimizing the norm of the system, a controller with robust performance can be obtained, thereby achieving control of the system. After linearizing the DP model, DP robust controllers can be obtained by solving linear matrix inequalities [12,87,88]. In addition, Hu et al. considered the sensor noise and ocean disturbances on marine crafts, combined DO and control, proposed a DP composite anti-disturbance controller, which provides considerable inspiration for DP robust control design [11].
3.5. Output Feedback Control Design
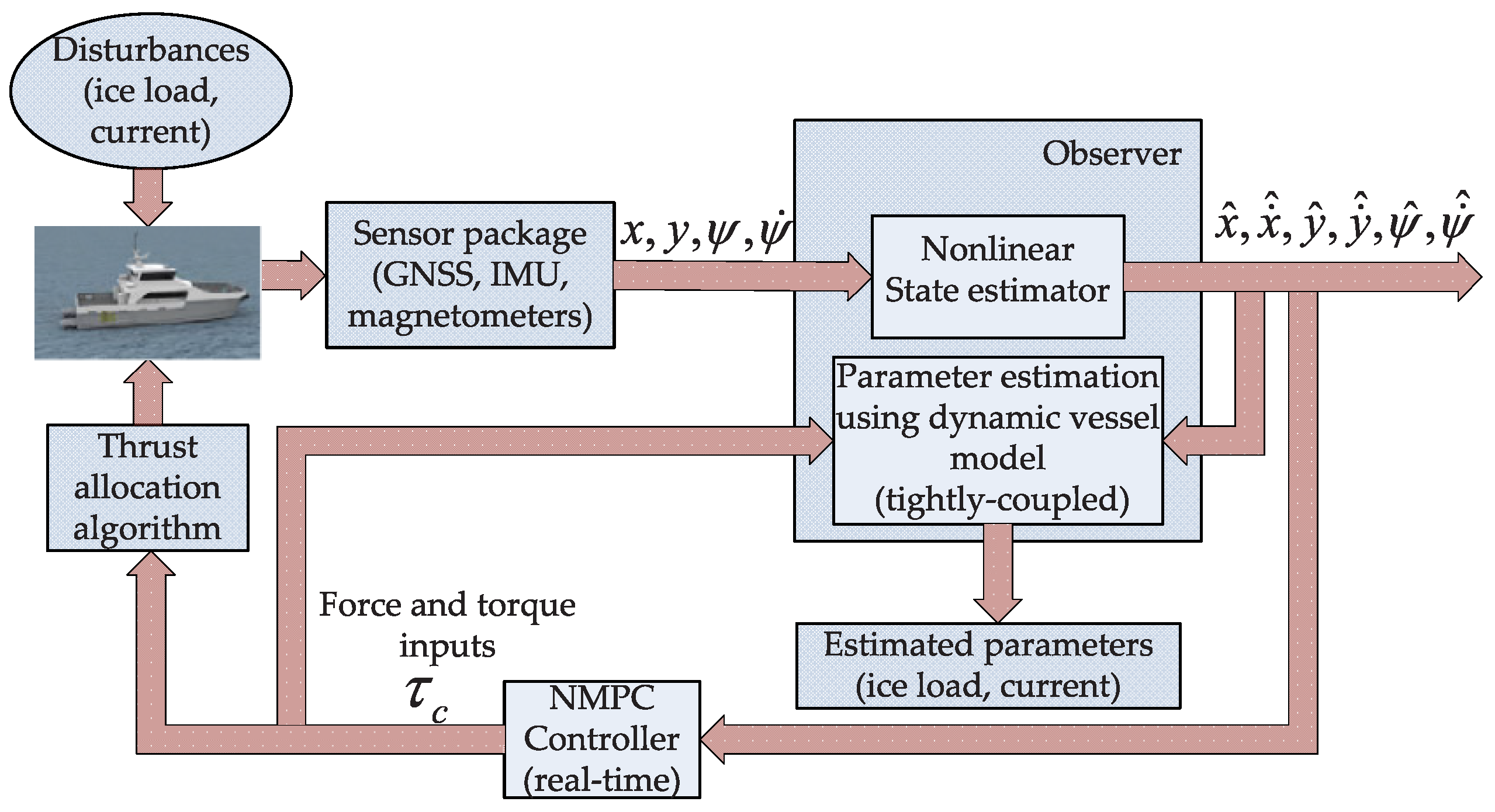
3.6. Optimal Control Design
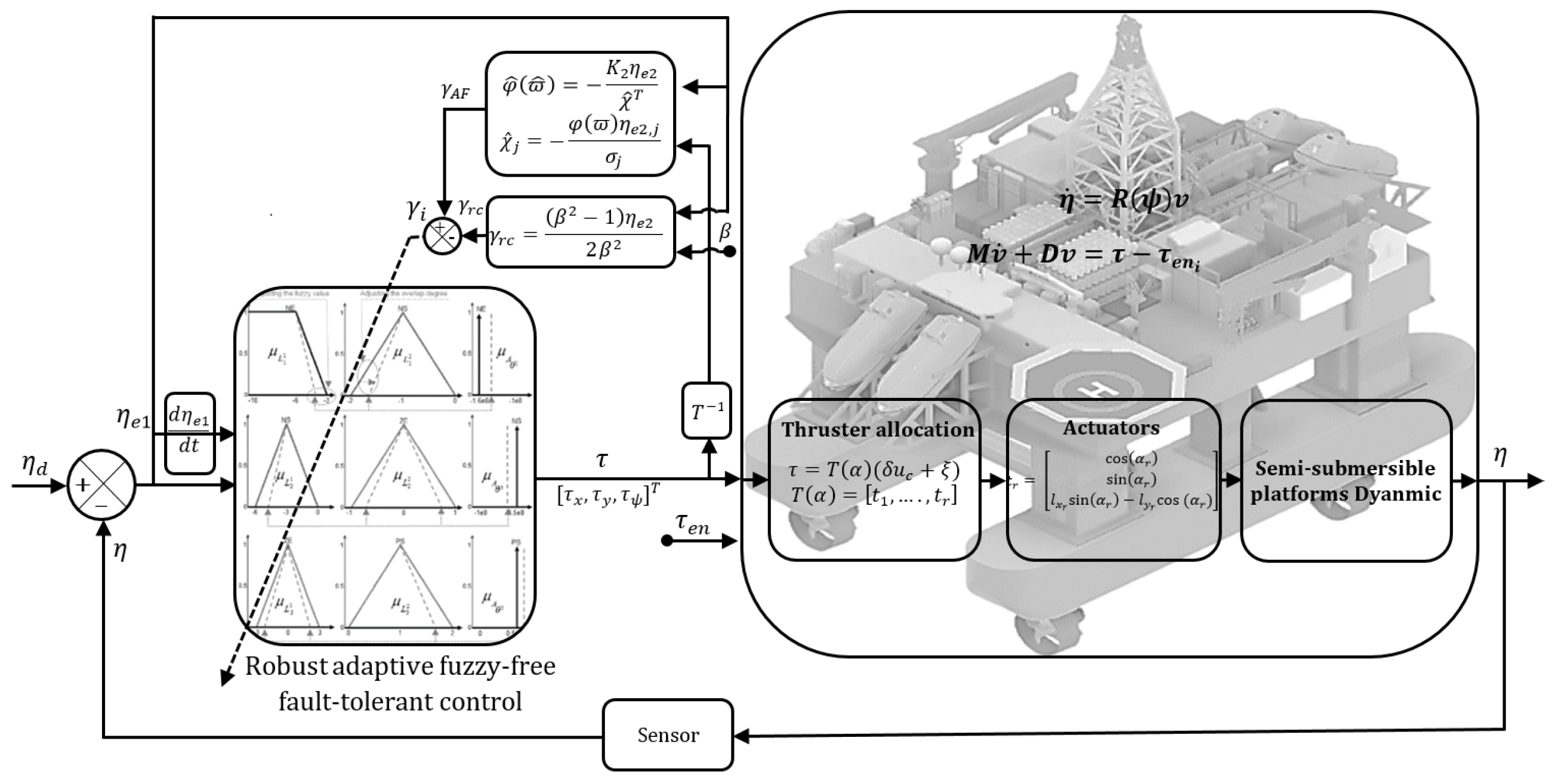
3.7. Fault-Tolerant Control Design
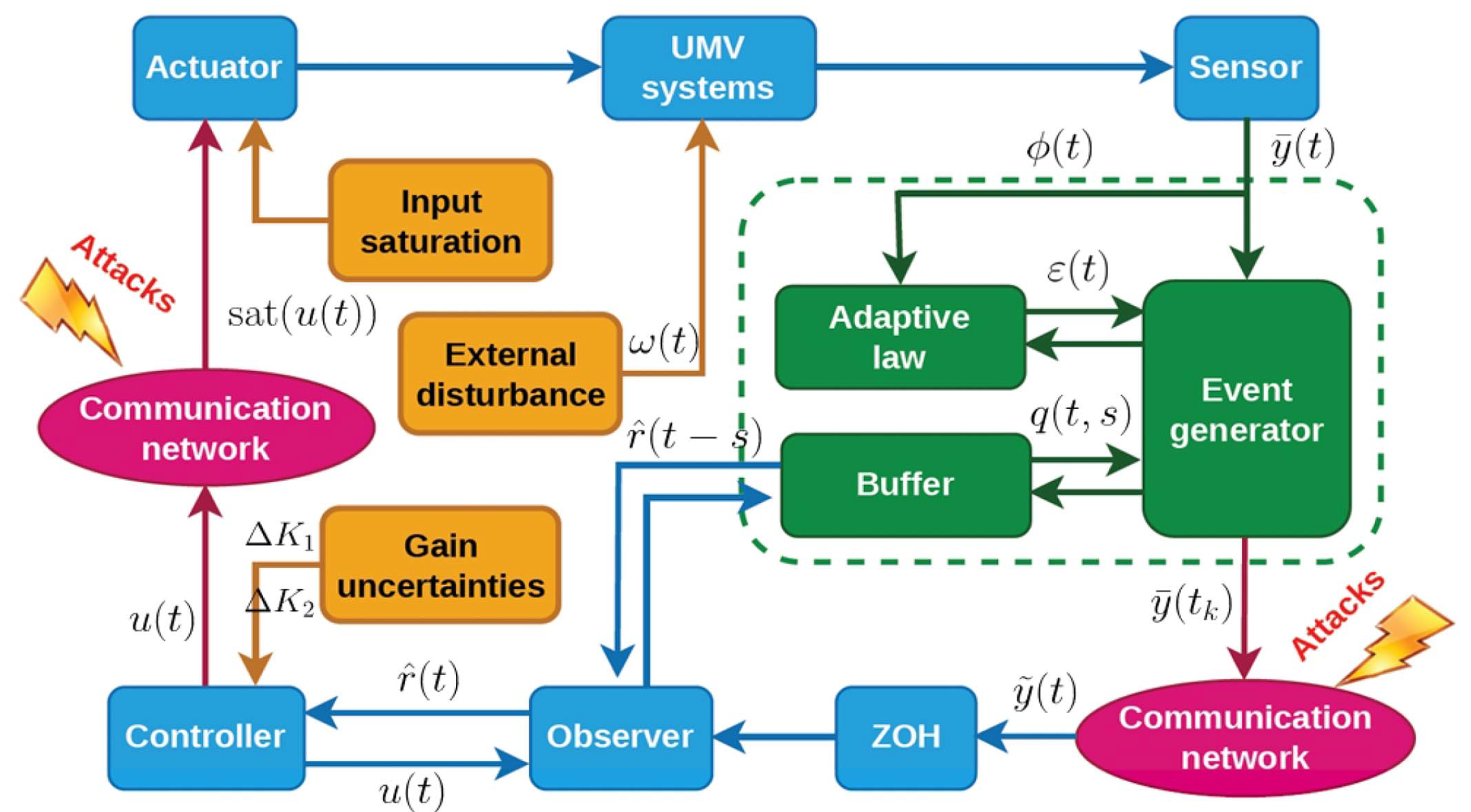
3.8. Security Control Design under Network Attack
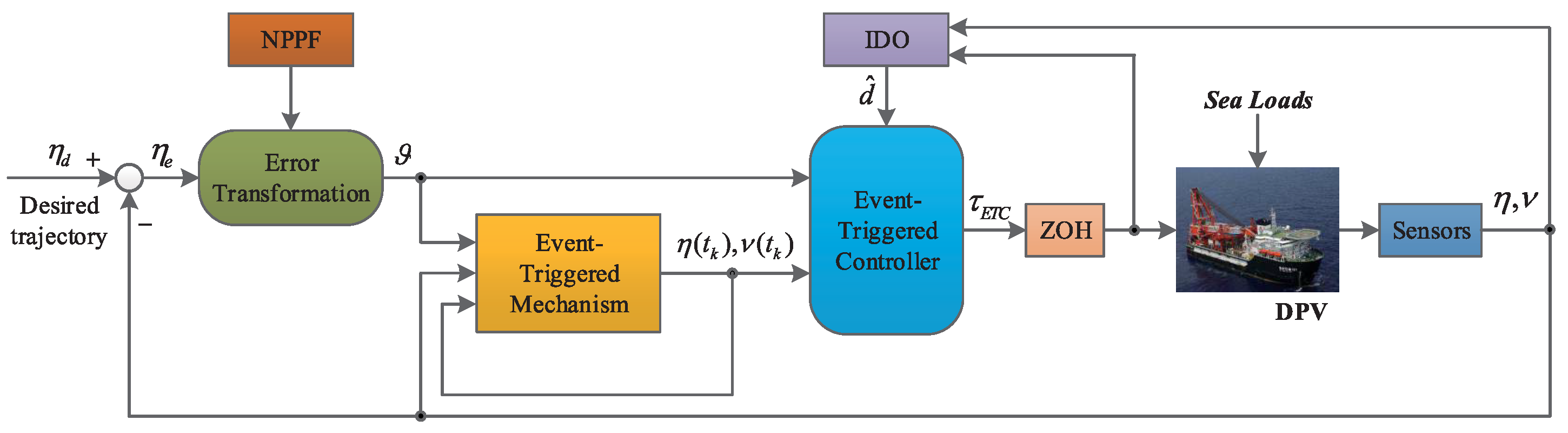
3.9. Constraint Control Design
3.10. Other Control Methods
4. Future Research Directions
4.1. Online Data-Driven Model-free Control Design
4.2. Intelligent Control Based on Man-Machine Combination
4.3. Composite Hierarchical Anti-Disturbance Control
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Xiao, Y.; Li, T. A survey of autonomous underwater vehicle formation: Performance, formation control, and communication capability. IEEE Commun. Surv. Tutor. 2018, 23, 815–841. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Sørensen, A.J. A survey of dynamic positioning control systems. Annu. Rev. Control 2011, 35, 123–136. [Google Scholar] [CrossRef]
- Shi, Y.; Shen, C.; Fang, H.; Li, H. Advanced control in marine mechatronic systems: A survey. IEEE/ASME Trans. Mechatron. 2017, 22, 1121–1131. [Google Scholar] [CrossRef]
- Liu, R.; Jin, Z.; Li, X.; Yuan, L. Dynamic Response Characteristics of the Hydraulic Rotary System of an Azimuth Thruster for a Dynamic Positioning Vessel. J. Mar. Sci. Eng. 2023, 11, 399. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, J.; Wang, D.; Han, Q. An Overview of Recent Advances in Coordinated Control of Multiple Autonomous Surface Vehicles. IEEE Trans. Ind. Inform. 2021, 17, 732–745. [Google Scholar] [CrossRef]
- He, S.; Kou, L.; Li, Y.; Xiang, J. Position tracking control of fully-actuated underwater vehicles with constrained attitude and velocities. IEEE Trans. Ind. Electron. 2022, 69, 13192–13202. [Google Scholar] [CrossRef]
- Gao, J.; Wu, P.; Li, T.; Proctor, A. Optimization-based model reference adaptive control for dynamic positioning of a fully actuated underwater vehicle. Nonlinear Dyn. 2017, 87, 2611–2623. [Google Scholar] [CrossRef]
- Panagou, D.; Kyriakopoulos, K.J. Dynamic positioning for an underactuated marine vehicle using hybrid control. Int. J. Control 2014, 87, 264–280. [Google Scholar] [CrossRef]
- Aguiar, A.P.; Pascoal, A.M. Dynamic positioning and way-point tracking of underactuated AUVs in the presence of ocean currents. Int. J. Control 2007, 80, 1092–1108. [Google Scholar] [CrossRef]
- Hu, X.; Wei, X.; Zhang, H.; Xie, W.; Zhang, Q. Composite anti-disturbance dynamic positioning of vessels with modelling uncertainties and disturbances. Appl. Ocean Res. 2020, 105, 102404. [Google Scholar] [CrossRef]
- Katebi, M.; Yamamoto, I.; Matsuura, M.; Grimble, M.; Hirayama, H.; Okamoto, N. Robust dynamic ship positioning control system design and applications. Int. J. Robust Nonlinear Control IFAC-Affil. J. 2001, 11, 1257–1284. [Google Scholar] [CrossRef]
- Du, J.; Hu, X.; Liu, H.; Chen, C.P. Adaptive robust output feedback control for a marine dynamic positioning system based on a high-gain observer. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2775–2786. [Google Scholar] [CrossRef]
- Yang, Y.; Guo, C.; Du, J. Robust adaptive NN-based output feedback control for a dynamic positioning ship using DSC approach. Sci. China Inf. Sci. 2014, 57, 1–13. [Google Scholar] [CrossRef]
- Gao, X.; Long, Y.; Li, T.; Hu, X.; Chen, C.P.; Sun, F. Optimal Fuzzy Output Feedback Control for Dynamic Positioning of Vessels With Finite-Time Disturbance Rejection Under Thruster Saturations. IEEE Trans. Fuzzy Syst. 2023, 31, 3447–3458. [Google Scholar] [CrossRef]
- Du, J.; Hu, X.; Krstić, M.; Sun, Y. Robust dynamic positioning of ships with disturbances under input saturation. Automatica 2016, 73, 207–214. [Google Scholar] [CrossRef]
- Shi, Q.; Li, X.; Dong, Q.; Yang, J.; Guo, X. Composite finite-time adaptive anti-disturbance control for dynamic positioning of vessels with output constraints. Ocean Eng. 2022, 255, 111414. [Google Scholar] [CrossRef]
- Yu, W.; Xu, H.; Han, X.; Chen, Y.; Zhu, M. Fault-tolerant control for dynamic positioning vessel with thruster faults based on the neural modified extended state observer. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 5905–5917. [Google Scholar] [CrossRef]
- Sørensen, A.J.; Sagatun, S.I.; Fossen, T.I. Design of a dynamic positioning system using model-based control. Control Eng. Pract. 1996, 4, 359–368. [Google Scholar] [CrossRef]
- Jayasiri, A.; Nandan, A.; Imtiaz, S.; Spencer, D.; Islam, S.; Ahmed, S. Dynamic positioning of vessels using a UKF-based observer and an NMPC-based controller. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1778–1785. [Google Scholar] [CrossRef]
- Fossen, T.I.; Grovlen, A. Nonlinear output feedback control of dynamically positioned ships using vectorial observer backstepping. IEEE Trans. Control. Syst. Technol. 1998, 6, 121–128. [Google Scholar] [CrossRef]
- Liang, K.; Lin, X.; Chen, Y.; Li, J.; Ding, F. Adaptive sliding mode output feedback control for dynamic positioning ships with input saturation. Ocean Eng. 2020, 206, 107245. [Google Scholar] [CrossRef]
- Wu, D.; Ren, F.; Qiao, L.; Zhang, W. Active disturbance rejection controller design for dynamically positioned vessels based on adaptive hybrid biogeography-based optimization and differential evolution. ISA Trans. 2018, 78, 56–65. [Google Scholar] [CrossRef]
- Wei, Y.; Fu, M.; Ning, J.; Sun, X. Quadratic programming thrust allocation and management for dynamic positioning ships. TELKOMNIKA Indones. J. Electr. Eng. 2013, 11, 1632–1638. [Google Scholar] [CrossRef]
- Fung, P.; Grimble, M. Dynamic ship positioning using a self-tuning Kalman filter. IEEE Trans. Autom. Control 1983, 28, 339–350. [Google Scholar] [CrossRef]
- Fotakis, J.; Grimble, M.J.; Kouvaritakis, B. A comparison of characteristic locus and optimal designs for dynamic ship positioning systems. IEEE Trans. Autom. Control 1982, 27, 1143–1157. [Google Scholar] [CrossRef]
- Gao, X.; Bai, W.; Li, T.; Yuan, L.; Long, Y. Broad learning system-based adaptive optimal control design for dynamic positioning of marine vessels. Nonlinear Dyn. 2021, 105, 1593–1609. [Google Scholar] [CrossRef]
- Gao, X.; Li, T.; Long, Y.; Huang, Z.; Yang, H. Optimal Adaptive Anti-Disturbance Control for DP of Vessels via Finite-Time Velocity Observer with Thruster Constrains. In Proceedings of the IECON 2023—49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023; pp. 1–6. [Google Scholar]
- Ma, L.; Wang, Y.L.; Han, Q.L. Event-triggered dynamic positioning for mass-switched unmanned marine vehicles in network environments. IEEE Trans. Cybern. 2020, 52, 3159–3171. [Google Scholar] [CrossRef]
- Wang, H.; Xie, W.; Wang, P.; Wang, Y.; Ge, S.S. Prescribed performance control for dynamic positioning vessels with a dynamic event-triggered mechanism. Ocean Eng. 2023, 281, 114878. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, B.; Hou, M.; Duan, G.R. Practical Prescribed-Time Stabilization of a Class of Nonlinear Systems by Event-Triggered and Self-Triggered Control. IEEE Trans. Autom. Control 2023. [Google Scholar] [CrossRef]
- Rokseth, B.; Utne, I.B.; Vinnem, J.E. A systems approach to risk analysis of maritime operations. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2017, 231, 53–68. [Google Scholar] [CrossRef]
- Yu, W.Z.; Xu, H.X.; Feng, H. Robust adaptive fault-tolerant control of dynamic positioning vessel with position reference system faults using backstepping design. Int. J. Robust Nonlinear Control 2018, 28, 403–415. [Google Scholar] [CrossRef]
- Ding, D.; Han, Q.L.; Xiang, Y.; Ge, X.; Zhang, X.M. A survey on security control and attack detection for industrial cyber-physical systems. Neurocomputing 2018, 275, 1674–1683. [Google Scholar] [CrossRef]
- Yang, X.; Li, T.; Long, Y.; Yang, H.; Chen, C.P. Switched-type unknown input observer-based fault-tolerant control for cyber-physical systems in the presence of denial of service attack. Inf. Sci. 2023, 647, 119457. [Google Scholar] [CrossRef]
- Hao, L.Y.; Zhang, H.; Li, T.S.; Lin, B.; Chen, C.L.P. Fault tolerant control for dynamic positioning of unmanned marine vehicles based on TS fuzzy model with unknown membership functions. IEEE Trans. Veh. Technol. 2020, 70, 146–157. [Google Scholar] [CrossRef]
- Zhang, D.; Ye, Z.; Feng, G.; Li, H. Intelligent event-based fuzzy dynamic positioning control of nonlinear unmanned marine vehicles under DoS attack. IEEE Trans. Cybern. 2021, 52, 13486–13499. [Google Scholar] [CrossRef] [PubMed]
- Song, W.; Li, Y.; Tong, S. Fuzzy Finite-Time H∞ Hybrid-Triggered Dynamic Positioning Control of Nonlinear Unmanned Marine Vehicles Under Cyber-Attacks. IEEE Trans. Intell. Veh. 2023. [Google Scholar] [CrossRef]
- Li, J.; Xiang, X.; Dong, D.; Yang, S. Saturated-command-deviation based finite-time adaptive control for dynamic positioning of USV with prescribed performance. Ocean Eng. 2022, 266, 112941. [Google Scholar] [CrossRef]
- Alagili, O.; Khan, M.A.I.; Ahmed, S.; Imtiaz, S.; Zaman, H.; Islam, M. An energy-efficient dynamic positioning controller for high sea conditions. Appl. Ocean Res. 2022, 129, 103331. [Google Scholar] [CrossRef]
- Li, M.Y.; Liu, L.T.; Xie, W.B.; Li, J.T. Collision avoidance fault-tolerant control for dynamic positioning vessels under thruster faults. Ocean Eng. 2023, 286, 115458. [Google Scholar] [CrossRef]
- Fossen, T.I. Marine Control Systems—Guidance. Navigation, and Control of Ships, Rigs and Underwater Vehicles; Number NO 985 195 005 MVA; Marine Cybernetics: Trondheim, Norway, 2002; ISBN 8292356002. Available online: www.marinecybernetics.com (accessed on 1 January 2002).
- Grovlen, A.; Fossen, T.I. Nonlinear control of dynamic positioned ships using only position feedback: An observer backstepping approach. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 11–13 December 1996; Volume 3, pp. 3388–3393. [Google Scholar]
- Pettersen, K.Y.; Fossen, T.I. Underactuated dynamic positioning of a ship-experimental results. IEEE Trans. Control Syst. Technol. 2000, 8, 856–863. [Google Scholar] [CrossRef]
- Girard, A.R.; Hedrick, J.K. Dynamic positioning of ships using nonlinear dynamic surface control. IFAC Proc. Vol. 2001, 34, 249–254. [Google Scholar] [CrossRef]
- Bertin, D.; Bittanti, S.; Meroni, S.; Savaresi, S.M. Dynamic positioning of a “single-thruster” vessel by feedback linearization. IFAC Proc. Vol. 2000, 33, 275–280. [Google Scholar] [CrossRef]
- Tannuri, E.A.; Donha, D.; Pesce, C. Dynamic positioning of a turret moored FPSO using sliding mode control. Int. J. Robust Nonlinear Control IFAC-Affil. J. 2001, 11, 1239–1256. [Google Scholar] [CrossRef]
- Cho, S.; Shim, H.; Kim, Y.S. Dynamical sliding mode control for robust dynamic positioning systems of FPSO vessels. J. Mar. Sci. Eng. 2022, 10, 474. [Google Scholar] [CrossRef]
- Tannuri, E.A.; Agostinho, A.; Morishita, H.; Moratelli, L., Jr. Dynamic positioning systems: An experimental analysis of sliding mode control. Control Eng. Pract. 2010, 18, 1121–1132. [Google Scholar] [CrossRef]
- Wang, Y.; Hao, L.Y.; Li, T.; Chen, C.P. Integral sliding mode-based fault-tolerant control for dynamic positioning of unmanned marine vehicles based on a TS fuzzy model. J. Mar. Sci. Eng. 2023, 11, 370. [Google Scholar] [CrossRef]
- Kumpati, S.N.; Kannan, P. Identification and control of dynamical systems using neural networks. IEEE Trans. Neural Netw. 1990, 1, 4–27. [Google Scholar]
- Gu, M.X.; Pao, Y.H.; Yip, P. Neural-net computing for real-time control of a ship’s dynamic positioning at sea. Control Eng. Pract. 1993, 1, 305–314. [Google Scholar]
- Fang, M.C.; Lee, Z.Y. Portable dynamic positioning control system on a barge in short-crested waves using the neural network algorithm. China Ocean Eng. 2013, 27, 469–480. [Google Scholar] [CrossRef]
- Hu, X.; Du, J.; Zhu, G.; Sun, Y. Robust adaptive NN control of dynamically positioned vessels under input constraints. Neurocomputing 2018, 318, 201–212. [Google Scholar] [CrossRef]
- How, B.V.E.; Ge, S.S.; Choo, Y.S. Dynamic load positioning for subsea installation via adaptive neural control. IEEE J. Ocean. Eng. 2010, 35, 366–375. [Google Scholar] [CrossRef]
- Tu, F.; Sam Ge, S.; Choo, Y.S.; Hang, C.C. Adaptive dynamic positioning control for accommodation vessels with multiple constraints. IET Control Theory Appl. 2017, 11, 329–340. [Google Scholar] [CrossRef]
- Yang, Y.S.; Wang, X.F. Adaptive H∞ tracking control for a class of uncertain nonlinear systems using radial-basis-function neural networks. Neurocomputing 2007, 70, 932–941. [Google Scholar] [CrossRef]
- Mu, D.; Feng, Y.; Wang, G.; Fan, Y.; Zhao, Y. Single-parameter-learning-based robust adaptive control of dynamic positioning ships considering thruster system dynamics in the input saturation state. Nonlinear Dyn. 2022, 110, 395–412. [Google Scholar] [CrossRef]
- Mu, D.; Feng, Y.; Wang, G. State-unknown single parameter learning adaptive output feedback control for ship dynamic positioning. Ocean Eng. 2022, 266, 112811. [Google Scholar] [CrossRef]
- Liang, K.; Lin, X.; Chen, Y.; Liu, Y.; Liu, Z.; Ma, Z.; Zhang, W. Robust adaptive neural networks control for dynamic positioning of ships with unknown saturation and time-delay. Appl. Ocean Res. 2021, 110, 102609. [Google Scholar] [CrossRef]
- Yuan, W.; Rui, X. Deep reinforcement learning-based controller for dynamic positioning of an unmanned surface vehicle. Comput. Electr. Eng. 2023, 110, 108858. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Hu, X.; Du, J.; Shi, J. Adaptive fuzzy controller design for dynamic positioning system of vessels. Appl. Ocean Res. 2015, 53, 46–53. [Google Scholar] [CrossRef]
- Lin, X.; Nie, J.; Jiao, Y.; Liang, K.; Li, H. Nonlinear adaptive fuzzy output-feedback controller design for dynamic positioning system of ships. Ocean Eng. 2018, 158, 186–195. [Google Scholar] [CrossRef]
- Nguyen, X.P.; Dang, X.K.; Do, V.D.; Corchado, J.M.; Truong, H.N. Robust Adaptive Fuzzy-Free Fault-Tolerant Path Planning Control for a Semi-Submersible Platform Dynamic Positioning System with Actuator Constraints. IEEE Trans. Intell. Transp. Syst. 2023, 24, 12701–12715. [Google Scholar] [CrossRef]
- Yamamoto, M.; Morooka, C. Dynamic positioning system of semi-submersible platform using fuzzy control. J. Braz. Soc. Mech. Sci. Eng. 2005, 27, 449–455. [Google Scholar] [CrossRef]
- Xiang, X.; Yu, C.; Lapierre, L.; Zhang, J.; Zhang, Q. Survey on fuzzy-logic-based guidance and control of marine surface vehicles and underwater vehicles. Int. J. Fuzzy Syst. 2018, 20, 572–586. [Google Scholar] [CrossRef]
- Fang, M.C.; Lee, Z.Y. Application of neuro-fuzzy algorithm to portable dynamic positioning control system for ships. Int. J. Nav. Archit. Ocean. Eng. 2016, 8, 38–52. [Google Scholar] [CrossRef]
- Xia, G.; Pang, C.; Xue, J. Fuzzy neural network-based robust adaptive control for dynamic positioning of underwater vehicles with input dead-zone. J. Intell. Fuzzy Syst. 2015, 29, 2585–2595. [Google Scholar] [CrossRef]
- Do, K.D. Global robust and adaptive output feedback dynamic positioning of surface ships. J. Mar. Sci. Appl. 2011, 10, 325–332. [Google Scholar] [CrossRef]
- Du, J.; Hu, X.; Krstic, M.; Sun, Y. Dynamic positioning of ships with unknown parameters and disturbances. Control Eng. Pract. 2018, 76, 22–30. [Google Scholar] [CrossRef]
- Bidikli, B. An adaptive control design for dynamic positioning of unmanned surface vessels having actuator dynamics. Ocean Eng. 2021, 229, 108948. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, W. Double-loop integral terminal sliding mode tracking control for UUVs with adaptive dynamic compensation of uncertainties and disturbances. IEEE J. Ocean. Eng. 2018, 44, 29–53. [Google Scholar] [CrossRef]
- Zhao, D.; Liang, H.; Spurgeon, S.K. Robust adaptive terminal sliding mode control for dynamic positioning of a semi-submersible offshore platform. Trans. Inst. Meas. Control 2019, 41, 1361–1372. [Google Scholar] [CrossRef]
- Hu, C.; Wu, D.; Liao, Y.; Hu, X. Sliding mode control unified with the uncertainty and disturbance estimator for dynamically positioned vessels subjected to uncertainties and unknown disturbances. Appl. Ocean Res. 2021, 109, 102564. [Google Scholar] [CrossRef]
- Veksler, A.; Johansen, T.A.; Borrelli, F.; Realfsen, B. Dynamic positioning with model predictive control. IEEE Trans. Control Syst. Technol. 2016, 24, 1340–1353. [Google Scholar] [CrossRef]
- Hu, X.; Du, J.; Sun, Y. Robust adaptive control for dynamic positioning of ships. IEEE J. Ocean. Eng. 2017, 42, 826–835. [Google Scholar] [CrossRef]
- Hu, X.; Du, J. Robust nonlinear control design for dynamic positioning of marine vessels with thruster system dynamics. Nonlinear Dyn. 2018, 94, 365–376. [Google Scholar] [CrossRef]
- Shi, Q.; Hu, C.; Li, X.; Guo, X.; Yang, J. Finite-time adaptive anti-disturbance constrained control design for dynamic positioning of marine vessels with simulation and model-scale tests. Ocean Eng. 2023, 277, 114117. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, X.; Wei, Y.; Hu, X. Anti-disturbance control for dynamic positioning system of ships with disturbances. Appl. Math. Comput. 2021, 396, 125929. [Google Scholar] [CrossRef]
- Fu, M.; Zhang, G.; Xu, Y.; Wang, L.; Dong, L. Discrete-time adaptive predictive sliding mode trajectory tracking control for dynamic positioning ship with input magnitude and rate saturations. Ocean Eng. 2023, 269, 113528. [Google Scholar] [CrossRef]
- Gong, C.; Su, Y.; Zhu, Q.; Zhang, D.; Hu, X. Finite-time dynamic positioning control design for surface vessels with external disturbances, input saturation and error constraints. Ocean Eng. 2023, 276, 114259. [Google Scholar] [CrossRef]
- Gong, C.; Su, Y.; Jia, F.; Zhang, D.; Hu, X. Fixed time prescribed performance dynamic positioning control design for surface vessels. Ocean Eng. 2023, 287, 115615. [Google Scholar] [CrossRef]
- Tang, L.; Liu, J.; Wang, L.; Wang, Y. Robust fixed-time trajectory tracking control of the dynamic positioning ship with actuator saturation. Ocean Eng. 2023, 284, 115199. [Google Scholar] [CrossRef]
- Xia, G.; Sun, C.; Zhao, B. Output feedback cooperative dynamic positioning control for an unactuated floating object using multiple vessels. J. Mar. Sci. Eng. 2021, 9, 463. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, W.; Wang, D.; Peng, Z. Event-triggered extended state observers design for dynamic positioning vessels subject to unknown sea loads. Ocean Eng. 2020, 209, 107242. [Google Scholar] [CrossRef]
- Liu, T.; Xiao, Y.; Feng, Y.; Li, J.; Huang, B. Guaranteed cost control for dynamic positioning of marine surface vessels with input saturation. Appl. Ocean Res. 2021, 116, 102868. [Google Scholar] [CrossRef]
- Hassani, V.; Sørensen, A.J.; Pascoal, A.M.; Athans, M. Robust dynamic positioning of offshore vessels using mixed-μ synthesis modeling, design, and practice. Ocean Eng. 2017, 129, 389–400. [Google Scholar] [CrossRef]
- Liming, H.; Zuohua, T.; Songjiao, S. Nonlinear observer-controller design for dynamic positioning of ships. J. Syst. Eng. Electron. 2004, 15, 359–363. [Google Scholar]
- Cui, J.; Yang, R.; Pang, C.; Zhang, Q. Observer-based adaptive robust stabilization of dynamic positioning ship with delay via Hamiltonian method. Ocean Eng. 2021, 222, 108439. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Li, M.; Wang, D.; Fu, M. Adaptive fuzzy controller design for dynamic positioning ship integrating prescribed performance. Ocean Eng. 2021, 219, 107956. [Google Scholar] [CrossRef]
- Gopmandal, F.; Ghosh, A.; Kumar, A. LQ optimal robust multivariable PID control for dynamic positioning of ships with norm-bounded parametric uncertainties. Ocean Eng. 2022, 266, 113054. [Google Scholar] [CrossRef]
- Lv, Y.; Li, H. Strong fixed-time dynamic inverse adaptive LQR integrated control strategy for dynamic positioning of ship. Ocean Eng. 2023, 288, 115969. [Google Scholar] [CrossRef]
- Tsopelakos, A.; Papadopoulos, E. Design and evaluation of dynamic positioning controllers with parasitic thrust reduction for an overactuated floating platform. IEEE Trans. Control Syst. Technol. 2016, 25, 145–160. [Google Scholar] [CrossRef]
- Luan, T.; Tan, Z.; Sun, M.; Wang, H.; Li, M.; Yao, H. Double-mode robust model predictive control of ship dynamic positioning system based on event-triggered mechanism. Ocean Eng. 2023, 286, 115536. [Google Scholar] [CrossRef]
- Shi, Y.; Shen, C.; Wei, H.; Zhang, K. Lyapunov-Based Model Predictive Control for Dynamic Positioning and Trajectory-Tracking Control of an AUV. In Advanced Model Predictive Control for Autonomous Marine Vehicles; Springer: Berlin/Heidelberg, Germany, 2023; pp. 49–75. [Google Scholar]
- Li, W.; Sun, Y.; Chen, H.; Wang, G. Model predictive controller design for ship dynamic positioning system based on state-space equations. J. Mar. Sci. Technol. 2017, 22, 426–431. [Google Scholar] [CrossRef]
- Gao, J.; Liu, C.; Proctor, A. Nonlinear model predictive dynamic positioning control of an underwater vehicle with an onboard USBL system. J. Mar. Sci. Technol. 2016, 21, 57–69. [Google Scholar] [CrossRef]
- Liu, C.; Sun, T.; Hu, Q. Synchronization control of dynamic positioning ships using model predictive control. J. Mar. Sci. Eng. 2021, 9, 1239. [Google Scholar] [CrossRef]
- Deng, F.; Yang, H.L.; Wang, L.J.; Yang, W.M. UKF based nonlinear offset-free model predictive control for ship dynamic positioning under stochastic disturbances. Int. J. Control Autom. Syst. 2019, 17, 3079–3090. [Google Scholar] [CrossRef]
- Yang, H.; Deng, F.; He, Y.; Jiao, D.; Han, Z. Robust nonlinear model predictive control for reference tracking of dynamic positioning ships based on nonlinear disturbance observer. Ocean Eng. 2020, 215, 107885. [Google Scholar] [CrossRef]
- Zheng, H.; Wu, J.; Wu, W.; Zhang, Y. Robust dynamic positioning of autonomous surface vessels with tube-based model predictive control. Ocean Eng. 2020, 199, 106820. [Google Scholar] [CrossRef]
- Cao, Y.; Li, T.; Hao, L. Nonlinear Model Predictive Control of Shipboard Boom Cranes Based on Moving Horizon State Estimation. J. Mar. Sci. Eng. 2023, 11, 4. [Google Scholar] [CrossRef]
- Cao, Y.; Li, T.; Hao, L.Y.; Gao, X. Nonlinear Antiswing Control of Shipboard Boom Cranes Using MPC-Based Auto-Tuning Mechanism with Full State Constraints. IEEE Trans. Intell. Transp. Syst. 2023. [Google Scholar] [CrossRef]
- Tang, L.; Wang, L.; Wang, Y.; Zhang, Y. An enhanced trajectory tracking control of the dynamic positioning ship based on nonlinear model predictive control and disturbance observer. Ocean Eng. 2022, 265, 112482. [Google Scholar] [CrossRef]
- Gao, S.; Liu, C.; Tuo, Y.; Chen, K.; Zhang, T. Augmented model-based dynamic positioning predictive control for underactuated unmanned surface vessels with dual-propellers. Ocean Eng. 2022, 266, 112885. [Google Scholar] [CrossRef]
- Huang, Z.; Bai, W.; Li, T.; Long, Y.; Chen, C.P.; Liang, H.; Yang, H. Adaptive reinforcement learning optimal tracking control for strict-feedback nonlinear systems with prescribed performance. Inf. Sci. 2023, 621, 407–423. [Google Scholar] [CrossRef]
- Huang, Z.; Gao, X.; Li, T.; Long, Y.; Yang, H. Prescribed performance event-triggered fuzzy optimal tracking control for strict-feedback nonlinear systems. Inf. Sci. 2024, 658, 120014. [Google Scholar] [CrossRef]
- Yuan, L.; Li, T.; Tong, S.; Xiao, Y.; Gao, X. NN adaptive optimal tracking control for a class of uncertain nonstrict feedback nonlinear systems. Neurocomputing 2022, 491, 382–394. [Google Scholar] [CrossRef]
- Su, Y.; Shan, Q.; Li, T.; Chen, C.L.P. Variable Separation-Based Fuzzy Optimal Control for Multiagent Systems in Nonstrict-Feedback Form. IEEE Trans. Fuzzy Syst. 2023. [Google Scholar] [CrossRef]
- Yuan, L.; Li, T.; Tong, S.; Xiao, Y.; Shan, Q. Broad Learning System Approximation-Based Adaptive Optimal Control for Unknown Discrete-Time Nonlinear Systems. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 5028–5038. [Google Scholar] [CrossRef]
- Werbos, P. Advanced forecasting methods for global crisis warning and models of intelligence. In General System Yearbook; The University of Chicago Press: Chicago, IL, USA, 1977; pp. 25–38. [Google Scholar]
- Gao, X.; Li, T.; Shan, Q.; Xiao, Y.; Yuan, L.; Liu, Y. Online optimal control for dynamic positioning of vessels via time-based adaptive dynamic programming. J. Ambient. Intell. Humaniz. Comput. 2019, 14, 15629–15641. [Google Scholar] [CrossRef]
- Gao, X.; Li, T.; Yuan, L.; Bai, W. Robust fuzzy adaptive output feedback optimal tracking control for dynamic positioning of marine vessels with unknown disturbances and uncertain dynamics. Int. J. Fuzzy Syst. 2021, 23, 2283–2296. [Google Scholar] [CrossRef]
- Wang, H.; Li, M.; Zhang, C.; Shao, X. Event-based prescribed performance control for dynamic positioning vessels. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2548–2552. [Google Scholar] [CrossRef]
- Zhu, G.; Ma, Y.; Yan, X. Event-triggered neuroadaptive predefined practical finite-time control for dynamic positioning vessels: A time-based generator approach. Fundam. Res. 2022, in press. [Google Scholar] [CrossRef]
- Hao, L.Y.; Zhang, H.; Li, H.; Li, T.S. Sliding mode fault-tolerant control for unmanned marine vehicles with signal quantization and time-delay. Ocean Eng. 2020, 215, 107882. [Google Scholar] [CrossRef]
- Liu, Q.; Long, Y.; Li, T.; Chen, C.L.P. Attack Resilient Fault Tolerant Control for T-S Fuzzy Cyber-Physical Systems. IEEE Trans. Fuzzy Syst. 2023. [Google Scholar] [CrossRef]
- Su, Y.; Zheng, C.; Mercorelli, P. Nonlinear PD fault-tolerant control for dynamic positioning of ships with actuator constraints. IEEE/ASME Trans. Mechatron. 2016, 22, 1132–1142. [Google Scholar] [CrossRef]
- Lin, Y.; Du, J.; Zhu, G.; Fang, H. Thruster fault-tolerant control for dynamic positioning of vessels. Appl. Ocean Res. 2018, 80, 118–124. [Google Scholar] [CrossRef]
- Lin, Y.; Du, J.; Li, J. Robust adaptive finite-time fault-tolerant control for dynamic positioning of vessels. Int. J. Control Autom. Syst. 2021, 19, 3168–3178. [Google Scholar] [CrossRef]
- Benetazzo, F.; Ippoliti, G.; Longhi, S.; Raspa, P. Advanced control for fault-tolerant dynamic positioning of an offshore supply vessel. Ocean Eng. 2015, 106, 472–484. [Google Scholar] [CrossRef]
- Li, H.; Lin, X. Robust finite-time fault-tolerant control for dynamic positioning of ships via nonsingular fast integral terminal sliding mode control. Appl. Ocean Res. 2022, 122, 103126. [Google Scholar] [CrossRef]
- Song, W.; Tong, S. Event-triggered fuzzy finite-time reliable control for dynamic positioning of nonlinear unmanned marine vehicles. Ocean Eng. 2022, 266, 113139. [Google Scholar] [CrossRef]
- Cheng, P.; Zhang, C.; Xie, W.; Zhang, W.; He, S. Network-based adaptive multievent-triggered fuzzy dynamic positioning controller design for unmanned surface vehicles against denial-of-service attacks. IEEE Trans. Control Netw. Syst. 2022, 10, 612–624. [Google Scholar] [CrossRef]
- Liu, Q.; Long, Y.; Li, T.; Park, J.H.; Chen, C.L.P. Fault Detection for Unmanned Marine Vehicles Under Replay Attack. IEEE Trans. Fuzzy Syst. 2023, 31, 1716–1728. [Google Scholar] [CrossRef]
- Han, S.; Zhu, H.; Zhong, Q.; Shi, K.; Kwon, O.M. Adaptive Event-Triggered Fuzzy Positioning Control for Unmanned Marine Vehicles with Actuator Saturation and Hybrid Attacks. IEEE Trans. Fuzzy Syst. 2023, 31, 3055–3068. [Google Scholar] [CrossRef]
- Su, Y.; Gong, C.; Zhang, D.; Hu, X. Simple Dynamic Positioning Control Design for Surface Vessels With Input Saturation and External Disturbances. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 1530–1534. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, D.; Yin, Z.; Yuan, Z.M. Design of UDE-based dynamic surface control for dynamic positioning of vessels with complex disturbances and input constraints. Ocean Eng. 2021, 220, 108487. [Google Scholar] [CrossRef]
- Li, J.; Du, J.; Hu, X. Robust adaptive prescribed performance control for dynamic positioning of ships under unknown disturbances and input constraints. Ocean Eng. 2020, 206, 107254. [Google Scholar] [CrossRef]
- Li, M.Y.; Xu, J.; Xie, W.B.; Wang, H.B. Finite-time composite learning control for trajectory tracking of dynamic positioning vessels. Ocean Eng. 2022, 262, 112288. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, X.; Liang, K. Robust tracking control for dynamic positioning ships subject to dynamic safety constraints. Ocean Eng. 2022, 266, 112710. [Google Scholar] [CrossRef]
- Gong, C.; Su, Y.; Zhang, D. Variable Gain Prescribed Performance Control for Dynamic Positioning of Ships with Positioning Error Constraints. J. Mar. Sci. Eng. 2022, 10, 74. [Google Scholar] [CrossRef]
- Wang, W.; Gao, X.; Li, T.; Wang, Y.; Chen, C.L.P. Observer-Based Platoon Formation Control With Prescribed Performance Guarantees for Unmanned Surface Vehicles in Presence of Nonsmooth Input Characteristics. IEEE Trans. Circuits Syst. II Express Briefs 2023. [Google Scholar] [CrossRef]
- Li, J.; Xiang, X.; Yang, S. Robust adaptive neural network control for dynamic positioning of marine vessels with prescribed performance under model uncertainties and input saturation. Neurocomputing 2022, 484, 1–12. [Google Scholar] [CrossRef]
- Li, M.Y.; Xie, W.B.; Wang, Y.L.; Hu, X. Prescribed performance trajectory tracking fault-tolerant control for dynamic positioning vessels under velocity constraints. Appl. Math. Comput. 2022, 431, 127348. [Google Scholar] [CrossRef]
- Brodtkorb, A.H.; Værnø, S.A.; Teel, A.R.; Sørensen, A.J.; Skjetne, R. Hybrid controller concept for dynamic positioning of marine vessels with experimental results. Automatica 2018, 93, 489–497. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, D.; Wang, J. Cooperative dynamic positioning of multiple marine offshore vessels: A modular design. IEEE/ASME Trans. Mechatron. 2015, 21, 1210–1221. [Google Scholar] [CrossRef]
- Xia, G.; Sun, C.; Zhao, B.; Xue, J. Cooperative control of multiple dynamic positioning vessels with input saturation based on finite-time disturbance observer. Int. J. Control Autom. Syst. 2019, 17, 370–379. [Google Scholar] [CrossRef]
- Ye, J.; Roy, S.; Godjevac, M.; Reppa, V.; Baldi, S. Robustifying dynamic positioning of crane vessels for heavy lifting operation. IEEE/CAA J. Autom. Sin. 2021, 8, 753–765. [Google Scholar] [CrossRef]
- Huang, H.; Sharma, S.; Zhuang, Y.; Xu, D. Dynamic positioning of an uninhabited surface vehicle using state-dependent Riccati equation and pseudospectral method. Ocean Eng. 2017, 133, 215–223. [Google Scholar] [CrossRef]
- Chen, L.; Liang, H.; Pan, Y.; Li, T. Human-in-the-loop consensus tracking control for UAV systems via an improved prescribed performance approach. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 8380–8391. [Google Scholar] [CrossRef]
- Shi, Z.; Chen, H.; Qu, T.; Yu, S. Human–Machine Cooperative Steering Control Considering Mitigating Human–Machine Conflict Based on Driver Trust. IEEE Trans.-Hum.-Mach. Syst. 2022, 52, 1036–1048. [Google Scholar] [CrossRef]
- Wei, X.; Guo, L. Composite disturbance-observer-based control and H∞ control for complex continuous models. Int. J. Robust Nonlinear Control IFAC-Affil. J. 2010, 20, 106–118. [Google Scholar] [CrossRef]
- Wei, X.; Chen, N. Composite hierarchical anti-disturbance control for nonlinear systems with DOBC and fuzzy control. Int. J. Robust Nonlinear Control 2014, 24, 362–373. [Google Scholar] [CrossRef]
- Guo, L.; Wen, X.Y. Hierarchical anti-disturbance adaptive control for non-linear systems with composite disturbances and applications to missile systems. Trans. Inst. Meas. Control 2011, 33, 942–956. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Li, T. Dynamic Positioning Control for Marine Crafts: A Survey and Recent Advances. J. Mar. Sci. Eng. 2024, 12, 362. https://doi.org/10.3390/jmse12030362
Gao X, Li T. Dynamic Positioning Control for Marine Crafts: A Survey and Recent Advances. Journal of Marine Science and Engineering. 2024; 12(3):362. https://doi.org/10.3390/jmse12030362
Chicago/Turabian StyleGao, Xiaoyang, and Tieshan Li. 2024. "Dynamic Positioning Control for Marine Crafts: A Survey and Recent Advances" Journal of Marine Science and Engineering 12, no. 3: 362. https://doi.org/10.3390/jmse12030362
APA StyleGao, X., & Li, T. (2024). Dynamic Positioning Control for Marine Crafts: A Survey and Recent Advances. Journal of Marine Science and Engineering, 12(3), 362. https://doi.org/10.3390/jmse12030362






